1. Introduction
In different astrophysical objects, we find “fast clump” or “interstellar bullet” flows with a long tail of material with linearly decreasing velocities towards the outflow source. For example, this kind of flow is found in planetary nebulae (PNe) or in proto-planetary nebulae (PPNe) (see, e.g., [
1,
2] and the review of [
3]).
Modelling high speed “bullet” flows in terms of winds, jets and clumps ejected from the central source has been presented by [
4,
5]. In a recent series of papers [
6,
7,
8], we showed that an ejection pulse with either of the following bulleted points result in the formation of a leading bow shock followed by a tail of material with an approximately linear velocity growth from the source position out to the emitting clump:
In the present paper, we show that a “clump flow” (with an initially spherical, dense clump with uniform density and velocity within the clump) can also produce a linear velocity vs. position tail. Such a tail is produced if the clump first travels within a dense region and then emerges into a much lower density environment.
In order to show that this is the case, we have computed axisymmetric numerical simulations (with the setup described in
Section 2) of a dense, high velocity clump traveling in a low density environment and of a clump first traveling in a high density environment and then emerging into a low density medium. The results of these simulations are described in
Section 3, and predictions of H
emission maps and position-velocity (PV) diagrams are shown in
Section 4. The results are summarized in
Section 5.
2. The Numerical Simulations
In order to present a first study of the problem, we have used a simple setup: We consider a domain in which H is always fully ionized and have used a parametrized cooling function (in particular, the one of [
9]) and impose a minimum temperature of
K in all grid cells at all times. This setup is a “poor man’s approach” for simulating flow within a photoionized region.
We use the adaptive grid “yguazú” code (see [
7]) to integrate the axisymmetric gasdynamic equations (with the cooling function described above) in a
cm (axial × radial, “
”) domain. A four-level, binary adaptive grid with a maximum number of
(axial × radial) is used.
The initial configuration has a dense sphere of radius cm and atom+ion number density cm centered at cm. The rest of the domain is filled with a uniform environment that flows along the x-axis at a velocity of km s (with an inflow boundary on the left and an outflow boundary condition on the right). The initial domain has a uniform temperature of K.
We run the following two simulations:
- A.
With an environment that is injected into the domain at all times with the cm density of the initial condition;
- B.
With an initial environment of density cm and for an injection with cm.
Model B is intended to model a clump that first travels within a dense circumstellar region of density and then emerges into a much lower density outer envelope of density .
From the results of the numerical integrations, we compute the recombination cascade H emission coefficient. With this emission coefficient, we calculate emission maps and position-velocity (PV) diagrams for a narrow spectrograph slit aligned with the projected symmetry axis.
3. Results
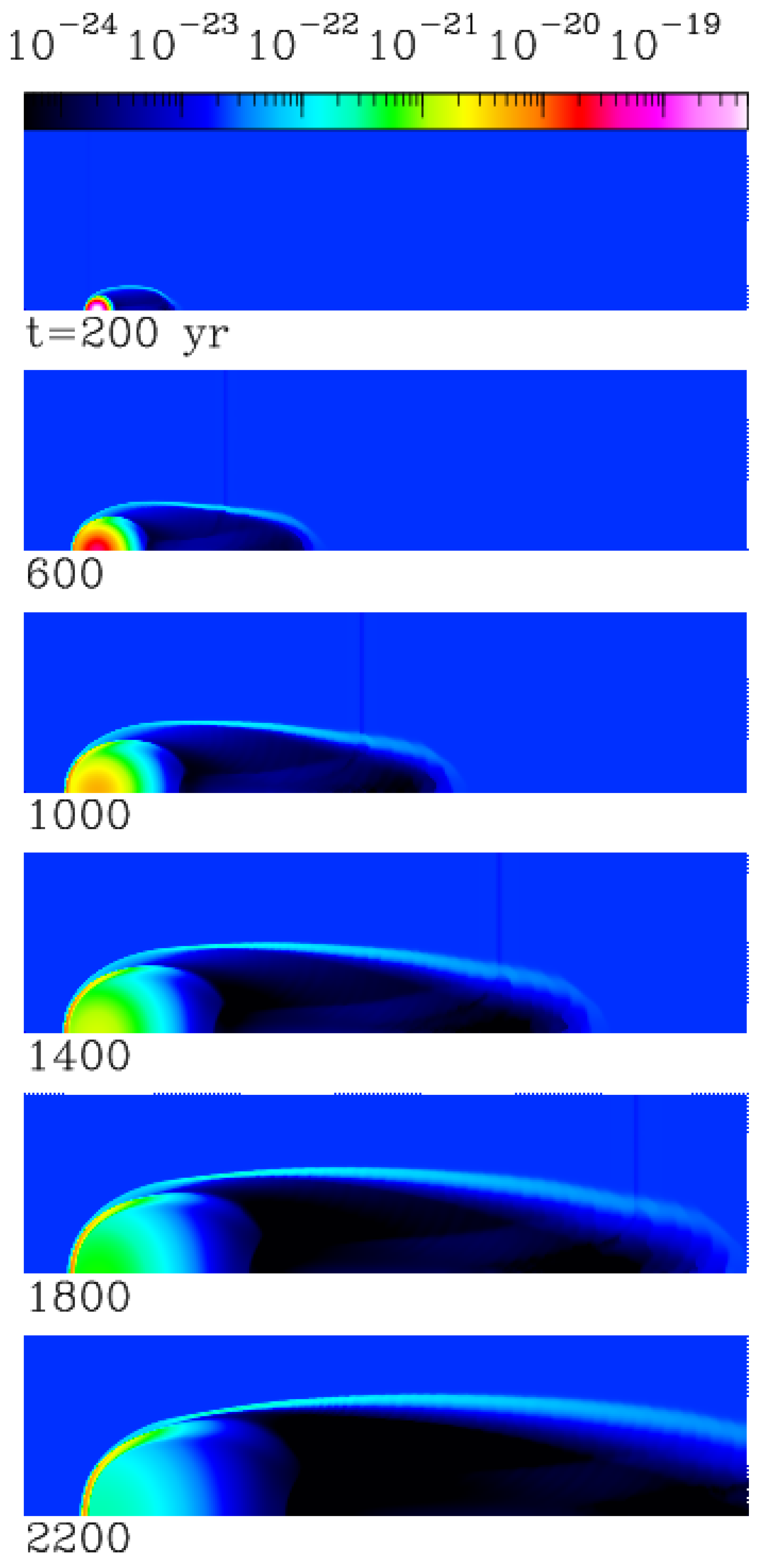
Figure 1 shows a time-sequence of the density structure obtained from model A. In this model, the highly overpressured cloud expands, and the streaming environment is deflected in a bow shock.
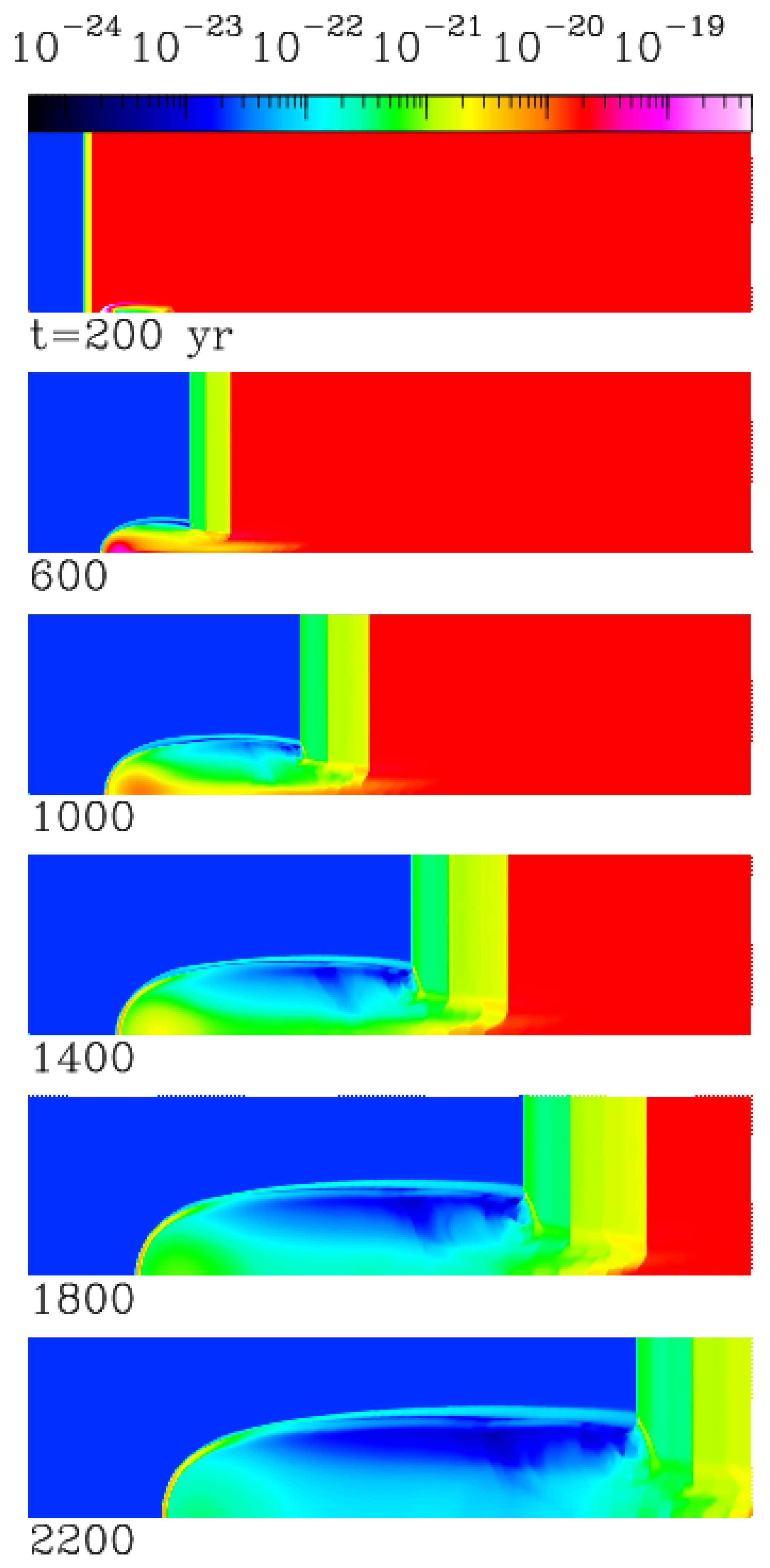
Figure 2 shows a similar time-sequence for model B. In the
yr frame, we observe that the cloud is confined by the streaming, dense environment. At
yr, the cloud has emerged into the low density, streaming environment region and has started to expand. By the end of the displayed time sequence (at
yr), the cloud has expanded, possessing a similar size to the cloud (at 2200 yr) of model A.
A notable difference between model A and B (
Figure 1 and
Figure 2, respectively) is that the region of the wake behind the cloud is much denser in model B. This dense, axial region is filled with materials belonging to the bow shock that was developed at early times when the clump traveled through the dense region of the environment (see the top frame of
Figure 2), which then emerges out of the dense region, trailing behind the cloud.
4. Intensity Maps and PV Diagrams
From density and temperature stratifications at
yr (bottom frames of
Figure 1 and
Figure 2), we have computed H
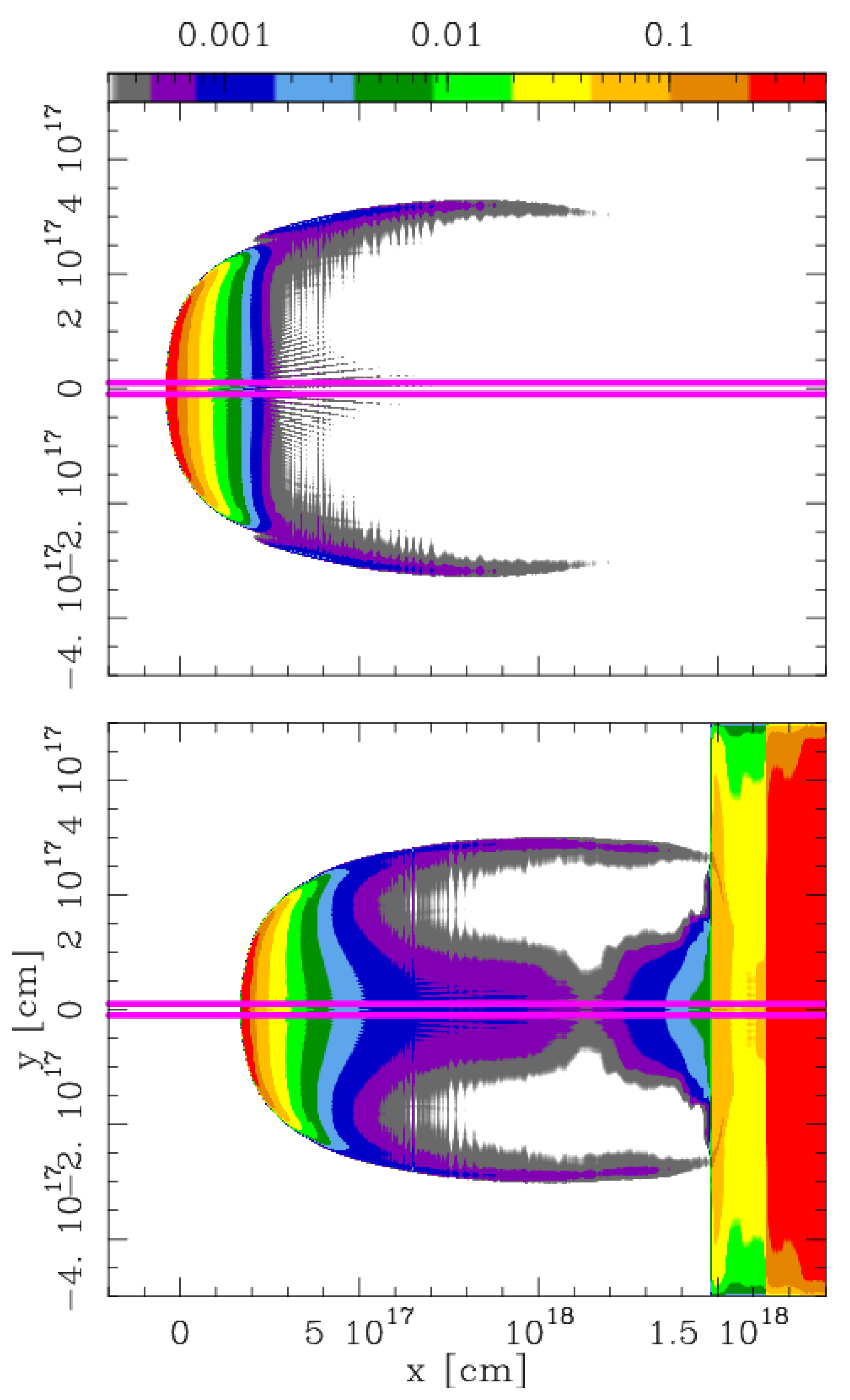
intensity maps for models A and B, assuming that the flow axis lies on the plane of the sky. The resulting maps are shown in
Figure 3.
The H
emission of model A only shows the bow shock. The map of model B shows a somewhat smaller bow shock. This map also shows emission from the dense environment (which has still not entirely left the computational domain, see
Figure 4) and the axial emission of the material dragged out by the confined bow shock (within the dense environment region) into the low density environment region.
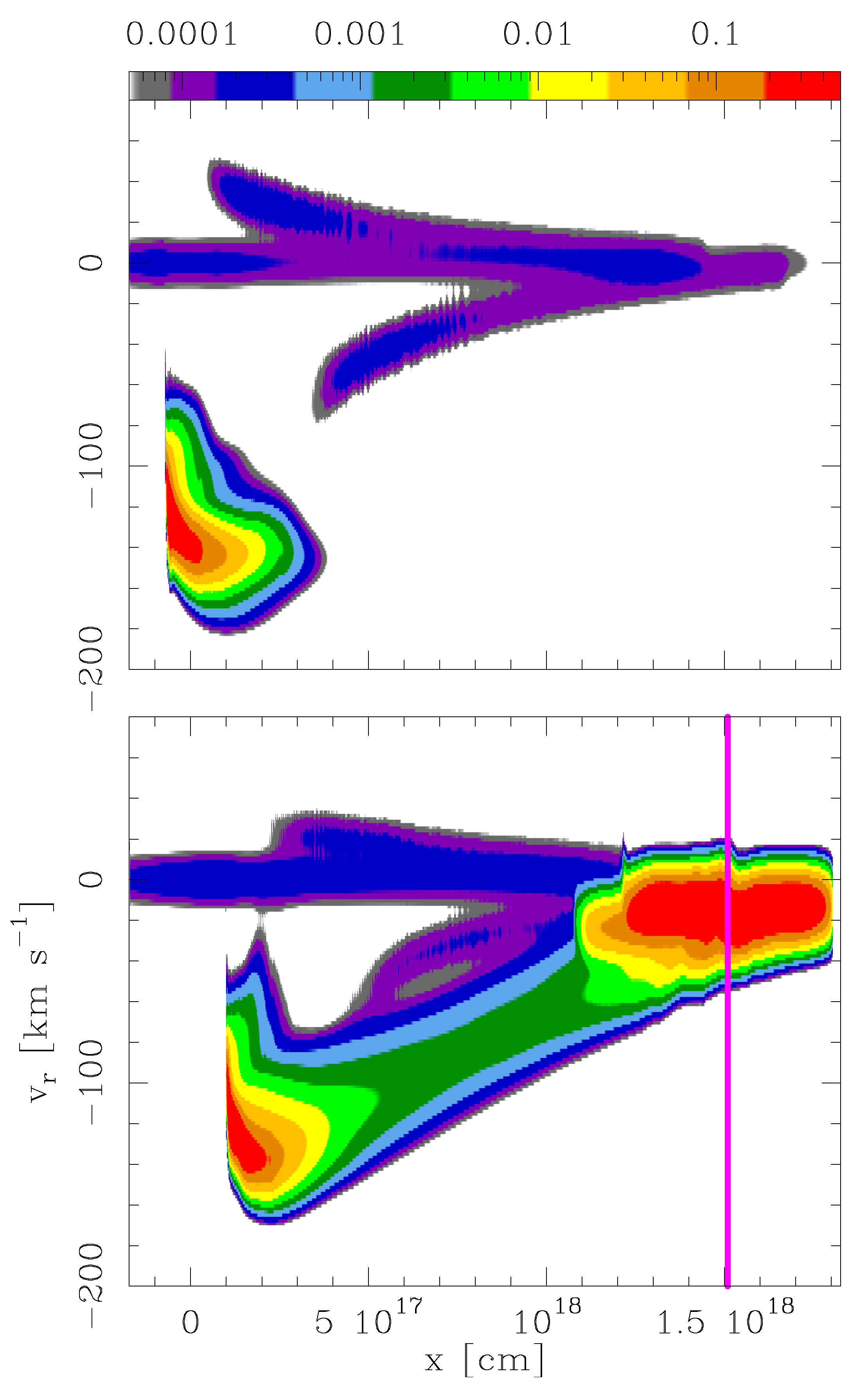
For the narrow spectrograph slits shown on H
intensity maps of
Figure 3, we have computed H
PV diagrams, which are shown in
Figure 4 (for an assumed angle of
towards the observed between the flow axis and the plane of the sky). The PV diagrams have been computed by placing the origin of the radial velocity axis at the projected velocity of the streaming environment so that the diagrams correspond to an observer at rest with respect to the environmental material.
In
Figure 4, we observe that the PV diagram of model A is dominated by the leading bow shock. The PV diagram of model B also shows the strong, zero radial velocity emission of the dense region of the environment, and an approximately linear ramp of emission joining the bow shock to the position at which the cloud emerged into the low density region (shown with a vertical purple line in the bottom frame of
Figure 4). This emission comes from the on-axis region of dragged out dense environment observed in model B’s density frames of
Figure 2 (and also observed in the corresponding H
map of
Figure 3).
The PV diagrams of
Figure 4 have of course been calculated for an arbitrary choice for the orientation angle (
between the outflow axis and the plane of the sky, see above). However, the same qualitative features (including the linear ramp in the model B PV diagram) are observed for orientation angles of ∼15
.
5. Discussion
We have presented a model for the production of clumps with a linear velocity vs. position tail. In order to produce the tail, a fast, high density clump initially travels through a high density region and then emerges into a low density medium. In the context of PNe, this could correspond to a fast, collimated ejection that first travels within a dense, inner region of the nebula and then emerges into a low density halo.
We have presented two simulations of photoionized bullets:
A. Traveling within a uniform, low density medium;
B. Initially traveling in a high density region and then emerging into a low density medium.
While model A produces a standard bow shock flow, with bow-shaped intensity maps and “comma shaped” PV diagrams (to use the description of [
4]), model B also shows a dense axial structure corresponding to material in the “confined bow shock” (produced when the bullet travels within the high density region) that emerges into the low density medium. As it emerges from the dense region, the released bow shock material moves approximately ballistically. A “velocity sorting” process occurs, with the fast bow shock region close to the clump head following the clump and the slower moving “bow shock wing” material trailing behind.
In this manner, model B has a “tail” of axially concentrated material. This tail shows up in PV diagrams as a linear ramp increasing from zero radial velocity at the point of emergence from the dense cloud up to the clump velocity (at the position of the clump).
This kind of flow clearly has applications to high velocity clumps in PNe followed by linear velocity ramps (e.g., in the classical example of OH 231.8 + 4.2, see [
1], and possibly also in multi-bullet flows in star formation regions (see, e.g., [
10] and references therein). Clearly, detailed models of specific objects will be necessary to observe if our model is indeed appropriate.
Author Contributions
The first author (A.C.R.) has contributed approximately 30%, and the other co-authors (J.C., A.C.-R., J.I.C., L.H.-M., A.R.-G., P.R.-O.) approximately 10% each of the reported work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the DGAPA (UNAM) grant number IG100422.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
A.Cas.R. acknowledges support from a CONACyT postdoctoral fellowship.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Alcolea, J.; Bujarrabal, V.; Sánchez Contreras, C.; Neri, R.; Zweigle, J. The highly collimated bipolar outflow of OH 231.8 + 4.2. Astron. Astrophys. 2001, 373, 932–949. [Google Scholar] [CrossRef]
- Bujarrabal, V.; Castro-Carrizo, A.; Alcolea, J.; Sánchez-Contreras, C. Mass, linear momentum and kinetic energy of bipolar flows in protoplanetary nebulae. Astron. Astrophys. 2001, 377, 868–897. [Google Scholar] [CrossRef]
- Balick, B.; Frank, A. Shapes and shaping of planetary nebulae. Annu. Rev. Astron. Astrophys. 2002, 40, 439–486. [Google Scholar] [CrossRef]
- Dennis, T.J.; Cunningham, A.J.; Frank, A.; Balick, B.; Blackman, E.G.; Mitran, S. Proto-planetary nebulae as explosions: Bullets versus jets and nebular shaping. Astrophys. J. 2008, 679, 1327. [Google Scholar] [CrossRef][Green Version]
- Lee, C.-F.; Sahai, R. Shaping proto-planetary and young planetary nebulae with collimated fast winds. Astrophys. J. 2003, 586, 319. [Google Scholar] [CrossRef]
- Castellanos-Ramírez, A.; Raga, A.C.; Cantó, J.; Rodríguez-González, A.; Hernández-Martínez, L. Velocity segregation in a clump-like outflow with a non-top hat velocity cross-section. RMxAA 2021, 57, 269. [Google Scholar] [CrossRef]
- Raga, A.C.; Rodríguez-González, A.; Hernández-Martínez, L.; Cantó, J.; Castellanos-Ramírez, A. A ‘head/tail’ plasmon model with a Hubble law velocity profile. Mon. Not. R. Astron. Soc. Lett. 2020, 499, L91–L95. [Google Scholar] [CrossRef]
- Raga, A.C.; Cantó, J.; Rodríguez-González, A.; Castellanos-Ramírez, A.; Hernández-Martínez, L. “Head/tail plasmon” produced by a Gaussian ejection velocity pulse. Revista Mexicana de Astronomıa y Astrofısica 2021, 57, 233–239. [Google Scholar] [CrossRef]
- Biro, S.; Raga, A.C. A numerical simulation of a variable velocity jet. Astrophys. J. 1994, 434, 221–231. [Google Scholar] [CrossRef]
- Zapata, L.A.; Ho, P.T.P.; Fernández-López, M.; Palau, A.; Estalella, R.; Osorio, M.; Anglada, G.; Huelamo, N. Tidal Interaction between the UX Tauri A/C Disk System Revealed by ALMA. Astrophys. J. 2020, 896, 132. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).