Optical Identification of Diabetic Retinopathy Using Hyperspectral Imaging
Abstract
1. Introduction
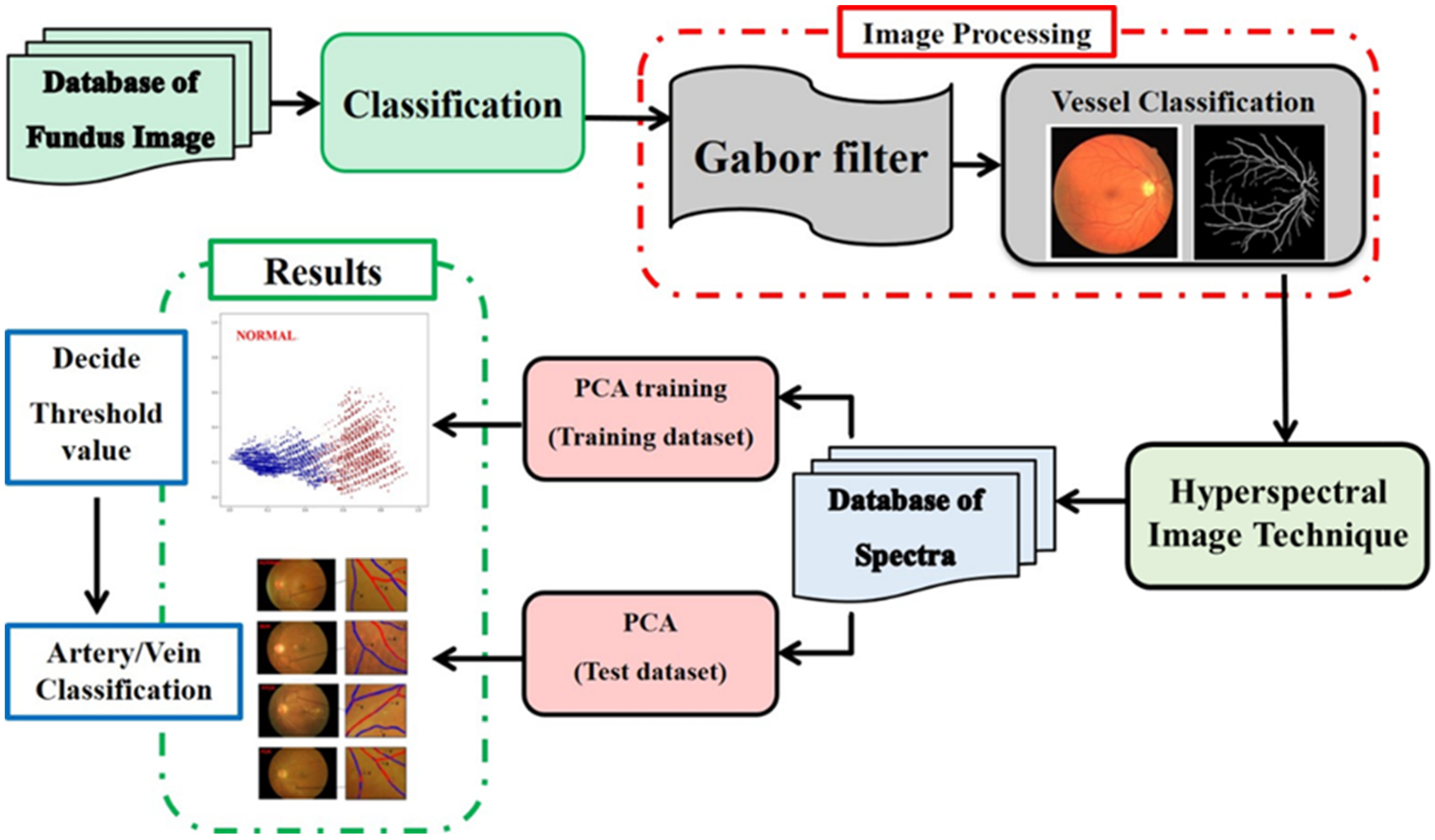
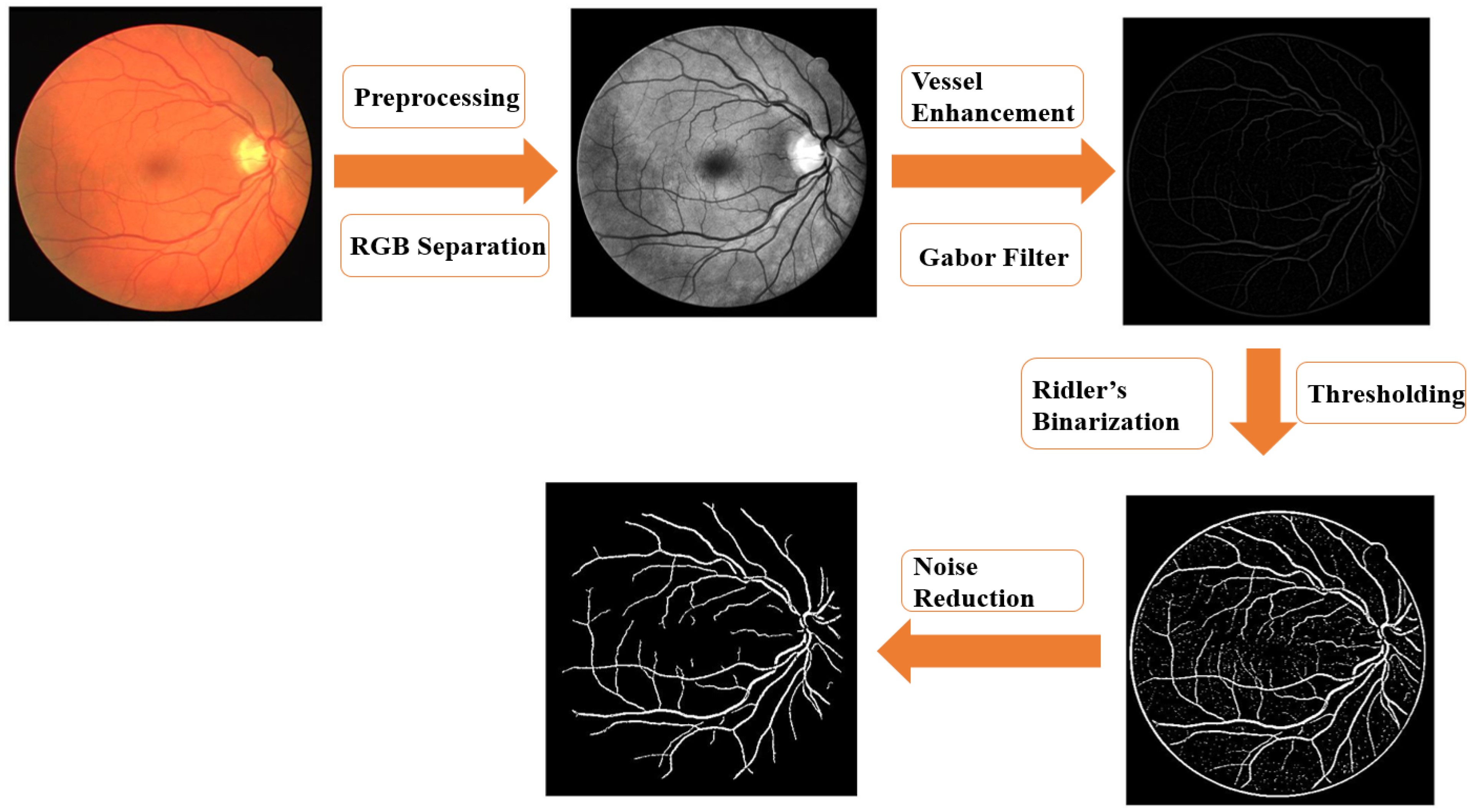
2. Materials and Methods
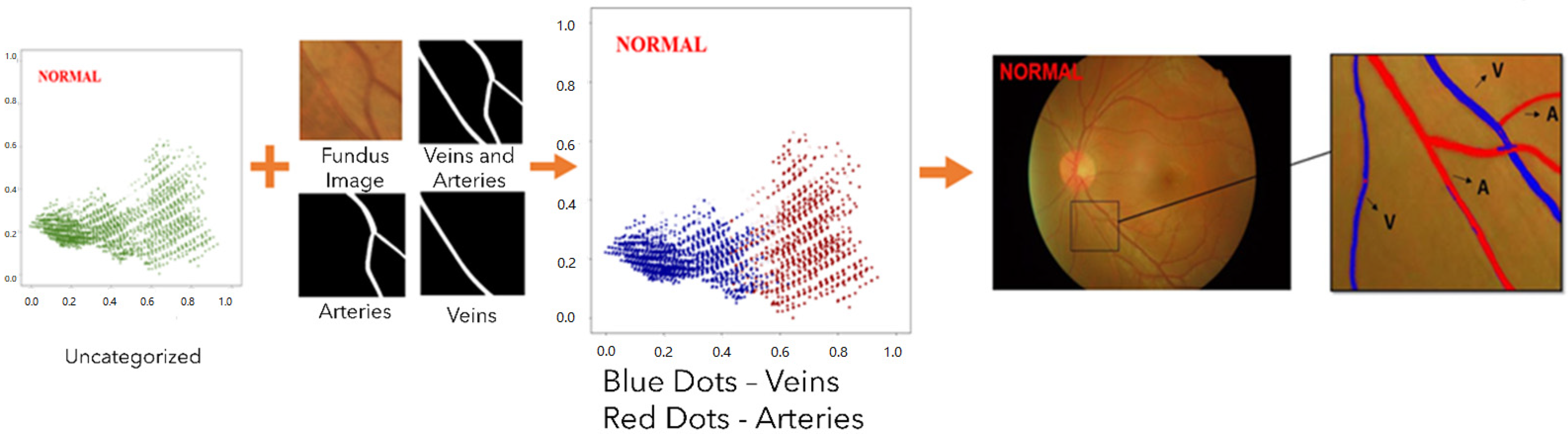
3. Results
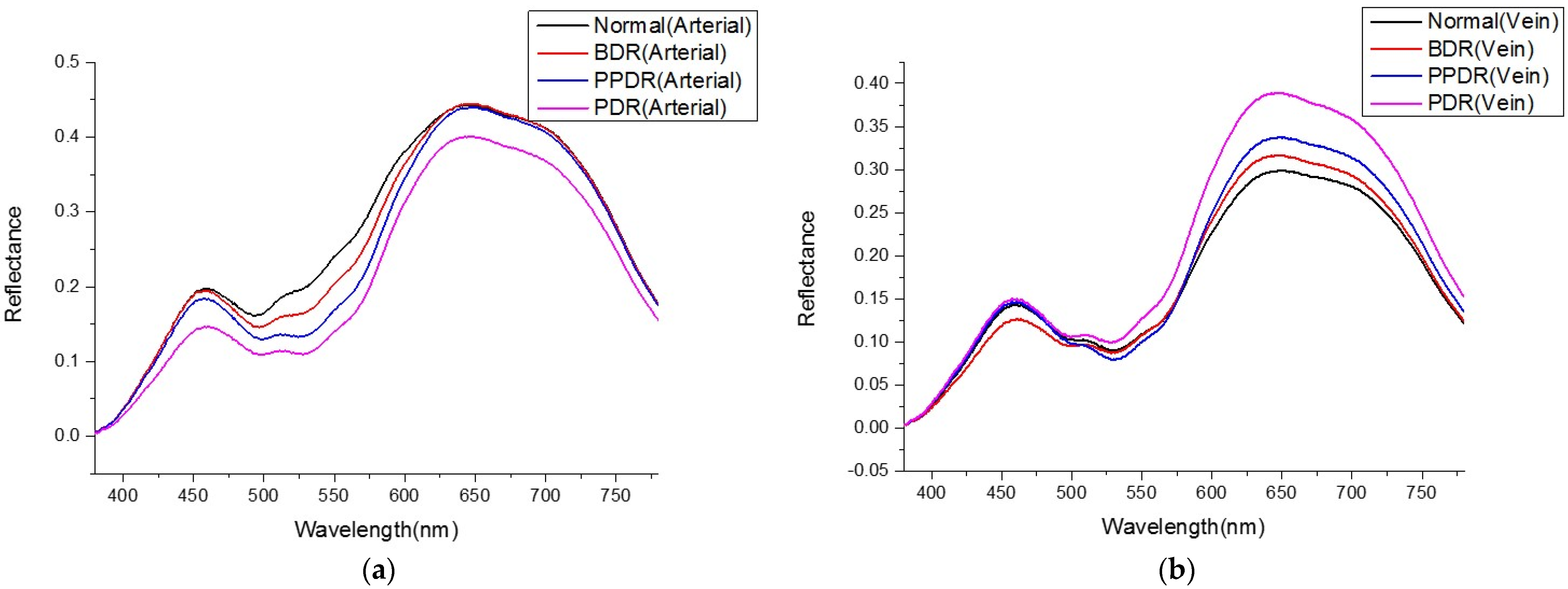
Average Reflectance Spectrum
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kanski, J.J. Clinical Ophthalmology: A Systematic Approach; Elsevier Brasil: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Abràmoff, M.D.; Garvin, M.K.; Sonka, M. Retinal imaging and image analysis. IEEE Rev. Biomed. Eng. 2010, 3, 169–208. [Google Scholar] [CrossRef] [PubMed]
- Galdran, A.; Meyer, M.; Costa, P.; Campilho, A. Uncertainty-aware artery/vein classification on retinal images. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 556–560. [Google Scholar]
- Girard, F.; Kavalec, C.; Cheriet, F. Joint segmentation and classification of retinal arteries/veins from fundus images. Artif. Intell. Med. 2019, 94, 96–109. [Google Scholar] [CrossRef] [PubMed]
- da Silva, A.V.B.; Gouvea, S.A.; da Silva, A.P.B.; Bortolon, S.; Rodrigues, A.N.; Abreu, G.R.; Herkenhoff, F.L. Changes in retinal microvascular diameter in patients with diabetes. Int. J. Gen. Med. 2015, 8, 267. [Google Scholar] [PubMed]
- Morano, J.; Hervella, Á.S.; Novo, J.; Rouco, J. Simultaneous segmentation and classification of the retinal arteries and veins from color fundus images. Artif. Intell. Med. 2021, 118, 102116. [Google Scholar] [CrossRef]
- Staal, J.; Abràmoff, M.D.; Niemeijer, M.; Viergever, M.A.; Van Ginneken, B. Ridge-based vessel segmentation in color images of the retina. IEEE Trans. Med. Imaging 2004, 23, 501–509. [Google Scholar] [CrossRef]
- Jiang, X.; Mojon, D. Adaptive local thresholding by verification-based multithreshold probing with application to vessel detection in retinal images. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 131–137. [Google Scholar] [CrossRef]
- Nain, D.; Yezzi, A.; Turk, G. Vessel segmentation using a shape driven flow. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Saint-Malo, France, 26–29 September 2004; pp. 51–59. [Google Scholar]
- Tolias, Y.A.; Panas, S.M. A fuzzy vessel tracking algorithm for retinal images based on fuzzy clustering. IEEE Trans. Med. Imaging 1998, 17, 263–273. [Google Scholar] [CrossRef]
- Sinthanayothin, C.; Boyce, J.F.; Cook, H.L.; Williamson, T.H. Automated localisation of the optic disc, fovea, and retinal blood vessels from digital colour fundus images. Br. J. Ophthalmol. 1999, 83, 902–910. [Google Scholar] [CrossRef]
- Marín, D.; Aquino, A.; Gegúndez-Arias, M.E.; Bravo, J.M. A new supervised method for blood vessel segmentation in retinal images by using gray-level and moment invariants-based features. IEEE Trans. Med. Imaging 2010, 30, 146–158. [Google Scholar] [CrossRef]
- Liskowski, P.; Krawiec, K. Segmenting retinal blood vessels with deep neural networks. IEEE Trans. Med. Imaging 2016, 35, 2369–2380. [Google Scholar] [CrossRef]
- Fu, H.; Xu, Y.; Lin, S.; Kee Wong, D.W.; Liu, J. Deepvessel: Retinal vessel segmentation via deep learning and conditional random field. In Proceedings of the International conference on medical image computing and computer-assisted intervention, Athens, Greece, 17–21 October 2016; pp. 132–139. [Google Scholar]
- Fu, H.; Xu, Y.; Wong, D.W.K.; Liu, J. Retinal vessel segmentation via deep learning network and fully-connected conditional random fields. In Proceedings of the 2016 IEEE 13th international symposium on biomedical imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 698–701. [Google Scholar]
- Dasgupta, A.; Singh, S. A fully convolutional neural network based structured prediction approach towards the retinal vessel segmentation. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, VIC, Australia, 18–21 April 2017; pp. 248–251. [Google Scholar]
- Jiang, Z.; Zhang, H.; Wang, Y.; Ko, S.-B. Retinal blood vessel segmentation using fully convolutional network with transfer learning. Comput. Med. Imaging Graph. 2018, 68, 1–15. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Mukundan, A.; Patel, A.; Saraswat, K.D.; Tomar, A.; Kuhn, T. Kalam Rover. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1047. [Google Scholar]
- Gross, W.; Queck, F.; Vögtli, M.; Schreiner, S.; Kuester, J.; Böhler, J.; Mispelhorn, J.; Kneubühler, M.; Middelmann, W. A multi-temporal hyperspectral target detection experiment: Evaluation of military setups. In Proceedings of the Target and Background Signatures VII, Online, Spain, 13–18 September 2021; pp. 38–48. [Google Scholar]
- Mukundan, A.; Feng, S.-W.; Weng, Y.-H.; Tsao, Y.-M.; Artemkina, S.B.; Fedorov, V.E.; Lin, Y.-S.; Huang, Y.-C.; Wang, H.-C. Optical and Material Characteristics of MoS2/Cu2O Sensor for Detection of Lung Cancer Cell Types in Hydroplegia. Int. J. Mol. Sci. 2022, 23, 4745. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, Y.-P.; Mukundan, A.; Chen, W.-C.; Wu, M.-T.; Hsieh, S.-C.; Wang, H.-C. Design of a Lab-On-Chip for Cancer Cell Detection through Impedance and Photoelectrochemical Response Analysis. Biosensors 2022, 12, 405. [Google Scholar] [CrossRef]
- Mukundan, A.; Tsao, Y.-M.; Artemkina, S.B.; Fedorov, V.E.; Wang, H.-C. Growth Mechanism of Periodic-Structured MoS2 by Transmission Electron Microscopy. Nanomaterials 2021, 12, 135. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-W.; Tseng, Y.-S.; Mukundan, A.; Wang, H.-C. Air Pollution: Sensitive Detection of PM2. 5 and PM10 Concentration Using Hyperspectral Imaging. Appl. Sci. 2021, 11, 4543. [Google Scholar] [CrossRef]
- Mukundan, A.; Huang, C.-C.; Men, T.-C.; Lin, F.-C.; Wang, H.-C. Air Pollution Detection Using a Novel Snap-Shot Hyperspectral Imaging Technique. Sensors 2022, 22, 6231. [Google Scholar] [CrossRef]
- Gerhards, M.; Schlerf, M.; Mallick, K.; Udelhoven, T. Challenges and future perspectives of multi-/Hyperspectral thermal infrared remote sensing for crop water-stress detection: A review. Remote Sens. 2019, 11, 1240. [Google Scholar] [CrossRef]
- Lee, C.-H.; Mukundan, A.; Chang, S.-C.; Wang, Y.-L.; Lu, S.-H.; Huang, Y.-C.; Wang, H.-C. Comparative Analysis of Stress and Deformation between One-Fenced and Three-Fenced Dental Implants Using Finite Element Analysis. J. Clin. Med. 2021, 10, 3986. [Google Scholar] [CrossRef]
- Stuart, M.B.; McGonigle, A.J.; Willmott, J.R. Hyperspectral imaging in environmental monitoring: A review of recent developments and technological advances in compact field deployable systems. Sensors 2019, 19, 3071. [Google Scholar] [CrossRef]
- Mukundan, A.; Wang, H.-C. Simplified Approach to Detect Satellite Maneuvers Using TLE Data and Simplified Perturbation Model Utilizing Orbital Element Variation. Appl. Sci. 2021, 11, 10181. [Google Scholar] [CrossRef]
- Tsai, C.-L.; Mukundan, A.; Chung, C.-S.; Chen, Y.-H.; Wang, Y.-K.; Chen, T.-H.; Tseng, Y.-S.; Huang, C.-W.; Wu, I.-C.; Wang, H.-C. Hyperspectral Imaging Combined with Artificial Intelligence in the Early Detection of Esophageal Cancer. Cancers 2021, 13, 4593. [Google Scholar] [CrossRef]
- Tsai, T.-J.; Mukundan, A.; Chi, Y.-S.; Tsao, Y.-M.; Wang, Y.-K.; Chen, T.-H.; Wu, I.-C.; Huang, C.-W.; Wang, H.-C. Intelligent Identification of Early Esophageal Cancer by Band-Selective Hyperspectral Imaging. Cancers 2022, 14, 4292. [Google Scholar] [CrossRef]
- Fang, Y.-J.; Mukundan, A.; Tsao, Y.-M.; Huang, C.-W.; Wang, H.-C. Identification of Early Esophageal Cancer by Semantic Segmentation. J. Pers. Med. 2022, 12, 1204. [Google Scholar] [CrossRef] [PubMed]
- Vangi, E.; D’Amico, G.; Francini, S.; Giannetti, F.; Lasserre, B.; Marchetti, M.; Chirici, G. The new hyperspectral satellite PRISMA: Imagery for forest types discrimination. Sensors 2021, 21, 1182. [Google Scholar] [CrossRef]
- Huang, S.-Y.; Mukundan, A.; Tsao, Y.-M.; Kim, Y.; Lin, F.-C.; Wang, H.-C. Recent Advances in Counterfeit Art, Document, Photo, Hologram, and Currency Detection Using Hyperspectral Imaging. Sensors 2022, 22, 7308. [Google Scholar] [CrossRef]
- Zhang, X.; Han, L.; Dong, Y.; Shi, Y.; Huang, W.; Han, L.; González-Moreno, P.; Ma, H.; Ye, H.; Sobeih, T. A deep learning-based approach for automated yellow rust disease detection from high-resolution hyperspectral UAV images. Remote Sens. 2019, 11, 1554. [Google Scholar] [CrossRef]
- Hennessy, A.; Clarke, K.; Lewis, M. Hyperspectral classification of plants: A review of waveband selection generalisability. Remote Sens. 2020, 12, 113. [Google Scholar] [CrossRef]
- Terentev, A.; Dolzhenko, V.; Fedotov, A.; Eremenko, D. Current State of Hyperspectral Remote Sensing for Early Plant Disease Detection: A Review. Sensors 2022, 22, 757. [Google Scholar] [CrossRef]
- De La Rosa, R.; Tolosana-Delgado, R.; Kirsch, M.; Gloaguen, R. Automated Multi-Scale and Multivariate Geological Logging from Drill-Core Hyperspectral Data. Remote Sens. 2022, 14, 2676. [Google Scholar] [CrossRef]
- Yao, H.-Y.; Tseng, K.-W.; Nguyen, H.-T.; Kuo, C.-T.; Wang, H.-C. Hyperspectral Ophthalmoscope Images for the Diagnosis of Diabetic Retinopathy Stage. J. Clin. Med. 2020, 9, 1613. [Google Scholar] [CrossRef] [PubMed]
- Whiting, D.R.; Guariguata, L.; Weil, C.; Shaw, J. IDF diabetes atlas: Global estimates of the prevalence of diabetes for 2011 and 2030. Diabetes Res. Clin. Pract. 2011, 94, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Fong, D.; Aiello, L.; Ferris, F. Klein RK Diabetic retinopathy. Ophthalmol. L 2004, 27, 2540–2553. [Google Scholar] [CrossRef]
- Wong, T.Y.; Sun, J.; Kawasaki, R.; Ruamviboonsuk, P.; Gupta, N.; Lansingh, V.C.; Maia, M.; Mathenge, W.; Moreker, S.; Muqit, M.M. Guidelines on diabetic eye care: The international council of ophthalmology recommendations for screening, follow-up, referral, and treatment based on resource settings. Ophthalmology 2018, 125, 1608–1622. [Google Scholar] [CrossRef] [PubMed]
- Solomon, S.D.; Chew, E.; Duh, E.J.; Sobrin, L.; Sun, J.K.; VanderBeek, B.L.; Wykoff, C.C.; Gardner, T.W. Diabetic retinopathy: A position statement by the American Diabetes Association. Diabetes Care 2017, 40, 412–418. [Google Scholar] [CrossRef] [PubMed]
- Simó, R.; Hernández, C. Advances in the medical treatment of diabetic retinopathy. Diabetes Care 2009, 32, 1556–1562. [Google Scholar] [CrossRef]
- Joussen, A.M.; Poulaki, V.; Le, M.L.; Koizumi, K.; Esser, C.; Janicki, H.; Schraermeyer, U.; Kociok, N.; Fauser, S.; Kirchhof, B. A central role for inflammation in the pathogenesis of diabetic retinopathy. FASEB J. 2004, 18, 1450–1452. [Google Scholar] [CrossRef]
- Li, N.; Liu, Y.; Yun, A.; Song, S. Correlation of Platelet Function with Postpartum Hemorrhage and Venous Thromboembolism in Patients with Gestational Hypertension Complicated with Diabetes. Comput. Math. Methods Med. 2022, 2022, 2423333. [Google Scholar] [CrossRef]
- Einer, S.G. Gradual painless visual loss: Retinal causes. Clin. Geriatr. Med. 1999, 15, 25–46. [Google Scholar] [CrossRef]
- Littmann, H. Die Zeiss Funduskamera Ber. 59. Zusammenkunft Deutsch. Ophthalmolog. Gesellsch., Heidelberg 1955; Verlag Bergmann: Munchen, Germany, 1995; p. 318. [Google Scholar]
- Morgner, U.; Drexler, W.; Kärtner, F.X.; Li, X.D.; Pitris, C.; Ippen, E.P.; Fujimoto, J.G. Spectroscopic optical coherencetomography. Opt. Lett. 2000, 25, 111–113. [Google Scholar] [CrossRef]
- Siddalingaswamy, P.C.; Prabhu, K.G. Automatic detection of multiple oriented blood vessels in retinal images. J. Biomed. Sci. Eng. 2010, 3, 101–107. [Google Scholar] [CrossRef]

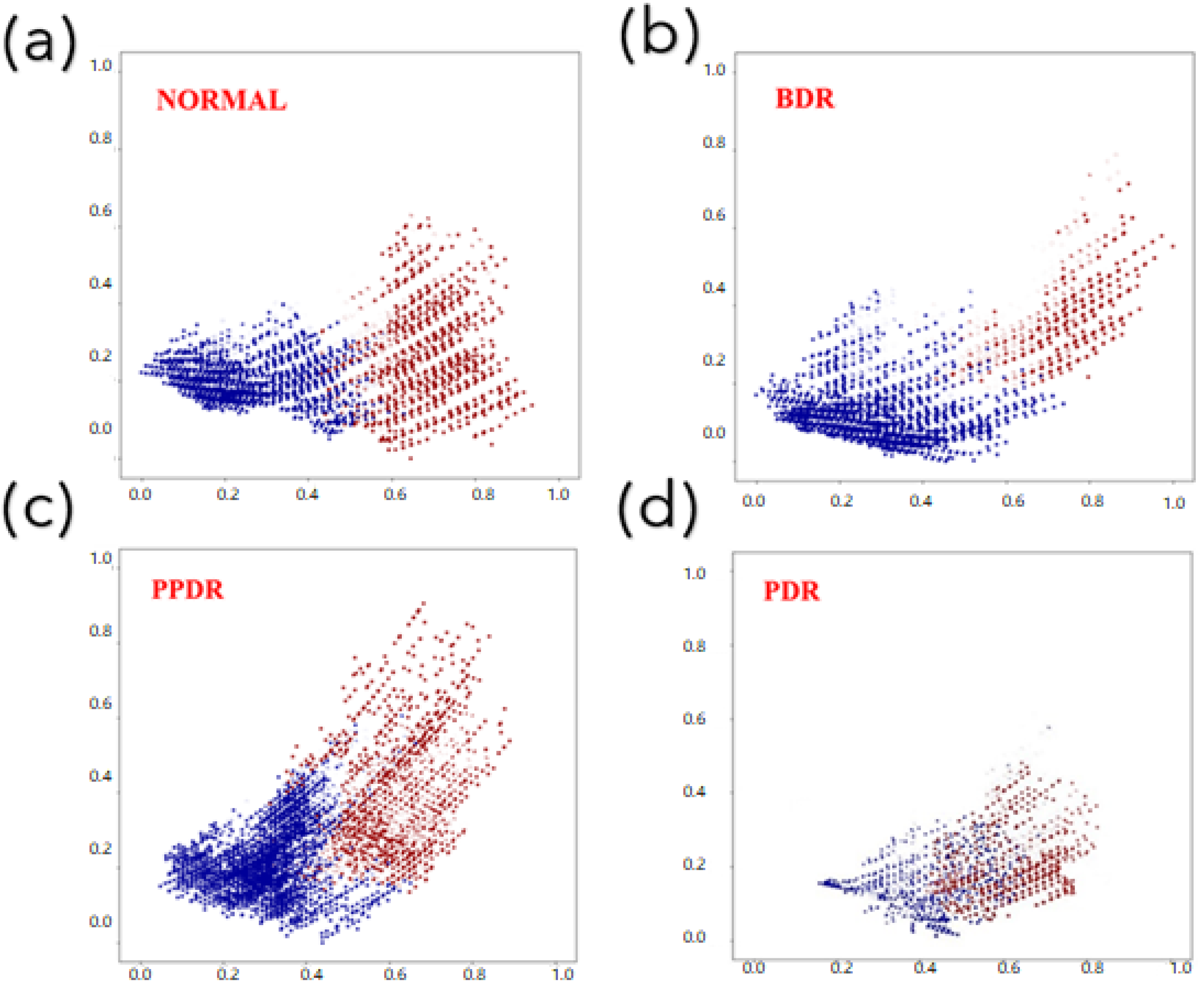
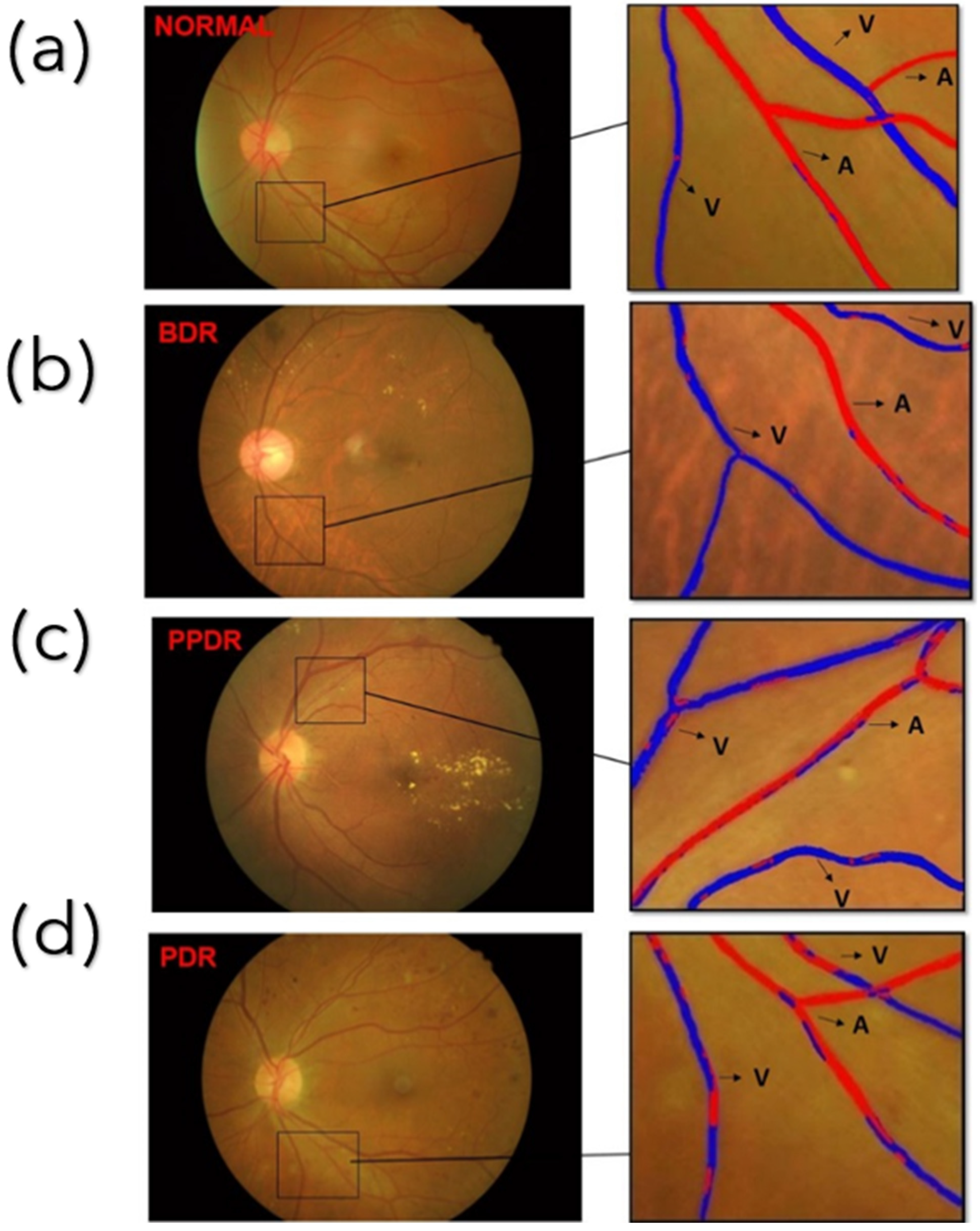
| Artery | Sensitivity (%) | Precision (%) | F1-Score (%) |
| NORMAL | 82.4 | 88.4 | 85.3 |
| BDR | 77.5 | 83.5 | 80.3 |
| PPDR | 78.1 | 80.7 | 79.4 |
| PDR | 72.9 | 73.4 | 73.1 |
| Veins | Sensitivity (%) | Precision (%) | F1-Score (%) |
| NORMAL | 88.5 | 82.6 | 85.4 |
| BDR | 85.4 | 81.2 | 83.2 |
| PPDR | 81.4 | 79.2 | 80.3 |
| PDR | 75.1 | 74.6 | 74.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-Y.; Mukundan, A.; Liu, Y.-S.; Tsao, Y.-M.; Lin, F.-C.; Fan, W.-S.; Wang, H.-C. Optical Identification of Diabetic Retinopathy Using Hyperspectral Imaging. J. Pers. Med. 2023, 13, 939. https://doi.org/10.3390/jpm13060939
Wang C-Y, Mukundan A, Liu Y-S, Tsao Y-M, Lin F-C, Fan W-S, Wang H-C. Optical Identification of Diabetic Retinopathy Using Hyperspectral Imaging. Journal of Personalized Medicine. 2023; 13(6):939. https://doi.org/10.3390/jpm13060939
Chicago/Turabian StyleWang, Ching-Yu, Arvind Mukundan, Yu-Sin Liu, Yu-Ming Tsao, Fen-Chi Lin, Wen-Shuang Fan, and Hsiang-Chen Wang. 2023. "Optical Identification of Diabetic Retinopathy Using Hyperspectral Imaging" Journal of Personalized Medicine 13, no. 6: 939. https://doi.org/10.3390/jpm13060939
APA StyleWang, C.-Y., Mukundan, A., Liu, Y.-S., Tsao, Y.-M., Lin, F.-C., Fan, W.-S., & Wang, H.-C. (2023). Optical Identification of Diabetic Retinopathy Using Hyperspectral Imaging. Journal of Personalized Medicine, 13(6), 939. https://doi.org/10.3390/jpm13060939








