Hybrid Bayesian Network-Based Modeling: COVID-19-Pneumonia Case
Abstract
:1. Introduction
1.1. Background
1.2. Related Works
1.3. The Research Question
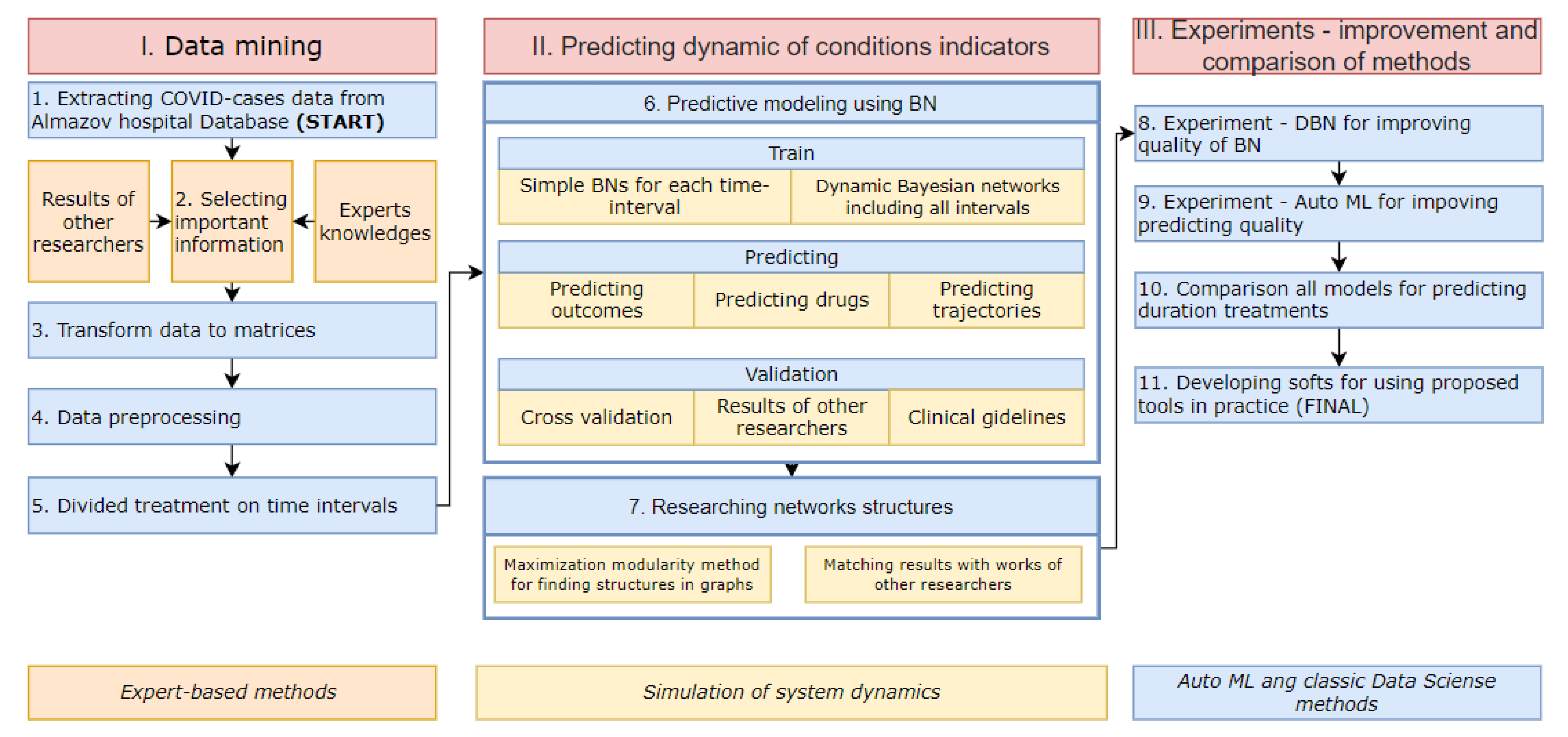
2. Materials and Methods
2.1. Simple Bayesian Networks
- Find statistical patterns between patients′ condition indicators.
- Select dynamical predictors (indicators and time of its measurement) of treatment outcomes.
- Predict treatment outcomes.
- The dataset is separated by 5 time periods—each period lasts 7 days. Patients′ conditions do not change every day. For researching statistically significant patterns, we, therefore, aggregate information for each interval.
- Learning the DAG. There are two approaches for finding the structure of the BN graph, score-based structure learning algorithms and constraint-based algorithms. We try to use two methods from the first approach—hillclimb search and Chow-liu and one method from the second approach—constraint-based search [27]. Hillclimb search performs a greedy local search that begins with default DAG without edges and proceeds by iteratively performing single-edge manipulations that maximally increase the score (BIC). Chow-liu is based on the hypothesis that networks have a tree structure. The tree structure shows the best metric, given that each node has at most one parent. The constraint-based approach identifies probabilistic dependencies in the data set based on hypothesis tests, such as chi-square.
- Learning the network parameters using the maximum likelihood estimation method [28].
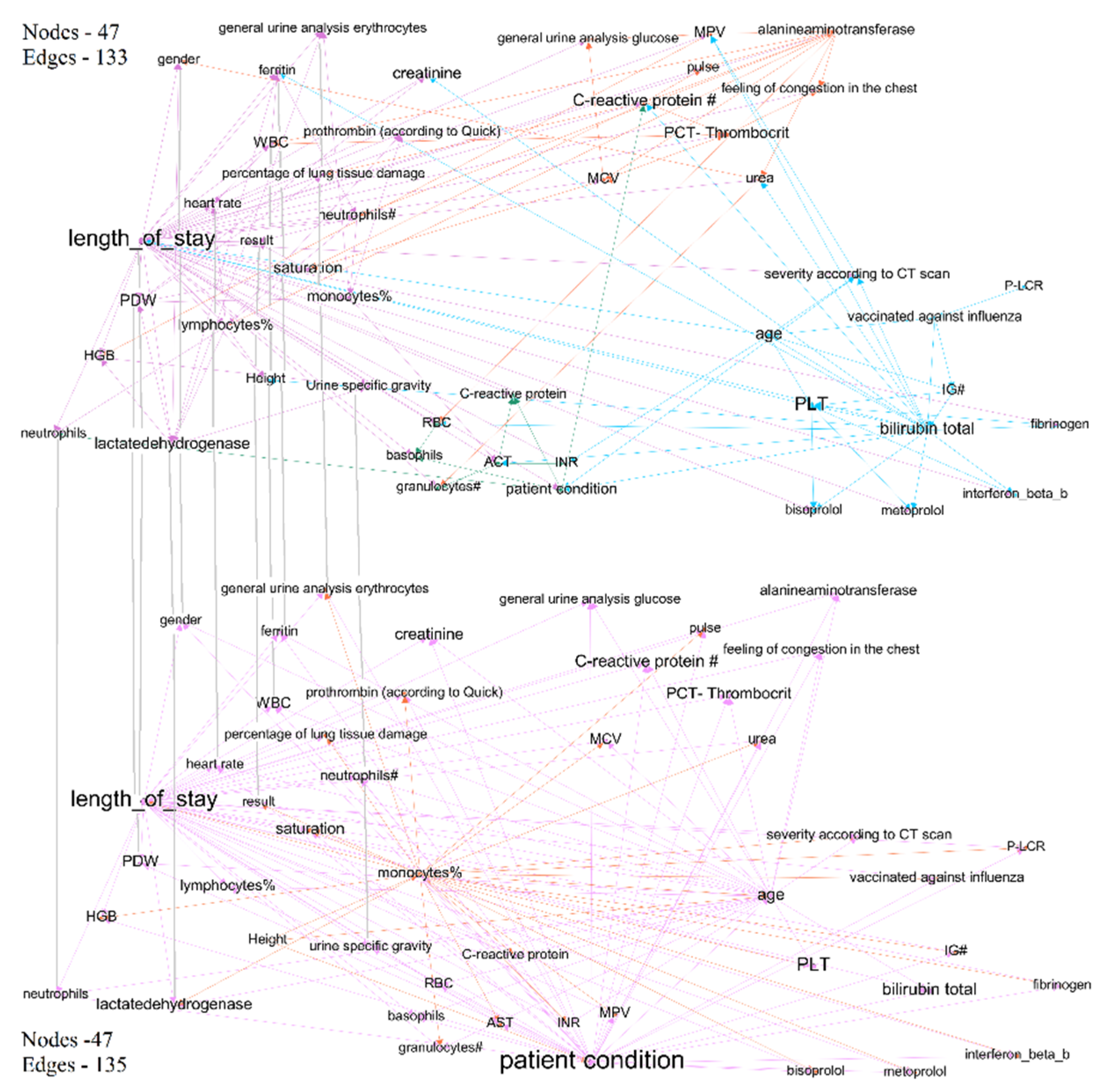
- Visualizing Bayesian networks as graphs. Nodes were clustered using the modularity maximization method. This method is based on the widely-used objective function to determine communities from a given network [29].
- Estimating the predictive quality of each network in terms of predicting treatment outcomes by using the classical metric of predictive tasks, including F1 score for the classification problem and mean absolute error (MSE) for regression.
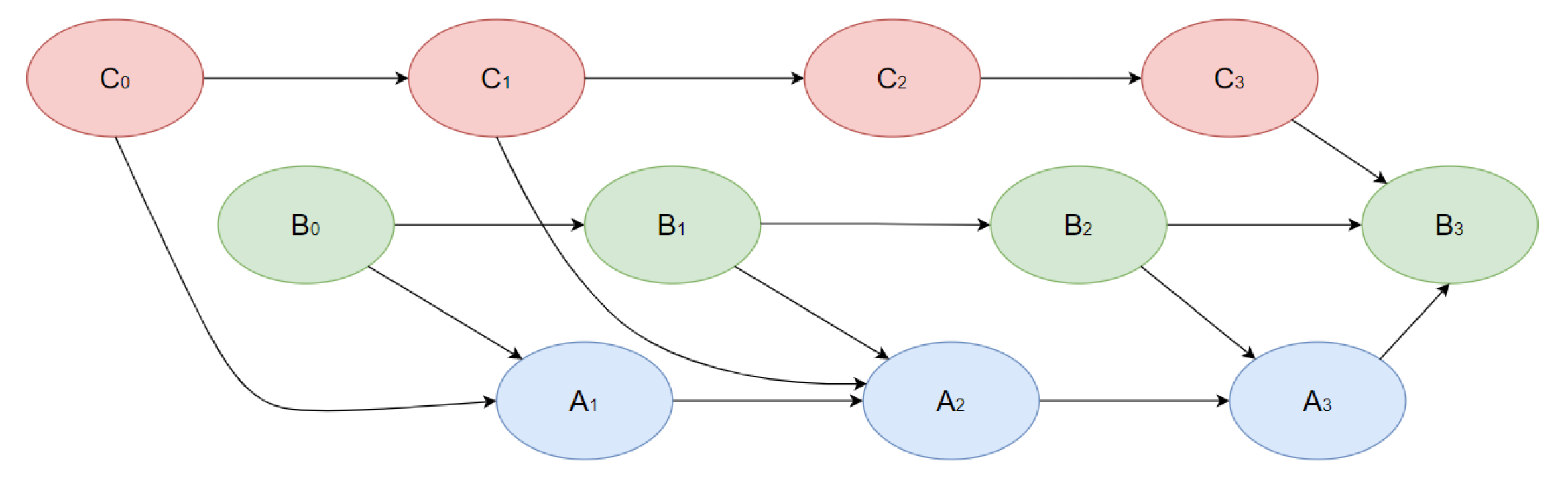
2.2. Dynamic Bayesian Networks
- Research of dynamical statistical patterns of treatment trajectories.
- Predicting the full future trajectory of important patients′ indicators
- Predicting the therapy effect in terms of treatment outcomes and length of stay (therapy included in factors of networks)
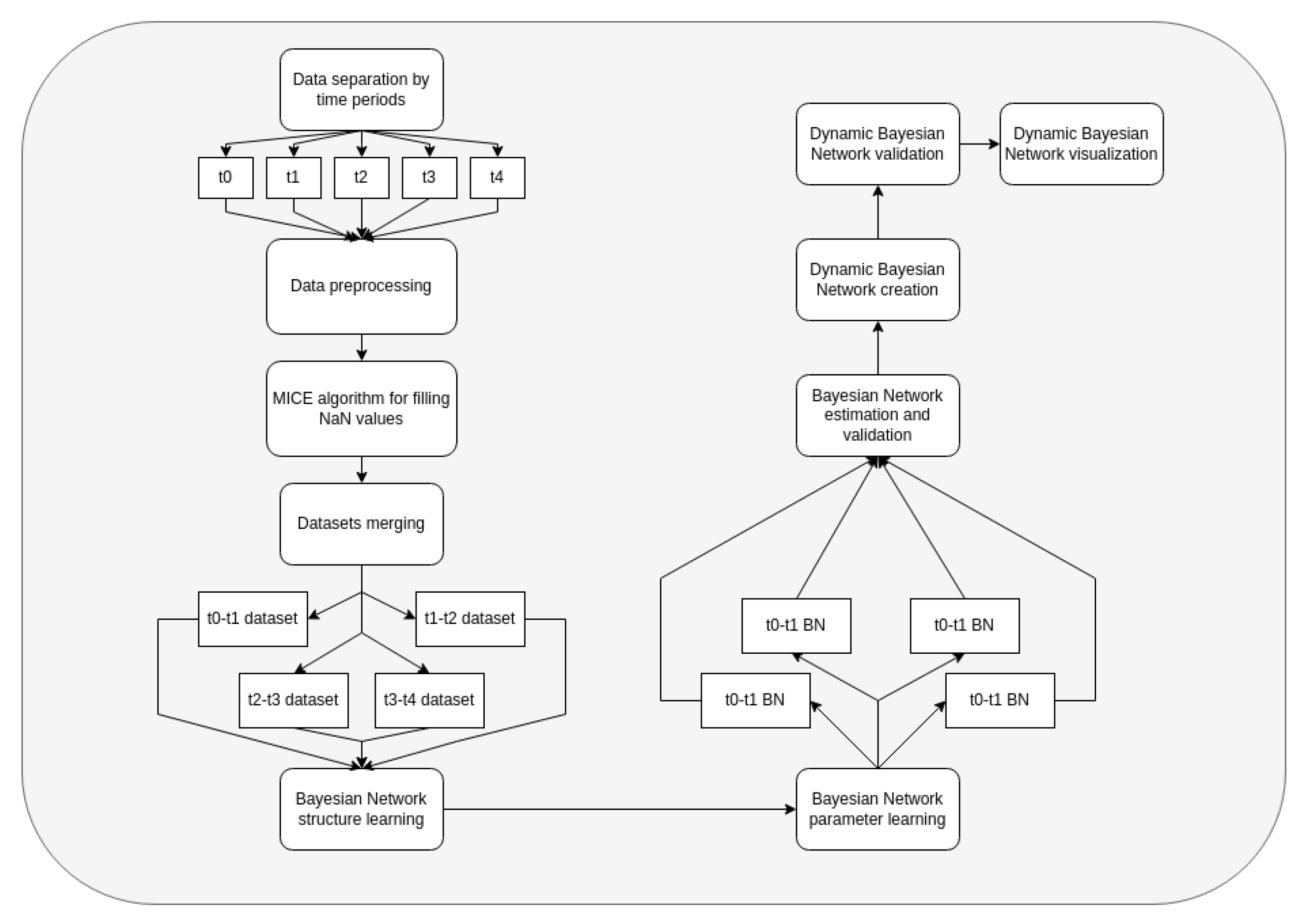
- The dataset is separated into 5 time periods, each of them with a 7-day length.
- The MICE algorithm is applied to fill the missing data, since real clinical data might contain missing values. Features without data are dropped.
- Information from day t to day t +1 is merged and used for the creation of Bayesian networks. Data are separated into train and test datasets for every time.
- We validate DBN using only test samples. Using models, we made predictions of the treatment outcomes and a series of important patient condition indicators using the following algorithm: using initial data from t-0 interval, we provide predictions of all the medical indicators for t-1 interval; using predicted indicators, we make predictions for the t-2-time interval, and so on. When we have predictions of the patients′ condition indicators, we predict the treatment outcomes.
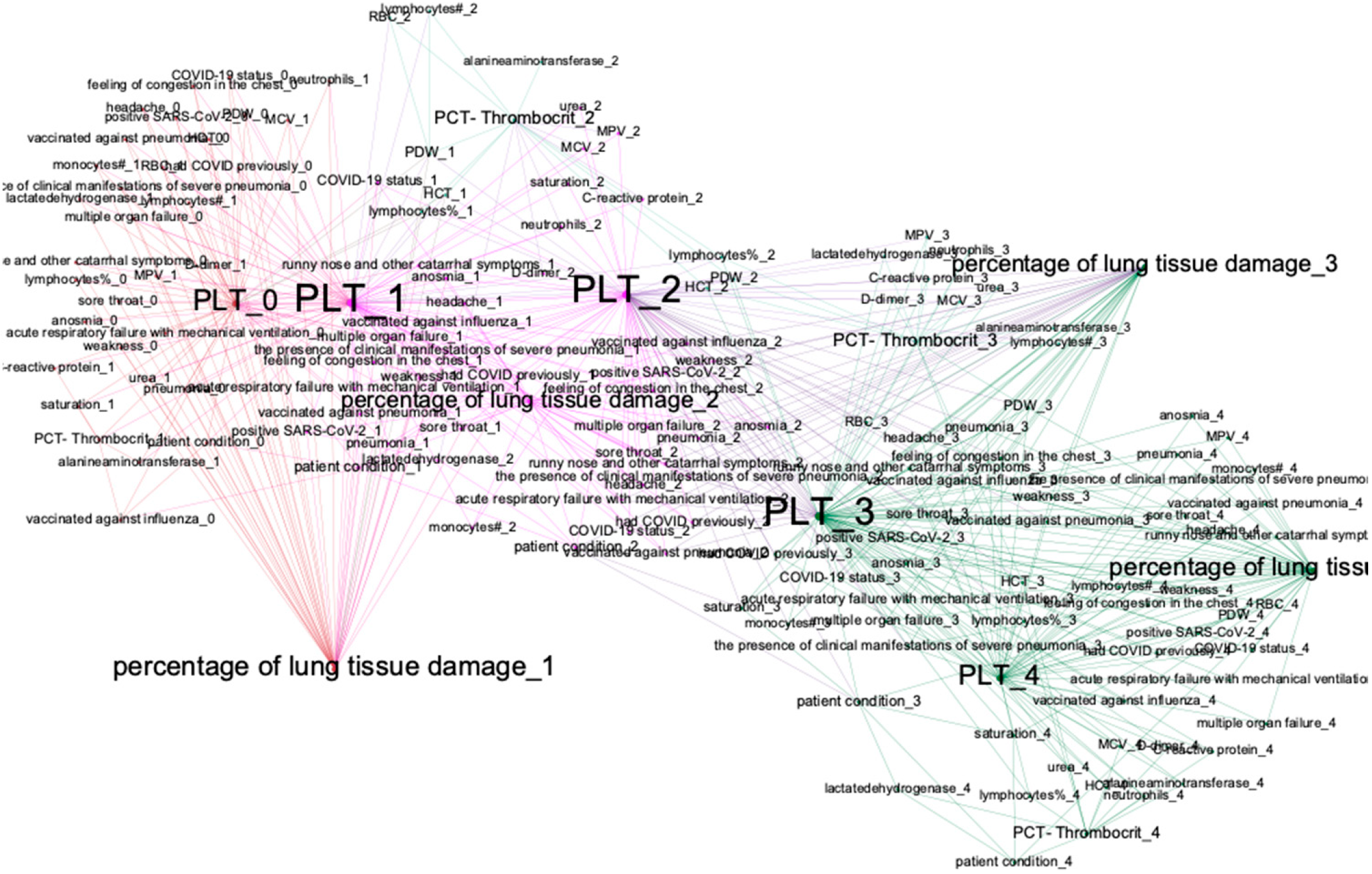
- For analyzing structures of trained DBN, we visualize it as a graph; we deploy the method of modularity maximization to divide networks into clusters and to analyze the model’s structure.
2.3. Data
3. Results
3.1. Simple Bayesian Network-Based Analysis
3.2. Dynamical Bayesian Network-Based Analysis
3.3. Hybrid Approach
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- COVID Live—Coronavirus Statistics—Worldometer. Available online: https://www.worldometers.info/coronavirus/ (accessed on 10 April 2022).
- Cummings, M.J.; Baldwin, M.R.; Abrams, D.; Jacobson, S.D.; Meyer, B.J.; Balough, E.M.; Aaron, J.G.; Claassen, J.; Rabbani, L.R.E.; Hastie, J.; et al. Epidemiology, clinical course, and outcomes of critically ill adults with COVID-19 in New York City: A prospective cohort study. Lancet 2020, 395, 1763–1770. [Google Scholar] [CrossRef]
- Shi, N.; Huang, C.; Zhang, Q.; Shi, C.; Liu, F.; Song, F.; Hou, Q.; Shen, J.; Shan, F.; Su, X.; et al. Longitudinal trajectories of pneumonia lesions and lymphocyte counts associated with disease severity among convalescent COVID-19 patients: A group-based multi-trajectory analysis. BMC Pulm. Med. 2021, 21, 233. [Google Scholar] [CrossRef] [PubMed]
- Symptoms of Coronavirus: Early Signs, Serious Symptoms and More. Available online: https://www.webmd.com/lung/covid-19-symptoms#1 (accessed on 10 April 2022).
- Bauer, T.T.; Ewig, S.; Rodloff, A.C.; Müller, E.E. Acute respiratory distress syndrome and pneumonia: A comprehensive review of clinical data. Clin. Infect. Dis. 2006, 43, 748–756. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ji Jung, K.; Yoo, S.J.; Yoon, S.H. Stratifying the early radiologic trajectory in dyspneic patients with COVID-19 pneumonia. PLoS ONE 2021, 16, e0259010. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; Sun, Y.; Xu, H.; Ye, Q. The emergence and epidemic characteristics of the highly mutated SARS-CoV-2 Omicron variant. J. Med. Virol. 2022, 94, 2376–2383. [Google Scholar] [CrossRef]
- Amrulloh, Y.A.; Triasih, R.; Setyati, A. Hidden markov model of cough from pediatric patients with respiratory infections. In Proceedings of the 2016 International Seminar on Application for Technology of Information and Communication (ISemantic), Semarang, Indonesia, 5–6 August 2016; pp. 341–345. [Google Scholar] [CrossRef]
- Ozonoff, A.; Sukpraprut, S.; Sebastiani, P. Modeling seasonality of influenza with Hidden Markov Models. Proc. Am. Stat. Assoc. 2006. Available online: https://www.researchgate.net/publication/267206133 (accessed on 4 May 2015).
- Heckerling, P.S.; Gerber, B.S.; Tape, T.G.; Wigton, R.S. Prediction of community-acquired pneumonia using artificial neural networks. Med. Decis. Mak. 2003, 23, 112–121. [Google Scholar] [CrossRef] [PubMed]
- Duchesne, S.; Gourdeau, D.; Archambault, P.; Chartrand-Lefebvre, C.; Dieumegarde, L.; Forghani, R.; Gagné, C.; Hains, A.; Hornstein, D.; Le, H.; et al. Tracking and predicting COVID-19 radiological trajectory using deep learning on chest X-rays: Initial accuracy testing. medRxiv 2020. [Google Scholar] [CrossRef]
- Ko, H.; Chung, H.; Kang, W.S.; Kim, K.W.; Shin, Y.; Kang, S.J.; Lee, J.H.; Kim, Y.J.; Kim, N.Y.; Jung, H.; et al. COVID-19 pneumonia diagnosis using a simple 2d deep learning framework with a single chest CT image: Model development and validation. J. Med. Internet Res. 2020, 22, e19569. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, Q.; Chen, F.; Luo, L.; Chen, L.; Zhang, W. Smooth Bayesian network model for the prediction of future high-cost patients with COPD. Int. J. Med. Inform. 2019, 126, 147–155. [Google Scholar] [CrossRef]
- Julia Flores, M.; Nicholson, A.E.; Brunskill, A.; Korb, K.B.; Mascaro, S. Incorporating expert knowledge when learning Bayesian network structure: A medical case study. Artif. Intell. Med. 2011, 53, 181–204. [Google Scholar] [CrossRef] [PubMed]
- Derevitskii, I.V.; Savitskaya, D.A.; Babenko, A.Y.; Kovalchuk, S.V. Hybrid predictive modelling: Thyrotoxic atrial fibrillation case. J. Comput. Sci. 2021, 51, 101365. [Google Scholar] [CrossRef]
- Mramorov, N.; Derevitskii, I.; Kovalchuk, S. Predictive Modeling of COVID and non-COVID Pneumonia Trajectories. Stud. Health Technol. Inform. 2021, 285, 112–117. [Google Scholar] [CrossRef] [PubMed]
- Gatti, E.; Luciani, D.; Stella, F. A continuous time Bayesian network model for cardiogenic heart failure. Flex. Serv. Manuf. J. 2012, 24, 496–515. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Hidden Markov Model. Effic. Learn. Mach. 2015, 263, 81–104. [Google Scholar] [CrossRef]
- van Buuren, S.; Groothuis-Oudshoorn, K. Mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Puga, J.L.; Krzywinski, M.; Altman, N. Points of Significance: Bayesian networks. Nat. Methods 2015, 12, 799–800. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Liu, Z.; Malone, B.; Yuan, C. Empirical evaluation of scoring functions for Bayesian network model selection. BMC Bioinform. 2012, 13 (Suppl. 1), 1–16. [Google Scholar] [CrossRef]
- De Campos, C.P.; Ji, Q. Efficient structure learning of Bayesian networks using constraints. J. Mach. Learn. Res. 2011, 12, 663–689. [Google Scholar]
- Park, E.; Chang, H.J.; Nam, H.S. A Bayesian network model for predicting post-stroke outcomes with available risk factors. Front. Neurol. 2018, 9, 699. [Google Scholar] [CrossRef] [PubMed]
- Van Der Gaag, L.C.; Renooij, S.; Feelders, A.; De Groote, A.; Eijkemans, M.J.C.; Broekmans, F.J.; Fauser, B.C.J.M. Aligning bayesian network classifiers with medical contexts. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2009; Volume 5632 LNAI, pp. 787–801. [Google Scholar] [CrossRef]
- Tong, L.L.; Gu, J.B.; Li, J.J.; Liu, G.X.; Jin, S.W.; Yan, A.Y. Application of Bayesian network and regression method in treatment cost prediction. BMC Med. Inform. Decis. Mak. 2021, 21, 284. [Google Scholar] [CrossRef] [PubMed]
- Package ‘bnlearn’ Type Package Title Bayesian Network Structure Learning, Parameter Learning and Inference. 2022. Available online: https://www.bnlearn.com/ (accessed on 10 April 2022).
- Ji, Z.; Xia, Q.; Meng, G. A Review of Parameter Learning Methods in Bayesian Network. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2015; Volume 9227, pp. 3–12. [Google Scholar] [CrossRef]
- Tsung, C.K.; Lee, S.L.; Ho, H.J.; Chou, S.K. A modularity-maximization-based approach for detecting multi-communities in social networks. Ann. Oper. Res. 2021, 303, 381–411. [Google Scholar] [CrossRef]
- Łupińska-Dubicka, A. Modeling dynamical systems by means of dynamic Bayesian networks. Sci. Bull. Bialystok Univ. Technol. Inform. 2012, 9, 77–92. [Google Scholar]
- Bubnova, A.V.; Deeva, I.; Kalyuzhnaya, A.V. MIxBN: Library for learning Bayesian networks from mixed data. Procedia Comput. Sci. 2021, 193, 494–503. [Google Scholar] [CrossRef]
- ITMO-NSS-Team/BAMT: Repository of a Data Modeling and Analysis Tool Based on Bayesian Networks. Available online: https://github.com/ITMO-NSS-team/BAMT (accessed on 12 April 2022).
- Tan, L.; Kang, X.; Ji, X.; Li, G.; Wang, Q.; Li, Y.; Wang, Q.; Miao, H. Validation of Predictors of Disease Severity and Outcomes in COVID-19 Patients: A Descriptive and Retrospective Study. Med 2020, 1, 128–138.e3. [Google Scholar] [CrossRef]
- Mukhtar, A.; Rady, A.; Hasanin, A.; Lotfy, A.; El Adawy, A.; Hussein, A.; El-Hefnawy, I.; Hassan, M.; Mostafa, H. Admission SpO2 and ROX index predict outcome in patients with COVID-19. Am. J. Emerg. Med. 2021, 50, 106–110. [Google Scholar] [CrossRef]
- Zeng, Z.Y.; Feng, S.D.; Chen, G.P.; Wu, J.N. Predictive value of the neutrophil to lymphocyte ratio for disease deterioration and serious adverse outcomes in patients with COVID-19: A prospective cohort study. BMC Infect. Dis. 2021, 21, 80. [Google Scholar] [CrossRef]
- Lentner, J.; Adams, T.; Knutson, V.; Zeien, S.; Abbas, H.; Moosavi, R.; Manuel, C.; Wallace, T.; Harmon, A.; Waters, R.; et al. C-reactive protein levels associated with COVID-19 outcomes in the United States. J. Osteopath. Med. 2021, 121, 869–873. [Google Scholar] [CrossRef]
- Mahboub, B.; Bataineh, M.T.A.; Alshraideh, H.; Hamoudi, R.; Salameh, L.; Shamayleh, A. Prediction of COVID-19 Hospital Length of Stay and Risk of Death Using Artificial Intelligence-Based Modeling. Front. Med. 2021, 8, 592336. [Google Scholar] [CrossRef]
- Lai, K.-L.; Hu, F.-C.; Wen, F.-Y.; Chen, J.-J. Lymphocyte count is a universal predictor to the health status and outcomes of patients with coronavirus disease 2019 (COVID-19): A systematic review and meta-regression analysis. medRxiv 2021. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Q.; Liu, T.; Luo, P.; Zhou, Y.; Liu, M.; Xiong, B.; Zhou, F. Development and Validation of Predictors for the Survival of Patients With COVID-19 Based on Machine Learning. Front. Med. 2021, 8, 683431. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, P.; Gajendran, M.; Perisetti, A.; Elkholy, K.O.; Chakraborti, A.; Lippi, G.; Goyal, H. Red Blood Cell Distribution Width in Hospitalized COVID-19 Patients. Front. Med. 2022, 8, 2531. [Google Scholar] [CrossRef] [PubMed]
- Kilercik, M.; Demirelce, Ö.; Serdar, M.A.; Mikailova, P.; Serteser, M. A new haematocytometric index: Predicting severity and mortality risk value in COVID-19 patients. PLoS ONE 2021, 16, e0254073. [Google Scholar] [CrossRef] [PubMed]
- Henry, B.M.; Aggarwal, G.; Wong, J.; Benoit, S.; Vikse, J.; Plebani, M.; Lippi, G. Lactate dehydrogenase levels predict coronavirus disease 2019 (COVID-19) severity and mortality: A pooled analysis. Am. J. Emerg. Med. 2020, 38, 1722–1726. [Google Scholar] [CrossRef]
- Tomasiuk, R.; Dabrowski, J.; Smykiewicz, J.; Wiacek, M. Predictors of COVID-19 Hospital Treatment Outcome. Int. J. Gen. Med. 2021, 14, 10247–10256. [Google Scholar] [CrossRef]
- Bommenahalli Gowda, S.; Gosavi, S.; Ananda Rao, A.; Shastry, S.; Raj, S.C.; Menon, S.; Suresh, A.; Sharma, A. Prognosis of COVID-19: Red Cell Distribution Width, Platelet Distribution Width, and C-Reactive Protein. Cureus 2021, 13, e13078. [Google Scholar] [CrossRef]
- Nikitin, N.O.; Vychuzhanin, P.; Sarafanov, M.; Polonskaia, I.S.; Revin, I.; Barabanova, I.V.; Maximov, G.; Kalyuzhnaya, A.V.; Boukhanovsky, A. Automated evolutionary approach for the design of composite machine learning pipelines. Future Gener. Comput. Syst. 2022, 127, 109–125. [Google Scholar] [CrossRef]
- nccr-itmo/FEDOT: Automated Modeling and Machine Learning Framework FEDOT. Available online: https://github.com/nccr-itmo/FEDOT (accessed on 11 April 2022).
- Probabilistic and Mean-Field Model of COVID-19 Epidemics with User Mobility and Contact Tracing | Semantic Scholar. Available online: https://www.semanticscholar.org/paper/Probabilistic-and-mean-field-model-of-COVID-19-with-Akian-Ganassali/9c8b962fb4ee58cb5cc3c25cbb29cbc30e2d583b (accessed on 28 July 2022).
- Alguliyev, R.; Aliguliyev, R.; Yusifov, F. Graph modelling for tracking the COVID-19 pandemic spread. Infect. Dis. Model. 2020, 6, 112–122. [Google Scholar] [CrossRef]
- Vepa, A.; Saleem, A.; Rakhshan, K.; Daneshkhah, A.; Sedighi, T.; Shohaimi, S.; Omar, A.; Salari, N.; Chatrabgoun, O.; Dharmaraj, D.; et al. Using Machine Learning Algorithms to Develop a Clinical Decision-Making Tool for COVID-19 Inpatients. Int. J. Environ. Res. Public Health 2021, 18, 6228. [Google Scholar] [CrossRef]
- Mihaljević, B.; Bielza, C.; Larrañaga, P. Bayesian networks for interpretable machine learning and optimization. Neurocomputing 2021, 456, 648–665. [Google Scholar] [CrossRef]


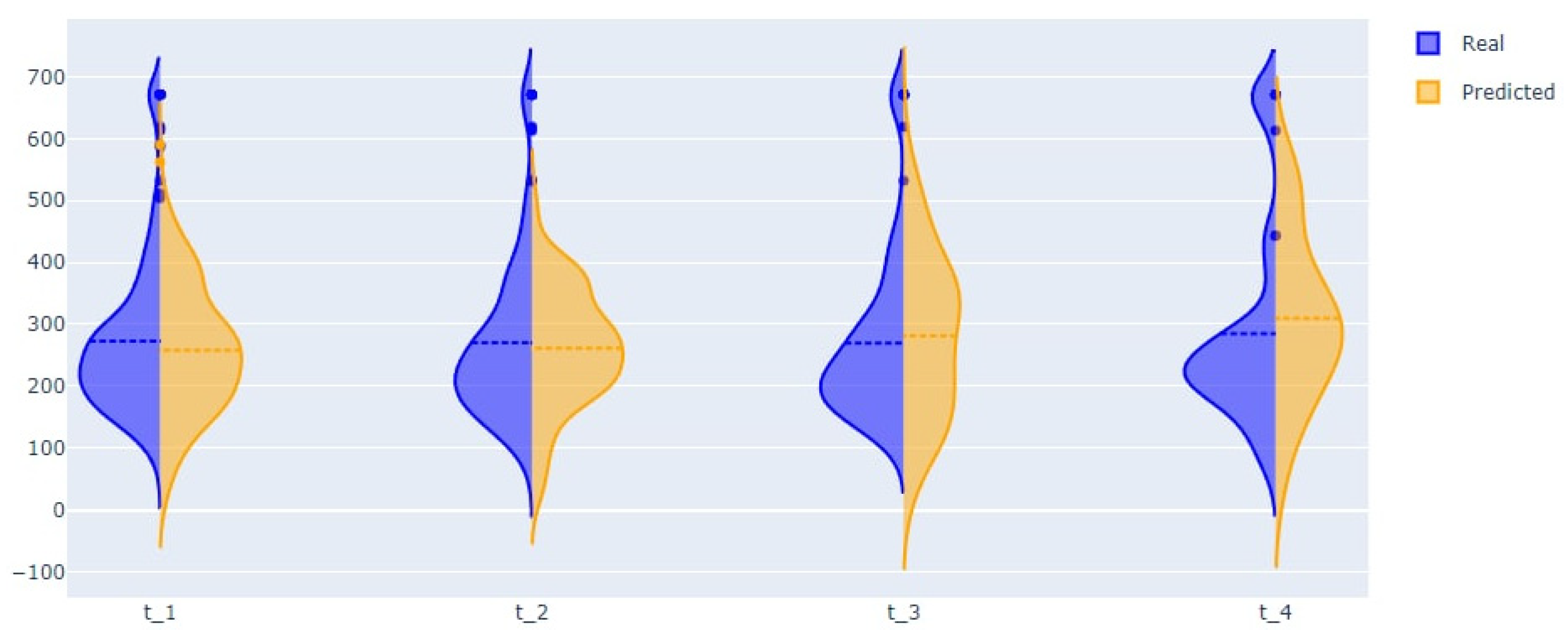
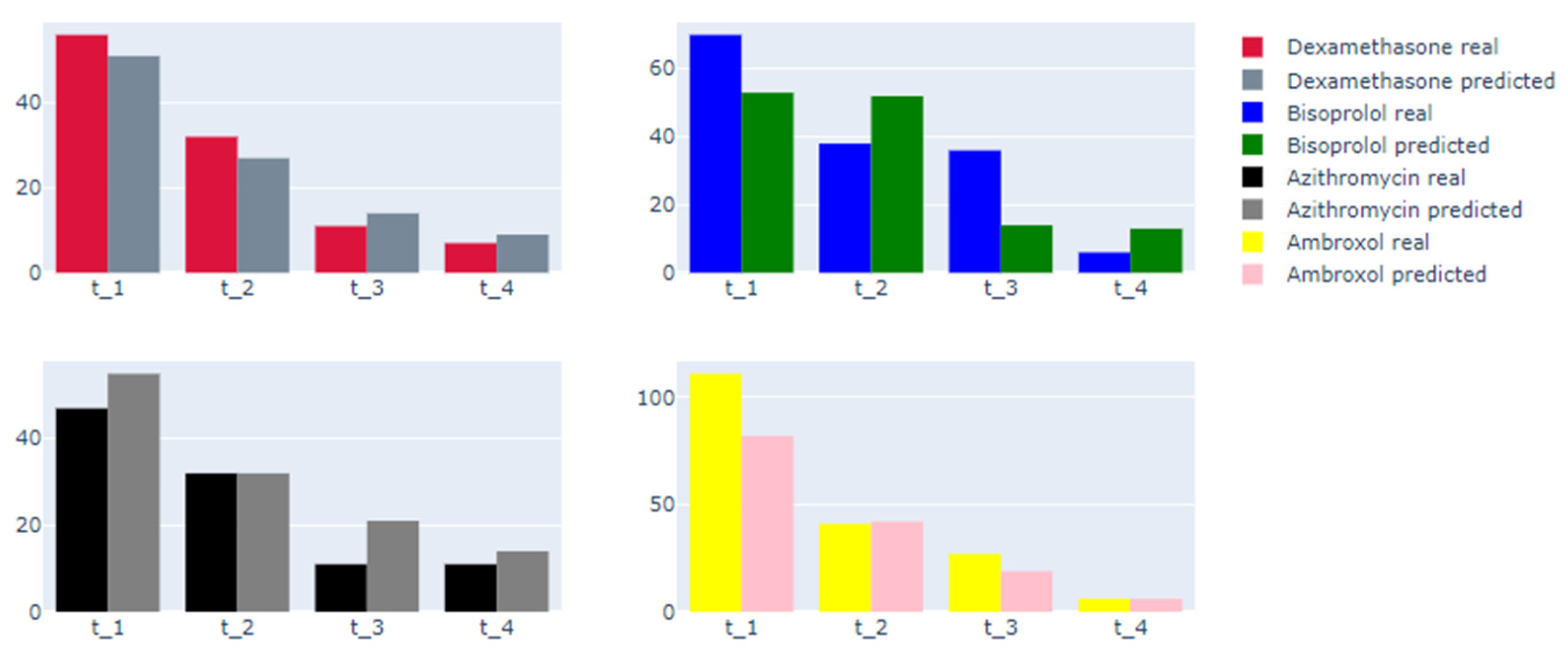
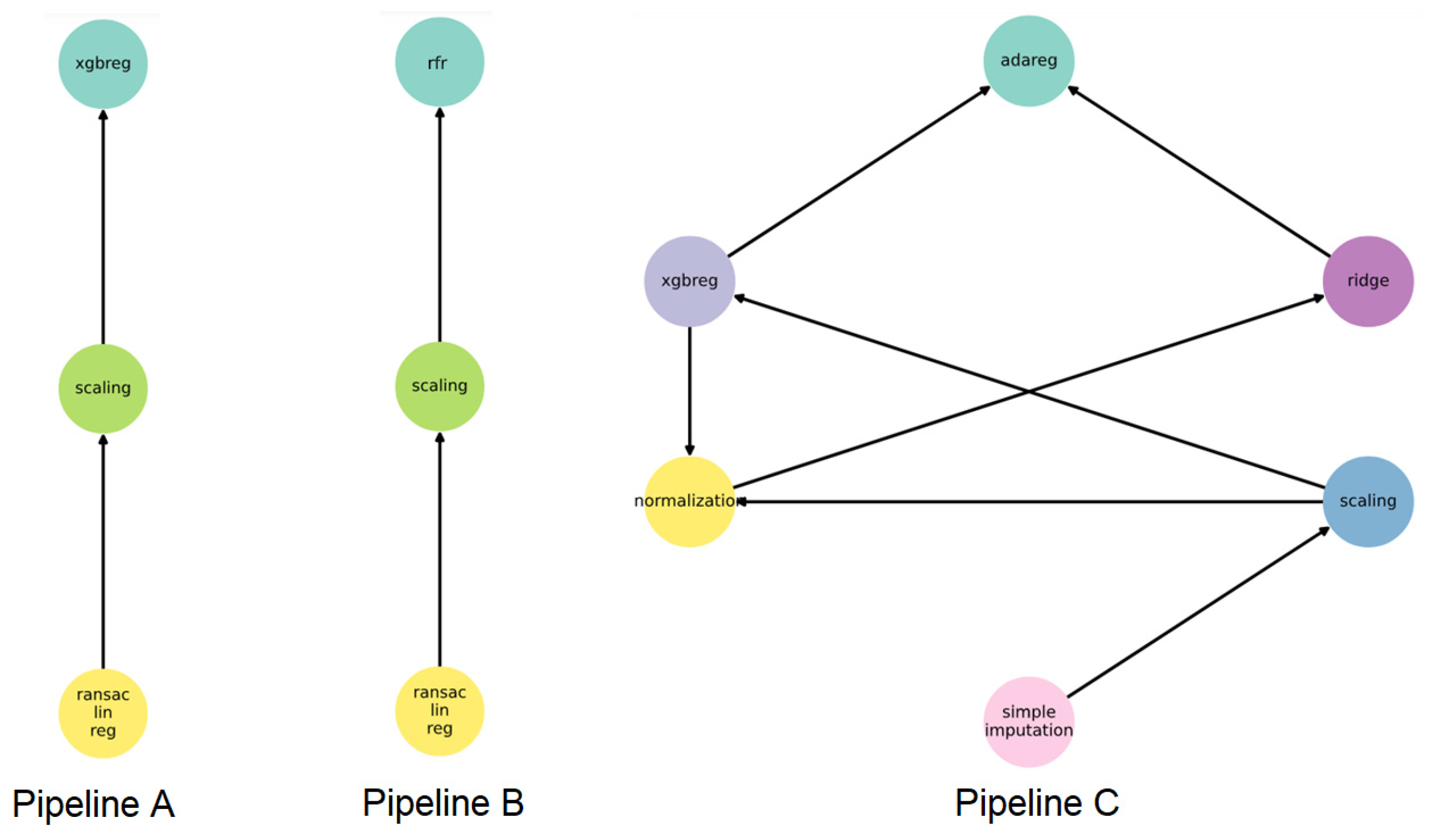
| Entry Criteria | Exclusion Criteria |
|---|---|
| 1. COVID-19-based pneumonia 2. Minimum length of stay is three days 3. Treatment outcomes include lethal outcome and hospital discharge 4. Treatment process was inpatient | 1. Observation period less than three days |
| Feature’s Group | Features |
|---|---|
| Anthropometrics parameters | Height, weight, gender, body mass index, body surface area. |
| Simple measurements | Systolic blood pressures (SBP), diastolic blood pressure; (DBP), heart rate, temperature, saturation (SPO2), respiratory rate. |
| Laboratory results | 101 indicators: different type of laboratory tests: venous and arterial blood tests, urine tests, cerebrospinal fluid tests, etc. |
| COVID-19 symptoms | Headache, unconsciousness, cough, sore throat, pus in the throat, feeling of congestion in the chest, type of breathing, weakness, decreased consciousness. |
| Results of diagnostic procedures | The presence of clinical manifestations of severe pneumonia, the percentage of lung tissue damage, the severity of the course, the patient’s condition, NEWS score, etc. |
| Vaccination | Flu, pneumonia, COVID-19 vaccination. |
| Complications | Multiple organ failure, septic shock, febrile fever, unstable hemodynamics. |
| COVID-19 therapy | Information of prescribed therapy for COVID-19 treatment drugs from clinical recommendations, including glucocorticosteroids, monoclonal antibodies, anticoagulants, antivirals, non-steroidal anti-inflammatory drugs and other drugs from current clinical recommendations. |
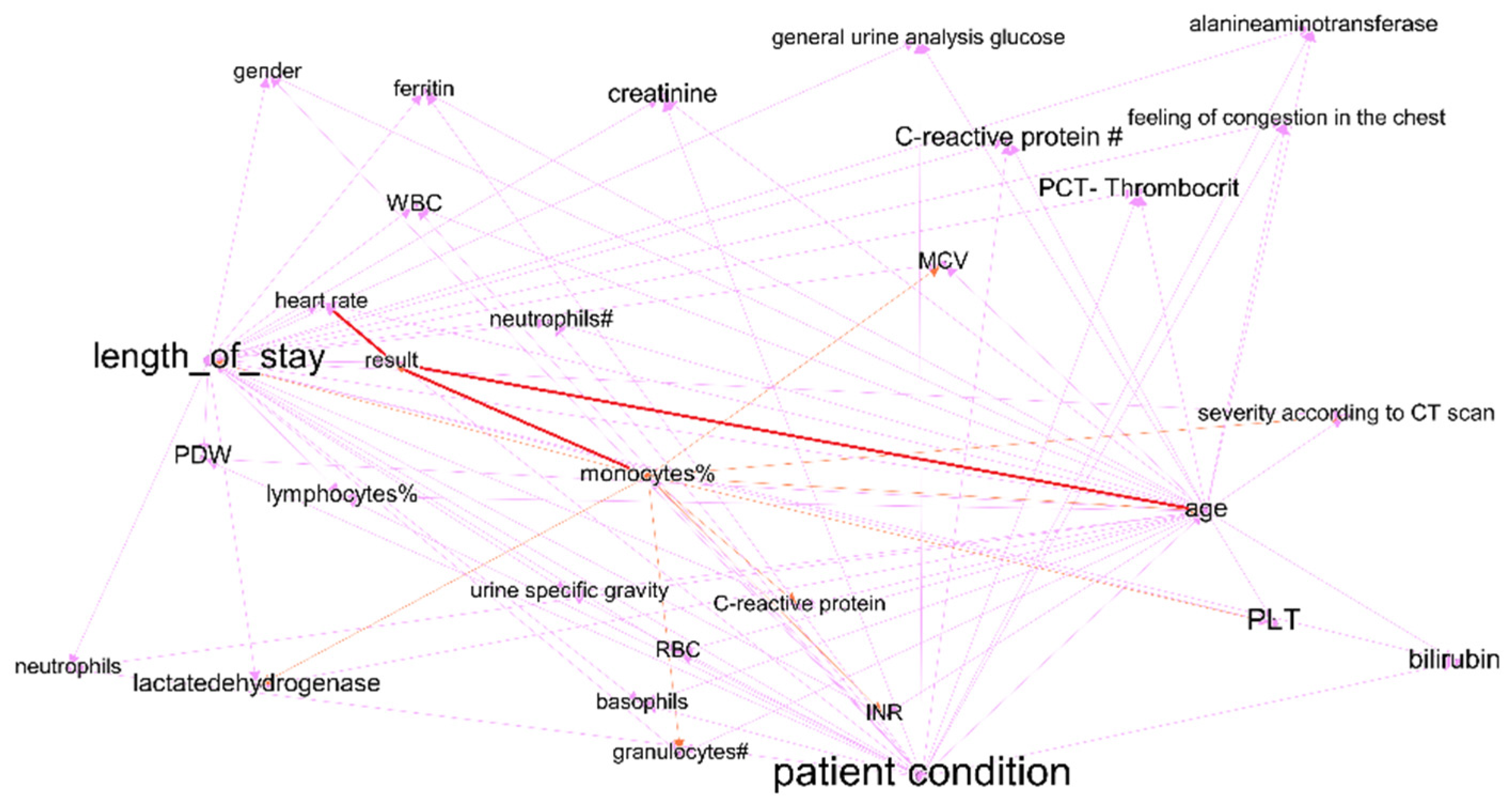
| Time Interval | Cluster | Description | Count of Nodes | Nodes with the Highest Power | Weighted Average Degree |
|---|---|---|---|---|---|
| First week of treatment | Purple | Includes predictors of treatment outcomes, and two outcome indicators—treatment outcomes and length of stay. | 21 | Duration of hospital stay (treatment outcome) | 19 |
| Fourth week of treatment | Purple | Includes predictors of treatment outcomes, and two outcome indicators—treatment results and length of stay. | 28 | Length of stay (treatment outcome) | 10 |
| First week of treatment | Orange | Some laboratory test results. Cluster does not include nodes with link to treatment outcomes. | 4 | PCT-plateletcrit | 8 |
| Fourth week of treatment | Orange | Some laboratory test results. Cluster includes nodes with link to treatment outcomes—monocyte% and saturation. | 18 | Saturation (link to treatment results) | 8 |
| First week of treatment | Green | C-reactive protein, RBC, basophils—indicators that have links to treatment outcomes (length of stay); however, they are not included in purple clusters. In the graph of the last period, this cluster joins with purple, part of indicators lose the link with treatment outcome. | 12 | C-reactive protein | 10 |
| First week of treatment | Blue | Patient condition and features that influence it—age, severity according to CT scan, bilirubin total, information of vaccination. In the fourth interval cluster, nodes transfer to purple cluster. | 7 | PLT | 15 |
| Outcome Feature | t0 | t1 | t2 | t3 |
|---|---|---|---|---|
| Treatment outcomes | Saturation | Lymphocytes [38] | Monocytes | Age |
| Treatment outcomes | Neutrophils [39] | Red blood cells [40] | Age | Patient condition |
| Length of stay | Feeling of congestion in the chest | Urea | MCV mean corpuscular volume [41] | C-reactive protein |
| Length of stay | PCT-plateletcrit | MCV mean corpuscular volume [41] | Alanineaminotransferase [39] | Lactatedehydrogenase [42] |
| Length of stay | Neutrophils | C-reactive protein [43] | C-reactive protein | PDW—platelet distribution width [44] |
| t0 | t1 | t2 | t3 | |
|---|---|---|---|---|
| Treatment outcomes—accuracy | 0.87 | 0.94 | 0.95 | 0.84 |
| Treatment outcomes—F1-score | 0.84 | 0.93 | 0.95 | 0.82 |
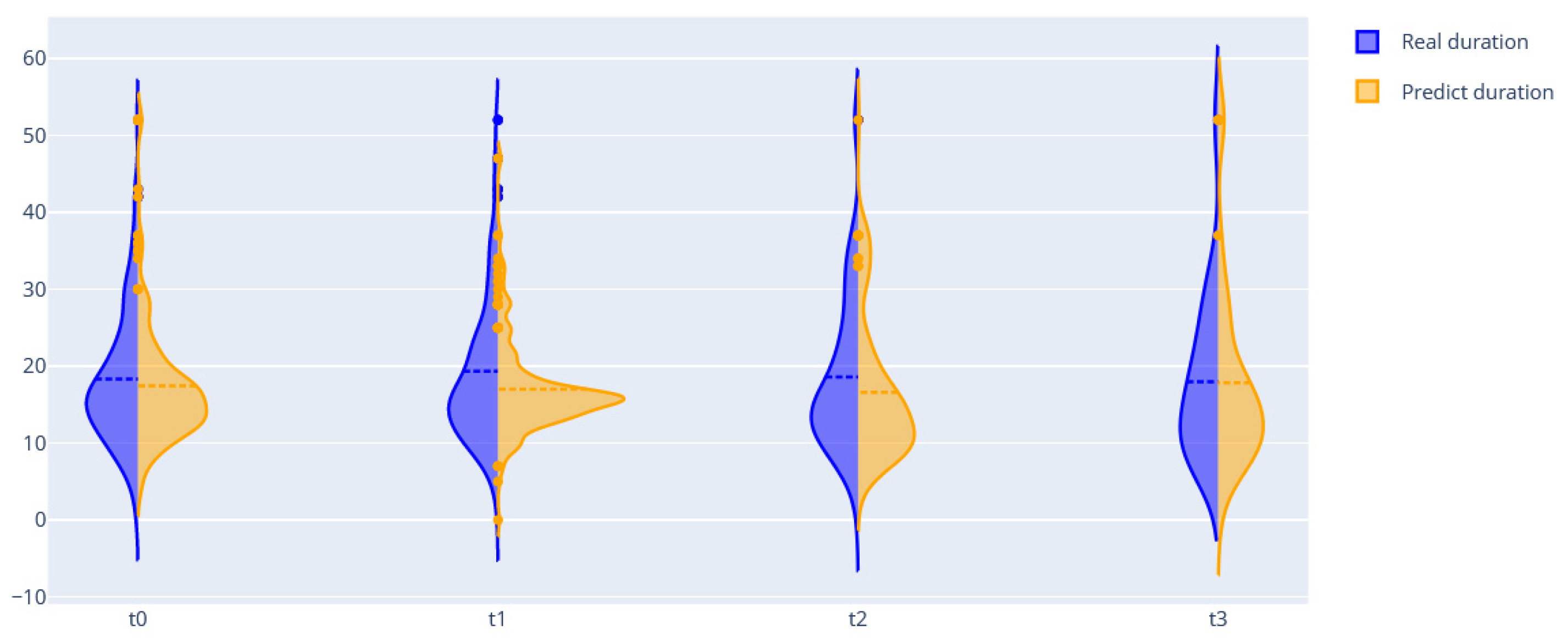
| Length of stay | 8.61 | 7.3 | 9.18 | 10.22 (needs improvement) |
| t-1 | t-2 | t-3 | t-4 | |
|---|---|---|---|---|
| F1-score—dexamethasone | 0.8421 | 0.8666 | 0.9 | 0.8333 |
| F1-score—ambroxol | 0.6516 | 0.6538 | 0.6136 | 0.998 |
| F1-score—azithromycin | 0.7481 | 0.8461 | 0.8421 | 0.4166 |
| F1-score—bisoprolol | 0.743 | 0.74 | 0.5133 | 0.909 |
| Methods | t-0 | t-1 | t-2 | t-3 |
|---|---|---|---|---|
| Set of ordinary BNs | 8.61 | 7.3 | 9.18 | 10.22 (8.12) |
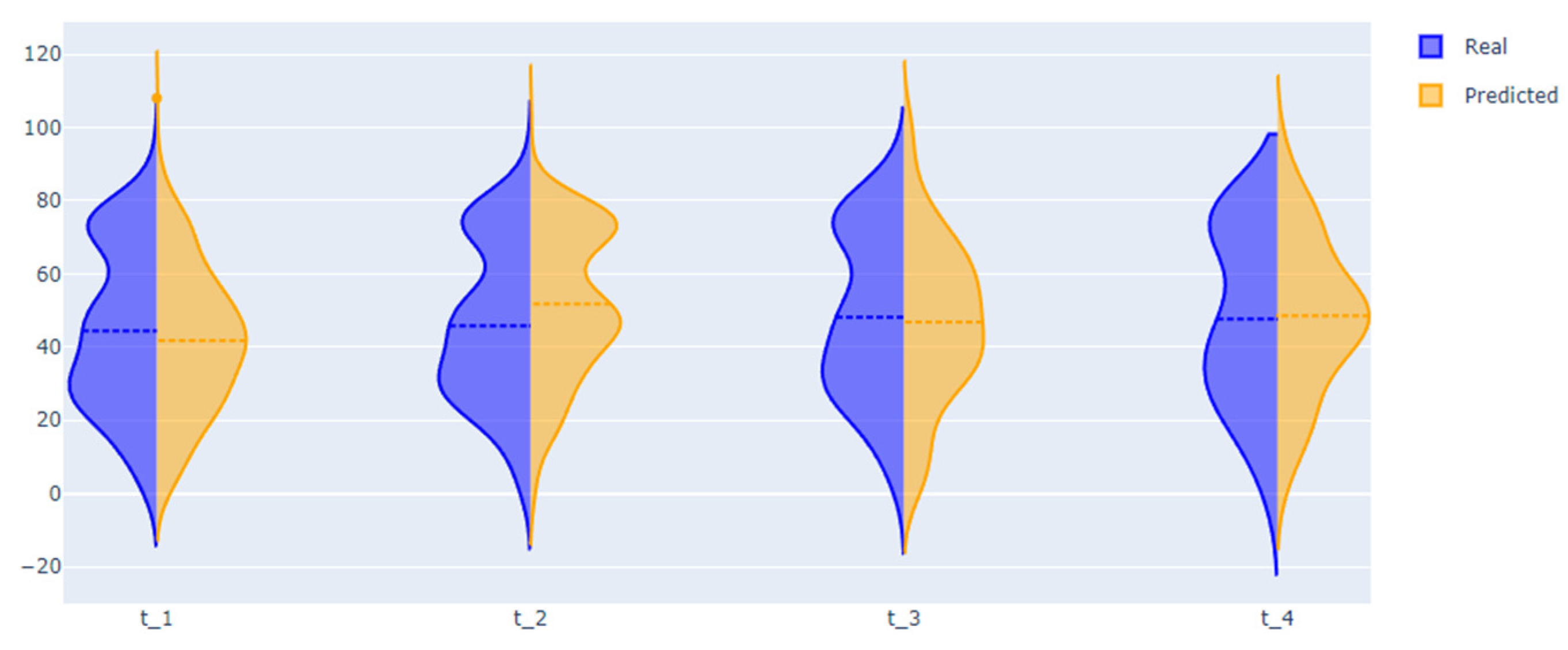
| FEDOT framework | 4.12 | 2.81 | 2.65 | 3.95 |
| FEDOT + DBN | 3.6 | 2.45 | 2.88 | 3.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derevitskii, I.V.; Mramorov, N.D.; Usoltsev, S.D.; Kovalchuk, S.V. Hybrid Bayesian Network-Based Modeling: COVID-19-Pneumonia Case. J. Pers. Med. 2022, 12, 1325. https://doi.org/10.3390/jpm12081325
Derevitskii IV, Mramorov ND, Usoltsev SD, Kovalchuk SV. Hybrid Bayesian Network-Based Modeling: COVID-19-Pneumonia Case. Journal of Personalized Medicine. 2022; 12(8):1325. https://doi.org/10.3390/jpm12081325
Chicago/Turabian StyleDerevitskii, Ilia Vladislavovich, Nikita Dmitrievich Mramorov, Simon Dmitrievich Usoltsev, and Sergey V. Kovalchuk. 2022. "Hybrid Bayesian Network-Based Modeling: COVID-19-Pneumonia Case" Journal of Personalized Medicine 12, no. 8: 1325. https://doi.org/10.3390/jpm12081325
APA StyleDerevitskii, I. V., Mramorov, N. D., Usoltsev, S. D., & Kovalchuk, S. V. (2022). Hybrid Bayesian Network-Based Modeling: COVID-19-Pneumonia Case. Journal of Personalized Medicine, 12(8), 1325. https://doi.org/10.3390/jpm12081325







