Abstract
Background/Objectives: Lung cancer is a leading cause of cancer-related mortalities, with early diagnosis crucial for survival. While biopsy is the gold standard, manual histopathological analysis is time-consuming. This research enhances lung cancer diagnosis through deep learning-based feature extraction, fusion, optimization, and classification for improved accuracy and efficiency. Methods: The study begins with image preprocessing using an adaptive fuzzy filter, followed by segmentation with a modified simple linear iterative clustering (SLIC) algorithm. The segmented images are input into deep learning architectures, specifically ResNet-50 (RN-50), ResNet-101 (RN-101), and ResNet-152 (RN-152), for feature extraction. The extracted features are fused using a deep-weighted averaging-based feature fusion (DWAFF) technique, producing ResNet-X (RN-X)-fused features. To further refine these features, particle swarm optimization (PSO) and red deer optimization (RDO) techniques are employed within the selective feature pooling layer. The optimized features are classified using various machine learning classifiers, including support vector machine (SVM), decision tree (DT), random forest (RF), K-nearest neighbor (KNN), SoftMax discriminant classifier (SDC), Bayesian linear discriminant analysis classifier (BLDC), and multilayer perceptron (MLP). A performance evaluation is performed using K-fold cross-validation with K values of 2, 4, 5, 8, and 10. Results: The proposed DWAFF technique, combined with feature selection using RDO and classification with MLP, achieved the highest classification accuracy of 98.68% when using K = 10 for cross-validation. The RN-X features demonstrated superior performance compared to individual ResNet variants, and the integration of segmentation and optimization significantly enhanced classification accuracy. Conclusions: The proposed methodology automates lung cancer classification using deep learning, feature fusion, optimization, and advanced classification techniques. Segmentation and feature selection enhance performance, improving diagnostic accuracy. Future work may explore further optimizations and hybrid models.
1. Introduction
Cancer is a complex set of diseases marked by uncontrolled growth and spread [1], unlike benign tumors, which remain localized, whereas malignant tumors invade and damage nearby tissues. Lung cancer is the leading type in men and the third in women, closely linked to smoking, and it is the primary contributor to cancer-associated mortality globally [2]. The WHO projected that cancer would become the top global cause of death by 2020 [3], with lung cancer alone causing around 1.80 million deaths. Projections indicate that, by 2035, lung cancer might contribute up to 60% of all cancer-related fatalities [4]. Early-stage cancers that are operable have a 5-year survival rate of approximately 34%, but for inoperable cases, the rate drops to under 10%. Lung cancer, which is predominantly classified into non-small-cell lung carcinoma (NSCLC) and small-cell lung carcinoma (SCLC) [5], shows varying characteristics. NSCLC, making up about 85% of cases, includes adenocarcinoma (ADC), squamous cell carcinoma (SCC), and large-cell carcinoma (LCC). The remaining 15% are SCLC cases.
Histopathological examination identifies lung cancer subtypes through biopsy reports [6], crucial for accurate diagnosis and effective treatment planning [7]. Computer-aided diagnosis (CAD) systems support pathologists by providing automated assessments to prevent misclassification [8]. Advances in artificial intelligence (AI) have enhanced both the precision and effectiveness of histopathological slide analysis. This study centers on categorizing lung cancer biopsy images into two distinct categories, adenocarcinoma and benign using deep learning frameworks.
Contribution of the Work
The major contribution of this research work can be summarized as follows:
- Histopathological images are preprocessed using an adaptive fuzzy filter and segmented using the modified SLIC algorithm.
- The segmented images are passed through deep learning models such as ResNet-50, ResNet-101, and ResNet-152 for feature extraction, followed by a proposed deep-weighted averaging feature fusion technique to generate RN-X features.
- The extracted features from the ResNet models and RN-X are put into a selective feature pooling layer, which leverages PSO and RDO optimization algorithms for feature selection.
- Finally, the classification layer implements the classifiers such as SVM, DT, RF, KNN, SDC, BLDC, and MLP, evaluated using K-fold cross-validation with K values of 2, 4, 5, 8, and 10.
This study is organized as follows: Section 2 provides a review of recent research on lung cancer detection. Section 3 presents the methodology. Section 4 details the proposed deep-weighted averaging feature fusion technique and discusses the selective feature pooling layer, incorporating PSO and RDO methods, along with the classification layer. Section 5 focuses on result comparisons. Finally, Section 6 highlights key findings and suggests directions for future research.
2. Review of Lung Cancer Detection
Over recent decades, various approaches have been proposed for the automated detection, segmentation, and classification of histopathological images using machine learning (ML) and deep learning (DL). Anthimopoulos et al. [9] developed a Convolutional Neural Network (CNN) with five convolutional layers using Leaky ReLU activation, average pooling, and three fully connected layers. Lizuka et al. [10] combined Inception v3 and an RNN to classify stomach and colon biopsies, incorporating regularization and augmentation for robustness. Wang et al. [11] used a CNN for lung cancer pathology, achieving 90.1% accuracy with Softmax activation. Gessert et al. [12] explored multiresolution EfficientNet for skin sore classification. Liu et al. [13] applied wavelet-based denoising to address noise in histopathological images, achieving 94.37% accuracy on the BreakHis dataset.
Zhou et al. [14] designed a hierarchical model using SVM and SURF features, achieving 91.14% accuracy, but performance at 400× magnification needed improvement. Wang et al. [15] introduced FE-BkCapsNet, combining CNNs with CapsNet and yielding up to 94.52% accuracy. Aresta et al. [16] used DenseNet121, achieving 87% accuracy on the BACH 2018 dataset. Spanhol et al. [17] combined CNN predictions, achieving 84% accuracy on BreakHis dataset at 200X magnification, while Filipczuk et al. [18] focused on nuclei segmentation and trained several classifiers using 25 shape and texture features.
Nada Mobarak et al. [19] created CoroNet, a CNN based on Xception, achieving 88.67% accuracy for breast cancer detection on the CBIS-DDSM dataset. Teresa et al. [20] applied CNN models to the Bioimaging 2015 dataset, segmenting images into 512 × 512-pixel patches and achieving up to 83.3% accuracy. Ahsan Rafiq et al. [21] proposed a three-CNN model for breast cancer classification, achieving 90.10% accuracy. Hameed et al. [22] fine-tuned Visual Geometry Group (VGG) models and used an ensemble approach, outperforming individual models. Wang et al. [23] achieved 96.19% accuracy using wavelet transforms and SVM with a genetic algorithm for feature selection.
3. Materials and Methods
This section offers an in-depth overview of the resources and methodologies employed in the classification of lung and colon cancers. The methodological framework of this study is illustrated in Figure 1.
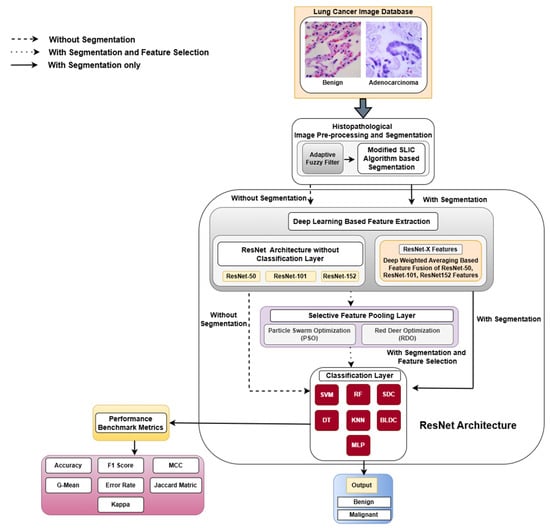
Figure 1.
Detailed workflow of the detection of lung cancer abnormalities. MCC—Matthews Correlation Coefficient.
3.1. Dataset Used
The LC25000 dataset, introduced in 2020 [24], contains 25,000 color images of five tissue types, expanded through augmentation from an original 1250 images of cancer. The images were resized to 768 × 768 pixels and verified for Health Insurance Portability and Accountability Act (HIPAA) compliance. This study focuses on 5000 benign and 5000 adenocarcinoma lung cancer images. Adenocarcinoma originates in glandular cells and often spreads to the alveoli. Benign tissues, while non-cancerous, typically require surgical removal and biopsy to confirm their nature.
3.2. Image Preprocessing
Histopathological image analysis is crucial for assessing tumor characteristics, clinical staging, and predicting patient survival [25]. However, these images face challenges such as complex geometric patterns and textures, critical textural features, image dimension and resolution variations, and color and noise issues. This study demonstrates that applying an adaptive fuzzy filter to resized images (224 × 224) enhances clarity by reducing noise and artifacts, resulting in more accurate diagnoses. The filtered images are then used for segmentation of the region of interest (ROI).
3.3. Modified SLIC Algorithm-Based Segmentation
A superpixel groups adjacent pixels that exhibit similar color, luminance, and texture properties to segment an image [26]. The SLIC algorithm allocates M initial seed points uniformly throughout the image. For an image with N pixels segmented into M superpixels, each superpixel contains N/M pixels. The separation between neighboring seed points is . The feature vector of the centroid is , combining the CIELAB color values and the pixel position . To enhance segmentation, the SLIC algorithm adjusts each centroid to the point with the minimal gradient in a 3 × 3 neighborhood. After initialization, it iteratively clusters pixels by assigning them to the nearest center and computing distances within a 2S × 2S neighborhood of each center. In the SLIC algorithm, the measure of proximity between a candidate pixel and the centroid of a cluster is expressed as
Here, denotes the centroid label, and denotes the pixel index in the 2S × 2S neighborhood. represents spatial similarity, represents color similarity, and is the total similarity with a lower signifying higher similarity. The parameter , where denotes the neighborhood size and indicates the compact factor balancing and , typically ranges from 1 to 40. This paper introduces a modified SLIC algorithm that simplifies calculations using a 3-dimensional feature vector consisting of spatial co-ordinates and grayscale feature (. The distance between a candidate pixel and the cluster centroid is revised as follows:
where denotes pixel similarity in grayscale values, and represents the overall similarity between the cluster centroid and the pixel co-ordinates. The algorithm of the modified SLIC superpixel segmentation is as follows.
Step 01: The microscopic color cell image is initially transformed into a grayscale format. It is then randomly split into segments. Given the grayscale probability distribution , and multiple thresholds (where ), the entropy for these segments can be expressed as follows:
The multiple thresholds for ideal classification for each segment adhere to the principle of maximum entropy, as follows:
These thresholds are determined using a conditional iteration algorithm.
Step 02: Using the optimal thresholds, the grayscale image is divided into intervals: , , and . Each interval is transformed into with a contrast-enhancing function, . The function is convex in and concave in , with turning point , where . is determined using the least squares principle:
To simplify image processing, grayscale transformation is modeled by the following function:
Here, . Varying generates different transformation curves. A higher improves gray equalization in the interval . By choosing appropriate and values, regional balance and contrast can be enhanced, leading to a more evenly adjusted and contrasted image.
Step 03: initialize clustering centers using grid superpixels with side length , and assign labels.
Step 04: move each center, , to the location with the minimum gradient within its 3 × 3 neighborhood.
Step 05: calculate the similarity distance, , from each pixel, , to within a radius, S, which matches the circular shape of the cell image.
Step 06: Set . If and is within range, update to , and assign the label to pixel .
Step 07: Repeat steps 4 to 6 until clustering converges. Recalculate each cluster’s mean grayscale and spatial features to update centers.
Step 08: merge isolated small superpixels using an adjacent merging strategy for improved fit and coherence.
Figure 2 shows the image progression from the (a) original to the (b) filtered image, followed by (c) original SLIC superpixel segmentation, (d) modified SLIC superpixel segmentation, and finally, the (e) modified SLIC segmentation result for the adenocarcinoma class (ACA).
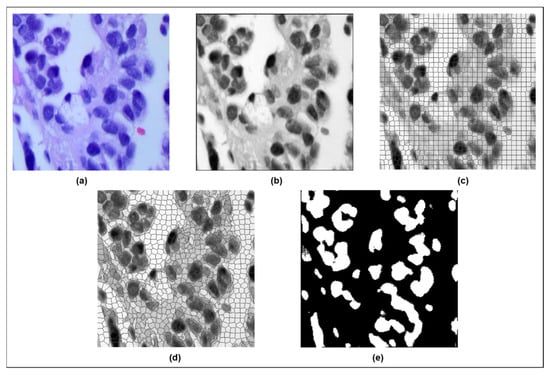
Figure 2.
(a) Original ACA image; (b) adaptive fuzzy filtered ACA image; (c) original SLIC superpixel segmentation; (d) modified SLIC superpixel segmentation; (e) modified SLIC segmentation result for the adenocarcinoma class (ACA).
4. Deep Learning Architecture
Deep learning networks are powerful but face challenges like saturation, accuracy degradation, and vanishing or exploding gradients. Architectures like ResNet-50 (RN-50), ResNet-101 (RN-101), and ResNet-152 (RN-152) address these issues using residual learning and identity mapping [27]. These architectures use shortcut connections that help mitigate the vanishing gradient problem and prevent overfitting [28]. The mapping function, as shown in Figure 3, is expressed as follows:
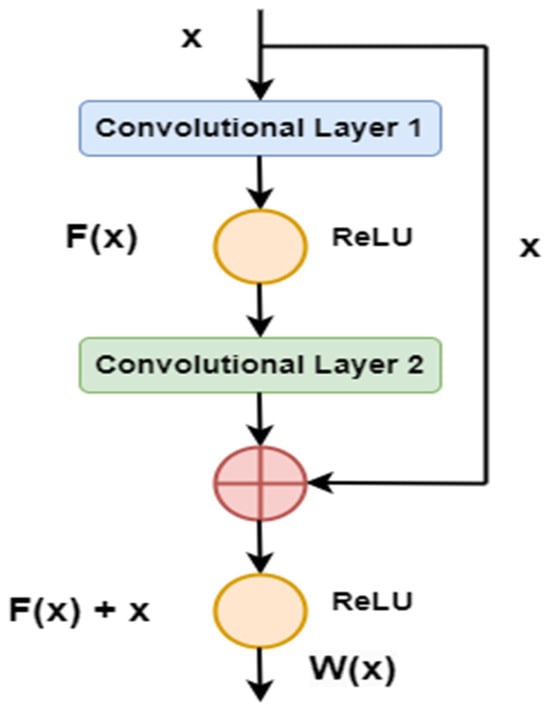
Figure 3.
Residual mapping function.
In Table 1, A, B, C, and D represent the number of blocks in the first, second, third, and fourth stages of the ResNet versions, respectively.

Table 1.
Residual blocks of ResNet versions.
The ResNet architecture configurations consist of different stages that are stacked across various ResNet versions, resulting in a 1D feature vector with 2048 elements for each image, as shown in Figure 4.
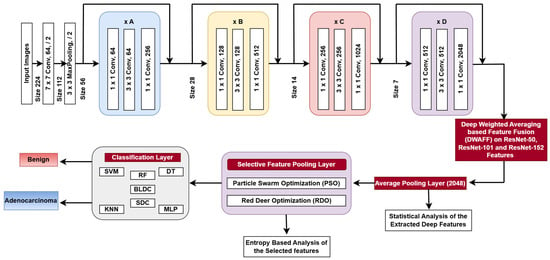
Figure 4.
Proposed ResNet-X architecture.
4.1. Proposed DWAFF Technique for ResNet-X Features
This study proposes a deep-weighted averaging-based feature fusion (DWAFF) technique. In this method, ResNet variants are evaluated, and weights are assigned to their feature vectors based on performance. By prioritizing contributions from each architecture, weights (ranging from 0 to 1) are adjusted in increments of 0.1 through trial and error. The final fused feature set for each image is computed using the weighted sum of the features as follows:
The optimal weight combination for feature fusion was determined using K-fold cross-validation on the dataset for each architecture—RN-50, RN-101, and RN-152—across various K values of 2, 4, 5, 8, and 10. Among these, ResNet 152 demonstrated the highest accuracy, followed by ResNet 101 and ResNet 50. The weight values for the architecture were chosen through a trial-and-error method, constrained to lie between 0 and 1, with their sum equal to 1. The best-performing combination was identified as 0.45 for RN-152 (), 0.35 for RN-101 (), and 0.20 for RN-50 (). These weights were subsequently applied to fuse features using Equation 11. Additionally, the mean value of the normal class is added to the normal features, and the mean value of the abnormal class, is added to the abnormal features, enhancing class separation and improving classification. The equation for generating DWAFF-based RN-X features is given by the following.
For normal cases,
For abnormal cases,
In this context, denotes the features extracted per image, represents the image index, for the normal class and for the abnormal class, and is the average of mean values from all three ResNet variants for normal images, while represents the same abnormal images. The Algorithm 1 for the proposed DWAFF technique for ResNet-X features is shown below.
| Algorithm 1. DWAFF Based Feature Fusion for ResNet-X Features | ||
| Step | Description | Details |
| Step 01 | Extract Features | Extract feature vectors for each image from ResNet-50, ResNet-101, and ResNet-152. Store the feature vectors: ResNet-50_feature [i, j], ResNet-101_feature [i, j], and ResNet-152_feature [i, j], where and . Perform K-fold Cross-Validation (K values are 2, 4, 5, 8, 10). Train the classifiers on the dataset set split. Evaluate performance of the classifiers for the different values of K using performance metrics. |
| Step 02 | Set Initial Weight Range | Initialize a range of possible weights, , and , based on the trial-and-error method, such that their sum must be equal to 1, based on the results obtained from K-fold cross-validation. |
| Step 03 | Identify Optimal Weights | For each weight combination, calculate the average performance across the K-folds. Select the weight combination that achieves the highest average performance. Optimal weights are identified as, 0.45 for ResNet-152 (), 0.35 for ResNet-101 (), and 0.20 for ResNet-50 (). |
| Step 04 | Compute Mean Values | Compute and , across all three ResNet variants. |
| Step 05 | Fuse Features for Final Feature Set | For normal cases (): fuse features of normal cases using Equation (12). For abnormal cases (): fuse features of abnormal cases using Equation (13). |
| Step 06 | Output Final Fused Features | The final fused feature set for both normal and abnormal cases, which are ResNet-X features, are used for subsequent classification tasks. |
Statistical Analysis
To enhance cancer classification accuracy with a reduced number of features, statistical measures play a crucial role in further analysis. The extracted features from ResNet-50, ResNet-101, ResNet-152, and the fused features from ResNet-X are analyzed by calculating statistical metrics such as the mean, variance, skewness, kurtosis, Pearson correlation coefficient (PCC), and canonical correlation analysis (CCA). These measures help assess how effectively the features capture lung cancer characteristics in both cancerous and non-cancerous data.
Table 2 presents the statistical parameters for the ResNet-50, ResNet-101, ResNet-152, and DWAFF-ResNet-X architectures for normal (N) and abnormal (ACA) cases. DWAFF-ResNet-X shows the best average performance with the highest mean values for both N (0.453891) and ACA (0.453709), outperforming the ResNet models, whose performance improves with depth. In terms of variance, DWAFF-ResNet-X has the lowest values (N: 0.380702; ACA: 0.444597), indicating more consistent performance compared to the higher variances in ResNet models, especially in ACA. For skewness, DWAFF-ResNet-X (N: 3.767961; ACA: 4.486885) shows a more symmetrical performance distribution, whereas ResNet models have higher skewness, indicating more inconsistent results. Kurtosis is also lower for DWAFF-ResNet-X (N: 21.14865; ACA: 33.4781), reflecting fewer extreme outliers than ResNet models, which have higher kurtosis values. PCC is highest in DWAFF-ResNet-X (N: 0.938638; ACA: 0.944338), indicating stronger alignment between predictions and outcomes compared to ResNet models. CCA also improves with model depth, with DWAFF-ResNet-X showing the highest CCA for ACA (0.8816). The dice coefficient values indicate the performance of the models in segmentation tasks. ResNet-50 shows moderate performance, with slightly better accuracy for normal cases. ResNet-101 outperforms ResNet-50, especially for normal cases. ResNet-152 demonstrates significant improvement, achieving higher accuracy for both normal and abnormal cases. DWAFF-ResNet-X delivers the best performance, with the highest dice coefficients for both normal and abnormal cases, making it the most effective model.

Table 2.
Statistical parameters of extracted deep features and fused features of benign and malignant data.
Figure 5 is the scatter plot matrix, which provides insights into feature relationships across different models, including ResNet-50, ResNet-101, ResNet-152, and the proposed RN-X method. ResNet-50 (RN-50-N and RN-50-ACA) exhibits a relatively compact feature distribution, indicating limited complexity in extracted features. ResNet-101 (RN-101-N and RN-101-ACA) shows a broader spread, capturing more diverse patterns compared to RN-50. ResNet-152 (RN-152-N and RN-152-ACA) further expands the feature space, suggesting that deeper network layers extract more complex and discriminative information. However, the proposed RN-X method (RN-X-N and RN-X-ACA) demonstrates a distinct feature distribution, influenced by deep-weighted averaging-based feature fusion (DWAFF). The ACA-based versions of all models (RN-50-ACA, RN-101-ACA, RN-152-ACA, and RN-X-ACA) introduce additional refinement, enhancing feature discrimination. Notably, RN-X-ACA exhibits the most unique distribution, reinforcing the effectiveness of feature fusion and optimization techniques in improving classification performance compared to standalone ResNet architectures.
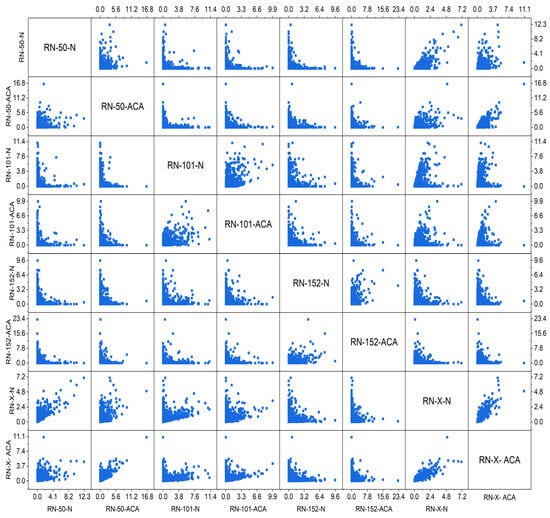
Figure 5.
Scatterplot matrix of ResNet-50, ResNet-101, ResNet-152, and ResNet-X for Cancerous and Non-Cancerous Data.
The violin plot in Figure 6 provides a detailed visualization of the feature distributions extracted by different ResNet models—ResNet-50, ResNet-101, ResNet-152, and the proposed ResNet-X—across normal (N) and abnormal (ACA) classes. ResNet-50 exhibits minimal variation with significant overlap between classes, indicating poor feature separability. ResNet-101 shows increased variation but still struggles with class differentiation due to substantial overlap. ResNet-152 presents more distinct distributions with reduced overlap, demonstrating improved feature extraction capabilities. In contrast, ResNet-X displays the widest distributions and the most pronounced class separation, suggesting superior feature discrimination. The progressive improvement from ResNet-50 to ResNet-X highlights the effectiveness of deeper architectures and feature fusion in enhancing classification performance for lung cancer diagnosis.
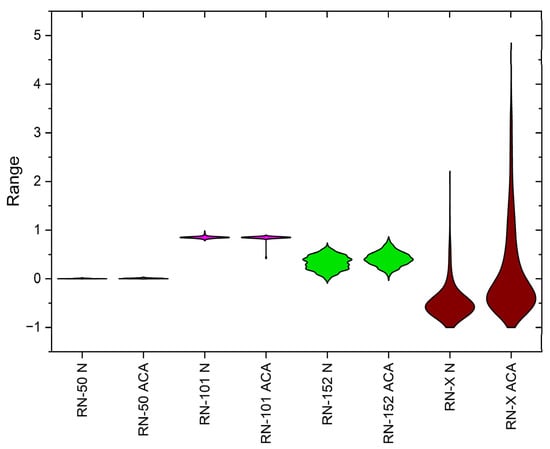
Figure 6.
Violin plot of class distributions from deep features extracted via ResNet variants and DWAFF-RN-X fused features.
4.2. Selective Feature Pooling Layer
The selective feature pooling layer is designed to condense the features of histopathological images into compact feature vectors, enhancing classifier performance and promoting high generalization capability. In lung cancer diagnosis [29], these techniques enhance accuracy using bio-inspired optimization algorithms like PSO and RDO.
4.2.1. Particle Swarm Optimization (PSO)
Particle swarm optimization (PSO), first proposed by Kennedy and Eberhart in 1995, mimics bird flock behavior to optimize problems. It begins by initializing particles and defining essential parameters [30]. The Algorithm 2 for the PSO as a Feature Selection with particle position and velocity updates is given below.
| Algorithm 2. Particle Swarm Optimization (PSO) as a Feature Selection | |||
| Step | Description | Details | |
| Step 01 | Initialization | - Maximum iteration count: - Inertia weight range: (, ) - Acceleration coefficients: c1, c2 - Set the position of each particle randomly: | |
| (14) | |||
| - Set the velocity of each particle randomly: | |||
| (15) | |||
| - Initialize the best position for an individual particle as and = the best of all . | |||
| Step 02 | Iteration Loop | for k = 0 to kmax − 1 do: for i = 1 to n do: Calculate the inertia weight: | |
| (16) | |||
| Update the velocity: | |||
| (17) | |||
| Update the position: | |||
| (18) | |||
| Update if the new position surpasses the previous Update if the new surpasses the current | |||
| Step 03 | Output | Output the final as the optimal solution. | |
In this study, the following parameter values are selected through an iterative process of experimentation and refinement: Inertia weight (wi)—between 0.45 and 0.9, maximum number of iterations—between 100 and 1000, random values (r1 and r2)—set to 0.85, cognitive component (c1) and social component (c2)—between 1.0 and 2.0.
4.2.2. Red Deer Optimization (RDO)
Red Deer Optimization (RDA), introduced in 2016 [31], emulates the courtship rituals of Scottish red deer. The algorithm starts with an initial population of “red deer” (RDs). The best RDs, called “RD males”, are split into “commanders” and “stags”, based on their initial performance. Commanders and stags compete for harems, with successful stags potentially becoming commanders. Commanders pair with hinds in their harems and others, while stags mate with nearby hinds. This process blends exploration and exploitation, generating new solutions and allowing weaker solutions to evolve. In terms of dimensionality reduction, RDA uses this evolutionary process to refine and optimize the solution space by iteratively improving and filtering candidate solutions. The Algorithm 3 for the Red Deer Optimization (RDO) as a Feature Selection is as follows.
| Algorithm 3. Red Deer Optimization (RDO) as a Feature Selection | |||
| Step | Description | Details | |
| Step 01 | Initial Population | - Define the solution space with dimensions: | |
| (19) | |||
| Here, represents the array size, set to 50. Each component corresponds to a vector of values for each of the 50 images, as defined by the equation below: - Initialize a random population of red deer (RDs). | |||
| Step 02 | Roaring Stage | - For each male RD: -- Calculate the new position based on fitness function (FF) value using | |
| (20) | |||
| Here, UL and LL represent the maximum and minimum boundaries of the search region, respectively. The factors a1, a2 and a3 are randomly selected from a uniform distribution between zero and one. -- Update the RD position and evaluate its fitness. -- Promote successful RDs to commander status if they show improved fitness. | |||
| Step 03 | Competition Stage | - Each commander competes with random stags: -- Compute new positions: | |
| (21) | |||
| (22) | |||
| Here and are the random numbers between 0 and 1 by uniform distribution function. -- Select the position with the best fitness function (FF) to update the commander status. | |||
| Step 04 | Harem Creation Phase | - For harems with -- A commander and several hinds based on the commander’s fitness. -- Calculate the number of hinds as: | |
| (23) | |||
| -- Stags do not participate in harems. | |||
| Step 05 | Mating Phase | - Commander Mating Within Harems: Each commander mates with a proportion () of its hinds - Commander Expansion Beyond Harems: Commanders mate with a percentage () of hinds from other harems. The parameter () ranges from 0 to 1. - Stag Mating: Stags mate with the closest hind. | |
| Step 06 | Offspring Creation | - Generate new offspring using: | |
| (24) | |||
| where is the new offspring RD, c is randomly chosen between 0 and 1. For -Stage mating, replace Com with Stag. | |||
| Step 07 | Next-Generation Solution | - Retain a percentage of the best male RDs. - Select hinds and offspring for the next generation using fitness-based methods. | |
| Step 08 | Stopping Criterion | - RDO’s stopping criteria include the following: 1. Fixed number of iterations. 2. Achievement of a quality threshold. 3. Exceeding a time limit. | |
The parameters of the RDO algorithm are described in the following table, Table 3.

Table 3.
Parameters of RDO.
4.2.3. Entropy-Based on Statistical Analysis
In biomedical applications, entropy has emerged as a widely used approach. When applied to feature selection, entropy-based techniques assess the relevance and significance of selected features by quantifying the amount of information each feature contributes to predicting the target variable. In this study, the selected features from the normal and abnormal classes are evaluated using Shannon Entropy and Fuzzy Entropy.
Approximate Entropy
Approximate Entropy is a statistical method for measuring the regularity and unpredictability of variations in time-series data [32]. It calculates the difference between the natural logarithms of repeating patterns of length n and n + 1 using the following formula:
Here, is the input feature length, and is the mean of all ranges. is given as
In the input vector of length , represents the number of features. A higher approximate entropy value indicates that the input feature vectors are more complex and less predictable.
Shannon Entropy
The Shannon Entropy of a random variable, S, containing values is determined by
Here, represents the probability function. If the entropy score is high, it means that the outcome is hard to predict because it is uncertain.
Fuzzy Entropy
Fuzzy Entropy, a statistical method used to quantify the uniformity of input feature vectors [33], is defined by the following formula:
Here, , and represents the membership value of the fuzzy set, and M is the total number of data points.
Table 4 compares the feature selection methods PSO and RDO in terms of entropy-based statistical parameters such as approximate entropy, Shannon entropy, and fuzzy entropy. Approximate entropy measures the regularity and predictability of time-series data. PSO, with lower approximate entropy values (1.2385 for N and 1.7816 for ACA) compared to RDO (2.0123 for N and 2.4893 for ACA), indicates more regularity and less complexity. RDO, with higher values, suggests greater variability and less predictability, possibly capturing more nuanced features. Shannon entropy reflects uncertainty or information content. RDO’s higher values (5.0821 for N and 5.8982 for ACA) show greater complexity and feature diversity compared to PSO’s lower values (3.8523 for N and 4.9891 for ACA), which suggest more structured data but less feature variety. Fuzzy entropy, which measures complexity in a fuzzy system, is higher for RDO (0.7283 for N and 0.9182 for ACA), indicating more ambiguity in feature relationships. PSO’s lower values (0.4862 for N and 0.5231 for ACA) suggest clearer, better-defined relationships with less uncertainty.

Table 4.
Entropy-based statistical measures for PSO and RDO DR techniques.
Table 5 compares the choice of hyperparameters of ResNet-50, ResNet-101, ResNet-152, and the proposed DWAFF method. All models use the Adam optimizer with increasing momentum values from 0.8 in ResNet-50 to 0.95 in DWAFF. The initial learning rate decreases progressively from 0.05 in ResNet-50 to 0.001 in DWAFF, with each model employing a different learning rate decay schedule. The learning rate is reduced by a factor of 10 at specified epochs, with ResNet-50 decaying every 4 epochs, ResNet-101 every 6, ResNet-152 every 8, and DWAFF every 10. Weight decay also decreases from 0.0005 in ResNet-50 to 0.00005 in DWAFF. All models maintain a batch size of 128. While the ResNet models utilize global average pooling, DWAFF incorporates a novel feature fusion approach. Each model is trained for 16 epochs, with a progressively decreasing learning rate schedule, where DWAFF exhibits a more gradual decay compared to the ResNet variants.

Table 5.
Hyperparameters of ResNet Architectures with DWAFF Method.
4.3. Classification Layer
Classifiers are essential for categorizing data, aiming for high accuracy and minimal errors while balancing computational complexity. This study utilized the following classifiers in the classification layer part of the ResNet architectures.
4.3.1. Support Vector Machine (SVM)
SVM is a set of supervised learning methods utilized for categorization, prediction, and anomaly detection due to its scalability and high performance [34]. Linear SVMs use a maximum-margin hyperplane (either hard or soft margin), while non-linear SVMs apply kernel functions for classification. The hyperplane is determined by
It is subject to Here, is the vector that is perpendicular to the hyperplane, is a data point, is a scalar, and are slack variables penalizing misclassifications. The decision function is . Various kernels such as linear, polynomial, RBF, and sigmoid are used in SVMs. This study uses the SVM-RBF kernel to enhance classification accuracy.
4.3.2. Decision Tree (DT)
A decision tree (DT) is a flexible algorithm for categorization and regression, using a tree structure with decision nodes based on features and leaf nodes for outcomes [34]. Starting at the root, the tree is traversed to make predictions. Nodes split data by feature and threshold, while leaf nodes provide final predictions. Key metrics for node impurity include the following:
where represents the feature, denotes the collection of instances at the node, and is the subset of instances with feature has the value . Gini impurity is given as follows:
where is the frequency of class k, and is the number of classes. The objective is to find the feature and threshold that minimize impurity, with the optimal split S given by the following:
Here, the values of and maximize the above expression, and denotes the impurity of the current node and subset , denoted the proportion of samples in subset relative to the total samples.
4.3.3. Random Forest (RF)
The random forest algorithm excels in image classification due to its accuracy and robustness [35]. It uses multiple independent decision trees, with key parameters including the number of trees and features considered by each tree. The final prediction is made by combining the decision from all trees with the following formula:
where is the final prediction, D is the number of trees, is the prediction from the tree, and is the class label.
4.3.4. K-Nearest Neighbor (KNN)
The KNN algorithm determines the category of a data point by comparing its distance to the K closest points in the training data and assigns it to the class that appears most frequently among these neighboring points. It requires no separate training phase and uses the entire dataset for classification. In weighted KNN, neighbors are weighted inversely to their distance from the query point [36]. The distance between two points and is calculated as follows:
In weighted KNN, is given by , with a small constant added to avoid division by zero. The classification of a query point is determined by the most common class among its K closest neighbors,
Here represents the set of K nearest neighbors, is the class label of neighbor , and is the indicator function. This study uses k = 5 with mixed Euclidean distance to improve classification accuracy by weighing closer neighbors more heavily.
4.3.5. Softmax Discriminant Classifier (SDC)
The SDC identifies and verifies the class of a test sample [37] by measuring its distance to training samples within each class. Given a training set, , where contains samples from class q, with . The samples used for testing are presumed to be , and then SDC is defined as
where measures the distinction between the test sample and class j. A penalty cost, λ > 0, is applied. If v and vn are similar, and y belongs to class i, is close to zero, making approach its maximum value.
4.3.6. Multi-Layer Perceptron (MLP)
Multilayer perceptron’s (MLPs) are used for function approximation tasks like regression [38]. The MLP structure consists of an input layer with n nodes, an intermediate layer, and an output layer. Input–output pairs are denoted as , where is the input vector, and is the target output; the output of the k-th hidden node is computed as follows:
The final output is given by
where represents the number of hidden units, θ denotes the bias at the output layer, and represents the weight connecting the k-th hidden unit to the output layer. This configuration results in (n + 2) j + 1 connections. The cost function for training the MLP is
In this study, a three-layer architecture was utilized, recognized for its effectiveness in approximating continuous functions [39].
4.3.7. BLDC
The Bayesian Linear Discriminant Classifier (BLDC) employs the Fisher linear discriminant alongside Bayes decision rule to reduce the probability of classification errors [40], effectively regularizing high-dimensional signals and enhancing computational efficiency. In Bayesian regression, the target a is defined as follows:
where q is the weight vector, and n is white Gaussian noise. The weighted likelihood function is
Here, is the target value, is the matrix of training feature vectors, and D combines and . is the inverse noise variance, and is the number of training samples. The prior distribution is given by
where N is the feature size, and denotes the (N+1) dimensional regularization diagonal matrix, represented as follows:
The posterior distribution of s is
This posterior distribution is Gaussian with covariance matrix H and mean vector U:
For the predictive variation of , the distribution on the regression target is
This predictive distribution is also Gaussian with mean and variance, as follows:
5. Results and Discussion
This study used deep learning-based feature extraction and feature fusion techniques, along with feature selection using PSO and RDO, to categorize histopathological images of lung cancer on a Windows 11 workstation with an AMD Ryzen 7 5700 G processor and integrated Radeon Graphics of 1 TB, running MATLAB 2018a.
5.1. Training and Testing of the Classifiers
In this study, K-fold cross-validation was used for classification. For instance, with K = 10, the dataset was divided into 10 equal segments, where each segment was used once as the test set and the remaining nine as the training set. Performance metrics were averaged across iterations. Different K values, such as 2, 4, 5, 8, and 10, were evaluated. The training data were partitioned into smaller batches, and classifiers such as SVM, DT, RF, KNN, and BLDC were trained iteratively on these smaller batches, while MLP and SDC were trained directly over epochs. After each epoch, performance was evaluated on both training and validation sets, and accuracy was recorded. Finally, the training and validation accuracies were plotted to visualize performance over epochs. Training stopped after a maximum of 15 epochs or when accuracy levels suggested potential overfitting. Testing ended once all batches were processed. Higher accuracy and lower error rates indicate better classifier performance. Table 6 lists the parameters selected for various classifiers, chosen through trial and error, with a maximum of 15 epochs to prevent overfitting.

Table 6.
Selection of optimal parameters for the classifiers.
5.2. Standard Benchmark Metrics of the Classifiers
In this study, several transfer learning models were assessed using a confusion matrix. The evaluation process involved using 90% of the input features for training and setting aside 10% for testing. In the context of lung cancer detection, the clinical scenarios related to the confusion matrix were defined as follows: true positive (TP), correctly identifying a patient’s tumor as benign. True negative (TN): correctly identifying a patient as having adenocarcinoma. False positive (FP): incorrectly classifying a patient’s adenocarcinoma as benign. False negative (FN): misclassifying a patient’s benign tumor as adenocarcinoma. The performance of the classifiers is evaluated using metrics such as accuracy, error rate, F1 score, Matthews correlation coefficient (MCC), Jaccard index, G-mean, and kappa. The mathematical formulations for these metrics are detailed in Table 7.

Table 7.
Performance metrics of the classifiers with their significance.
5.3. Performance Analysis of the Classifiers in Terms of Accuracy for Different K Values
In this study, the performance of seven classifiers—SVM, KNN, random forest, decision tree, softmax discriminant, MLP, and BLDC—was evaluated for cancer image classification across K values of 2, 4, 5, 8, and 10.
In the first scenario, without segmentation, as shown in Figure 7, the ResNet-X based feature fusion technique, combined with an MLP model, achieved an accuracy of 58.610% at K = 2 and 63.150% at K = 4. The ResNet-50-based feature extraction with the MLP model reached its highest accuracy of 65.230% at K = 5, while the ResNet-152-based feature extraction with the MLP model attained a peak accuracy of 68.783% at K = 8. Additionally, the ResNet-X based feature fusion technique combined with the MLP model achieved a top accuracy of 69.610% at K = 10.
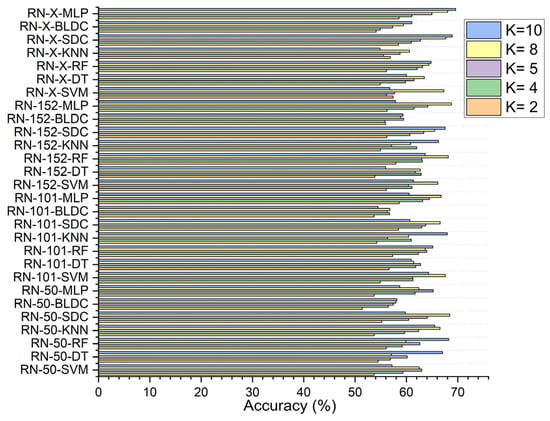
Figure 7.
Classifier performance in accuracy for K = 2, 4, 5, 8, 10—without segmentation.
In the second scenario, with segmentation as shown in Figure 8, ResNet-152-based feature extraction combined with the MLP model achieved 66.920% accuracy at K = 2 and 74.380% at K = 5. The ResNet-101 based feature extraction with the MLP reached 72.910% at K = 4, while the ResNet-50 based feature extraction with the MLP peaked at 83.730% at K = 8. Additionally, the ResNet-X based feature fusion technique combined with the MLP attained a top accuracy of 86.460% at K = 10.
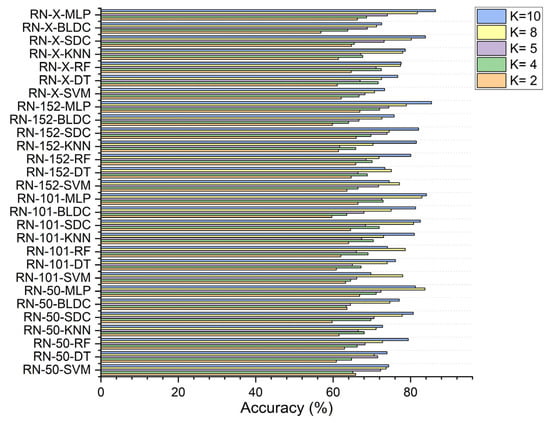
Figure 8.
Classifier performance in accuracy for K = 2, 4, 5, 8, 10—with segmentation.
In the third scenario, with segmentation and feature selection, applying PSO for feature selection resulted in a ResNet-50-based feature extraction with the MLP achieving 72.250% accuracy at K = 2. The ResNet-152-based feature extraction with the MLP attained 76.432% at K = 4, 79.490% at K = 5, and 93.508% at K = 8, while the ResNet-X-based feature fusion technique combined with the MLP reached 96.490% at K = 10, as shown in Figure 9.
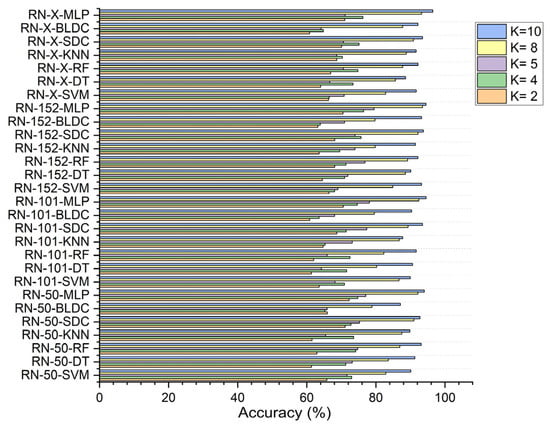
Figure 9.
Classifier performance in accuracy for K = 2, 4, 5, 8, 10—with segmentation and PSO feature selection.
Using RDO for feature selection, the ResNet-50 based feature extraction with the MLP achieved 77.980% accuracy at K = 2. The ResNet-152-based feature extraction with the MLP reached 87.240% at K = 5, while the ResNet-X based feature fusion technique combined with the MLP recorded 82.810% at K = 4, 94.531% at K = 8, and 98.680% at K = 10, as shown in Figure 10.
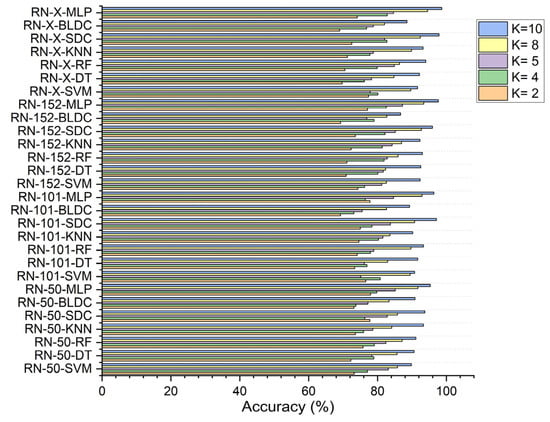
Figure 10.
Classifier performance in accuracy for K = 2, 4, 5, 8, 10—with segmentation and RDO feature selection.
Across all scenarios, ResNet-X-based feature fusion technique combined with the MLP consistently achieved the highest accuracy, demonstrating its effective deep-weighted averaging feature fusion capabilities.
5.4. Performance Analysis of Classifiers for K = 10
Without segmentation, the ResNet-X-based feature fusion technique combined with MLP classifiers achieved the highest performance, with an accuracy of 69.610%, an F1 score of 73.184%, a Jaccard index of 57.709%, a G-Mean of 68.321%, and an error rate of 30.390%. In contrast, the ResNet-101-based feature extraction with BLDC classifiers had the lowest accuracy at 54.450%, an F1 score of 54.345%, a Jaccard index of 37.310%, a G-mean of 54.449%, and a high error rate of 45.550%, as shown in Figure 11.
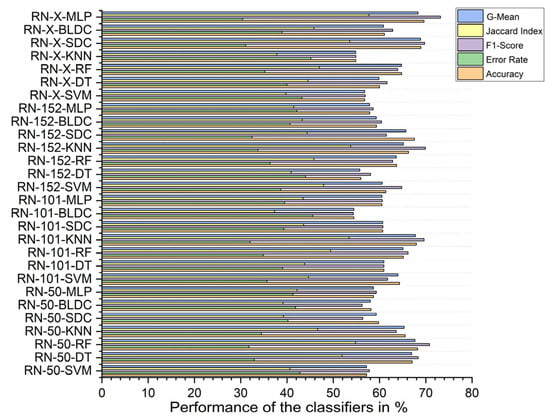
Figure 11.
Classifier performance when K = 10—without segmentation.
With segmentation, as shown in Figure 12, the ResNet-X-based feature fusion technique with MLP classifiers performed best, achieving 86.460% accuracy, an F1 score of 86.317%, a Jaccard index of 75.928%, a G-mean of 86.453%, and an error rate of 13.540%. On the other hand, the ResNet-101-based feature extraction combined with SVM classifiers achieved the lowest performance, with 69.760% accuracy, an F1 score of 66.622%, a Jaccard index of 49.950%, a G-mean of 69.123%, and an error rate of 30.240%.
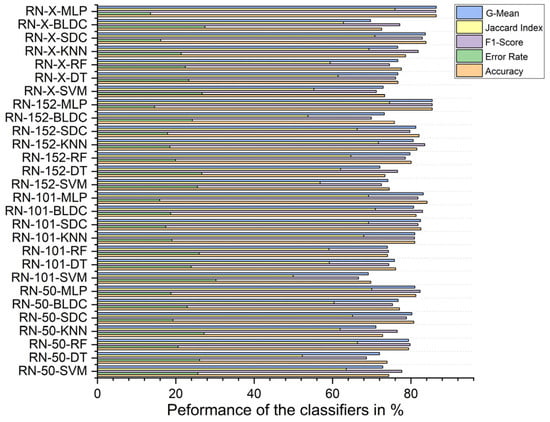
Figure 12.
Classifier performance when K = 10—with segmentation.
Using PSO feature selection, the ResNet-X-based feature fusion technique combined with MLP classifiers achieved the highest accuracy at 96.490%, with an F1 score of 96.476%, a Jaccard index of 93.192%, a G-mean of 96.489%, and an error rate of 3.510%. In contrast, the ResNet-50-based feature extraction with BLDC classifiers achieved the lowest accuracy at 87.100%, an F1 score of 86.483%, a Jaccard index of 76.186%, a G-mean of 86.980%, and an error rate of 12.900%, as shown in Figure 13 below.
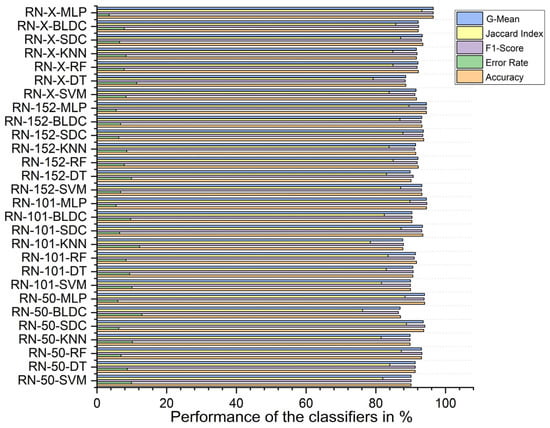
Figure 13.
Classifier performance when K = 10—with segmentation and PSO feature selection.
Using RDO feature selection, the ResNet-X-based feature fusion technique with MLP classifiers again achieved the highest performance, with 98.680% accuracy, an F1 score of 98.669%, a Jaccard index of 97.347%, a G-mean of 98.677%, and an error rate of 1.320%. The lowest accuracy was recorded for the ResNet-152-based feature extraction with BLDC classifiers, which had an accuracy of 86.710%, an F1 score of 85.863%, a Jaccard index of 75.228%, a G-mean of 86.502%, and an error rate of 13.290%, as shown in Figure 14 below.
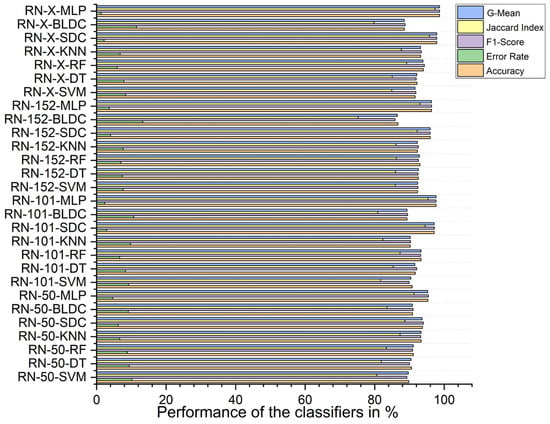
Figure 14.
Classifier performance when K = 10—with segmentation and RDO feature selection.
Figure 15 presents the training and validation loss (dotted lines) alongside training and validation accuracy (solid lines) over 16 epochs. The blue markers represent training performance, while the red markers indicate validation performance. The training accuracy shows a consistent upward trend, reaching nearly 98.8% by epoch 16, while the training loss decreases, reflecting proper model learning. However, validation accuracy fluctuates, with its highest peak at epoch 15, suggesting optimal generalization at that point. The validation loss decreases initially but shows oscillations, indicating some variance in performance. The best epoch is identified as 15, balancing high accuracy and low loss before potential overfitting. This analysis highlights the importance of early stopping to ensure robust model generalization.
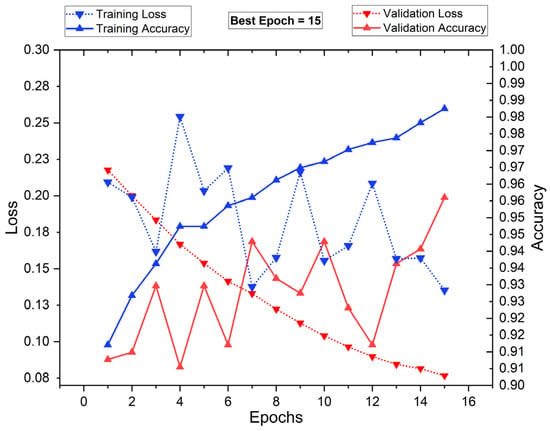
Figure 15.
Training vs. validation performance plot: with segmentation and PSO FS.
Figure 16 illustrates the training and validation loss (dotted lines), along with training and validation accuracy (solid lines) over 16 epochs. The blue markers represent training metrics, while the red markers indicate validation performance. Initially, training loss is high but drops sharply within the first few epochs, stabilizing around epoch 4. The validation loss follows a similar pattern, indicating a smooth learning process. Training and validation accuracy increase rapidly, reaching nearly 100% by epoch 11, which is identified as the best epoch. Beyond this point, the accuracy plateaus, suggesting that further training does not yield significant improvements. The close alignment of training and validation metrics suggests minimal overfitting, demonstrating strong generalization.
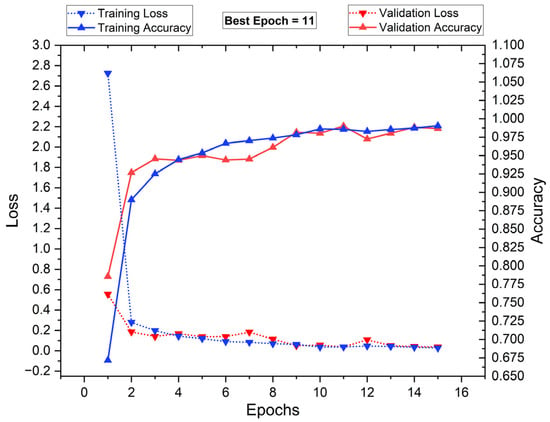
Figure 16.
Training vs. validation performance plot: with segmentation and RDO FS.
Figure 17 and Figure 18 show radar plots that evaluate the performance of classifiers using ResNet-based deep feature extraction and optimization techniques in the selective feature pooling layer for feature selection, with K = 10 in K-fold cross-validation. The analysis compares input images with segmentation, without segmentation, and with segmentation combined with PSO- and RDO-based feature selection. The results indicate that ResNet-X-MLP achieves the highest accuracy of 69.610% without segmentation and 86.460% with segmentation alone. When feature selection is applied, ResNet-X-MLP achieves 96.490% with PSO and 98.680% with RDO. RDO shows more consistent performance across epochs, while PSO demonstrates instability, as shown in Figure 15 and Figure 16, making ResNet-X-MLP with RDO the more stable choice for classification.
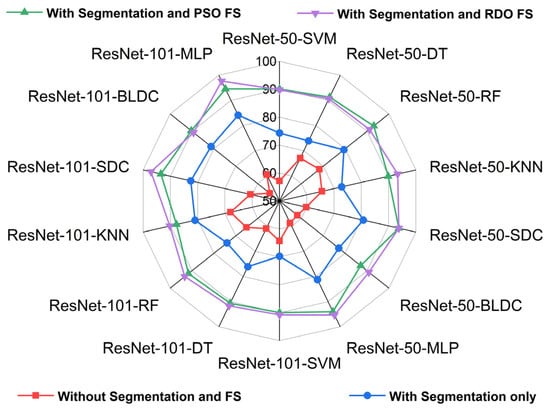
Figure 17.
Radar plot for performance analysis of ResNet-50 and ResNet-101 with classifiers for K = 10.
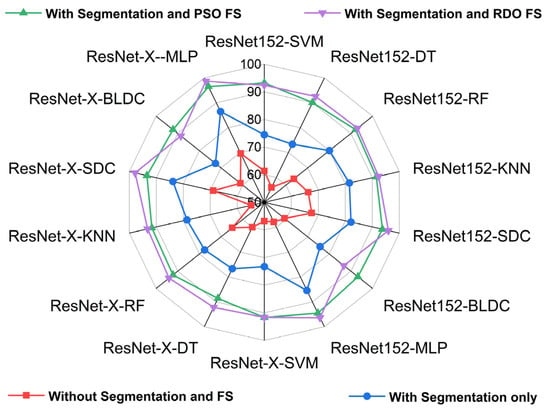
Figure 18.
Radar plot for performance analysis of ResNet-152 and DWAFF-based ResNet-X with classifiers for K = 10.
Figure 19 shows the Jaccard index and F1 score performance for K = 10 across the classifiers. It reveals a strong positive linear relationship in scenarios with no segmentation, with segmentation alone, and with both segmentation and feature selection using PSO and RDO. The R2 value of 0.993 indicates an almost perfect linear correlation. The regression line shows that the F1 Score deviation increases slightly less than the Jaccard index deviation, with a near-zero intercept suggesting minimal deviation from the mean. Table 8 details the previous work carried out in lung cancer detection on various datasets.
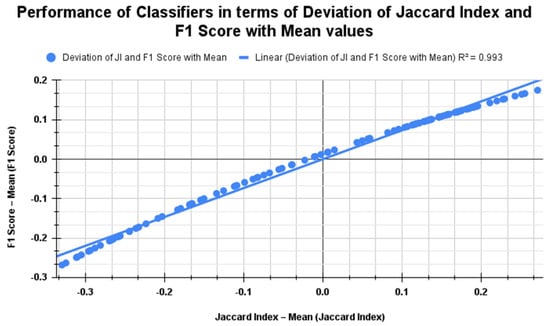
Figure 19.
Comparison of classifier performance using Jaccard index vs. F1 score metrics for all three cases when K = 10.

Table 8.
Comparison of classifier performance with different datasets.
5.5. Major Outcomes and Limitations
This research may have faced limitations due to the specific histopathological images used, which might not be generalizable to other image types or healthcare settings. Issues such as reliance on intensity values from segmented images, outliers, and data overlap could impact classification accuracy. Despite these challenges, the study’s approach, which combines various feature extraction methods, shows promise for identifying cancerous cells in histopathological images. A significant outcome is the creation of a comprehensive lung cancer screening database, which could enhance early detection and improve patient outcomes. Overall, this research provides valuable insights into early lung cancer detection and paves the way for further exploration.
5.6. Computational Complexity
This study evaluates the computational complexity of ResNet-50, ResNet-101, and ResNet-152-based feature extraction, as well as deep-weighted averaging-based feature fusion (DWAFF) features, in combination with feature selection techniques like PSO and RDO across various classifiers, using Big O notation.
In k-fold cross-validation, training on one-fold has a time complexity of , as the model is trained k times. Complexity grows with input size n, where signifies minimal complexity, while denotes logarithmic growth. Table 9 details the computational complexity and execution times for pretrained transfer learning architectures with various classifiers and feature extraction methods. DWAFF-based ResNet-X fused features with an MLP classifier, using RDO feature selection, achieves the highest complexity at and the longest execution time of 480 s due to the extensive training across multiple layers.

Table 9.
Computational complexity of the classifiers.
6. Conclusions
Lung cancer represents a major worldwide health issue, leading significantly to illness and mortality. Although treatment advancements have been made, early detection and prevention remain vital for addressing this serious public health issue. This study implements the deep-weighted averaging-based feature fusion (DWAFF) technique on ResNet-50, ResNet-101, and ResNet-152 architectures for deep feature extraction. Additionally, a selective feature pooling layer is applied after feature extraction to reduce the feature set, which is then fed into seven classifiers for the effective classification of adenocarcinoma and benign images from the LC25000 dataset. Performance is measured using standard benchmark metrics, demonstrating strong results in classifying complex lung cancer images. Training and testing were conducted with K-fold cross-validation. The DWAFF-based ResNet-X fused features combined with MLP classifiers for the RDO feature selection method achieved the highest performance, with an accuracy of 98.68%, an F1 score of 98.67%, a Jaccard index of 97.37%, and a G-mean value of 98.68% at K = 10. Future research will focus on extending this approach to multiclass classification and other cancers, such as colon cancer, and exploring the incorporation of RNN models like LSTM and Bi-LSTM to further improve classification accuracy and support ongoing clinical monitoring.
Author Contributions
Conceptualization, K.S.; methodology, K.S.; software, K.S.; validation, H.R. and K.S.; formal analysis, H.R.; investigation, H.R. and K.S.; resources, H.R. and K.S.; data curation, H.R.; writing—original draft preparation, K.S.; writing—review and editing, H.R.; visualization, H.R. and K.S.; supervision, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Who Report on Cancer: Setting Priorities, Investing Wisely and Providing Care for All 2020. Available online: http://apps.who.int/bookorders (accessed on 24 February 2024).
- Siegel, R.L.; Giaquinto, A.N.; Jemal, A. Cancer statistics, 2024. CA Cancer J. Clin. 2024, 74, 12–49. [Google Scholar] [CrossRef] [PubMed]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Araghi, M.; Soerjomataram, I.; Jenkins, M.; Brierley, J.; Morris, E.; Bray, F.; Arnold, M. Global trends in colorectal cancer mortality: Projections to the year 2035. Int. J. Cancer 2019, 144, 2992–3000. [Google Scholar] [CrossRef] [PubMed]
- WHO Classification of Tumours Editorial Board (Ed.) WHO Classification of Tumours. In Thoracic Tumours, 5th ed.; International Agency for Research on Cancer: Lyon, France, 2021; ISBN 978-92-832-4506-3. [Google Scholar]
- Andreadis, D.A.; Pavlou, A.M.; Panta, P. Biopsy and oral squamous cell carcinoma histopathology. In Oral Cancer Detection: Novel Strategies and Clinical Impact; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 133–151. [Google Scholar] [CrossRef]
- Ozdemir, O.; Russell, R.L.; Berlin, A.A. A 3D Probabilistic Deep Learning System for Detection and Diagnosis of Lung Cancer Using Low-Dose CT Scans. IEEE Trans Med. Imaging 2020, 39, 1419–1429. [Google Scholar] [CrossRef]
- Teramoto, A.; Tsukamoto, T.; Kiriyama, Y.; Fujita, H. Automated Classification of Lung Cancer Types from Cytological Images Using Deep Convolutional Neural Networks. Biomed Res. Int. 2017, 2017, 4067832. [Google Scholar] [CrossRef]
- Anthimopoulos, M.; Christodoulidis, S.; Ebner, L.; Christe, A.; Mougiakakou, S. Lung Pattern Classification for Interstitial Lung Diseases Using a Deep Convolutional Neural Network. IEEE Trans Med. Imaging 2016, 35, 1207–1216. [Google Scholar] [CrossRef]
- Iizuka, O.; Kanavati, F.; Kato, K.; Rambeau, M.; Arihiro, K.; Tsuneki, M. Deep Learning Models for Histopathological Classification of Gastric and Colonic Epithelial Tumours. Sci. Rep. 2020, 10, 1504. [Google Scholar] [CrossRef]
- Wang, S.; Wang, T.; Yang, L.; Yang, D.M.; Fujimoto, J.; Yi, F.; Luo, X.; Yang, Y.; Yao, B.; Lin, S.; et al. ConvPath: A software tool for lung adenocarcinoma digital pathological image analysis aided by a convolutional neural network. EBioMedicine 2019, 50, 103–110. [Google Scholar] [CrossRef]
- Gessert, N.; Nielsen, M.; Shaikh, M.; Werner, R.; Schlaefer, A. Skin lesion classification using ensembles of multi-resolution EfficientNets with meta data. MethodsX 2020, 7, 100864. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Qi, Y. Adaptive Threshold Learning in Frequency Domain for Classification of Breast Cancer Histopathological Images. Int. J. Intell. Syst. 2024, 1–13. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, C.; Gao, S. Breast Cancer Classification from Histopathological Images Using Resolution Adaptive Network. IEEE Access 2022, 10, 35977–35991. [Google Scholar] [CrossRef]
- Wang, P.; Wang, J.; Li, Y.; Li, P.; Li, L.; Jiang, M. Automatic classification of breast cancer histopathological images based on deep feature fusion and enhanced routing. Biomed. Signal Process Control 2021, 65, 102341. [Google Scholar] [CrossRef]
- Aresta, G.; Araújo, T.; Kwok, S.; Chennamsetty, S.S.; Safwan, M.; Alex, V.; Aguiar, P. BACH: Grand challenge on breast cancer histology images. Med. Image Anal. 2019, 56, 122–139. [Google Scholar] [CrossRef]
- Spanhol, F.A.; Oliveira, L.S.; Petitjean, C.; Heutte, L. Breast cancer histopathological image classification using Convolutional Neural Networks. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 2560–2567. [Google Scholar] [CrossRef]
- Filipczuk, P.; Fevens, T.; Krzyzak, A.; Monczak, R. Computer-aided breast cancer diagnosis based on the analysis of cytological images of fine needle biopsies. IEEE Trans Med. Imaging 2013, 32, 2169–2178. [Google Scholar] [CrossRef]
- Mobark, N.; Hamad, S.; Rida, S.Z. CoroNet: Deep Neural Network-Based End-to-End Training for Breast Cancer Diagnosis. Appl. Sci. 2022, 12, 7080. [Google Scholar] [CrossRef]
- Araújo, T.; Aresta, G.; Castro, E.; Rouco, J.; Aguiar, P.; Eloy, C.; Campilho, A. Classification of breast cancer histology images using convolutional neural networks. PLoS ONE 2017, 12, 6. [Google Scholar] [CrossRef]
- Rafiq, A.; Chursin, A.; Awad Alrefaei, W.; Rashed Alsenani, T.; Aldehim, G.; Abdel Samee, N.; Menzli, L.J. Detection and Classification of Histopathological Breast Images Using a Fusion of CNN Frameworks. Diagnostics 2023, 13, 1700. [Google Scholar] [CrossRef]
- Hameed, Z.; Zahia, S.; Garcia-Zapirain, B.; Aguirre, J.J.; Vanegas, A.M. Breast cancer histopathology image classification using an ensemble of deep learning models. Sensors 2020, 20, 4373. [Google Scholar] [CrossRef]
- Wang, P.; Hu, X.; Li, Y.; Liu, Q.; Zhu, X. Automatic cell nuclei segmentation and classification of breast cancer histopathology images. Signal Process. 2016, 122, 1–13. [Google Scholar] [CrossRef]
- Borkowski, A.A.; Bui, M.M.; Thomas, L.B.; Wilson, C.P.; Deland, L.A.; Mastorides, S.M. Lung and Colon Cancer Histopathological Image Dataset (LC25000). Available online: https://github.com/beamandrew/medical-data (accessed on 24 February 2024).
- Boumaraf, S.; Liu, X.; Zheng, Z.; Ma, X.; Ferkous, C. A new transfer learning-based approach to magnification dependent and independent classification of breast cancer in histopathological images. Biomed. Signal Process Control 2021, 63, 102192. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans Pattern Anal. Mach. Intell. 2012, 34, 2274–2281. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Theckedath, D.; Sedamkar, R.R. Detecting Affect States Using VGG16, ResNet50 and SE-ResNet50 Networks. SN Comput. Sci. 2020, 1, 79. [Google Scholar] [CrossRef]
- Alinsaif, S.; Lang, J. Texture features in the Shearlet domain for histopathological image classification. BMC Med. Inf. Decis. Mak. 2020, 20, 312. [Google Scholar] [CrossRef] [PubMed]
- Goel, L.; Patel, P. Improving YOLOv6 using advanced PSO optimizer for weight selection in lung cancer detection and classification. Multimed. Tools Appl. 2024, 83, 78059–78092. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R. Red deer algorithm (RDA): A new nature-inspired meta-heuristic. Soft Comput. 2020, 24, 14637–14665. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Kosko, B. Fuzzy entropy and conditioning. Inf. Sci. 1986, 40, 165–174. [Google Scholar] [CrossRef]
- Rachel, V.M.; Chokkalingam, S. Efficiency of Decision Tree Algorithm for Lung Cancer CT-Scan Images Comparing with SVM Algorithm. In Proceedings of the 2022 3rd International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 20–22 October 2022; pp. 1561–1565. [Google Scholar] [CrossRef]
- Lavanya, C.; Pooja, S.; Kashyap, A.H.; Rahaman, A.; Niranjan, S.; Niranjan, V. Novel Biomarker Prediction for Lung Cancer Using Random Forest Classifiers. Cancer Inform. 2023, 22, 11769351231167992. [Google Scholar] [CrossRef]
- Song, Y.; Huang, J.; Zhou, D.; Zha, H.; Giles, C.L. LNAI 4702—IKNN: Informative K-Nearest Neighbor Pattern Classification. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4702. [Google Scholar] [CrossRef]
- Zang, F.; Zhang, J.S. Softmax discriminant classifier. In Proceedings of the 3rd International Conference on Multimedia Information Networking and Security, MINES 2011, Shanghai, China, 4–6 November 2011; pp. 16–19. [Google Scholar] [CrossRef]
- Liu, M.; Li, L.; Wang, H.; Guo, X.; Liu, Y.; Li, Y.; Song, K.; Shao, Y.; Wu, F.; Zhang, J.; et al. A multilayer perceptron-based model applied to histopathology image classification of lung adenocarcinoma subtypes. Front. Oncol. 2023, 13, 1172234. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signal Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Kalaiyarasi, M.; Rajaguru, H.; Ravi, S. PFCM Approach for Enhancing Classification of Colon Cancer Tumors using DNA Microarray Data. In Proceedings of the 2023 Third International Conference on Smart Technologies, Communication and Robotics (STCR), Sathyamangalam, India, 9–10 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Jain, D.K.; Lakshmi, K.M.; Varma, K.P.; Ramachandran, M.; Bharati, S. Lung Cancer Detection Based on Kernel PCA-Convolution Neural Network Feature Extraction and Classification by Fast Deep Belief Neural Network in Disease Management Using Multimedia Data Sources. Comput. Intell. Neurosci. 2022, 2022, 3149406. [Google Scholar] [CrossRef] [PubMed]
- Civit-Masot, J.; Bañuls-Beaterio, A.; Domínguez-Morales, M.; Rivas-Pérez, M.; Muñoz-Saavedra, L.; Corral, J.M.R. Non-small cell lung cancer diagnosis aid with histopathological images using Explainable Deep Learning techniques. Comput. Methods Programs Biomed. 2022, 226, 107108. [Google Scholar] [CrossRef]
- Naseer, I.; Masood, T.; Akram, S.; Jaffar, A.; Rashid, M.; Iqbal, M.A. Lung Cancer Detection Using Modified AlexNet Architecture and Support Vector Machine. Comput. Mater. Contin. 2023, 74, 2039–2054. [Google Scholar] [CrossRef]
- Wang, Z.; Bi, Y.; Pan, T.; Wang, X.; Bain, C.; Bassed, R.; Song, J. Targeting tumor heterogeneity: Multiplex-detection-based multiple instances learning for whole slide image classification. Bioinformatics 2023, 39, btad114. [Google Scholar] [CrossRef]
- Masud, M.; Sikder, N.; Al Nahid, A.; Bairagi, A.K.; Alzain, M.A. A machine learning approach to diagnosing lung and colon cancer using a deep learning-based classification framework. Sensors 2021, 21, 748. [Google Scholar] [CrossRef]
- Wahid, R.R.; Nisa, C.; Amaliyah, R.P.; Puspaningrum, E.Y. Lung and colon cancer detection with convolutional neural networks on histopathological images. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2023. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, M.K.; Shabaz, M.; Sharma, A. Deep Learning Techniques for Cancer Classification Using Microarray Gene Expression Data; Frontiers Media S.A.: Lausanne, Switzerland, 2022. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Song, K.; Sun, M.; Shao, Y.; Xue, S.; Zhang, T. CroReLU: Cross-Crossing Space-Based Visual Activation Function for Lung Cancer Pathology Image Recognition. Cancers 2022, 14, 5181. [Google Scholar] [CrossRef]
- Wang, X.; Yu, G.; Yan, Z.; Wan, L.; Wang, W.; Cui, L. Lung Cancer Subtype Diagnosis by Fusing Image-Genomics Data and Hybrid Deep Networks. IEEE/ACM Trans Comput. Biol. Bioinform 2023, 20, 512–523. [Google Scholar] [CrossRef]
- Mastouri, R.; Khlifa, N.; Neji, H.; Hantous-Zannad, S. A bilinear convolutional neural network for lung nodules classification on CT images. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 91–101. [Google Scholar] [CrossRef]
- Phankokkruad, M. Ensemble Transfer Learning for Lung Cancer Detection. In Proceedings of the ACM International Conference Proceeding Series, Montreal, Canada, 18–22 October 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 438–442. [Google Scholar] [CrossRef]
- Bukhari, S.U.K.; Syed, A.; Bokhari, S.K.A.; Hussain, S.S.; Armaghan, S.U.; Shah, S.S.H. The Histological Diagnosis of Colonic Adenocarcinoma by Applying Partial Self Supervised Learning. medRxiv 2020, arXiv:15.20175760. [Google Scholar] [CrossRef]
- Anjum, S.; Ahmed, I.; Asif, M.; Aljuaid, H.; Alturise, F.; Ghadi, Y.Y.; Elhabob, R. Lung Cancer Classification in Histopathology Images Using Multiresolution Efficient Nets. Comput. Intell. Neurosci. 2023, 2023, 7282944. [Google Scholar] [CrossRef]
- Shourie, P.; Anand, V.; Gupta, S. Colon and Lung Cancer Classification of Histopathological Images Using Efficientnetb7. In Proceedings of the 2023 3rd Asian Conference on Innovation in Technology (ASIANCON), Ravet, India, 25–27 August 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Diosdado, J.; Gilabert, P.; Seguí, S.; Borrego, H. LungHist700: A dataset of histological images for deep learning in pulmonary pathology. Sci. Data 2024, 11, 1088. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).