Robustness of Machine Learning Predictions for Determining Whether Deep Inspiration Breath-Hold Is Required in Breast Cancer Radiation Therapy
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Population
2.2. Data Collection
2.3. ML Models
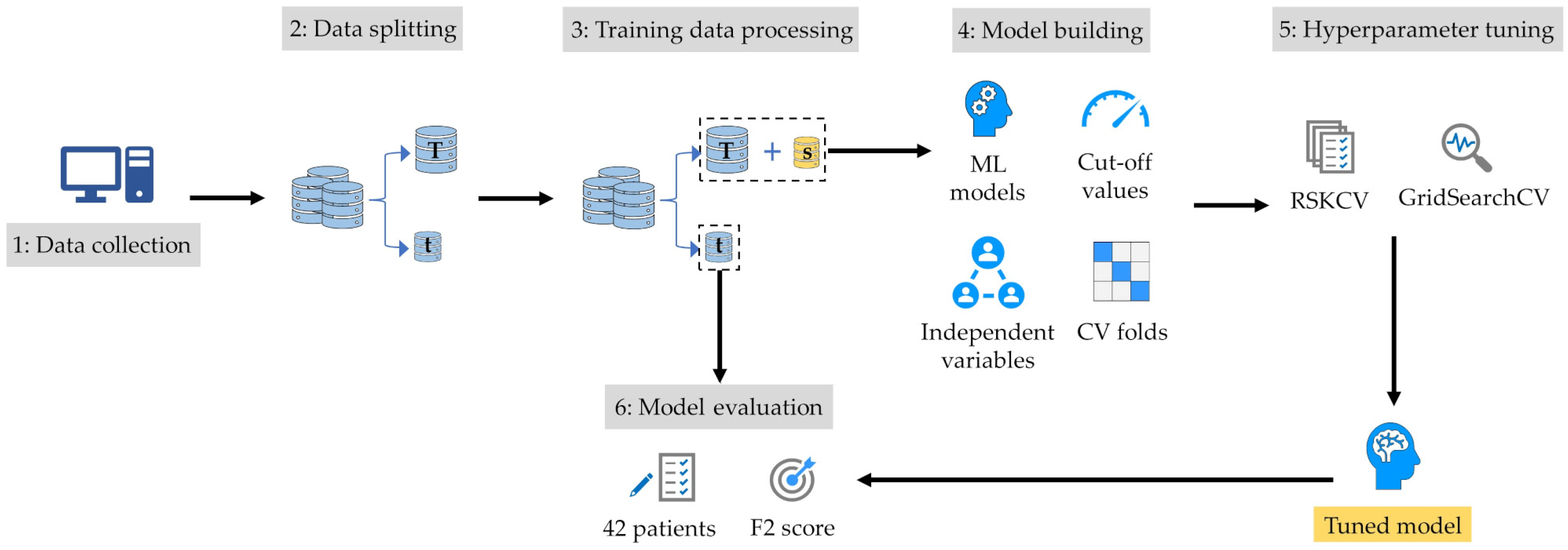
2.4. Model-Building Process
2.5. Model Evaluation
2.6. Predicted DIBH
3. Results
3.1. Patient Characteristics
3.2. Model Performance and Robustness
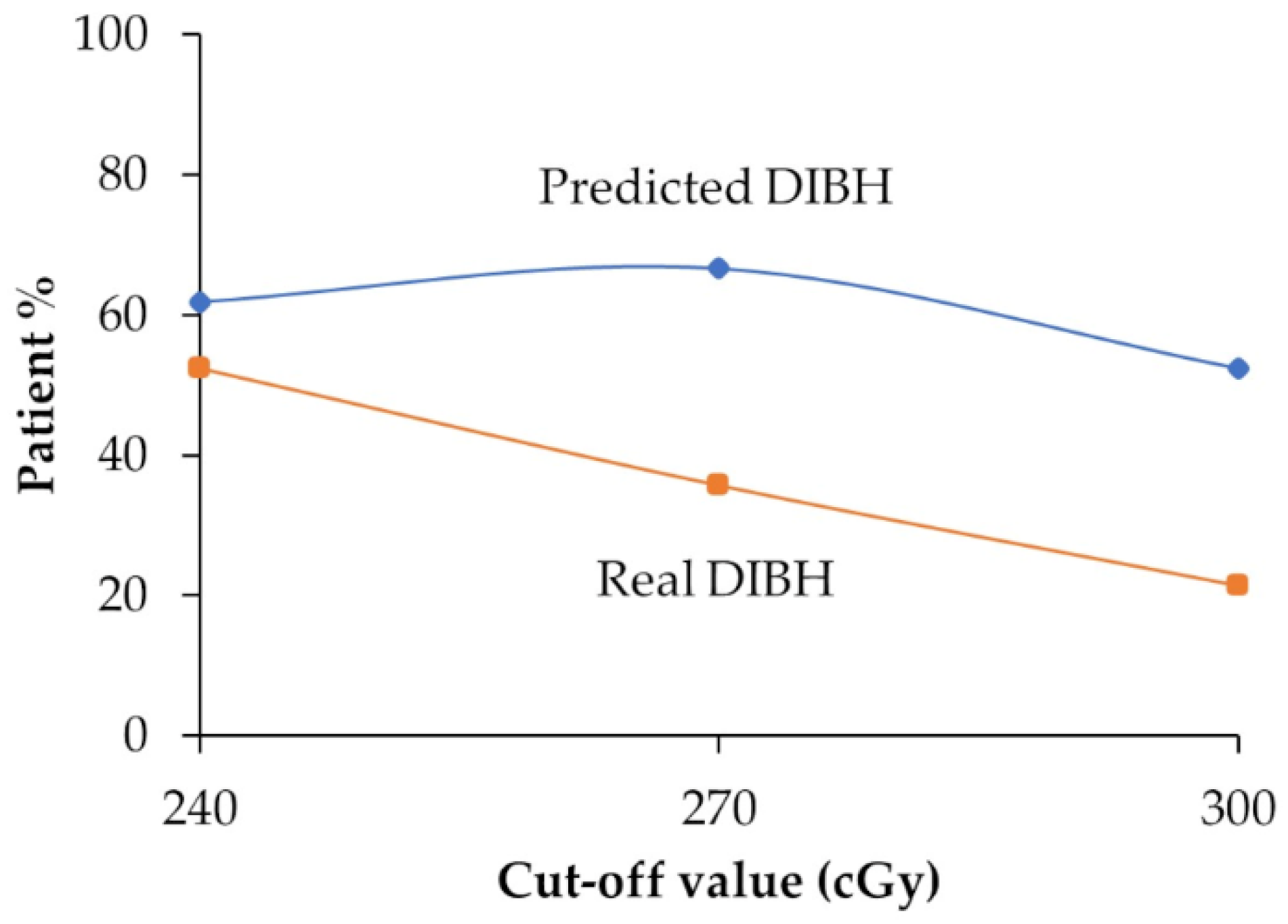
3.3. Comparison Between Predicted DIBH and Real DIBH
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Darby, S.; McGale, P.; Correa, C.; Taylor, C.; Arriagada, R.; Clarke, M.; Cutter, D.; Davies, C.; Ewertz, M.; Godwin, J.; et al. Effect of radiotherapy after breast-conserving surgery on 10-year recurrence and 15-year breast cancer death: Meta-analysis of individual patient data for 10,801 women in 17 randomised trials. Lancet 2011, 378, 1707–1716. [Google Scholar] [CrossRef] [PubMed]
- Clarke, M.; Collins, R.; Darby, S.; Davies, C.; Elphinstone, P.; Evans, V.; Godwin, J.; Gray, R.; Hicks, C.; James, S.; et al. Effects of radiotherapy and of differences in the extent of surgery for early breast cancer on local recurrence and 15-year survival: An overview of the randomised trials. Lancet 2005, 366, 2087–2106. [Google Scholar] [CrossRef] [PubMed]
- Sardar, P.; Kundu, A.; Chatterjee, S.; Nohria, A.; Nairooz, R.; Bangalore, S.; Mukherjee, D.; Aronow, W.S.; Lavie, C.J. Long-term cardiovascular mortality after radiotherapy for breast cancer: A systematic review and meta-analysis. Clin. Cardiol. 2017, 40, 73–81. [Google Scholar] [CrossRef]
- Taylor, C.; Correa, C.; Duane, F.K.; Aznar, M.C.; Anderson, S.J.; Bergh, J.; Dodwell, D.; Ewertz, M.; Gray, R.; Jagsi, R.; et al. Estimating the risks of breast cancer radiotherapy: Evidence from modern radiation doses to the lungs and heart and from previous randomized trials. J. Clin. Oncol. 2017, 35, 1641–1649. [Google Scholar] [CrossRef]
- Drost, L.; Yee, C.; Lam, H.; Zhang, L.; Wronski, M.; McCann, C.; Lee, J.; Vesprini, D.; Leung, E.; Chow, E. A systematic review of heart dose in breast radiotherapy. Clin. Breast Cancer 2018, 18, e819–e824. [Google Scholar] [CrossRef]
- Jacob, S.; Camilleri, J.; Derreumaux, S.; Walker, V.; Lairez, O.; Lapeyre, M.; Bruguière, E.; Pathak, A.; Bernier, M.O.; Laurier, D.; et al. Is mean heart dose a relevant surrogate parameter of left ventricle and coronary arteries exposure during breast cancer radiotherapy: A dosimetric evaluation based on individually-determined radiation dose (BACCARAT study). Radiat. Oncol. 2019, 14, 29. [Google Scholar] [CrossRef] [PubMed]
- Beaton, L.; Bergman, A.; Nichol, A.; Aparicio, M.; Wong, G.; Gondara, L.; Speers, C.; Weir, L.; Davis, M.; Tyldesley, S. Cardiac death after breast radiotherapy and the QUANTEC cardiac guidelines. Clin. Transl. Radiat. Oncol. 2019, 19, 39–45. [Google Scholar] [CrossRef]
- Kirli Bolukbas, M.; Karaca, S.; Coskun, V. Cardiac protective techniques in left breast radiotherapy: Rapid selection criteria for routine clinical decision making. Eur. J. Med. Res. 2023, 28, 504. [Google Scholar] [CrossRef]
- McWilliam, A.; Khalifa, J.; Vasquez Osorio, E.; Banfill, K.; Abravan, A.; Faivre-Finn, C.; van Herk, M. Novel Methodology to Investigate the Effect of Radiation Dose to Heart Substructures on Overall Survival. Int. J. Radiat. Oncol. Biol. Phys. 2020, 108, 1073–1081. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, D.; Zhang, X.; Teng, Y.; Yuan, W.; Zhang, Y.; He, R.; Tang, F.; Pang, J.; Han, B.; et al. Comparison of deep inspiration breath hold versus free breathing in radiotherapy for left sided breast cancer. Front. Oncol. 2022, 12, 845037. [Google Scholar] [CrossRef]
- Falco, M.; Masojć, B.; Macała, A.; Łukowiak, M.; Woźniak, P.; Malicki, J. Deep inspiration breath hold reduces the mean heart dose in left breast cancer radiotherapy. Radiol. Oncol. 2021, 55, 212–220. [Google Scholar] [CrossRef]
- Yamauchi, R.; Mizuno, N.; Itazawa, T.; Saitoh, H.; Kawamori, J. Dosimetric evaluation of deep inspiration breath hold for left-sided breast cancer: Analysis of patient-specific parameters related to heart dose reduction. J. Radiat. Res. 2020, 61, 447–456. [Google Scholar] [CrossRef] [PubMed]
- Gaál, S.; Kahán, Z.; Paczona, V.; Kószó, R.; Drencsényi, R.; Szabó, J.; Rónai, R.; Antal, T.; Deák, B.; Varga, Z. Deep-inspirational breath-hold (DIBH) technique in left-sided breast cancer: Various aspects of clinical utility. Radiat. Oncol. 2021, 16, 89. [Google Scholar] [CrossRef] [PubMed]
- Darapu, A.; Balakrishnan, R.; Sebastian, P.; Kather Hussain, M.R.; Ravindran, P.; John, S. Is the deep inspiration breath-hold technique superior to the free breathing technique in cardiac and lung sparing while treating both left-sided post-mastectomy chest wall and supraclavicular regions. Case Rep. Oncol. 2017, 10, 37–51. [Google Scholar] [CrossRef] [PubMed]
- Al-Hammad, W.E.; Kuroda, M.; Kamizaki, R.; Tekiki, N.; Ishizaka, H.; Kuroda, K.; Sugimoto, K.; Oita, M.; Tanabe, Y.; Barham, M.; et al. Mean heart dose prediction using parameters of single-slice computed tomography and body mass index: Machine learning approach for radiotherapy of left-sided breast cancer of Asian patients. Curr. Oncol. 2023, 30, 7412–7424. [Google Scholar] [CrossRef]
- Koide, Y.; Aoyama, T.; Shimizu, H.; Kitagawa, T.; Miyauchi, R.; Tachibana, H.; Kodaira, T. Development of deep learning chest X-ray model for cardiac dose prediction in left-sided breast cancer radiotherapy. Sci. Rep. 2022, 12, 13706. [Google Scholar] [CrossRef]
- West, D.; Mangiameli, P.; Rampal, R.; West, V. Ensemble strategies for a medical diagnostic decision support system: A breast cancer diagnosis application. Eur. J. Oper. Res. 2005, 162, 532–551. [Google Scholar] [CrossRef]
- Freiesleben, T.; Grote, T. Beyond generalization: A theory of robustness in machine learning. Synthese 2023, 202, 109. [Google Scholar] [CrossRef]
- Lloyd, E.A. Confirmation and robustness of climate models. Philos. Sci. 2010, 77, 971–984. [Google Scholar] [CrossRef]
- Tekiki, N.; Kuroda, M.; Ishizaka, H.; Khasawneh, A.; Barham, M.; Hamada, K.; Konishi, K.; Sugimoto, K.; Katsui, K.; Sugiyama, S.; et al. New field-in-field with two reference points method for whole breast radiotherapy: Dosimetric analysis and radiation-induced skin toxicities assessment. Mol. Clin. Oncol. 2021, 15, 193. [Google Scholar] [CrossRef]
- Alghamdi, M.; Al-Mallah, M.; Keteyian, S.; Brawner, C.; Ehrman, J.; Sakr, S. Predicting diabetes mellitus using SMOTE and ensemble machine learning approach: The Henry Ford ExercIse Testing (FIT) project. Liu B, editor. PLoS ONE 2017, 12, e0179805. [Google Scholar] [CrossRef]
- Khushi, M.; Shaukat, K.; Alam, T.M.; Hameed, I.A.; Uddin, S.; Luo, S.; Yang, X.; Reyes, M.C. A comparative performance analysis of data resampling methods on imbalance medical data. IEEE Access 2021, 9, 109960–109975. [Google Scholar] [CrossRef]
- Kaliappan, J.; Bagepalli, A.R.; Almal, S.; Mishra, R.; Hu, Y.C.; Srinivasan, K. Impact of cross-validation on machine learning models for early detection of intrauterine fetal demise. Diagnostics 2023, 13, 1692. [Google Scholar] [CrossRef] [PubMed]
- Charilaou, P.; Battat, R. Machine learning models and over-fitting considerations. World J. Gastroenterol. 2020, 28, 605–607. [Google Scholar] [CrossRef]
- Chhatwal, J.; Alagoz, O.; Lindstrom, M.J.; Kahn, C.E., Jr.; Shaffer, K.A.; Burnside, E.S. A logistic regression model based on the national mammography database format to aid breast cancer diagnosis. AJR Am. J. Roentgenol. 2009, 192, 1117–1127. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random forest. R News 2002, 2, 18–22. [Google Scholar]
- Wickramasinghe, I.; Kalutarage, H. Naive bayes: Applications, variations, and vulnerabilities: A review of literature with code snippets for implementation. Soft Comput. 2021, 25, 2277–2293. [Google Scholar] [CrossRef]
- Rodriguez, D.; Nayak, T.; Chen, Y.; Krishnan, R.; Huang, Y. On the role of deep learning model complexity in adversarial robustness for medical images. BMC Med. Inform. Decis. Mak. 2022, 22, 160. [Google Scholar] [CrossRef]
- Koçak, B.; Cuocolo, R.; dos Santos, D.P.; Stanzione, A.; Ugga, L. Must-have qualities of clinical research on artificial intelligence and machine learning. Balkan Med. J. 2023, 40, 3–12. [Google Scholar] [CrossRef]
- Campagner, A.; Famiglini, L.; Carobene, A.; Cabitza, F. Everything is varied: The surprising impact of instantial variation on ML reliability. Appl. Soft Comput. 2023, 146, 110644. [Google Scholar] [CrossRef]
- Bouthillier, X.; Laurent, C.; Vincent, P. Unreproducible research is reproducible. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 725–734. Available online: https://proceedings.mlr.press/v97/bouthillier19a.html (accessed on 18 June 2024).
- Goodfellow, I.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, M.C. Obtaining optimal cutoff values for tree classifiers using multiple biomarkers. Biometrics 2022, 78, 128–140. [Google Scholar] [CrossRef] [PubMed]
- Kamizaki, R.; Kuroda, M.; Al-Hammad, W.E.; Tekiki, N.; Ishizaka, H.; Kuroda, K.; Sugimoto, K.; Oita, M.; Tanabe, Y.; Barham, M.; et al. Evaluation of the accuracy of heart dose prediction by machine learning for selecting patients not requiring deep inspiration breath-hold radiotherapy after breast cancer surgery. Exp. Ther. Med. 2023, 26, 536. [Google Scholar] [CrossRef] [PubMed]
- Aluja-Banet, T.; Nafria, E. Stability and scalability in decision trees. Comput. Stat. 2023, 18, 505–520. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Terui, Y.; Nochioka, K.; Ota, H.; Tada, H.; Sato, H.; Miyata, S.; Toyoda, S.; Shimojima, M.; Izumiya, Y.; Kitai, T.; et al. CHECH HEART-BC. Risk prediction model of cardiotoxicity in breast cancer patients; the multicenter prospective CHECK HEART-BC (comprehensive heart imaging to evaluate cardiac damage linked with chemotherapy in breast). Eur. Heart J. 2023, 44 (Suppl. S2), ehad655.2680. [Google Scholar] [CrossRef]
- Ferini, G.; Valenti, V.; Viola, A.; Umana, G.E.; Martorana, E. A critical overview of predictors of heart sparing by deep-inspiration-breath-hold irradiation in left-sided breast cancer patients. Cancers 2022, 14, 3477. [Google Scholar] [CrossRef]
| Characteristic | Value |
|---|---|
| Age (mean ± SD, years) | 55.3 ± 11.1 |
| Body mass index (mean ± SD) | 22.9 ± 3.9 |
| Tumor location (%) | |
| Upper-inner quadrant | 27.1% |
| Lower-inner quadrant | 9.2% |
| Upper-outer quadrant | 51.7% |
| Lower-outer quadrant | 4.8% |
| Central portion | 7.2% |
| Radiation method (%) | |
| FIF-1RP | 33.8% |
| FIF-2RP | 66.2% |
| Breast separation (mean ± SD, cm) | 18.8 ± 2.6 |
| Chest wall thickness (mean ± SD, cm) | 6.0 ± 1.2 |
| Mean heart dose (mean ± SD, cGy) | 251 ± 81 |
| High | 106 *1, 74 *2, 43 *3 |
| Low | 101 *1, 133 *2, 164 *3 |
| Cut-Off Value | # of Variables | Folds | GB | DT | Bagging | DNN | RF | KNN | SVM | NB | LR | RC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 240 cGy | 3 variables | 3-fold | 0.846 | 0.701 | 0.707 | 0.601 | 0.607 | 0.528 | 0.560 | 0.528 | 0.528 | 0.485 |
| 4-fold | 0.846 | 0.701 | 0.707 | 0.560 | 0.663 | 0.528 | 0.560 | 0.528 | 0.528 | 0.485 | ||
| 5-fold | 0.392 | 0.701 | 0.714 | 0.636 | 0.607 | 0.607 | 0.560 | 0.528 | 0.485 | 0.485 | ||
| 6 variables | 3-fold | 0.846 | 0.739 | 0.582 | 0.652 | 0.566 | 0.571 | 0.681 | 0.550 | 0.544 | 0.544 | |
| 4-fold | 0.799 | 0.701 | 0.660 | 0.619 | 0.571 | 0.630 | 0.544 | 0.594 | 0.588 | 0.544 | ||
| 5-fold | 0.846 | 0.701 | 0.540 | 0.625 | 0.648 | 0.630 | 0.544 | 0.594 | 0.544 | 0.544 | ||
| Median | 0.846 | 0.701 | 0.683 | 0.622 | 0.607 | 0.589 | 0.560 | 0.539 | 0.536 | 0.514 | ||
| Q1 | 0.811 | 0.701 | 0.602 | 0.606 | 0.580 | 0.539 | 0.548 | 0.528 | 0.528 | 0.485 | ||
| Q3 | 0.846 | 0.701 | 0.707 | 0.633 | 0.638 | 0.624 | 0.560 | 0.583 | 0.544 | 0.544 | ||
| IQR | 0.035 | 0.000 | 0.106 | 0.028 | 0.058 | 0.085 | 0.012 | 0.055 | 0.016 | 0.059 | ||
| Maximum | 0.846 | 0.739 | 0.714 | 0.652 | 0.663 | 0.630 | 0.681 | 0.594 | 0.588 | 0.544 | ||
| Minimum | 0.392 | 0.701 | 0.540 | 0.560 | 0.566 | 0.528 | 0.544 | 0.528 | 0.485 | 0.485 | ||
| Model instability | 0.454 * | 0.038 | 0.174 * | 0.092 | 0.097 | 0.102 * | 0.137 * | 0.066 | 0.103 * | 0.059 | ||
| 270 cGy | 3 variables | 3-fold | 0.735 | 0.786 | 0.687 | 0.625 | 0.731 | 0.679 | 0.555 | 0.679 | 0.679 | 0.679 |
| 4-fold | 0.735 | 0.786 | 0.687 | 0.632 | 0.823 | 0.679 | 0.722 | 0.679 | 0.731 | 0.679 | ||
| 5-fold | 0.823 | 0.786 | 0.679 | 0.625 | 0.687 | 0.670 | 0.740 | 0.679 | 0.679 | 0.679 | ||
| 6 variables | 3-fold | 0.735 | 0.804 | 0.625 | 0.523 | 0.687 | 0.705 | 0.714 | 0.639 | 0.609 | 0.555 | |
| 4-fold | 0.000 | 0.804 | 0.740 | 0.641 | 0.687 | 0.654 | 0.632 | 0.639 | 0.609 | 0.555 | ||
| 5-fold | 0.804 | 0.804 | 0.687 | 0.555 | 0.687 | 0.639 | 0.647 | 0.639 | 0.555 | 0.555 | ||
| Median | 0.735 | 0.795 | 0.687 | 0.625 | 0.687 | 0.674 | 0.680 | 0.659 | 0.644 | 0.617 | ||
| Q1 | 0.735 | 0.786 | 0.681 | 0.573 | 0.687 | 0.658 | 0.636 | 0.639 | 0.609 | 0.555 | ||
| Q3 | 0.787 | 0.804 | 0.687 | 0.630 | 0.720 | 0.679 | 0.720 | 0.679 | 0.679 | 0.679 | ||
| IQR | 0.052 | 0.018 | 0.006 | 0.058 | 0.033 | 0.021 | 0.084 | 0.040 | 0.070 | 0.124 | ||
| Maximum | 0.823 | 0.804 | 0.740 | 0.641 | 0.823 | 0.705 | 0.740 | 0.679 | 0.731 | 0.679 | ||
| Minimum | 0.000 | 0.786 | 0.625 | 0.523 | 0.687 | 0.639 | 0.555 | 0.639 | 0.555 | 0.555 | ||
| Model instability | 0.823 * | 0.018 | 0.115 | 0.118 | 0.136 * | 0.066 | 0.185 * | 0.040 | 0.176 * | 0.124 * | ||
| 300 cGy | 3 variables | 3-fold | 0.603 | 0.725 | 0.789 | 0.689 | 0.737 | 0.762 | 0.762 | 0.714 | 0.714 | 0.714 |
| 4-fold | 0.762 | 0.725 | 0.789 | 0.789 | 0.775 | 0.775 | 0.762 | 0.714 | 0.714 | 0.714 | ||
| 5-fold | 0.576 | 0.306 | 0.510 | 0.689 | 0.775 | 0.775 | 0.750 | 0.714 | 0.701 | 0.714 | ||
| 6 variables | 3-fold | 0.727 | 0.666 | 0.714 | 0.526 | 0.775 | 0.737 | 0.409 | 0.535 | 0.526 | 0.526 | |
| 4-fold | 0.520 | 0.689 | 0.803 | 0.454 | 0.686 | 0.737 | 0.545 | 0.535 | 0.526 | 0.526 | ||
| 5-fold | 0.510 | 0.666 | 0.803 | 0.614 | 0.737 | 0.517 | 0.526 | 0.614 | 0.526 | 0.526 | ||
| Median | 0.590 | 0.678 | 0.789 | 0.652 | 0.756 | 0.750 | 0.648 | 0.664 | 0.614 | 0.620 | ||
| Q1 | 0.534 | 0.666 | 0.733 | 0.548 | 0.737 | 0.737 | 0.531 | 0.555 | 0.526 | 0.526 | ||
| Q3 | 0.696 | 0.716 | 0.800 | 0.689 | 0.775 | 0.772 | 0.759 | 0.714 | 0.711 | 0.714 | ||
| IQR | 0.162 | 0.050 | 0.067 | 0.141 | 0.038 | 0.035 | 0.228 | 0.159 | 0.185 | 0.188 | ||
| Maximum | 0.762 | 0.725 | 0.803 | 0.789 | 0.775 | 0.775 | 0.762 | 0.714 | 0.714 | 0.714 | ||
| Minimum | 0.510 | 0.306 | 0.510 | 0.454 | 0.686 | 0.517 | 0.409 | 0.535 | 0.526 | 0.526 | ||
| Model instability | 0.252 | 0.419 * | 0.293 * | 0.335 * | 0.089 | 0.258 * | 0.353 * | 0.179 | 0.188 | 0.188 |
| Cut-off value = 240 cGy | ||||||||||
| Model | GB | DT | Bagging | DNN | RF | KNN | SVM | NB | LR | RC |
| GB | N/A | |||||||||
| DT | 0.61 | N/A | ||||||||
| Bagging | 0.206 | 0.121 | N/A | |||||||
| DNN | 0.102 | 0.002 * | 0.292 | N/A | ||||||
| RF | 0.08 | 0.002 * | 0.26 | 0.807 | N/A | |||||
| KNN | 0.035 * | 0.002 * | 0.087 | 0.186 | 0.294 | N/A | ||||
| SVM | 0.052 | 0.002 * | 0.061 | 0.132 | 0.225 | 0.82 | N/A | |||
| NB | 0.015 * | 0.002 * | 0.032 * | 0.013 * | 0.026 * | 0.253 | 0.539 | N/A | ||
| LR | 0.015 * | 0.002 * | 0.015 * | 0.004 * | 0.006 * | 0.082 | 0.143 | 0.409 | N/A | |
| RC | 0.015 * | 0.002 * | 0.009 * | 0.002 * | 0.002 * | 0.024 * | 0.022 * | 0.069 | 0.364 | N/A |
| Cut-off value = 270 cGy | ||||||||||
| Model | GB | DT | Bagging | DNN | RF | KNN | SVM | NB | LR | RC |
| GB | N/A | |||||||||
| DT | 0.067 | N/A | ||||||||
| Bagging | 0.994 | 0.002 * | N/A | |||||||
| DNN | 0.905 | 0.002 * | 0.011 * | N/A | ||||||
| RF | 0.944 | 0.015 * | 0.349 | 0.002 * | N/A | |||||
| KNN | 1 | 0.002 * | 0.496 | 0.004 * | 0.058 | N/A | ||||
| SVM | 0.994 | 0.002 * | 0.66 | 0.058 | 0.217 | 0.937 | N/A | |||
| NB | 1 | 0.002 * | 0.197 | 0.009 * | 0.002 * | 0.372 | 0.76 | N/A | ||
| LR | 1 | 0.002 * | 0.195 | 0.223 | 0.048 * | 0.351 | 0.55 | 0.63 | N/A | |
| RC | 0.955 | 0.002 * | 0.054 | 0.649 | 0.002 * | 0.139 | 0.225 | 0.182 | 0.589 | N/A |
| Cut-off value = 300 cGy | ||||||||||
| Model | GB | DT | Bagging | DNN | RF | KNN | SVM | NB | LR | RC |
| GB | N/A | |||||||||
| DT | 0.887 | N/A | ||||||||
| Bagging | 0.097 | 0.251 | N/A | |||||||
| DNN | 0.883 | 0.985 | 0.132 | N/A | ||||||
| RF | 0.024 * | 0.013 * | 0.924 | 0.048 * | N/A | |||||
| KNN | 0.132 | 0.364 | 0.619 | 0.182 | 0.727 | N/A | ||||
| SVM | 0.887 | 0.974 | 0.175 | 1 | 0.128 | 0.336 | N/A | |||
| NB | 0.714 | 0.924 | 0.147 | 0.82 | 0.022 * | 0.149 | 0.903 | N/A | ||
| LR | 0.981 | 0.972 | 0.093 | 0.935 | 0.013 * | 0.069 | 0.97 | 0.589 | N/A | |
| RC | 0.948 | 0.981 | 0.095 | 0.952 | 0.022 * | 0.069 | 0.987 | 0.61 | 1 | N/A |
 | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Hammad, W.E.; Kuroda, M.; Al Jamal, G.; Fujikura, M.; Kamizaki, R.; Kuroda, K.; Yoshida, S.; Nakamura, Y.; Oita, M.; Tanabe, Y.; et al. Robustness of Machine Learning Predictions for Determining Whether Deep Inspiration Breath-Hold Is Required in Breast Cancer Radiation Therapy. Diagnostics 2025, 15, 668. https://doi.org/10.3390/diagnostics15060668
Al-Hammad WE, Kuroda M, Al Jamal G, Fujikura M, Kamizaki R, Kuroda K, Yoshida S, Nakamura Y, Oita M, Tanabe Y, et al. Robustness of Machine Learning Predictions for Determining Whether Deep Inspiration Breath-Hold Is Required in Breast Cancer Radiation Therapy. Diagnostics. 2025; 15(6):668. https://doi.org/10.3390/diagnostics15060668
Chicago/Turabian StyleAl-Hammad, Wlla E., Masahiro Kuroda, Ghaida Al Jamal, Mamiko Fujikura, Ryo Kamizaki, Kazuhiro Kuroda, Suzuka Yoshida, Yoshihide Nakamura, Masataka Oita, Yoshinori Tanabe, and et al. 2025. "Robustness of Machine Learning Predictions for Determining Whether Deep Inspiration Breath-Hold Is Required in Breast Cancer Radiation Therapy" Diagnostics 15, no. 6: 668. https://doi.org/10.3390/diagnostics15060668
APA StyleAl-Hammad, W. E., Kuroda, M., Al Jamal, G., Fujikura, M., Kamizaki, R., Kuroda, K., Yoshida, S., Nakamura, Y., Oita, M., Tanabe, Y., Sugimoto, K., Sugianto, I., Barham, M., Tekiki, N., Hisatomi, M., & Asaumi, J. (2025). Robustness of Machine Learning Predictions for Determining Whether Deep Inspiration Breath-Hold Is Required in Breast Cancer Radiation Therapy. Diagnostics, 15(6), 668. https://doi.org/10.3390/diagnostics15060668





