A Novel Method to Represent the Three-Dimensional Inclination of the Distal Radius Joint Surface
Abstract
1. Introduction
2. Methods
2.1. Three-Dimensional Bone Morphology and Analysis
2.2. Statistical Analysis
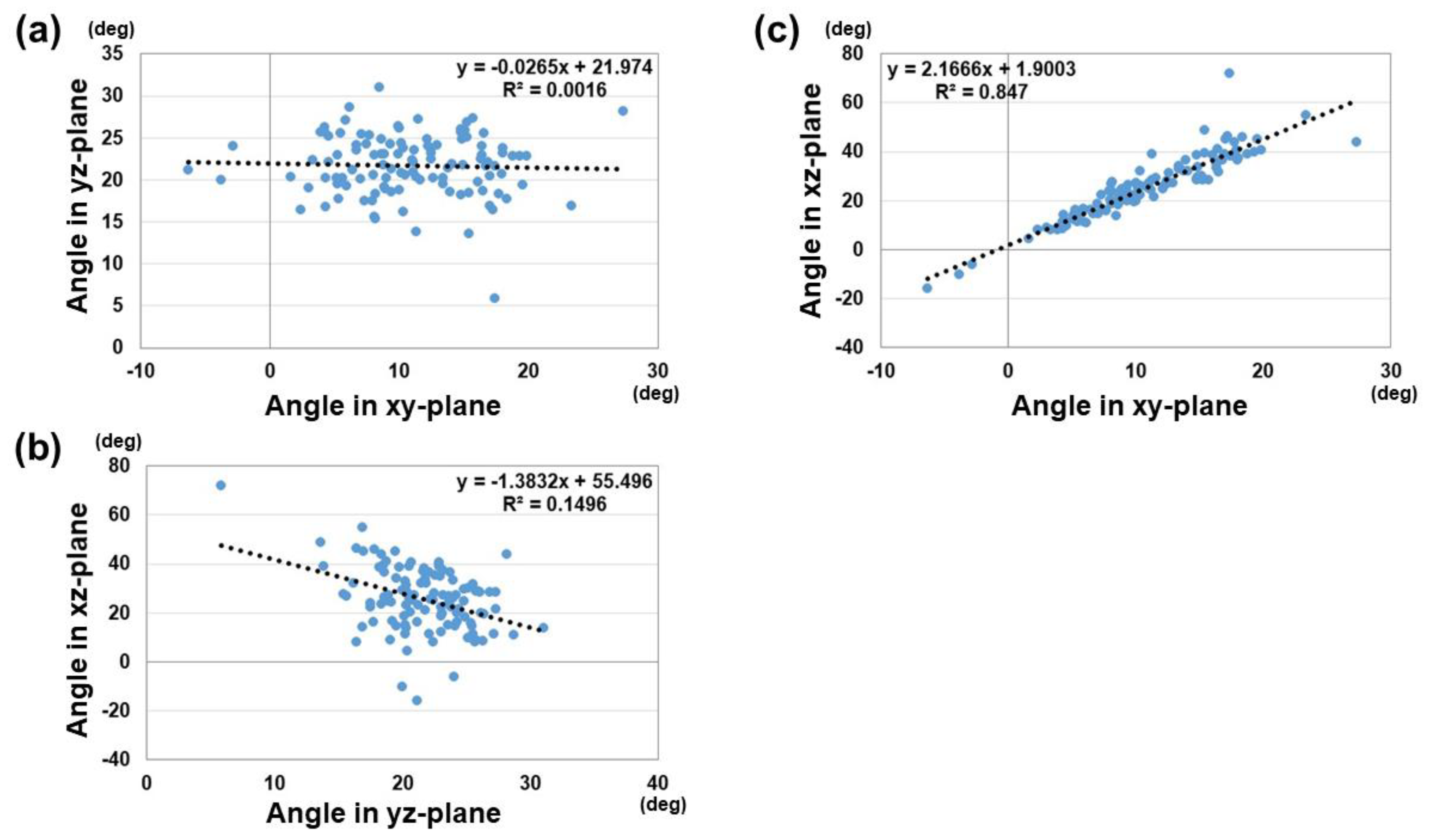
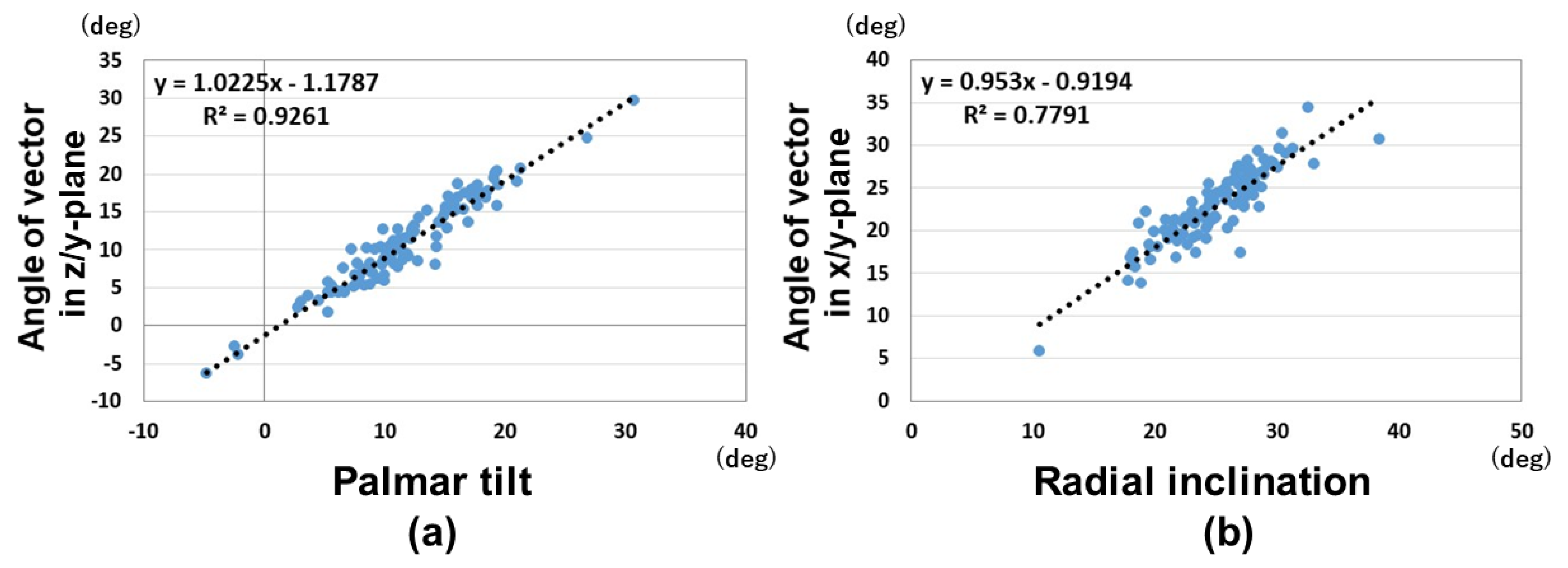
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hubbard, J.; Berry, D.; Chauhan, A.; Casstevens, C.; Shin, A.Y.; Abrams, R.A. A three-dimensional computed tomography study of the palmar ulnar corner fragment in distal radial fractures. J. Hand Surg. Eur. 2024, 49, 300–309. [Google Scholar] [CrossRef] [PubMed]
- Roner, S.; Fürnstahl, P.; Scheibler, A.G.; Sutter, R.; Nagy, L.; Carrillo, F. Three-Dimensional Automated Assessment of the Distal Radioulnar Joint Morphology According to Sigmoid Notch Surface Orientation. J. Hand Surg. Am. 2020, 45, 1083.e1–1083.e11. [Google Scholar] [CrossRef] [PubMed]
- Baumbach, S.F.; Binder, J.; Synek, A.; Mück, F.G.; Chevalier, Y.; Euler, E.; Langs, G.; Fischer, L. Analysis of the three-dimensional anatomical variance of the distal radius using 3D shape models. BMC Med. Imaging 2017, 17, 23. [Google Scholar] [CrossRef]
- Petrie, K.A.; Burbank, K.; Sizer, P.S.; James, C.R.; Zumwalt, M. Considerations of Sex Differences in Musculoskeletal Anatomy Between Males and Females. In The Active Female: Health Issues Throughout the Lifespan; Robert-McComb, J.J., Zumwalt, M., Fernandez-del-Valle, M., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 3–24. [Google Scholar]
- Eda, Y.; Asai, R.; Kohyama, S.; Ikumi, A.; Totoki, Y.; Yoshii, Y. Three-Dimensional Morphometric Analysis of the Volar Cortical Shape of the Lunate Facet of the Distal Radius. Diagnostics 2024, 14, 1802. [Google Scholar] [CrossRef]
- Geeta Anasuya, D.; Kumar, A.; Arasu, S.; Shanmugam, J.; Vijaianand, M.; Praveen, D. Radiographic Morphometric Analysis of the Distal Radius in the Tamil Nadu Population: A Retrospective Study. Cureus 2024, 16, e62226. [Google Scholar] [CrossRef]
- Maass, P.; Friedling, L.J. Radius morphology variation in an adult South African cadaveric sample. Anthr. Anz. 2022, 79, 289–299. [Google Scholar] [CrossRef]
- Kumar, A.; Rastogi, S.; Haider, Y.; Kumar, S.; Chauhan, S.; Passey, J. Morphometric variations of the lateral surface of calcaneus: Can standard plate sizes fit all? J. Clin. Orthop. Trauma 2021, 13, 156–162. [Google Scholar] [CrossRef]
- Gras, F.; Gottschling, H.; Schröder, M.; Marintschev, I.; Reimers, N.; Burgkart, R. Sex-specific differences of the infraacetabular corridor: A biomorphometric CT-based analysis on a database of 523 pelves. Clin. Orthop. Relat. Res. 2015, 473, 361–369. [Google Scholar] [CrossRef]
- Weaver, A.A.; Schoell, S.L.; Stitzel, J.D. Morphometric analysis of variation in the ribs with age and sex. J. Anat. 2014, 225, 246–261. [Google Scholar] [CrossRef]
- Ikumi, A.; Yoshii, Y.; Eda, Y.; Ishii, T. Computer-Aided Assessment of Three-Dimensional Standard Bone Morphology of the Distal Radius. Diagnostics 2022, 12, 3212. [Google Scholar] [CrossRef]
- Asai, R.; Ikumi, A.; Eda, Y.; Kohyama, S.; Ogawa, T.; Yoshii, Y. Relationship between Physical Characteristics and Morphological Features of the Articular Radius Surface: A Retrospective Single-Center Study. Diagnostics 2024, 14, 2005. [Google Scholar] [CrossRef] [PubMed]
- Yoshii, Y.; Totoki, Y.; Shigi, A.; Oka, K.; Ogawa, T.; Murase, T.; Ishii, T. Computer-Aided Assessment of Displacement and Reduction of Distal Radius Fractures. Diagnostics 2021, 11, 719. [Google Scholar] [CrossRef] [PubMed]
- Oura, K.; Oka, K.; Kawanishi, Y.; Sugamoto, K.; Yoshikawa, H.; Murase, T. Volar morphology of the distal radius in axial planes: A quantitative analysis. J. Orthop. Res. 2015, 33, 496–503. [Google Scholar] [CrossRef] [PubMed]
- Lorensen, W.; Cline, H. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph. Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Stockmans, F.; Dezillie, M.; Vanhaecke, J. Accuracy of 3D Virtual Planning of Corrective Osteotomies of the Distal Radius. J. Wrist Surg. 2013, 2, 306–314. [Google Scholar]
- Kong, L.; Zhang, Z.; Lu, J.; Zhang, B.; Zhou, Y.; Tian, D. Clinical Utility of 3-Dimensional Reconstruction Images to Predict Conservative Treatment Outcomes of Intra-Articular Distal Radius Fractures. Med. Sci. Monit. 2020, 26, e926894. [Google Scholar] [CrossRef]
- Dankelman, L.H.M.; Barvelink, B.; Verhofstad, M.H.J.; Wijffels, M.M.E.; Colaris, J.W. Traditional radiography versus computed tomography to assess reduced distal radius fractures. Eur. J. Trauma Emerg. Surg. 2024, 50, 2313–2321. [Google Scholar] [CrossRef]
- Assink, N.; Meesters, A.M.L.; Duis, K.T.; Harbers, J.S.; Ijpma, F.F.A.; van der Veen, H.C.; Doornberg, J.N.; Pijpker, P.A.J.; Kraeima, J. A Two-Step Approach for 3D-Guided Patient-Specific Corrective Limb Osteotomies. J. Pers. Med. 2022, 12, 1458. [Google Scholar] [CrossRef]
- Oldhoff, M.G.E.; Assink, N.; Kraeima, J.; de Vries, J.-P.P.M.; Duis, K.T.; Meesters, A.M.L.; Ijpma, F.F.A. 3D-assisted corrective osteotomies of the distal radius: A comparison of pre-contoured conventional implants versus patient-specific implants. Eur. J. Trauma Emerg. Surg. 2024, 50, 37–47. [Google Scholar] [CrossRef]
- Yan, H.; Sato, K.; Takahashi, G.; Mimata, Y.; Murakami, K.; Doita, M. Load Distribution in Dorsally-Angulated Distal Radius Deformity Using Finite Element Analysis. J. Hand Surg. Am. 2023, 48, 1062.e1–1062.e6. [Google Scholar] [CrossRef]
- Matsuura, Y.; Rokkaku, T.; Kuniyoshi, K.; Takahashi, K.; Suzuki, T.; Kanazuka, A.; Akasaka, T.; Hirosawa, N.; Iwase, M.; Yamazaki, A.; et al. Smith’s fracture generally occurs after falling on the palm of the hand. J. Orthop. Res. 2017, 35, 2435–2441. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, Y.Q.; Wang, G.H.; Li, K.; Wang, J.; Ni, M. Melone’s concept revisited in comminuted distal radius fractures: The three-dimensional CT mapping. J. Orthop. Surg. Res. 2020, 15, 222. [Google Scholar] [CrossRef] [PubMed]
- Brink, P.R.; Rikli, D.A. Four-Corner Concept: CT-Based Assessment of Fracture Patterns in Distal Radius. J. Wrist Surg. 2016, 5, 147–151. [Google Scholar] [PubMed]
- Smees, C.J.; van Es, E.M.; Tuijthof, G.J.M.; Colaris, J.W.; de Graaff, F.; Vochteloo, A.J.H. A comparison of 3-D CT and 2-D plain radiograph measurements of the wrist in extra-articular malunited fractures of the distal radius. J. Hand Surg. Eur. 2024, 49, 546–553. [Google Scholar] [CrossRef]
- Garcia-Elias, M.; An, K.N.; Amadio, P.C.; Cooney, W.P.; Linscheid, R.L. Reliability of carpal angle determinations. J. Hand Surg. Am. 1989, 14, 1017–1021. [Google Scholar] [CrossRef]
- Victor, J. Rotational alignment of the distal femur: A literature review. Orthop. Traumatol. Surg. Res. 2009, 95, 365–372. [Google Scholar] [CrossRef]
- Cirpar, M.; Gudemez, E.; Cetik, O.; Turker, M.; Eksioglu, F. Rotational deformity affects radiographic measurements in distal radius malunion. Eur. J. Orthop. Surg. Traumatol. 2011, 21, 13–20. [Google Scholar] [CrossRef]
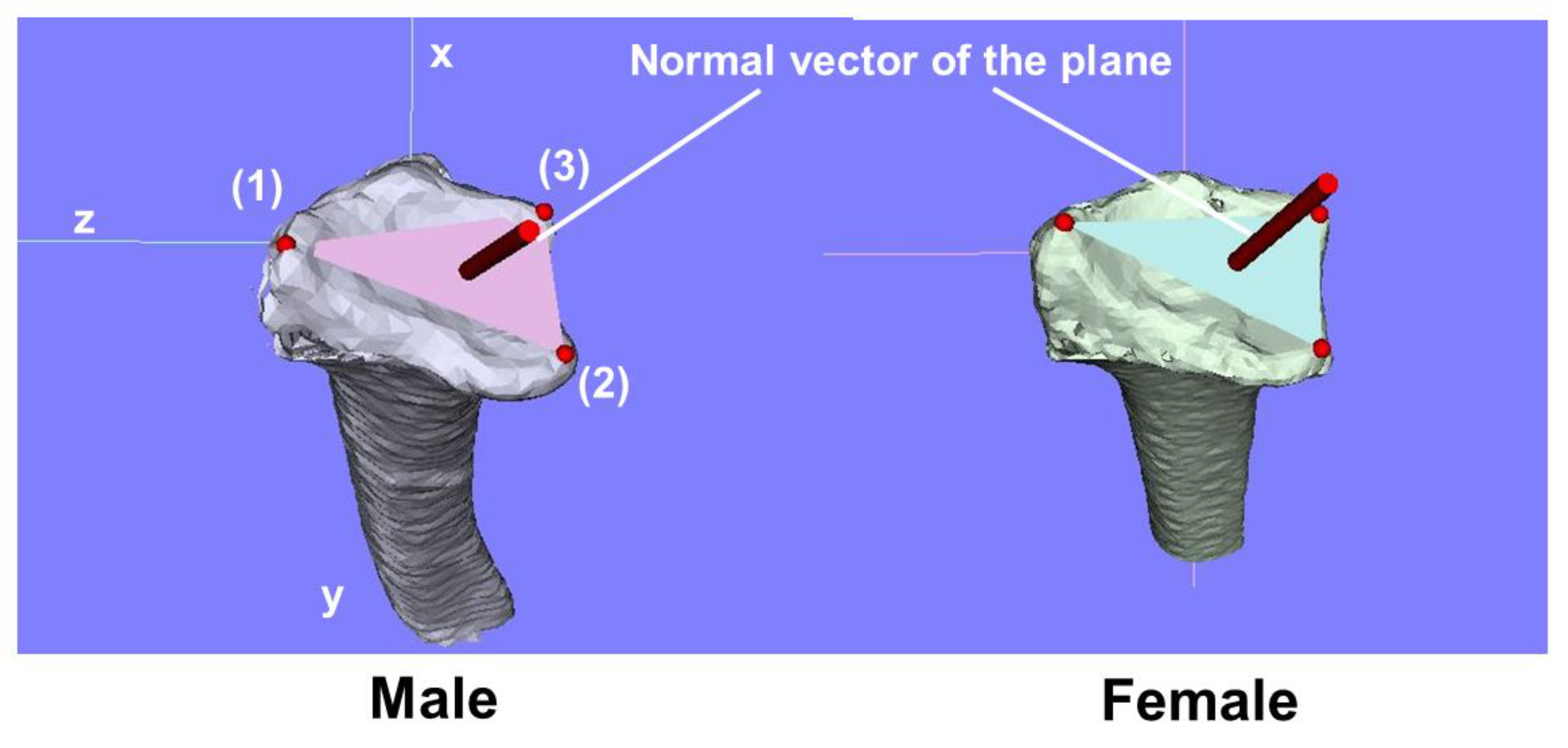
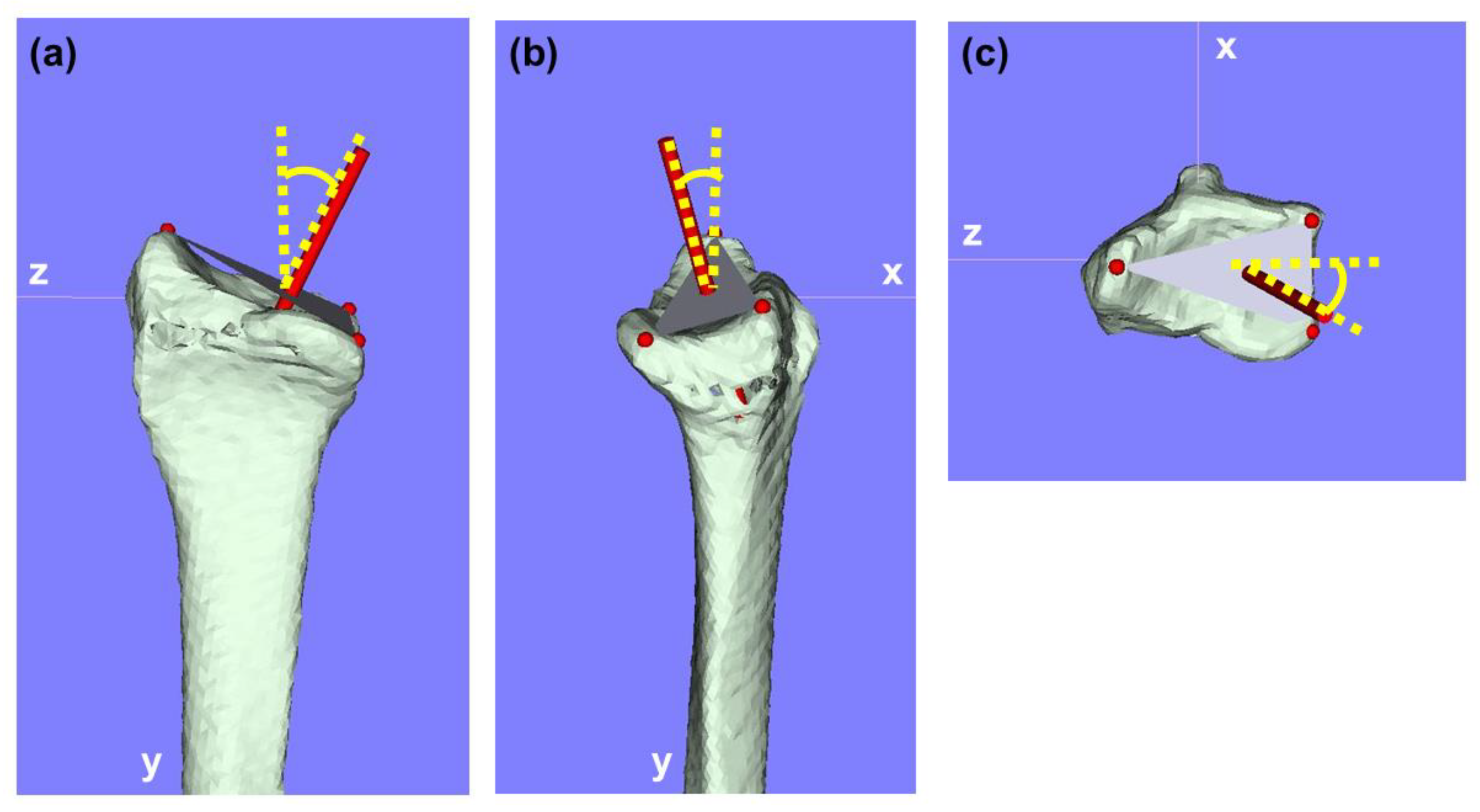

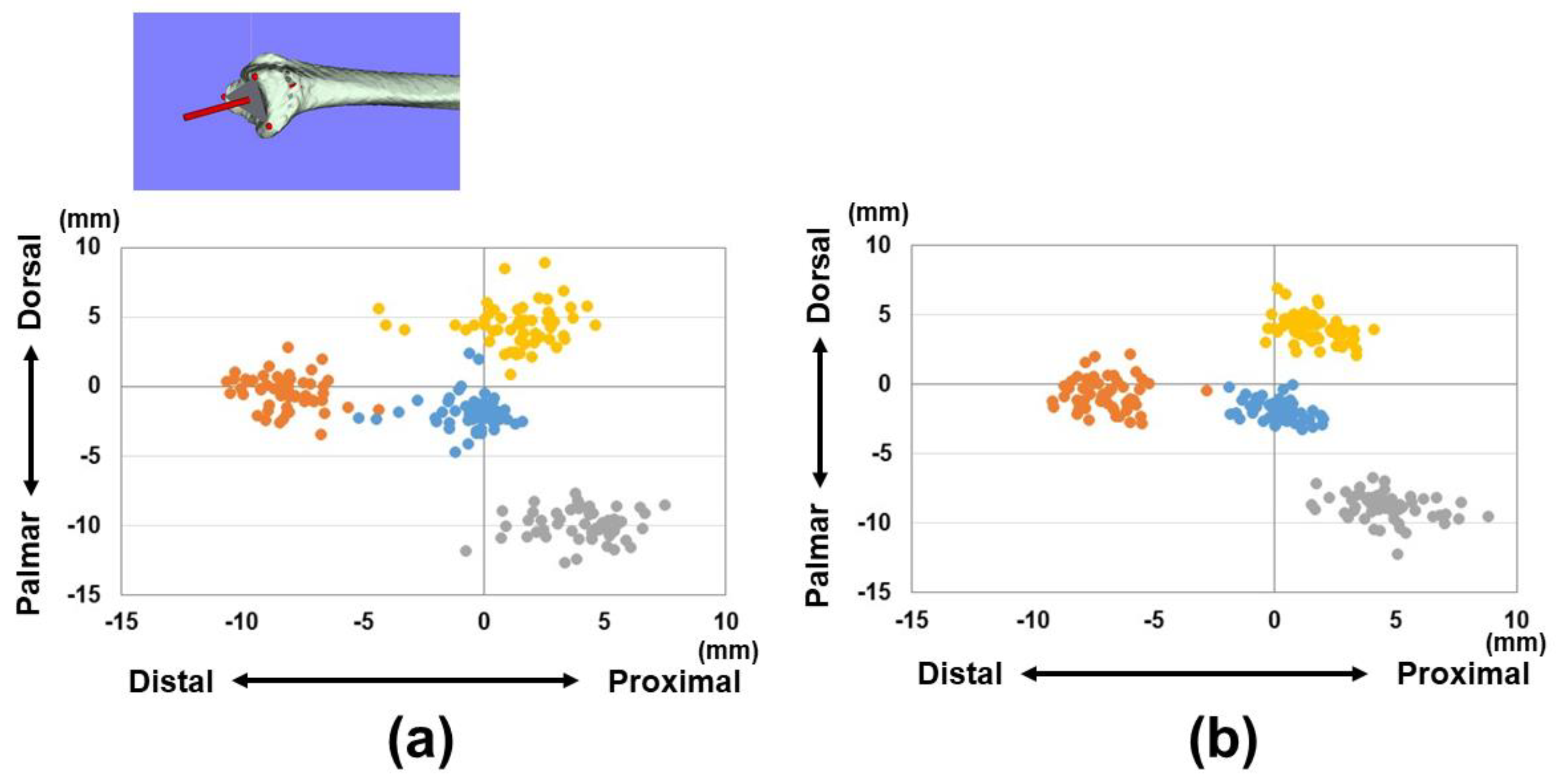

| Male | Female | |||||||
|---|---|---|---|---|---|---|---|---|
| Avg. (SD) (mm) | x | y | z | Total | X | y | z | Total |
| Reference points | ||||||||
| 1 | −0.5 (1.2) | −8.2 (1.3) | 11.6 (1.4) | 14.3 (1.4) | −0.8 (1.1) | −7.0 (1.2) | 10.5 (1.0) | 12.6 (1.0) |
| 2 | −10.0 (1.1) | 4.1 (1.6) | −16.2 (1.5) | 19.4 (1.4) | −8.9 (1.0) | 4.6 (1.5) | −13.7 (1.0) | 16.9 (1.2) |
| 3 | 4.4 (1.5) | 1.4 (1.8) | −15.0 (1.4) | 15.7 (1.6) | 4.0 (1.0) | 1.6 (1.1) | −13.4 (0.9) | 14.1 (0.8) |
| Barycenter | −2.0 (1.2) | −0.5 (1.3) | −5.0 (1.7) | 5.6 (1.7) | −1.9 (0.7) | 0.2 (0.9) | −4.1 (1.2) | 4.7 (1.1) |
| Parameters | Male | Female |
| Vector components | ||
| A | −0.14 ± 0.09 | −0.21 ± 0.08 * |
| B | −0.92 ± 0.02 | −0.90 ± 0.03 * |
| C | −0.36 ± 0.07 | −0.36 ± 0.05 |
| Angles of vectors | ||
| xy-plane | 8.9 ± 5.4° | 12.9 ± 5.0° * |
| yz-plane | 21.3 ± 4.1° | 22.1 ± 3.2° |
| xz-plane | 22.2 ± 14.8° | 28.8 ± 10.1° * |
| Angle parameters | ||
| 3D-RI | 24.0 ± 3.9° | 25.9 ± 3.7° |
| 3D-PT | 10.6 ± 5.4° | 13.4 ± 5.3° * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikumi, A.; Asai, R.; Eda, Y.; Uchida, T.; Kohyama, S.; Ogawa, T.; Yoshii, Y. A Novel Method to Represent the Three-Dimensional Inclination of the Distal Radius Joint Surface. Diagnostics 2025, 15, 345. https://doi.org/10.3390/diagnostics15030345
Ikumi A, Asai R, Eda Y, Uchida T, Kohyama S, Ogawa T, Yoshii Y. A Novel Method to Represent the Three-Dimensional Inclination of the Distal Radius Joint Surface. Diagnostics. 2025; 15(3):345. https://doi.org/10.3390/diagnostics15030345
Chicago/Turabian StyleIkumi, Akira, Reo Asai, Yusuke Eda, Tooru Uchida, Sho Kohyama, Takeshi Ogawa, and Yuichi Yoshii. 2025. "A Novel Method to Represent the Three-Dimensional Inclination of the Distal Radius Joint Surface" Diagnostics 15, no. 3: 345. https://doi.org/10.3390/diagnostics15030345
APA StyleIkumi, A., Asai, R., Eda, Y., Uchida, T., Kohyama, S., Ogawa, T., & Yoshii, Y. (2025). A Novel Method to Represent the Three-Dimensional Inclination of the Distal Radius Joint Surface. Diagnostics, 15(3), 345. https://doi.org/10.3390/diagnostics15030345






