Validation of Body Surface Area Equations for Estimating Fat-Free Mass by Dual X-Ray Absorptiometry in a Regional Chilean Sample Aged 4 to 85 Years
Abstract
1. Introduction
2. Materials and Methods
2.1. Type of Study and Sample
2.2. Techniques and Procedures
2.2.1. Anthropometry
2.2.2. iDXA Analysis
2.2.3. Statistics
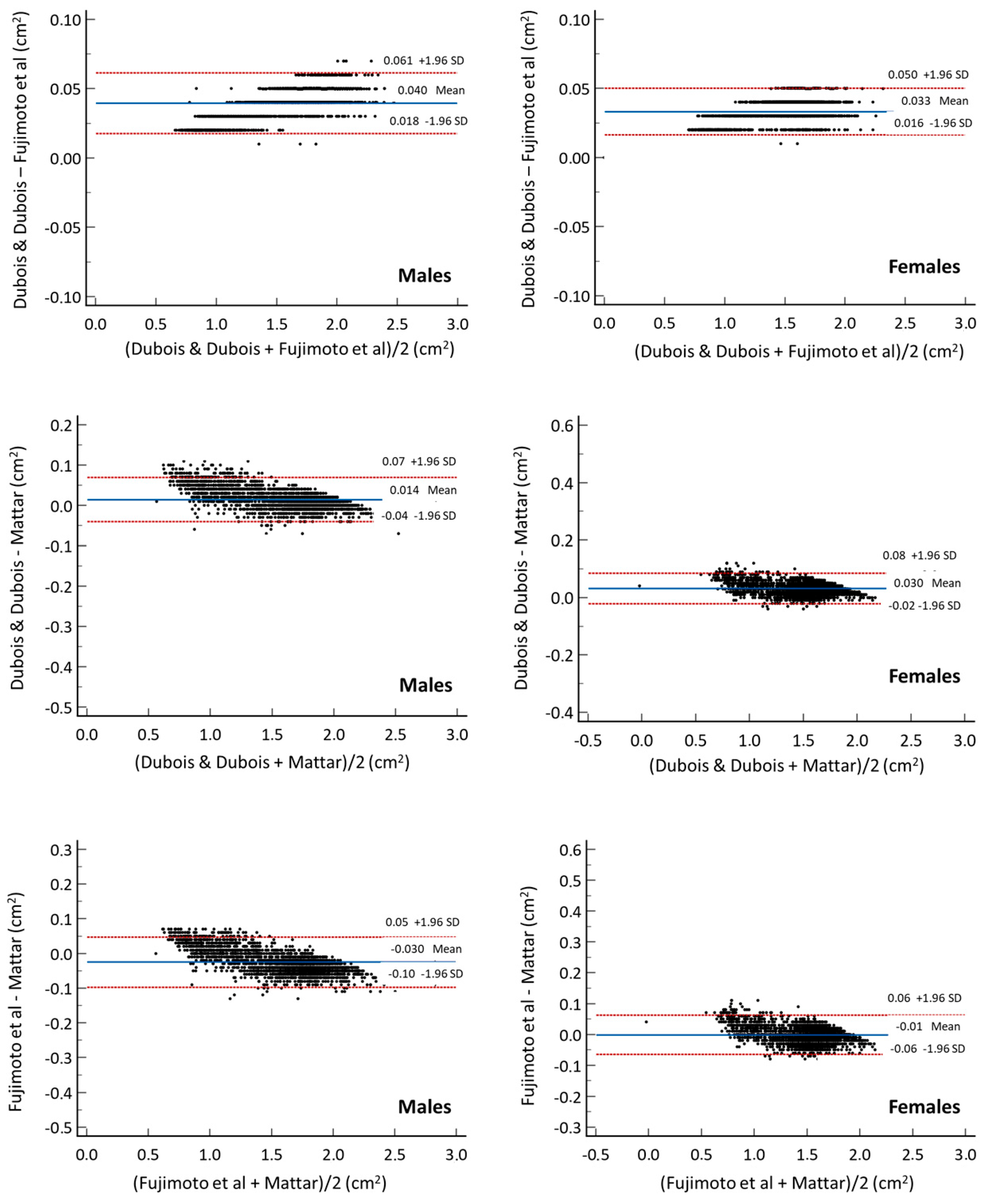
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oliver, C.J.; Climstein, M.; Rosic, N.; Bosy-Westphal, A.; Tinsley, G.; Myers, S. Fat-Free Mass: Friend or Foe to Metabolic Health? J. Cachexia Sarcopenia Muscle 2025, 16, e13714. [Google Scholar] [CrossRef]
- Heymsfield, S.B.; Brown, J.; Ramirez, S.; Prado, C.M.; Tinsley, G.M.; Gonzalez, M.C. Are Lean Body Mass and Fat-Free Mass the Same or Different Body Components? A Critical Perspective. Adv. Nutr. 2024, 15, 100335. [Google Scholar] [CrossRef]
- de Moraes, A.M.; Vidal-Espinoza, R.; Bergamo, R.R.; Gómez-Campos, R.; de Lazari, E.; de Campos, L.F.C.C.; Sulla-Torres, J.; Cossio-Bolaños, M. Prediction of fat-free mass from body surface area in young basketball players. BMC Sports Sci. Med. Rehabil. 2024, 16, 65. [Google Scholar] [CrossRef]
- Katzmarzyk, P.T.; Heymsfield, S.B.; Bouchard, C. Clinical utility of visceral adipose tissue for the identification of cardiometabolic risk in white and African American adults. Am. J. Clin. Nutr. 2013, 97, 480–486. [Google Scholar] [CrossRef] [PubMed]
- Kuriyan, R. Body composition techniques. Indian J. Med. Res. 2018, 148, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Ofenheimer, A.; Breyer-Kohansal, R.; Hartl, S.; Burghuber, O.C.; Krach, F.; Schrott, A.; Wouters, E.F.M.; Franssen, F.M.E.; Breyer, M.K. Reference values of body composition parameters and visceral adipose tissue (VAT) by DXA in adults aged 18–81 years-results from the LEAD cohort. Eur. J. Clin. Nutr. 2020, 74, 1181–1191. [Google Scholar] [CrossRef] [PubMed]
- Scafoglieri, A.; Clarys, J.P. Dual energy X-ray absorptiometry: Gold standard for muscle mass? J. Cachexia Sarcopenia Muscle 2018, 9, 786–787. [Google Scholar] [CrossRef]
- Poortmans, J.R.; Boisseau, N.; Moraine, J.J.; Moreno-Reyes, R.; Goldman, S. Estimation of total-body skeletal muscle mass in children and adolescents. Med. Sci. Sports Exerc. 2005, 37, 316–322. [Google Scholar] [CrossRef]
- Henriksson, P.; Cadenas-Sanchez, C.; Leppänen, M.H.; Delisle Nyström, C.; Ortega, F.B.; Pomeroy, J.; Ruiz, J.R.; Löf, M. Associations of Fat Mass and Fat-Free Mass with Physical Fitness in 4-Year-Old Children: Results from the MINISTOP Trial. Nutrients 2016, 8, 473. [Google Scholar] [CrossRef]
- Córdoba-Rodríguez, D.P.; Iglesia, I.; Gomez-Bruton, A.; Rodríguez, G.; Casajús, J.A.; Morales-Devia, H.; Moreno, L.A. Fat-free/lean body mass in children with insulin resistance or metabolic syndrome: A systematic review and meta-analysis. BMC Pediatr. 2022, 22, 58. [Google Scholar] [CrossRef] [PubMed]
- Pezoa-Fuentes, P.; Cossio-Bolaños, M.; Urra-Albornoz, C.; Alvear-Vasquez, F.; Lazari, E.; Urzua-Alul, L.; de Campos, L.F.C.C.; Gomez-Campos, R. Fat-free mass and maturity status are determinants of physical fitness performance in schoolchildren and adolescents. J. Pediatr. 2023, 99, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Wood, R.J.; Gregory, S.M.; Sawyer, J.; Milch, C.M.; Matthews, T.D.; Headley, S.A. Preservation of fat-free mass after two distinct weight loss diets with and without progressive resistance exercise. Metab. Syndr. Relat. Disord. 2012, 10, 167–174. [Google Scholar] [CrossRef]
- Bai, M.; Wang, R.; Zhu, L.; Li, G.; Yuan, D.; Wang, L.; Jin, T. Age-related differences in limb fat-free mass and fat mass in healthy Chinese Adults. Sci. Rep. 2018, 8, 8013. [Google Scholar] [CrossRef]
- Walowski, C.O.; Braun, W.; Maisch, M.J.; Jensen, B.; Peine, S.; Norman, K.; Müller, M.J.; Bosy-Westphal, A. Reference Values for Skeletal Muscle Mass—Current Concepts and Methodological Considerations. Nutrients 2020, 12, 755. [Google Scholar] [CrossRef] [PubMed]
- Rogeri, P.S.; Zanella, R., Jr.; Martins, G.L.; Garcia, M.D.A.; Leite, G.; Lugaresi, R.; Gasparini, S.O.; Sperandio, G.A.; Ferreira, L.H.B.; Souza-Junior, T.P.; et al. Strategies to Prevent Sarcopenia in the Aging Process: Role of Protein Intake and Exercise. Nutrients 2021, 14, 52. [Google Scholar] [CrossRef]
- Rush, E.C.; Chandu, V.; Plank, L.D. Prediction of fat-free mass by bioimpedance analysis in migrant Asian Indian men and women: A cross validation study. Int. J. Obes. 2006, 30, 1125–1131. [Google Scholar] [CrossRef]
- Dasgupta, R.; Anoop, S.; Samuel, P.; Kurian, M.E.; Inbakumari, M.; Finney, G.; Thomas, N. Bioimpedance analysis with a novel predictive equation—A reliable technique to estimate fat free mass in birth weight based cohorts of Asian Indian males. Diabetes Metab. Syndr. 2019, 13, 738–742. [Google Scholar] [CrossRef]
- Kawakami, R.; Miyachi, M.; Tanisawa, K.; Ito, T.; Usui, C.; Midorikawa, T.; Torii, S.; Ishii, K.; Suzuki, K.; Sakamoto, S.; et al. Development and validation of a simple anthropometric equation to predict appendicular skeletal muscle mass. Clin. Nutr. 2021, 40, 5523–5530. [Google Scholar] [CrossRef]
- Teixeira, P.J.; Sardinha, L.B.; Going, S.B.; Lohman, T.G. Total and regional fat and serum cardiovascular disease risk factors in lean and obese children and adolescents. Obes. Res. 2001, 9, 432–442. [Google Scholar] [CrossRef] [PubMed]
- Wells, J.C.; Fewtrell, M.S. Measuring body composition. Arch. Dis. Child. 2006, 91, 612–617. [Google Scholar] [CrossRef]
- Sheikhsaraf, B.; Allah, N.H.; Ali, A.M. Association of body surface area and body composition with heart structural characteristics of female swimmers. Int. J. Exerc. Sci. 2010, 3, 97–101. [Google Scholar] [CrossRef]
- Zanforlini, B.M.; Alessi, A.; Pontarin, A.; De Rui, M.; Zoccarato, F.; Seccia, D.M.; Trevisan, C.; Brunello, A.; Basso, U.; Manzato, E.; et al. Association of body surface area with fat mass, free fat mass and total weight in healthy individuals, and implications for the dosage of cytotoxic drugs. Clin. Nutr. ESPEN 2021, 43, 471–477. [Google Scholar] [CrossRef]
- Looney, D.P.; Potter, A.W.; Arcidiacono, D.M.; Santee, W.R.; Friedl, K.E. Body surface area equations for physically active men and women. Am. J. Hum. Biol. 2023, 35, e23823. [Google Scholar] [CrossRef]
- Gibson, S.; Numa, A. The importance of metabolic rate and the folly of body surface area calculations. Anaesthesia 2003, 58, 50–55. [Google Scholar] [CrossRef]
- Agache, P.; Fanian, F. Body Surface Area. In Agache’s Measuring the Skin; Humbert, P., Fanian, F., Maibach, H., Agache, P., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- United Nations Development Programme (UNDP). Human Development Report 2019. Beyond Income, Beyond Averages, Beyond Today: Inequalities in Human Development in the 21st Century. UNDP 2019. Available online: https://hdr.undp.org/content/human-development-report-2019 (accessed on 8 April 2025).
- Ross, W.D.; Marfell-Jones, M.J. Kinanthropometry. In Physiological Testing of Eliteathlete; MacDougall, J.D., Wenger, H.A., Geeny, H.J., Eds.; Human Kinetics: London, UK, 1991; Volume 223, pp. 308–314. [Google Scholar]
- DuBois, D.; DuBois, E.F. Clinical calorimetry: Tenth paper a formula to estimate the approximate surface area if height and weight be known. Arch. Intern. Med. 1916, 17, 863–871. [Google Scholar] [CrossRef]
- Boyd, E. The Growth of the Surface Area of the Human Body; University of Minnesota Press: Minneapolis, MN, USA, 1935. [Google Scholar]
- Costeff, H. A simple empirical formula for calculating approximate surface area in children. Arch. Dis. Child. 1966, 41, 681–683. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, S.; Watanabe, T.; Sakamoto, A.; Yukawa, K.; Morimoto, K. Studies on the Physical Surface Area of Japanese. Nihon Eiseigaku zasshi. Jpn. J. hygiene 1968, 23, 443–450. [Google Scholar] [CrossRef]
- Haycock, G.B.; Schwartz, G.J.; Wisotsky, D.H. Geometric method for measuring body surface area: A height-weight formula validated in infants, children, and adults. J. Pediatr. 1978, 93, 62–66. [Google Scholar] [CrossRef] [PubMed]
- Mosteller, R.D. Simplified calculation of body-surface area. N. Engl. J. Med. 1987, 317, 1098. [Google Scholar] [CrossRef]
- Mattar, J.A. A simple calculation to estimate body surface area in adults and its correlation with the Du Bois formula. Crit. Care Med. 1989, 17, 846–847. [Google Scholar] [CrossRef] [PubMed]
- Nana, A.; Slater, G.J.; Hopkins, W.G.; Burke, L.M. Effects of daily activities on dual-energy X-ray absorptiometry measurements of body composition in active people. Med. Sci. Sports Exerc. 2012, 44, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.I. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [PubMed]
- Pan, H.; Cole, T. LMS Chartmaker. 2006. Available online: http://www.healthforallchildren.co.uk (accessed on 28 March 2025).
- Cole, T.J.; Bellizzi, M.C.; Flegal, K.M.; Dietz, W.H. Establishing a standard definition for child overweight and obesity worldwide: International survey. BMJ (Clin. Res. Ed.) 2000, 320, 1240–1243. [Google Scholar] [CrossRef]
- Fujimoto, S.; Watanabe, T. Studies on the Body Surface Area of Japanese. Acta Med. Nagasaki. 1969, 13, 1–13. [Google Scholar]
- Zafar, M.A.; Li, Y.; Rizzo, J.A.; Charilaou, P.; Saeyeldin, A.; Velasquez, C.A.; Mansour, A.M.; Bin Mahmood, S.U.; Ma, W.G.; Brownstein, A.J.; et al. Height alone, rather than body surface area, suffices for risk estimation in ascending aortic aneurysm. J. Thorac. Cardiovasc. Surg. 2018, 155, 1938–1950. [Google Scholar] [CrossRef]
- Hull, H.R.; Thornton, J.; Wang, J.; Pierson, R.N., Jr.; Kaleem, Z.; Pi-Sunyer, X.; Heymsfield, S.; Albu, J.; Fernandez, J.R.; Vanitallie, T.B.; et al. Fat-free mass index: Changes and race/ethnic differences in adulthood. Int. J. Obes. 2011, 35, 121–127. [Google Scholar] [CrossRef]
- Glass, D.; Roubenoff, R. Recent advances in the biology and therapy of muscle wasting. Ann. N. Y Acad. Sci. 2010, 1211, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Alabadi, B.; Civera, M.; De la Rosa, A.; Martinez-Hervas, S.; Gomez-Cabrera, M.C.; Real, J.T. Low Muscle Mass Is Associated with Poorer Glycemic Control and Higher Oxidative Stress in Older Patients with Type 2 Diabetes. Nutrients 2023, 15, 3167. [Google Scholar] [CrossRef]
- Hoffmann, M.D.; Colley, R.C.; Doyon, C.Y.; Wong, S.L.; Tomkinson, G.R.; Lang, J.J. Normative-referenced percentile values for physical fitness among Canadians. Health Rep. 2019, 30, 14–22. [Google Scholar] [CrossRef]
- Kuczmarski, R.J.; Ogden, C.L.; Grummer-Strawn, L.M.; Flegal, K.M.; Guo, S.S.; Wei, R.; Mei, Z.; Curtin, L.R.; Roche, A.F.; Johnson, C.L. CDC growth charts: United States. Adv. Data 2000, 314, 1–27. [Google Scholar]
- Fryar, C.D.; Gu, Q.; Ogden, C.L.; Flegal, K.M. Anthropometric Reference Data for Children and Adults: United States, 2011-2014. Vital Health Stat. 3 Anal. Stud. 2016, 39, 1–46. [Google Scholar]
- Amaral, M.A.; Mundstock, E.; Scarpatto, C.H.; Cañon-Montañez, W.; Mattiello, R. Reference percentiles for bioimpedance body composition parameters of healthy individuals: A cross-sectional study. Clinics 2022, 77, 100078. [Google Scholar] [CrossRef] [PubMed]
- Amuna, P.; Zotor, F.B. Epidemiological and nutrition transition in developing countries: Impact on human health and development. Proc. Nutr. Soc. 2008, 67, 82–90. [Google Scholar] [CrossRef] [PubMed]
| n° | Authors | Years | Subjects | Equation |
|---|---|---|---|---|
| 1 | Dubois & Dubois [28] | 1916 | All ages | BSA = 0.007184 × weight (kg)0.425 × height (cm)0.725 |
| 2 | Boyd [29] | 1935 | Children | BSA = 4.688 × weight (kg)(0.8168−0.0154×log weight (kg)) |
| 3 | Costeff [30] | 1966 | All ages | BSA = (4 × weight (kg) + 7)/90 + weight (kg) |
| 4 | Fujimoto et al. [31] | 1969 | All ages | BSA = 0.008883 × Weight0.444 × Height0.663 |
| 5 | Haycock et al. [32] | 1978 | All ages | BSA = 0.024265 × Weight0.5378 × Height0.3964 |
| 6 | Mosteller [33] | 1987 | Adults | BSA = √(weight (kg) × height (cm))/3600 |
| 7 | Mattar [34] | 1981 | Adults | BSA = (Height + Weight − 60)/100 |
| Age (Years) | n | Anthropometry | BSA Equations | DXA | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weight (kg) | Height (cm) | Dubois & Dubois [28] (m2) | Boyd [29] (m2) | Costeff [30] (m2) | Fujimoto et al. [31] (m2) | Haycock et al. [32] (m2) | Mosteller [33] (m2) | Mattar [34] (m2) | LBM (kg) | ||||||||||||
| X | SD | X | SD | X | SD | X | SD | X | SD | X | SD | X | SD | X | SD | X | SD | X | SD | ||
| Males | |||||||||||||||||||||
| 4–7 | 300 | 26.1 | 6.8 | 120.2 | 8.2 | 0.92 | 0.1 | 0.95 | 0.2 | 0.95 | 0.2 | 0.9 | 0.1 | 0.93 | 0.2 | 0.93 | 0.1 | 0.86 | 0.1 | 19.21 | 5.5 |
| 8–11 | 498 | 39.1 | 11 | 139.1 | 9.3 | 1.22 | 0.2 | 1.24 | 0.2 | 1.25 | 0.2 | 1.19 | 0.2 | 1.22 | 0.2 | 1.22 | 0.2 | 1.18 | 0.2 | 27.16 | 6.9 |
| 12–15 | 754 | 57.9 | 12 | 163.2 | 11 | 1.62 | 0.2 | 1.62 | 0.2 | 1.6 | 0.2 | 1.57 | 0.2 | 1.61 | 0.2 | 1.61 | 0.2 | 1.61 | 0.2 | 44.46 | 9.6 |
| 16–19 | 784 | 71.3 | 12 | 171.8 | 6.8 | 1.83 | 0.2 | 1.85 | 0.2 | 1.8 | 0.2 | 1.79 | 0.2 | 1.85 | 0.2 | 1.84 | 0.2 | 1.83 | 0.2 | 55.27 | 7.6 |
| 20–39 | 362 | 77.9 | 12 | 173.4 | 7 | 1.92 | 0.2 | 1.95 | 0.2 | 1.89 | 0.2 | 1.87 | 0.2 | 1.94 | 0.2 | 1.93 | 0.2 | 1.91 | 0.2 | 58.66 | 9.0 |
| 40–59 | 75 | 85.8 | 13 | 169.7 | 6.2 | 1.97 | 0.2 | 2.04 | 0.2 | 1.98 | 0.2 | 1.92 | 0.2 | 2.03 | 0.2 | 2.01 | 0.2 | 1.95 | 0.2 | 57.92 | 8 |
| 60–79 | 75 | 80.9 | 13 | 167 | 6.6 | 1.9 | 0.2 | 1.97 | 0.2 | 1.92 | 0.2 | 1.85 | 0.2 | 1.95 | 0.2 | 1.86 | 0.2 | 1.88 | 0.2 | 53.72 | 9.4 |
| >80 y | 20 | 72.2 | 3 | 163.6 | 4.5 | 1.78 | 0.1 | 1.84 | 0.1 | 1.82 | 0 | 1.74 | 0.1 | 1.83 | 0.1 | 1.71 | 0.2 | 1.76 | 0.1 | 49.12 | 3.7 |
| Females | |||||||||||||||||||||
| 4–7 | 248 | 25.8 | 6 | 119.4 | 11 | 0.91 | 0.1 | 0.94 | 0.1 | 0.94 | 0.2 | 0.89 | 0.1 | 0.92 | 0.1 | 0.92 | 0.1 | 0.85 | 0.2 | 17.8 | 4.4 |
| 8–11 | 438 | 40.2 | 10 | 141.1 | 12 | 1.24 | 0.2 | 1.27 | 0.2 | 1.27 | 0.2 | 1.21 | 0.2 | 1.25 | 0.2 | 1.25 | 0.2 | 1.21 | 0.2 | 26.19 | 6.0 |
| 12–15 | 427 | 57 | 11 | 157.2 * | 6.8 | 1.56 | 0.2 | 1.59 | 0.2 | 1.58 | 0.2 | 1.52 | 0.2 | 1.58 | 0.2 | 1.57 | 0.2 | 1.54 | 0.2 | 37.42 * | 6.2 |
| 16–19 | 360 | 62.9 * | 12 | 158.9 * | 5.6 | 1.64 * | 0.2 | 1.69 * | 0.2 | 1.68 * | 0.2 | 1.60 * | 0.2 | 1.67 * | 0.2 | 1.66 * | 0.2 | 1.62 * | 0.2 | 39.56 * | 5.3 |
| 20–39 | 313 | 65.68 * | 13 | 160.4 * | 6.6 | 1.68 * | 0.2 | 1.73 * | 0.2 | 1.72 * | 0.2 | 1.64 * | 0.2 | 1.72 * | 0.2 | 1.7 * | 0.2 | 1.66 * | 0.2 | 41.45 * | 7.6 |
| 40–59 | 278 | 70.6 * | 13 | 156.4 * | 7.9 | 1.7 * | 0.1 | 1.79 * | 0.2 | 1.79 * | 0.2 | 1.67 * | 0.1 | 1.77 * | 0.2 | 1.74 * | 0.2 | 1.67 * | 0.2 | 41.22 * | 7.4 |
| 60–79 | 539 | 69.1 * | 12 | 152.2 * | 6.5 | 1.65 * | 0.2 | 1.75 * | 0.2 | 1.77 * | 0.2 | 1.62 * | 0.2 | 1.72 * | 0.2 | 1.71 * | 0.2 | 1.61 * | 0.2 | 37.78 * | 9.2 |
| >80 y | 22 | 66.7 * | 14 | 153.5 * | 7.3 | 1.64 * | 0.2 | 1.72 * | 0.2 | 1.73 * | 0.2 | 1.61 * | 0.2 | 1.7 * | 0.2 | 1.69 * | 0.2 | 1.6 * | 0.2 | 35.50 * | 5.2 |
| BSA/Age (Years) | Males | Females | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | SD | R | R2 | SEE | %EE | X | SD | R | R2 | SEE | %EE | |
| Dubois & Dubois [28] | ||||||||||||
| 4.0–11.9 y | 1.10 | 0.22 | 0.761 | 0.58 | 0.049 | 4.39 | 1.12 | 0.23 | 0.855 | 0.73 | 0.035 | 3.13 |
| 12.0–19.9 y | 1.73 | 0.21 | 0.786 | 0.62 | 0.063 | 3.66 | 1.60 | 0.16 | 0.771 | 0.59 | 0.038 | 2.35 |
| 20.0–39.9 y | 1.92 | 0.16 | 0.613 | 0.38 | 0.080 | 4.15 | 1.68 | 0.16 | 0.546 | 0.30 | 0.064 | 3.77 |
| 40.0–59.9 | 1.97 | 0.16 | 0.733 | 0.54 | 0.055 | 2.80 | 1.70 | 0.14 | 0.608 | 0.37 | 0.059 | 3.46 |
| >60 y | 1.88 | 0.16 | 0.664 | 0.44 | 0.068 | 3.63 | 1.65 | 0.18 | 0.492 | 0.24 | 0.088 | 5.33 |
| All ages | 1.59 | 0.37 | 0.910 | 0.83 | 0.061 | 3.85 | 1.51 | 0.30 | 0.83 | 0.69 | 0.055 | 3.66 |
| Fujimoto et al. [31] | ||||||||||||
| 4.0–11.9 y | 1.08 | 0.22 | 0.760 | 0.58 | 0.049 | 4.50 | 1.10 | 0.23 | 0.855 | 0.73 | 0.035 | 3.20 |
| 12.0–19.9 y | 1.68 | 0.21 | 0.784 | 0.61 | 0.063 | 3.77 | 1.56 | 0.16 | 0.769 | 0.59 | 0.038 | 2.41 |
| 20.0–39.9 y | 1.87 | 0.16 | 0.611 | 0.37 | 0.080 | 4.26 | 1.64 | 0.16 | 0.543 | 0.30 | 0.064 | 3.87 |
| 40.0–59.9 | 1.92 | 0.15 | 0.733 | 0.54 | 0.055 | 2.86 | 1.67 | 0.14 | 0.609 | 0.37 | 0.059 | 3.52 |
| > 60 y | 1.84 | 0.16 | 0.663 | 0.44 | 0.069 | 3.72 | 1.62 | 0.18 | 0.493 | 0.24 | 0.088 | 5.43 |
| All ages | 1.55 | 0.36 | 0.911 | 0.83 | 0.061 | 3.95 | 1.47 | 0.29 | 0.833 | 0.69 | 0.055 | 3.75 |
| Mattar [34] | ||||||||||||
| 4.0–11.9 y | 1.06 | 0.23 | 0.761 | 0.58 | 0.049 | 4.57 | 1.08 | 0.25 | 0.846 | 0.72 | 0.036 | 3.34 |
| 12.0–19.9 y | 1.72 | 0.21 | 0.791 | 0.63 | 0.063 | 3.63 | 1.58 | 0.16 | 0.767 | 0.59 | 0.038 | 2.39 |
| 20.0–39.9 y | 1.91 | 0.17 | 0.614 | 0.38 | 0.079 | 4.15 | 1.66 | 0.17 | 0.548 | 0.30 | 0.063 | 3.82 |
| 40.0–59.9 | 1.95 | 0.17 | 0.739 | 0.55 | 0.055 | 2.79 | 1.67 | 0.15 | 0.618 | 0.38 | 0.058 | 3.49 |
| >60 y | 1.87 | 0.17 | 0.668 | 0.45 | 0.068 | 3.65 | 1.61 | 0.20 | 0.484 | 0.24 | 0.088 | 5.50 |
| All ages | 1.57 | 0.39 | 0.922 | 0.84 | 0.060 | 3.82 | 1.47 | 0.31 | 0.833 | 0.69 | 0.055 | 3.76 |
| L | M | S | P3 | P5 | P10 | P15 | P25 | P50 | P75 | P85 | P90 | P95 | P97 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Males | ||||||||||||||
| 4 | −0.0074 | 0.669 | 0.0012 | 0.54 | 0.55 | 0.58 | 0.59 | 0.62 | 0.67 | 0.73 | 0.77 | 0.79 | 0.83 | 0.86 |
| 5 | −0.0064 | 0.7585 | 0.0012 | 0.61 | 0.63 | 0.65 | 0.67 | 0.7 | 0.76 | 0.83 | 0.87 | 0.89 | 0.94 | 0.97 |
| 6 | −0.0055 | 0.8485 | 0.0012 | 0.69 | 0.7 | 0.73 | 0.75 | 0.78 | 0.85 | 0.92 | 0.97 | 1.00 | 1.05 | 1.08 |
| 7 | −0.0044 | 0.939 | 0.0012 | 0.76 | 0.78 | 0.81 | 0.83 | 0.87 | 0.94 | 1.02 | 1.07 | 1.1 | 1.15 | 1.19 |
| 8 | −0.0033 | 10.308 | 0.0012 | 0.83 | 0.86 | 0.89 | 0.92 | 0.95 | 1.03 | 1.12 | 1.17 | 1.2 | 1.26 | 1.3 |
| 9 | −0.0022 | 11.268 | 0.0012 | 0.91 | 0.94 | 0.97 | 1.00 | 1.04 | 1.13 | 1.22 | 1.27 | 1.31 | 1.37 | 1.41 |
| 10 | −0.0012 | 12.282 | 0.0011 | 1.00 | 1.02 | 1.06 | 1.09 | 1.14 | 1.23 | 1.33 | 1.38 | 1.42 | 1.48 | 1.52 |
| 11 | −0.0002 | 13.332 | 0.0011 | 1.08 | 1.11 | 1.16 | 1.19 | 1.24 | 1.33 | 1.44 | 1.5 | 1.54 | 1.6 | 1.64 |
| 12 | 0.0007 | 14.393 | 0.0011 | 1.17 | 1.2 | 1.25 | 1.29 | 1.34 | 1.44 | 1.55 | 1.61 | 1.65 | 1.72 | 1.76 |
| 13 | 0.0012 | 15.426 | 0.001 | 1.27 | 1.3 | 1.35 | 1.38 | 1.44 | 1.54 | 1.65 | 1.72 | 1.76 | 1.83 | 1.87 |
| 14 | 0.0011 | 16.377 | 0.001 | 1.35 | 1.39 | 1.44 | 1.47 | 1.53 | 1.64 | 1.75 | 1.82 | 1.86 | 1.93 | 1.97 |
| 15 | 0.0005 | 17.185 | 0.001 | 1.43 | 1.46 | 1.52 | 1.55 | 1.61 | 1.72 | 1.83 | 1.9 | 1.95 | 2.01 | 2.06 |
| 16 | −0.0004 | 17.811 | 0.0009 | 1.49 | 1.53 | 1.58 | 1.62 | 1.67 | 1.78 | 1.9 | 1.96 | 2.01 | 2.08 | 2.13 |
| 17 | −0.0014 | 18.257 | 0.0009 | 1.54 | 1.57 | 1.63 | 1.66 | 1.72 | 1.83 | 1.94 | 2.01 | 2.05 | 2.12 | 2.17 |
| 18 | −0.0023 | 18.569 | 0.0009 | 1.58 | 1.61 | 1.66 | 1.7 | 1.75 | 1.86 | 1.97 | 2.04 | 2.08 | 2.15 | 2.2 |
| 19 | −0.003 | 18.793 | 0.0009 | 1.6 | 1.63 | 1.68 | 1.72 | 1.77 | 1.88 | 1.99 | 2.06 | 2.11 | 2.18 | 2.22 |
| 20–39 | −0.0036 | 18.954 | 0.0009 | 1.62 | 1.65 | 1.7 | 1.74 | 1.79 | 1.9 | 2.01 | 2.07 | 2.12 | 2.19 | 2.24 |
| 40–59 | −0.004 | 19.055 | 0.0008 | 1.63 | 1.66 | 1.71 | 1.75 | 1.8 | 1.91 | 2.02 | 2.08 | 2.13 | 2.2 | 2.25 |
| 60–79 | −0.0043 | 1.911 | 0.0008 | 1.64 | 1.67 | 1.72 | 1.75 | 1.81 | 1.91 | 2.02 | 2.09 | 2.13 | 2.2 | 2.25 |
| >80 | −0.0045 | 1.915 | 0.0008 | 1.65 | 1.68 | 1.73 | 1.76 | 1.81 | 1.91 | 2.03 | 2.09 | 2.13 | 2.2 | 2.25 |
| Females | ||||||||||||||
| 4 | −0.0011 | 0.6711 | 0.0012 | 0.53 | 0.55 | 0.57 | 0.59 | 0.62 | 0.67 | 0.73 | 0.76 | 0.79 | 0.82 | 0.85 |
| 5 | 0.0004 | 0.7633 | 0.0012 | 0.61 | 0.63 | 0.65 | 0.67 | 0.7 | 0.76 | 0.83 | 0.86 | 0.89 | 0.93 | 0.96 |
| 6 | 0.0018 | 0.8573 | 0.0012 | 0.68 | 0.7 | 0.73 | 0.76 | 0.79 | 0.86 | 0.93 | 0.97 | 1.00 | 1.04 | 1.07 |
| 7 | 0.0032 | 0.9547 | 0.0012 | 0.76 | 0.78 | 0.82 | 0.84 | 0.88 | 0.95 | 1.03 | 1.08 | 1.11 | 1.15 | 1.18 |
| 8 | 0.0046 | 1.056 | 0.0012 | 0.84 | 0.87 | 0.91 | 0.93 | 0.98 | 1.06 | 1.14 | 1.19 | 1.22 | 1.27 | 1.3 |
| 9 | 0.0058 | 11.606 | 0.0011 | 0.92 | 0.95 | 1.00 | 1.03 | 1.07 | 1.16 | 1.25 | 1.3 | 1.34 | 1.39 | 1.42 |
| 10 | 0.0068 | 12.646 | 0.0011 | 1.01 | 1.04 | 1.09 | 1.12 | 1.17 | 1.26 | 1.36 | 1.41 | 1.45 | 1.5 | 1.54 |
| 11 | 0.0075 | 13.618 | 0.0011 | 1.09 | 1.12 | 1.17 | 1.21 | 1.26 | 1.36 | 1.46 | 1.52 | 1.56 | 1.61 | 1.65 |
| 12 | 0.0079 | 14.456 | 0.0011 | 1.16 | 1.2 | 1.25 | 1.29 | 1.34 | 1.45 | 1.55 | 1.61 | 1.65 | 1.71 | 1.74 |
| 13 | 0.0078 | 15.112 | 0.0011 | 1.22 | 1.26 | 1.31 | 1.35 | 1.4 | 1.51 | 1.62 | 1.68 | 1.72 | 1.78 | 1.82 |
| 14 | 0.007 | 15.593 | 0.001 | 1.27 | 1.3 | 1.36 | 1.4 | 1.45 | 1.56 | 1.67 | 1.73 | 1.77 | 1.83 | 1.87 |
| 15 | 0.0054 | 15.928 | 0.001 | 1.3 | 1.34 | 1.39 | 1.43 | 1.49 | 1.59 | 1.7 | 1.76 | 1.8 | 1.87 | 1.91 |
| 16 | 0.0032 | 16.151 | 0.001 | 1.33 | 1.37 | 1.42 | 1.46 | 1.51 | 1.62 | 1.72 | 1.79 | 1.83 | 1.89 | 1.93 |
| 17 | 0.0007 | 16.294 | 0.001 | 1.36 | 1.39 | 1.44 | 1.47 | 1.53 | 1.63 | 1.74 | 1.8 | 1.84 | 1.91 | 1.95 |
| 18 | −0.002 | 16.387 | 0.001 | 1.37 | 1.4 | 1.45 | 1.49 | 1.54 | 1.64 | 1.75 | 1.81 | 1.85 | 1.92 | 1.97 |
| 19 | −0.0045 | 16.433 | 0.0009 | 1.39 | 1.41 | 1.46 | 1.49 | 1.54 | 1.64 | 1.75 | 1.82 | 1.86 | 1.93 | 1.98 |
| 20–39 | −0.0067 | 16.412 | 0.0009 | 1.39 | 1.42 | 1.46 | 1.49 | 1.54 | 1.64 | 1.75 | 1.81 | 1.86 | 1.93 | 1.98 |
| 40–59 | −0.0086 | 16.308 | 0.0009 | 1.39 | 1.41 | 1.46 | 1.49 | 1.53 | 1.63 | 1.74 | 1.8 | 1.85 | 1.92 | 1.97 |
| 60–79 | −0.0103 | 16.134 | 0.0009 | 1.37 | 1.4 | 1.44 | 1.47 | 1.52 | 1.61 | 1.72 | 1.79 | 1.83 | 1.91 | 1.96 |
| >80 | −0.012 | 15.944 | 0.0009 | 1.36 | 1.39 | 1.43 | 1.46 | 1.5 | 1.59 | 1.7 | 1.77 | 1.81 | 1.89 | 1.94 |
| Age | L | M | S | P3 | P5 | P10 | P15 | P25 | P50 | P75 | P85 | P90 | P95 | P97 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Males | ||||||||||||||
| 4 | −1.789 | 14.09 | 0.1999 | 10.57 | 10.88 | 11.41 | 11.81 | 12.49 | 14.09 | 16.44 | 18.25 | 19.85 | 23.14 | 26.3 |
| 5 | −14.052 | 159.255 | 0.1987 | 11.79 | 12.17 | 12.81 | 13.29 | 14.09 | 15.93 | 18.47 | 20.31 | 21.83 | 24.67 | 27.05 |
| 6 | −10.211 | 177.979 | 0.1975 | 12.99 | 13.44 | 14.21 | 14.78 | 15.71 | 17.8 | 20.54 | 22.39 | 23.85 | 26.41 | 28.39 |
| 7 | −0.6372 | 197.242 | 0.1961 | 14.16 | 14.71 | 15.62 | 16.29 | 17.37 | 19.72 | 22.65 | 24.52 | 25.94 | 28.3 | 30.03 |
| 8 | −0.2552 | 218.182 | 0.1944 | 15.38 | 16.04 | 17.14 | 17.93 | 19.18 | 21.82 | 24.93 | 26.83 | 28.22 | 30.46 | 32.03 |
| 9 | 0.1264 | 242.611 | 0.1922 | 16.76 | 17.57 | 18.89 | 19.83 | 21.29 | 24.26 | 27.59 | 29.53 | 30.92 | 33.08 | 34.55 |
| 10 | 0.5009 | 272.184 | 0.1891 | 18.4 | 19.41 | 21.02 | 22.14 | 23.86 | 27.22 | 30.8 | 32.81 | 34.21 | 36.34 | 37.76 |
| 11 | 0.8521 | 307.896 | 0.1849 | 20.38 | 21.65 | 23.63 | 24.98 | 26.99 | 30.79 | 34.66 | 36.77 | 38.21 | 40.35 | 41.76 |
| 12 | 11.715 | 348.865 | 0.1796 | 22.69 | 24.28 | 26.68 | 28.28 | 30.61 | 34.89 | 39.07 | 41.28 | 42.77 | 44.96 | 46.37 |
| 13 | 14.455 | 392.445 | 0.1732 | 25.27 | 27.19 | 30.03 | 31.88 | 34.53 | 39.24 | 43.72 | 46.03 | 47.57 | 49.82 | 51.25 |
| 14 | 16.537 | 434.999 | 0.1659 | 28.05 | 30.26 | 33.47 | 35.53 | 38.44 | 43.5 | 48.2 | 50.61 | 52.19 | 54.49 | 55.94 |
| 15 | 17.955 | 472.828 | 0.1584 | 30.87 | 33.27 | 36.73 | 38.92 | 41.99 | 47.28 | 52.14 | 54.6 | 56.22 | 58.55 | 60.03 |
| 16 | 1.878 | 503.156 | 0.1514 | 33.48 | 35.97 | 39.53 | 41.78 | 44.92 | 50.32 | 55.24 | 57.73 | 59.37 | 61.72 | 63.21 |
| 17 | 19.067 | 525.393 | 0.1453 | 35.71 | 38.19 | 41.74 | 43.99 | 47.14 | 52.54 | 57.48 | 59.98 | 61.61 | 63.97 | 65.46 |
| 18 | 18.885 | 541.051 | 0.1403 | 37.55 | 39.96 | 43.43 | 45.65 | 48.75 | 54.11 | 59.03 | 61.52 | 63.16 | 65.53 | 67.02 |
| 19 | 18.371 | 551.457 | 0.1364 | 38.98 | 41.29 | 44.66 | 46.82 | 49.86 | 55.15 | 60.04 | 62.53 | 64.17 | 66.54 | 68.05 |
| 20–39 | 17.662 | 557.421 | 0.1333 | 40.03 | 42.25 | 45.49 | 47.58 | 50.54 | 55.74 | 60.59 | 63.08 | 64.72 | 67.09 | 68.6 |
| 40–59 | 16.892 | 559.433 | 0.1304 | 40.76 | 42.86 | 45.97 | 47.99 | 50.86 | 55.94 | 60.72 | 63.19 | 64.82 | 67.18 | 68.69 |
| 60–79 | 1.613 | 559.143 | 0.1277 | 41.27 | 43.27 | 46.24 | 48.18 | 50.96 | 55.91 | 60.61 | 63.04 | 64.65 | 67 | 68.49 |
| >80 | 15.371 | 558.224 | 0.125 | 41.7 | 43.6 | 46.45 | 48.32 | 51 | 55.82 | 60.43 | 62.82 | 64.41 | 66.74 | 68.22 |
| Females | ||||||||||||||
| 4 | −14.802 | 124.277 | 0.1924 | 9.3 | 9.59 | 10.07 | 10.44 | 11.04 | 12.43 | 14.35 | 15.74 | 16.89 | 19.04 | 20.87 |
| 5 | −11.996 | 143.388 | 0.1902 | 10.65 | 10.99 | 11.58 | 12.01 | 12.73 | 14.34 | 16.48 | 17.96 | 19.13 | 21.22 | 22.88 |
| 6 | −0.9176 | 16.301 | 0.188 | 12 | 12.42 | 13.11 | 13.63 | 14.46 | 16.3 | 18.65 | 20.2 | 21.4 | 23.45 | 24.99 |
| 7 | −0.6357 | 183.935 | 0.1857 | 13.42 | 13.91 | 14.74 | 15.34 | 16.31 | 18.39 | 20.96 | 22.58 | 23.81 | 25.83 | 27.3 |
| 8 | −0.359 | 207.033 | 0.1831 | 14.96 | 15.55 | 16.53 | 17.23 | 18.35 | 20.7 | 23.49 | 25.2 | 26.45 | 28.47 | 29.9 |
| 9 | −0.0977 | 233.007 | 0.1801 | 16.7 | 17.4 | 18.55 | 19.37 | 20.65 | 23.3 | 26.33 | 28.13 | 29.43 | 31.47 | 32.88 |
| 10 | 0.1339 | 261.335 | 0.1767 | 18.6 | 19.43 | 20.76 | 21.71 | 23.17 | 26.13 | 29.41 | 31.32 | 32.67 | 34.76 | 36.18 |
| 11 | 0.3191 | 290.277 | 0.173 | 20.59 | 21.54 | 23.07 | 24.13 | 25.77 | 29.03 | 32.55 | 34.56 | 35.96 | 38.11 | 39.56 |
| 12 | 0.4497 | 316.974 | 0.1689 | 22.5 | 23.56 | 25.24 | 26.41 | 28.2 | 31.7 | 35.42 | 37.52 | 38.97 | 41.18 | 42.66 |
| 13 | 0.5244 | 338.785 | 0.1646 | 24.16 | 25.3 | 27.09 | 28.33 | 30.22 | 33.88 | 37.74 | 39.89 | 41.38 | 43.64 | 45.14 |
| 14 | 0.5493 | 355.188 | 0.1602 | 25.55 | 26.72 | 28.56 | 29.84 | 31.77 | 35.52 | 39.45 | 41.64 | 43.15 | 45.43 | 46.94 |
| 15 | 0.5312 | 366.847 | 0.1559 | 26.67 | 27.85 | 29.7 | 30.98 | 32.92 | 36.68 | 40.64 | 42.83 | 44.35 | 46.65 | 48.17 |
| 16 | 0.4836 | 374.865 | 0.1517 | 27.57 | 28.73 | 30.56 | 31.83 | 33.75 | 37.49 | 41.42 | 43.62 | 45.14 | 47.45 | 48.98 |
| 17 | 0.424 | 380.398 | 0.1481 | 28.28 | 29.42 | 31.21 | 32.46 | 34.35 | 38.04 | 41.95 | 44.14 | 45.66 | 47.96 | 49.5 |
| 18 | 0.3699 | 384.462 | 0.1452 | 28.83 | 29.94 | 31.71 | 32.93 | 34.8 | 38.45 | 42.33 | 44.51 | 46.02 | 48.33 | 49.87 |
| 19 | 0.3358 | 387.136 | 0.143 | 29.2 | 30.3 | 32.04 | 33.25 | 35.1 | 38.71 | 42.57 | 44.74 | 46.25 | 48.55 | 50.09 |
| 20–39 | 0.3334 | 387.587 | 0.1417 | 29.32 | 30.41 | 32.14 | 33.34 | 35.17 | 38.76 | 42.58 | 44.73 | 46.23 | 48.51 | 50.03 |
| 40–59 | 0.3689 | 384.961 | 0.1411 | 29.12 | 30.2 | 31.93 | 33.12 | 34.94 | 38.5 | 42.27 | 44.39 | 45.86 | 48.1 | 49.58 |
| 60–79 | 0.4274 | 379.892 | 0.1408 | 28.68 | 29.77 | 31.48 | 32.67 | 34.48 | 37.99 | 41.7 | 43.77 | 45.2 | 47.38 | 48.83 |
| >80 | 0.4891 | 374.306 | 0.1407 | 28.19 | 29.28 | 30.99 | 32.18 | 33.96 | 37.43 | 41.07 | 43.09 | 44.49 | 46.6 | 48.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cossio-Bolaños, M.; Vidal Espinoza, R.; Sulla-Torres, J.; Urra-Albornoz, C.; Sanchez-Macedo, L.; de Arruda, M.; Alvear-Vasquez, F.; Lazari, E.; Gomez-Campos, R. Validation of Body Surface Area Equations for Estimating Fat-Free Mass by Dual X-Ray Absorptiometry in a Regional Chilean Sample Aged 4 to 85 Years. Diagnostics 2025, 15, 2982. https://doi.org/10.3390/diagnostics15232982
Cossio-Bolaños M, Vidal Espinoza R, Sulla-Torres J, Urra-Albornoz C, Sanchez-Macedo L, de Arruda M, Alvear-Vasquez F, Lazari E, Gomez-Campos R. Validation of Body Surface Area Equations for Estimating Fat-Free Mass by Dual X-Ray Absorptiometry in a Regional Chilean Sample Aged 4 to 85 Years. Diagnostics. 2025; 15(23):2982. https://doi.org/10.3390/diagnostics15232982
Chicago/Turabian StyleCossio-Bolaños, Marco, Rubén Vidal Espinoza, Jose Sulla-Torres, Camilo Urra-Albornoz, Lucila Sanchez-Macedo, Miguel de Arruda, Fernando Alvear-Vasquez, Evandro Lazari, and Rossana Gomez-Campos. 2025. "Validation of Body Surface Area Equations for Estimating Fat-Free Mass by Dual X-Ray Absorptiometry in a Regional Chilean Sample Aged 4 to 85 Years" Diagnostics 15, no. 23: 2982. https://doi.org/10.3390/diagnostics15232982
APA StyleCossio-Bolaños, M., Vidal Espinoza, R., Sulla-Torres, J., Urra-Albornoz, C., Sanchez-Macedo, L., de Arruda, M., Alvear-Vasquez, F., Lazari, E., & Gomez-Campos, R. (2025). Validation of Body Surface Area Equations for Estimating Fat-Free Mass by Dual X-Ray Absorptiometry in a Regional Chilean Sample Aged 4 to 85 Years. Diagnostics, 15(23), 2982. https://doi.org/10.3390/diagnostics15232982








