Prediction of Recurrence and Rupture Risk of Ruptured and Unruptured Intracranial Aneurysms of the Posterior Circulation: A Machine Learning-Based Analysis
Abstract
1. Introduction
2. Materials and Methods
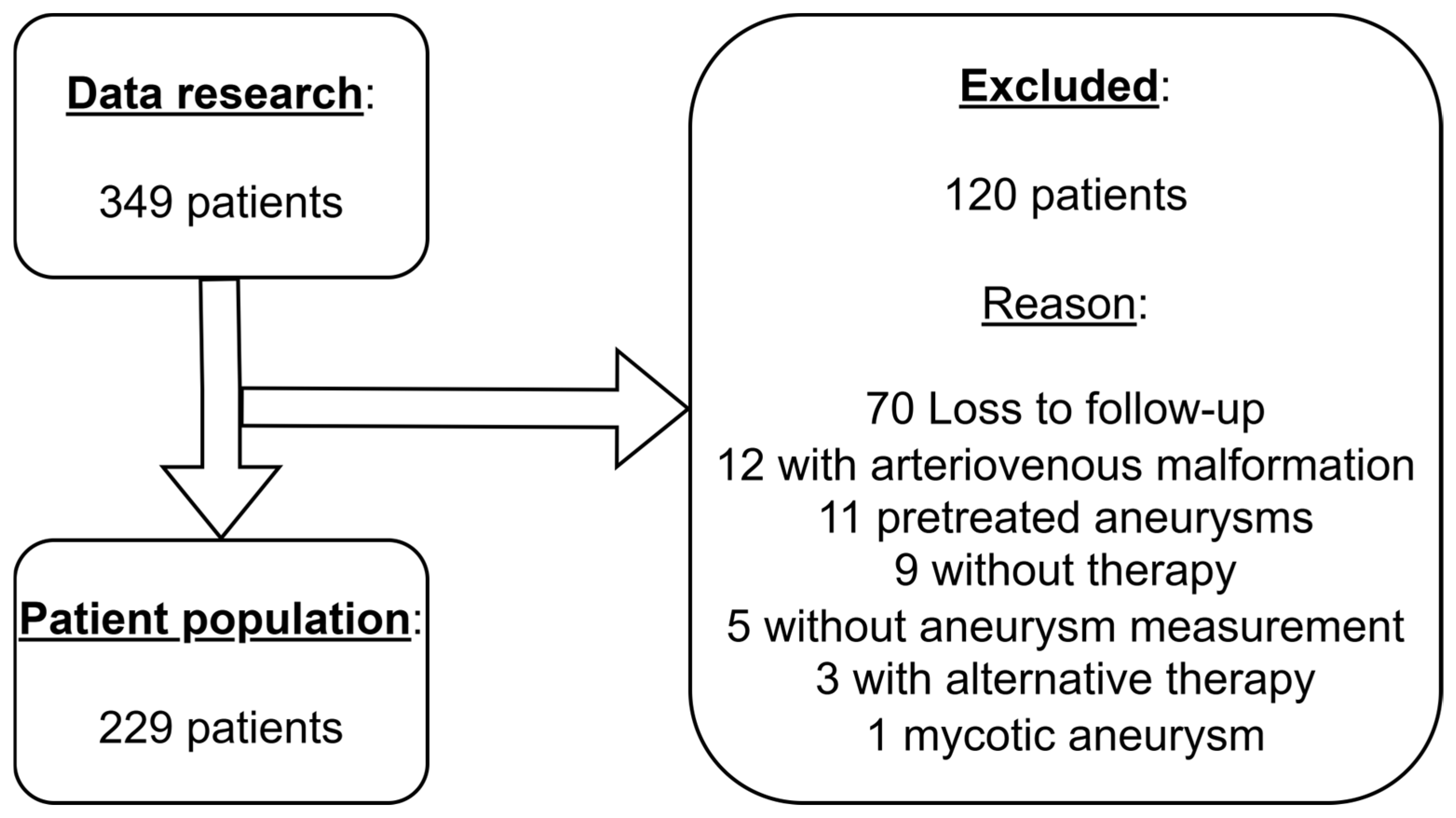
2.1. Patient Population
2.2. Data Collection
2.3. Criteria of Medical Evaluation
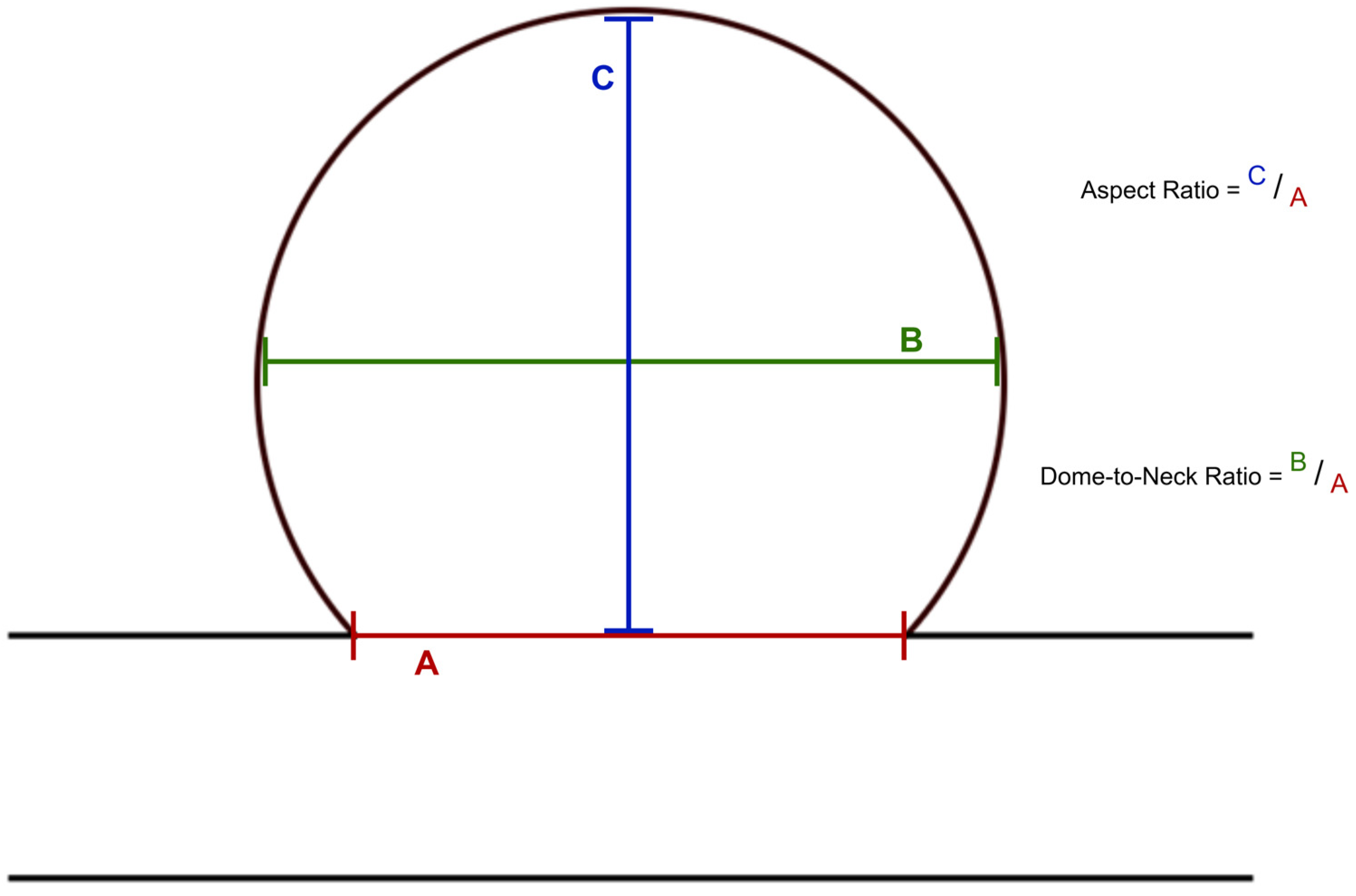
2.4. Image Analysis
2.5. Machine Learning
2.6. Descriptive Statistics
3. Results
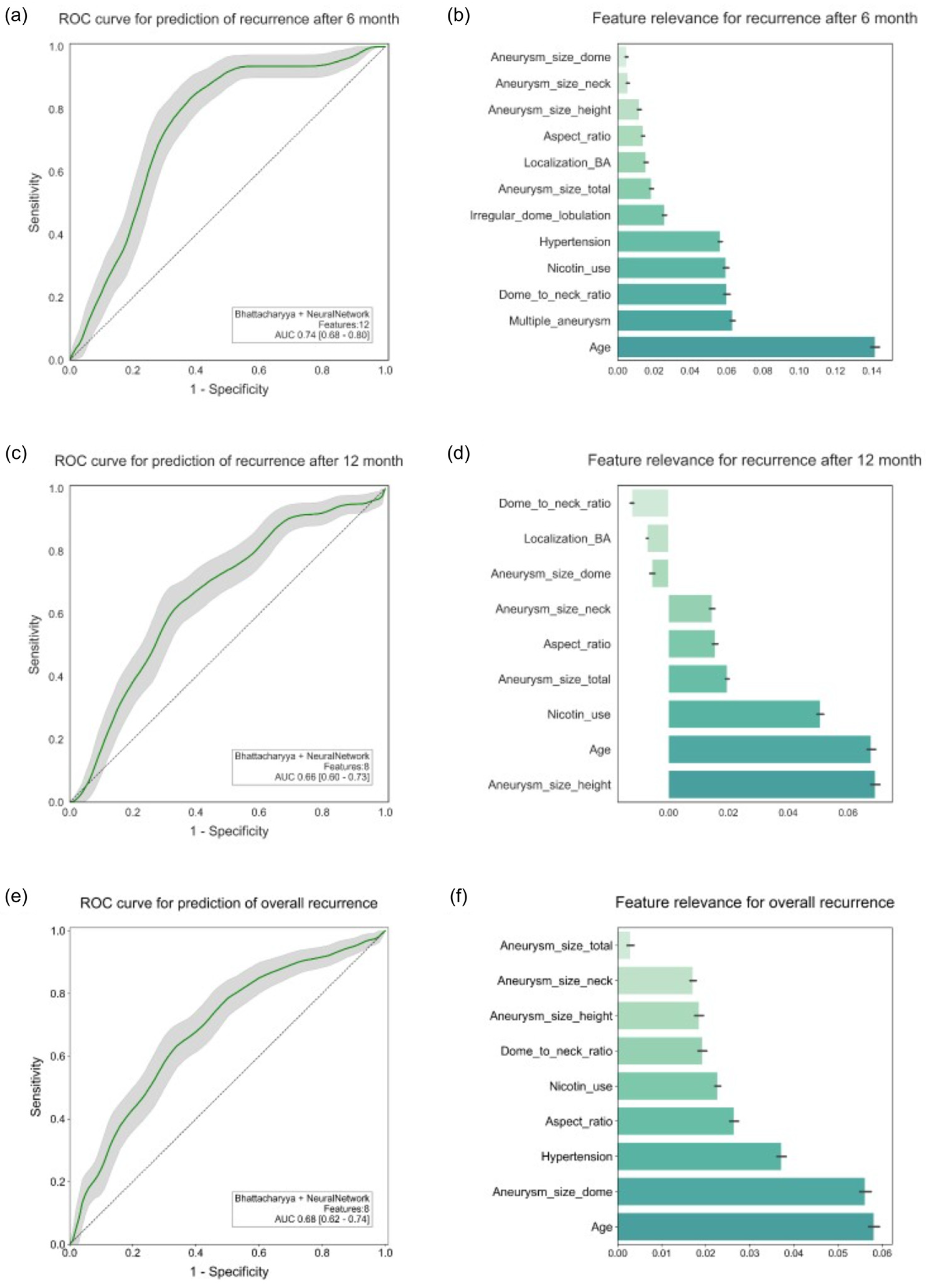
3.1. Recurrence
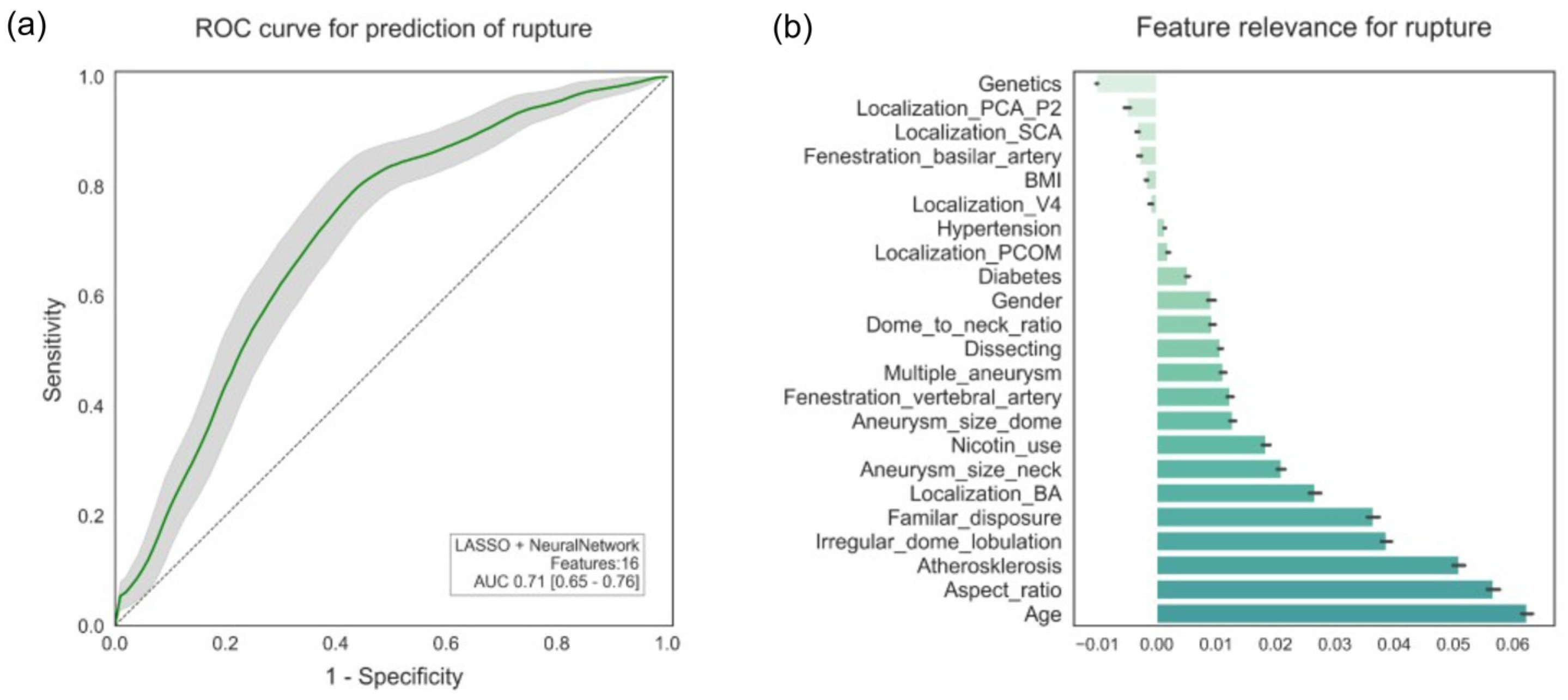
3.2. Rupture
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| SAH | Subarachnoid Hemorrhage |
| g | gram |
| RIS | Radiology Information System |
| BMI | Body Mass Index |
| PACS | Picture Archiving and Communication System |
| H&H | Hunt and Hess |
| GCS | Glasgow Coma Scale |
| DSA | Digital Subtraction Angiography |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| ANOVA | Analysis of Variance |
| MIM | Mutual Information |
| MRMRe | Minimum Redundancy, Maximum Relevance Ensemble |
| SVM | Support Vector Machine |
| RBF | Radial Basis Function |
| ROC | Receiver Operating Characteristics |
| AUC | Area Under the Curve |
| SD | Standard Deviation |
| CI | Confidence Interval |
| kg | kilogram |
| m | meter |
| cm | centimeter |
| UCAS | Unruptured Cerebral Aneurysm Study |
| mm | millimeter |
References
- Wiebers, D.O.; Whisnant, J.P.; Sundt, T.M., Jr.; O’Fallon, W.M. The significance of unruptured intracranial saccular aneurysms. J. Neurosurg. 1987, 66, 23–29. [Google Scholar] [CrossRef]
- Vlak, M.H.; Algra, A.; Brandenburg, R.; Rinkel, G.J. Prevalence of unruptured intracranial aneurysms, with emphasis on sex, age, comorbidity, country, and time period: A systematic review and meta-analysis. Lancet Neurol. 2011, 10, 626–636. [Google Scholar] [CrossRef]
- Lempert, T.E.; Malek, A.M.; Halbach, V.V.; Phatouros, C.C.; Meyers, P.M.; Dowd, C.F.; Higashida, R.T. Endovascular treatment of ruptured posterior circulation cerebral aneurysms: Clinical and angiographic outcomes. Stroke 2000, 31, 100–110. [Google Scholar] [CrossRef]
- Schievink, W.I.; Katzmann, J.A.; Piepgras, D.G.; Schaid, D.J. Alpha-1-antitrypsin phenotypes among patients with intracranial aneurysms. J. Neurosurg. 1996, 84, 781–784. [Google Scholar] [CrossRef]
- Wiebers, D.O.; Torres, V.E. Screening for unruptured intracranial aneurysms in autosomal dominant polycystic kidney disease. N. Engl. J. Med. 1992, 327, 953–955. [Google Scholar] [CrossRef]
- Feigin, V.; Parag, V.; Lawes, C.M.; Rodgers, A.; Suh, I.; Woodward, M.; Jamrozik, K.; Ueshima, H.; Asia Pacific Cohort Studies Collaboration. Smoking and elevated blood pressure are the most important risk factors for subarachnoid hemorrhage in the Asia-Pacific region: An overview of 26 cohorts involving 306,620 participants. Stroke 2005, 36, 1360–1365. [Google Scholar] [CrossRef]
- Juvela, S.; Hillbom, M.; Numminen, H.; Koskinen, P. Cigarette smoking and alcohol consumption as risk factors for aneurysmal subarachnoid hemorrhage. Stroke 1993, 24, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Inci, S.; Spetzler, R.F. Intracranial aneurysms and arterial hypertension: A review and hypothesis. Surg. Neurol. 2000, 53, 530–540; Discussion 532–540. [Google Scholar] [CrossRef]
- Orz, Y.; Kobayashi, S.; Osawa, M.; Tanaka, Y. Aneurysm size: A prognostic factor for rupture. Br. J. Neurosurg. 1997, 11, 144–149. [Google Scholar] [CrossRef] [PubMed]
- Sonobe, M.; Yamazaki, T.; Yonekura, M.; Kikuchi, H. Small unruptured intracranial aneurysm verification study: SUAVe study, Japan. Stroke 2010, 41, 1969–1977. [Google Scholar] [CrossRef] [PubMed]
- Linn, F.H.; Rinkel, G.J.; Algra, A.; van Gijn, J. Headache characteristics in subarachnoid haemorrhage and benign thunderclap headache. J. Neurol. Neurosurg. Psychiatry 1998, 65, 791–793. [Google Scholar] [CrossRef]
- Wanke, I.; Egelhof, T.; Dörfler, A.; Forsting, M. Intrakranielle Aneurysmen: Entstehung, Rupturrisiko, Behandlungsoptionen. Rofo 2003, 175, 1064–1070. [Google Scholar] [CrossRef]
- Quinsten, A.S.; Heße, D. Informationstechnologie und Künstliche Intelligenz in der Radiologie; Deutscher Ärzteverlag: Cologne, Germany, 2022. [Google Scholar]
- Shi, Z.; Chen, G.Z.; Mao, L.; Li, X.L.; Zhou, C.S.; Xia, S.; Zhang, Y.X.; Zhang, B.; Hu, B.; Lu, G.M.; et al. Machine Learning-Based Prediction of Small Intracranial Aneurysm Rupture Status Using CTA-Derived Hemodynamics: A Multicenter Study. AJNR Am. J. Neuroradiol. 2021, 42, 648–654. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Gu, D.; Qi, P.; Cao, X.; Wu, D.; Chen, L.; Qu, G.; Wang, J.; Pan, X.; Wang, X.; et al. Evaluation of an automated intracranial aneurysm detection and rupture analysis approach using cascade detection and classification networks. Comput. Med. Imaging Graph. 2022, 102, 102126. [Google Scholar] [CrossRef]
- Kim, H.C.; Rhim, J.K.; Ahn, J.H.; Park, J.J.; Moon, J.U.; Hong, E.P.; Kim, M.R.; Kim, S.G.; Lee, S.H.; Jeong, J.H.; et al. Machine Learning Application for Rupture Risk Assessment in Small-Sized Intracranial Aneurysm. J. Clin. Med. 2019, 8, 683. [Google Scholar] [CrossRef] [PubMed]
- Malik, K.; Alam, F.; Santamaria, J.; Krishnamurthy, M.; Malik, G. Toward Grading Subarachnoid Hemorrhage Risk Prediction: A Machine Learning-Based Aneurysm Rupture Score. World Neurosurg. 2023, 172, e19–e38. [Google Scholar] [CrossRef]
- Feigin, V.L.; Rinkel, G.J.; Lawes, C.M.; Algra, A.; Bennett, D.A.; van Gijn, J.; Anderson, C.S. Risk factors for subarachnoid hemorrhage: An updated systematic review of epidemiological studies. Stroke 2005, 36, 2773–2780. [Google Scholar] [CrossRef]
- Morita, A.; Kirino, T.; Hashi, K.; Aoki, N.; Fukuhara, S.; Hashimoto, N.; Nakayama, T.; Sakai, M.; Teramoto, A.; Tominari, S.; et al. The natural course of unruptured cerebral aneurysms in a Japanese cohort. N. Engl. J. Med. 2012, 366, 2474–2482. [Google Scholar] [CrossRef]
- Fernandez Zubillaga, A.; Guglielmi, G.; Vinuela, F.; Duckwiler, G.R. Endovascular occlusion of intracranial aneurysms with electrically detachable coils: Correlation of aneurysm neck size and treatment results. AJNR Am. J. Neuroradiol. 1994, 15, 815–820. [Google Scholar]
- Brinjikji, W.; Cloft, H.J.; Kallmes, D.F. Difficult aneurysms for endovascular treatment: Overwide or undertall? AJNR Am. J. Neuroradiol. 2009, 30, 1513–1517. [Google Scholar] [CrossRef] [PubMed]
- Webb, G.I. Naïve bayes. In Encyclopedia of Machine Learning and Data Mining; Springer: Berlin/Heidelberg, Germany, 2017; pp. 895–896. [Google Scholar]
- Cox, D.R. The regression analysis of binary sequences. J. R. Stat. Soc. Ser. B Stat. Methodol. 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Scholkopf, B.; Sung, K.-K.; Burges, C.J.; Girosi, F.; Niyogi, P.; Poggio, T.; Vapnik, V. Comparing support vector machines with Gaussian kernels to radial basis function classifiers. IEEE Trans. Signal Process. 1997, 45, 2758–2765. [Google Scholar] [CrossRef]
- Amigo, N.; Valencia, A.; Wu, W.; Patnaik, S.; Finol, E. Cerebral aneurysm rupture status classification using statistical and machine learning methods. Proc. Inst. Mech. Eng. H. 2021, 235, 655–662. [Google Scholar] [CrossRef]
- Detmer, F.J.; Luckehe, D.; Mut, F.; Slawski, M.; Hirsch, S.; Bijlenga, P.; von Voigt, G.; Cebral, J.R. Comparison of statistical learning approaches for cerebral aneurysm rupture assessment. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 141–150. [Google Scholar] [CrossRef]
- Ueda, D.; Yamamoto, A.; Nishimori, M.; Shimono, T.; Doishita, S.; Shimazaki, A.; Katayama, Y.; Fukumoto, S.; Choppin, A.; Shimahara, Y.; et al. Deep Learning for MR Angiography: Automated Detection of Cerebral Aneurysms. Radiology 2019, 290, 187–194. [Google Scholar] [CrossRef]
- Hamalawi, B.E. Endovaskuläre Embolisation Intrakranieller Aneurysmen im Vertebrobasilären Stromgebiet mit Elektrolytisch Ablösbaren Platinspiralen (Guglielmi Detachable Coils): Klinische und Angiographische Ergebnisse bei 91 Patienten. Ph.D. Thesis, Universität Duisburg-Essen, Duisburg, Germany, 2009. [Google Scholar]
- Rinkel, G.J.; Djibuti, M.; Algra, A.; van Gijn, J. Prevalence and risk of rupture of intracranial aneurysms: A systematic review. Stroke 1998, 29, 251–256. [Google Scholar] [CrossRef] [PubMed]
- Greving, J.P.; Wermer, M.J.; Brown, R.D., Jr.; Morita, A.; Juvela, S.; Yonekura, M.; Ishibashi, T.; Torner, J.C.; Nakayama, T.; Rinkel, G.J.; et al. Development of the PHASES score for prediction of risk of rupture of intracranial aneurysms: A pooled analysis of six prospective cohort studies. Lancet Neurol. 2014, 13, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Jiang, P.; Jiang, Y.; Ge, H.; Li, S.; Jin, H.; Li, Y. Prediction of aneurysm stability using a machine learning model based on PyRadiomics-derived morphological features. Stroke 2019, 50, 2314–2321. [Google Scholar] [CrossRef]
- Bonita, R. Cigarette smoking, hypertension and the risk of subarachnoid hemorrhage: A population-based case-control study. Stroke 1986, 17, 831–835. [Google Scholar] [CrossRef]
- Chen, S.; Mao, J.; Chen, X.; Li, Z.; Zhu, Z.; Li, Y.; Jiang, Z.; Zhao, W.; Wang, Z.; Zhong, P. Association between body mass index and intracranial aneurysm rupture: A multicenter retrospective study. Front. Aging Neurosci. 2021, 13, 716068. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zou, X.; Zhao, Y.; Jin, Z.; Tu, J.; Ning, X.; Li, J.; Yang, X.; Wang, J. Prevalence and Risk Factors for Unruptured Intracranial Aneurysms in the Population at High Risk for Aneurysm in the Rural Areas of Tianjin. Front. Neurol. 2022, 13, 853054. [Google Scholar] [CrossRef]
- Rosi Junior, J.; Gomes dos Santos, A.; da Silva, S.A.; Iglesio, R.F.; Caldas, J.G.M.P.; Rabelo, N.N.; Teixeira, M.J.; Preul, M.C.; Spetzler, R.F.; Figueiredo, E.G. Multiple and mirror intracranial aneurysms: Study of prevalence and associated risk factors. Br. J. Neurosurg. 2021, 35, 780–784. [Google Scholar] [CrossRef]
- Forsting, M.; Wanke, I. Intracranial Vascular Malformations and Aneurysms; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Leng, B.; Zheng, Y.; Ren, J.; Xu, Q.; Tian, Y.; Xu, F. Endovascular treatment of intracranial aneurysms with detachable coils: Correlation between aneurysm volume, packing, and angiographic recurrence. J. Neurointerv. Surg. 2014, 6, 595–599. [Google Scholar] [CrossRef]
- Beck, J.; Rohde, S.; el Beltagy, M.; Zimmermann, M.; Berkefeld, J.; Seifert, V.; Raabe, A. Difference in configuration of ruptured and unruptured intracranial aneurysms determined by biplanar digital subtraction angiography. Acta Neurochir. 2003, 145, 861–865; Discussion 865. [Google Scholar] [CrossRef] [PubMed]
- Piotin, M.; Spelle, L.; Mounayer, C.; Salles-Rezende, M.T.; Giansante-Abud, D.; Vanzin-Santos, R.; Moret, J. Intracranial aneurysms: Treatment with bare platinum coils—Aneurysm packing, complex coils, and angiographic recurrence. Radiology 2007, 243, 500–508. [Google Scholar] [CrossRef]
- Lin, S.; Zou, Y.; Hu, J.; Xiang, L.; Guo, L.; Lin, X.; Zou, D.; Gao, X.; Liang, H.; Zou, J.; et al. Development and assessment of machine learning models for predicting recurrence risk after endovascular treatment in patients with intracranial aneurysms. Neurosurg. Rev. 2022, 45, 1521–1531. [Google Scholar] [CrossRef]
- Ou, C.; Liu, J.; Qian, Y.; Chong, W.; Zhang, X.; Liu, W.; Su, H.; Zhang, N.; Zhang, J.; Duan, C.Z.; et al. Rupture Risk Assessment for Cerebral Aneurysm Using Interpretable Machine Learning on Multidimensional Data. Front. Neurol. 2020, 11, 570181. [Google Scholar] [CrossRef] [PubMed]
| Feature Selection | Type | Hyperparameters |
|---|---|---|
| Analysis of Variance (ANOVA) | Filtering | - |
| Bhattacharyya | Filtering | - |
| Fisher Score | Filtering | - |
| Least Absolute Shrinkage and Selection Operator (LASSO) | Wrapper | Regularization parameter C = 1 |
| Mutual Information (MIM) | Filtering | - |
| Minimum Redundancy, Maximum Relevance Ensemble (MRMRe) | Filtering | - |
| None | Filtering | - |
| Pearson Correlation | Filtering | - |
| ReliefF | Filtering | - |
| t-Score | Filtering | - |
| Classifier | Hyperparameters |
|---|---|
| Logistic Regression | Regularization parameter C in 2^(−6, −5, …, 5, 6) |
| Naïve Bayes | - |
| Neural Network (with three layers) | Number of neurons in Layers 1, 2, 3 in (2, 4, 8, 16, 32, 64) |
| Random Forest | Number of Trees in 50, 125, 250 |
| Radial Basis Function-SVM (RBF-SVM) | Regularization parameter C and kernel parameter γ in 2^(−6, −5, …, 5, 6) |
| Characteristics | Total Patients (n = 229) |
|---|---|
| Gender [female] | 164 (71.6%) |
| Age [years] | 54.0 [18.0; 81.0] |
| Hypertension | 166 (72.5%) |
| Nicotine consumption | 126 (55.0%) |
| Atherosclerosis | 57 (24.9%) |
| BMI [kg/m2] | |
| ≤25 | 124 (54.1%) |
| 25–30 | 69 (30.1%) |
| 30–35 | 25 (10.9%) |
| 35–40 | 6 (2.6%) |
| >40 | 5 (2.2%) |
| Characteristics | Total Patients (n = 229) |
|---|---|
| Aneurysm localization [basilar artery] | 119 (52.0%) |
| Aneurysm size—dome width [mm] | 5.70 [1.50; 44.0] |
| Aneurysm size—dome height [mm] | 6.40 [1.50; 24.6] |
| Aneurysm size—neck width [mm] | 3.90 [0.90; 44.4] |
| Dome-to-neck ratio | 1.50 [0.20; 4.60] |
| Aspect ratio | 1.60 [0.20; 5.50] |
| Multiple aneurysms | 88 (38.4%) |
| Irregular dome configuration—lobulation | 96 (41.9%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Növer, M.; Styczen, H.; Jabbarli, R.; Dammann, P.; Köhrmann, M.; Hagenacker, T.; Moenninghoff, C.; Forsting, M.; Li, Y.; Wanke, I.; et al. Prediction of Recurrence and Rupture Risk of Ruptured and Unruptured Intracranial Aneurysms of the Posterior Circulation: A Machine Learning-Based Analysis. Diagnostics 2025, 15, 2365. https://doi.org/10.3390/diagnostics15182365
Növer M, Styczen H, Jabbarli R, Dammann P, Köhrmann M, Hagenacker T, Moenninghoff C, Forsting M, Li Y, Wanke I, et al. Prediction of Recurrence and Rupture Risk of Ruptured and Unruptured Intracranial Aneurysms of the Posterior Circulation: A Machine Learning-Based Analysis. Diagnostics. 2025; 15(18):2365. https://doi.org/10.3390/diagnostics15182365
Chicago/Turabian StyleNöver, Martin, Hanna Styczen, Ramazan Jabbarli, Philipp Dammann, Martin Köhrmann, Tim Hagenacker, Christoph Moenninghoff, Michael Forsting, Yan Li, Isabel Wanke, and et al. 2025. "Prediction of Recurrence and Rupture Risk of Ruptured and Unruptured Intracranial Aneurysms of the Posterior Circulation: A Machine Learning-Based Analysis" Diagnostics 15, no. 18: 2365. https://doi.org/10.3390/diagnostics15182365
APA StyleNöver, M., Styczen, H., Jabbarli, R., Dammann, P., Köhrmann, M., Hagenacker, T., Moenninghoff, C., Forsting, M., Li, Y., Wanke, I., Demircioğlu, A., & Deuschl, C. (2025). Prediction of Recurrence and Rupture Risk of Ruptured and Unruptured Intracranial Aneurysms of the Posterior Circulation: A Machine Learning-Based Analysis. Diagnostics, 15(18), 2365. https://doi.org/10.3390/diagnostics15182365







