Comparative Evaluation of 24 LDL-C Estimation Equations Against Direct Assays in Two Independent Cohorts
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Demographic and Laboratory Characteristics
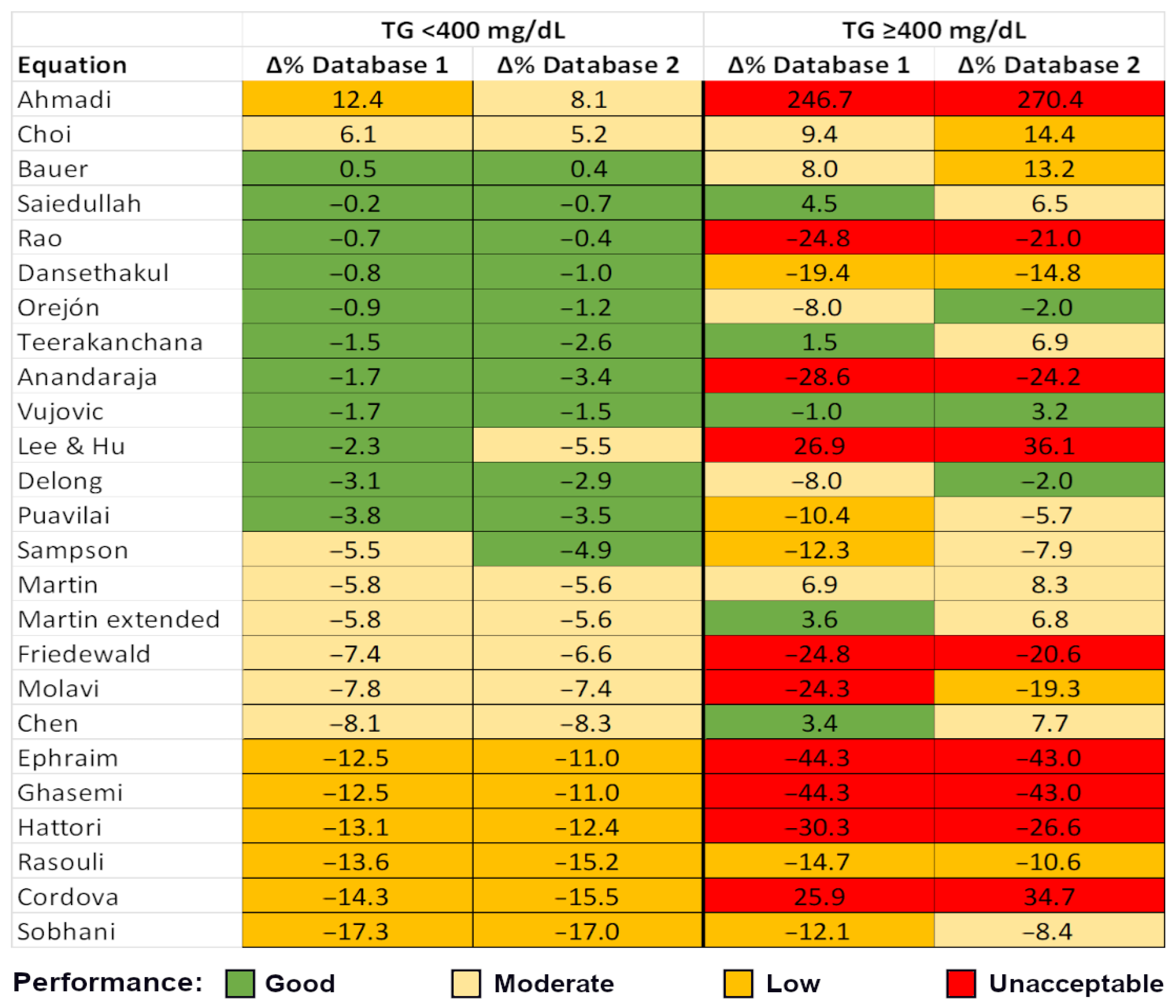
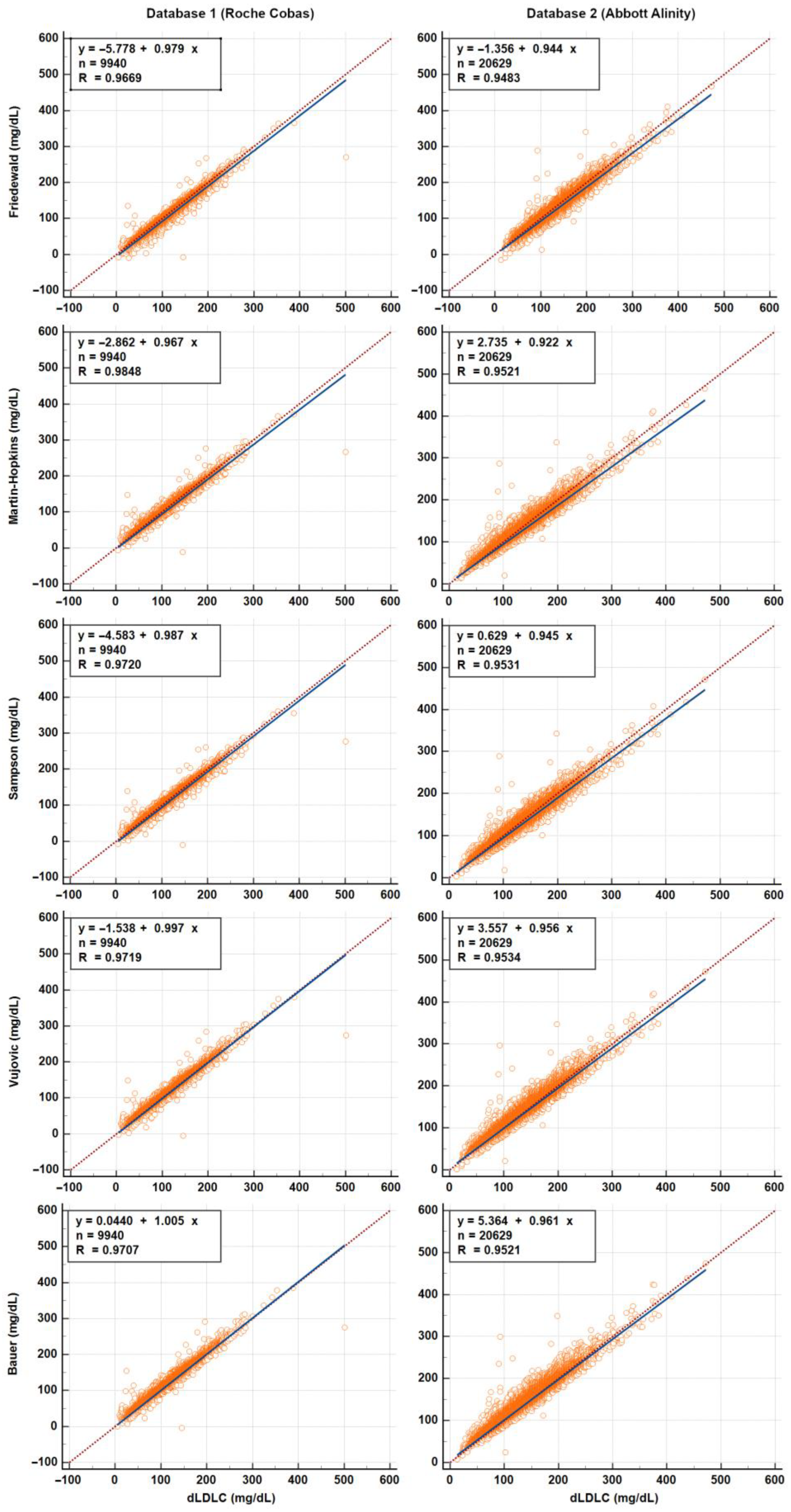
3.2. Calculated and Measured LDL-C—Accuracy of LDL-C Equations
3.3. Calculated and Measured LDL-C—Categorical Agreement for Risk Stratification
4. Discussion
4.1. Advantages and Limitations of Direct Assays
4.2. Direct Assays as De Facto Reference Methods
4.3. Differences Between Laboratory Databases
4.4. Performance and Bias of LDL-C Equations
4.5. Classification Performance of LDL-C Equations
4.6. Net Gain in Classification Accuracy: Is It Enough to Replace the Friedewald Equation?
4.7. Strengths and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LDL-C | Low-density lipoprotein cholesterol |
| FW | Friedwald equation |
| SN | Sampson equation |
| MH | Martin–Hopkins equation |
| TC | Total cholesterol |
| HDL-C | High-density lipoprotein cholesterol |
| TG | Triglycerides |
| dLDL-C | Directly measured low-density lipoprotein cholesterol |
| NonHDL-C | Non-HDL-cholesterol |
| RC | Remnant cholesterol |
References
- Miller, W.G.; Myers, G.L.; Sakurabayashi, I.; Bachmann, L.M.; Caudill, S.P.; Dziekonski, A.; Edwards, S.; Kimberly, M.M.; Korzun, W.J.; Leary, E.T.; et al. Seven direct methods for measuring HDL and LDL cholesterol compared with ultracentrifugation reference measurement procedures. Clin. Chem. 2010, 56, 977–986. [Google Scholar] [CrossRef]
- Ikezaki, H.; Fisher, V.A.; Lim, E.; Ai, M.; Liu, C.T.; Cupples, L.A.; Nakajima, K.; Asztalos, B.F.; Furusyo, N.; Schaefer, E.J. Direct versus calculated LDL cholesterol and C-reactive protein in cardiovascular disease risk assessment in the Framingham offspring study. Clin. Chem. 2019, 65, 1102–1114. [Google Scholar] [CrossRef]
- Steyn, N.; Rossouw, H.M.; Pillay, T.S.; Martins, J. Comparability of calculated LDL-C with directly measured LDL-C in selected paediatric and adult cohorts. Clin. Chim. Acta 2022, 531, 148–154. [Google Scholar] [CrossRef]
- Martins, J.; Olorunju, S.A.S.; Murray, L.M.; Pillay, T.S. Comparison of equations for the calculation of LDL-cholesterol in hospitalized patients. Clin. Chim. Acta 2020, 504, 132–137. [Google Scholar] [CrossRef]
- Martins, J.; Steyn, N.; Rossouw, H.M.; Pillay, T.S. Best practice for LDL-cholesterol: When and how to calculate. J. Clin. Pathol. 2023, 76, 145–150. [Google Scholar] [CrossRef]
- Cemin, R.; Casablanca, S.; Ermacora, D.; Daves, M. The importance of being aware of intrinsic methods’ limitation in low-density lipoprotein cholesterol determination to correctly identify cardiovascular risk: Is direct determination obtained with the Roche system systematically overestimating LDL in very high-risk patients with triglycerides concentration <2.25 mmol/L? J. Clin. Med. 2023, 12, 4419. [Google Scholar] [CrossRef]
- Friedewald, W.T.; Levy, R.I.; Fredrickson, D.S. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin. Chem. 1972, 18, 499–502. [Google Scholar] [CrossRef]
- Rodríguez-Domínguez, J.; Piedra-Aguilera, Á.; Martínez-Bujidos, M.; Malumbres-Serrano, S.; Morales-Indiano, C.; Fernández-Prendes, C. Direct LDL cholesterol assay vs. estimated equations in patients with hypertriglyceridemia or low LDL cholesterol levels. Ann. Lab. Med. 2024, 44, 363–366. [Google Scholar] [CrossRef] [PubMed]
- Sathiyakumar, V.; Blumenthal, R.S.; Elshazly, M.B. New information on accuracy of LDLC estimation: The impact of triglycerides and LDLC levels on Friedewald and alternative equations. J. Am. Coll. Cardiol. 2020. Epub ahead of print. [Google Scholar]
- Khan, M.R.; Sowmithri, K.D.; Shazia, A.; Nawaz, M.; Khaveyya, P.K.; Parkavi, B. Correlation analysis of direct LDL measurement and calculated LDL methods in lipid profile assessment: A comprehensive study. EJIFCC 2024, 35, 244–264. [Google Scholar] [PubMed]
- Samuel, C.; Park, J.; Sajja, A.; Michos, E.D.; Blumenthal, R.S.; Jones, S.R.; Martin, S.S. Accuracy of 23 equations for estimating LDL cholesterol in a clinical laboratory database of 5,051,467 patients. Glob. Heart 2023, 18, 36. [Google Scholar] [CrossRef] [PubMed]
- Karkhaneh, A.; Bagherieh, M.; Sadeghi, S.; Nikbakht, H.; Azhang, N.; Pourmoghaddas, M. Evaluation of eight formulas for LDL-C estimation in Iranian subjects with different metabolic health statuses. Lipids Health Dis. 2019, 18, 231. [Google Scholar] [CrossRef]
- Lindsey, C.C.; Graham, M.R.; Johnston, T.P.; Kiroff, C.G.; Freshley, A. A clinical comparison of calculated versus direct measurement of low-density lipoprotein cholesterol level. Pharmacotherapy 2004, 24, 167–172. [Google Scholar] [CrossRef]
- Sampson, M.; Ling, C.; Sun, Q.; Harb, R.; Ashmaig, M.; Warnick, R.; Sethi, A.; Fleming, J.K.; Otvos, J.D.; Meeusen, J.W.; et al. A new equation for calculation of low-density lipoprotein cholesterol in patients with normolipidemia and/or hypertriglyceridemia. JAMA Cardiol. 2020, 5, 540–548. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.S.; Blaha, M.J.; Elshazly, M.B.; Toth, P.P.; Kwiterovich, P.O.; Blumenthal, R.S.; Jones, S.R. Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA 2013, 310, 2061–2068. [Google Scholar] [CrossRef]
- Sajja, A.; Park, J.; Sathiyakumar, V.; Varghese, B.; Pallazola, V.A.; Marvel, F.A.; Kulkarni, K.; Muthukumar, A.; Joshi, P.H.; Gianos, E.; et al. Comparison of Methods to Estimate Low-Density Lipoprotein Cholesterol in Patients With High Triglyceride Levels. JAMA Netw. Open 2021, 4, e2128817. [Google Scholar] [CrossRef]
- Azimi, V.; Farnsworth, C.W.; Roper, S.M. Comparison of the Friedewald equation with Martin and Sampson equations for estimating LDL cholesterol in hypertriglyceridemic adults. Clin. Biochem. 2022, 108, 1–4. [Google Scholar] [CrossRef]
- Mach, F.; Baigent, C.; Catapano, A.L.; Koskinas, K.C.; Casula, M.; Badimon, L.; Chapman, M.J.; De Backer, G.G.; Delgado, V.; Ference, B.A.; et al. 2019 ESC/EAS Guidelines for the management of dyslipidaemias: Lipid modification to reduce cardiovascular risk: The Task Force for the management of dyslipidaemias of the European Society of Cardiology (ESC) and European Atherosclerosis Society (EAS). Eur. Heart J. 2020, 41, 111–188. [Google Scholar] [CrossRef]
- Grundy, S.M.; Stone, N.J.; Bailey, A.L.; Beam, C.; Birtcher, K.K.; Blumenthal, R.S.; Braun, L.T.; de Ferranti, S.; Faiella-Tommasino, J.; Forman, D.E.; et al. 2018 AHA/ACC Guideline on the Management of Blood Cholesterol: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. J. Am. Coll. Cardiol. 2019, 73, 3168–3209. [Google Scholar] [CrossRef] [PubMed]
- Miller, W.G.; Waymack, P.P.; Anderson, F.P.; Ethridge, S.F.; Jayne, E.C. Performance of four homogeneous direct methods for LDL-cholesterol. Clin. Chem. 2002, 48, 489–498. [Google Scholar] [CrossRef]
- Ahmadi, S.A.; Boroumand, M.A.; Gohari-Moghaddam, K.; Tajik, P.; Dibaj, S.M. The impact of low serum triglyceride on LDL-cholesterol estimation. Arch. Iran. Med. 2008, 11, 318–321. [Google Scholar] [PubMed]
- Anandaraja, S.; Narang, R.; Godeswar, R.; Laksmy, R.; Talwar, K.K. Low-density lipoprotein cholesterol estimation by a new formula in Indian population. Int. J. Cardiol. 2005, 102, 117–120. [Google Scholar] [CrossRef] [PubMed]
- Bauer, F.; Seibert, F.S.; Rohn, B.; Babel, N.; Westhoff, T.H. Estimation of LDL cholesterol in chronic kidney disease. Eur. J. Prev. Cardiol. 2021, 28, 1402–1408. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Pan, B.; Jin, X.; Yao, H.; Chen, B.; Zou, Y.; Ge, J.; Chen, H. A modified formula for calculating low-density lipoprotein cholesterol values. Lipids Health Dis. 2010, 9, 52. [Google Scholar] [CrossRef] [PubMed]
- Choi, R.; Park, M.J.; Oh, Y.; Kim, S.H.; Lee, S.G.; Lee, E.H. Validation of multiple equations for estimating low-density lipoprotein cholesterol levels in Korean adults. Lipids Health Dis. 2021, 20, 111. [Google Scholar] [CrossRef]
- de Cordova, C.M.; de Cordova, M.M. A new accurate, simple formula for LDL-cholesterol estimation based on directly measured blood lipids from a large cohort. Ann. Clin. Biochem. 2013, 50, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Dansethakul, P.; Thapanathamchai, L.; Saichanma, S.; Worachartcheewan, A.; Pidetcha, P. Determining a new formula for calculating low-density lipoprotein cholesterol: Data mining approach. EXCLI J. 2015, 14, 478–483. [Google Scholar] [CrossRef]
- DeLong, D.M.; DeLong, E.R.; Wood, P.D.; Lippel, K.; Rifkind, B.M. A comparison of methods for the estimation of plasma low- and very low-density lipoprotein cholesterol: The Lipid Research Clinics Prevalence Study. JAMA 1986, 256, 2372–2377. [Google Scholar] [CrossRef]
- Ephraim, R.K.D.; Acheampong, E.; Swaray, S.M.; Odame Anto, E.; Agbodzakey, H.; Adoba, P.; Afranie, B.O.; Batu, E.N.; Adu, P.; Fondjo, L.A.; et al. Developing a modified low-density lipoprotein (M-LDL-C) Friedewald’s equation as a substitute for direct LDL-C measure in a Ghanaian population: A comparative study. J. Lipids 2018, 2018, 7078409. [Google Scholar] [CrossRef]
- Ghasemi, A.; Asgari, S.; Hadaegh, F.; Kheirandish, M.; Azimzadeh, I.; Azizi, F.; Tohidi, M. New modified Friedewald formulae for estimating low-density lipoprotein cholesterol according to triglyceride levels: Extraction and validation. Endocrine 2018, 62, 404–411. [Google Scholar] [CrossRef]
- Hattori, Y.; Suzuki, M.; Tsushima, M.; Yoshida, M.; Tokunaga, Y.; Wang, Y.; Zhao, D.; Takeuchi, M.; Hara, Y.; Ryomoto, K.I.; et al. Development of approximate formula for LDL-chol, LDL-apo B and LDL-chol/LDL-apo B as indices of hyperapobetalipoproteinemia and small dense LDL. Atherosclerosis 1998, 138, 289–299. [Google Scholar] [CrossRef]
- Hu, C.Y.; Lee, C.L.; Sheu, W.H.; Wang, J.S.; Lee, I.T.; Song, Y.M.; Fu, C.-P.; Ling, J.-T.; Li, Y.-F.; Lin, S.-Y. A new formula for estimation of low-density lipoprotein cholesterol in an ethnic Chinese population. Clin. Chem. Lab. Med. 2015, 53, 1871–1879. [Google Scholar] [CrossRef]
- Molavi, F.; Namazi, N.; Asadi, M.; Sanjari, M.; Motlagh, M.E.; Shafiee, G.; Qorbani, M.; Heshmat, R.; Kelishadi, R. Comparison common equations for LDL-C calculation with direct assay and developing a novel formula in Iranian children and adolescents: The CASPIAN V study. Lipids Health Dis. 2020, 19, 129. [Google Scholar] [CrossRef] [PubMed]
- Saldaña Orejón, I.M.; Benites Ricra, M.A.; Chipana Huallpa, J.A. Derivación y validación de una ecuación para estimar el colesterol ligado a lipoproteínas de baja densidad en una población de Lima, Perú. An. Fac. Med. 2017, 78, 41–48. [Google Scholar] [CrossRef]
- Puavilai, W.; Laorugpongse, D.; Deerochanawong, C.; Muthapongthavorn, N.; Srilert, P. The accuracy in using modified Friedewald equation to calculate LDL from non-fast triglyceride: A pilot study. J. Med. Assoc. Thail. 2009, 92, 182–187. [Google Scholar]
- Rao, A.; Parker, A.H.; el-Sheroni, N.A.; Babelly, M.M. Calculation of low-density lipoprotein cholesterol with use of triglyceride/cholesterol ratios in lipoproteins compared with other calculation methods. Clin. Chem. 1988, 34, 2532–2534. [Google Scholar] [CrossRef]
- Rasouli, M.; Mokhtari, H. Calculation of LDL-cholesterol vs. direct homogenous assay. J. Clin. Lab. Anal. 2017, 31, e22057. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, N.; Saiedullah, M.; Khan, M.A.; Rahman, M.R. Comparison of modified Friedewald’s formula with direct measurement of low-density lipoprotein cholesterol in Bangladeshi population. Bangladesh Med. Res. Counc. Bull. 2013, 39, 120–123. [Google Scholar] [CrossRef]
- Sobhani, S.A.; Kheirandish, M.; Rafati, S.; Rafat, M.; Shahbazi, R.; Azarbad, A.; Mahmoodi, M.; Eftekhar, E.; Kheirandish, S. Development of a Modified Friedewald’s Formula to Calculate Low-Density Lipoprotein in an Iranian Population. Iran. J. Med. Sci. 2023, 48, 484–492. [Google Scholar] [CrossRef]
- Teerakanchana, T.; Puavilai, W.; Suriyaprom, K.; Tungtrongchitr, R. Comparative study of LDL-cholesterol levels in Thai patients by the direct method and using the Friedewald formula. Southeast Asian J. Trop. Med. Public Health 2007, 38, 519–527. [Google Scholar]
- Vujovic, A.; Kotur-Stevuljevic, J.; Spasic, S.; Bujisic, N.; Martinovic, J.; Vujovic, M.; Spasojevic-Kalimanovska, V.; Zeljkovic, A.; Pajic, D. Evaluation of different formulas for LDL-C calculation. Lipids Health Dis. 2010, 9, 27. [Google Scholar] [CrossRef] [PubMed]
- Miida, T.; Nishimura, K.; Okamura, T.; Hirayama, S.; Ohmura, H.; Yoshida, H.; Miyashita, Y.; Ai, M.; Tanaka, A.; Sumino, H.; et al. A multicenter study on the precision and accuracy of homogeneous assays for LDL-cholesterol: Comparison with a beta-quantification method using fresh serum obtained from non-diseased and diseased subjects. Atherosclerosis 2012, 225, 208–215. [Google Scholar] [CrossRef]
- Yamada, K.; Tsuji, N.; Fujita, T.; Tanaka, M.; Kuribayashi, K.; Kobayashi, D.; Watanabe, N. Comparison of four direct homogeneous methods for the measurement of low-density lipoprotein cholesterol. Clin. Lab. 2010, 56, 327–333. [Google Scholar] [PubMed]
- Mănescu, I.B.; Demian, L.; Dobreanu, M. Low-density lipoprotein cholesterol gymnastics: Exploring the advantages and limitations of the Friedewald, Martin-Hopkins, and Sampson equations for personalized lipid management. J. Pers. Med. 2024, 14, 1000. [Google Scholar] [CrossRef] [PubMed]
- Drobnik, S.; Scharnagl, H.; Samani, N.J.; Braund, P.S.; Nelson, C.P.; Hollstein, T.; Kassner, U.; Dressel, A.; Drobnik, W.; März, W. Evaluation of current indirect methods for measuring LDL-cholesterol. Clin. Chem. Lab. Med. 2025, 63, 1099–1108. [Google Scholar] [CrossRef] [PubMed]
| Database 1 (n = 10,174) | Database 2 (n = 21,091) | p Value * | |||||
|---|---|---|---|---|---|---|---|
| Male | Female | All | Male | Female | All | ||
| Sex (n, %) | 4958 (48.7%) | 5216 (51.3%) | 10,174 | 9995 (47.4%) | 11,096 (52.6%) | 21,091 | 0.026 |
| Age (years) | 60.0 [49.0–71.0] (0.0–96.0) | 62.0 [49.0–72.0] (0.0–97.0) | 61.0 [49.0–71.0] (0.0–97.0) | 54.0 [43.0–65.0] (1.0–96.0) | 58.0 [45.0–67.0] (1.0–94.0) | 56.0 [44.0–66.0] (1.0–96.0) | <0.0001 |
| Triglycerides | 119.0 [84.8–176.0] (23.6–1745.0) | 112.0 [82.2–158.0] (24.6–1943.0) | 116.0 [83.0–166.0] (23.6–1943.0) | 128.0 [91.0–186.0] (17.0–3490.0) | 107.0 [77.0–150.0] (24.0–3690.0) | 116.0 [83.0–166.0] (17.0–3690.0) | 0.75 |
| Total cholesterol | 174.0 [140.0–209.0] (43.8–765.0) | 189.0 [156.0–224.0] (59.1–463.0) | 182.0 [148.0–217.0] (43.8–765.0) | 192.0 [159.0–227.0] (75.0–554.0) | 204.0 [172.0–239.0] (33.0–730.0) | 198.0 [166.0–233.0] (33.0–730.0) | <0.0001 |
| HDL-cholesterol | 44.2 [36.9–53.7] (4.0–189.0) | 53.4 [44.4–63.8] (7.1–149.0) | 48.9 [39.8–59.6] (4.0–189.0) | 44.0 [37.0–51.0] (5.0–123.0) | 54.0 [46.0–63.0] (5.0–131.0) | 49.0 [41.0–58.0] (5.0–131.0) | 0.85 |
| dLDL-cholesterol | 107.0 [77.6–138.0] (10.1–388.0) | 116.0 [87.2–148.0] (4.3–501.0) | 112.0 [82.4–143.0] (4.3–501.0) | 125.0 [95.0–158.0] (23.0–472.0) | 131.0 [102.0–165.0] (13.0–378.0) | 129.0 [99.0–162.0] (13.0–472.0) | <0.0001 |
| Non-HDL-cholesterol | 126.7 [93.5–161.6] (24.8–760.9) | 131.2 [101.6–167.9] (1.0–403.4) | 128.9 [97.9–164.5] (1.0–760.9) | 146.0 [114.0–181.0] (39.0–488.0) | 147.0 [118.0–182.5] (26.0–696.0) | 147.0 [116.0–182.0] (26.0–696.0) | <0.0001 |
| Remnant cholesterol | 16.8 [9.9–25.6] (0.0–717.7) | 15.2 [9.0–22.9] (0.0–339.5) | 15.9 [9.5–24.2] (0.0–717.7) | 17.0 [10.0–27.0] (0.0–423.0) | 15.0 [8.0–23.0] (0.0–658.0) | 16.0 [9.0–24.0] (0.0–658.0) | 0.06 |
| TG ≥ 400 mg/dL (n, %) | 155 (1.52%) | 79 (0.77%) | 234 (2.29%) | 349 (1.65%) | 113 (0.53%) | 462 (2.18%) | - |
| Equation [Reference] | LDL-C Category (mg/dL) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| <40 (n = 230) | 40–54 (n = 512) | 55–69 (n = 847) | 70–99 (n = 2479) | 100–129 (n = 2558) | 130–159 (n = 1986) | 160–189 (n = 1004) | ≥190 (n = 558) | Overall (n = 10,174) | |
| Ahmadi [21] | 33.9 | 20.5 | 21.5 | 37.4 | 33.0 | 30.8 | 29.6 | 89.1 | 34.8 |
| Anandaraja [22] | 65.7 | 38.9 | 41.8 | 64.1 | 62.2 | 60.5 | 56.5 | 69.2 | 59.3 |
| Bauer [23] | 65.7 | 67.6 | 74.4 | 86.6 | 84.0 | 82.3 | 82.9 | 91.0 | 82.5 |
| Chen [24] | 75.2 | 75.0 | 69.7 | 81.1 | 67.8 | 54.2 | 40.9 | 56.6 | 65.8 |
| Choi [25] | 44.3 | 42.8 | 50.5 | 74.0 | 76.3 | 77.9 | 79.5 | 97.8 | 73.0 |
| Cordova [26] | 60.4 | 66.0 | 57.3 | 67.6 | 40.6 | 21.5 | 10.8 | 29.2 | 43.0 |
| Dansethakul [27] | 65.7 | 67.0 | 69.7 | 84.5 | 82.8 | 79.8 | 75.6 | 79.6 | 79.4 |
| Delong [28] | 79.6 | 73.6 | 73.1 | 84.1 | 80.5 | 76.7 | 72.5 | 81.5 | 78.9 |
| Ephraim [29] | 87.8 | 37.1 | 29.8 | 57.6 | 48.6 | 40.7 | 32.7 | 48.6 | 46.4 |
| Friedewald [7] | 88.7 | 63.9 | 53.8 | 74.4 | 67.2 | 62.2 | 54.6 | 64.7 | 65.8 |
| Ghasemi [30] | 87.8 | 37.1 | 29.8 | 57.6 | 48.6 | 40.7 | 32.7 | 48.6 | 46.4 |
| Hattori [31] | 91.7 | 48.4 | 34.6 | 60.6 | 46.5 | 34.8 | 23.0 | 42.8 | 45.3 |
| Lee & Hu [32] | 37.8 | 40.2 | 49.6 | 76.1 | 75.5 | 63.4 | 47.3 | 55.6 | 64.6 |
| Martin [15] | 81.7 | 65.4 | 63.0 | 81.9 | 75.6 | 69.2 | 59.0 | 68.6 | 72.4 |
| Martin extdended [16] | 81.7 | 65.6 | 63.1 | 82.0 | 75.8 | 69.3 | 58.6 | 68.1 | 72.5 |
| Molavi [33] | 88.7 | 67.4 | 59.1 | 75.8 | 65.8 | 58.0 | 48.4 | 59.7 | 64.7 |
| Orejón [34] | 63.0 | 67.0 | 73.3 | 88.2 | 85.6 | 81.5 | 75.5 | 81.5 | 81.7 |
| Puavilai [35] | 82.6 | 73.0 | 71.3 | 83.0 | 79.4 | 74.6 | 69.2 | 78.3 | 77.4 |
| Rao [36] | 82.2 | 67.0 | 68.1 | 81.1 | 79.8 | 78.4 | 77.5 | 86.4 | 78.4 |
| Rasouli [37] | 66.5 | 78.1 | 74.9 | 78.0 | 44.9 | 14.0 | 2.3 | 18.6 | 45.9 |
| Saiedullah [38] | 33.5 | 44.5 | 64.2 | 86.8 | 85.9 | 81.4 | 76.7 | 81.0 | 79.0 |
| Sampson [14] | 87.4 | 68.6 | 63.9 | 80.2 | 76.1 | 70.2 | 62.4 | 69.9 | 73.1 |
| Sobhani [39] | 90.9 | 47.7 | 25.3 | 51.4 | 31.4 | 15.6 | 5.2 | 28.9 | 32.1 |
| Teerakanchana [40] | 59.1 | 60.0 | 70.5 | 88.2 | 87.5 | 80.0 | 70.1 | 75.4 | 80.4 |
| Vujovic [41] | 73.5 | 72.7 | 74.7 | 86.7 | 83.5 | 80.9 | 78.4 | 86.6 | 81.9 |
| Equation | LDL-C Category (mg/dL) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| <40 (n = 84) | 40–54 (n = 349) | 55–69 (n = 966) | 70–99 (n = 4010) | 100–129 (n = 5301) | 130–159 (n = 4837) | 160–189 (n = 3325) | ≥190 (n = 2219) | Overall (n = 21,091) | |
| Ahmadi [21] | 23.8 | 20.3 | 18.0 | 37.9 | 35.4 | 32.6 | 32.6 | 83.1 | 38.7 |
| Anandaraja [22] | 38.1 | 29.2 | 34.2 | 59.5 | 59.0 | 55.9 | 49.2 | 61.0 | 55.3 |
| Bauer [23] | 40.5 | 47.9 | 58.0 | 81.3 | 80.8 | 77.2 | 72.4 | 83.4 | 77.3 |
| Chen [24] | 59.5 | 69.3 | 75.1 | 84.2 | 69.0 | 50.3 | 36.4 | 47.0 | 60.4 |
| Choi [25] | 26.2 | 21.2 | 30.2 | 64.0 | 72.2 | 75.0 | 74.6 | 92.8 | 70.9 |
| Cordova [26] | 41.7 | 62.2 | 68.7 | 72.1 | 37.8 | 19.9 | 10.3 | 23.4 | 36.2 |
| Dansethakul [27] | 34.5 | 41.0 | 52.7 | 79.9 | 79.6 | 74.9 | 68.0 | 74.1 | 74.1 |
| Delong [28] | 54.8 | 63.0 | 65.7 | 83.8 | 79.2 | 71.6 | 65.0 | 73.3 | 74.5 |
| Ephraim [29] | 63.1 | 49.3 | 45.2 | 65.5 | 52.8 | 41.3 | 33.1 | 47.1 | 48.5 |
| Friedewald [7] | 57.1 | 60.7 | 59.8 | 79.3 | 69.3 | 58.9 | 52.0 | 60.3 | 64.5 |
| Ghasemi [30] | 63.1 | 49.3 | 45.2 | 65.5 | 52.8 | 41.3 | 33.1 | 47.1 | 48.5 |
| Hattori [31] | 61.9 | 57.3 | 50.9 | 69.5 | 50.8 | 34.2 | 23.5 | 39.0 | 45.2 |
| Lee & Hu [32] | 22.6 | 23.8 | 41.8 | 70.9 | 70.3 | 53.2 | 36.2 | 42.1 | 55.9 |
| Martin [15] | 61.9 | 66.8 | 70.9 | 84.2 | 75.2 | 64.1 | 54.0 | 60.5 | 69.1 |
| Martin extdended [16] | 60.7 | 67.0 | 71.0 | 84.2 | 75.3 | 63.7 | 54.0 | 60.3 | 69.0 |
| Molavi [33] | 52.4 | 61.3 | 61.4 | 80.0 | 67.9 | 54.5 | 45.1 | 55.3 | 61.7 |
| Orejón [34] | 35.7 | 44.1 | 56.0 | 82.8 | 82.1 | 75.6 | 67.7 | 73.6 | 75.6 |
| Puavilai [35] | 57.1 | 62.8 | 65.6 | 83.5 | 77.8 | 69.9 | 62.6 | 71.4 | 73.1 |
| Rao [36] | 45.2 | 48.7 | 51.6 | 76.8 | 74.9 | 72.8 | 69.1 | 81.6 | 73.0 |
| Rasouli [37] | 44.0 | 61.9 | 70.2 | 80.9 | 45.7 | 15.9 | 4.5 | 17.6 | 37.5 |
| Saiedullah [38] | 19.0 | 21.8 | 46.3 | 82.9 | 84.2 | 76.6 | 67.6 | 74.0 | 75.5 |
| Sampson [14] | 67.9 | 71.3 | 67.5 | 82.5 | 75.1 | 65.9 | 58.3 | 65.0 | 70.2 |
| Sobhani [39] | 75.0 | 67.0 | 45.7 | 61.3 | 32.8 | 15.8 | 8.2 | 25.3 | 31.0 |
| Teerakanchana [40] | 41.7 | 40.1 | 54.9 | 81.2 | 80.6 | 70.7 | 59.4 | 63.8 | 71.3 |
| Vujovic [41] | 52.4 | 59.3 | 65.3 | 83.6 | 81.1 | 74.9 | 68.3 | 78.1 | 76.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Györfi, I.; Oprea, O.R.; Mănescu, I.B.; Curici, A.; Dobreanu, M. Comparative Evaluation of 24 LDL-C Estimation Equations Against Direct Assays in Two Independent Cohorts. Diagnostics 2025, 15, 2298. https://doi.org/10.3390/diagnostics15182298
Györfi I, Oprea OR, Mănescu IB, Curici A, Dobreanu M. Comparative Evaluation of 24 LDL-C Estimation Equations Against Direct Assays in Two Independent Cohorts. Diagnostics. 2025; 15(18):2298. https://doi.org/10.3390/diagnostics15182298
Chicago/Turabian StyleGyörfi, Imola, Oana Roxana Oprea, Ion Bogdan Mănescu, Antoanela Curici, and Minodora Dobreanu. 2025. "Comparative Evaluation of 24 LDL-C Estimation Equations Against Direct Assays in Two Independent Cohorts" Diagnostics 15, no. 18: 2298. https://doi.org/10.3390/diagnostics15182298
APA StyleGyörfi, I., Oprea, O. R., Mănescu, I. B., Curici, A., & Dobreanu, M. (2025). Comparative Evaluation of 24 LDL-C Estimation Equations Against Direct Assays in Two Independent Cohorts. Diagnostics, 15(18), 2298. https://doi.org/10.3390/diagnostics15182298







