Predicting the Recurrence of Differentiated Thyroid Cancer Using Whale Optimization-Based XGBoost Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Acquisition
2.2. Dataset Preprocessing
2.3. Feature Selection
2.3.1. Basic Whale Optimization Algorithm
- is the best position;
- is the current position;
- and are coefficient vectors;
- is linearly decreased from 2 to 0 over the course of iterations;
- is a random vector;
- is the distance between the best and current positions.
- is the distance of ith whale to the best solution obtained so far;
- indicates the updated position of whales during optimization;
- b defines the logarithmic spiral shape;
- l is a random number;
- p determines whether the population encircles or spirals to attack.
2.3.2. Modified Whale Optimization Algorithm
- (a)
- Inertia weight (w)
- w is the inertia weight coefficient;
- t is the current iteration number in the optimization algorithm;
- is the maximum number of iterations in the algorithm;
- n is a constant parameter that affects the frequency of oscillation.
- represents the position of the whale at iteration t;
- is the best solution so far;
- is a coefficient vector controlling the balance between exploration and exploitation;
- w is the inertia weight.
- (b)
- Piecewise linear chaotic map
- and β refers to the initial condition and control parameters, respectively.
2.4. Model Trained Using XGBoost Classifier Algorithm
Hyperparameter Tuning
2.5. Performance Analysis
3. Results
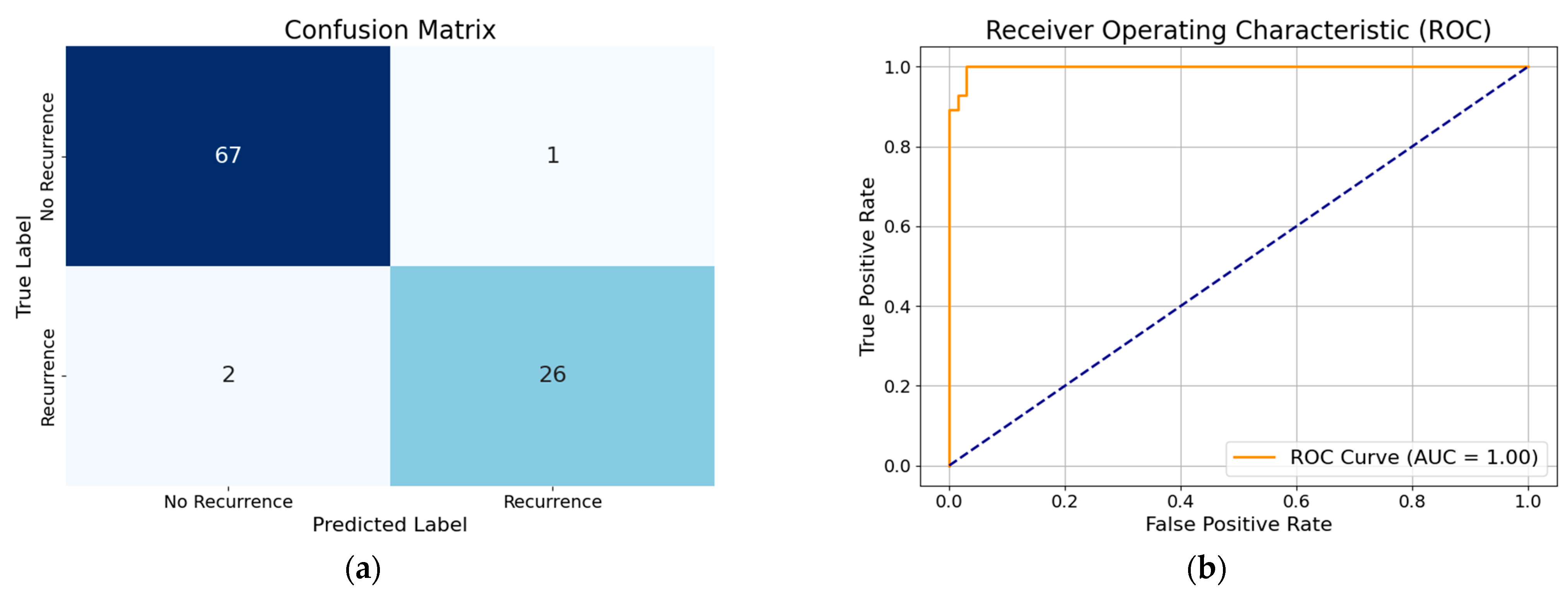
3.1. Performance of XGBoost Model with All Features
3.2. Performance of XGBoost Model with Selected Features



3.3. Overfitting Prevention and Model Robustness Evaluation
- Feature Selection: Our Modified WOA selected only two key features (‘Pathology’ and ‘Response’). This significantly reduced model complexity and the risk of overfitting.
- Hyperparameter Optimization: The WOA also tuned important XGBoost parameters such as max_depth and learning_rate, which are known to control model complexity and regularization.
- Fitness Function with Regularization: Our fitness function included a penalty for using more features, encouraging the model to favor simpler, more generalizable solutions.
- Cross-Validation: We used 5-fold cross-validation during training to evaluate the performance of each candidate model configuration. This provided a robust estimate of generalization ability. The best configuration achieved a mean F1-score of 0.8823 ± 0.0505 on the training data.
- Independent Test Set Evaluation: After optimization, the final model was tested on an unseen dataset, achieving an F1-score of 0.9231 and accuracy of 0.9583, confirming strong generalization to new data.
3.4. Model Performance Comparison
| Model | Accuracy | Precision | Recall | F1 Score | AUC-ROC |
|---|---|---|---|---|---|
| XGBoost with all features | 96% | 94% | 96% | 95% | 1.00 |
| Optimized XGBoost by basic WOA with all features | 99% | 99% | 97% | 98% | 0.97 |
| Optimized XGBoost by modified WOA with all features | 97% | 100% | 89% | 94% | 1.00 |
| Optimized XGBoost by modified WOA with selected features | 96% | 100% | 85% | 92% | 0.99 |
| Optimized XGBoost by basic WOA with selected features | 96% | 97% | 93% | 95% | 0.99 |
3.5. Comparison with Previous Works
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DTC | Differentiated thyroid cancer |
| WOA | Whale optimization algorithm |
| AI | Artificial intelligence |
| PWLCM | Piecewise linear chaotic map |
References
- Mazzaferri, E.L. Empirically treating high serum thyroglobulin levels. J. Nucl. Med. 2005, 46, 1079–1088. [Google Scholar] [PubMed]
- Burns, W.R.; Zeiger, M.A. Differentiated thyroid cancer. In Seminars in Oncology; WB Saunders: Philadelphia, PA, USA, 2010; pp. 557–566. [Google Scholar]
- Schlumberger, M.; Leboulleux, S. Current practice in patients with differentiated thyroid cancer. Nat. Rev. Endocrinol. 2021, 17, 176–188. [Google Scholar] [CrossRef] [PubMed]
- Haugen, B.R. 2015 American Thyroid Association management guidelines for adult patients with thyroid nodules and differentiated thyroid cancer: What is new and what has changed? Cancer 2017, 123, 372–381. [Google Scholar] [CrossRef] [PubMed]
- Hollenbeak, C.S.; Boltz, M.M.; Schaefer, E.W.; Saunders, B.D.; Goldenberg, D. Recurrence of differentiated thyroid cancer in the elderly. Eur. J. Endocrinol. 2013, 168, 549–556. [Google Scholar] [CrossRef]
- Zahedi, A.; Bondaz, L.; Rajaraman, M.; Leslie, W.D.; Jefford, C.; Young, J.E.; Pathak, K.A.; Bureau, Y.; Rachinsky, I.; Badreddine, M. Risk for thyroid cancer recurrence is higher in men than in women independent of disease stage at presentation. Thyroid 2020, 30, 871–877. [Google Scholar] [CrossRef]
- Medas, F.; Canu, G.L.; Boi, F.; Lai, M.L.; Erdas, E.; Calò, P.G. Predictive factors of recurrence in patients with differentiated thyroid carcinoma: A retrospective analysis on 579 patients. Cancers 2019, 11, 1230. [Google Scholar] [CrossRef]
- Borzooei, S.; Briganti, G.; Golparian, M.; Lechien, J.R.; Tarokhian, A. Machine learning for risk stratification of thyroid cancer patients: A 15-year cohort study. Eur. Arch. Oto-Rhino-Laryngol. 2024, 281, 2095–2104. [Google Scholar] [CrossRef]
- Chattopadhyay, S. Towards Predicting Recurrence Risk of Differentiated Thyroid Cancer with a Hybrid Machine Learning Model. Medinformatics 2024. [Google Scholar] [CrossRef]
- Setiawan, K.E. Predicting recurrence in differentiated thyroid cancer: A comparative analysis of various machine learning models including ensemble methods with chi-squared feature selection. Commun. Math. Biol. Neurosci. 2024, 2024, 5. [Google Scholar]
- Clark, E.; Price, S.; Lucena, T.; Haberlein, B.; Wahbeh, A.; Seetan, R. Predictive Analytics for Thyroid Cancer Recurrence: A Machine Learning Approach. Knowledge 2024, 4, 557–570. [Google Scholar] [CrossRef]
- Rajni, G.; Pankaj, R. XGBoost for Heart Disease Prediction: Achieving High Accuracy with Robust Machine Learning Techniques. Int. J. Innov. Sci. Eng. Manag. 2024, 3, 7–14. Available online: https://ijisem.com/journal/index.php/ijisem/article/view/17 (accessed on 19 July 2024).
- Latif, M.A.; Mushtaq, Z.; Arif, S.; Rehman, S.; Qureshi, M.F.; Samee, N.A.; Alabdulhafith, M.; Al-masni, M.A. Improving Thyroid Disorder Diagnosis via Ensemble Stacking and Bidirectional Feature Selection. Comput. Mater. Contin. 2024, 78, 4225–4241. [Google Scholar] [CrossRef]
- Oture, O.; Iqbal, M.Z.; Wang, X. Enhanced diagnosis of thyroid diseases through advanced machine learning methodologies. Sci 2025, 7, 66. [Google Scholar] [CrossRef]
- Afshan, N.; Mushtaq, Z.; Alamri, F.S.; Qureshi, M.F.; Khan, N.A.; Siddique, I. Efficient thyroid disorder identification with weighted voting ensemble of super learners by using adaptive synthetic sampling technique. AIMS Math. 2023, 8, 24274–24309. [Google Scholar] [CrossRef]
- Akhtar, T.; Gilani, S.O.; Mushtaq, Z.; Arif, S.; Jamil, M.; Ayaz, Y.; Butt, S.I.; Waris, A. Effective voting ensemble of homogenous ensembling with multiple attribute-selection approaches for improved identification of thyroid disorder. Electronics 2021, 10, 3026. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Springer International Publishing: Cham, Switzerland, 2015; Volume 72. [Google Scholar]
- Hastie, T. The elements of statistical learning: Data mining, inference, and prediction. J. Am. Stat. Assoc. 2009, 99, 567. [Google Scholar]
- Kuhn, M. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Chakraborty, S.; Saha, A.K.; Chakraborty, R.; Saha, M. An enhanced whale optimization algorithm for large scale optimization problems. Know.-Based Syst. 2021, 233, 29. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Guo, W.; Liu, T.; Dai, F.; Xu, P. An Improved Whale Optimization Algorithm for Feature Selection. Comput. Mater. Contin. 2020, 62, 337. [Google Scholar] [CrossRef]
- Chao, I.M.; Hsiung, S.-C.; Liu, J.-L. Improved Whale Optimization Algorithm Based on Inertia Weights for Solving Global Optimization Problems. Adv. Technol. Innov. 2020, 5, 147. [Google Scholar] [CrossRef]
- Saiki, Y.; Takahasi, H.; Yorke, J.A. Piecewise linear maps with heterogeneous chaos. Nonlinearity 2021, 34, 5744. [Google Scholar] [CrossRef]
- Alzahrani, J.S.; Rizwanullah, M.; Osman, A.E. Piece-Wise Linear Chaotic Mapping-based Beluga Whale Optimization Algorithm-based Indoor Activity Monitoring for Elderly and Visually Impaired Persons. J. Disabil. Res. 2023, 2, 112–119. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Nandini, S. Comparative Study of Machine Learning Algorithms in Detecting Cardiovascular Diseases. arXiv 2024, arXiv:2405.17059. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
- Abbad Ur Rehman, H.; Lin, C.-Y.; Mushtaq, Z. Effective K-nearest neighbor algorithms performance analysis of thyroid disease. J. Chin. Inst. Eng. 2021, 44, 77–87. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks. Studies in Computational Intelligence; Springer: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Feoktistov, V. Differential Evolution; Springer: Boston, MA, USA, 2006. [Google Scholar]
- Hossain, M.S.; Muhammad, G.; Guizani, N. Explainable AI and mass surveillance system-based healthcare framework to combat COVID-I9 like pandemics. IEEE Netw. 2020, 34, 126–132. [Google Scholar] [CrossRef]
- Lundberg, S. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-precision model-agnostic explanations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]





| Category | Details | Count |
|---|---|---|
| Total samples | - | 383 |
| Recurrence | - | 120 |
| Cancer Stages | Stage I | 333 |
| Stage II | 32 | |
| Stage III | 4 | |
| Stage IV A | 3 | |
| Stage IV B | 11 | |
| Pathology | Papillary Carcinoma | 287 |
| Micro Papillary Carcinoma | 48 | |
| Follicular Carcinoma | 28 | |
| Hurthel Cell Carcinoma | 20 | |
| Tumor Size (T) | T0 | 0 |
| T1 | 92 | |
| -T1a | 49 | |
| -T1b | 43 | |
| T2 | 149 | |
| T3 | 110 | |
| -T3a | 94 | |
| -T3b | 16 | |
| T4 | 26 | |
| Lymph Node (N) | N0 | 264 |
| N1 | 119 | |
| N2 | 0 | |
| N3 | 0 | |
| Metastasis (M) | M0 | 365 |
| M1 | 18 |
| Work | Dataset Used | Model Used | Accuracy | F1-Score | Precision | Recall |
|---|---|---|---|---|---|---|
| [10] | DTC (All f.) [8] | RF | 96% | 94% | 94% | 94% |
| [9] | DTC (All f.) [8] | MLR | 78.32% | - | - | - |
| [11] | DTC (All f.) [8] | RF | 95% | 95% | 95% | 96% |
| [15] | KEEL and hypothyroid dataset | SL ensemble | 99.602% | 98.565% | 99.785% | 97.413% |
| [16] | DHQ [31] | SFM | 100% | 100% | 100% | 100% |
| Our | DTC (All f.) [8] | XGBoost | 99% | 98% | 99% | 97% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrestha, K.; Rifat, H.M.J.O.; Biswas, U.; Tiang, J.-J.; Nahid, A.-A. Predicting the Recurrence of Differentiated Thyroid Cancer Using Whale Optimization-Based XGBoost Algorithm. Diagnostics 2025, 15, 1684. https://doi.org/10.3390/diagnostics15131684
Shrestha K, Rifat HMJO, Biswas U, Tiang J-J, Nahid A-A. Predicting the Recurrence of Differentiated Thyroid Cancer Using Whale Optimization-Based XGBoost Algorithm. Diagnostics. 2025; 15(13):1684. https://doi.org/10.3390/diagnostics15131684
Chicago/Turabian StyleShrestha, Keshika, H. M. Jabed Omur Rifat, Uzzal Biswas, Jun-Jiat Tiang, and Abdullah-Al Nahid. 2025. "Predicting the Recurrence of Differentiated Thyroid Cancer Using Whale Optimization-Based XGBoost Algorithm" Diagnostics 15, no. 13: 1684. https://doi.org/10.3390/diagnostics15131684
APA StyleShrestha, K., Rifat, H. M. J. O., Biswas, U., Tiang, J.-J., & Nahid, A.-A. (2025). Predicting the Recurrence of Differentiated Thyroid Cancer Using Whale Optimization-Based XGBoost Algorithm. Diagnostics, 15(13), 1684. https://doi.org/10.3390/diagnostics15131684










