A Tumor Volume Segmentation Algorithm Based on Radiomics Features in FDG-PET in Lung Cancer Patients, Validated Using Surgical Specimens
Abstract
1. Introduction
2. Materials and Methods
2.1. Patient Population
2.2. Imaging
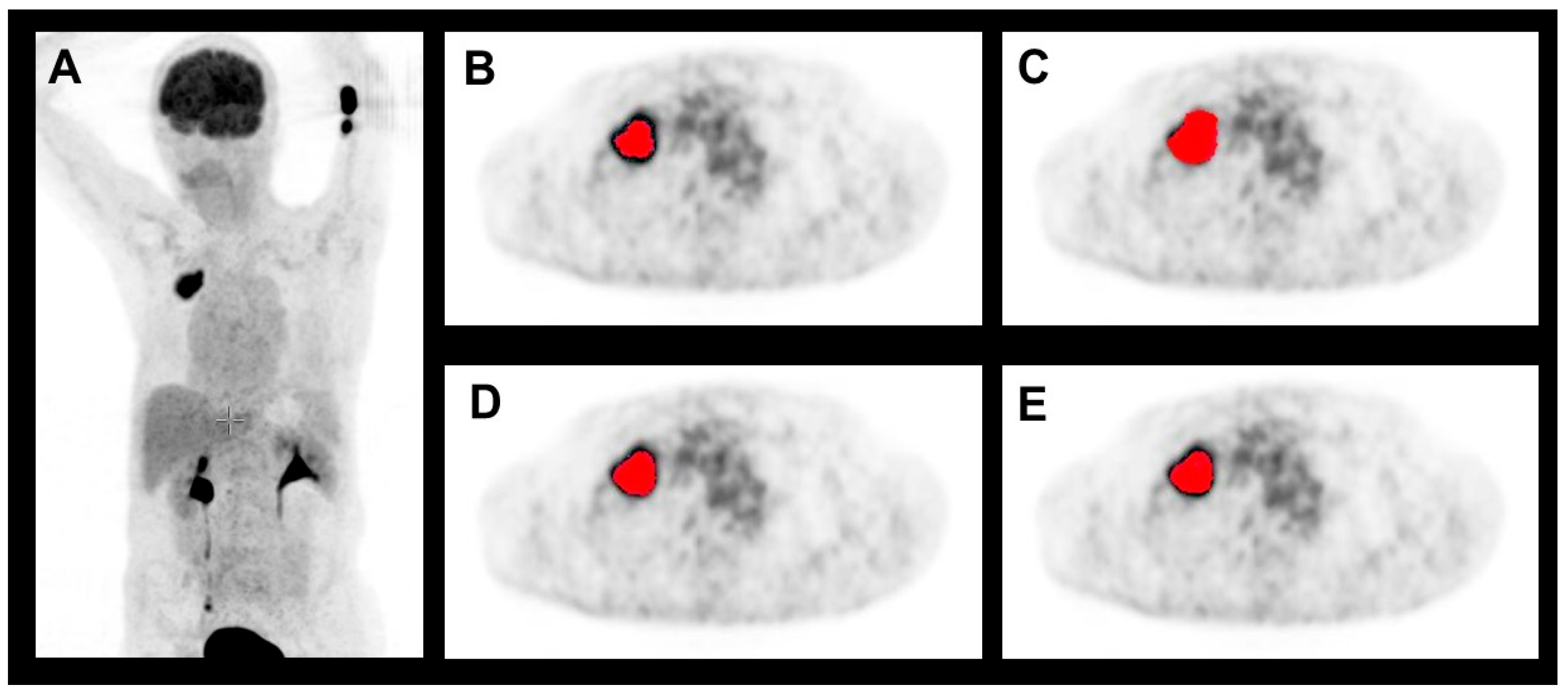
2.3. Target Volume Segmentation
2.4. Pathological Workup
2.5. Statistical Analysis
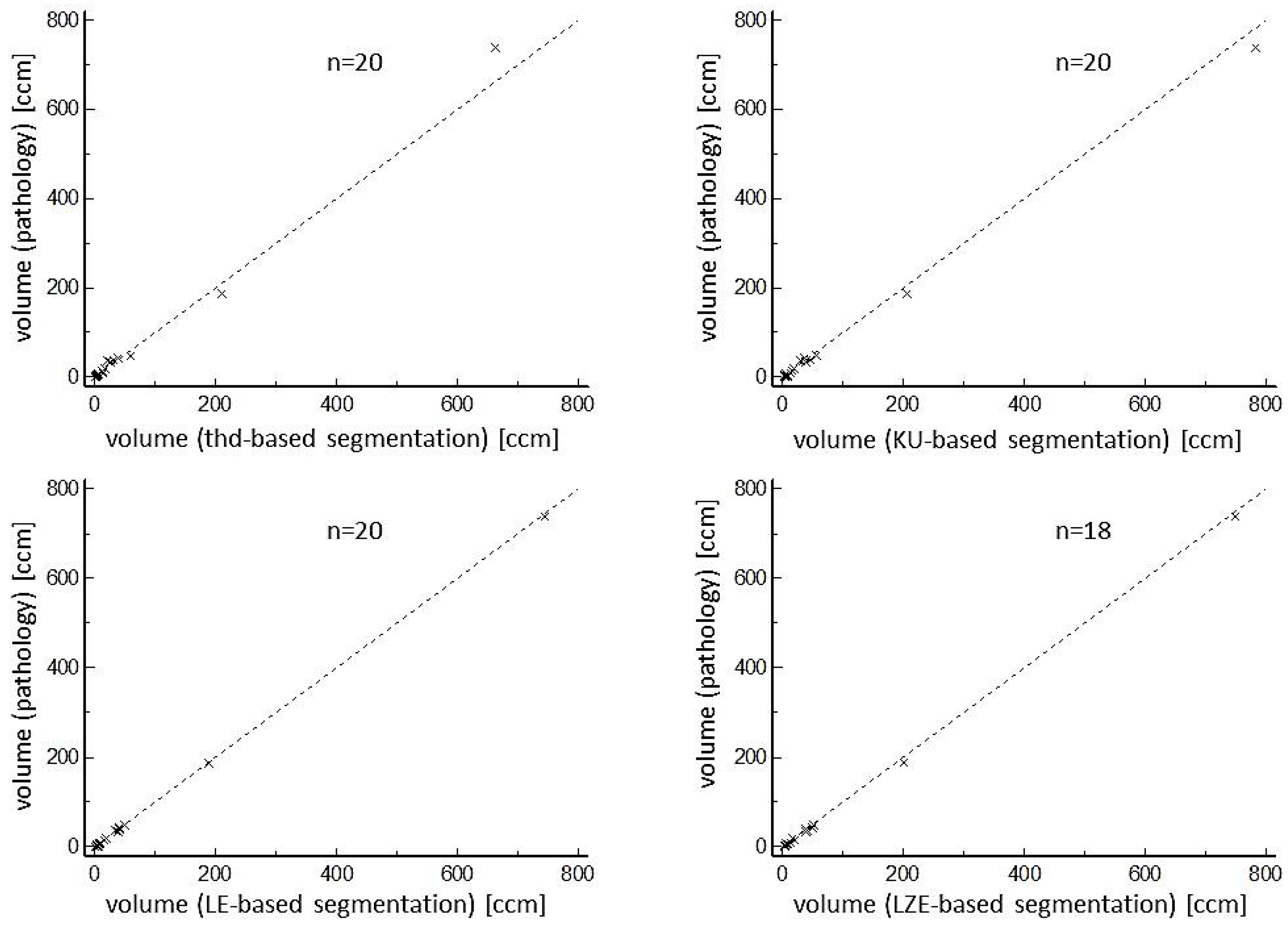
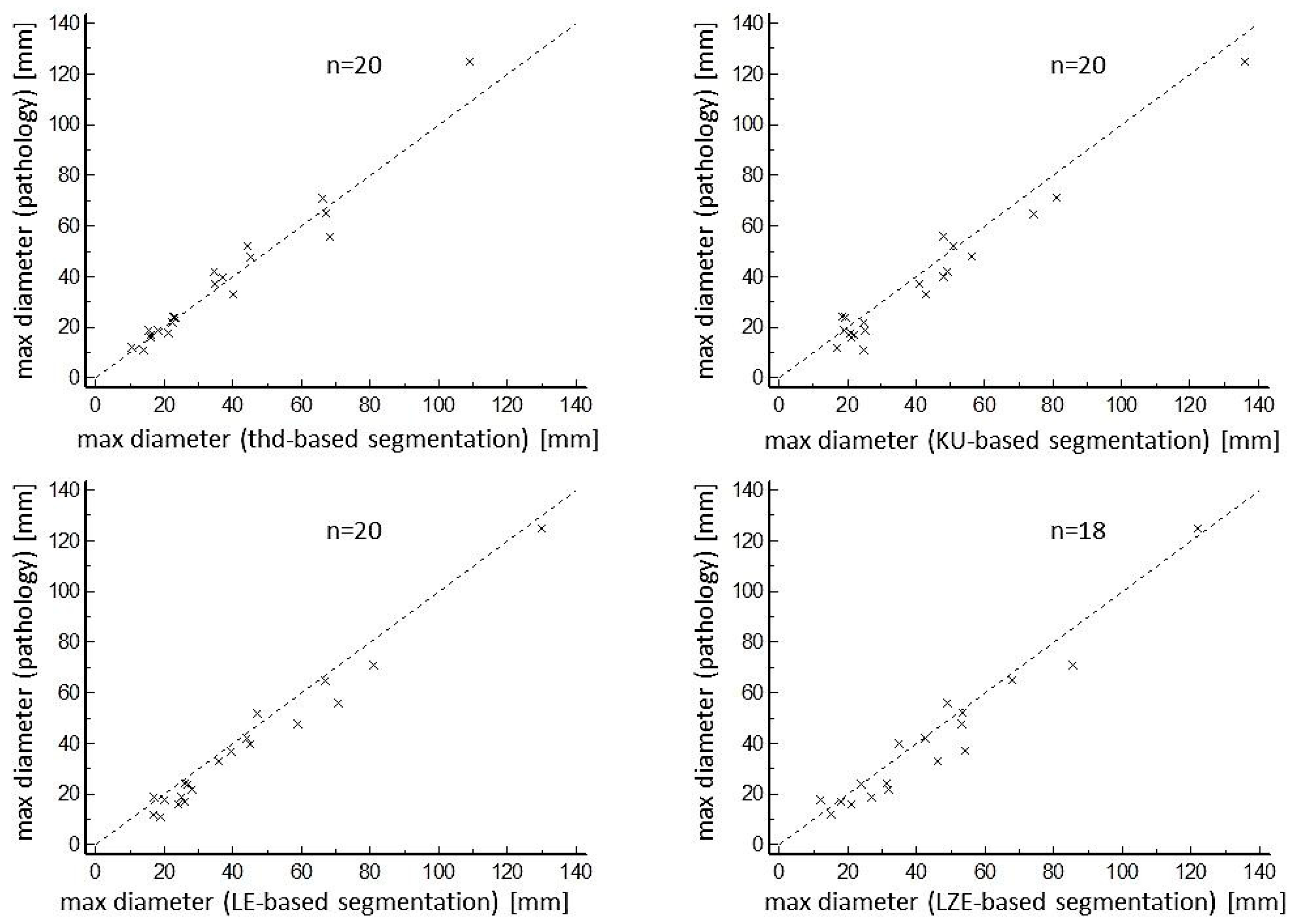
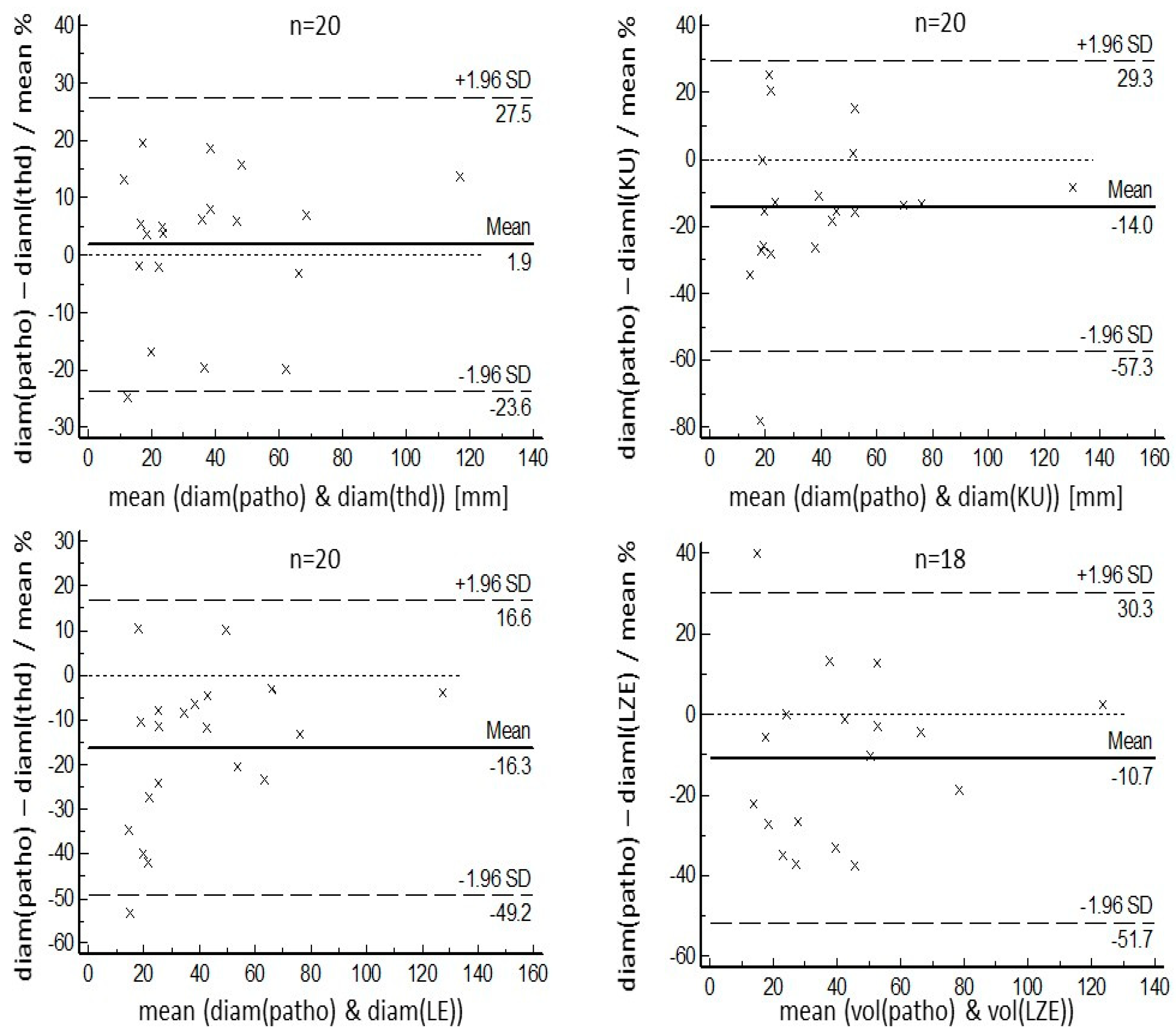
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Unterrainer, M.; Eze, C.; Ilhan, H.; Marschner, S.; Roengvoraphoj, O.; Schmidt-Hegemann, N.S.; Walter, F.; Kunz, W.G.; Rosenschöld, P.M.; Jeraj, R.; et al. Recent advances of PET imaging in clinical radiation oncology. Radiat. Oncol. 2020, 15, 88. [Google Scholar] [CrossRef] [PubMed]
- Fonti, R.; Conson, M.; Del Vecchio, S. PET/CT in radiation oncology. Semin. Oncol. 2019, 46, 202–209. [Google Scholar] [CrossRef] [PubMed]
- Laack, N.N.; Pafundi, D.; Anderson, S.K.; Kaufmann, T.; Lowe, V.; Hunt, C.; Vogen, D.; Yan, E.; Sarkaria, J.; Brown, P.; et al. Initial Results of a Phase 2 Trial of (18)F-DOPA PET-Guided Dose-Escalated Radiation Therapy for Glioblastoma. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 1383–1395. [Google Scholar] [CrossRef] [PubMed]
- Ganem, J.; Thureau, S.; Gardin, I.; Modzelewski, R.; Hapdey, S.; Vera, P. Delineation of lung cancer with FDG PET/CT during radiation therapy. Radiat. Oncol. 2018, 13, 219. [Google Scholar] [CrossRef]
- Mac Manus, M.P.; Hicks, R.J. Impact of PET on radiation therapy planning in lung cancer. Radiol. Clin. N. Am. 2007, 45, 627–638. [Google Scholar] [CrossRef]
- Nestle, U.; Schimek-Jasch, T.; Kremp, S.; Schaefer-Schuler, A.; Mix, M.; Kusters, A.; Tosch, M.; Hehr, T.; Eschmann, S.M.; Bultel, Y.P.; et al. Imaging-based target volume reduction in chemoradiotherapy for locally advanced non-small-cell lung cancer (PET-Plan): A multicentre, open-label, randomised, controlled trial. Lancet Oncol. 2020, 21, 581–592. [Google Scholar] [CrossRef]
- Pyka, T.; Bundschuh, R.A.; Andratschke, N.; Mayer, B.; Specht, H.M.; Papp, L.; Zsoter, N.; Essler, M. Textural features in pre-treatment [F18]-FDG-PET/CT are correlated with risk of local recurrence and disease-specific survival in early stage NSCLC patients receiving primary stereotactic radiation therapy. Radiat. Oncol. 2015, 10, 100. [Google Scholar] [CrossRef]
- Vees, H.; Senthamizhchelvan, S.; Miralbell, R.; Weber, D.C.; Ratib, O.; Zaidi, H. Assessment of various strategies for 18F-FET PET-guided delineation of target volumes in high-grade glioma patients. Eur. J. Nucl. Med. Mol. Imaging 2009, 36, 182–193. [Google Scholar] [CrossRef]
- Bundschuh, R.A.; Delso, G.; Essler, M.; Martínez-Möller, A.; Astner, S.T.; Nekolla, S.G.; Ziegler, S.I.; Schwaiger, M. Biological target volume for lesions with inhomogeneous activity distribution in PET. Radiother. Oncol. 2008, 88, S31. [Google Scholar]
- Milker-Zabel, S.; Zabel-du Bois, A.; Henze, M.; Huber, P.; Schulz-Ertner, D.; Hoess, A.; Haberkorn, U.; Debus, J. Improved target volume definition for fractionated stereotactic radiotherapy in patients with intracranial meningiomas by correlation of CT, MRI, and [68Ga]-DOTATOC-PET. Int. J. Radiat. Oncol. Biol. Phys. 2006, 65, 222–227. [Google Scholar] [CrossRef]
- Hatt, M.; Lee, J.A.; Schmidtlein, C.R.; Naqa, I.E.; Caldwell, C.; De Bernardi, E.; Lu, W.; Das, S.; Geets, X.; Gregoire, V.; et al. Classification and evaluation strategies of auto-segmentation approaches for PET: Report of AAPM task group No. 211. Med. Phys. 2017, 44, e1–e42. [Google Scholar] [CrossRef] [PubMed]
- Mercieca, S.; Belderbos, J.S.A.; van Herk, M. Challenges in the target volume definition of lung cancer radiotherapy. Transl. Lung Cancer Res. 2021, 10, 1983–1998. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, M.; Garcia, D.V.; Kramer, G.M.; Frings, V.; Smit, E.F.; Dierckx, R.; Hoekstra, O.S.; Boellaard, R. Variability and Repeatability of Quantitative Uptake Metrics in (18)F-FDG PET/CT of Non-Small Cell Lung Cancer: Impact of Segmentation Method, Uptake Interval, and Reconstruction Protocol. J. Nucl. Med. 2019, 60, 600–607. [Google Scholar] [CrossRef] [PubMed]
- Thie, J.A. Understanding the standardized uptake value, its methods, and implications for usage. J. Nucl. Med. 2004, 45, 1431–1434. [Google Scholar]
- Boellaard, R.; Krak, N.C.; Hoekstra, O.S.; Lammertsma, A.A. Effects of noise, image resolution, and ROI definition on the accuracy of standard uptake values: A simulation study. J. Nucl. Med. 2004, 45, 1519–1527. [Google Scholar]
- Nestle, U.; Kremp, S.; Schaefer-Schuler, A.; Sebastian-Welsch, C.; Hellwig, D.; Rübe, C.; Kirsch, C.-M. Comparison of Different Methods for Delineation of 18F-FDG PET-Positive Tissue for Target Volume Definition in Radiotherapy of Patients with Non-Small Cell Lung Cancer. J. Nucl. Med. 2005, 46, 1342–1348. [Google Scholar]
- Daisne, J.F.; Sibomana, M.; Bol, A.; Doumont, T.; Lonneux, M.; Gregoire, V. Tri-dimensional automatic segmentation of PET volumes based on measured source-to-background ratios: Influence of reconstruction algorithms. Radiother. Oncol. 2003, 69, 247–250. [Google Scholar] [CrossRef]
- Jentzen, W.; Freudenberg, L.; Eising, E.G.; Heinze, M.; Brandau, W.; Bockisch, A. Segmentation of PET volumes by iterative image thresholding. J. Nucl. Med. 2007, 48, 108–114. [Google Scholar]
- Geets, X.; Lee, J.A.; Bol, A.; Lonneux, M.; Gregoire, V. A gradient-based method for segmenting FDG-PET images: Methodology and validation. Eur. J. Nucl. Med. Mol. Imaging 2007, 34, 1427–1438. [Google Scholar] [CrossRef]
- Besson, F.L.; Henry, T.; Meyer, C.; Chevance, V.; Roblot, V.; Blanchet, E.; Arnould, V.; Grimon, G.; Chekroun, M.; Mabille, L.; et al. Rapid Contour-based Segmentation for 18F-FDG PET Imaging of Lung Tumors by Using ITK-SNAP: Comparison to Expert-based Segmentation. Radiology 2018, 288, 277–284. [Google Scholar] [CrossRef]
- Rundo, L.; Stefano, A.; Militello, C.; Russo, G.; Sabini, M.G.; D’Arrigo, C.; Marletta, F.; Ippolito, M.; Mauri, G.; Vitabile, S.; et al. A fully automatic approach for multimodal PET and MR image segmentation in gamma knife treatment planning. Comput. Methods Programs Biomed. 2017, 144, 77–96. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Shen, C.; Zhou, Z.; Maquilan, G.; Albuquerque, K.; Folkert, M.R.; Wang, J. Automatic PET cervical tumor segmentation by combining deep learning and anatomic prior. Phys. Med. Biol. 2019, 64, 085019. [Google Scholar] [CrossRef]
- Li, L.; Zhao, X.; Lu, W.; Tan, S. Deep Learning for Variational Multimodality Tumor Segmentation in PET/CT. Neurocomputing 2020, 392, 277–295. [Google Scholar] [CrossRef]
- Bundschuh, L.; Prokic, V.; Guckenberger, M.; Tanadini-Lang, S.; Essler, M.; Bundschuh, R.A. A Novel Radiomics-Based Tumor Volume Segmentation Algorithm for Lung Tumors in FDG-PET/CT after 3D Motion Correction-A Technical Feasibility and Stability Study. Diagnostics 2022, 12, 576. [Google Scholar] [CrossRef]
- Tunali, I.; Gillies, R.J.; Schabath, M.B. Application of Radiomics and Artificial Intelligence for Lung Cancer Precision Medicine. Cold Spring Harb. Perspect. Med. 2021, 11, a039537. [Google Scholar] [CrossRef]
- Wu, G.; Jochems, A.; Refaee, T.; Ibrahim, A.; Yan, C.; Sanduleanu, S.; Woodruff, H.C.; Lambin, P. Structural and functional radiomics for lung cancer. Eur. J. Nucl. Med. Mol. Imaging 2021, 48, 3961–3974. [Google Scholar] [CrossRef]
- Jouanjan, L.A.; Thomas, L.; Zsoter, N.; Essler, M.; Bundschuh, R.A. FDG-PET bei Lungenkrebs; kann uns die Texturanalyse helfen, malignes Gewebe besser abzugrenzen? Nuklearmedizin 2020, 59, 170. [Google Scholar]
- Brooks, F.J.; Grigsby, P.W. The effect of small tumor volumes on studies of intratumoral heterogeneity of tracer uptake. J. Nucl. Med. 2014, 55, 37–42. [Google Scholar] [CrossRef]
- Bazanez-Borgert, M.; Bundschuh, R.A.; Herz, M.; Martinez, M.J.; Schwaiger, M.; Ziegler, S.I. Radioactive spheres without inactive wall for lesion simulation in PET. Z. Med. Phys. 2008, 18, 37–42. [Google Scholar] [CrossRef]
- Wang, F.; Liu, C.; Vidal, I.; Mana-Ay, M.; Voter, A.F.; Solnes, L.B.; Ross, A.E.; Gafita, A.; Schaeffer, E.M.; Bivalacqua, T.J.; et al. Comparison of Multiple Segmentation Methods for Volumetric Delineation of Primary Prostate Cancer with Prostate-Specific Membrane Antigen-Targeted (18)F-DCFPyL PET/CT. J. Nucl. Med. 2024, 65, 87–93. [Google Scholar] [CrossRef]
- Grefve, J.; Soderkvist, K.; Gunnlaugsson, A.; Sandgren, K.; Jonsson, J.; Keeratijarut Lindberg, A.; Nilsson, E.; Axelsson, J.; Bergh, A.; Zackrisson, B.; et al. Histopathology-validated gross tumor volume delineations of intraprostatic lesions using PSMA-positron emission tomography/multiparametric magnetic resonance imaging. Phys. Imaging Radiat. Oncol. 2024, 31, 100633. [Google Scholar] [CrossRef] [PubMed]
- Bundschuh, R.A.; Wendl, C.M.; Weirich, G.; Eiber, M.; Souvatzoglou, M.; Treiber, U.; Kubler, H.; Maurer, T.; Gschwend, J.E.; Geinitz, H.; et al. Tumour volume delineation in prostate cancer assessed by [(11)C]choline PET/CT: Validation with surgical specimens. Eur. J. Nucl. Med. Mol. Imaging 2013, 40, 824–831. [Google Scholar] [CrossRef] [PubMed]
- Daisne, J.F.; Duprez, T.; Weynand, B.; Lonneux, M.; Hamoir, M.; Reychler, H.; Gregoire, V. Tumor volume in pharyngolaryngeal squamous cell carcinoma: Comparison at CT, MR imaging, and FDG PET and validation with surgical specimen. Radiology 2004, 233, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Tixier, F.; Le Rest, C.C.; Hatt, M.; Albarghach, N.; Pradier, O.; Metges, J.P.; Corcos, L.; Visvikis, D. Intratumor heterogeneity characterized by textural features on baseline 18F-FDG PET images predicts response to concomitant radiochemotherapy in esophageal cancer. J. Nucl. Med. 2011, 52, 369–378. [Google Scholar] [CrossRef]
- Cook, G.J.; Yip, C.; Siddique, M.; Goh, V.; Chicklore, S.; Roy, A.; Marsden, P.; Ahmad, S.; Landau, D. Are Pretreatment 18F-FDG PET Tumor Textural Features in Non-Small Cell Lung Cancer Associated with Response and Survival After Chemoradiotherapy? J. Nucl. Med. 2013, 54, 19–26. [Google Scholar] [CrossRef]
- Nestle, U.; Schaefer-Schuler, A.; Kremp, S.; Groeschel, A.; Hellwig, D.; Rube, C.; Kirsch, C.M. Target volume definition for 18F-FDG PET-positive lymph nodes in radiotherapy of patients with non-small cell lung cancer. Eur. J. Nucl. Med. Mol. Imaging 2007, 34, 453–462. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Applying the right statistics: Analyses of measurement studies. Ultrasound Obstet. Gynecol. 2003, 22, 85–93. [Google Scholar] [CrossRef]
- Hyslop, N.P.; White, W.H. Estimating precision using duplicate measurements. J. Air Waste Manag. Assoc. 2009, 59, 1032–1039. [Google Scholar] [CrossRef]
- Forkman, J. Estimator and Tests for Common Coefficients of Variation in Normal Distributions. Commun. Stat.—Theory Methods 2009, 38, 233–251. [Google Scholar] [CrossRef]
- Zwanenburg, A. Radiomics in nuclear medicine: Robustness, reproducibility, standardization, and how to avoid data analysis traps and replication crisis. Eur. J. Nucl. Med. Mol. Imaging 2019, 46, 2638–2655. [Google Scholar] [CrossRef] [PubMed]
- Whybra, P.; Zwanenburg, A.; Andrearczyk, V.; Schaer, R.; Apte, A.P.; Ayotte, A.; Baheti, B.; Bakas, S.; Bettinelli, A.; Boellaard, R.; et al. The Image Biomarker Standardization Initiative: Standardized Convolutional Filters for Reproducible Radiomics and Enhanced Clinical Insights. Radiology 2024, 310, e231319. [Google Scholar] [CrossRef] [PubMed]
- Gang, G.J.; Deshpande, R.; Stayman, J.W. Standardization of histogram- and gray-level co-occurrence matrices-based radiomics in the presence of blur and noise. Phys. Med. Biol. 2021, 66, 074004. [Google Scholar] [CrossRef] [PubMed]

| Paper | Comments | |
|---|---|---|
| Threshold-based segmentation | [12,13,16] | Stable; fixed uptake threshold does not represent variability of glucose metabolism; problem with highly variable background depending on lesion location |
| Threshold-based with background adaption | [17,18] | Takes into account variations in lesion uptake and background; limited efficacy with heterogeneous tumors; strongly dependent on the system and reconstruction algorithm |
| Gradient-based algorithms | [19,20] | Closer to human observation, i.e., looks into changes in imaging more than intensity; use in practice limited to small lesions |
| Combination of functional and morphological imaging | [21] | Seems to work well in special applications but limited data available; requires high-quality anatomical data, preferably MRI |
| Segmentation based on machine learning | [22,23] | Promising results, but many open questions concerning standardization; large data sets necessary for training |
| Proposed method: Radiomics-based | Expected advantages
| |
| Mean Pathological Volume [mL] | Mean Segmented Volume [mL] | Relative Difference [%] | r | COV [%] | |
|---|---|---|---|---|---|
| All lesions (n = 20 (18) *) | |||||
| Volume Threshold-based | 59.9 (0.7–737.9) | 56.2 (0.6–663.0) | 22.4 (5.0–62.7) | 0.997 | 16.2 |
| Volume KU-based | 59.9 (0.7–737.9) | 64.9 (3.5–782.9) | 31.2 (0.7–80.0) | 0.999 | 44.6 |
| Volume LE-based | 59.9 (0.7–737.9) | 61.2(1.5–745.0) | 17.9 (0.9–60.9) | 0.999 | 26.2 |
| Volume LZE-based | 59.9 (0.7–737.9) | 70.0 (3.1–749.1) | 24.8 (0.8–82.4) | 0.999 | 32.8 |
| Lesions > 3 ccm (n = 14) ** | |||||
| Volume Threshold-based | 84.9 (3.1–737.9) | 79.5 (2.5–663.0) | 22.1 (5.0–62.7) | 0.997 | 16.8 |
| Volume KU-based | 84.9 (3.1–737.9) | 90.5 (4.2–782.9) | 16.2 (0.7–63.1) | 0.999 | 20.6 |
| Volume LE-based | 84.9 (3.1–737.9) | 86.1 (4.1–745.0) | 7.2 (0.9–31.1) | 0.999 | 8.3 |
| Volume LZE-based | 84.9 (3.1–737.9) | 88.9 (3.3–749.1) | 17.5 (0.8–39.8) | 0.999 | 17.7 |
| Lesions > 45 ccm (n = 3) ** | |||||
| Volume Threshold-based | 324.3 (47.7–737.9) | 310.9 (59.2–663.0) | 13.9 (11.1–19.3) | 0.999 | 10.8 |
| Volume KU-based | 324.3 (47.7–737.9) | 348.2 (55.9–782.9) | 9.7 (5.8–14.5) | 0.999 | 7.8 |
| Volume LE-based | 324.3 (47.7–737.9) | 327.7 (49.0–745.0) | 1.4 (0.9–2.5) | 0.999 | 1.2 |
| Volume LZE-based | 324.3 (47.7–737.9) | 333.9 (51.6–749.1) | 5.2 (1.5–7.4) | 0.999 | 4.3 |
| Mean Pathological Maximum Diameter [mm] | Mean Segmented Maximum Diameter [mm] | Relative Difference [%] | r | COV [%] | |
|---|---|---|---|---|---|
| All lesions (n = 20 (18) *) | |||||
| Volume Threshold-based | 38 (11–125) | 36 (11–109) | 10.8 (1.8–22.0) | 0.989 | 9.1 |
| Volume KU-based | 38 (11–125) | 42 (17–136) | 18.3 (0.0–56.0) | 0.981 | 18.1 |
| Volume LE-based | 38 (11–125) | 42 (17–130) | 16.2 (3.0–42.1) | 0.987 | 16.3 |
| Volume LZE-based | 38 (11–125) | 44 (12–122) | 17.2 (0.0–50.0) | 0.968 | 16.2 |
| Lesions > 3 ccm (n = 14) ** | |||||
| Volume Threshold-based | 47 (18–125) | 46 (21–109) | 10.4 (1.8–20.7) | 0.973 | 8.6 |
| Volume KU-based | 47 (18–125) | 51 (19–136) | 14.9 (2.0–29.0) | 0.983 | 11.6 |
| Volume LE-based | 47 (18–125) | 51 (20–130) | 10.7 (3.0–21.4) | 0.987 | 9.3 |
| Volume LZE-based | 47 (18–125) | 51 (12–122) | 16.5 (0.0–50.0) | 0.960 | 15.8 |
| Lesions > 45 ccm (n = 3) ** | |||||
| Volume Threshold-based | 87 (65–125) | 81 (66–109) | 8.4 (3.1–14.7) | 0.994 | 6.4 |
| Volume KU-based | 87 (65–125) | 97 (75–136) | 11.1 (8.1–12.8) | 0.999 | 8.5 |
| Volume LE-based | 87 (65–125) | 93 (67–130) | 6.4 (3.0–12.4) | 0.993 | 5.7 |
| Volume LZE-based | 87 (65–125) | 92 (68–122) | 8.0 (2.5–17.2) | 0.972 | 7.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bundschuh, L.; Buermann, J.; Toma, M.; Schmidt, J.; Kristiansen, G.; Essler, M.; Bundschuh, R.A.; Prokic, V. A Tumor Volume Segmentation Algorithm Based on Radiomics Features in FDG-PET in Lung Cancer Patients, Validated Using Surgical Specimens. Diagnostics 2024, 14, 2654. https://doi.org/10.3390/diagnostics14232654
Bundschuh L, Buermann J, Toma M, Schmidt J, Kristiansen G, Essler M, Bundschuh RA, Prokic V. A Tumor Volume Segmentation Algorithm Based on Radiomics Features in FDG-PET in Lung Cancer Patients, Validated Using Surgical Specimens. Diagnostics. 2024; 14(23):2654. https://doi.org/10.3390/diagnostics14232654
Chicago/Turabian StyleBundschuh, Lena, Jens Buermann, Marieta Toma, Joachim Schmidt, Glen Kristiansen, Markus Essler, Ralph Alexander Bundschuh, and Vesna Prokic. 2024. "A Tumor Volume Segmentation Algorithm Based on Radiomics Features in FDG-PET in Lung Cancer Patients, Validated Using Surgical Specimens" Diagnostics 14, no. 23: 2654. https://doi.org/10.3390/diagnostics14232654
APA StyleBundschuh, L., Buermann, J., Toma, M., Schmidt, J., Kristiansen, G., Essler, M., Bundschuh, R. A., & Prokic, V. (2024). A Tumor Volume Segmentation Algorithm Based on Radiomics Features in FDG-PET in Lung Cancer Patients, Validated Using Surgical Specimens. Diagnostics, 14(23), 2654. https://doi.org/10.3390/diagnostics14232654







