Prediction of Coronary Artery Disease Using Machine Learning Techniques with Iris Analysis
Abstract
1. Introduction
1.1. Related Work on IRIS
1.2. Research Gaps of Previous Work on IRIS/CAD
1.3. Contribution of This Paper
- A novel diagnostic approach is proposed for the non-invasive detection of CAD using iris images.
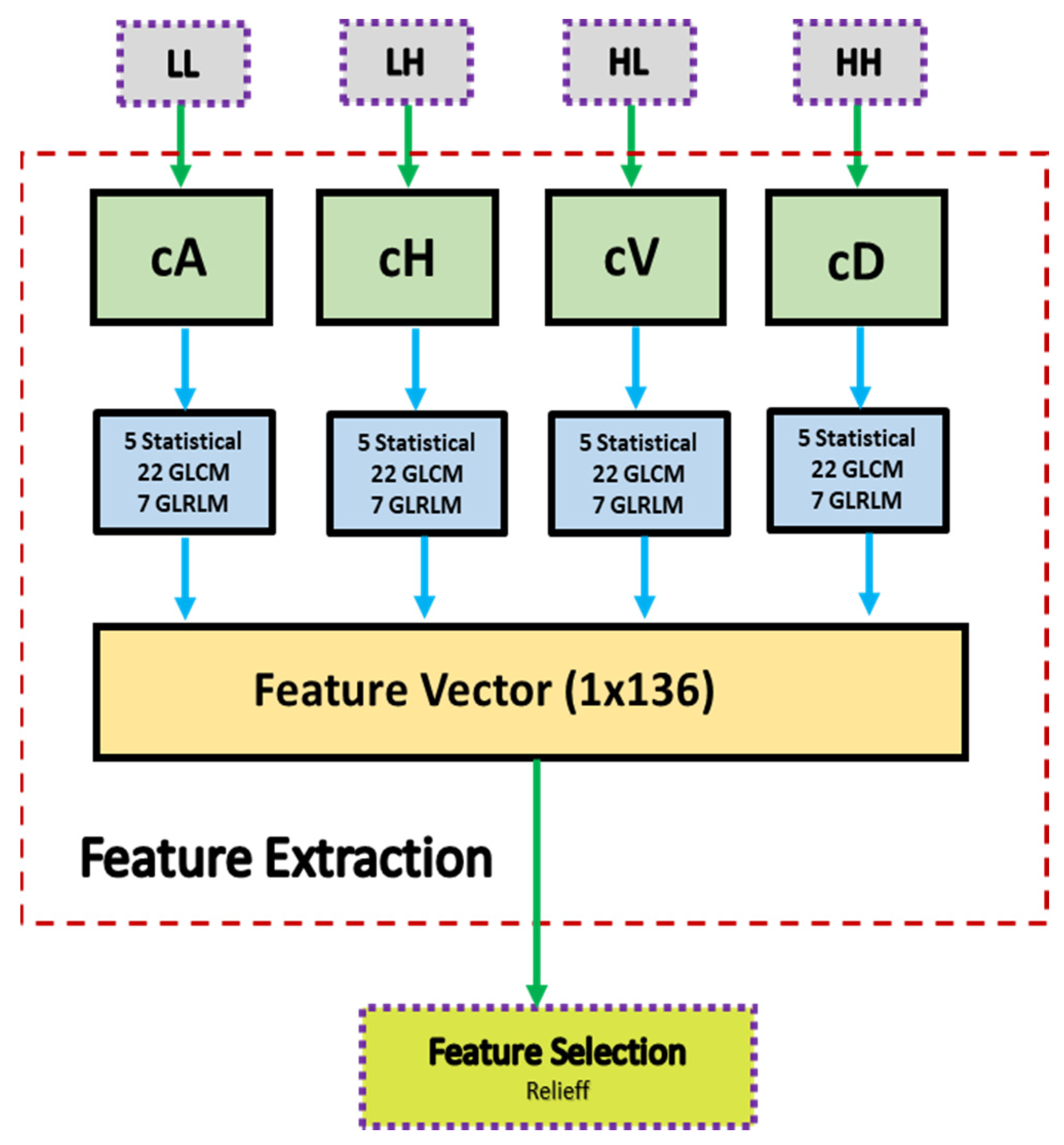
- The Relieff feature selection method based on wavelet transform is introduced, resulting in 136 features including statistical, GLCM, and GLRLM features.
- A comparison is made between different classifiers, such as DT, NB, SVM, kNN, and NN, and the best-performing classifier is identified.
- The proposed model was compared with existing models and was more successful in detecting CAD.
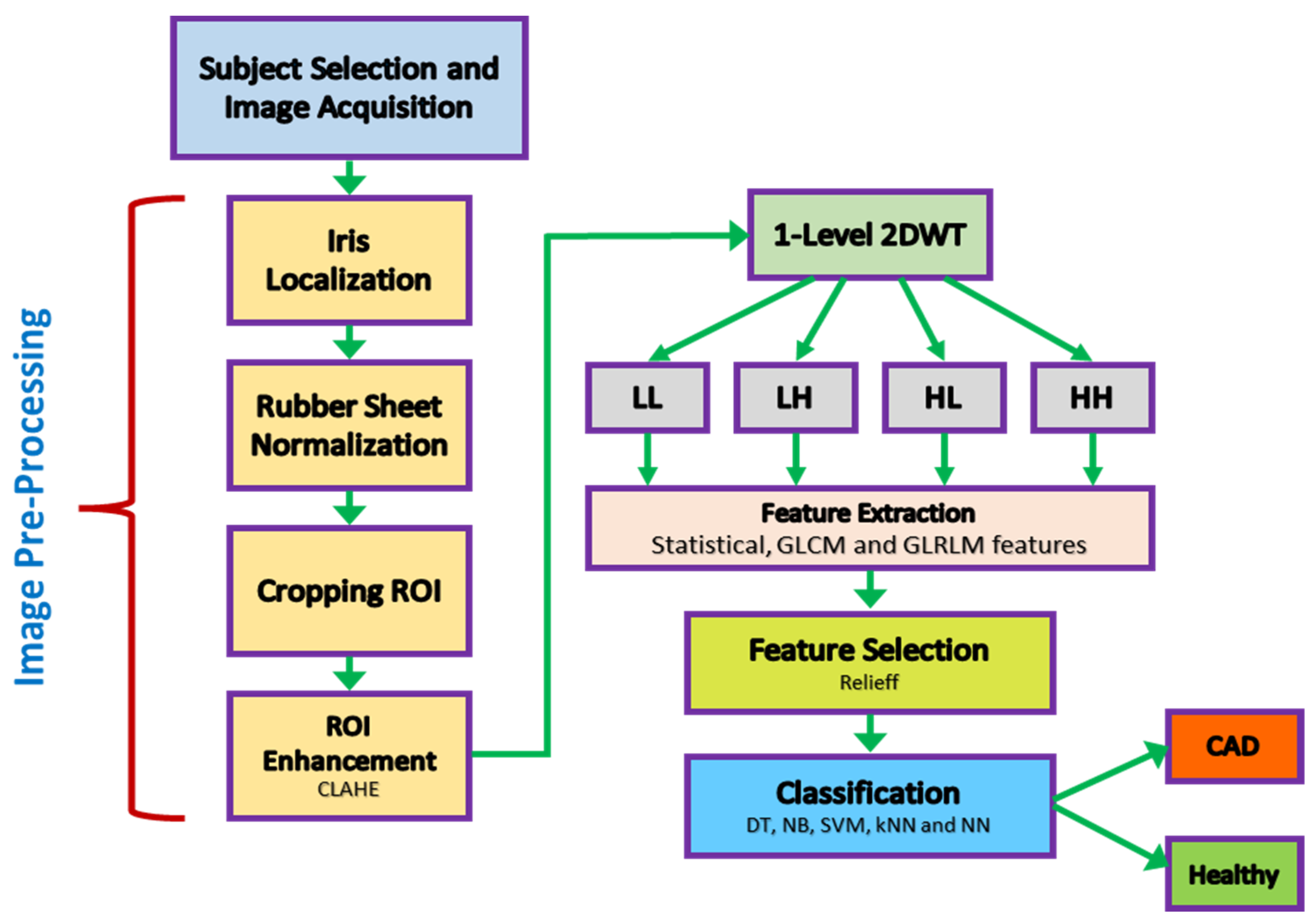
2. Materials and Methods
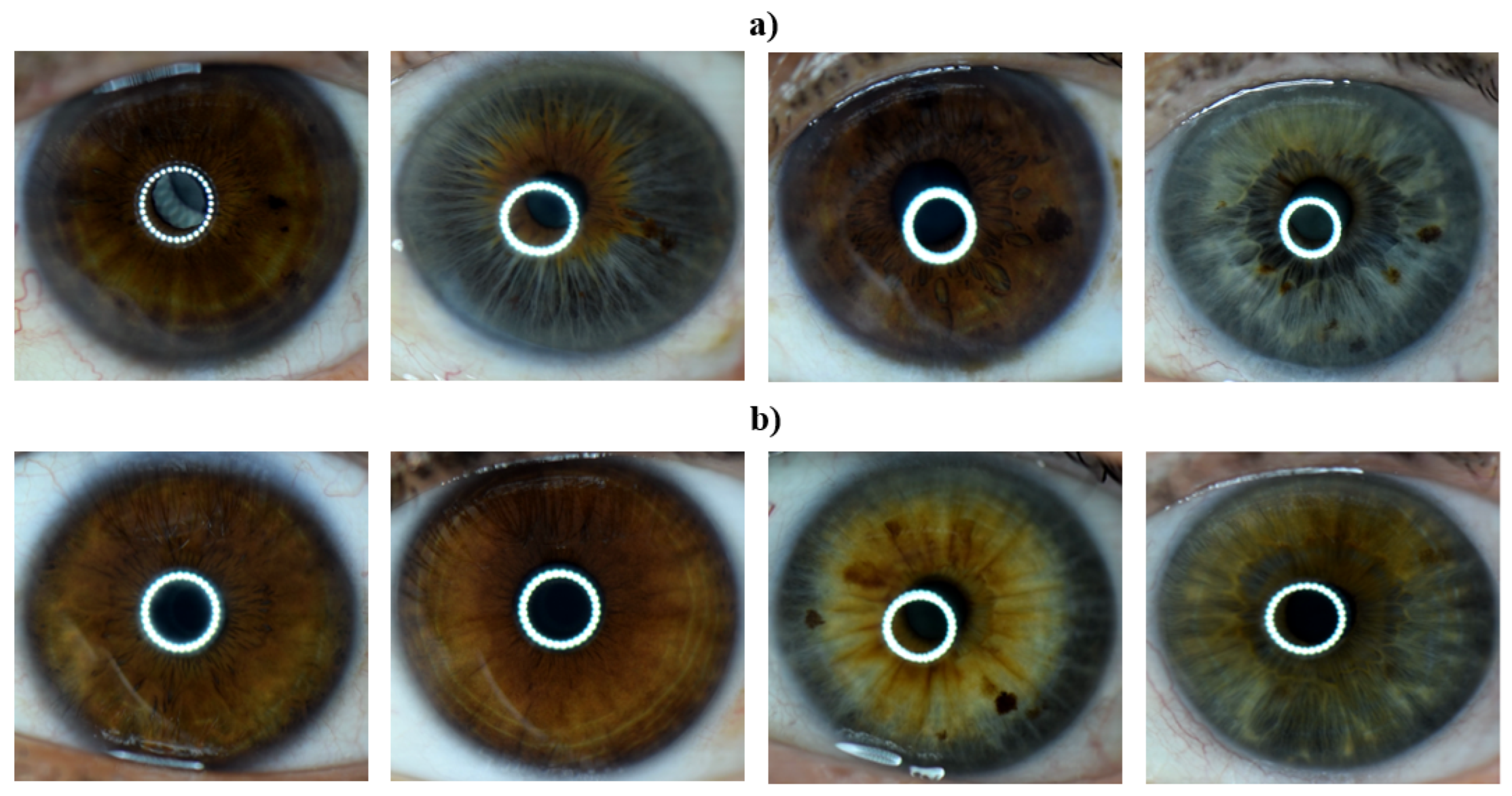
2.1. Subject Selection for Data Acquisition
2.2. Eye Image Acquisition
2.3. Eye Image Pre-Processing
| Algorithm 1 Eye image pre-processing algorithm |
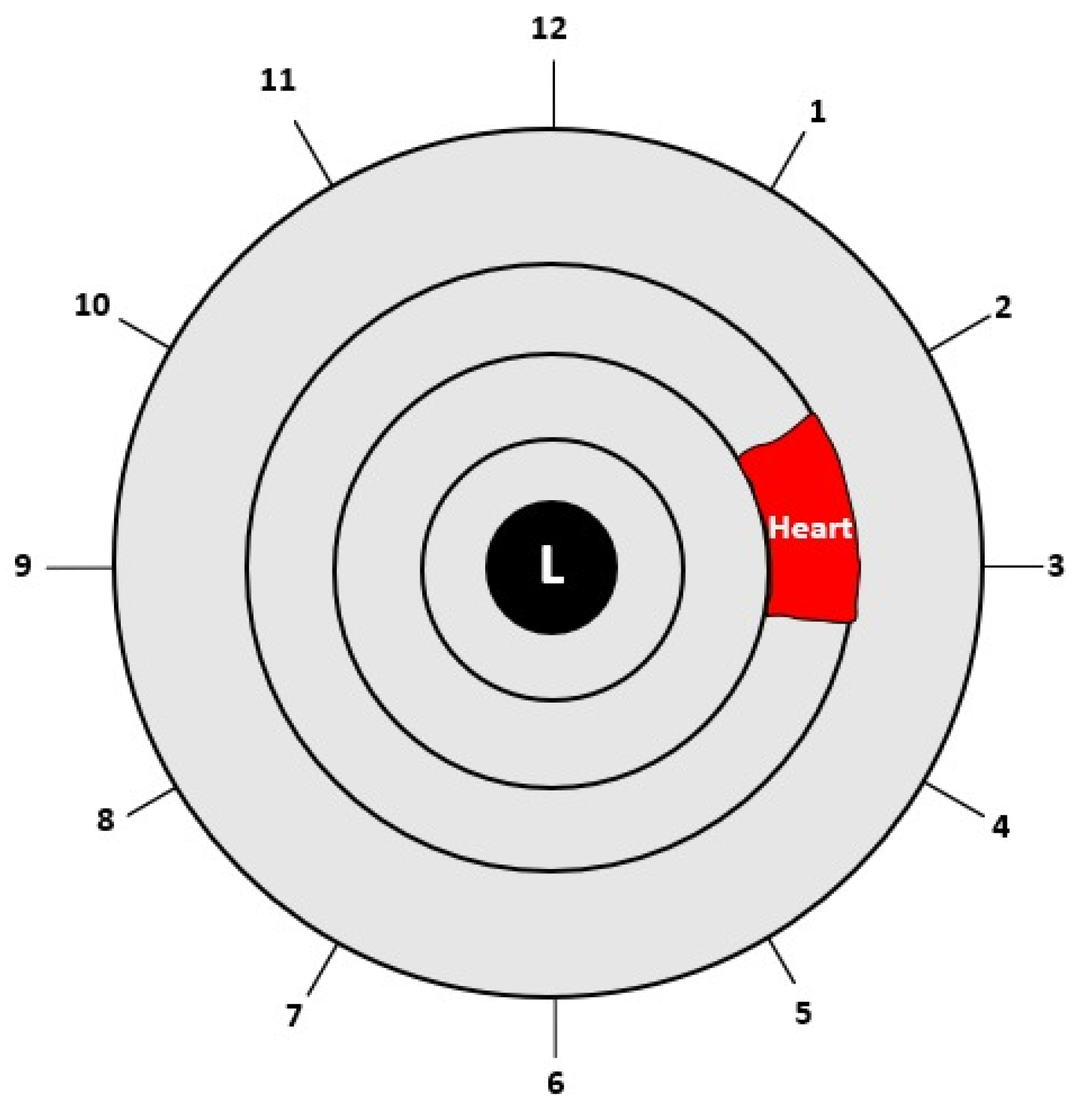
| (1) Input: Eye image (2) Iris localization from the eye image (a) Localization pupil using Daugman’s Integral Differential Operator (b) Localization iris using Daugman’s Integral Differential Operator (3) Iris normalization using Daugman’s rubber sheet Technique - Normalized iris becomes a fixed size: 360 × 720 (4) ROI cropped according to the iris map in Figure 4 - The ROI size is 190 × 120 (5) ROI enhancement using the CLAHE method (6) Output: ROI image |
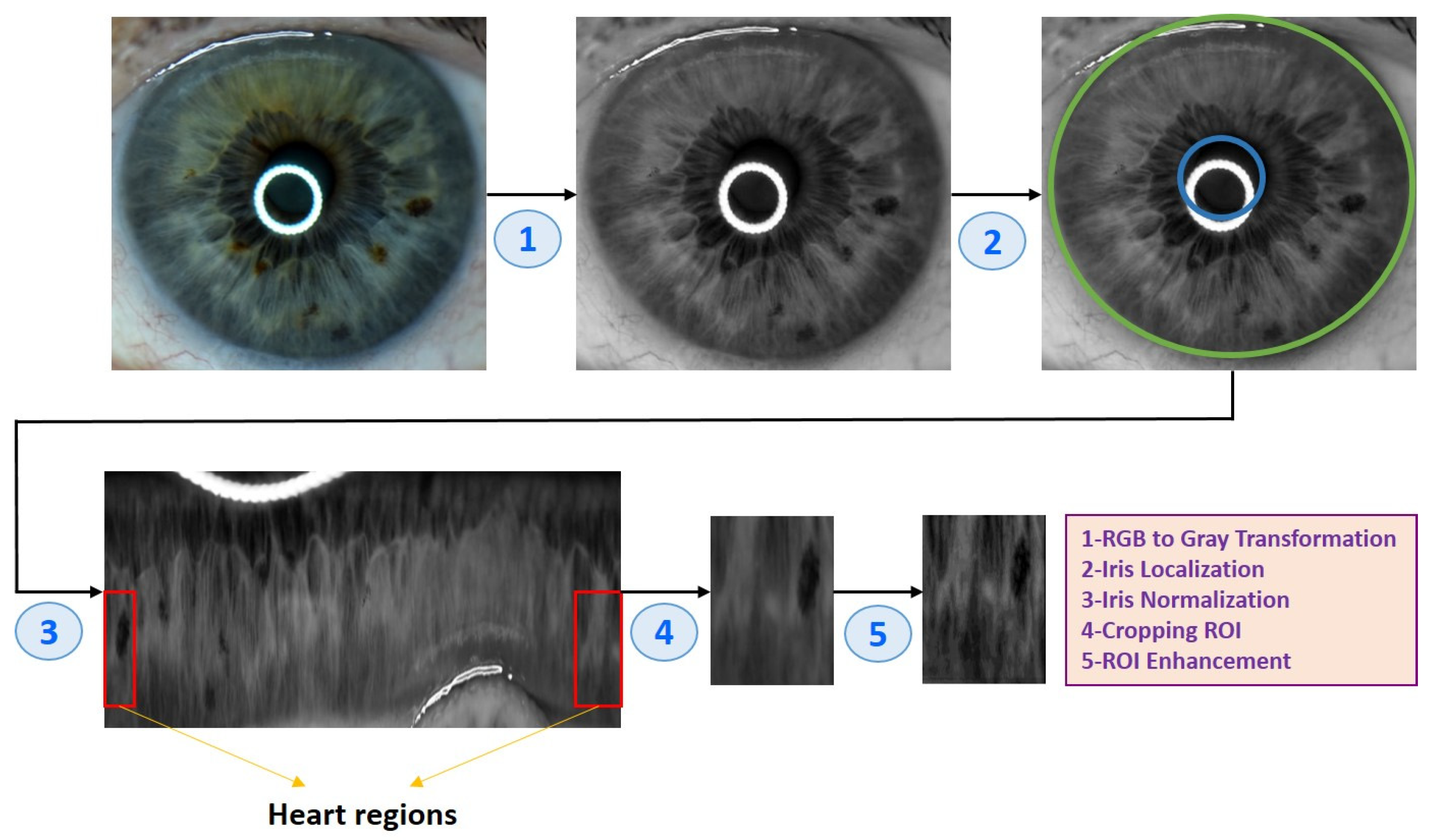
2.3.1. Iris Localization
2.3.2. Iris Normalization
2.3.3. Region of Interest (ROI)
2.3.4. Enhancement of ROI
2.4. Iris Feature Extraction
| Algorithm 2 Feature extraction process |
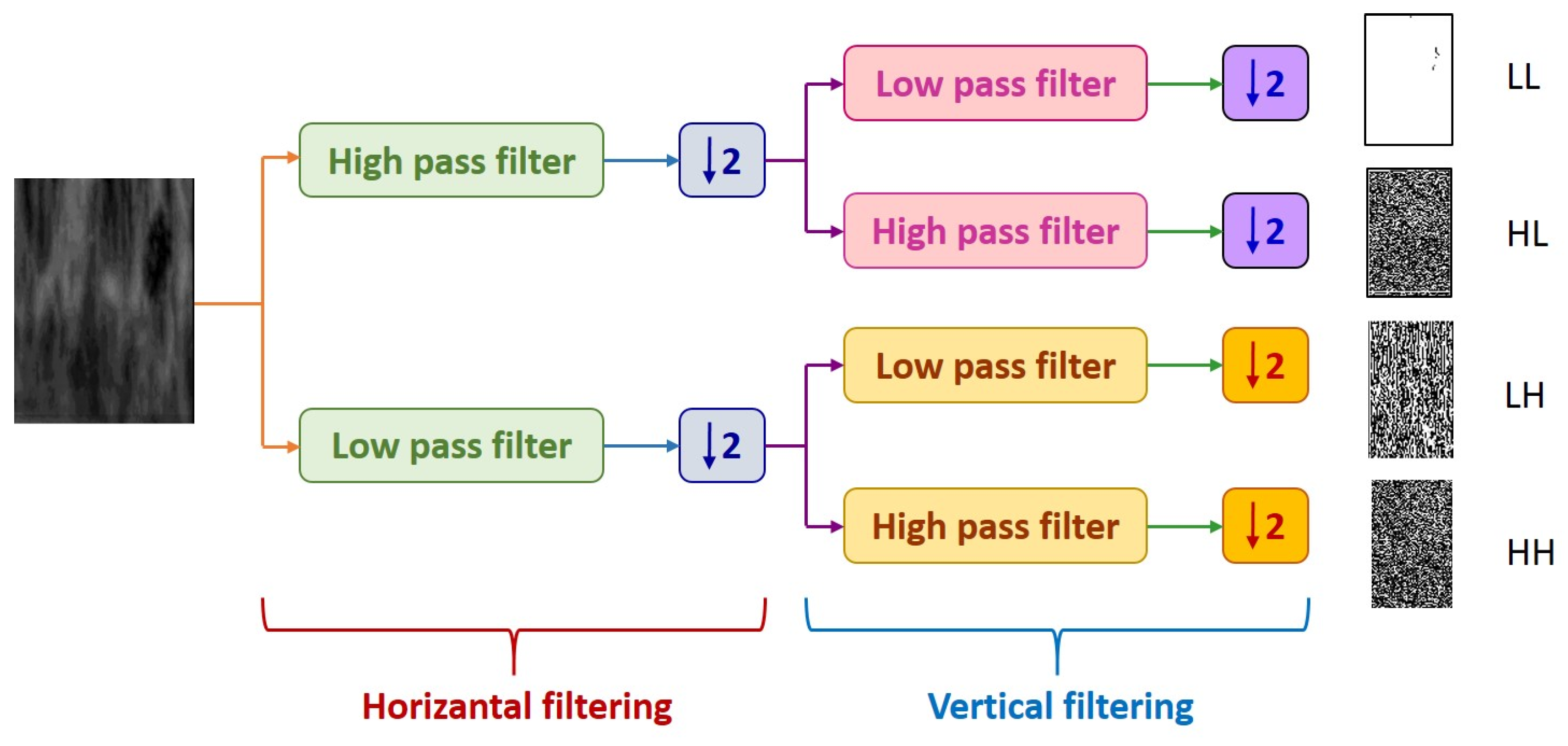
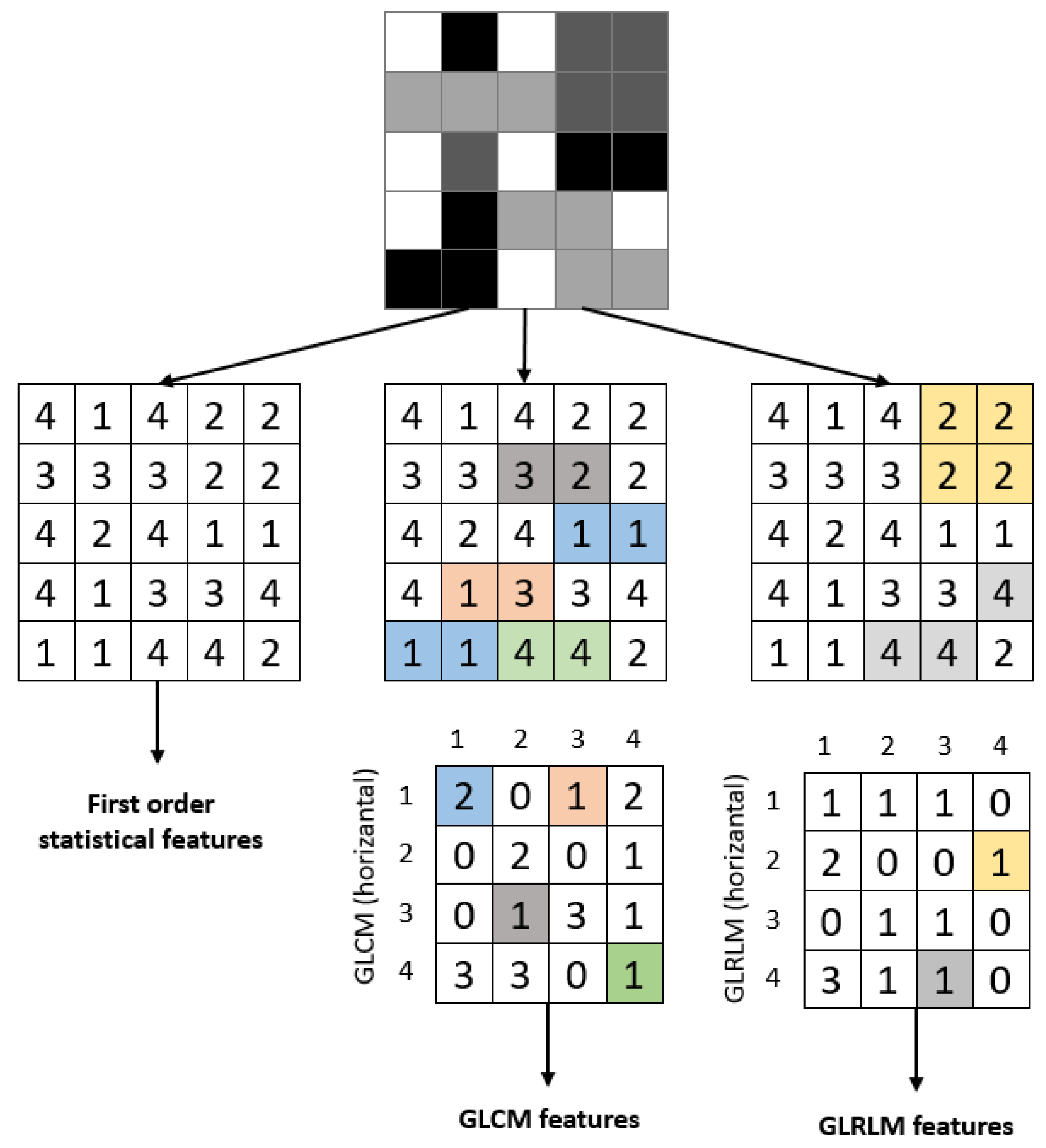
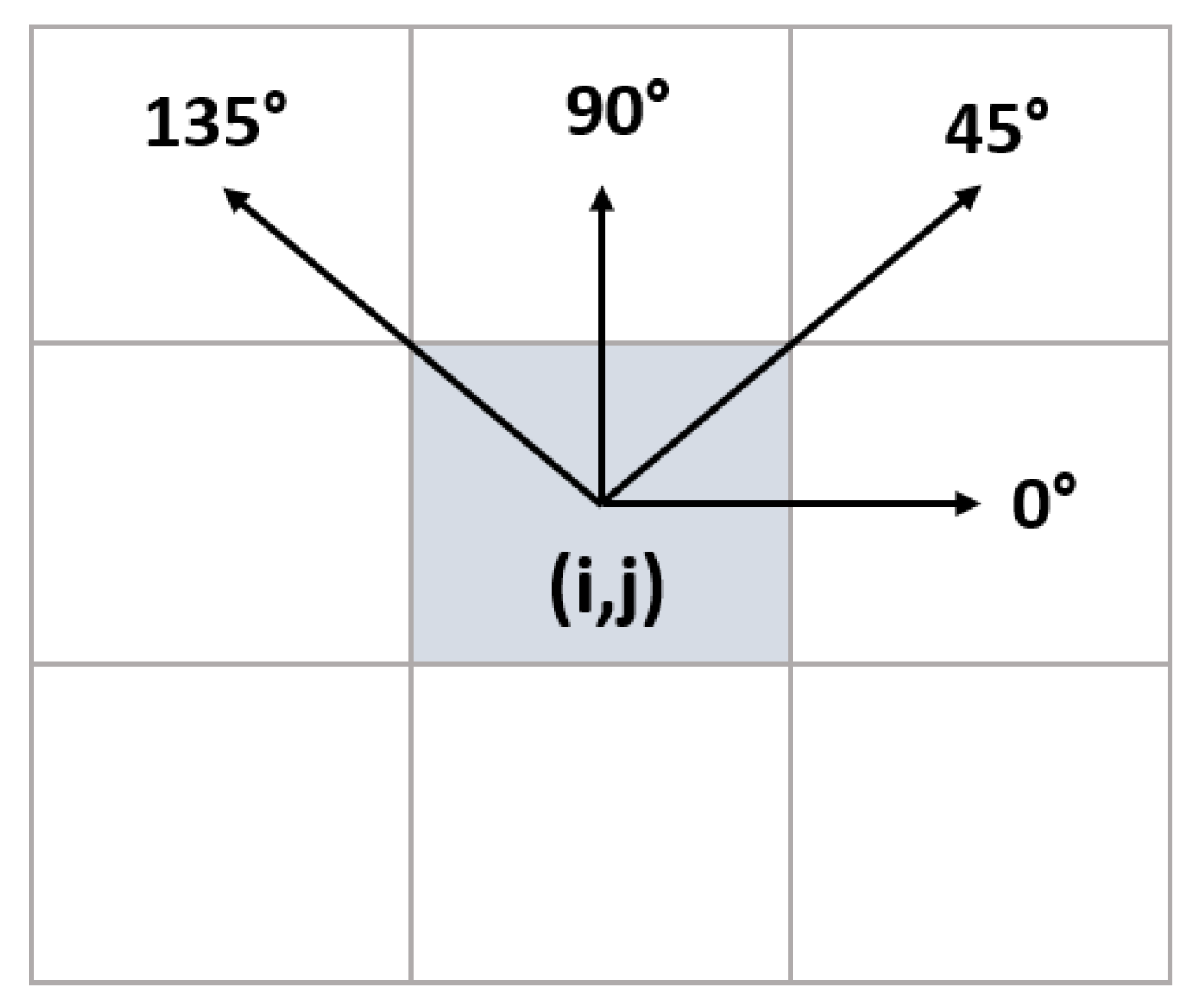
| (1) Input: ROI Image (2) Perform 1 Level 2D-DWT to ROI image - Four sub-bands occur (cA, cV, cD, cH) (3) Extract features from sub-bands (a) Extract 5 first-order statistical features as shown in Table 2 (b) Extract 22 GLCM-based features as shown in Table 3 - Formation of the 8 × 8 GLC matrix using θ = (00, 450, 900, 1350) with d = 1. Values for each direction are found and averaged (c) Extract 7 GLRLM-based features as shown in Table 4 - Formation of the GLRL matrix using θ = (00, 450, 900, 1350) with quantize level = 16. Values for each direction are found and averaged (4) Fusion of features (5 statistical + 22 GLCM + 7 GLRLM = 34 features for each sub-band) (5) Output: feature vector with 136 features |
2.4.1. Statistical Features
| Feature Name | Formula | Feature Name | Formula |
|---|---|---|---|
| Mean intensity | Skewness | ||
| Standard deviation | Kurtosis | ||
| Entropy |
2.4.2. Gray-Level Co-Occurrence Matrix (GLCM) Features
| Feature Name | Formula | Feature Name | Formula |
|---|---|---|---|
| Auto correlation | Information measure of correlation 1 | ||
| Cluster prominence | Information measure of correlation 2 | ||
| Cluster shade | Inverse difference moment | ||
| Contrast | Maximum probability | ||
| Correlation | Sum average | ||
| Difference entropy | Sum entropy | ||
| Difference variance | Sum of squares | ||
| Dissimilarity | Sum variance | ||
| Energy | Maximal correlation coefficient | ||
| Entropy | Inverse difference normalized | ||
| Homogeneity | Inverse difference moment normalized |
2.4.3. Gray-Level Run Length (GLRL) Matrix Features
| Feature Name | Formula | Feature Name | Formula |
|---|---|---|---|
| Short Run Emphasis (SRE) | Run Length Non-Uniformity (RLN) | ||
| Long Run Emphasis (LRE) | Low Gray-Level Run Emphasis (LGRE) | ||
| Gray-Level Non-Uniformity (GLN) | High Gray-Level Run Emphasis (HGRE) | ||
| Run Percentage (RP) |
2.5. Feature Selection
2.6. Classification
- (a)
- Decision Trees: Fine, Medium, and Coarse Trees
- (b)
- Naive Bayes: Gaussian and Kernel types
- (c)
- Support Vector Machines with four kernels: Quadratic, Cubic, Fine Gaussian, Medium Gaussian, and Coarse Gaussian
- (d)
- k-Nearest Neighborhood (kNN): Fine, Medium, Coarse, Cosine, Cubic, and Weighted
- (e)
- Neural Networks: Narrow, Medium, Wide, Bilayered, and Trilayered
2.7. Performance Evaluation
3. Results and Discussion
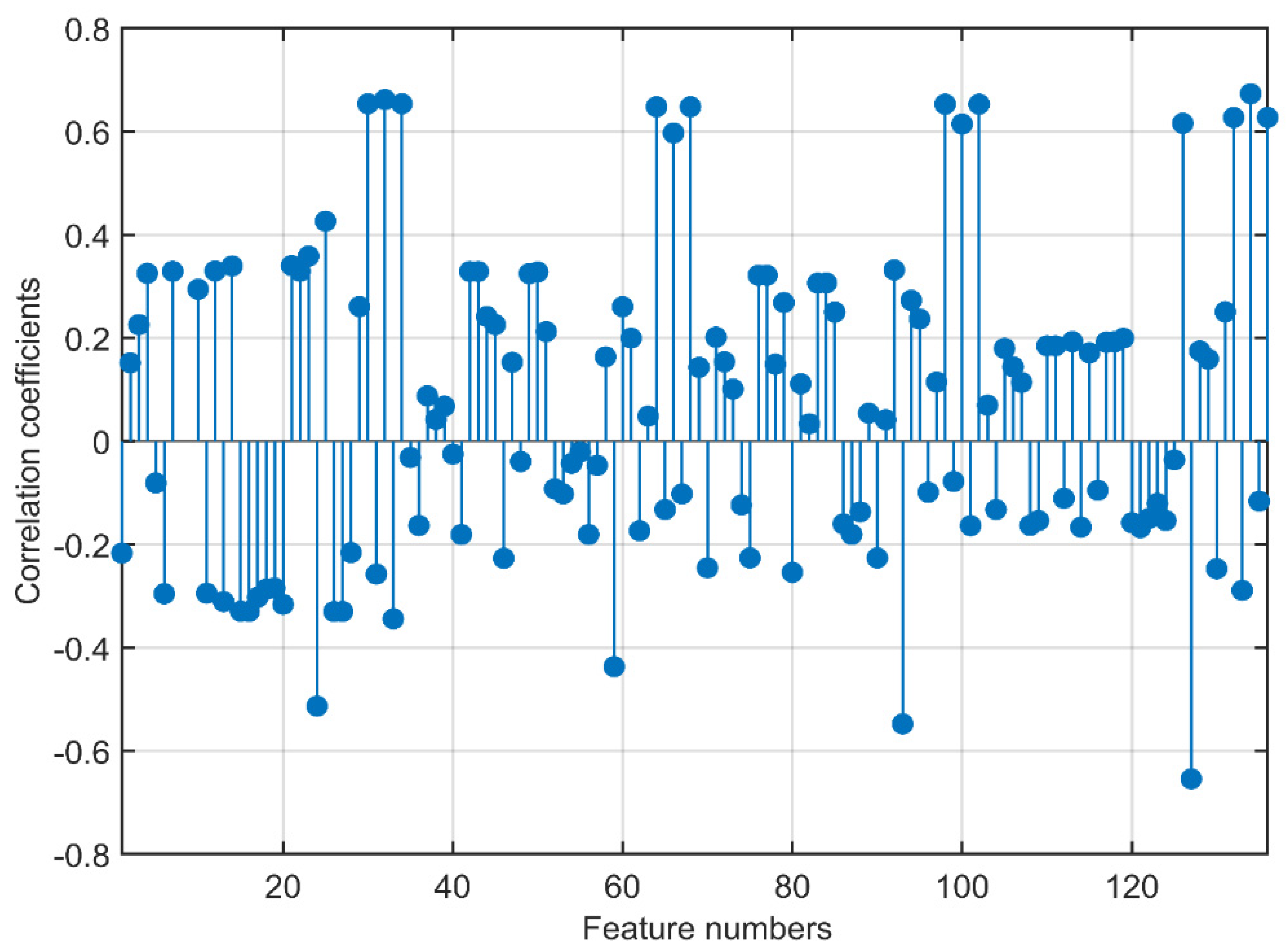
3.1. Feature Analysis
3.2. Results after Feature Selection
3.3. Comparison with Studies in the Literature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Virani, S.S.; Alonso, A.; Benjamin, E.J.; Bittencourt, M.S.; Callaway, C.W.; Carson, A.P.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Delling, F.N. Heart disease and stroke statistics—2020 update: A report from the American Heart Association. Circulation 2020, 141, e139–e596. [Google Scholar] [CrossRef]
- Benjamin, E.J.; Muntner, P.; Alonso, A.; Bittencourt, M.S.; Callaway, C.W.; Carson, A.P.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Das, S.R. Heart disease and stroke statistics—2019 update: A report from the American Heart Association. Circulation 2019, 139, e56–e528. [Google Scholar] [CrossRef] [PubMed]
- Nowbar, A.N.; Gitto, M.; Howard, J.P.; Francis, D.P.; Al-Lamee, R. Mortality from ischemic heart disease: Analysis of data from the World Health Organization and coronary artery disease risk factors From NCD Risk Factor Collaboration. Circ. Cardiovasc. Qual. Outcomes 2019, 12, e005375. [Google Scholar] [CrossRef] [PubMed]
- Malakar, A.K.; Choudhury, D.; Halder, B.; Paul, P.; Uddin, A.; Chakraborty, S. A review on coronary artery disease, its risk factors, and therapeutics. J. Cell. Physiol. 2019, 234, 16812–16823. [Google Scholar] [CrossRef]
- Bauersachs, R.; Zeymer, U.; Brière, J.-B.; Marre, C.; Bowrin, K.; Huelsebeck, M. Burden of coronary artery disease and peripheral artery disease: A literature review. Cardiovasc. Ther. 2019, 2019, 8295054. [Google Scholar] [CrossRef] [PubMed]
- Novak, R.; Hrkac, S.; Salai, G.; Bilandzic, J.; Mitar, L.; Grgurevic, L. The role of ADAMTS-4 in atherosclerosis and vessel wall abnormalities. J. Vasc. Res. 2022, 59, 69–77. [Google Scholar] [CrossRef]
- Ghiasi, M.M.; Zendehboudi, S.; Mohsenipour, A.A. Decision tree-based diagnosis of coronary artery disease: CART model. Comput. Methods Programs Biomed. 2020, 192, 105400. [Google Scholar] [CrossRef]
- Alizadehsani, R.; Zangooei, M.H.; Hosseini, M.J.; Habibi, J.; Khosravi, A.; Roshanzamir, M.; Khozeimeh, F.; Sarrafzadegan, N.; Nahavandi, S. Coronary artery disease detection using computational intelligence methods. Knowl.-Based Syst. 2016, 109, 187–197. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms and Applications; Pearson Education India: London, UK, 2006. [Google Scholar]
- Jensen, B. Iridology Simplified; Book Publishing Company: New York, NY, USA, 2012. [Google Scholar]
- Sivasankar, K.; Sujaritha, M.; Pasupathi, P.; Muthukumar, S. FCM based iris image analysis for tissue imbalance stage identification. In Proceedings of the 2012 International Conference on Emerging Trends in Science, Engineering and Technology (INCOSET), Himeji, Japan, 5–7 November 2012; pp. 210–215. [Google Scholar]
- Kurnaz, Ç.; Gül, B.K. Determination of the relationship between sodium ring width on iris and cholesterol level. J. Fac. Eng. Archit. Gazi Univ. 2018, 33, 1557–1568. [Google Scholar]
- Ma, L.; Zhang, D.; Li, N.; Cai, Y.; Zuo, W.; Wang, K. Iris-based medical analysis by geometric deformation features. IEEE J. Biomed. Health Inform. 2012, 17, 223–231. [Google Scholar]
- Samant, P.; Agarwal, R. Machine learning techniques for medical diagnosis of diabetes using iris images. Comput. Methods Programs Biomed. 2018, 157, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Samant, P.; Agarwal, R. Analysis of computational techniques for diabetes diagnosis using the combination of iris-based features and physiological parameters. Neural Comput. Appl. 2019, 31, 8441–8453. [Google Scholar] [CrossRef]
- Bansal, A.; Agarwal, R.; Sharma, R. Determining diabetes using iris recognition system. Int. J. Diabetes Dev. Ctries. 2015, 35, 432–438. [Google Scholar] [CrossRef]
- Önal, M.N.; Güraksin, G.E.; Duman, R. Convolutional neural network-based diabetes diagnostic system via iridology technique. Multimed. Tools Appl. 2022, 82, 173–194. [Google Scholar] [CrossRef]
- Rehman, M.U.; Najam, S.; Khalid, S.; Shafique, A.; Alqahtani, F.; Baothman, F.; Shah, S.Y.; Abbasi, Q.H.; Imran, M.A.; Ahmad, J. Infrared sensing based non-invasive initial diagnosis of chronic liver disease using ensemble learning. IEEE Sens. J. 2021, 21, 19395–19406. [Google Scholar] [CrossRef]
- Muzamil, S.; Hussain, T.; Haider, A.; Waraich, U.; Ashiq, U.; Ayguadé, E. An intelligent iris based chronic kidney identification system. Symmetry 2020, 12, 2066. [Google Scholar] [CrossRef]
- Hernández, F.; Vega, R.; Tapia, F.; Morocho, D.; Fuertes, W. Early detection of Alzheimer’s using digital image processing through iridology, an alternative method. In Proceedings of the 2018 13th Iberian Conference on Information Systems and Technologies (CISTI), Caceres, Spain, 13–16 June 2018; pp. 1–7. [Google Scholar]
- Ozbilgin, F.; Kurnaz, C. An alternative approach for determining the cholesterol level: Iris analysis. Int. J. Imaging Syst. Technol. 2022, 32, 1159–1171. [Google Scholar] [CrossRef]
- Özbilgin, F. Determination of Iris Symptoms of Systemic Diseases by Iris Analysis Method. Master’s Thesis, Ondokuz Mayıs University, Samsun, Türkiye, 2019. [Google Scholar]
- Ramlee, R.; Ranjit, S. Using iris recognition algorithm, detecting cholesterol presence. In Proceedings of the 2009 International Conference on Information Management and Engineering, Banff, AB, Canada, 6–8 July 2009; pp. 714–717. [Google Scholar]
- Gunawan, V.A.; Putra, L.S.A.; Imansyah, F.; Kusumawardhani, E. Identification of Coronary Heart Disease through Iris using Gray Level Co-occurrence Matrix and Support Vector Machine Classification. Int. J. Adv. Comput. Sci. Appl. 2022, 13. [Google Scholar] [CrossRef]
- Putra, L.S.A.; Isnanto, R.R.; Triwiyatno, A.; Gunawan, V.A. Identification of Heart Disease with Iridology Using Backpropagation Neural Network. In Proceedings of the 2018 2nd Borneo International Conference on Applied Mathematics and Engineering (BICAME), Balikpapan, Indonesia, 10–11 December 2018; pp. 138–142. [Google Scholar]
- Permatasari, L.I.; Novianty, A.; Purboyo, T.W. Heart disorder detection based on computerized iridology using support vector machine. In Proceedings of the 2016 International Conference on Control, Electronics, Renewable Energy and Communications (ICCEREC), Bandung, Indonesia, 13–15 September 2016; pp. 157–161. [Google Scholar]
- Kusuma, F.D.; Kusumaningtyas, E.M.; Barakbah, A.R.; Hermawan, A.A. Heart abnormalities detection through iris based on mobile. In Proceedings of the 2018 International Electronics Symposium on Knowledge Creation and Intelligent Computing (IES-KCIC), Lombok Island, Indonesia, 29–30 October 2018; pp. 152–157. [Google Scholar]
- Daugman, J. How iris recognition works. In The Essential Guide to Image Processing; Elsevier: Amsterdam, The Netherlands, 2009; pp. 715–739. [Google Scholar]
- Reza, A.M. Realization of the contrast limited adaptive histogram equalization (CLAHE) for real-time image enhancement. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2004, 38, 35–44. [Google Scholar] [CrossRef]
- Diwakar, M.; Tripathi, A.; Joshi, K.; Sharma, A.; Singh, P.; Memoria, M. A comparative review: Medical image fusion using SWT and DWT. Mater. Today Proc. 2021, 37, 3411–3416. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, B.K. DWT based color image watermarking using maximum entropy. Multimed. Tools Appl. 2021, 80, 15487–15510. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Soh, L.-K.; Tsatsoulis, C. Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices. IEEE Trans. Geosci. Remote Sens. 1999, 37, 780–795. [Google Scholar] [CrossRef]
- Clausi, D.A. An analysis of co-occurrence texture statistics as a function of grey level quantization. Can. J. Remote Sens. 2002, 28, 45–62. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. A practical approach to feature selection. In Machine Learning Proceedings 1992; Elsevier: Amsterdam, The Netherlands, 1992; pp. 249–256. [Google Scholar]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In Proceedings of the European Conference on Machine Learning, Catania, Italy, 6–8 April 1994; pp. 171–182. [Google Scholar]
- Luque, A.; Carrasco, A.; Martín, A.; de Las Heras, A. The impact of class imbalance in classification performance metrics based on the binary confusion matrix. Pattern Recognit. 2019, 91, 216–231. [Google Scholar] [CrossRef]
- Chicco, D.; Tötsch, N.; Jurman, G. The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation. BioData Min. 2021, 14, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Room, C. Confusion Matrix. Mach. Learn 2019, 6, 27. [Google Scholar]
- Hasan, M.K.; Alam, M.A.; Das, D.; Hossain, E.; Hasan, M. Diabetes prediction using ensembling of different machine learning classifiers. IEEE Access 2020, 8, 76516–76531. [Google Scholar] [CrossRef]
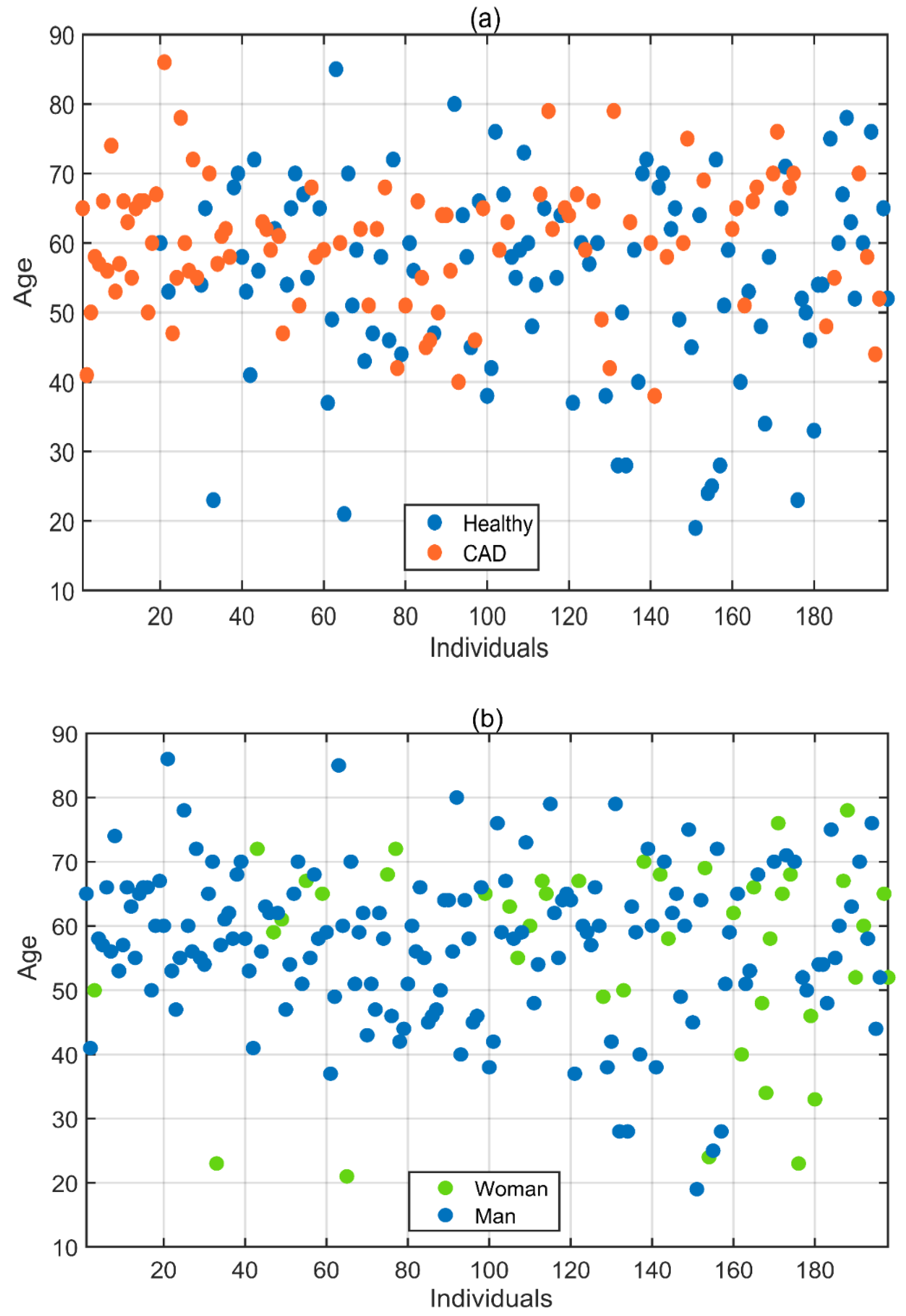


| Subject | Number of Men | Number of Women | Mean Age | Standard Deviation | Total |
|---|---|---|---|---|---|
| Healthy | 77 | 27 | 55 | 14.2 | 104 |
| CAD | 79 | 15 | 60 | 9.4 | 94 |
| Metric | Symbol | Formula |
|---|---|---|
| Sensitivity | SNS | |
| Specificity | SPC | |
| Precision | PRC | |
| Accuracy | ACC | |
| F1 score | F1 | |
| Geometric Mean | GM |
| Group | Feature Numbers |
|---|---|
| 1 | 103, 105, 31, 28, 32, 5, 70, 127, 126, 135, 35, 134, 98, 102, 24, 69, 33, 30, 34, 37, 125, 29, 107, 66, 116 |
| 2 | 81, 89, 123, 82, 85, 109, 124, 115, 121, 129, 120, 122, 108, 51, 3, 114, 119, 128, 38, 106, 117, 4, 118, 101, 72 |
| 3 | 1, 112, 53, 52, 104, 47, 56, 41, 61, 113, 75, 90, 71, 91, 95, 23, 87, 130, 17, 55, 15, 16, 54, 46, 14 |
| Classifiers | Performance Metrics | |||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Sensitivity | Specificity | Precision | Fscore | Gmean | AUC | ||
| Decision Tree | Fine Tree | 0.88 | 0.84 | 0.91 | 0.88 | 0.86 | 0.88 | 0.87 |
| Medium Tree | 0.88 | 0.84 | 0.91 | 0.88 | 0.86 | 0.88 | 0.87 | |
| Coarse Tree | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.86 | |
| Naive Bayes | Gaussian | 0.85 | 0.80 | 0.88 | 0.83 | 0.82 | 0.84 | 0.95 |
| Kernel | 0.81 | 0.96 | 0.71 | 0.71 | 0.81 | 0.82 | 0.87 | |
| SVM | Linear | 0.86 | 0.92 | 0.82 | 0.79 | 0.85 | 0.87 | 0.95 |
| Quadratic | 0.88 | 0.92 | 0.85 | 0.82 | 0.87 | 0.89 | 0.92 | |
| Cubic | 0.86 | 0.92 | 0.82 | 0.79 | 0.85 | 0.87 | 0.93 | |
| Fine Gaussian | 0.64 | 0.28 | 0.91 | 0.70 | 0.40 | 0.51 | 0.75 | |
| Medium Gaussian | 0.88 | 0.92 | 0.85 | 0.82 | 0.87 | 0.89 | 0.96 | |
| Coarse Gaussian | 0.85 | 0.84 | 0.85 | 0.81 | 0.82 | 0.85 | 0.96 | |
| kNN | Fine | 0.71 | 0.72 | 0.71 | 0.64 | 0.68 | 0.71 | 0.71 |
| Medium | 0.86 | 0.88 | 0.85 | 0.81 | 0.85 | 0.87 | 0.94 | |
| Coarse | 0.85 | 0.80 | 0.88 | 0.83 | 0.82 | 0.84 | 0.95 | |
| Cosine | 0.83 | 0.76 | 0.88 | 0.83 | 0.79 | 0.82 | 0.93 | |
| Cubic | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.93 | |
| Weighted | 0.85 | 0.88 | 0.82 | 0.79 | 0.83 | 0.85 | 0.94 | |
| Neural Network | Narrow | 0.90 | 0.92 | 0.88 | 0.85 | 0.88 | 0.90 | 0.91 |
| Medium | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.9 | |
| Wide | 0.86 | 0.88 | 0.85 | 0.81 | 0.85 | 0.87 | 0.9 | |
| Bilayered | 0.81 | 0.84 | 0.79 | 0.75 | 0.79 | 0.82 | 0.9 | |
| Trilayered | 0.88 | 0.92 | 0.85 | 0.82 | 0.87 | 0.89 | 0.88 | |
| Classifiers | Performance Metrics | |||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Sensitivity | Specificity | Precision | Fscore | Gmean | AUC | ||
| Decision Tree | Fine Tree | 0.88 | 0.84 | 0.91 | 0.88 | 0.86 | 0.88 | 0.87 |
| Medium Tree | 0.88 | 0.84 | 0.91 | 0.88 | 0.86 | 0.88 | 0.87 | |
| Coarse Tree | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.86 | |
| Naive Bayes | Gaussian | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.97 |
| Kernel | 0.83 | 0.96 | 0.74 | 0.73 | 0.83 | 0.84 | 0.87 | |
| SVM | Linear | 0.88 | 0.92 | 0.85 | 0.82 | 0.87 | 0.89 | 0.96 |
| Quadratic | 0.90 | 0.92 | 0.88 | 0.85 | 0.88 | 0.90 | 0.94 | |
| Cubic | 0.90 | 0.88 | 0.91 | 0.88 | 0.88 | 0.90 | 0.96 | |
| Fine Gaussian | 0.73 | 0.36 | 1.00 | 1.00 | 0.53 | 0.60 | 0.9 | |
| Medium Gaussian | 0.92 | 0.96 | 0.88 | 0.86 | 0.91 | 0.92 | 0.96 | |
| Coarse Gaussian | 0.85 | 0.84 | 0.85 | 0.81 | 0.82 | 0.85 | 0.96 | |
| kNN | Fine | 0.78 | 0.68 | 0.85 | 0.77 | 0.72 | 0.76 | 0.77 |
| Medium | 0.86 | 0.84 | 0.88 | 0.84 | 0.84 | 0.86 | 0.95 | |
| Coarse | 0.85 | 0.76 | 0.91 | 0.86 | 0.81 | 0.83 | 0.94 | |
| Cosine | 0.86 | 0.84 | 0.88 | 0.84 | 0.84 | 0.86 | 0.96 | |
| Cubic | 0.86 | 0.84 | 0.88 | 0.84 | 0.84 | 0.86 | 0.94 | |
| Weighted | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.95 | |
| Neural Network | Narrow | 0.86 | 0.92 | 0.82 | 0.79 | 0.85 | 0.87 | 0.87 |
| Medium | 0.86 | 0.88 | 0.85 | 0.81 | 0.85 | 0.87 | 0.91 | |
| Wide | 0.92 | 0.96 | 0.88 | 0.86 | 0.91 | 0.92 | 0.92 | |
| Bilayered | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.89 | |
| Trilayered | 0.88 | 0.92 | 0.85 | 0.82 | 0.87 | 0.89 | 0.89 | |
| Classifiers | Performance Metrics | |||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Sensitivity | Specificity | Precision | Fscore | Gmean | AUC | ||
| Decision Tree | Fine Tree | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.84 |
| Medium Tree | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.84 | |
| Coarse Tree | 0.83 | 0.80 | 0.85 | 0.80 | 0.80 | 0.83 | 0.86 | |
| Naive Bayes | Gaussian | 0.90 | 0.88 | 0.91 | 0.88 | 0.88 | 0.90 | 0.98 |
| Kernel | 0.83 | 0.92 | 0.76 | 0.74 | 0.82 | 0.84 | 0.87 | |
| Support Vector Machine | Linear | 0.90 | 0.92 | 0.88 | 0.85 | 0.88 | 0.90 | 0.96 |
| Quadratic | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.95 | |
| Cubic | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.93 | |
| Fine Gaussian | 0.69 | 0.36 | 0.94 | 0.82 | 0.50 | 0.58 | 0.91 | |
| Medium Gaussian | 0.93 | 1.00 | 0.88 | 0.86 | 0.93 | 0.94 | 0.96 | |
| Coarse Gaussian | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.96 | |
| kNN | Fine | 0.80 | 0.72 | 0.85 | 0.78 | 0.75 | 0.78 | 0.79 |
| Medium | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.93 | |
| Coarse | 0.80 | 0.64 | 0.91 | 0.84 | 0.73 | 0.76 | 0.94 | |
| Cosine | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.95 | |
| Cubic | 0.88 | 0.88 | 0.88 | 0.85 | 0.86 | 0.88 | 0.93 | |
| Weighted | 0.90 | 0.92 | 0.88 | 0.85 | 0.88 | 0.90 | 0.94 | |
| Neural Network | Narrow | 0.85 | 0.84 | 0.85 | 0.81 | 0.82 | 0.85 | 0.89 |
| Medium | 0.85 | 0.88 | 0.82 | 0.79 | 0.83 | 0.85 | 0.89 | |
| Wide | 0.85 | 0.92 | 0.79 | 0.77 | 0.84 | 0.85 | 0.91 | |
| Bilayered | 0.83 | 0.88 | 0.79 | 0.76 | 0.81 | 0.84 | 0.87 | |
| Trilayered | 0.88 | 0.96 | 0.82 | 0.80 | 0.87 | 0.89 | 0.93 | |
| References | Feature Extraction | Classifier | Evaluation Metrics | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Sensitivity | Specificity | Precision | Fscore | Gmean | AUC | |||
| Gunawan et al. [24] | GLCM | SVM | 0.91 | - | - | - | - | - | - |
| Putra et al. [25] | GLCM | NN | 0.78 | - | - | - | - | - | - |
| PCA | NN | 0.90 | - | - | - | - | - | - | |
| Kusuma et al. [27] | B&W Ratio | Threshold | 0.83 | - | - | - | - | - | - |
| Permatasari et al. [26] | PCA | SVM | 0.80 | - | - | - | - | - | - |
| This study | Statistical, GLCM, GLRLM | KNN | 0.90 | 0.92 | 0.88 | 0.85 | 0.88 | 0.90 | 0.94 |
| Naive Bayes | 0.90 | 0.88 | 0.91 | 0.88 | 0.88 | 0.90 | 0.98 | ||
| SVM | 0.93 | 1.00 | 0.88 | 0.86 | 0.93 | 0.94 | 0.96 | ||
| DT | 0.88 | 0.84 | 0.91 | 0.88 | 0.86 | 0.88 | 0.87 | ||
| NN | 0.92 | 0.96 | 0.88 | 0.86 | 0.91 | 0.92 | 0.92 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özbilgin, F.; Kurnaz, Ç.; Aydın, E. Prediction of Coronary Artery Disease Using Machine Learning Techniques with Iris Analysis. Diagnostics 2023, 13, 1081. https://doi.org/10.3390/diagnostics13061081
Özbilgin F, Kurnaz Ç, Aydın E. Prediction of Coronary Artery Disease Using Machine Learning Techniques with Iris Analysis. Diagnostics. 2023; 13(6):1081. https://doi.org/10.3390/diagnostics13061081
Chicago/Turabian StyleÖzbilgin, Ferdi, Çetin Kurnaz, and Ertan Aydın. 2023. "Prediction of Coronary Artery Disease Using Machine Learning Techniques with Iris Analysis" Diagnostics 13, no. 6: 1081. https://doi.org/10.3390/diagnostics13061081
APA StyleÖzbilgin, F., Kurnaz, Ç., & Aydın, E. (2023). Prediction of Coronary Artery Disease Using Machine Learning Techniques with Iris Analysis. Diagnostics, 13(6), 1081. https://doi.org/10.3390/diagnostics13061081






