Comparison of Automated Keratometer and Scheimpflug Tomography for Predicting Refractive Astigmatism in Pseudophakic Eyes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Patients and Surgical Procedures
2.2. Postoperative Measurements
2.3. Astigmatism Analysis
2.4. Statistical Analysis
3. Results
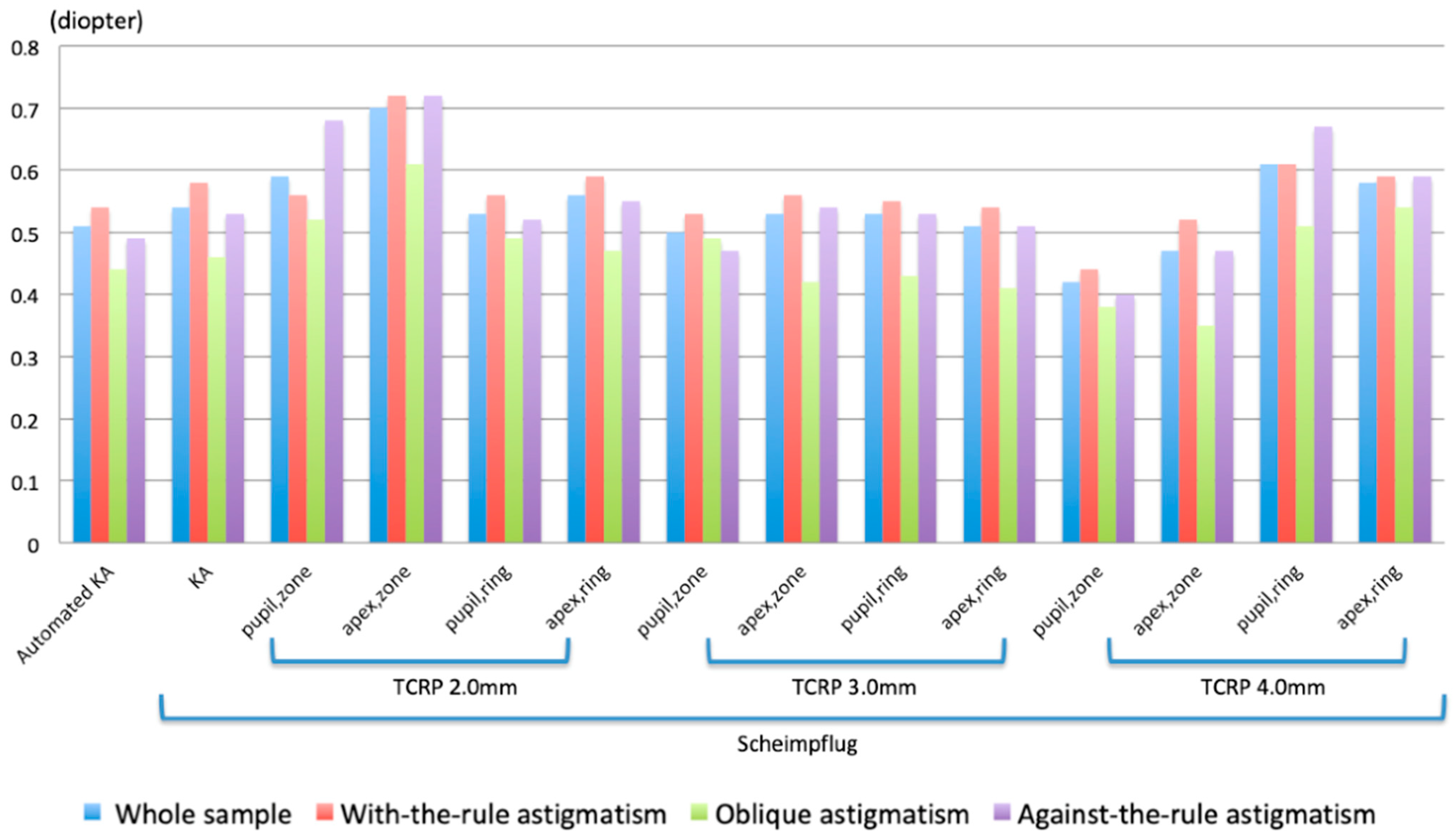
3.1. Comparing Refractive and Corneal Magnitudes of Astigmatism
3.2. Comparing Refractive and Corneal Astigmatism Using the Steep Corneal Meridian as the Reference Plane
4. Discussion
KP(Φ)RA = −0.04 + 0.94 × KP(Φ)KA+ 0.39 × cos(2α)
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ferrer-Blasco, T.; Montés-Micó, R.; Peixoto-de-Matos, S.C.; González-Méijome, J.M.; Cerviño, A. Prevalence of corneal astigmatism before cataract surgery. J. Cataract Refract. Surg. 2009, 35, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Nemeth, G.; Szalai, E.; Berta, A.; Modis, L., Jr. Astigmatism prevalence and biometric analysis in normal population. Eur. J. Ophthalmol. 2013, 23, 779–783. [Google Scholar] [CrossRef] [PubMed]
- Savini, G.; Barboni, P.; Carbonelli, M.; Hoffer, K.J. Comparison of methods to measure corneal power for intraocular lens power calculation using a rotating Scheimpflug camera. J. Cataract Refract. Surg. 2013, 39, 598–604. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.D.; Tsai, C.Y.; Liou, S.W. Accuracy of corneal astigmatism estimation by neglecting the posterior corneal surface measurement. Am. J. Ophthalmol. 2009, 147, 788–795. [Google Scholar] [CrossRef] [PubMed]
- Koch, D.D.; Ali, S.F.; Weikert, M.P.; Shirayama, M.; Jenkins, R.; Wang, L. Contribution of posterior corneal astigmatism to total corneal astigmatism. J. Cataract Refract. Surg. 2012, 38, 2080–2087. [Google Scholar] [CrossRef] [PubMed]
- Savini, G.; Versaci, F.; Vestri, G.; Ducoli, P.; Næser, K. Influence of posterior corneal astigmatism on total corneal astigmatism in eyes with moderate to high astigmatism. J. Cataract Refract. Surg. 2014, 40, 1645–1653. [Google Scholar] [CrossRef] [PubMed]
- Tonn, B.; Klaproth, O.K.; Kohnen, T. Anterior surface-based keratometry compared with Scheimpflug tomography-based total corneal astigmatism. Invest. Ophthalmol. Vis. Sci. 2014, 56, 291–298. [Google Scholar] [CrossRef]
- Alpins, N.; Ong, J.K.; Stamatelatos, G. Corneal topographic astigmatism (CorT) to quantify total corneal astigmatism. J. Refract. Surg. 2015, 31, 182–186. [Google Scholar] [CrossRef]
- De Castro, A.; Rosales, P.; Marcos, S. Tilt and decentration of intraocular lenses in vivo from Purkinje and Scheimpflug imaging. Validation study. J. Cataract Refract. Surg. 2007, 33, 418–429. [Google Scholar] [CrossRef]
- Kránitz, K.; Miháltz, K.; Sándor, G.L.; Takacs, A.; Knorz, M.C.; Nagy, Z.Z. Intraocular lens tilt and decentration measured by Scheimpflug camera following manual or femtosecond laser-created continuous circular capsulotomy. J. Refract. Surg. 2012, 28, 259–263. [Google Scholar] [CrossRef]
- Naeser, K. Combining refractive and topographic data in corneal refractive surgery for astigmatism: A new method based on polar value analysis and mathematical optimization. Acta Ophthalmol. 2012, 90, 768–772. [Google Scholar] [CrossRef] [PubMed]
- Naeser, K. Assessment and statistics of surgically induced astigmatism. Acta Ophthalmol. 2008, 86 (Suppl. S1), 5–28. [Google Scholar] [CrossRef] [PubMed]
- Bregnhøj, J.F.; Mataji, P.; Naeser, K. Refractive, anterior corneal and internal astigmatism in the pseudophakic eye. Acta Ophthalmol. 2015, 93, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Abulafia, A.; Koch, D.D.; Holladay, J.T.; Wang, L.; Hill, W. Pursuing perfection in intraocular lens calculations: IV. Rethinking astigmatism analysis for intraocular lens-based surgery: Suggested terminology, analysis, and standards for outcome reports. J. Cataract Refract. Surg. 2018, 44, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Tejedor, J.; Guirao, A. Agreement between refractive and corneal astigmatism in pseudophakic eyes. Cornea 2013, 32, 783–790. [Google Scholar] [CrossRef]
- Whang, W.J.; Byun, Y.S.; Joo, C.K. Comparison of refractive outcomes using five devices for the assessment of preoperative corneal power. Clin. Exp. Ophthalmol. 2012, 40, 425–432. [Google Scholar] [CrossRef]
- Klijn, S.; Reus, N.J.; van der Sommen, C.M.; Sicam, V.A. Accuracy of Total Corneal Astigmatism Measurements With a Scheimpflug Imager and a Color Light-Emitting Diode Corneal Topographer. Am. J. Ophthalmol. 2016, 167, 72–78. [Google Scholar] [CrossRef]
- Savini, G.; Næser, K.; Schiano-Lomoriello, D.; Ducoli, P. Optimized keratometry and total corneal astigmatism for toric intraocular lens calculation. J. Cataract Refract. Surg. 2017, 43, 1140–1148. [Google Scholar] [CrossRef]
- Holladay, J.T.; Piers, P.A.; Koranyi, G.; van der Mooren, M.; Norrby, N.E. A new intraocular lens design to reduce spherical aberration of pseudophakic eyes. J. Refract. Surg. 2002, 18, 683–691. [Google Scholar] [CrossRef]
- Piers, P.A.; Weeber, H.A.; Artal, P.; Norrby, S. Theoretical comparison of aberration-correcting customized and aspheric intraocular lenses. J. Refract. Surg. 2007, 23, 374–384. [Google Scholar] [CrossRef]
- Rosales, P.; De Castro, A.; Jiménez-Alfaro, I.; Marcos, S. Intraocular lens alignment from purkinje and Scheimpflug imaging. Clin. Exp. Optom. 2010, 93, 400–408. [Google Scholar] [CrossRef] [PubMed]


| Absolute Value | ||
|---|---|---|
| Standard Deviation | Range | |
| Horizontal decentration (mm) | 0.16 0.11 | 0~0.38 |
| Vertical decentration (mm) | 0.14 0.11 | 0~0.35 |
| Total decentration (mm) | 0.24 0.12 | 0~0.39 |
| Horizontal tilt (degrees) | 1.25 0.95 | 0~3.0 |
| Vertical tilt (degrees) | 1.46 1.08 | 0~3.5 |
| Parameter | SD | Difference with RA | p Value * | |
|---|---|---|---|---|
| RA | 0.70 0.61 | |||
| Automated K | 0.72 0.56 | −0.02 0.45 | 0.845 | |
| Scheimpflug KA | 0.73 0.56 | −0.03 0.42 | 0.576 | |
| Scheimpflug TCRP 2.0 mm | pupil/zone | 0.78 0.60 | −0.08 0.47 | 0.148 |
| apex/zone | 1.03 0.67 | −0.33 0.50 | <0.001 | |
| pupil/ring | 0.87 0.64 | −0.17 0.41 | 0.001 | |
| apex/ring | 0.86 0.61 | −0.16 0.41 | 0.001 | |
| Scheimpflug TCRP 3.0 mm | pupil/zone | 0.84 0.61 | −0.14 0.39 | 0.233 |
| apex/zone | 0.80 0.59 | −0.10 0.40 | 0.033 | |
| pupil/ring | 0.80 0.55 | −0.10 0.39 | 0.023 | |
| apex/ring | 0.83 0.64 | −0.13 0.41 | 0.007 | |
| Scheimpflug TCRP 4.0 mm | pupil/zone | 0.75 0.60 | −0.05 0.35 | 0.300 |
| apex/zone | 0.75 0.57 | −0.04 0.37 | 0.357 | |
| pupil/ring | 0.81 0.55 | −0.11 0.45 | 0.037 | |
| apex/ring | 0.81 0.59 | −0.11 0.45 | 0.064 | |
| Difference between parameters (p value) ** | <0.001 | |||
| Keratometric Measurement | (D) ± SD | Difference from Zero (p Value) † | (D) ± SD | Mean DA (D @ Degree) | (D) ± SD | Range of DA (D) | Percentage of DA Magnitude within 0.50 D | ||
|---|---|---|---|---|---|---|---|---|---|
| Automated KA | −0.13 0.46 | 0.005 | −0.04 0.31 | 0.579 | 0.14 @ 98 | 0.51 0.25 | 0–1.25 | 51.6 | |
| Scheimpflug KA | −0.22 0.40 | <0.001 | −0.01 0.37 | 0.799 | 0.22 @ 91 | 0.54 0.23 | 0–1.20 | 46.3 | |
| Scheimpflug TCRP 2.0 mm | pupil/zone | −0.28 0.49 | <0.001 | 0.04 0.42 | 0.189 | 0.28 @ 86 | 0.59 0.37 | 0.09–2.03 | 49.5 |
| apex/zone | −0.52 0.51 | <0.001 | 0.06 0.37 | 0.077 | 0.52 @ 87 | 0.70 0.42 | 0.07–2.03 | 37.9 | |
| pupil/ring | −0.33 0.40 | <0.001 | 0.08 0.32 | 0.017 | 0.34 @ 84 | 0.53 0.31 | 0–1.50 | 52.6 | |
| apex/ring | −0.34 0.39 | <0.001 | 0.10 0.37 | 0.007 | 0.35 @ 82 | 0.56 0.31 | 0.02–1.50 | 49.5 | |
| Scheimpflug TCRP 3.0 mm | pupil/zone | −0.29 0.38 | <0.001 | 0.07 0.32 | 0.018 | 0.30 @ 83 | 0.50 0.29 | 0.05–1.30 | 54.7 |
| apex/zone | −0.27 0.38 | <0.001 | 0.11 0.36 | 0.004 | 0.29 @ 79 | 0.53 0.29 | 0.05–1.30 | 55.8 | |
| pupil/ring | −0.26 0.39 | <0.001 | 0.13 0.34 | 0.001 | 0.29 @ 77 | 0.53 0.28 | 0.03–1.38 | 51.6 | |
| apex/ring | −0.27 0.40 | <0.001 | 0.11 0.32 | 0.002 | 0.29 @ 79 | 0.51 0.29 | 0–1.39 | 54.7 | |
| Scheimpflug TCRP 4.0 mm | pupil/zone | −0.16 0.33 | <0.001 | 0.07 0.30 | 0.013 | 0.18 @ 78 | 0.42 0.24 | 0.03–1.10 | 62.1 |
| apex/zone | −0.19 0.37 | <0.001 | 0.10 0.33 | 0.007 | 0.21 @ 76 | 0.47 0.26 | 0.02–1.07 | 51.6 | |
| pupil/ring | −0.34 0.47 | <0.001 | 0.08 0.38 | 0.059 | 0.35 @ 83 | 0.61 0.34 | 0.03–1.40 | 43.2 | |
| apex/ring | −0.31 0.45 | <0.001 | 0.05 0.39 | 0.338 | 0.31 @ 85 | 0.58 0.33 | 0.07–1.44 | 45.3 | |
| Difference between parameters (p value) * | <0.001 | 0.027 | <0.001 | ||||||
| Keratometric Measurement | (D) ± SD | Difference from Zero (p Value) † | (D) ± SD | Difference from Zero (p Value) † | Mean DA (D @ Degree) | (D) ± SD | Range of DA (D) | Percentage of DA within 0.50 D | |
|---|---|---|---|---|---|---|---|---|---|
| Automated KA | −0.44 0.32 | <0.001 | −0.02 0.28 | 0.905 | 0.44 @ 0 | 0.54 0.28 | 0.08–1.25 | 46.7 | |
| Scheimpflug KA | −0.47 0.28 | <0.001 | 0.01 0.33 | 0.915 | 0.38 @ 0 | 0.58 0.26 | 0.09–1.20 | 40.0 | |
| Scheimpflug TCRP 2.0 mm | pupil/zone | −0.42 0.37 | <0.001 | 0.11 0.31 | 0.029 | 0.06 @ 52 | 0.56 0.32 | 0.09–1.50 | 55.6 |
| apex/zone | −0.61 0.42 | <0.001 | 0.12 0.33 | 0.041 | 0.01 @ 169 | 0.72 0.38 | 0.16–1.95 | 33.3 | |
| pupil/ring | −0.43 0.35 | <0.001 | 0.11 0.29 | 0.023 | 0.07 @ 34 | 0.56 0.30 | 0.05–1.40 | 51.1 | |
| apex/ring | −0.47 0.33 | <0.001 | 0.15 0.31 | 0.002 | 0.05 @ 49 | 0.59 0.30 | 0.07–1.44 | 44.4 | |
| Scheimpflug TCRP 3.0 mm | pupil/zone | −0.40 0.33 | <0.001 | 0.11 0.29 | 0.021 | 0.07 @ 28 | 0.53 0.28 | 0.15~1.30 | 55.6 |
| apex/zone | −0.43 0.31 | <0.001 | 0.15 0.32 | 0.005 | 0.06 @ 35 | 0.56 0.27 | 0.09–1.30 | 51.1 | |
| pupil/ring | −0.38 0.40 | <0.001 | 0.10 0.28 | 0.019 | 0.08 @ 11 | 0.55 0.29 | 0.05–1.18 | 46.7 | |
| apex/ring | −0.36 0.41 | <0.001 | 0.09 0.28 | 0.027 | 0.12 @ 7 | 0.54 0.30 | 0.09–1.31 | 51.1 | |
| Scheimpflug TCRP 4.0 mm | pupil/zone | −0.26 0.34 | <0.001 | 0.08 0.28 | 0.020 | 0.11 @ 11 | 0.44 0.26 | 0.05–1.10 | 55.6 |
| apex/zone | −0.33 0.36 | <0.001 | 0.10 0.30 | 0.043 | 0.10 @ 15 | 0.52 0.27 | 0.09–1.03 | 48.9 | |
| pupil/ring | −0.45 0.44 | <0.001 | 0.06 0.30 | 0.240 | 0.19 @ 1 | 0.61 0.34 | 0.10–1.40 | 40.0 | |
| apex/ring | −0.41 0.45 | <0.001 | 0.04 0.30 | 0.464 | 0.23 @ 179 | 0.59 0.33 | 0.07–1.40 | 44.4 | |
| Difference between parameters (p value) * | <0.001 | 0.030 | <0.001 | ||||||
| Keratometric Measurement | (D) ± SD | Difference from Zero (p Value) † | (D) ± SD | Difference from Zero (p Value) † | Mean DA (D @ Degree) | (D) ± SD | Range of DA (D) | Percentage of DA within 0.50 D | |
|---|---|---|---|---|---|---|---|---|---|
| Automated KA | −0.10 0.29 | 0.148 | −0.09 0.38 | 0.469 | 0.29 @ 172 | 0.44 0.20 | 0.05–0.97 | 68.8 | |
| Scheimpflug KA | −0.19 0.31 | 0.028 | 0.03 0.38 | 0.753 | 0.31 @ 169 | 0.46 0.23 | 0.00–0.84 | 62.5 | |
| Scheimpflug TCRP 2.0 mm | pupil/zone | −0.09 0.51 | 0.642 | −0.04 0.39 | 0.433 | 0.16 @ 4 | 0.52 0.38 | 0.12–1.25 | 50.0 |
| apex/zone | −0.38 0.58 | 0.039 | 0.04 0.32 | 0.875 | 0.08 @ 157 | 0.61 0.44 | 0.07–1.53 | 50.0 | |
| pupil/ring | −0.27 0.46 | 0.061 | 0.06 0.27 | 0.666 | 0.05 @ 136 | 0.49 0.34 | 0.00–1.19 | 56.3 | |
| apex/ring | −0.21 0.42 | 0.063 | 0.09 0.33 | 0.470 | 0.09 @ 167 | 0.47 0.32 | 0.02–1.11 | 56.3 | |
| Scheimpflug TCRP 3.0 mm | pupil/zone | −0.28 0.44 | 0.049 | 0.08 0.27 | 0.382 | 0.02 @ 159 | 0.49 0.33 | 0.06~1.16 | 50.0 |
| apex/zone | −0.12 0.41 | 0.278 | 0.07 0.29 | 0.510 | 0.10 @ 6 | 0.42 0.30 | 0.05~1.01 | 62.5 | |
| pupil/ring | −0.20 0.32 | 0.026 | 0.12 0.29 | 0.158 | 0.02 @ 151 | 0.43 0.21 | 0.14–0.88 | 62.5 | |
| apex/ring | −0.18 0.29 | 0.023 | 0.09 0.29 | 0.328 | 0.04 @ 133 | 0.41 0.19 | 0.15–0.73 | 68.8 | |
| Scheimpflug TCRP 4.0 mm | pupil/zone | −0.14 0.29 | 0.079 | 0.10 0.30 | 0.365 | 0.08 @ 169 | 0.38 0.22 | 0.07–0.80 | 68.8 |
| apex/zone | −0.10 0.33 | 0.098 | 0.10 0.26 | 0.198 | 0.07 @ 5 | 0.35 0.25 | 0.03–0.88 | 62.5 | |
| pupil/ring | −0.37 0.28 | 0.001 | 0.13 0.39 | 0.638 | 0.11 @ 4 | 0.51 0.35 | 0.03–1.30 | 62.5 | |
| apex/ring | −0.29 0.30 | 0.003 | 0.01 0.49 | 0.730 | 0.28 @ 169 | 0.54 0.34 | 0.10–1.44 | 50.0 | |
| Difference between parameters (p value) * | 0.026 | 0.389 | 0.330 | ||||||
| Keratometric Measurement | (D) ± SD | Difference from Zero (p Value) † | (D) ± SD | Difference from Zero (p Value) † | Mean DA (D @ Degree) | (D) ± SD | Range of DA (D) | Percentage of DA within 0.50 D | |
|---|---|---|---|---|---|---|---|---|---|
| Automated KA | 0.26 0.37 | <0.001 | −0.03 0.32 | 0.784 | 0.30 @ 177 | 0.49 0.24 | 0.00–1.07 | 50.0 | |
| Scheimpflug KA | 0.09 0.35 | 0.209 | −0.06 0.44 | 0.477 | 0.37 @ 178 | 0.53 0.19 | 0.10–0.91 | 47.1 | |
| Scheimpflug TCRP 2.0 mm | pupil/zone | −0.19 0.57 | 0.066 | −0.01 0.53 | 0.859 | 0.17 @ 170 | 0.68 0.42 | 0.12–2.03 | 41.2 |
| apex/zone | −0.46 0.58 | <0.001 | −0.01 0.45 | 0.822 | 0.17 @ 89 | 0.72 0.47 | 0.12–2.03 | 38.2 | |
| pupil/ring | −0.22 0.42 | 0.010 | 0.04 0.38 | 0.445 | 0.10 @ 53 | 0.52 0.31 | 0.05–1.50 | 52.9 | |
| apex/ring | −0.23 0.41 | 0.004 | 0.04 0.44 | 0.449 | 0.07 @ 38 | 0.55 0.33 | 0.06–1.50 | 52.9 | |
| Scheimpflug TCRP 3.0 mm | pupil/zone | −0.16 0.38 | 0.043 | 0.02 0.38 | 0.487 | 0.07 @ 47 | 0.47 0.29 | 0.05–1.15 | 55.9 |
| apex/zone | −0.14 0.40 | 0.074 | 0.07 0.45 | 0.268 | 0.12 @ 18 | 0.54 0.29 | 0.06–1.15 | 58.8 | |
| pupil/ring | −0.13 0.38 | 0.089 | 0.16 0.43 | 0.048 | 0.29 @ 13 | 0.53 0.29 | 0.03–1.38 | 52.9 | |
| apex/ring | −0.19 0.41 | 0.008 | 0.14 0.38 | 0.042 | 0.18 @ 29 | 0.51 0.31 | 0–1.39 | 52.9 | |
| Scheimpflug TCRP 4.0 mm | pupil/zone | −0.05 0.30 | 0.478 | 0.05 0.34 | 0.334 | 0.11 @ 22 | 0.40 0.20 | 0.03–0.85 | 67.6 |
| apex/zone | −0.04 0.33 | 0.407 | 0.09 0.40 | 0.184 | 0.20 @ 15 | 0.47 0.23 | 0.02–1.07 | 50.0 | |
| pupil/ring | −0.18 0.55 | 0.077 | 0.09 0.48 | 0.221 | 0.39 @ 11 | 0.67 0.32 | 0.17–1.36 | 38.2 | |
| apex/ring | −0.17 0.48 | 0.032 | 0.08 0.45 | 0.327 | 0.26 @ 9 | 0.59 0.32 | 0.11–1.20 | 44.1 | |
| Difference between parameters (p value) * | <0.001 | <0.001 | |||||||
| Keratometric Measurement | Linear Regression Equation | r2 | * p Value | |
|---|---|---|---|---|
| Automated KA | −0.04 + 0.92 KP(Φ) + 0.39 cos(2α) | 0.76 | <0.001 | |
| Scheimpflug KA | −0.17 + 0.99 KP(Φ) + 0.36 cos(2α) | 0.81 | <0.001 | |
| Scheimpflug TCRP 2.0 mm | pupil/zone | −0.13 + 0.78 KP(Φ) + 0.09 cos(2α) | 0.50 | <0.001 |
| apex/zone | −0.23 + 0.71 KP(Φ) + 0.04 cos(2α) | 0.50 | <0.001 | |
| pupil/ring | −0.22 + 0.86 KP(Φ) + 0.07 cos(2α) | 0.66 | <0.001 | |
| apex/ring | −0.26 + 0.90 KP(Φ) + 0.05 cos(2α) | 0.66 | <0.001 | |
| Scheimpflug TCRP 3.0 mm | pupil/zone | −0.24 + 0.91 KP(Φ) + 0.07 cos(2α) | 0.69 | <0.001 |
| apex/zone | −0.22 + 0.91 KP(Φ) + 0.09 cos(2α) | 0.68 | <0.001 | |
| pupil/ring | −0.24 + 0.95 KP(Φ) + 0.14 cos(2α) | 0.67 | <0.001 | |
| apex/ring | −0.15 + 0.84 KP(Φ) + 0.12 cos(2α) | 0.68 | <0.001 | |
| Scheimpflug TCRP 4.0 mm | pupil/zone | −0.13 + 0.93 KP(Φ) + 0.13 cos(2α) | 0.77 | <0.001 |
| apex/zone | −0.16 + 0.94 KP(Φ) + 0.15 cos(2α) | 0.71 | <0.001 | |
| pupil/ring | −0.29 + 0.94 KP(Φ) + 0.27 cos(2α) | 0.63 | <0.001 | |
| apex/ring | −0.19 + 0.86 KP(Φ) + 0.26 cos(2α) | 0.65 | <0.001 | |
| Keratometric Measurement | (D) ± SD | Difference from Zero (p Value) † | (D) ± SD | Difference from Zero (p Value) † | Mean DA (D @ Degree) | (D) ± SD | Range of DA (D) | Percentage of DA Magnitude within 0.50 D | |
|---|---|---|---|---|---|---|---|---|---|
| Automated KA | 0.00 0.32 | 0.509 | −0.04 0.31 | 0.579 | 0.04 @ 133 | 0.38 0.23 | 0.03–1.30 | 71.6 | |
| Scheimpflug KA | 0.00 0.30 | 0.844 | −0.01 0.37 | 0.799 | 0.01 @ 146 | 0.42 0.21 | 0.02–0.94 | 67.4 | |
| Scheimpflug TCRP 2.0 mm | pupil/zone | 0.00 0.47 | 0.994 | 0.04 0.42 | 0.189 | 0.04 @ 43 | 0.53 0.33 | 0.01–1.60 | 54.7 |
| apex/zone | 0.00 0.48 | 0.994 | 0.06 0.37 | 0.077 | 0.06 @ 44 | 0.53 0.29 | 0.01–1.39 | 50.5 | |
| pupil/ring | 0.00 0.39 | 0.724 | 0.08 0.32 | 0.017 | 0.08 @ 46 | 0.45 0.23 | 0.02–1.14 | 65.3 | |
| apex/ring | 0.00 0.39 | 0.897 | 0.10 0.37 | 0.007 | 0.10 @ 45 | 0.47 0.26 | 0.04–1.31 | 64.2 | |
| Scheimpflug TCRP 3.0 mm | pupil/zone | 0.00 0.37 | 0.622 | 0.07 0.32 | 0.018 | 0.07 @ 42 | 0.44 0.22 | 0.03–1.02 | 65.3 |
| apex/zone | 0.00 0.38 | 0.867 | 0.11 0.36 | 0.004 | 0.11 @ 44 | 0.47 0.25 | 0.04–1.19 | 57.9 | |
| pupil/ring | 0.00 0.38 | 0.667 | 0.13 0.34 | 0.001 | 0.13 @ 44 | 0.46 0.25 | 0–1.10 | 58.9 | |
| apex/ring | 0.00 0.37 | 0.758 | 0.11 0.32 | 0.002 | 0.11 @ 46 | 0.44 0.25 | 0.01–1.09 | 63.2 | |
| Scheimpflug TCRP 4.0 mm | pupil/zone | 0.00 0.31 | 0.683 | 0.07 0.30 | 0.013 | 0.07 @ 45 | 0.38 0.21 | 0.02–0.88 | 73.7 |
| apex/zone | 0.00 0.35 | 0.705 | 0.10 0.33 | 0.007 | 0.10 @ 46 | 0.43 0.23 | 0.03–0.99 | 61.1 | |
| pupil/ring | 0.00 0.42 | 0.956 | 0.08 0.38 | 0.059 | 0.08 @ 45 | 0.50 0.28 | 0.01–1.14 | 55.8 | |
| apex/ring | 0.00 0.40 | 0.962 | 0.05 0.39 | 0.338 | 0.05 @ 46 | 0.49 0.27 | 0.01–1.27 | 54.7 | |
| Difference between parameters (p value) * | 0.746 | 0.027 | <0.001 | ||||||
| Keratometric Measurement | (D) ± SD | Difference between Automated KA and TCRP 4.0 mm, Pupil/Zone (p Value) * | (D) ± SD | Difference between Automated KA and TCRP 4.0 mm, Pupil/Zone (p Value) * | (D) ± SD | Difference between Parameters (p Value) * | |
|---|---|---|---|---|---|---|---|
| Before optimization | Automated KA | −0.13 0.46 | 0.662 | −0.04 0.31 | 0.003 | 0.51 0.25 | 0.001 |
| TCRP 4.0 mm Pupil/zone | −0.16 0.33 | 0.07 0.30 | 0.42 0.24 | ||||
| After optimization | Automated KA | 0.00 0.32 | 0.499 | −0.04 0.31 | 0.003 | 0.38 0.23 | 0.733 |
| TCRP 4.0 mm Pupil/zone | 0.00 0.31 | 0.07 0.30 | 0.38 0.21 | ||||
| Difference according to optimization (p value) * | Automated KA | <0.001 | 1.00 | <0.001 | |||
| TCRP 4.0 mm Pupil/zone | <0.001 | 0.054 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, K.-S.; Savini, G.; Whang, W.-J.; Næser, K. Comparison of Automated Keratometer and Scheimpflug Tomography for Predicting Refractive Astigmatism in Pseudophakic Eyes. Diagnostics 2023, 13, 3687. https://doi.org/10.3390/diagnostics13243687
Na K-S, Savini G, Whang W-J, Næser K. Comparison of Automated Keratometer and Scheimpflug Tomography for Predicting Refractive Astigmatism in Pseudophakic Eyes. Diagnostics. 2023; 13(24):3687. https://doi.org/10.3390/diagnostics13243687
Chicago/Turabian StyleNa, Kyung-Sun, Giacomo Savini, Woong-Joo Whang, and Kristian Næser. 2023. "Comparison of Automated Keratometer and Scheimpflug Tomography for Predicting Refractive Astigmatism in Pseudophakic Eyes" Diagnostics 13, no. 24: 3687. https://doi.org/10.3390/diagnostics13243687
APA StyleNa, K.-S., Savini, G., Whang, W.-J., & Næser, K. (2023). Comparison of Automated Keratometer and Scheimpflug Tomography for Predicting Refractive Astigmatism in Pseudophakic Eyes. Diagnostics, 13(24), 3687. https://doi.org/10.3390/diagnostics13243687





