Machine Learning Models for Prediction of Sex Based on Lumbar Vertebral Morphometry
Abstract
:1. Introduction
2. Materials and Methods
2.1. Selection of the Study Lot, Criteria for Inclusion and Exclusion
2.2. Recording Information in the Database
2.3. Working Methodology
2.4. Data Analysis and Machine Learning Methodology
- learn_rate (learning rate);
- loss_reduction (min reduction in the loss function for continuing the tree split);
- tree_depth (max tree depth);
- sample_size (random samples size);
- min_n and mtry (as for RF models).
3. Results
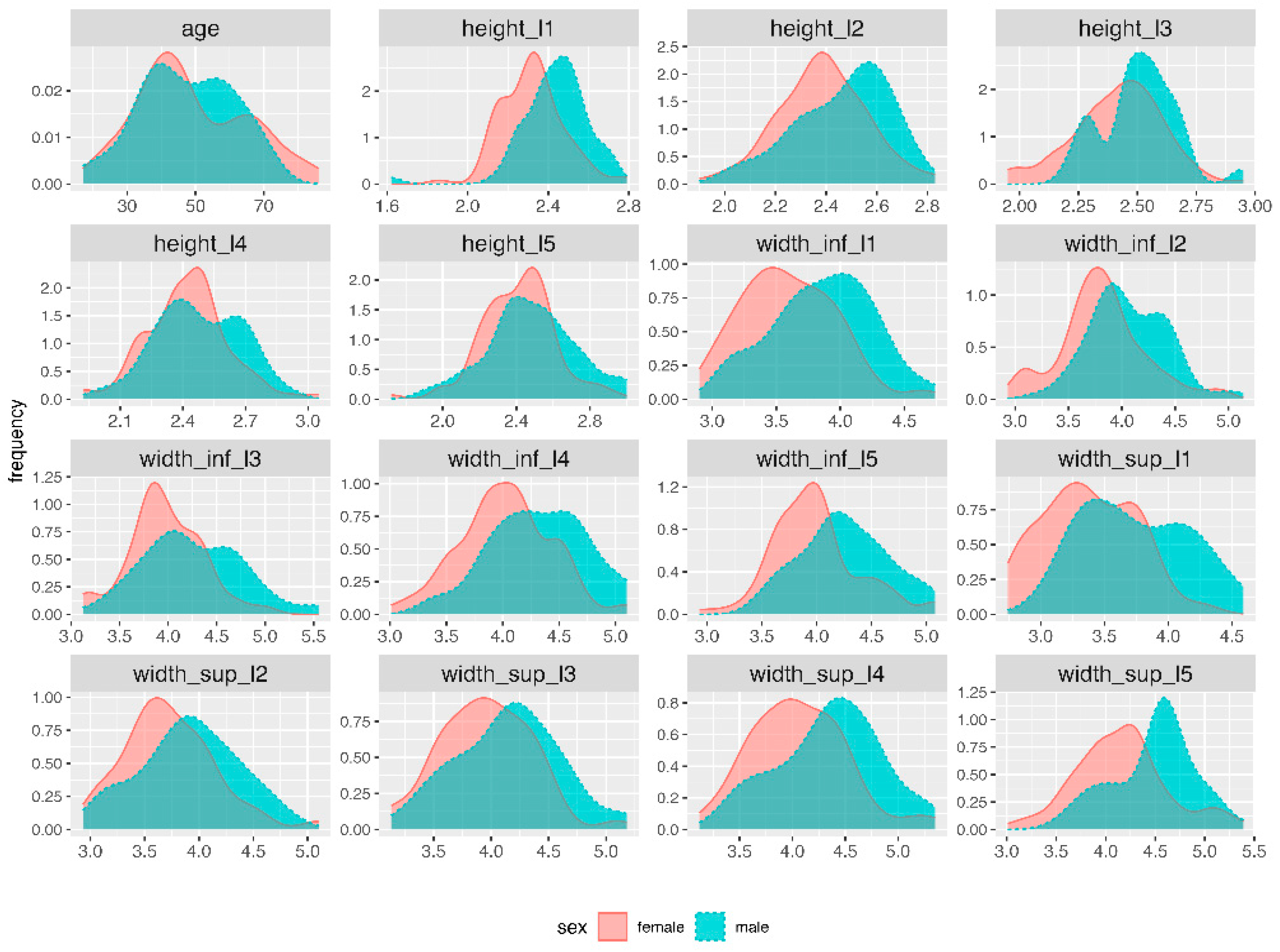
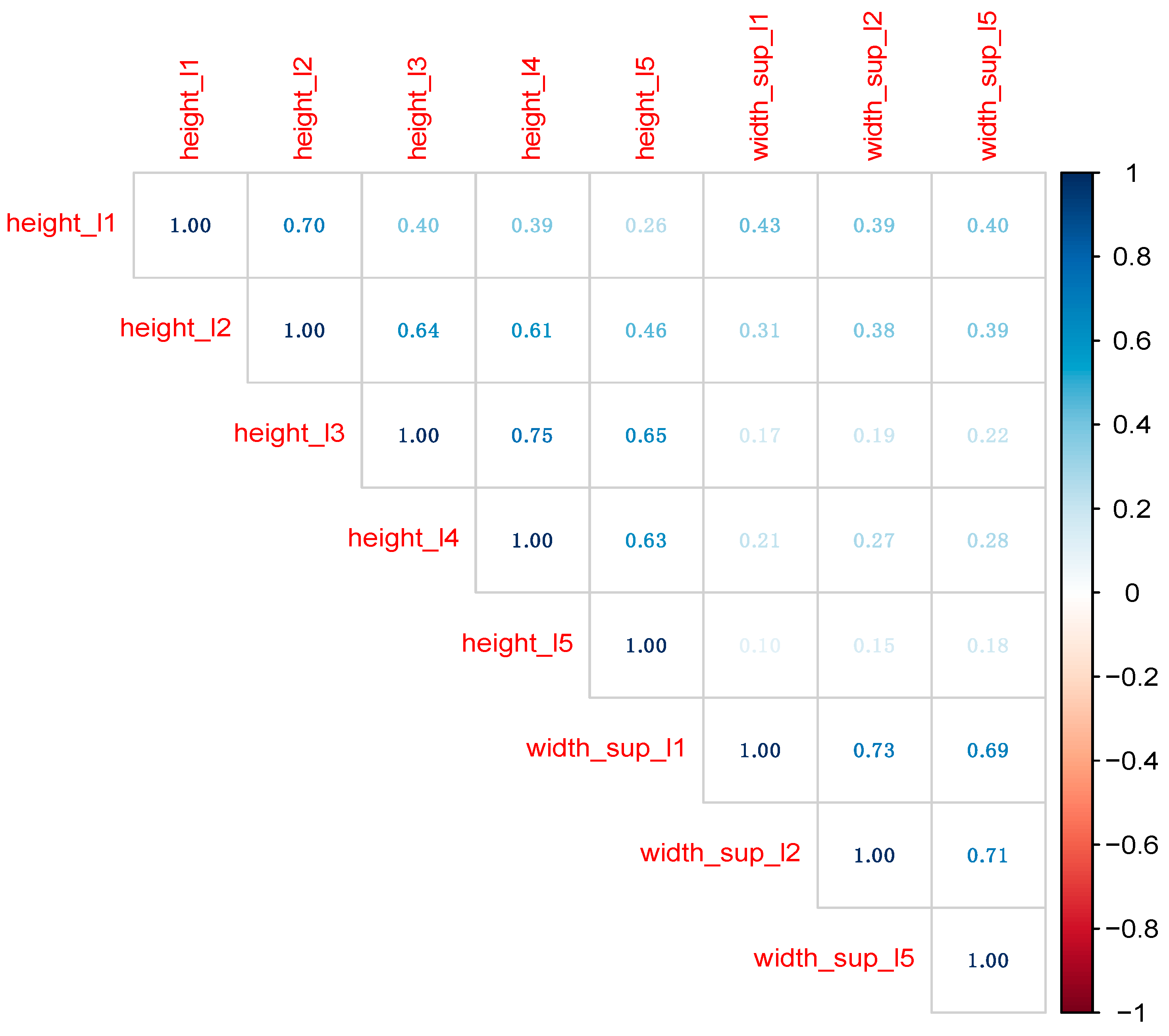
3.1. Data Distribution Correlation among Predictors
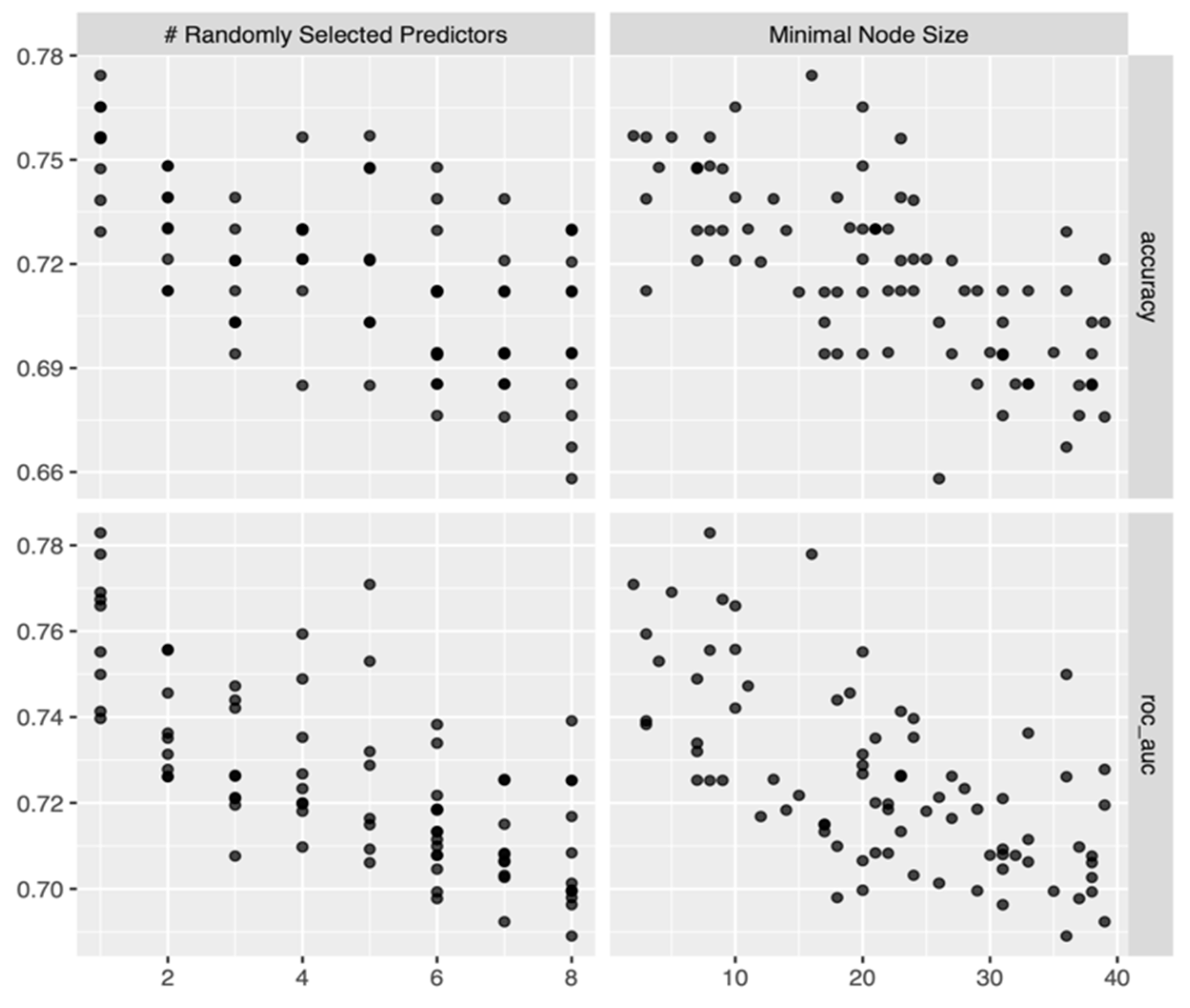
3.2. Model Building and Refinement
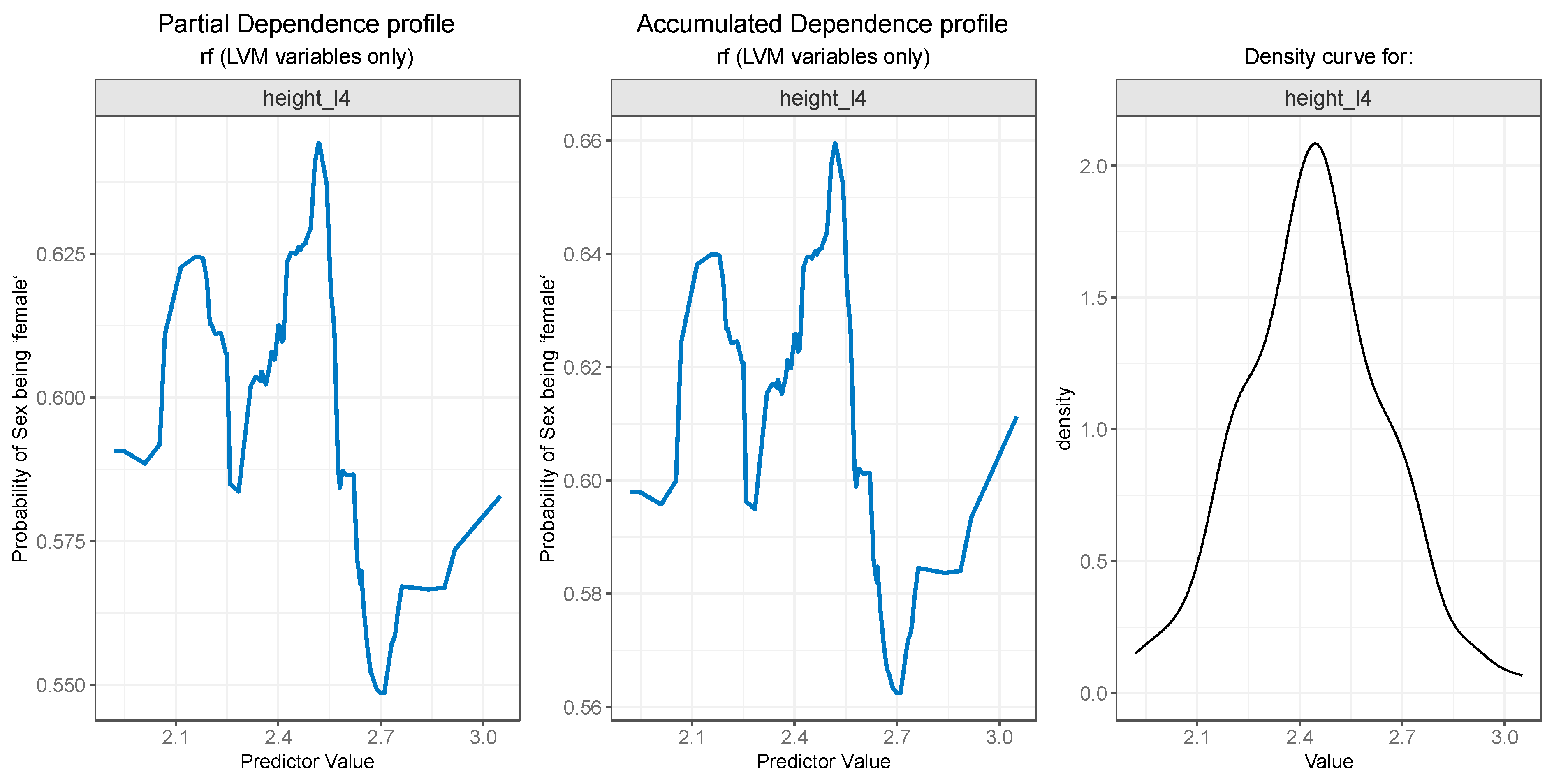
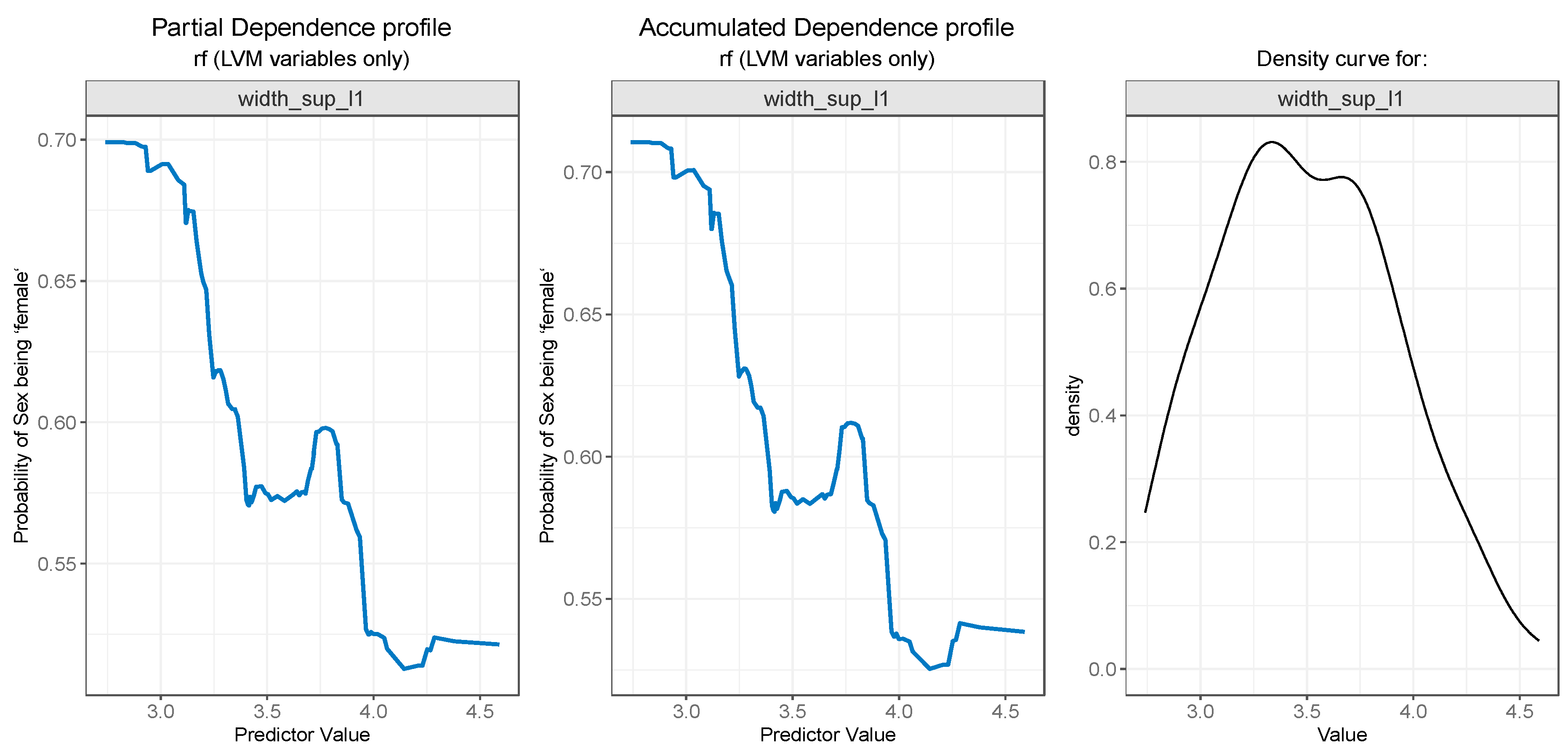
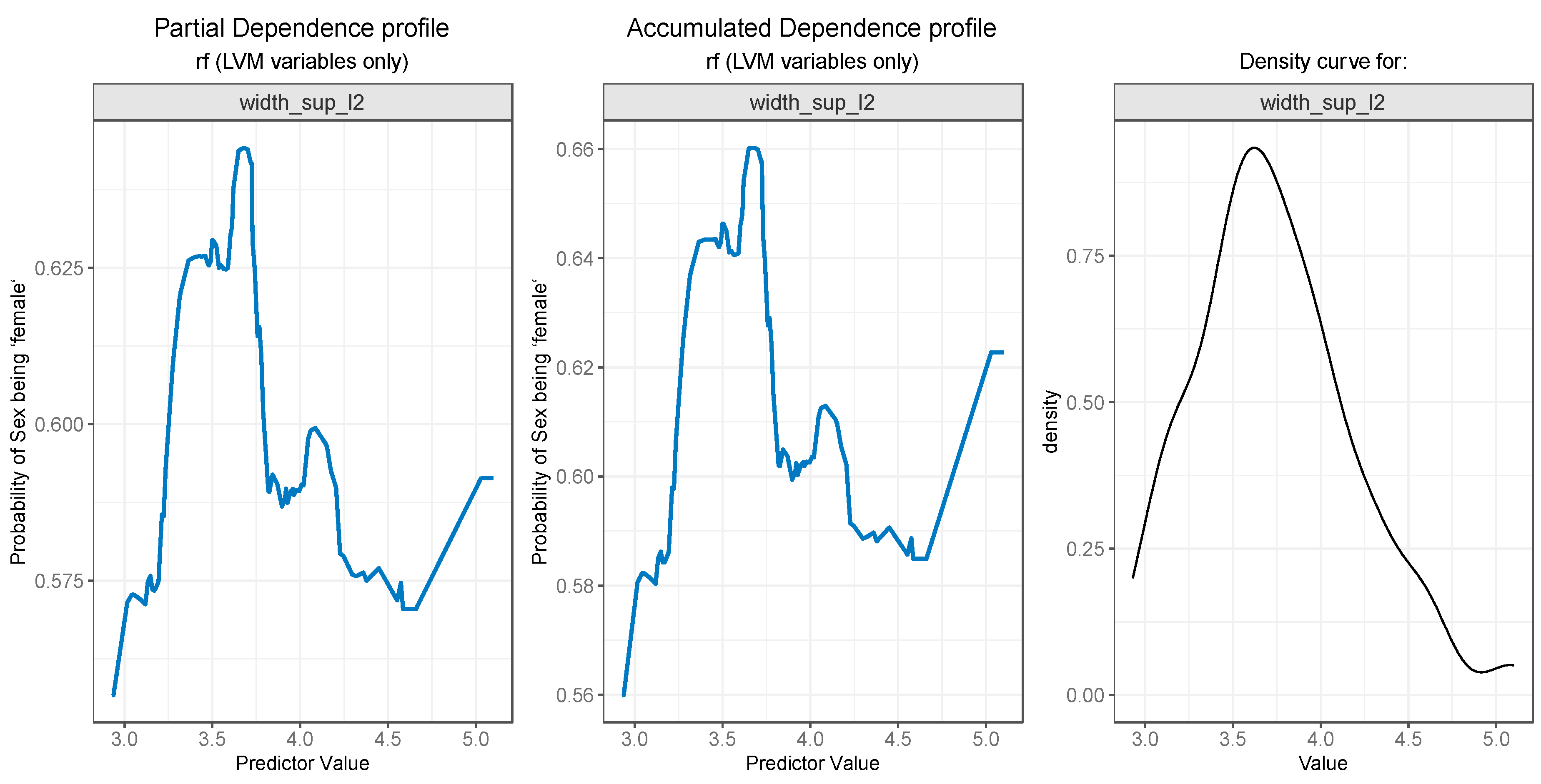
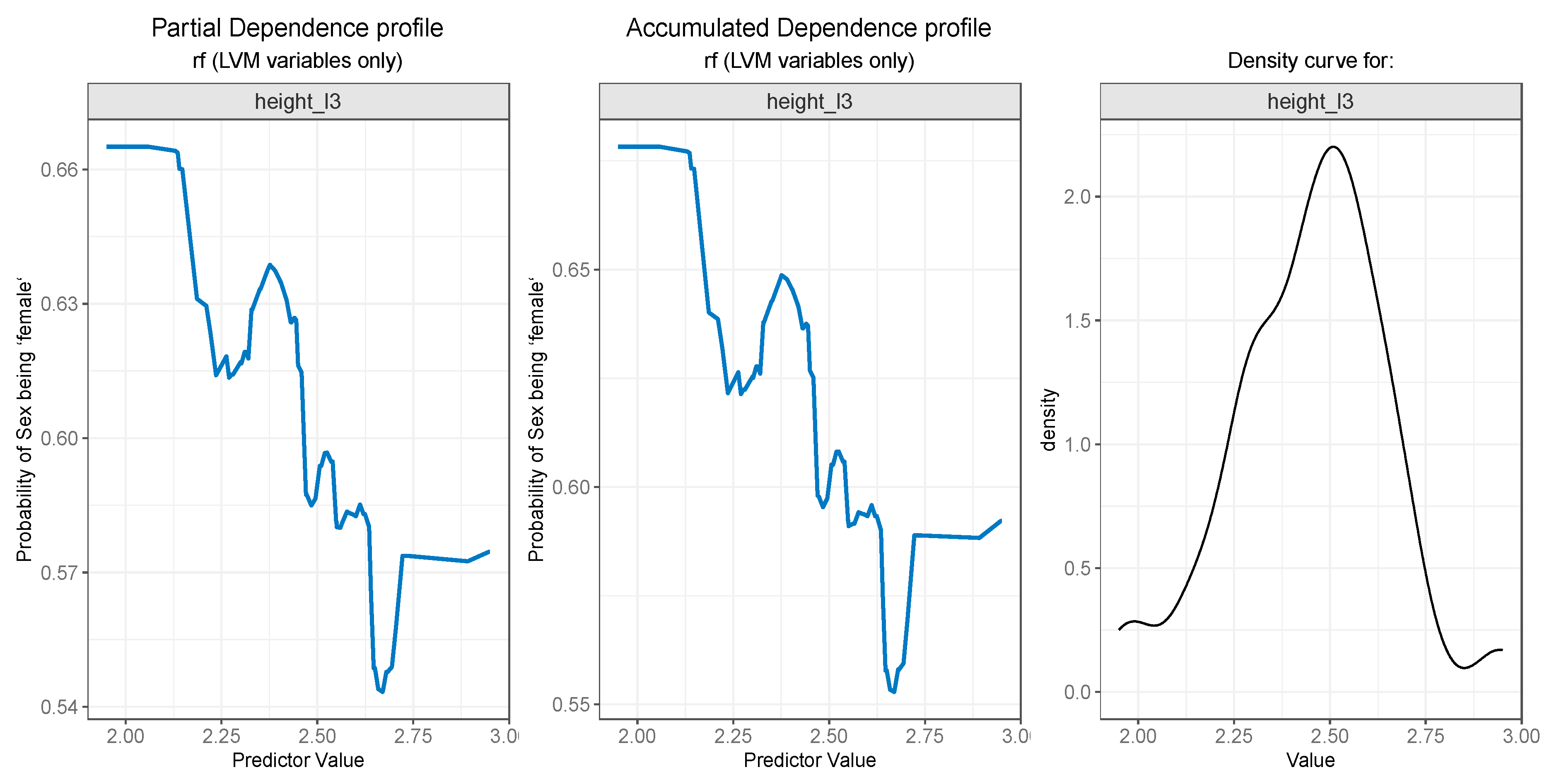
3.3. Model Interpretation
4. Discussion
Limits of the Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cattaneo, C. Forensic anthropology: Developments of a classical discipline in the new millennium. Forensic Sci. Int. 2007, 165, 185–193. [Google Scholar] [CrossRef]
- Diac, M.M.; Iov, T.; Damian, S.I.; Knieling, A.; Girlesccu, N.; Lucasievici, C.; David, S.; Kranioti, E.F.; Iliescu, D.B. Estimation of stature from tibia length for Romanian adult population. Appl. Sci. 2021, 11, 11962. [Google Scholar] [CrossRef]
- Diac, M.M.; Hunea, I.; Girlescu, N.; Knieling, A.; Damian, S.I.; Iliescu, D.B. Morphometry of the foramen magnum for sex estimation in Romanian adult population. Brain 2020, 11, 231–243. [Google Scholar] [CrossRef]
- Blau, S.; Robertson, S.; Johnstone, M. Disaster victim identification: New applications for post-mortem computed tomography. J. Forensic Sci. 2008, 53, 956–961. [Google Scholar] [CrossRef] [PubMed]
- Toy, S.; Secgin, Y.; Oner, Z.; Turan, M.K.; Oner, S.; Senol, D. A study on sex estimation by using machine learning algorithms with parameters obtained from computerized tomography images of the cranium. Sci. Rep. 2022, 12, 4278. [Google Scholar] [CrossRef] [PubMed]
- Grant, J.P.; Oxland, T.R.; Dvorak, M.F. Mapping the structural properties of the lumbosacral vertebral endplates. Spine 2001, 26, 889–896. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.G.; Sun, Y.; Boonen, S.; Nicholson, P.H.; Brys, P.; Dequeker, J.; Felsenberg, D. Measurements of vertebral shape by radiographic morphometry: Sex differences and relationships with vertebral level and lumbar lordosis. Skelet. Radiol. 1998, 27, 380–384. [Google Scholar] [CrossRef] [PubMed]
- Decker, S.J.; Foley, R.; Hazelton, J.M.; Ford, J.M. 3D analysis of computed tomography (CT)–derived lumbar spine models for the estimation of sex. Int. J. Leg. Med. 2019, 133, 1497–1506. [Google Scholar] [CrossRef]
- Garoufi, N.; Bertsatos, A.; Chovalopoulou, M.E.; Villa, C. Forensic sex estimation using the vertebrae: An evaluation on two European populations. Int. J. Leg. Med. 2020, 134, 2307–2318. [Google Scholar] [CrossRef]
- Sevinc, O.; Barut, C.; Is, M.; Eryoruk, N.; Safak, A.A. Influence of age and sex on lumbar vertebral morphometry determined using sagittal magnestic resonance imaging. Ann. Anat. 2008, 190, 277–283. [Google Scholar] [CrossRef]
- Rohmani, A.; Shafie, M.S.; Mohd Nor, F. Sex estimation using the human vertebra: A systemtic review. Egyptian J. Forensic Sci. 2021, 25, 25. [Google Scholar] [CrossRef]
- Davy-Jow, S.L.; Decker, S.J. Virtual anthropology and virtopsy in human identification. In Advances in Forensic Human Identification; Mallet, X., Blythe, T., Berry, R., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 271–289. [Google Scholar]
- Dedouit, F.; Savall, F.; Mokrane, F.Z.; Rousseau, H.; Crubezy, E.; Rouge, D. Virtual anthropology and forensic identification using multidetector CT. British J. Radiol. 2014, 87, 20130468. [Google Scholar] [CrossRef] [PubMed]
- Tukey, J.W. We need both exploratory and confirmatory. Am. Stat. 1980, 34, 23–25. [Google Scholar]
- Behrens, J.T. Principles and procedures of exploratory data analysis. Psychol. Methods 1997, 2, 131. [Google Scholar] [CrossRef]
- Dettling, M.; Bühlmann, P. Boosting for tumor classification with gene expression data. Bioinformatics 2003, 19, 1061–1069. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, C.; Koenig, T.; Jelic, V.; Prichep, L.; John, R.E.; Wahlund, L.O.; Dodge, Y.; Dierks, T. Application and comparison of classification algorithms for recognition of Alzheimer’s disease in electrical brain activity (EEG). J. Neurosci. Methods 2007, 161, 342–350. [Google Scholar] [CrossRef] [PubMed]
- Zaunseder, S.; Huhle, R.; Malberg, H. CinC Challenge—Assessing the Usability of ECG by Ensemble Decision Trees. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; pp. 277–280. [Google Scholar]
- Austin, P.C.; Lee, D.S.; Steyerberg, E.W.; Tu, J.V. Regression trees for predicting mortality in patients with cardiovascular disease: What improvement is achieved by using ensemble-based methods? Biom J. 2012, 54, 657–673. [Google Scholar] [CrossRef]
- Abreu, P.H.; Santos, M.S.; Abreu, M.H.; Andrade, B.; Silva, D.C. Predicting breast cancer recurrence using machine learning techniques: A systematic review. ACM Comput. Surv. 2016, 49, 40. [Google Scholar] [CrossRef]
- Lorenzoni, G.; Sabato, S.S.; Lanera, C.; Bottigliengo, D.; Minto, C.; Ocagli, H. Comparison of machine learning techniques for prediction of hospitalization in heart failure patients. J. Clin. Med. 2019, 8, 1298. [Google Scholar] [CrossRef]
- Mpanya, D.; Celik, T.; Klug, E.; Ntsinjana, H. Predicting mortality and hospitalization in heart failure using machine learning: A systematic literature review. IJC Heart Vasc. 2021, 34, 100773. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall: Wadsworth, NY, USA, 1984. [Google Scholar]
- Loh, W.Y. Fifty years of classification and regression trees. Int. Statist. Rev. 2014, 82, 329–348. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, R.D.; Stevens, J.R. Random forests. Ensemble Machine Learning; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Freund, Y.; Schapire, R. A short introduction to boosting. J. Jpn. Soc. Artif. Intellig. 1999, 14, 771–780. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), ACM, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Statist. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 5. [Google Scholar]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. WIREs Data Mining. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Degenhardt, F.; Seifert, S.; Szymczak, S. Evaluation of variable selection methods for random forests and omics data sets. Brief. Bioinform. 2019, 20, 492–503. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Xgboost: Extreme Gradient Boosting, R Package Version 1.3.2.1. Available online: https://CRAN.R-project.org/package=xgboost (accessed on 10 August 2021).
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why should I trust you? Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lipton, Z.C. The doctor just won’t accept that! arXiv 2017, arXiv:1711.08037. [Google Scholar]
- Du, M.; Liu, N.; Hu, X. Techniques for interpretable machine learning. Commun. ACM 2019, 63, 68–77. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Herrera, F. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G.; et al. Explainable AI (XAI): Core ideas, techniques, and solutions. ACM Comput. Surv. 2023, 55, 1–33. [Google Scholar] [CrossRef]
- Biecek, P.; Burzykowski, T. Explanatory Model Analysis; Chapman and Hall/CRC: New York, NY, USA, 2021. [Google Scholar]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 2nd ed.; Independently Published, LeanPublishing Process, ebook; 2022. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing, Vienna, Austria: R Foundation for Statistical Computing. R version 4.3.0. Available online: https://www.R-project.org (accessed on 30 August 2023).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; D’Agostino McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J. Welcome to the Tidyverse. J. Open-Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Sjoberg, D.D.; Whiting, K.; Curry, M.; Lavery, J.A.; Larmarange, J. Reproducible summary tables with the gtsummary package. R J. 2021, 13, 570–580. [Google Scholar] [CrossRef]
- Kuhn, M.; Wickham, H. Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles. 2022. Available online: https://www.tidymodels.org (accessed on 1 February 2022).
- Kuhn, M.; Silge, J. Tidy Modeling with R; O’Reilly Media: Sebastopol, CA, USA, 2022. [Google Scholar]
- Wright, M.N.; Ziegler, A. Ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Statist. Soft. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Biecek, P. DALEX: Explainers for complex predictive models in R. J. Mach. Learn. Res. 2018, 19, 3245–3249. [Google Scholar]
- Biecek, P.; Baniecki, H. Ingredients: Effects and Importances of Model Ingredients. R package Version 2.3.0. 2023. Available online: https://CRAN.R-project.org/package=ingredients (accessed on 30 October 2023).
- McQueen, R.J.; Holmes, G.; Hunt, L. User satisfaction with machine learning as a data analysis method in agricultural research. New Zealand J. Agric. Res. 1998, 41, 577–584. [Google Scholar] [CrossRef]
- Taylor, J.; Twomey, L. Sexual dimorphism in human vertebral body shape. J. Anat. 1984, 138, 281–286. [Google Scholar]
- Pastor, R.F. Sexual dimorphism in vertebral dimensions at the T12/L1 junction. In Proceedings of the American Academy of Forensic Sciences 57th Annual Scientific Meeting, New Orleans, LA, USA, 21–26 February 2005. [Google Scholar]
- Ostrofsky, K.R.; Churchill, S.E. Sex determination by discriminant function analysis of lumbar vertebrae. J. Forensic Sci. 2015, 60, 21–28. [Google Scholar] [CrossRef]
- Zheng, W.X.; Cheng, F.B.; Cheng, K.L.; Tian, Y.; Lai, Y.; Zhang, W.S. Sex assessment using measurements of the first lumbar vertebra. Forensic Sci. Int. 2012, 219, 285.e1–285.e5. [Google Scholar] [CrossRef]
- Oura, P.; Karppinen, J.; Niinimäki, J.; Junno, J.A. Sex estimation from dimensions of the fourth lumbar vertebra in Northern Finns of 20, 30, and 46 years of age. Forensic Sci. Int. 2018, 290, 350.e1–350.e6. [Google Scholar] [CrossRef] [PubMed]
- MacLaughlin, S.M.; Oldale, K.N.M. Vertebral body diameters and sex prediction. Ann. Hum. Biol. 1992, 19, 285–292. [Google Scholar] [CrossRef] [PubMed]
- Gilsanz, V.; Wren, T.A.L.; Ponrartana, S.; Mora, S.; Rosen, C.J. Sexual dimorphism and the origins of human spinal health. Endocr. Rev. 2018, 39, 221–239. [Google Scholar] [CrossRef] [PubMed]
- Ponrartana, S.; Aggabao, P.C.; Dharmavaram, N.L.; Fisher, C.L.; Friedlich, P.; Devaskar, S.U. Sexual dimorphism in newborn vertebrae and its potential implications. J. Pediatr. 2015, 167, 416–421. [Google Scholar] [CrossRef] [PubMed]
- Steyn, M.; Iscan, M.Y. Sex determination from the femur and tibia in South African whites. Forensic Sci. Int. 1997, 90, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Mall, G.; Graw, M.; Gehring, K.; Hubig, M. Determination of sex from femora. Forensic Sci. Int. 2000, 113, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Asala, S.A.; Bidmos, M.A.; Dayal, M.R. Discriminant function sexing of fragmentary femur of South African blacks. Forensic Sci. Int. 2004, 145, 25–29. [Google Scholar] [CrossRef]
- Iscan, M.Y.; Yoshino, M.; Kato, S. Sex determination from the tibia: Standards for contemporary Japan. J. Forensic Sci. 1994, 39, 785–792. [Google Scholar] [CrossRef]
- Dayal, M.R.; Bidmos, M.A. Discriminating sex in South African blacks using patella dimensions. J. Forensic Sci. 2005, 50, 1294–1297. [Google Scholar] [CrossRef]
- Introna, F.; DiVella, G.; Campobasso, C.P. Sex determination by discriminant analysis of patella measurements. Forensic Sci. Int. 1998, 95, 39–45. [Google Scholar] [CrossRef]
- Frutos, L.R. Metric determination of sex from the humerus in a Guatemalan forensic sample. Forensic Sci. Int. 2005, 147, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Kranioti, E.F.; Michalodimitrakis, M. Sexual dimorphism of the humerus in contemporary Cretans—A population-specific study and a review of the literature. J. Forensic Sci. 2009, 54, 996–1000. [Google Scholar] [CrossRef] [PubMed]
- Barrier, I.L.; L’Abbe, E.N. Sex determination from the radius and ulna in a modern South African sample. Forensic Sci. Int. 2008, 179, 85.e1–85.e7. [Google Scholar] [CrossRef] [PubMed]
- Mastrangelo, P.; Luca, S.D.; Sánchez-Mejorada, G. Sex assessment from carpals bones: Discriminant function analysis in a contemporary Mexican sample. Forensic Sci. Int. 2011, 209, 196.e1–196.e15. [Google Scholar] [CrossRef]
- Barrio, P.A.; Trancho, G.J.; Sánchez, J.A. Metacarpal sexual determination in a Spanish Population. J. Forensic Sci. 2006, 51, 990–995. [Google Scholar] [CrossRef]
- Bidmos, M.A.; Asala, S.A. Sexual dimorphism of the calcaneus of South African blacks. J. Forensic Sci. 2004, 49, 446–450. [Google Scholar] [CrossRef]





| Measurement | Abbreviation | Vertebrae | Definition |
|---|---|---|---|
| Width of superior endplate | Width_sup_lx | L1–L5 | Distance between the most lateral edges of the superior plate of the vertebrae |
| Width of inferior endplate | Width_inf_lx | L1–L5 | Distance between the most lateral edges of the inferior plate of the vertebrae |
| Posterior height of the vertebral body | Heigth_lx | L1–L5 | Posterior height of the vertebral body from the left bisecting plane at the posterior part of the vertebral body at the point which can get the largest height |
| Variable | Min | Q1 | Median | Q3 | Max | Mean | SD |
|---|---|---|---|---|---|---|---|
| age | 17 | 38 | 46 | 60 | 86 | 48 | 15 |
| height_l1 | 1.62 | 2.26 | 2.36 | 2.47 | 2.79 | 2.36 | 0.17 |
| width_sup_l1 | 2.74 | 3.22 | 3.47 | 3.78 | 4.59 | 3.52 | 0.43 |
| width_inf_l1 | 2.90 | 3.41 | 3.70 | 3.98 | 4.74 | 3.69 | 0.40 |
| height_l2 | 1.90 | 2.30 | 2.41 | 2.55 | 2.83 | 2.42 | 0.18 |
| width_sup_l2 | 2.93 | 3.49 | 3.77 | 4.05 | 5.10 | 3.80 | 0.44 |
| width_inf_l2 | 2.93 | 3.67 | 3.86 | 4.18 | 5.14 | 3.91 | 0.40 |
| height_l3 | 1.95 | 2.32 | 2.47 | 2.56 | 2.95 | 2.45 | 0.19 |
| width_sup_l3 | 3.13 | 3.73 | 4.02 | 4.32 | 5.18 | 4.03 | 0.43 |
| width_inf_l3 | 3.12 | 3.79 | 4.05 | 4.34 | 5.55 | 4.08 | 0.45 |
| height_l4 | 1.92 | 2.32 | 2.44 | 2.57 | 3.05 | 2.44 | 0.20 |
| width_sup_l4 | 3.12 | 3.82 | 4.19 | 4.48 | 5.35 | 4.17 | 0.48 |
| width_inf_l4 | 3.01 | 3.86 | 4.12 | 4.49 | 5.10 | 4.14 | 0.44 |
| height_l5 | 1.72 | 2.31 | 2.44 | 2.56 | 3.00 | 2.44 | 0.22 |
| width_sup_l5 | 3.01 | 3.96 | 4.27 | 4.59 | 5.39 | 4.28 | 0.47 |
| width_inf_l5 | 2.93 | 3.80 | 4.05 | 4.41 | 5.08 | 4.09 | 0.42 |
| Algorithm | Metric | Estimate |
|---|---|---|
| rf | accuracy | 0.78947 |
| xgb | accuracy | 0.81579 |
| rf | roc_auc | 0.96308 |
| xgb | roc_auc | 0.86770 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diac, M.M.; Toma, G.M.; Damian, S.I.; Fotache, M.; Romanov, N.; Tabian, D.; Sechel, G.; Scripcaru, A.; Hancianu, M.; Iliescu, D.B. Machine Learning Models for Prediction of Sex Based on Lumbar Vertebral Morphometry. Diagnostics 2023, 13, 3630. https://doi.org/10.3390/diagnostics13243630
Diac MM, Toma GM, Damian SI, Fotache M, Romanov N, Tabian D, Sechel G, Scripcaru A, Hancianu M, Iliescu DB. Machine Learning Models for Prediction of Sex Based on Lumbar Vertebral Morphometry. Diagnostics. 2023; 13(24):3630. https://doi.org/10.3390/diagnostics13243630
Chicago/Turabian StyleDiac, Madalina Maria, Gina Madalina Toma, Simona Irina Damian, Marin Fotache, Nicolae Romanov, Daniel Tabian, Gabriela Sechel, Andrei Scripcaru, Monica Hancianu, and Diana Bulgaru Iliescu. 2023. "Machine Learning Models for Prediction of Sex Based on Lumbar Vertebral Morphometry" Diagnostics 13, no. 24: 3630. https://doi.org/10.3390/diagnostics13243630
APA StyleDiac, M. M., Toma, G. M., Damian, S. I., Fotache, M., Romanov, N., Tabian, D., Sechel, G., Scripcaru, A., Hancianu, M., & Iliescu, D. B. (2023). Machine Learning Models for Prediction of Sex Based on Lumbar Vertebral Morphometry. Diagnostics, 13(24), 3630. https://doi.org/10.3390/diagnostics13243630







