Detection of Atrial Fibrillation Episodes based on 3D Algebraic Relationships between Cardiac Intervals
Abstract
:1. Introduction
1.1. Existing Diagnostics Techniques for Atrial Fibrillation
1.2. Perfect Matrices of Lagrange Differences as a Method for ECG Signal Analysis
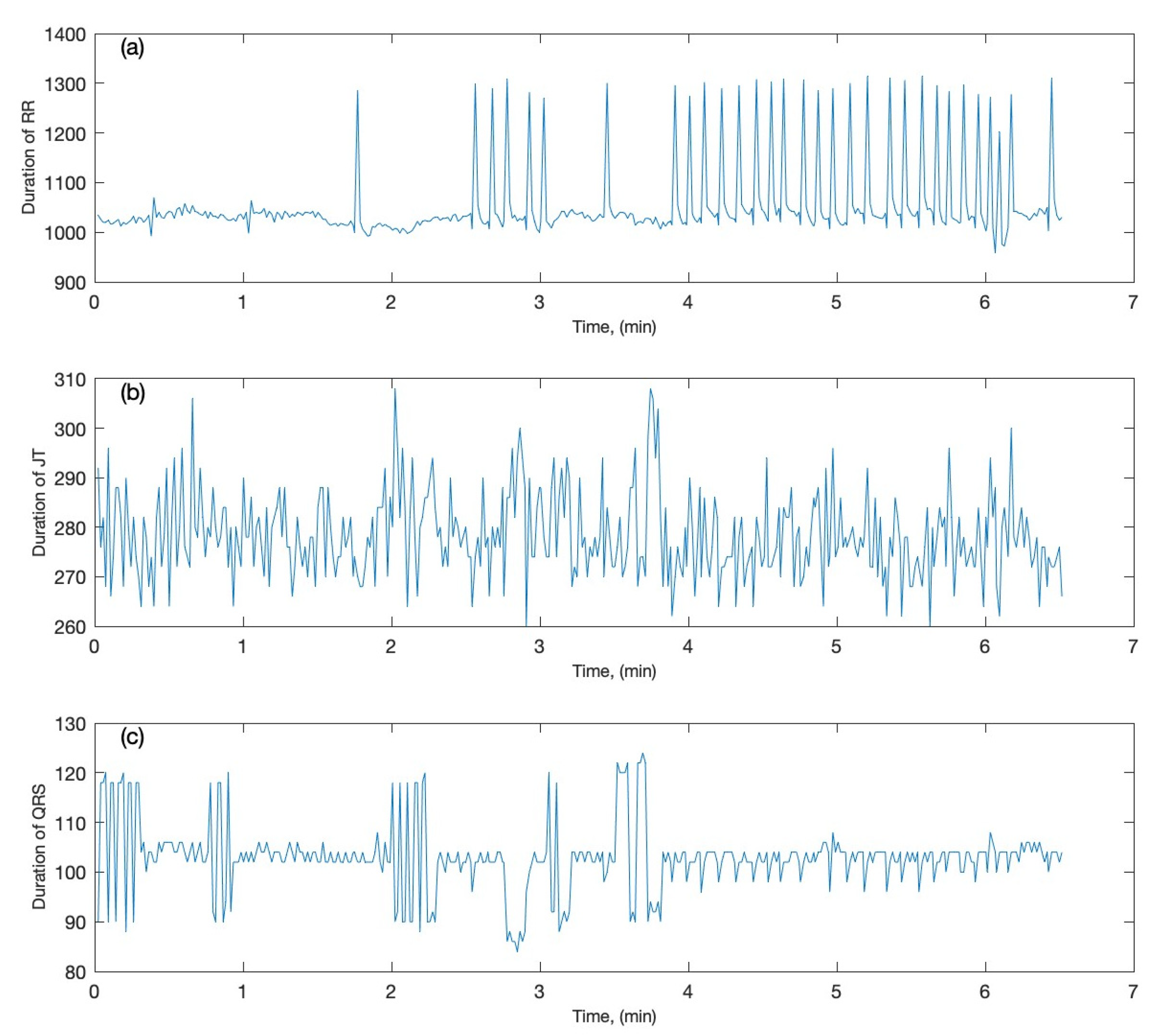
2. Methods
2.1. The Description of the Experimental Setup
2.2. Participants
2.3. Ethics Statement
2.4. The Description of the Proposed Algorithm
2.4.1. Preliminary Synopsis
2.4.2. The Architecture of Third-Order Square Matrices of Lagrange Differences
- All elements of the matrix must be different.
- Zeroth-order differences are located on the main diagonal.
- First-order differences are located on the secondary diagonal.
- The matrix is balanced with respect to time (the sum of all time lags is equal to zero).
- The matrix is balanced with respect to lexicographic variables (the number of different symbols must be the same).
2.4.3. The Sensitivity of the Proposed Algorithm
2.4.4. Trials Computed upon the Dataset with Different Combination Patterns
2.4.5. The Development of the Decision Support System
3. Results and Discussion
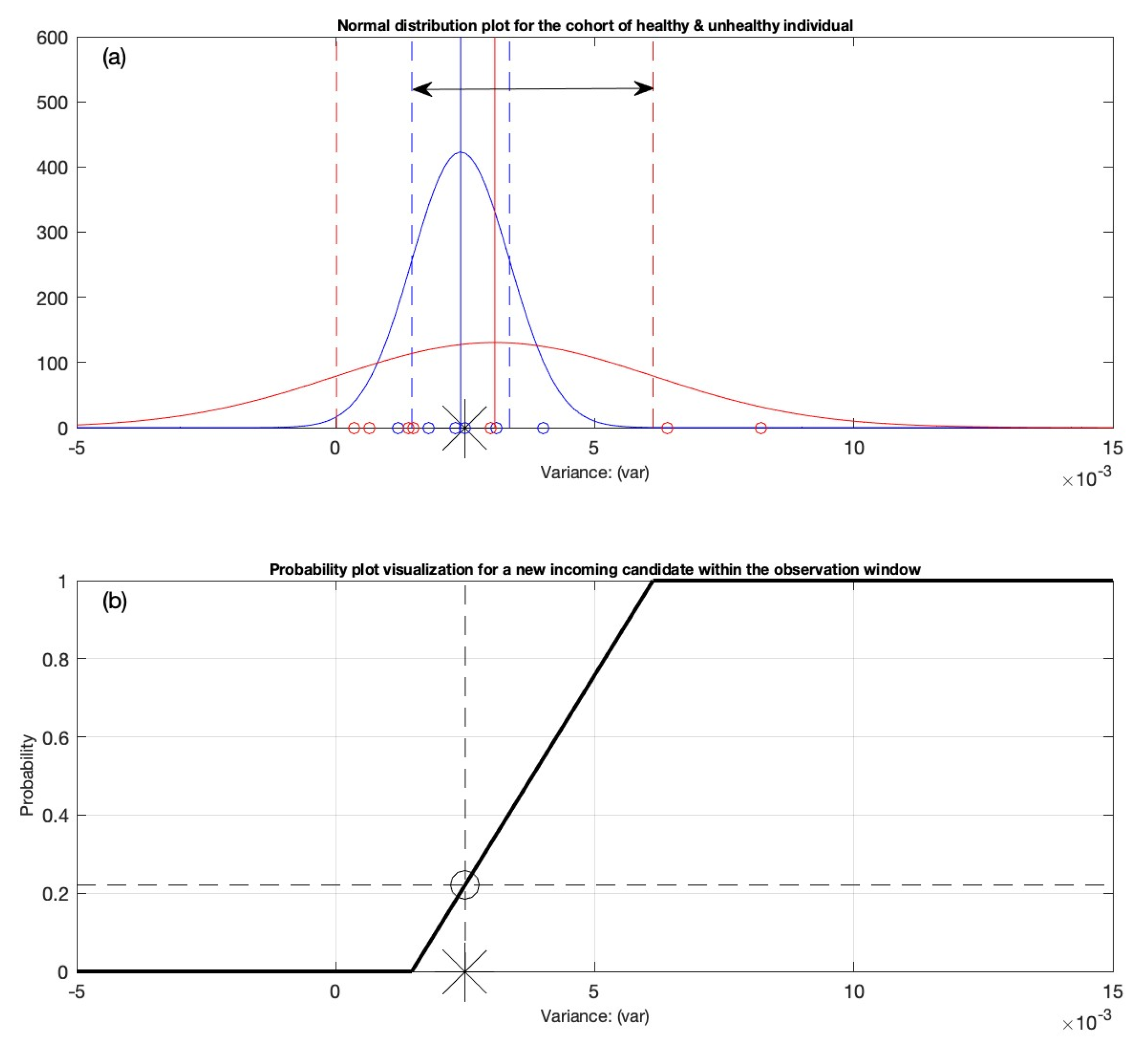
3.1. Performing the Statistical Analysis
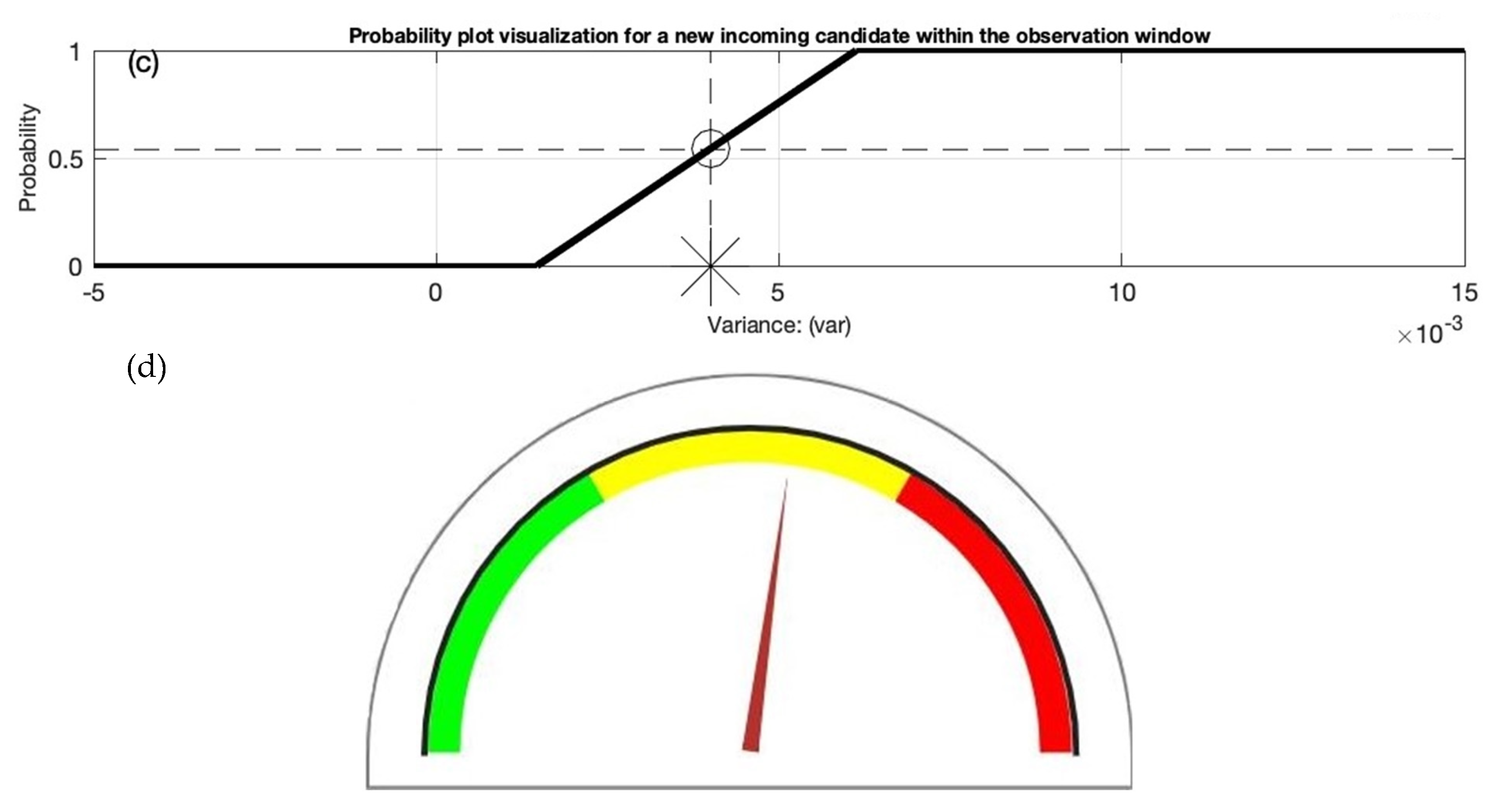
3.2. Generation of the Variation Interval
3.2.1. Condition 1
3.2.2. Condition 2
3.2.3. Condition 3
3.3. First Test Candidate
3.4. Second Test Candidate
4. Limitations
5. Conclusions
6. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cunha, S.; Antunes, E.; Antoniou, S.; Tiago, S.; Relvas, R.; Fernandez-Llimós, F.; da Costa, F.A. Raising awareness and early detection of atrial fibrillation, an experience resorting to mobile technology centred on informed individuals. Res. Soc. Adm. Pharm. 2020, 16, 787–792. [Google Scholar] [CrossRef] [PubMed]
- Odutayo, A.; Wong, C.X.; Hsiao, A.J.; Hopewell, S.; Altman, D.G.; Emdin, C.A. Atrial fibrillation and risks of cardiovascular disease, renal disease, and death: Systematic review and meta-analysis. BMJ 2016, 354, i4482. [Google Scholar] [CrossRef] [Green Version]
- Rho, R.W.; Page, R.L. Asymptomatic atrial fibrillation. Prog. Cardiovasc. Dis. 2005, 48, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Savelieva, I.; Camm, A.J. Clinical relevance of silent atrial fibrillation: Prevalence, prognosis, quality of life, and management. J. Interv. Card. Electrophysiol. 2000, 4, 369–382. [Google Scholar] [CrossRef] [PubMed]
- Camm, A.J.; Corbucci, G.; Padeletti, L. Usefulness of continuous electrocardiographic monitoring for atrial fibrillation. Am. J. Cardiol. 2012, 110, 270–276. [Google Scholar] [CrossRef]
- Developed with the Special Contribution of the European Heart Rhythm Association (EHRA); Camm, A.J.; Kirchhof, P.; Lip, G.Y.; Schotten, U.; Savelieva, I.; Ernst, S.; Van Gelder, I.C.; Al-Attar, N.; Hindricks, G.; et al. Guidelines for the management of atrial fibrillation: The Task Force for the Management of Atrial Fibrillation of the European Society of Cardiology (ESC). Eur. Heart J. 2010, 31, 2369–2429. [Google Scholar]
- Members, W.G.; Wann, L.S.; Curtis, A.B.; January, C.T.; Ellenbogen, K.A.; Lowe, J.E.; Estes, N.M., III; Page, R.L.; Ezekowitz, M.D.; Slotwiner, D.J. 2011 ACCF/AHA/HRS focused update on the management of patients with atrial fibrillation (updating the 2006 guideline) a report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines. Circulation 2011, 123, 104–123. [Google Scholar] [CrossRef]
- Guidera, S.A.; Steinberg, J.S. The signal-averaged P wave duration: A rapid and noninvasive marker of risk of atrial fibrillation. J. Am. Coll. Cardiol. 1993, 21, 1645–1651. [Google Scholar] [CrossRef] [Green Version]
- Mehta, S.; Lingayat, N.; Sanghvi, S. Detection and delineation of P and T waves in 12-lead electrocardiograms. Expert Syst. 2009, 26, 125–143. [Google Scholar] [CrossRef]
- Qammar, N.W.; Orinaitė, U.; Šiaučiūnaitė, V.; Vainoras, A.; Šakalytė, G.; Ragulskis, M. The Complexity of the Arterial Blood Pressure Regulation during the Stress Test. Diagnostics 2022, 12, 1256. [Google Scholar] [CrossRef]
- Ziaukas, P.; Alabdulgader, A.; Vainoras, A.; Navickas, Z.; Ragulskis, M. New approach for visualization of relationships between RR and JT intervals. PLoS ONE 2017, 12, e0174279. [Google Scholar] [CrossRef] [PubMed]
- Houssein, E.H.; Kilany, M.; Hassanien, A.E. ECG signals classification: A review. Int. J. Intell. Eng. Inform. 2017, 5, 376–396. [Google Scholar] [CrossRef]
- Malik, M.; Färbom, P.; Batchvarov, V.; Hnatkova, K.; Camm, A. Relation between QT and RR intervals is highly individual among healthy subjects: Implications for heart rate correction of the QT interval. Heart 2002, 87, 220–228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lyon, A.; Mincholé, A.; Martínez, J.P.; Laguna, P.; Rodriguez, B. Computational techniques for ECG analysis and interpretation in light of their contribution to medical advances. J. R. Soc. Interface 2018, 15, 20170821. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, Z.; Loni, M.; Daneshtalab, M.; Gharehbaghi, A. A review on deep learning methods for ECG arrhythmia classification. Expert Syst. Appl. X 2020, 7, 100033. [Google Scholar] [CrossRef]
- Gupta, V.; Mittal, M.; Mittal, V.; Saxena, N.K. A critical review of feature extraction techniques for ECG signal analysis. J. Inst. Eng. Ser. B 2021, 102, 1049–1060. [Google Scholar] [CrossRef]
- Noujaim, S.F.; Lucca, E.; Muñoz, V.; Persaud, D.; Berenfeld, O.; Meijler, F.L.; Jalife, J. From mouse to whale: A universal scaling relation for the PR Interval of the electrocardiogram of mammals. Circulation 2004, 110, 2802–2808. [Google Scholar] [CrossRef] [Green Version]
- Bonomini, M.P.; Arini, P.D.; Gonzalez, G.E.; Buchholz, B.; Valentinuzzi, M.E. The allometric model in chronic myocardial infarction. Theor. Biol. Med. Model. 2012, 9, 15. [Google Scholar] [CrossRef] [Green Version]
- Captur, G.; Karperien, A.L.; Hughes, A.D.; Francis, D.P.; Moon, J.C. The fractal heart—Embracing mathematics in the cardiology clinic. Nat. Rev. Cardiol. 2017, 14, 56–64. [Google Scholar] [CrossRef]
- Jafari, A. Sleep apnoea detection from ECG using features extracted from reconstructed phase space and frequency domain. Biomed. Signal Process. Control. 2013, 8, 551–558. [Google Scholar] [CrossRef]
- Casaleggio, A.; Braiotta, S.; Corana, A. Study of the Lyapunov exponents of ECG signals from MIT-BIH database. In Proceedings of the Computers in Cardiology 1995, Vienna, Austria, 10–13 September 1995; pp. 697–700. [Google Scholar]
- Übeyli, E.D. Detecting variabilities of ECG signals by Lyapunov exponents. Neural Comput. Appl. 2009, 18, 653–662. [Google Scholar] [CrossRef]
- Casaleggio, A.; Corana, A.; Ridella, S. Correlation dimension estimation from electrocardiograms. Chaos Solitons Fractals 1995, 5, 713–726. [Google Scholar] [CrossRef]
- Acharya, R.; Lim, C.; Joseph, P. Heart rate variability analysis using correlation dimension and detrended fluctuation analysis. Itbm-Rbm 2002, 23, 333–339. [Google Scholar] [CrossRef]
- Fojt, O.; Holcik, J. Applying nonlinear dynamics to ECG signal processing. IEEE Eng. Med. Biol. Mag. 1998, 17, 96–101. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-M.; Kim, D.-J.; Kim, I.-Y.; Park, K.-S.; Kim, S.I. Detrended fluctuation analysis of EEG in sleep apnea using MIT/BIH polysomnography data. Comput. Biol. Med. 2002, 32, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Houshyarifar, V.; Amirani, M.C. Early detection of sudden cardiac death using Poincaré plots and recurrence plot-based features from HRV signals. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 1541–1553. [Google Scholar] [CrossRef]
- Saunoriene, L.; Siauciunaite, V.; Vainoras, A.; Bertasiute, V.; Navickas, Z.; Ragulskis, M. The characterization of the transit through the anaerobic threshold based on relationships between RR and QRS cardiac intervals. PLoS ONE 2019, 14, e0216938. [Google Scholar] [CrossRef]
- Duan, J.; Wang, Q.; Zhang, B.; Liu, C.; Li, C.; Wang, L. Accurate detection of atrial fibrillation events with RR intervals from ECG signals. PLoS ONE 2022, 17, e0271596. [Google Scholar] [CrossRef]
- de Godoy, M.F. Nonlinear analysis of heart rate variability: A comprehensive review. J. Cardiol. Ther. 2016, 3, 528–533. [Google Scholar] [CrossRef]
- Skinner, J.E.; Anchin, J.M.; Weiss, D.N. Nonlinear analysis of the heartbeats in public patient ECGs using an automated PD2i algorithm for risk stratification of arrhythmic death. Ther. Clin. Risk Manag. 2008, 4, 549. [Google Scholar] [CrossRef]
- Vainoras, A. Kardiovaskulinė sistema ir sportinė veikla. Kardiovaskulinė Sist. Sport. Veikla. Vilnius 1996, 3, 8. [Google Scholar]

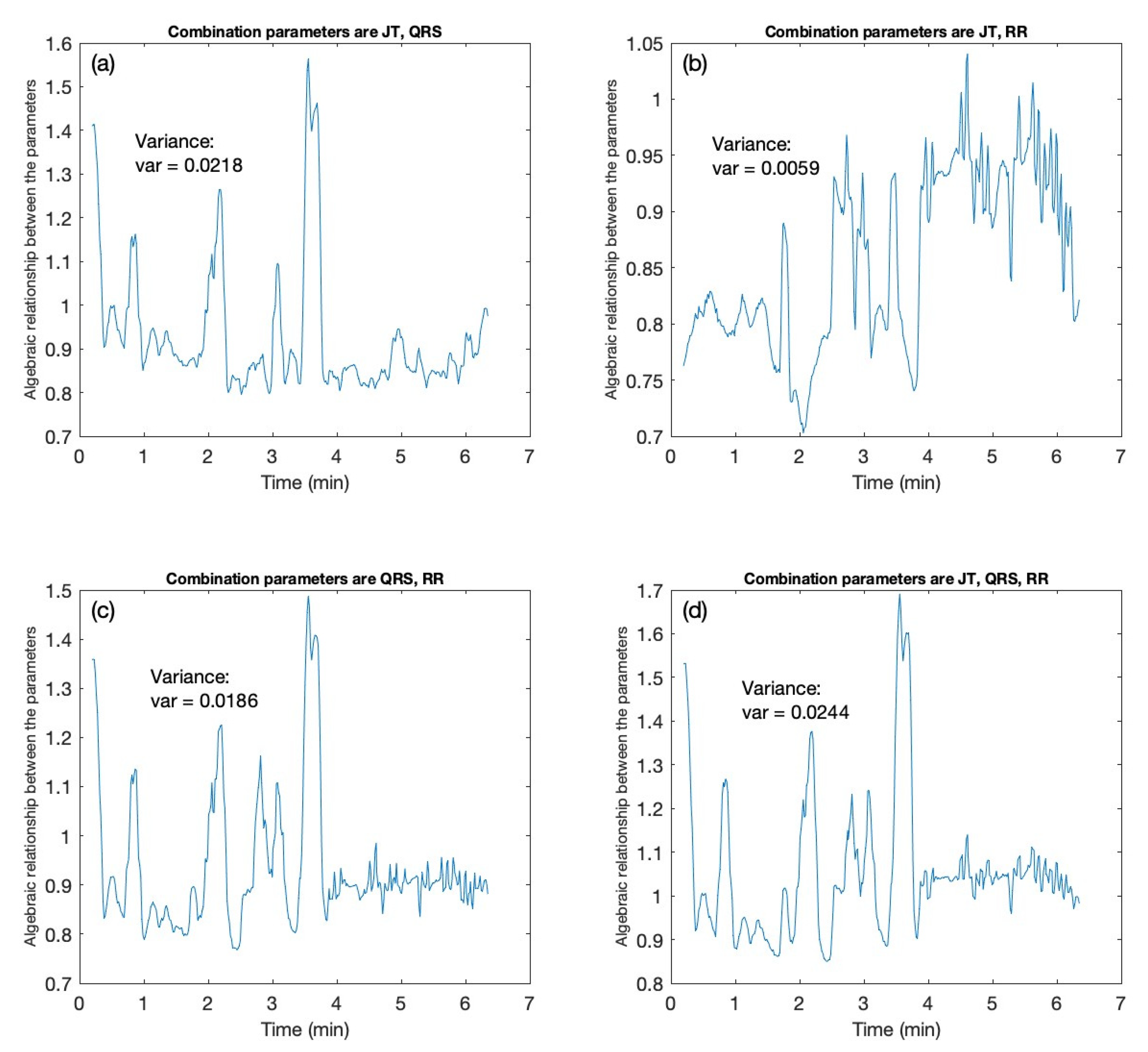



| Candidate | Variance Values | |||
|---|---|---|---|---|
| Combination of JT–QRS Interval | Combination of JT–RR Interval | Combination of QRS–RR Interval | Combination of JT–QRS–RR Interval | |
| 0.0218 | 0.0059 | 0.0186 | 0.0244 | |
| Healthy Candidates (H) | Unhealthy Candidates (UH) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00080583 | 0.736 | 0.734 | 0.028 | 0.763 | 0.707 | 0.359 | 0.0003 | 1.168 | 1.164 | 0.018 | 1.182 | 0.004 | 0.769 |
| 0.0016751 | 0.827 | 0.821 | 0.041 | 0.863 | 0.781 | 1.100 | 0.0002 | 1.281 | 1.279 | 0.015 | 1.294 | 1.264 | 0.875 |
| 0.0015197 | 0.917 | 0.916 | 0.039 | 0.956 | 0.878 | −0.376 | 0.0061 | 1.018 | 1.012 | 0.078 | 1.091 | 0.935 | 2.062 |
| 0.00073806 | 1.031 | 1.031 | 0.027 | 1.059 | 1.004 | 0.254 | 0.0006 | 0.932 | 0.936 | 0.025 | 0.962 | 0.912 | −1.217 |
| 0.0015323 | 1.024 | 1.027 | 0.039 | 1.067 | 0.989 | −1.307 | 0.0141 | 1.422 | 1.409 | 0.119 | 1.528 | 1.291 | 1.461 |
| 0.0010183 | 0.875 | 0.875 | 0.032 | 0.907 | 0.843 | 0.148 | 0.0027 | 0.822 | 0.811 | 0.052 | 0.864 | 0.760 | 2.422 |
| 0.010428 | 1.317 | 1.307 | 0.102 | 1.41 | 1.206 | 1.508 | 0.0015 | 1.011 | 1.006 | 0.039 | 1.045 | 0.967 | 1.466 |
| 0.0060534 | 0.899 | 0.881 | 0.078 | 0.959 | 0.804 | 4.437 | |||||||
| Healthy Candidates (H) | Unhealthy Candidates (UH) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.000792 | 0.736 | 0.736 | 0.028 | 0.764 | 0.708 | 0.242 | 0.0003 | 1.168 | 1.164 | 0.018 | 1.182 | 1.146 | 0.775 |
| 0.001677 | 0.827 | 0.821 | 0.041 | 0.862 | 0.780 | 1.147 | 0.0002 | 1.282 | 1.279 | 0.015 | 1.294 | 1.264 | 0.896 |
| 0.001713 | 0.921 | 0.922 | 0.041 | 0.963 | 0.880 | −0.494 | 0.0061 | 1.016 | 1.011 | 0.078 | 1.089 | 0.932 | 2.051 |
| 0.000767 | 1.033 | 1.033 | 0.026 | 1.061 | 1.005 | 0.310 | 0.0006 | 0.933 | 0.937 | 0.025 | 0.962 | 0.911 | −1.264 |
| 0.001689 | 1.031 | 1.034 | 0.041 | 1.075 | 0.999 | −1.086 | 0.0141 | 1.424 | 1.411 | 0.119 | 1.529 | 1.292 | 1.477 |
| 0.001000 | 0.881 | 0.879 | 0.032 | 0.911 | 0.848 | 0.231 | 0.0027 | 0.823 | 0.812 | 0.052 | 0.864 | 0.759 | 2.434 |
| 0.01042 | 1.319 | 1.310 | 0.102 | 1.412 | 1.208 | 1.525 | 0.0015 | 1.012 | 1.006 | 0.039 | 1.046 | 0.967 | 1.478 |
| 0.006422 | 0.906 | 0.891 | 0.080 | 0.976 | 0.810 | 4.392 | |||||||
| Healthy Candidates (H) | Unhealthy Candidates (UH) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0013 | 0.698 | 0.694 | 0.037 | 0.731 | 0.658 | 1.565 | 0.0006 | 1.397 | 1.393 | 0.025 | 1.418 | 1.367 | 0.9204 |
| 0.0030 | 0.882 | 0.880 | 0.055 | 0.934 | 0.825 | 0.527 | 0.0004 | 1.539 | 1.535 | 0.019 | 1.554 | 1.516 | 1.1994 |
| 0.0025 | 1.039 | 1.032 | 0.050 | 1.082 | 0.982 | 1.427 | 0.0090 | 1.051 | 1.043 | 0.095 | 1.138 | 0.948 | 2.2968 |
| 0.0014 | 1.165 | 1.168 | 0.037 | 1.206 | 1.131 | −0.806 | 0.0014 | 1.070 | 1.077 | 0.037 | 1.114 | 1.040 | −2.2801 |
| 0.0043 | 1.169 | 1.184 | 0.066 | 1.250 | 1.119 | −5.280 | 0.0067 | 1.293 | 1.283 | 0.082 | 1.365 | 1.201 | 1.1756 |
| 0.0029 | 0.905 | 0.909 | 0.054 | 0.963 | 0.856 | −0.469 | 0.0031 | 0.900 | 0.900 | 0.056 | 0.956 | 0.845 | 0.6442 |
| 0.0031 | 1.441 | 1.446 | 0.055 | 1.502 | 1.391 | −1.105 | 0.0014 | 1.140 | 1.139 | 0.038 | 1.177 | 1.101 | 0.5454 |
| 0.0021 | 1.003 | 0.998 | 0.046 | 1.044 | 0.953 | 1.300 | |||||||
| Healthy Candidates (H) | Unhealthy Candidates (UH) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0012 | 0.692 | 0.689 | 0.035 | 0.724 | 0.654 | 1.370 | 0.0006424 | 1.397 | 1.393 | 0.025 | 1.418 | 1.367 | 0.904 |
| 0.0030 | 0.881 | 0.880 | 0.055 | 0.934 | 0.825 | 0.435 | 0.0003502 | 1.538 | 1.535 | 0.019 | 1.553 | 1.516 | 1.219 |
| 0.0023 | 1.032 | 1.025 | 0.048 | 1.073 | 0.978 | 1.565 | 0.0082 | 1.038 | 1.031 | 0.091 | 1.122 | 0.940 | 2.147 |
| 0.0014 | 1.161 | 1.164 | 0.037 | 1.201 | 1.127 | −0.773 | 0.0015 | 1.065 | 1.073 | 0.039 | 1.112 | 1.034 | −2.483 |
| 0.0040 | 1.162 | 1.176 | 0.064 | 1.240 | 1.113 | −5.041 | 0.0064 | 1.285 | 1.274 | 0.080 | 1.354 | 1.194 | 1.532 |
| 0.0025 | 0.894 | 0.895 | 0.050 | 0.945 | 0.845 | 0.042 | 0.0030 | 0.897 | 0.900 | 0.055 | 0.955 | 0.844 | 0.355 |
| 0.0031 | 1.431 | 1.437 | 0.056 | 1.493 | 1.382 | −1.224 | 0.0014 | 1.135 | 1.134 | 0.038 | 1.172 | 1.096 | 0.548 |
| 0.0018 | 0.991 | 0.987 | 0.042 | 1.029 | 0.945 | 1.159 | |||||||
| Condition 1 | Condition 2 | Condition 3 | |
|---|---|---|---|
| If | C | ||
| Then, indicator is |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qammar, N.W.; Šiaučiūnaitė, V.; Zabiela, V.; Vainoras, A.; Ragulskis, M. Detection of Atrial Fibrillation Episodes based on 3D Algebraic Relationships between Cardiac Intervals. Diagnostics 2022, 12, 2919. https://doi.org/10.3390/diagnostics12122919
Qammar NW, Šiaučiūnaitė V, Zabiela V, Vainoras A, Ragulskis M. Detection of Atrial Fibrillation Episodes based on 3D Algebraic Relationships between Cardiac Intervals. Diagnostics. 2022; 12(12):2919. https://doi.org/10.3390/diagnostics12122919
Chicago/Turabian StyleQammar, Naseha Wafa, Vaiva Šiaučiūnaitė, Vytautas Zabiela, Alfonsas Vainoras, and Minvydas Ragulskis. 2022. "Detection of Atrial Fibrillation Episodes based on 3D Algebraic Relationships between Cardiac Intervals" Diagnostics 12, no. 12: 2919. https://doi.org/10.3390/diagnostics12122919
APA StyleQammar, N. W., Šiaučiūnaitė, V., Zabiela, V., Vainoras, A., & Ragulskis, M. (2022). Detection of Atrial Fibrillation Episodes based on 3D Algebraic Relationships between Cardiac Intervals. Diagnostics, 12(12), 2919. https://doi.org/10.3390/diagnostics12122919








