Radiomics-Based Detection of COVID-19 from Chest X-ray Using Interpretable Soft Label-Driven TSK Fuzzy Classifier
Abstract
:1. Introduction
- (1)
- When classic TSK fuzzy systems are applied to classification tasks, margins between different classes are expected to be as large as possible after they are transformed into their label space. However, this assumption is too rigid to learn a discriminative transformation matrix. Additionally, excessive label fitting may cause overfitting. To address these issues, label softening and the compactness class graph are embedded into the objective function of the classic TSK fuzzy systems, which can bring two advantages: firstly, the new method can enlarge the margins between different classes as much as possible, and it has more freedom to fit the labels better. Secondly, to avoid the problem of overfitting, the new method uses the class compactness graph to guarantee that the samples from the same class can be kept close together in the transformed space.
- (2)
- Five state-of-the-art algorithms are introduced for comparison studies, and experimental results are reported from the perspectives of classification performance, sensitivity and interpretability. The proposed algorithm significantly performs better than the state-of-the-art algorithm in terms of accuracy and macro F1-score due to the introduced label soften and the compactness class graph. What is more, the improved generalization ability can be observed from the lower accuracy difference between training and testing. In addition, radiomics features have physical meaning; with the help of transparent fuzzy rules generated by the proposed algorithm, the interpretability can be guaranteed.
2. ZERO-TSK-FS for Classification
3. LR-ZERO-TSK-FS
3.1. Objective Function
3.2. Optimization
3.3. Algorithm
| Algorithm 1 LR-ZERO-TSK-FS |
Input: Training set , number of fuzzy rules K, regularized parameters and Output: Transformation matrix and non-negative label soften matrix Procedures:
1 Use clustering technique, e.g., FCM (Fuzzy C-Mean) to learn the antecedent parameters, i.e., and in (4) of fuzzy rules.
2 Use (3) to get , and further .
3 Use (13) and to compute the graph Laplacian matrix .
4 Randomize under the constraint .
5 Set .
Repeat 6 Update by (19) with current .
7 Update by (21) with current .
8 .
Until 9 With and , the output can be computed by .
|
4. Experimental Studies
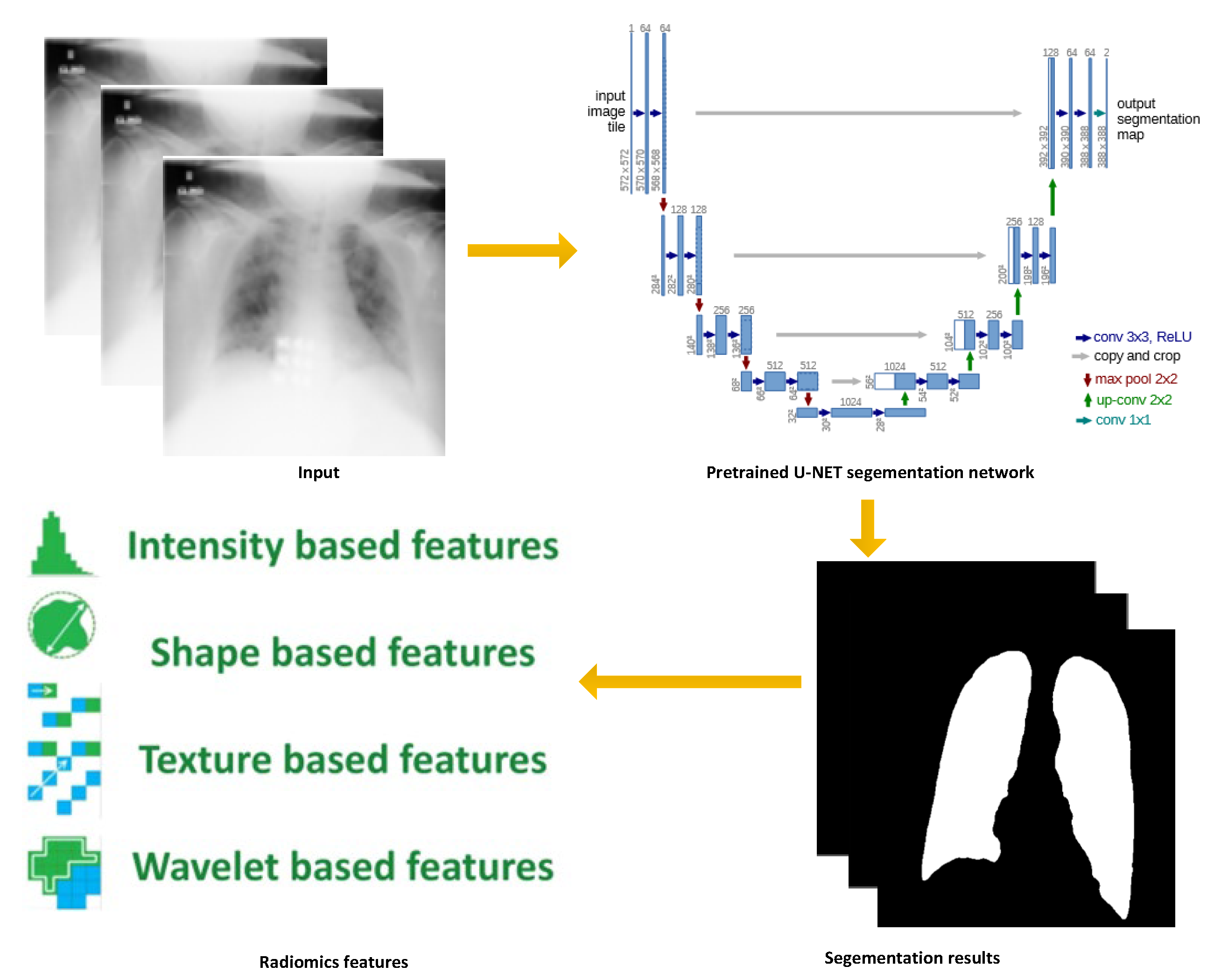
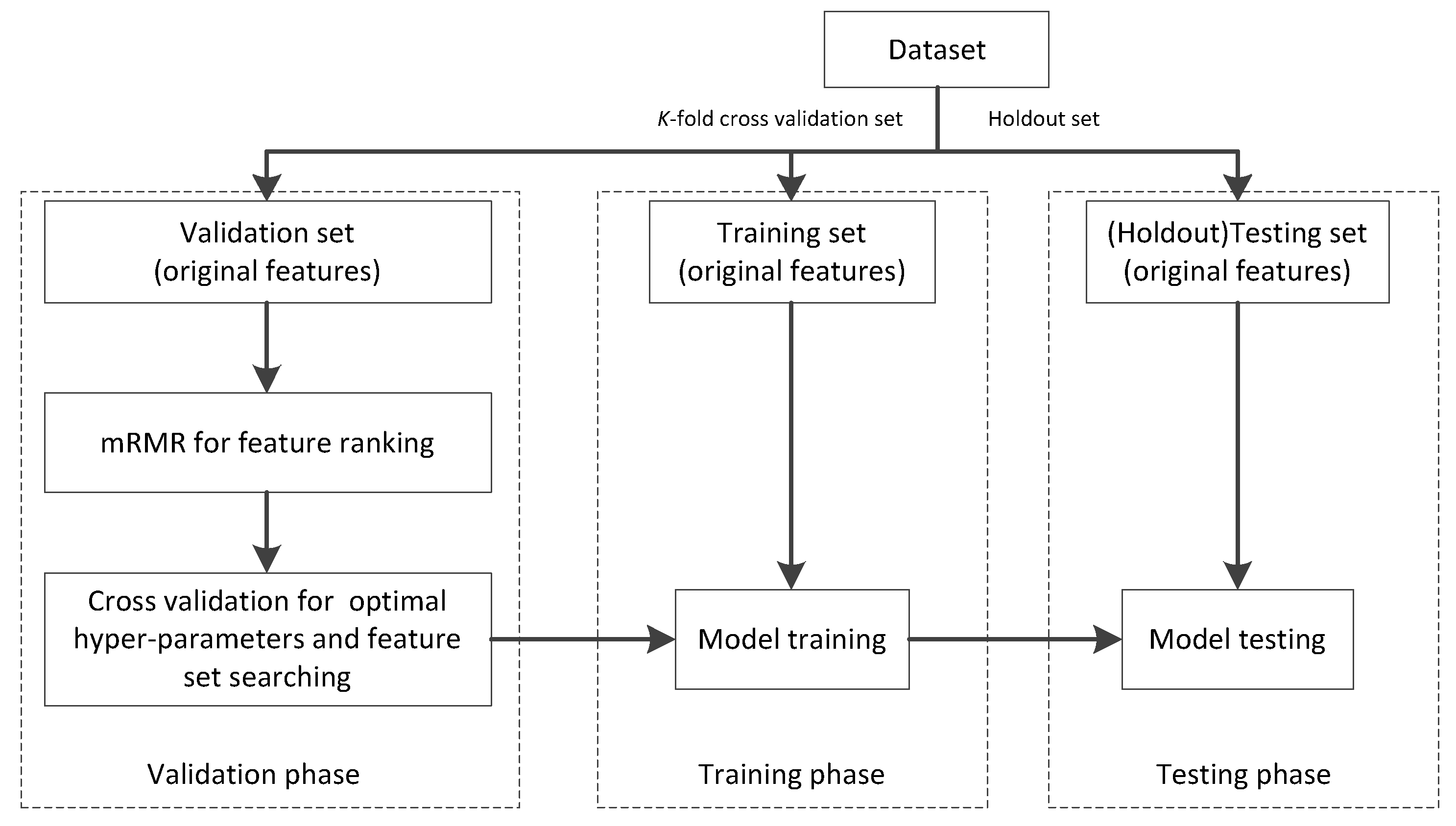
4.1. Data Preprocessing
4.2. Settings
4.3. Experimental Results
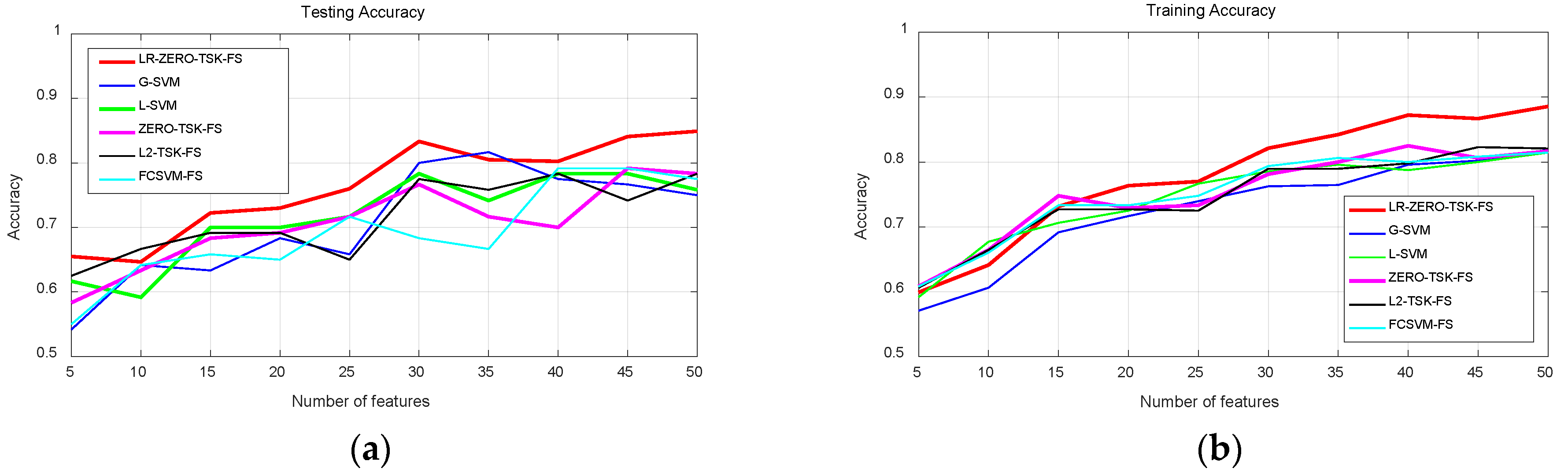
4.3.1. Classification Performance Analysis
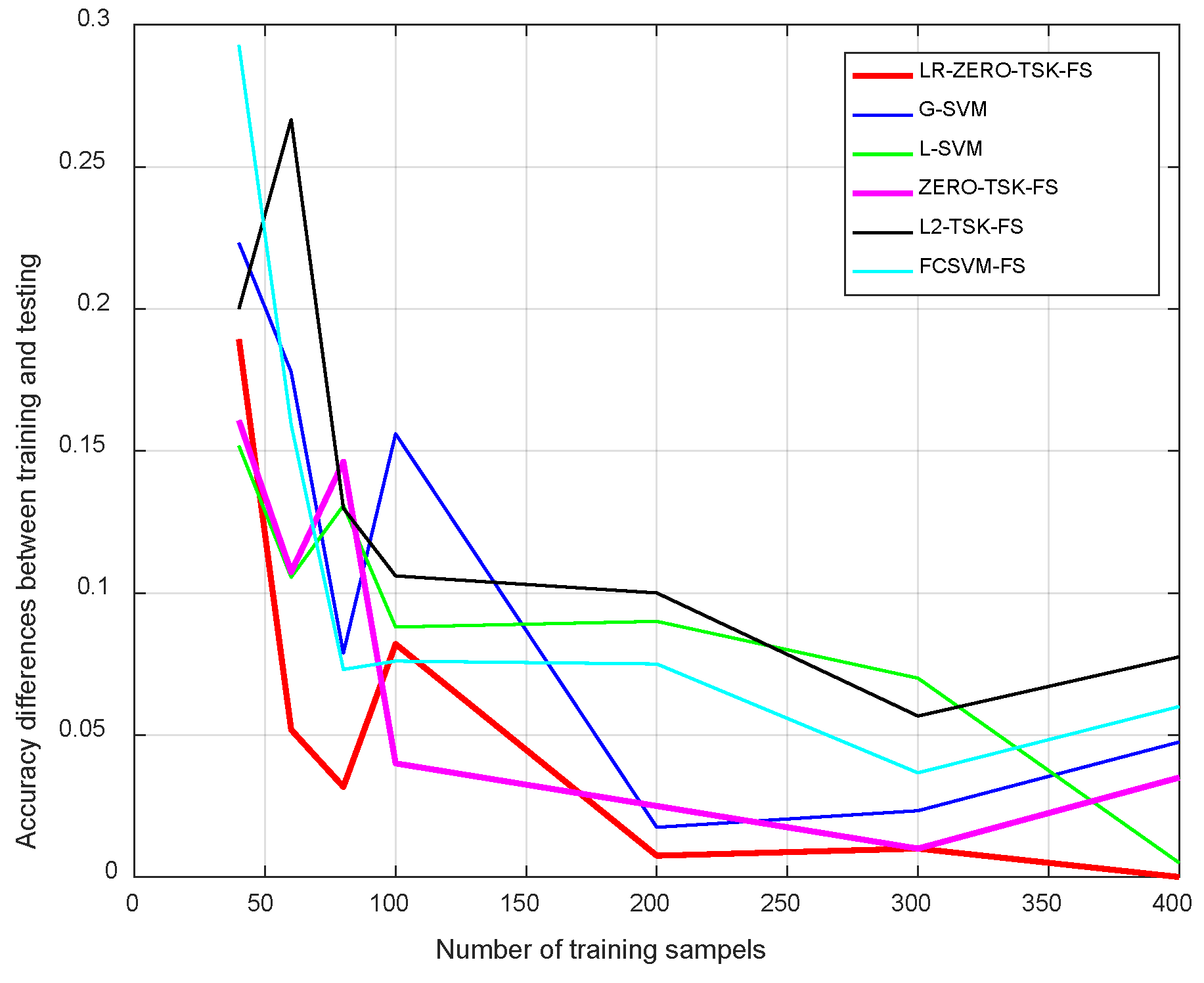
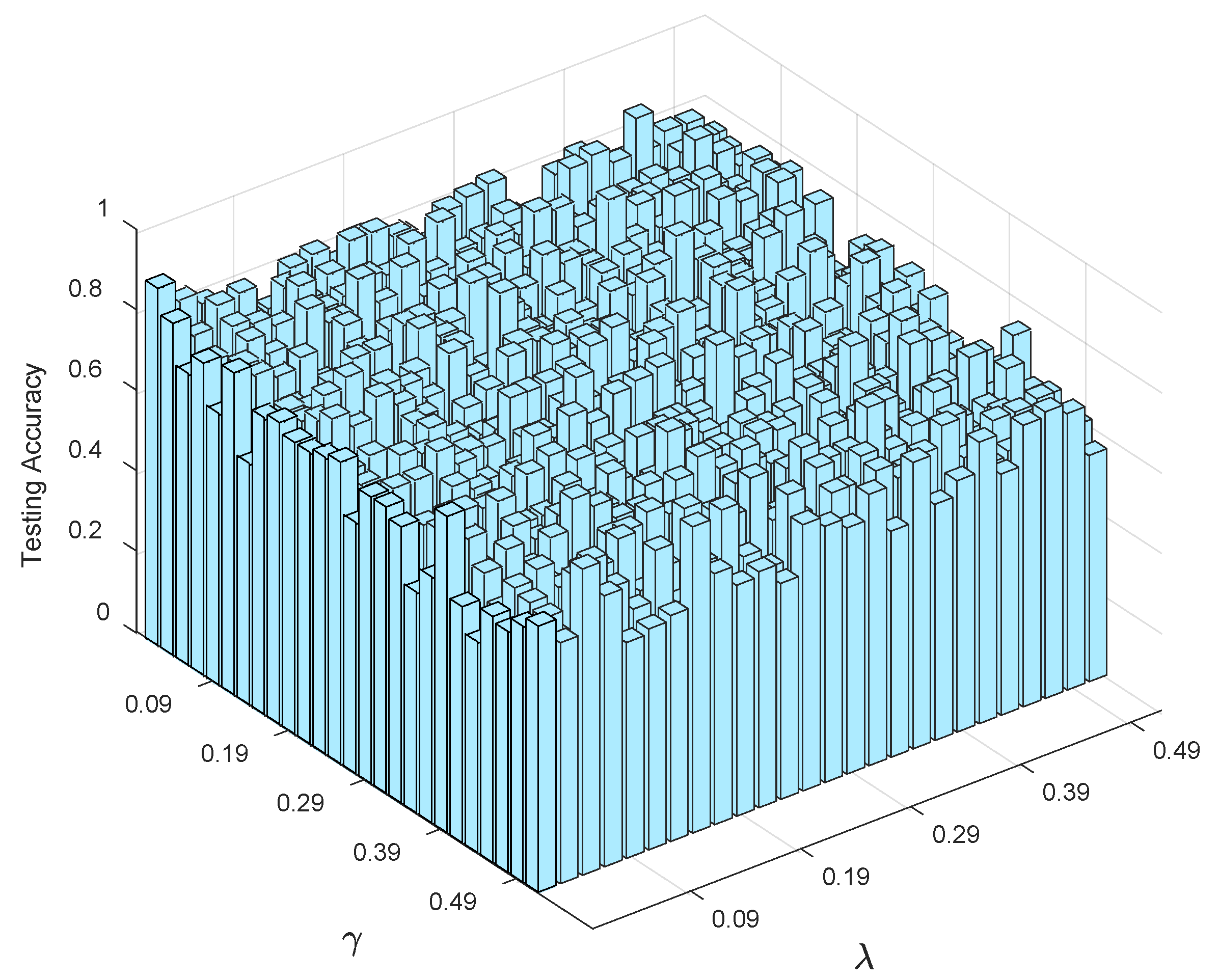
4.3.2. Sensitivity Analysis
- (1)
- Streamlined classification accuracy owing to the introduction of a soft strategy to adaptively relax the binary matrix during label transformation, rendering more flexibility during label transformation and capability in enlarging the margins between different classes.
- (2)
- Alleviated risk of model overfitting in virtue of the adoption of a class compactness graph during manifold learning, based on the assumption that samples sharing the same labels should be kept as close as possible when they are transformed into the label space.
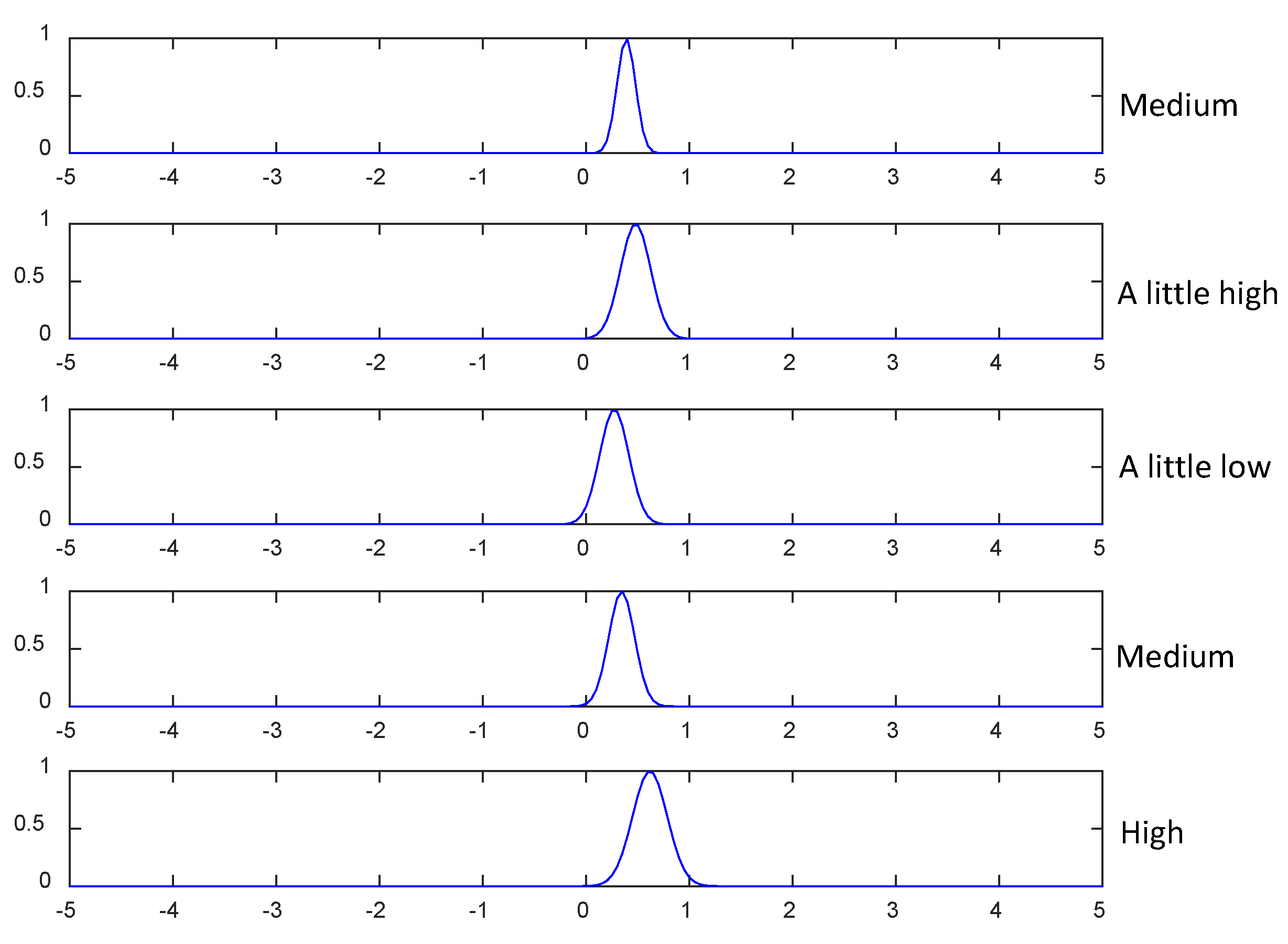
4.3.3. Interpretability Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Consent to Participate
Consent for Publication
Abbreviations
| Abbreviations | |
| COVID-19 | Corona Virus Disease 2019 |
| CXR | Chest X-Ray |
| TSK | Takagi–Sugeno–Kang |
| RT-PCR | Reverse Transcription Polymerase Chain Reaction |
| AI | Artificial Intelligence |
| ZERO-TSK-FS | Zero Order TSK Fuzzy System |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| LR-ZERO-TSK-FS | Label Relaxation Zero Order TSK Fuzzy System |
| mRMR | Minimum-Redundancy-Maximum-Relevance |
| Symbols | |
| Training set | |
| One training sample (vector) and the corresponding label. | |
| N | Number of training samples. |
| C | Number of classes. |
| Non-negative label soften matrix | |
| Luxury matrix | |
| Transformation matrix | |
| Weight matrix | |
| Graph Laplacian matrix | |
References
- Wang, W.; Xu, Y.; Gao, R.; Lu, R.; Han, K.; Wu, G.; Tan, W. Detection of SARS-CoV-2 in Different Types of Clinical Specimens. JAMA 2020, 323, 1843–1844. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Yang, M.; Yuan, J.; Wang, F.; Wang, Z.; Li, J.; Zhang, M.; Xing, L.; Wei, J.; Peng, L.; et al. Laboratory diagnosis and monitoring the viral shedding of 2019-nCoV infections. Innovation 2020, 1, 100061. [Google Scholar] [CrossRef]
- Kanne, J.P.; Little, B.P.; Chung, J.H.; Elicker, B.M.; Ketai, L.H. Essentials for Radiologists on COVID-19: An Update—Radiology Scientific Expert Panel. Radiology 2020, 296, E113–E114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodrigues, J.; Hare, S.; Edey, A.; Devaraj, A.; Jacob, J.; Johnstone, A.; McStay, R.; Nair, A.; Robinson, G.; Rodrigues, J.; et al. An update on COVID-19 for the radiologist-A British society of Thoracic Imaging statement. Clin. Radiol. 2020, 75, 323–325. [Google Scholar] [CrossRef] [Green Version]
- Haghanifar, A.; Majdabadi, M.M.; Choi, Y.; Deivalakshmi, S.; Ko, S. COVID-CXNet: Detecting COVID-19 in frontal chest X-ray images using deep learning. Multimed. Tools Appl. 2022, 81, 30615–30645. [Google Scholar] [CrossRef] [PubMed]
- Umer, M.; Ashraf, I.; Ullah, S.; Mehmood, A.; Choi, G.S. COVINet: A convolutional neural network approach for predicting COVID-19 from chest X-ray images. J. Ambient Intell. Humaniz. Comput. 2022, 13, 535–547. [Google Scholar] [CrossRef]
- Zhang, Y.-D.; Satapathy, S.C.; Liu, S.; Li, G.-R. A five-layer deep convolutional neural network with stochastic pooling for chest CT-based COVID-19 diagnosis. Mach. Vis. Appl. 2021, 32, 14. [Google Scholar] [CrossRef]
- Khan, M.A.; Hussain, N.; Majid, A.; Alhaisoni, M.; Bukhari, S.A.C.; Kadry, S.; Nam, Y.; Zhang, Y.-D. Classification of Positive COVID-19 CT Scans using Deep Learning. Comput. Mater. Contin. 2021, 66, 2923–2938. [Google Scholar] [CrossRef]
- Wang, S.-H.; Nayak, D.R.; Guttery, D.S.; Zhang, X.; Zhang, Y.-D. COVID-19 classification by CCSHNet with deep fusion using transfer learning and discriminant correlation analysis. Inf. Fusion 2021, 68, 131–148. [Google Scholar] [CrossRef]
- Minaee, S.; Kafieh, R.; Sonka, M.; Yazdani, S.; Soufi, G.J. Deep-COVID: Predicting COVID-19 from chest X-ray images using deep transfer learning. Med. Image Anal. 2020, 65, 101794. [Google Scholar] [CrossRef] [PubMed]
- Ozturk, T.; Talo, M.; Yildirim, E.A.; Baloglu, U.B.; Yildirim, O.; Acharya, U.R. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020, 121, 103792. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Ren, L.; Cai, J. Clinical implementation of AI technologies will require interpretable AI models. Med. Phys. 2020, 47, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Jiang, X.; Ma, C.; Du, P.; Li, X.; Lv, S.; Yu, L.; Chen, Y.; Su, J.; Lang, G. Deep Learning System to Screen novel Coronavirus Disease 2019 Pneumonia. Engineering 2020, 6, 1122–1129. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C.; Deng, X.; Fu, Q.; Zhou, Q.; Feng, J.; Ma, H.; Liu, W.; Wang, X. Deep learning-based detection for COVID-19 from chest CT using weak label. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Kang, B.; Ma, J.; Zeng, X.; Xiao, M.; Guo, J.; Cai, M.; Yang, J.; Li, Y.; Meng, X.; et al. A deep learning algorithm using CT images to screen for Corona Virus Disease (COVID-19). MedRxiv 2021, 31, 6096–6104. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, S.; Li, L.; Zhang, X.; Zhang, X.; Huang, Z.; Chen, J.; Zhao, H.; Jie, Y.; Wang, R. Deep learning Enables Accurate Diagnosis of Novel Coronavirus (COVID-19) with CT images. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 18, 2775–2780. [Google Scholar] [CrossRef]
- Narin, A.; Kaya, C.; Pamuk, Z. Automatic detection of coronavirus disease (COVID-19) using X-ray images and deep convolutional neural networks. Pattern Anal. Appl. 2021, 24, 1207–1220. [Google Scholar] [CrossRef]
- Hemdan, E.E.D.; Shouman, M.A.; Karar, M.E. Covidx-net: A framework of deep learning classifiers to diagnose covid-19 in X-ray images. arXiv 2020, arXiv:2003.11055. [Google Scholar]
- Kumar, P.; Kumari, S. Detection of coronavirus disease (COVID-19) based on deep features and support vector machine. Preprints 2020, 2020030300. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Lin, Z.Q.; Wong, A. COVID-Net: A tailored deep convolutional neural network design for detection of COVID-19 cases from chest X-ray images. Sci. Rep. 2020, 10, 19549. [Google Scholar] [CrossRef]
- Apostolopoulos, I.D.; Mpesiana, T.A. Covid-19: Automatic detection from X-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020, 43, 635–640. [Google Scholar] [CrossRef] [PubMed]
- Karim, M.R.; Döhmen, T.; Cochez, M.; Beyan, O.; Rebholz-Schuhmann, D.; Decker, S. Deepcovidex-plainer: Explainable COVID-19 diagnosis from chest X-ray images. In Proceedings of the 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Seoul, Korea, 16–19 December 2020; pp. 1034–1037. [Google Scholar]
- Brunese, L.; Mercaldo, F.; Reginelli, A.; Santone, A. Explainable Deep Learning for Pulmonary Disease and Coronavirus COVID-19 Detection from X-rays. Comput. Methods Programs Biomed. 2020, 196, 105608. [Google Scholar] [CrossRef]
- Deng, Z.; Jiang, Y.; Choi, K.-S.; Chung, F.-L.; Wang, S. Knowledge-Leverage-Based TSK Fuzzy System Modeling. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ishibuchi, H.; Wang, S. Deep Takagi–Sugeno–Kang Fuzzy Classifier with Shared Linguistic Fuzzy Rules. IEEE Trans. Fuzzy Syst. 2017, 26, 1535–1549. [Google Scholar] [CrossRef]
- Xia, K.; Zhang, Y.; Jiang, Y.; Qian, P.; Dong, J.; Yin, H.; Muzic, R.F. TSK Fuzzy System for Multi-View Data Discovery Underlying Label Relaxation and Cross-Rule & Cross-View Sparsity Regularizations. IEEE Trans. Ind. Inform. 2021, 17, 3282–3291. [Google Scholar] [CrossRef]
- Jiang, Y.; Deng, Z.; Chung, F.-L.; Wang, G.; Qian, P.; Choi, K.-S.; Wang, S. Recognition of Epileptic EEG Signals Using a Novel Multiview TSK Fuzzy System. IEEE Trans. Fuzzy Syst. 2016, 25, 3–20. [Google Scholar] [CrossRef]
- Lin, C.-L.; Hsieh, S.-T. Work-In-Progress: An intelligent diagnosis influenza system based on adaptive neuro-fuzzy inference system. In Proceedings of the 2015 1st International Conference on Industrial Networks and Intelligent Systems (INISCom), Tokyo, Japan, 2–4 March 2015; pp. 177–180. [Google Scholar] [CrossRef] [Green Version]
- Khayamnia, M.; Yazdchi, M.; Vahidiankamyad, A.; Foroughipour, M. The recognition of migraine headache by designation of fuzzy expert system and usage of LFE learning algorithm. In Proceedings of the 2017 5th Iranian Joint Congress on Fuzzy and Intelligent Sys-tems (CFIS), Qazvin, Iran, 7–9 March 2017; pp. 50–53. [Google Scholar] [CrossRef]
- Shao, L.; Liu, L.; Li, X. Feature Learning for Image Classification via Multiobjective Genetic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2013, 25, 1359–1371. [Google Scholar] [CrossRef]
- Fan, Z.; Xu, Y.; Zhang, D. Local Linear Discriminant Analysis Framework Using Sample Neighbors. IEEE Trans. Neural Netw. 2011, 22, 1119–1132. [Google Scholar] [CrossRef]
- Łęski, J. Ho–Kashyap classifier with generalization control. Pattern Recognit. Lett. 2003, 24, 2281–2290. [Google Scholar] [CrossRef]
- Deng, Z.; Choi, K.-S.; Jiang, Y.; Wang, S. Generalized Hidden-Mapping Ridge Regression, Knowledge-Leveraged Inductive Transfer Learning for Neural Networks, Fuzzy Systems and Kernel Methods. IEEE Trans. Cybern. 2014, 44, 2585–2599. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Y.; Li, X.; Lai, Z.; Wong, W.K.; Fang, B. Regularized Label Relaxation Linear Regression. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1006–1018. [Google Scholar] [CrossRef]
- Liu, J.; Chung, F.-L.; Wang, S. Bayesian zero-order TSK fuzzy system modeling. Appl. Soft Comput. 2017, 55, 253–264. [Google Scholar] [CrossRef]
- Juang, C.-F.; Chiu, S.-H.; Shiu, S.-J. Fuzzy System Learned Through Fuzzy Clustering and Support Vector Machine for Human Skin Color Segmentation. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2007, 37, 1077–1087. [Google Scholar] [CrossRef]
- Tsang, I.W.; Kwok, J.T.; Cheung, P.M.; Cristianini, N. Core vector machines: Fast SVM training on very large data sets. J. Mach. Learn. Res. 2005, 6, 363–392. [Google Scholar]
- Yang, C.; Deng, Z.; Choi, K.-S.; Wang, S. Takagi–Sugeno–Kang Transfer Learning Fuzzy Logic System for the Adaptive Recognition of Epileptic Electroencephalogram Signals. IEEE Trans. Fuzzy Syst. 2015, 24, 1079–1094. [Google Scholar] [CrossRef]


| Studies | Modalities | Number of Cases | AI Models | Best Performance |
|---|---|---|---|---|
| COVID-19 detection from healthy and pneumonia cases [13]. | CCT * | 219 COVID-19 cases (S) 224 Pneumonia cases 175 Healthy cases | ResNet with location attention mechanism | Overall accuracy rate was 86.7%. |
| Severity rating [14]. | CCT | 313 COVID-19 cases (S) 229 COVID-19 cases (M) | UNet and 3D Deep Network | The model obtained a testing AUC of 0.975. |
| Severity rating [15]. | CCT | 195 COVID-19 cases (S) 258 COVID-19 cases (M) | M-Inception | The external testing dataset showed a total accuracy of 79.3% with a specificity of 0.83 and sensitivity of 0.67. |
| COVID-19 detection from healthy cases [16]. | CCT | 777 COVID-19 cases (S) 708 Healthy cases | DRE-Net | The model discriminated the COVID-19 patients from the bacteria pneumonia patients with an AUC of 0.95, recall (sensitivity) of 0.96, and precision of 0.79. |
| Severity rating [17]. | CXR ** | 50 COVID-19 cases (S) 50 COVID-19 cases (M) | Deep CNN and ResNet-50 | The model achieved 99.7% accuracy for automatic detection of COVID-19. |
| COVID-19 detection from healthy cases [18]. | CXR | 25 COVID-19 cases (S) 25 Healthy cases | COVIDX-Net | The model achieved f1-scores of 0.89 and 0.91 for normal and COVID-19, respectively. |
| COVID-19 detection from healthy cases [19]. | CXR | 25 COVID-19 cases (S) 25 COVID-19 cases (M) | ResNet50 and SVM | The highest accuracy achieved by ResNet50 plus SVM is 98.66%. |
| COVID-19 detection from healthy cases [20]. | CXR | 53 COVID-19 cases (S) 5526 COVID-19 cases (M) | COVID-Net | COVID-Net achieves good accuracy by achieving 93.3% test accuracy. |
| COVID-19 detection from healthy and pneumonia cases [21]. | CXR | 224 COVID-19 cases (S) 700 Pneumonia cases 504 Healthy cases | VGG-19 | The best accuracy, sensitivity, and specificity obtained is 96.78%, 98.66%, and 96.46% respectively. |
| COVID-19 detection from healthy and pneumonia cases [22] | CXR | 15,959 CXR images of 15,854 patients, covering normal, pneumonia, and COVID-19 cases. | Deep CNN | The model achieved best positive predictive value of 91.6%, 92.45%, and 96.12%, respectively for normal, pneumonia, and COVID-19 cases, respectively. |
| COVID-19 detection from healthy and pneumonia cases [23] | CXR | 250 COVID-19 cases 2753 pulmonary cases 3520 healthy cases. | Deep CNN | The best accuracy is 0.99. |
| Model | Parameter Settings |
|---|---|
| ZERO-TSK-FS | FCM is used to learn the antecedent parameters. The optimal number of fuzzy rules is determined by cross-validation from [2, 4, 6, …, 30]. |
| L2-TSK-FS | FCM is used to learn the antecedent parameters. The optimal number of fuzzy rules is determined by cross-validation from [2, 4, 6, …, 30]. |
| FS-FCSVM | FCM is used to learn the antecedent parameters. The optimal number of fuzzy rules is determined by cross-validation from [2, 4, 6, …, 30]. The learning threshold parameter is determined by cross-validation from [0.2, 0.3, …, 0.8]. The regularization parameter is determined by cross-validation from [2−3, 2−2, …, 25, 27]. |
| L-SVM | The regularization parameter C is determined by cross-validation from [10−3, 2−2, …, 103]. |
| G-SVM | The regularization parameter C is determined by cross-validation from [10−3, 2−2, …, 103]. The kernel width σ is determined by cross-validation from [10−3, 10−2, …, 103]. |
| LR-ZERO-TSK-FS | FCM is used to learn the antecedent parameters. The optimal number of fuzzy rules is determined by cross-validation from [2, 4, 6, …, 30]. The regularization parameter and are both determined by cross-validation from [0.01, 0.03, …, 1]. |
| Software and hardware settings | |
| Development platform: Python 3.9.8 (pyRadiomics for radiomics feature extraction), Matlab 2012b (LR-ZERO-TSK-FS coding) System OS: Windows 10 Hardware: Intel(R) Core (TM) i5-7200U CPU @ 2.50 GHz 2.71 GHz, 16 G RAM | |
| Number of Features | G-SVM | L-SVM | ZERO-TSK-FS | L2-TSK-FS | FCSVM-FS |
|---|---|---|---|---|---|
| 5 | * | * | * | * | * |
| 10 | * | * | |||
| 15 | * | * | * | * | * |
| 20 | * | * | * | * | * |
| 25 | * | * | * | * | * |
| 30 | * | * | * | * | * |
| 35 | * | * | * | * | |
| 40 | * | * | * | * | |
| 45 | * | * | * | * | * |
| 50 | * | * | * | * | * |
| Number of Features | G-SVM | L-SVM | ZERO-TSK-FS | L2-TSK-FS | FCSVM-FS | LR-ZERO-TSK-FS |
|---|---|---|---|---|---|---|
| 5 | 0.5289 | 0.5947 | 0.5674 | 0.6088 | 0.5098 | 0.6145 |
| 10 | 0.6287 | 0.5792 | 0.6065 | 0.6474 | 0.6045 | 0.6024 |
| 15 | 0.6159 | 0.6801 | 0.6543 | 0.6612 | 0.6181 | 0.6887 |
| 20 | 0.6701 | 0.6810 | 0.6803 | 0.6704 | 0.6251 | 0.6912 |
| 25 | 0.6342 | 0.7031 | 0.7032 | 0.6305 | 0.6831 | 0.7253 |
| 30 | 0.7801 | 0.7603 | 0.7454 | 0.6504 | 0.6448 | 0.7923 |
| 35 | 0.7956 | 0.7251 | 0.7002 | 0.6405 | 0.6523 | 0.7664 |
| 40 | 0.7406 | 0.7602 | 0.6803 | 0.7603 | 0.7503 | 0.7661 |
| 45 | 0.7510 | 0.7604 | 0.7711 | 0.7303 | 0.7803 | 0.8047 |
| 50 | 0.7301 | 0.7402 | 0.7600 | 0.7600 | 0.7589 | 0.8232 |
| Number of Features | G-SVM | L-SVM | ZERO-TSK-FS | L2-TSK-FS | FCSVM-FS | LR-ZERO-TSK-FS |
|---|---|---|---|---|---|---|
| 5 | 0.5512 | 0.5798 | 0.5925 | 0.5923 | 0.5923 | 0.5812 |
| 10 | 0.5823 | 0.6612 | 0.6487 | 0.6487 | 0.6487 | 0.6256 |
| 15 | 0.6741 | 0.7361 | 0.7367 | 0.7118 | 0.7123 | 0.7220 |
| 20 | 0.7019 | 0.7012 | 0.7010 | 0.7012 | 0.7124 | 0.7489 |
| 25 | 0.7189 | 0.7490 | 0.7102 | 0.7001 | 0.7302 | 0.7491 |
| 30 | 0.7478 | 0.7731 | 0.7612 | 0.7742 | 0.7781 | 0.8024 |
| 35 | 0.7476 | 0.7800 | 0.7803 | 0.7732 | 0.7921 | 0.8215 |
| 40 | 0.7803 | 0.7586 | 0.8137 | 0.7803 | 0.7803 | 0.8510 |
| 45 | 0.7897 | 0.7898 | 0.7911 | 0.8021 | 0.7923 | 0.8454 |
| 50 | 0.8005 | 0.8005 | 0.8008 | 0.8009 | 0.8001 | 0.8702 |
| Number of Features | G-SVM | L-SVM | ZERO-TSK-FS | L2-TSK-FS | FCSVM-FS |
|---|---|---|---|---|---|
| 5 | 1.76 | 1.43 | 2.11 | 1.98 | 2.03 |
| 10 | 2.32 | 2.67 | 3.33 | 2.99 | 2.92 |
| 15 | 2.91 | 3.04 | 3.50 | 3.14 | 3.24 |
| 20 | 3.64 | 2.98 | 4.11 | 4.04 | 3.96 |
| 25 | 7.21 | 6.23 | 5.55 | 5.98 | 6.01 |
| 30 | 7.87 | 6.65 | 6.04 | 7.13 | 7.27 |
| 35 | 8.03 | 7.75 | 7.56 | 8.09 | 7.85 |
| 40 | 10.43 | 9.84 | 7.99 | 9.43 | 8.43 |
| 45 | 13.67 | 13.48 | 16.09 | 15.43 | 16.22 |
| 50 | 16.47 | 15.99 | 16.73 | 17.48 | 17.78 |
| No. | Feature Name | No. | Feature Name |
|---|---|---|---|
| 1 | ‘wavelet-HH_glrlm_GrayLevelVariance’ | 16 | ‘logarithm_gldm_GrayLevelVariance’ |
| 2 | ‘squareroot_glrlm_GrayLevelNonUniformityNormalized’ | 17 | ‘wavelet-HL_glrlm_GrayLevelNonUniformityNormalized’ |
| 3 | ‘exponential_firstorder_RobustMeanAbsoluteDeviation’ | 18 | ‘wavelet-HL_ngtdm_Busyness’ |
| 4 | ‘gradient_glcm_ClusterProminence’ | 19 | ‘squareroot_glszm_LargeAreaEmphasis’ |
| 5 | ‘squareroot_glcm_MCC’ | 20 | ‘squareroot_glrlm_LongRunLowGrayLevelEmphasis’ |
| 6 | ‘squareroot_glcm_ClusterProminence’ | 21 | ‘wavelet-LH_glrlm_RunEntropy’ |
| 7 | ‘gradient_glszm_GrayLevelVariance’ | 22 | ‘wavelet-LH_glrlm_GrayLevelNonUniformityNormalized’ |
| 8 | ‘wavelet-LH_gldm_LowGrayLevelEmphasis’ | 23 | ‘wavelet-HH_gldm_DependenceNonUniformityNormalized’ |
| 9 | ‘exponential_firstorder_Range’ | 24 | ‘exponential_glszm_LargeAreaHighGrayLevelEmphasis’ |
| 10 | ‘wavelet-LH_glszm_SmallAreaEmphasis’ | 25 | ‘square_glcm_DifferenceEntropy’ |
| 11 | ‘square_gldm_DependenceNonUniformityNormalized’ | 26 | ‘original_glcm_SumSquares’ |
| 12 | ‘gradient_glcm_JointAverage’ | 27 | ‘squareroot_glcm_Autocorrelation’ |
| 13 | ‘logarithm_glrlm_LongRunHighGrayLevelEmphasis’ | 28 | ‘logarithm_glrlm_LongRunEmphasis’ |
| 14 | ‘wavelet-LH_glrlm_LongRunLowGrayLevelEmphasis’ | 29 | ‘wavelet-HH_firstorder_90Percentile’ |
| 15 | ‘wavelet-LH_glszm_HighGrayLevelZoneEmphasis’ | 30 | ‘wavelet-LH_glrlm_RunEntropy’ |
| LR-ZERO-TSK-FS | ||
|---|---|---|
| No. | Antecedent | Consequent |
| 1 | [0.3888, 0.4187, 0.0043, 0.3884, 0.2543, …] [0.0080, 0.0051, 0.0011, 0.0079, 0.0034, …] | [0.0340, 0.0087, 0.0024] |
| 2 | [0.4791, 0.5709, 0.0008, 0.4801, 0.2732, …] [0.0214, 0.0105, 0.0005, 0.0213, 0.0068, …] | [0.0096, 0.0148, 0.0119] |
| 3 | [0.2726, 0.4477, 0.0018, 0.2746, 0.2200, …] [0.0199, 0.0088, 0.0007, 0.0198, 0.0050, …] | [0.0100, 0.0108, 0.0077] |
| 4 | [0.3443, 0.2711, 0.0072, 0.3471, 0.1323, …] [0.0156, 0.0104, 0.0015, 0.0153, 0.0042, …] | [0.0048, 0.0189, 0.0202] |
| 5 | [0.6174, 0.3593, 0.0018, 0.6172, 0.1463, …] [0.0283, 0.0094, 0.0007, 0.0279, 0.0048, …] | [0.0026, 0.0109, 0.0165] |
| Rule No. | If Part | Then Part |
|---|---|---|
| 1 | No.1 is “low”, No.2 is “low”, No.3 is “a little low”, No.4 is “a little low”, No.5 is “a litter low”, … | for class 1,for class 2 andfor class 3. |
| 2 | No.1 is “low”, No.2 is “low”, No.3 is “a little low”, No.4 is “a little low”, No.5 is “a little low”, … | for class 1,for class 2 andfor class 3. |
| 3 | No.1 is “low”, No.2 is “low”, No.3 is “a little low”, No.4 is “a little low”, No.5 is “a little low”, … | for class 1,for class 2 andfor class 3. |
| 4 | No.1 is “low”, No.2 is “low”, No.3 is “a little low”, No.4 is “a little low”, No.5 is “a litter low”, … | for class 1,for class 2 andfor class 3. |
| 5 | No.1 is “low”, No.2 is “low”, No.3 is “a little low”, No.4 is “a little low”, No.5 is “a little low”, … | for class 1,for class 2 andfor class 3. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, D.; Lam, S.; Li, B.; Teng, X.; Zhang, J.; Zhou, T.; Ma, Z.; Ying, T.-C.; Cai, J. Radiomics-Based Detection of COVID-19 from Chest X-ray Using Interpretable Soft Label-Driven TSK Fuzzy Classifier. Diagnostics 2022, 12, 2613. https://doi.org/10.3390/diagnostics12112613
Zhang Y, Yang D, Lam S, Li B, Teng X, Zhang J, Zhou T, Ma Z, Ying T-C, Cai J. Radiomics-Based Detection of COVID-19 from Chest X-ray Using Interpretable Soft Label-Driven TSK Fuzzy Classifier. Diagnostics. 2022; 12(11):2613. https://doi.org/10.3390/diagnostics12112613
Chicago/Turabian StyleZhang, Yuanpeng, Dongrong Yang, Saikit Lam, Bing Li, Xinzhi Teng, Jiang Zhang, Ta Zhou, Zongrui Ma, Tin-Cheung (Michael) Ying, and Jing Cai. 2022. "Radiomics-Based Detection of COVID-19 from Chest X-ray Using Interpretable Soft Label-Driven TSK Fuzzy Classifier" Diagnostics 12, no. 11: 2613. https://doi.org/10.3390/diagnostics12112613
APA StyleZhang, Y., Yang, D., Lam, S., Li, B., Teng, X., Zhang, J., Zhou, T., Ma, Z., Ying, T.-C., & Cai, J. (2022). Radiomics-Based Detection of COVID-19 from Chest X-ray Using Interpretable Soft Label-Driven TSK Fuzzy Classifier. Diagnostics, 12(11), 2613. https://doi.org/10.3390/diagnostics12112613






