Minimal Cardinality Diagnosis in Problems with Multiple Observations
Abstract
1. Introduction
2. Background and Related Work
2.1. Model-Based Diagnosis
2.2. Related Work
3. MBD with Multiple Observations
4. Intermittent and Non-Intermittent Faults
4.1. Between Fault Modes and Intermittency
4.1.1. Int+WFM
4.1.2. NotInt+WFM
4.1.3. Int+SFM
4.1.4. NotInt+SFM
5. Finding Diagnoses
5.1. SAT-Based MBD Algorithm
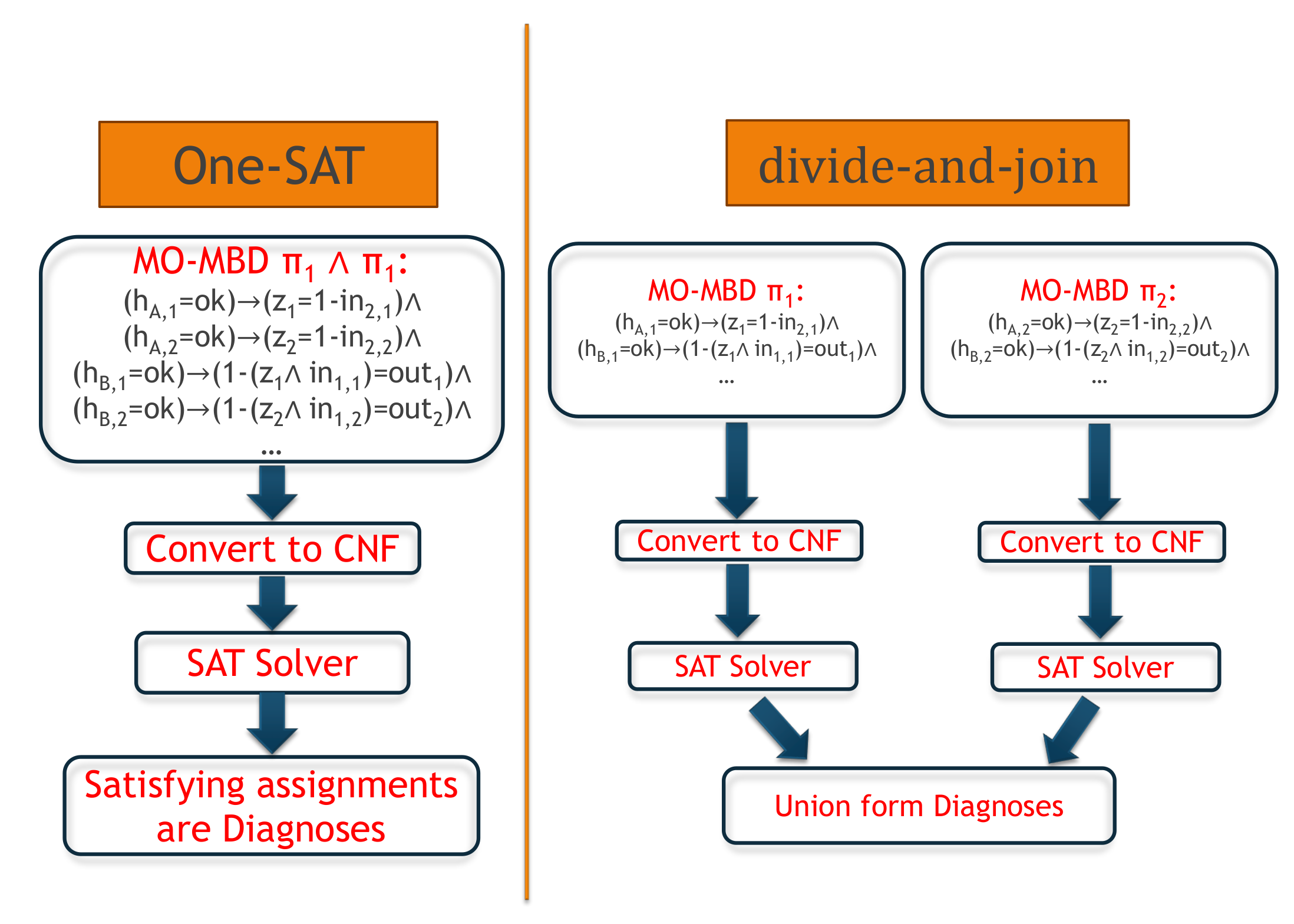
5.2. One Formula for Multiple Observations
5.3. Joining Diagnoses of Multiple Observations
5.3.1. Finding Minimal Diagnoses
5.3.2. Finding MC Diagnoses with Divide-and-Join
| Algorithm 1:Divide-and-Join-MC |
 |
6. Empirical Evaluation
Discussion
- divide-and-join approach is faster than one-SAT for the harder problems (with larger set of components).
- The time gap between finding the first diagnosis and all diagnoses is significant in one-SAT but less so in divide-and-join.
- The divide-and-join algorithm is especially suited for diagnosis problems with low cardinality.
- divide-and-join is faster for cases with fewer abnormal behaviors—smaller MC and , while one-SAT is more appropriate for cases in which there are many abnormal behaving components.
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Kleer, J.; Williams, B.C. Diagnosis with Behavioral Modes. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), San Francisco, CA, USA, 20–25 August 1989; pp. 1324–1330. [Google Scholar]
- Palma, J.; Juarez, J.M.; Campos, M.; Marin, R. Fuzzy theory approach for temporal model-based diagnosis: An application to medical domains. Artif. Intell. Med. 2006, 38, 197–218. [Google Scholar] [CrossRef] [PubMed]
- Mirsky, R.; Hibah, S.; Hadad, M.; Gorenstein, A.; Kalech, M. “PhysIt”—A Diagnosis and Troubleshooting Tool for Physiotherapists in Training. Diagnostics 2020, 10, 72. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Jiang, B.; Ding, S.X.; Huang, B. Data-driven fault diagnosis for traction systems in high-speed trains: A survey, challenges, and perspectives. IEEE Trans. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Williams, B.C.; Nayak, P.P. A model-based approach to reactive self-configuring systems. In Proceedings of the AAAI Conference on Artificial Intelligence, Portland, OR, USA, 4 August 1996; pp. 971–978. [Google Scholar]
- Raiman, O.; de Kleer, J.; Saraswat, V.A.; Shirley, M. Characterizing Non-Intermittent Faults. In Proceedings of the AAAI Conference on Artificial Intelligence, Anaheim, CA, USA, 14–19 July 1991; pp. 849–854. [Google Scholar]
- de Kleer, J. Diagnosing Multiple Persistent and Intermittent Faults. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Pasadena, CA, USA, 11–17 July 2009; pp. 733–738. [Google Scholar]
- Pill, I.; Wotawa, F. Computing Multi-Scenario Diagnoses. International Workshop on Principles of Diagnosis (DX). Available online: http://dx-2020.org/papers/DX-2020_paper_1.pdf (accessed on 1 February 2021).
- Siddiqi, S.A.; Huang, J. Sequential diagnosis by abstraction. J. Artif. Intell. Res. (JAIR) 2011, 41, 329–365. [Google Scholar] [CrossRef]
- Ignatiev, A.; Morgado, A.; Weissenbacher, G.; Marques-Silva, J. Model-Based Diagnosis with Multiple Observations. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Macao, China, 10–16 August 2019; pp. 1108–1115. [Google Scholar]
- Metodi, A.; Stern, R.; Kalech, M.; Codish, M. A novel SAT-based approach to model based diagnosis. J. Artif. Intell. Res. (JAIR) 2014, 51, 377–411. [Google Scholar] [CrossRef]
- Marques-Silva, J.; Janota, M.; Ignatiev, A.; Morgado, A. Efficient model based diagnosis with maximum satisfiability. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Buenos Aires, Argentina, 25 July–1 August 2015. [Google Scholar]
- Williams, B.C.; Ragno, R.J. Conflict-directed A* and its role in model-based embedded systems. Discret. Appl. Math. 2007, 155, 1562–1595. [Google Scholar] [CrossRef]
- Stern, R.; Kalech, M.; Feldman, A.; Provan, G.M. Exploring the Duality in Conflict-Directed Model-Based Diagnosis. In Proceedings of the AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22 July 2012. [Google Scholar]
- Torasso, P.; Torta, G. Model-based diagnosis through obdd compilation: A complexity analysis. In Reasoning, Action and Interaction in AI Theories and Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 287–305. [Google Scholar]
- Darwiche, A. Model-based diagnosis using structured system descriptions. J. Artif. Intell. Res. (JAIR) 1998, 8, 165–222. [Google Scholar] [CrossRef]
- Jannach, D.; Schmitz, T.; Shchekotykhin, K.M. Parallel Model-Based Diagnosis on Multi-Core Computers. J. Artif. Intell. Res. (JAIR) 2016, 55, 835–887. [Google Scholar] [CrossRef]
- Shchekotykhin, K.; Jannach, D.; Schmitz, T. Parallel Model-Based Diagnosis. In Handbook of Parallel Constraint Reasoning; Springer: Berlin/Heidelberg, Germany, 2018; pp. 547–580. [Google Scholar]
- De Kleer, J.; Williams, B.C. Diagnosing multiple faults. Artif. Intell. 1987, 32, 97–130. [Google Scholar] [CrossRef]
- De Kleer, J. An assumption-based TMS. Artif. Intell. 1986, 28, 127–162. [Google Scholar] [CrossRef]
- Rui Abreu, A.J.V.G. Diagnosing multiple intermittent failures using maximum likelihood estimation. Artif. Intell. 2010, 174, 1481–1497. [Google Scholar] [CrossRef][Green Version]
- Pearson, S.; Campos, J.; Just, R.; Fraser, G.; Abreu, R.; Ernst, M.D.; Pang, D.; Keller, B. Evaluating and improving fault localization. In Proceedings of the International Conference on Software Engineering (ICSE), Buenos Aires, Argentina, 20–28 May 2017; pp. 609–620. [Google Scholar]
- Elmishali, A.; Stern, R.; Kalech, M. Data-augmented software diagnosis. In Proceedings of the Innovative Application of Artficial Intelligence Conference (IAAI), Phoenix, AZ USA, 12–7 February 2016. [Google Scholar]
- Elmishali, A.; Stern, R.; Kalech, M. An Artificial Intelligence paradigm for troubleshooting software bugs. Eng. Appl. Artif. Intell. 2018, 69, 147–156. [Google Scholar] [CrossRef]
- Ignatiev, A.; Morgado, A.; Marques-Silva, J. Model Based Diagnosis of Multiple Observations with Implicit Hitting Sets. arXiv 2017, arXiv:1707.01972. [Google Scholar]
- Cai, B.; Liu, Y.; Xie, M. A dynamic-Bayesian-network-based fault diagnosis methodology considering transient and intermittent faults. IEEE Trans. Autom. Sci. Eng. 2016, 14, 276–285. [Google Scholar] [CrossRef]
- Bouziat, V.; Pucel, X.; Roussel, S.; Travé-Massuyés, L. Preferential discrete model-based diagnosis for intermittent and permanent faults. In Proceedings of the 29th International Workshop on Principles of Diagnosis (DX 2018), Warsaw, Poland, August 2018. [Google Scholar]
- Zhou, D.; Zhao, Y.; Wang, Z.; He, X.; Gao, M. Review on Diagnosis Techniques for Intermittent Faults in Dynamic Systems. IEEE Trans. Ind. Electron. 2019, 67, 2337–2347. [Google Scholar] [CrossRef]
- Gómez, L.R.; Cook, A.; Indlekofer, T.; Hellebrand, S.; Wunderlich, H.J. Adaptive Bayesian Diagnosis of Intermittent Faults. J. Electron. Test. 2014, 30, 527–540. [Google Scholar] [CrossRef]
- Feldman, A.; Provan, G.; van Gemund, A. A model-based active testing approach to sequential diagnosis. J. Artif. Intell. Res. (JAIR) 2010, 39, 301. [Google Scholar] [CrossRef]
- Shchekotykhin, K.M.; Schmitz, T.; Jannach, D. Efficient Sequential Model-Based Fault-Localization with Partial Diagnoses. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), New York, NY, USA, 9–15 July 2016; pp. 1251–1257. [Google Scholar]
- Rodler, P. On Active Learning Strategies for Sequential Diagnosis. In Proceedings of the 28th International Workshop on Principles of Diagnosis (DX’17), Brescia, Italy, 26–29 September 2017; Volume 4, pp. 264–283. [Google Scholar]
- Rodler, P.; Schmid, W.; Schekotihin, K. Inexpensive cost-optimized measurement proposal for sequential model-based diagnosis. arXiv 2017, arXiv:1705.09879. [Google Scholar]
- Feldman, A.; De Castro, H.V.; Van Gemund, A.; Provan, G. Model-based diagnostic decision-support system for satellites. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–14. [Google Scholar]
- Breuer, M.A. Testing for intermittent faults in digital circuits. IEEE Trans. Comput. 1973, 100, 241–246. [Google Scholar] [CrossRef]
- Koren, I.; Kohavi, Z. Diagnosis of intermittent faults in combinational networks. IEEE Comput. Archit. Lett. 1977, 26, 1154–1158. [Google Scholar] [CrossRef]
- Smith, A.; Veneris, A.; Ali, M.F.; Viglas, A. Fault diagnosis and logic debugging using Boolean satisfiability. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2005, 24, 1606–1621. [Google Scholar] [CrossRef]
- Bailleux, O.; Boufkhad, Y. Efficient CNF Encoding of Boolean Cardinality Constraints. In Lecture Notes in Computer Science, Proceedings of the International Conference on Principles and Practice of Constraint Programming (CP), Kinsale, Ireland, 29 September–3 October 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 108–122. [Google Scholar]
- Silva, J.; Lynce, I. Towards Robust CNF Encodings of Cardinality Constraints. In Lecture Notes in Computer Science, Proceedings of the International Conference on Principles and Practice of Constraint Programming (CP), Providence, RI, USA, 23–27 September 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 483–497. [Google Scholar]
- Pill, I.; Quaritsch, T. Behavioral Diagnosis of LTL Specifications at Operator Level. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Beijing, China, 3–9 August 2013. [Google Scholar]
- Rintanen, J.; Grastien, A. Diagnosability Testing with Satisfiability Algorithms. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Hyderabad, India, 6–12 January 2007; pp. 532–537. [Google Scholar]
- Hansen, M.C.; Yalcin, H.; Hayes, J.P. Unveiling the ISCAS-85 Benchmarks: A Case Study in Reverse Engineering. IEEE Des. Test 1999, 16, 72–80. [Google Scholar] [CrossRef]
- Brglez, F.; Bryan, D.; Kozminski, K. Combinatorial profiles of sequential benchmark circuits. In Proceedings of the IEEE International Symposium on Circuits and Systems, Portland, OR, USA, 8–11 May 1989; pp. 1929–1934. [Google Scholar]
- Feldman, A.; Provan, G.; van Gemund, A. Approximate model-based diagnosis using greedy stochastic search. J. Artif. Intell. Res. (JAIR) 2010, 38, 371. [Google Scholar] [CrossRef]
- Stern, R.T.; Kalech, M.; Rogov, S.; Feldman, A. How Many Diagnoses Do We Need? In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 1618–1624. [Google Scholar]
- Cazes, D.; Kalech, M. Model-Based Diagnosis with Uncertain Observations. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 2766–2773. [Google Scholar]
- Dean, C.; Meir, K. Model-based diagnosis with uncertain observations. Int. J. Intell. Syst. 2021. [Google Scholar] [CrossRef]
- Abreu, R.; Zoeteweij, P.; van Gemund, A.J.C. Simultaneous debugging of software faults. J. Syst. Softw. 2011, 84, 573–586. [Google Scholar] [CrossRef]
- Khalastchi, E.; Kalech, M. On fault detection and diagnosis in robotic systems. ACM Comput. Surv. (CSUR) 2018, 51, 1–24. [Google Scholar] [CrossRef]
- Kalech, M. Diagnosis of coordination failures: A matrix-based approach. Auton. Agents Multi-Agent Syst. 2012, 24, 69–103. [Google Scholar] [CrossRef]
- Felfernig, A.; Schubert, M.; Zehentner, C. An efficient diagnosis algorithm for inconsistent constraint sets. Artif. Intell. Eng. Des. Anal. Manuf. (AI EDAM) 2012, 26, 53. [Google Scholar] [CrossRef]
- Felfernig, A.; Zehentner, C.; Blazek, P. Corediag: Eliminating redundancy in constraint sets. arXiv 2021, arXiv:2102.12151. [Google Scholar]




| WFM | SFM | |
|---|---|---|
| Int. | Faulty behavior is unconstrained | Must follow a behavior mode but mode can differ between observations |
| Non-Int. | Not constrained by faulty behavior modes but must be consistent across observations | Must follow a single behavior mode across all observations |
| Name | |COMPS| | in | out |
|---|---|---|---|
| 74181 | 65 | 14 | 8 |
| 74283 | 36 | 9 | 5 |
| c432 | 160 | 36 | 7 |
| c880 | 383 | 60 | 26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalech, M.; Stern, R.; Lazebnik, E. Minimal Cardinality Diagnosis in Problems with Multiple Observations. Diagnostics 2021, 11, 780. https://doi.org/10.3390/diagnostics11050780
Kalech M, Stern R, Lazebnik E. Minimal Cardinality Diagnosis in Problems with Multiple Observations. Diagnostics. 2021; 11(5):780. https://doi.org/10.3390/diagnostics11050780
Chicago/Turabian StyleKalech, Meir, Roni Stern, and Ester Lazebnik. 2021. "Minimal Cardinality Diagnosis in Problems with Multiple Observations" Diagnostics 11, no. 5: 780. https://doi.org/10.3390/diagnostics11050780
APA StyleKalech, M., Stern, R., & Lazebnik, E. (2021). Minimal Cardinality Diagnosis in Problems with Multiple Observations. Diagnostics, 11(5), 780. https://doi.org/10.3390/diagnostics11050780







