A Simulation-Based Methodology of Developing 3D Printed Anthropomorphic Phantoms for Microwave Imaging Systems
Abstract
1. Introduction
2. Materials and Methods
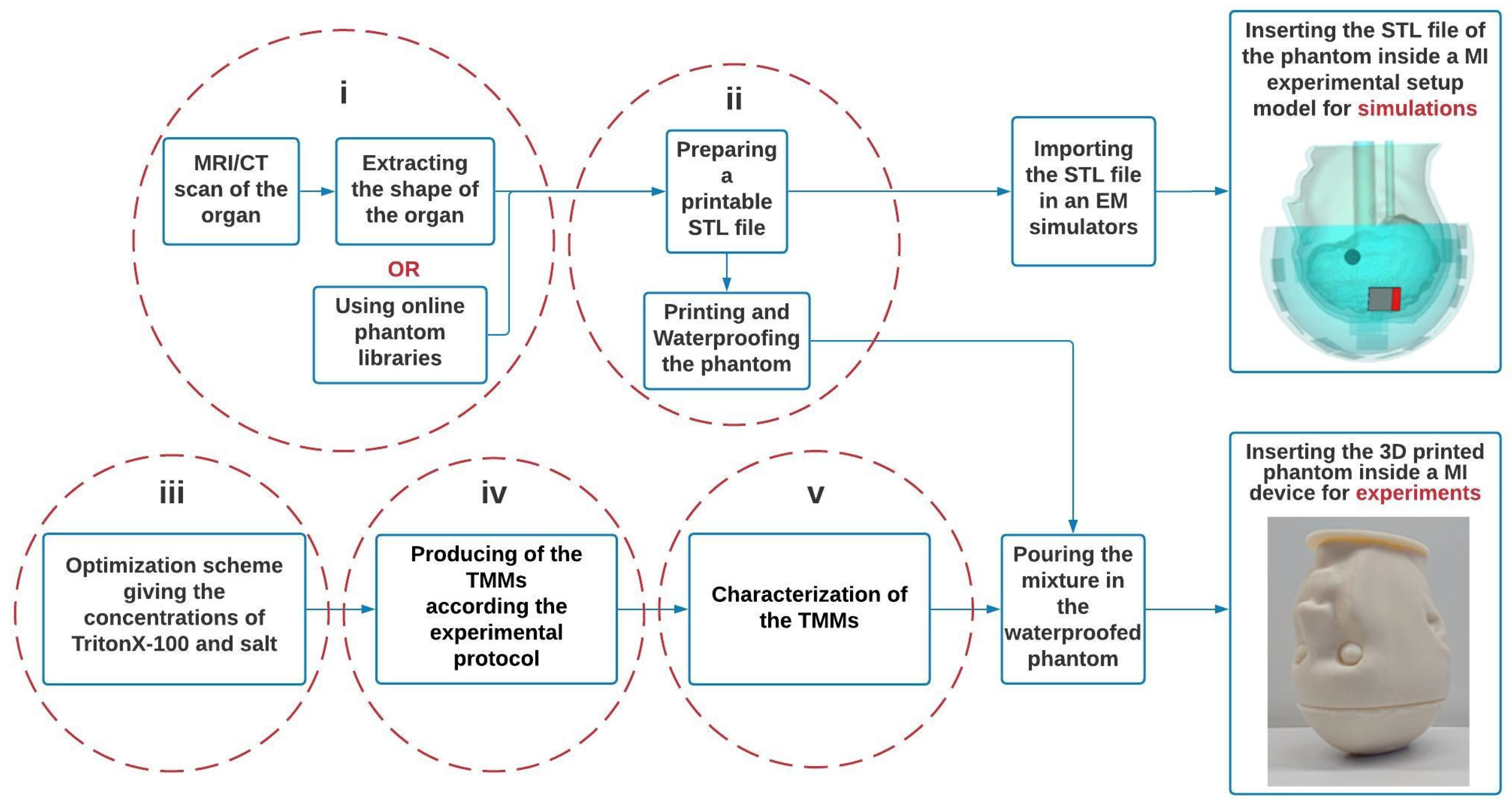
2.1. Flowchart
2.2. Tissue Mimicking Material (TMM) for 10 Biological Tissues
2.2.1. Introduction
2.2.2. Development
- Optimization Scheme
- Experimental protocol
- -
- Tare the balance while the empty beaker is upon the balance.
- -
- The masses of NaCl and deionized water should be added successively considering that taring during the adding process is necessary.
- -
- Using a magnetic bar for stirring will result in a homogenous solution. Tare the balance.
- -
- Add the mass of TritonX-100. Heat up TritonX-100 in a 45 ° C water bath since the liquid is very viscous and needs to be fluid.
- -
- Use the magnetic bar again while the solution is in a hot water bath to obtain a homogeneous mixture.
- -
- Keep the solution in a container at room temperature and away from light for its conservation.
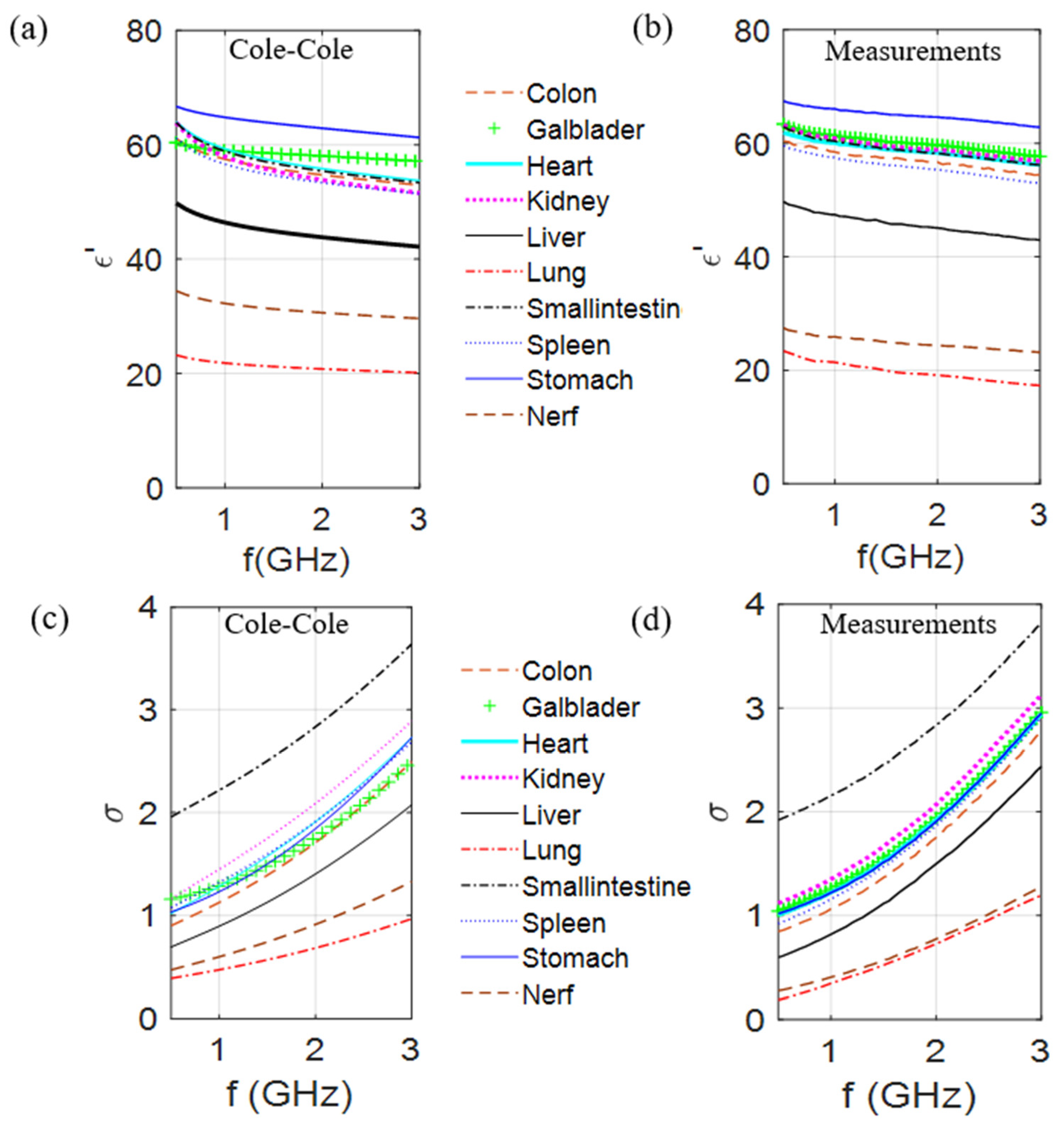
2.2.3. Dielectric Characterization
3. Results and Discussion
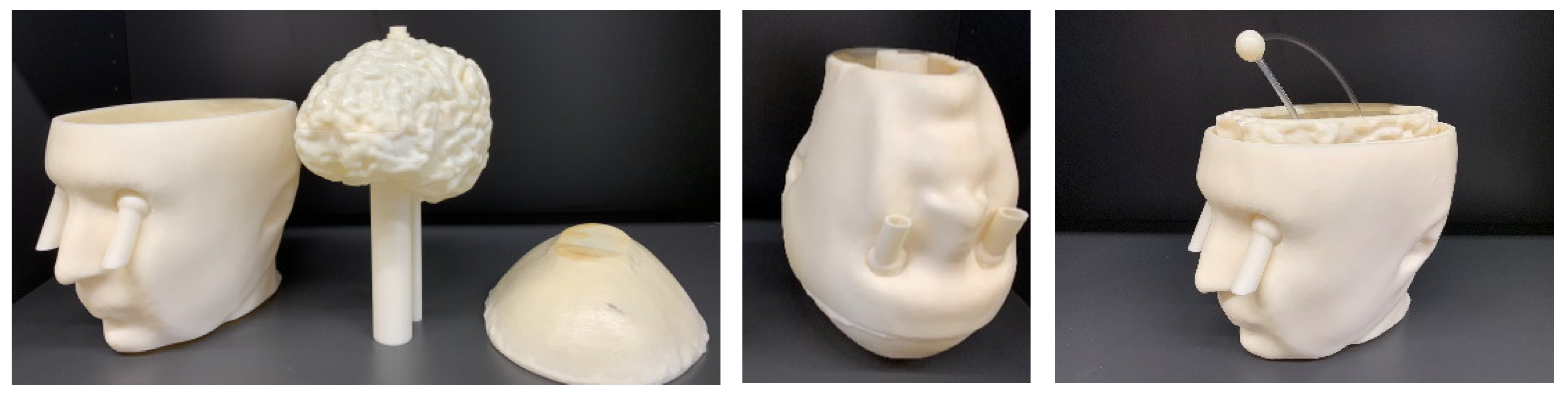
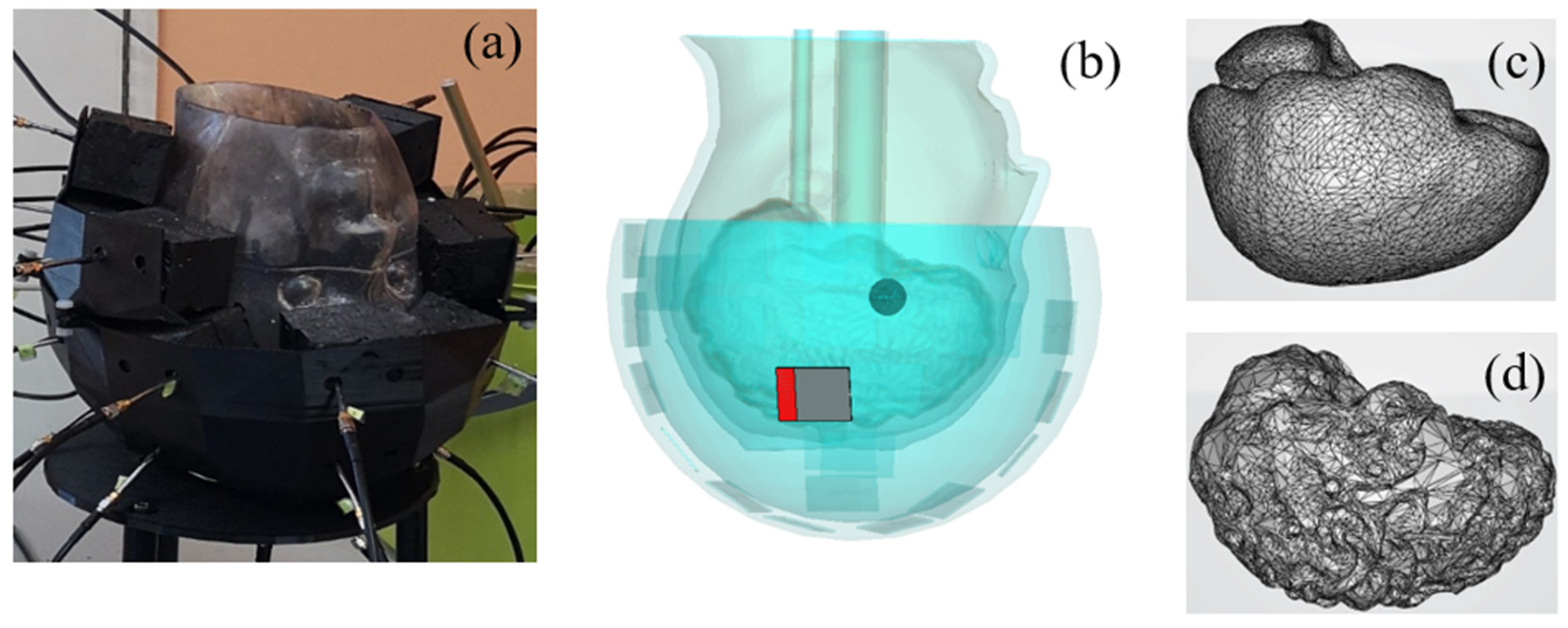
3.1. Description of the Test Case
3.2. TMM
3.3. Numerical Simulations of the Electric Field Inside and Outside the Head Phantom—Monopole Antenna Excitation
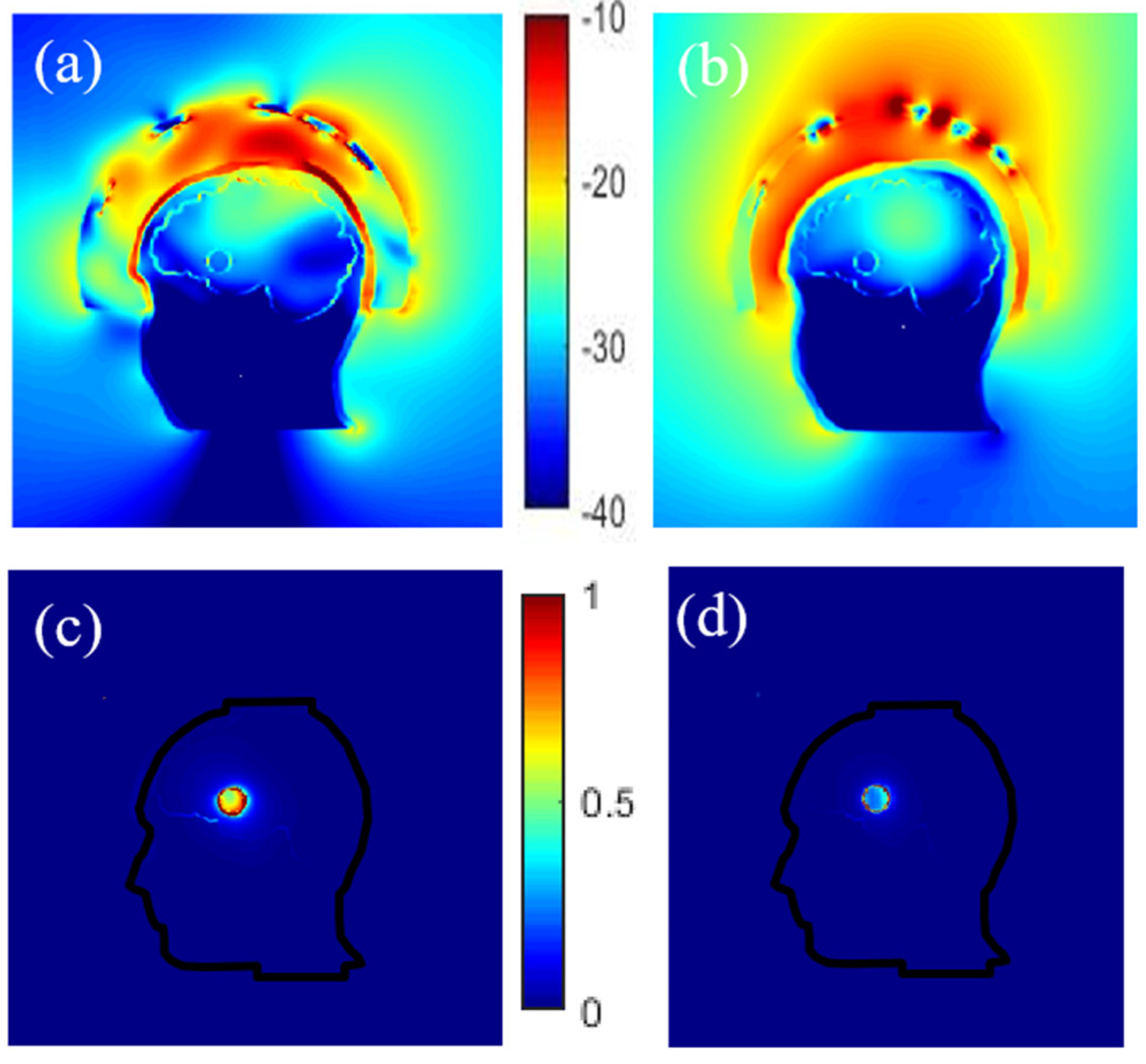
3.3.1. Effect of the Coupling Medium
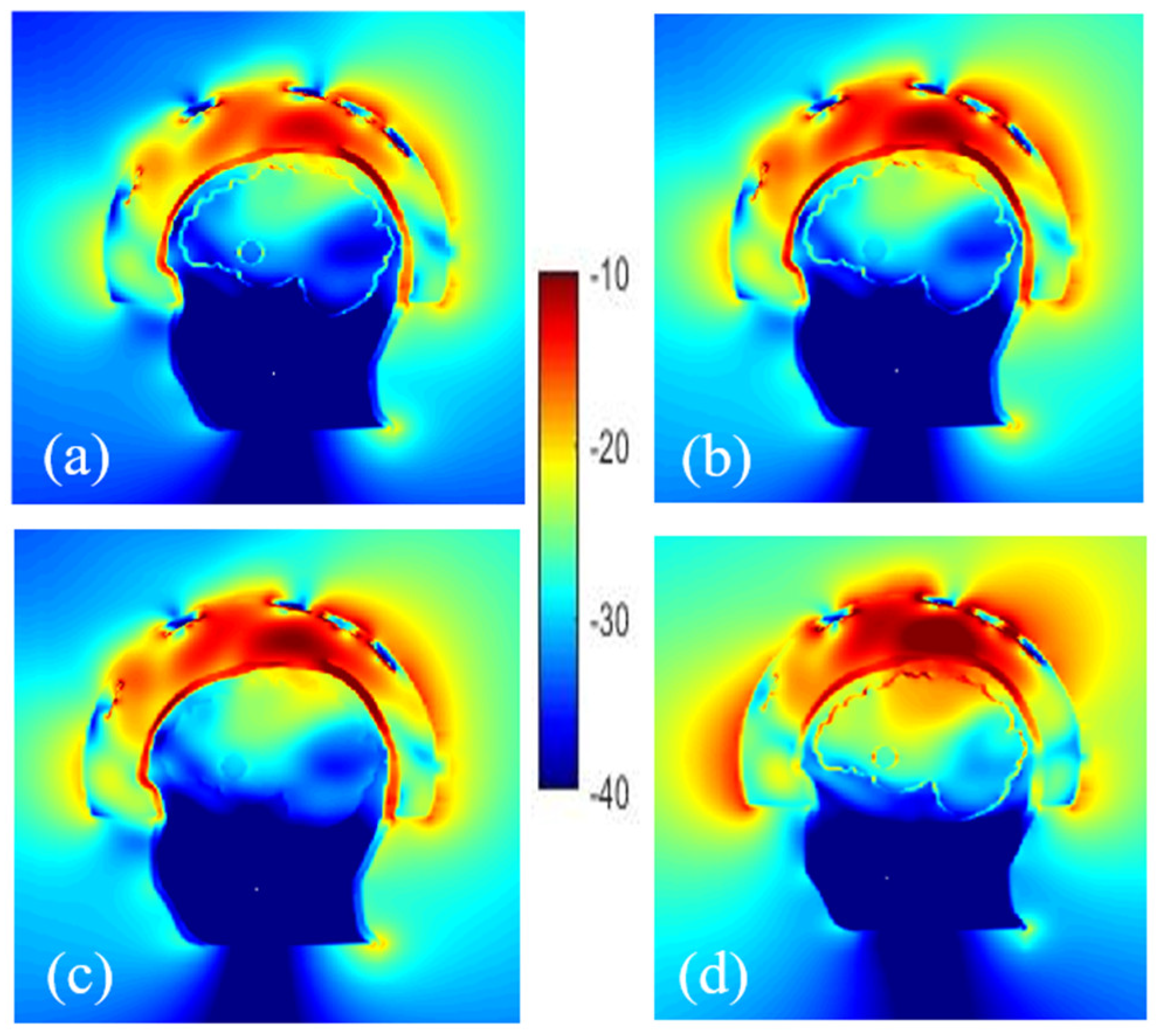
3.3.2. Effect of the Plastic
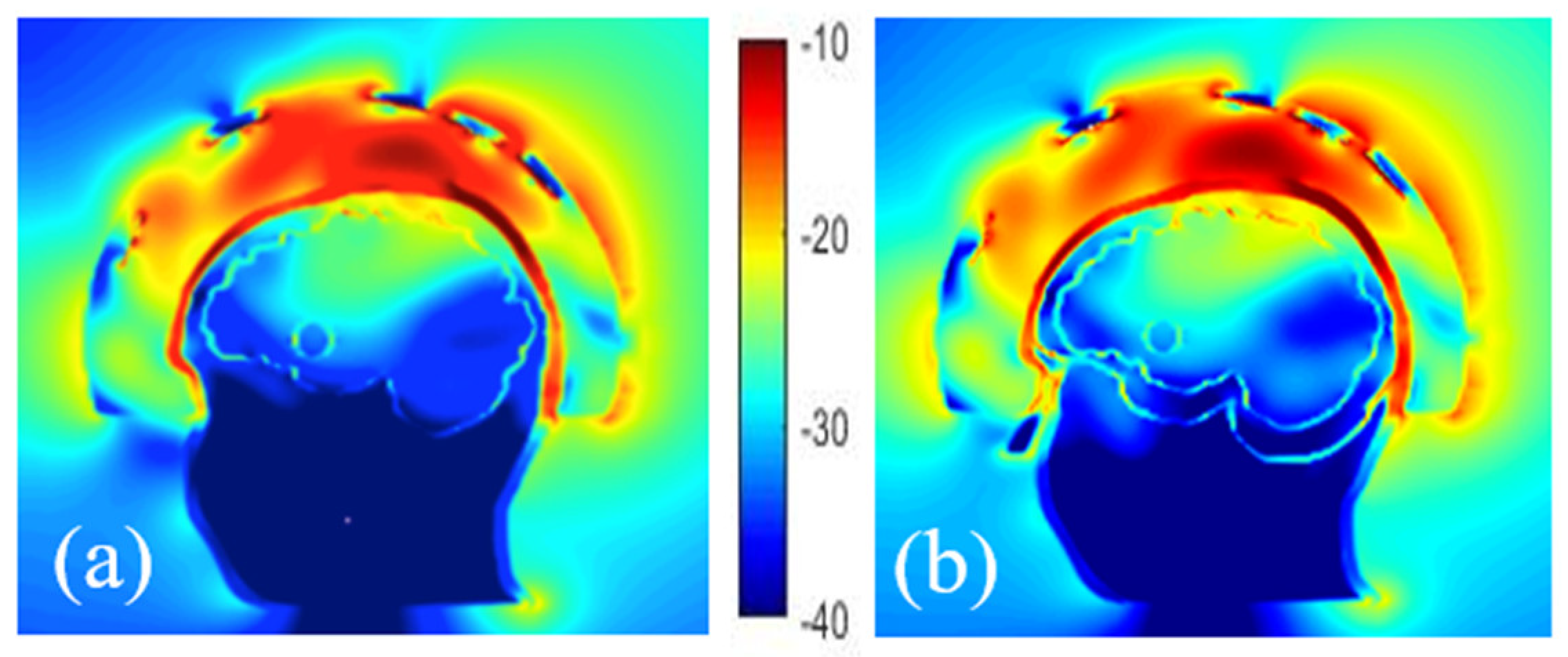
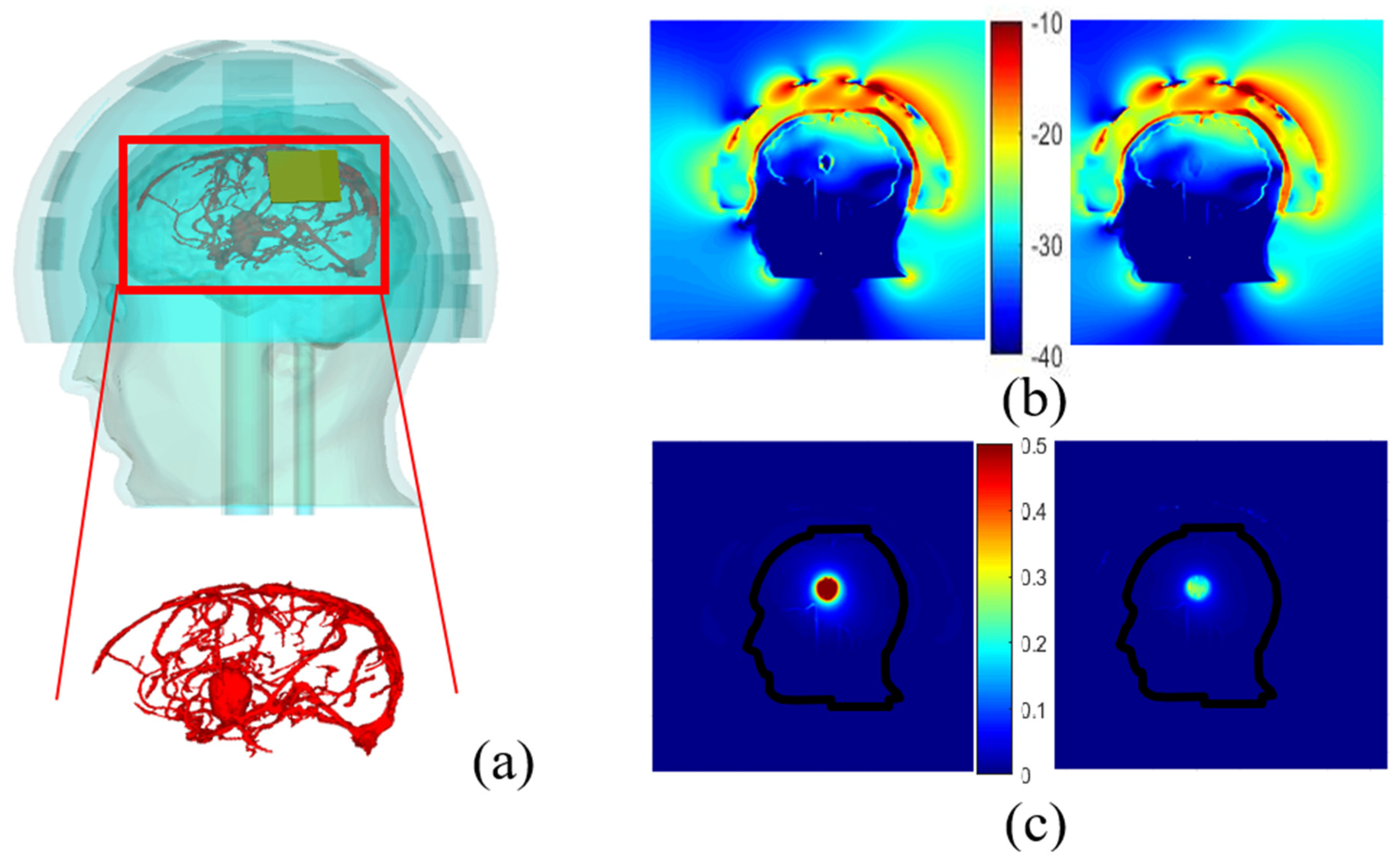
3.3.3. Effect of Phantom Complexity
- Number of cavities
- Vessels around a randomly shaped stroke
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Chandra, R.; Zhou, H.; Balasingham, I.; Narayanan, R.M. On the Opportunities and Challenges in Microwave Medical Sensing and Imaging. IEEE Trans. Biomed. Eng. 2015, 62, 1667–1682. [Google Scholar] [CrossRef] [PubMed]
- O’laughlin, D.; O’Halloran, M.; Maloney, B.M.; Glavin, M.; Jones, E.; Elahi, M.A. Microwave breast imaging: Clinical ad-vances and remaining challenges. IEEE Trans. Biomed. Eng. 2018, 65, 2580–2590. [Google Scholar] [CrossRef]
- Bolomey, J.C. Crossed viewpoints on microwave-based imaging for medical diagnosis: From genesis to earliest clinical outcomes, Chap.16. In The World of Applied Electromagnetics; Lakhtakia, A., Furse, C.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Shao, W.; McCollough, T. Advances in Microwave Near-Field Imaging: Prototypes, Systems, and Applications. IEEE Microw. Mag. 2020, 21, 94–119. [Google Scholar] [CrossRef]
- Vasquez, J.A.T.; Scapaticci, R.; Turvani, G.; Bellizzi, G.; Rodriguez-Duarte, D.O.; Joachimowicz, N.; Duchêne, B.; Tedeschi, E.; Casu, M.R.; Crocco, L.; et al. A Prototype Microwave System for 3D Brain Stroke Imaging. Sensors 2020, 20, 2607. [Google Scholar] [CrossRef] [PubMed]
- Crocco, L.; Vipiana, F. An Innovative Framework for Advancing Microwave Medical Imaging: The EM-ERALD European Network. In Proceedings of the 13th European Conference on Antennas and Propagation (EuCAP) IEEE, Krakow, Poland, 31 March–5 April 2019. [Google Scholar]
- Persson, M.; Fhager, A.; Trefná, H.D.; Yu, Y.; McKelvey, T.; Pegenius, G.; Karlsson, J.E.; Elam, M. Micro-wave-based stroke diagnosis making global prehospital thrombolytic treatment possible. IEEE Trans. Bio-Med Eng. 2014, 61, 2806–2817. [Google Scholar] [CrossRef] [PubMed]
- Mobashsher, A.T.; Bialkowski, K.S.; Abbosh, A.M.; Crozier, S. Design and experimental evaluation of a non-invasive microwave head imaging system for intracranial hemorrhage detection. PLoS ONE 2016, 11, e0152351. [Google Scholar]
- Hopfer, M.; Planas, R.; Hamidipour, A.; Henriksson, T.; Semenov, S. Electromagnetic Tomography for Detection, Differentiation, and Monitoring of Brain Stroke: A Virtual Data and Human Head Phantom Study. IEEE Antennas Propag. Mag. 2017, 59, 86–97. [Google Scholar] [CrossRef]
- Fhager, A.; Candefjord, S.; Elam, M.; Persson, M. Microwave Diagnostics Ahead: Saving Time and the Lives of Trauma and Stroke Patients. IEEE Microw. Mag. 2018, 19, 78–90. [Google Scholar] [CrossRef]
- Bieniosek, M.F.; Lee, B.J.; Levin, C.S. Technical Note: Characterization of custom 3D printed multimodality imaging phantoms. Med Phys. 2015, 42, 5913–5918. [Google Scholar] [CrossRef]
- Burfeindt, M.J.; Colgan, T.J.; Mays, R.O.; Shea, J.D.; Behdad, N.; Van Veen, B.D.; Hagness, S.C. MRI-Derived 3-D-Printed Breast Phantom for Microwave Breast Imaging Validation. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1610–1613. [Google Scholar] [CrossRef]
- Joachimowicz, N.; Duchêne, B.; Conessa, C.; Meyer, O. Easy-to-produce adjustable realistic breast phantoms for microwave imaging. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–4. [Google Scholar]
- Rydholm, T.; Fhager, A.; Persson, M.; Meaney, P.M. A First Evaluation of the Realistic Supelec-Breast Phantom. IEEE J. Electromagn. Rf Microw. Med. Biol. 2017, 1, 59–65. [Google Scholar] [CrossRef]
- Koutsoupidou, M.; Karanasiou, I.S.; Kakoyiannis, C.G.; Groumpas, E.; Conessa, C.; Joachimowicz, N.; Duchêne, B. Evaluation of a tumor detection microwave system with a realistic breast phantom. Microw. Opt. Technol. Lett. 2017, 59, 6–10. [Google Scholar] [CrossRef]
- Casu, M.R.; Vacca, M.; Tobon Vasquez, J.A.; Pulimeno, A.; Sarwar, I.; Solimene, R.; Vipiana, F.A. COTS-based mi-crowave imaging system for breast-cancer detection. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 804–814. [Google Scholar] [CrossRef]
- Felicio, J.M.; Bioucas-Dias, J.M.; Costa, J.R.; Fernandes, C.A. Microwave Breast Imaging Using a Dry Setup. IEEE Trans. Comput. Imaging 2019, 6, 167–180. [Google Scholar] [CrossRef]
- Reimer, T.; Solis-Nepote, M.; Pistorius, S. The Application of an Iterative Structure to the Delay-and-Sum and the Delay-Multiply-and-Sum Beamformers in Breast Microwave Imaging. Diagnostics 2020, 10, 411. [Google Scholar] [CrossRef] [PubMed]
- Joachimowicz, N.; Duchêne, B.; Conessa, C.; Meyer, O. Anthropomorphic breast and head phantoms for microwave imaging. Diagnostics 2018, 8, 85. [Google Scholar] [CrossRef]
- Abedi, S.; Joachimowicz, N.; Meyer, O.; Picard, D.; Roussel, H. Phantoms for a Novel Generation of Medical Microwave Imaging Devices. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–4. [Google Scholar]
- Kraszewski, A. Prediction of the Dielectric Properties of Two-Phase Mixtures. J. Microw. Power 1977, 12, 216–222. [Google Scholar] [CrossRef]
- Graedel, N.N.; Polimeni, J.R.; Guerin, B.; Gagoski, B.; Wald, L.L. An anatomically realistic temperature phantom for radiofrequency heating measurements. Magn. Reson. Med. 2015, 73, 442–450. [Google Scholar] [CrossRef]
- Wang, K.; Ho, C.-C.; Zhang, C.; Wang, B. A Review on the 3D Printing of Functional Structures for Medical Phantoms and Regenerated Tissue and Organ Applications. Engineering 2017, 3, 653–662. [Google Scholar] [CrossRef]
- Haleem, A.; Javaid, M.; Vaishya, R. 3D printing applications for the treatment of cancer. Clin. Epidemiol. Glob. Heal. 2020, 8, 1072–1076. [Google Scholar] [CrossRef]
- Asfia, A.; Novak, J.I.; Mohammed, M.I.; Rolfe, B.; Kron, T. A review of 3D printed patient specific immobilisation devices in radiotherapy. Phys. Imaging Radiat. Oncol. 2020, 13, 30–35. [Google Scholar] [CrossRef] [PubMed]
- Filippou, V.; Tsoumpas, C. Recent advances on the development of phantoms using 3D printing for imaging with CT, MRI, PET, SPECT, and ultrasound. Med Phys. 2018, 45, e740–e760. [Google Scholar] [CrossRef]
- Mobashsher, A.T.; Abbosh, A.M. Artificial Human Phantoms: Human Proxy in Testing Microwave Apparatuses That Have Electromagnetic Interaction with the Human Body. IEEE Microw. Mag. 2015, 16, 42–62. [Google Scholar] [CrossRef]
- Pokorny, T.; Tesarik, J. 3D Printed Multi-layer Molds of Human Head Tissue Phantoms for Microwave Stroke Detection. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium-Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 1424–1427. [Google Scholar]
- Garrett, J.; Fear, E. A New Breast Phantom with a Durable Skin Layer for Microwave Breast Imaging. IEEE Trans. Antennas Propag. 2015, 63, 1693–1700. [Google Scholar] [CrossRef]
- McDermott, B.; Porter, E.; Santorelli, A.; Divilly, B.; Morris, L.; Jones, M.; McGinley, B.; O’Halloran, M. Anatomically and Dielectrically Realistic Microwave Head Phantom with Circulation and Reconfigurable Lesions. Prog. Electromagn. Res. 2017, 78, 47–60. [Google Scholar] [CrossRef]
- Khuda, I.E. A Comprehensive Review on Design and Development of Human Breast Phantoms for Ultra-Wide Band Breast Cancer Imaging Systems. Eng. J. 2017, 21, 183–206. [Google Scholar] [CrossRef][Green Version]
- Joachimowicz, N.; Vasquez, J.T.; Turvani, G.; Dassano, G.; Casu, M.R.; Vipiana, F.; Duchene, B.; Scapaticci, R.; Crocco, L. Head Phantoms for a Microwave Imaging System Dedicated to Cerebrovascular Disease Monitoring. In Proceedings of the 2018 IEEE Conference on Antenna Measurements & Applications (CAMA), Vasteras, Sweden, 3–6 September 2018; pp. 1–3. [Google Scholar]
- Joachimowicz, N.; Conessa, C.; Henriksson, T.; Duchene, B. Breast Phantoms for Microwave Imaging. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1333–1336. [Google Scholar] [CrossRef]
- Abedi, S.; Savazzi, M.; Istuk, N.; Porter, E.; O’Halloran, M.; Conceição, R.C.; Felício, J.M.; Fernandes, C.A.; Roussel, H.; Joachimowicz, N. An anthropomorphic axillary region phantom. In Proceedings of the ICEAA-IEEE APWC 2020, Honolulu, HI, USA, 10–14 August 2020. [Google Scholar]
- Savazzi, M.; Abedi, S.; Ištuk, N.; Joachimowicz, N.; Roussel, H.; Porter, E.; O’Halloran, M.; Costa, J.R.; Fernandes, C.A.; Felício, J.M.; et al. Development of an Anthropomorphic Phantom of the Axillary Region for Micro-wave Imaging Assessment. Sensors 2020, 20, 4968. [Google Scholar] [CrossRef]
- Bjelogrlic, M.; Volery, M.; Fuchs, B.; Thiran, J.-P.; Mosig, J.R.; Mattes, M. Stratified spherical model for microwave imaging of the brain: Analysis and experimental validation of transmitted power. Microw. Opt. Technol. Lett. 2018, 60, 1042–1048. [Google Scholar] [CrossRef]
- Fasoula, A.; Duchesne, L.; Gil Cano, J.D.; Lawrence, P.; Robin, G.; Bernard, J.-G. On-Site Validation of a Microwave Breast Imaging System, before First Patient Study. Diagnostics 2018, 8, 53. [Google Scholar] [CrossRef]
- Amin, B.; Kelly, D.; Shahzad, A.; O’Halloran, M.; Elahi, M.A. Microwave calcaneus phantom for bone imaging applications. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–5. [Google Scholar]
- Amin, B.; Shahzad, A.; Kelly, D.; O’Halloran, M.; Elahi, A. Anthropomorphic Calcaneus Phantom for Microwave Bone Imaging Applications. IEEE J. Electromagn. Rf Microw. Med. Biol. 2020, 1. [Google Scholar] [CrossRef]
- WIPL-D d.o.o. Wipl-d pro description. Available online: https://wipl-d.com/products/wipl-d-pro/ (accessed on 28 February 2020).
- Meaney, P.M.; Fox, C.J.; Geimer, S.D.; Paulsen, K.D. Electrical Characterization of Glycerin: Water Mixtures: Implications for Use as a Coupling Medium in Microwave Tomography. IEEE Trans. Microw. Theory Tech. 2017, 65, 1471–1478. [Google Scholar] [CrossRef] [PubMed]
- Hartsgrove, G.; Kraszewski, A.; Surowiec, A. Simulated biological materials for electromagnetic radiation absorption studies. Bioelectromagn. 1987, 8, 29–36. [Google Scholar] [CrossRef]
- Chou, C.K.; Chen, G.W.; Guy, A.W.; Luk, K.H. Formulas for preparing phantom muscle tissue at various radiofrequencies. Bioelectromagnetics: Journal of the Bioelectromagnetics Society, The Society for Physical Regulation in Biology and Medicine. Eur. Bioelectromagn. Assoc. 1984, 5, 435–441. [Google Scholar] [CrossRef]
- Oziel, M.; Hjouj, M.; Rubinsky, B.; Korenstein, R. Multifrequency Analysis of Single Inductive Coil Measurements Across a Gel Phantom Simulation of Internal Bleeding in the Brain. Bioelectromagnetics 2020, 41, 21–33. [Google Scholar] [CrossRef]
- Mashal, A.; Gao, F.; Hagness, S.C. Heterogeneous anthropomorphic phantoms with realistic dielectric properties for microwave breast imaging experiments. Microw. Opt. Technol. Lett. 2011, 53, 1896–1902. [Google Scholar] [CrossRef]
- Porter, E.; Fakhoury, J.; Oprisor, R.; Coates, M.; Popovic, M. Improved tissue phantoms for experimental validation of microwave breast cancer detection. In Proceedings of the 4th European Conference on Antennas and Propagation (EuCAP), Barcelona, Spain, 12–16 April 2010; pp. 1–5. [Google Scholar]
- Kobayashi, T.; Nojima, T.; Yamada, K.; Uebayashi, S. Dry phantom composed of ceramics and its application to SAR estimation. IEEE Trans. Microw. Theory Tech. 1993, 41, 136–140. [Google Scholar] [CrossRef]
- Lazebnik, M.; Okoniewski, M.; Booske, J.H.; Hagness, S.C. Highly Accurate Debye Models for Normal and Malignant Breast Tissue Dielectric Properties at Microwave Frequencies. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 822–824. [Google Scholar] [CrossRef]
- Stogryn, A. Equations for Calculating the Dielectric Constant of Saline Water (Correspondence). IEEE Trans. Microw. Theory Tech. 1971, 19, 733–736. [Google Scholar] [CrossRef]
- Greffe, J.L.; Grosse, C. Static permittivity of emulsions. In Dielectric Properties of Heterogeneous Materials; Elsevier: Amsterdam, The Netherlands, 1992; pp. 41–100. [Google Scholar]
- IFAC. Available online: http://niremf.ifac.cnr.it/tissprop/htmlclie/htmlclie.php (accessed on 28 May 2020).
- Walter, E. Numerical Methods and Optimization: A Consumer Guide; Springer: Cham, Switzerland, 2014. [Google Scholar]
- La Gioia, A.; Porter, E.; Merunka, I.; Shahzad, A.; Salahuddin, S.; Jones, M.; O’Halloran, M. Open-Ended Coaxial Probe Technique for Dielectric Measurement of Biological Tissues: Challenges and Common Practices. Diagnostics 2018, 8, 40. [Google Scholar] [CrossRef]
- Scapaticci, R.; Tobon, J.; Bellizzi, G.; Vipiana, F.; Crocco, L. Design and Numerical Characterization of a Low-Complexity Microwave Device for Brain Stroke Monitoring. IEEE Trans. Antennas Propag. 2018, 66, 7328–7338. [Google Scholar] [CrossRef]
- Rodriguez-Duarte, D.O.; Vasquez, J.A.T.; Scapaticci, R.; Crocco, L.; Vipiana, F. Brick-Shaped Antenna Module for Microwave Brain Imaging Systems. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 2057–2061. [Google Scholar] [CrossRef]
- Rydholm, T.; Fhager, A.; Persson, M.; Geimer, S.D.; Meaney, P.M. Effects of the plastic of the realistic GeePS-L2S-Breast phantom. Diagnostics 2018, 8, 61. [Google Scholar] [CrossRef]
- Faenger, B.; Ley, S.; Helbig, M.; Sachs, J.; Hilger, I. Breast phantom with a conductive skin layer and conductive 3D-printed anatomical structures for microwave imaging. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 1065–1068. [Google Scholar]
- Geffrin, J.-M.; Sabouroux, P.; Eyraud, C. Free space experimental scattering database continuation: Experimental set-up and measurement precision. Inverse Probl. 2005, 21, S117–S130. [Google Scholar] [CrossRef]
- Mallorqui, J.; Joachimowicz, N.; Bolomey, J.; Broquetas, A. Database of "In Vivo" Measurements for Quantitative Microwave Imaging and Reconstruction Algorithms. IEEE Antennas Propag. Mag. 1995, 37, 87. [Google Scholar] [CrossRef][Green Version]
- Singh, T.; Abedi, S.; Nikovic, B.; Stevanovic, M.; joachimowicz, N.; Roussel, H.; Kolundzjja, B. Smart simplification of Anthropomorphic Head Phantom Aimed for Microwave imaging. In Proceedings of the 15th European Conference on Antenna and Propagation (EuCAP), Dusseldorf, Germany, 22–26 March 2021. (Accepted). [Google Scholar]

| Mixture Components Given by the Kraszewski and Böttcher’s Binary Laws | Kraszewski–Böttcher and Cole–Cole Dielectic Properties | |||
|---|---|---|---|---|
| Tissue | TX-100 (vol %) | NaCl (g/L) | (S/m) | |
| Kraszewski–Böttcher | Kraszewski–Böttcher | Binary law–Ref [51] | Binary law–Ref [51] | |
| Brain | 34–36 | 6.8–6.9 | 41–42 | 1.0–1.0 |
| CSF | 5–6 | 13.9–14.0 | 68–68 | 2.5–2.5 |
| Muscle | 21–22 | 5.5–5.4 | 54–55 | 1.0–1.0 |
| Bone | 80–75 | 1.0–2.0 | 12–12 | 0.2–0.2 |
| Blood | 14–14 | 9.2–9.0 | 60–61 | 1.6–1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abedi, S.; Joachimowicz, N.; Phillips, N.; Roussel, H. A Simulation-Based Methodology of Developing 3D Printed Anthropomorphic Phantoms for Microwave Imaging Systems. Diagnostics 2021, 11, 376. https://doi.org/10.3390/diagnostics11020376
Abedi S, Joachimowicz N, Phillips N, Roussel H. A Simulation-Based Methodology of Developing 3D Printed Anthropomorphic Phantoms for Microwave Imaging Systems. Diagnostics. 2021; 11(2):376. https://doi.org/10.3390/diagnostics11020376
Chicago/Turabian StyleAbedi, Soroush, Nadine Joachimowicz, Nicolas Phillips, and Hélène Roussel. 2021. "A Simulation-Based Methodology of Developing 3D Printed Anthropomorphic Phantoms for Microwave Imaging Systems" Diagnostics 11, no. 2: 376. https://doi.org/10.3390/diagnostics11020376
APA StyleAbedi, S., Joachimowicz, N., Phillips, N., & Roussel, H. (2021). A Simulation-Based Methodology of Developing 3D Printed Anthropomorphic Phantoms for Microwave Imaging Systems. Diagnostics, 11(2), 376. https://doi.org/10.3390/diagnostics11020376







