Automated COVID-19 and Heart Failure Detection Using DNA Pattern Technique with Cough Sounds
Abstract
:1. Introduction
- New local feature generator based on graph theory and the chemical structure of nucleotide basic units of the DNA molecule, which we labelled as DNA pattern-based.
- New prospectively acquired dataset comprising cough sounds recorded from healthy subjects, COVID-19, and HF patients using basic smart phone microphones, which we divided into standardized one-second sound segments for analysis.
- To the best our knowledge, this is the first work to automatically classify healthy subjects, HF and COVID-19 patients using cough sounds signals.
- The major contributions of this study include:
- Three distinct clinically relevant classification problems were defined: Case 1, COVID-19 vs. healthy; Case 2, HF vs. healthy; and Case 3, COVID-19 vs. HF vs. healthy.
- The DNA pattern- and ImRMR-based model combined with the standard kNN classifier attained excellent results, with greater than 99% accuracy for every Case.
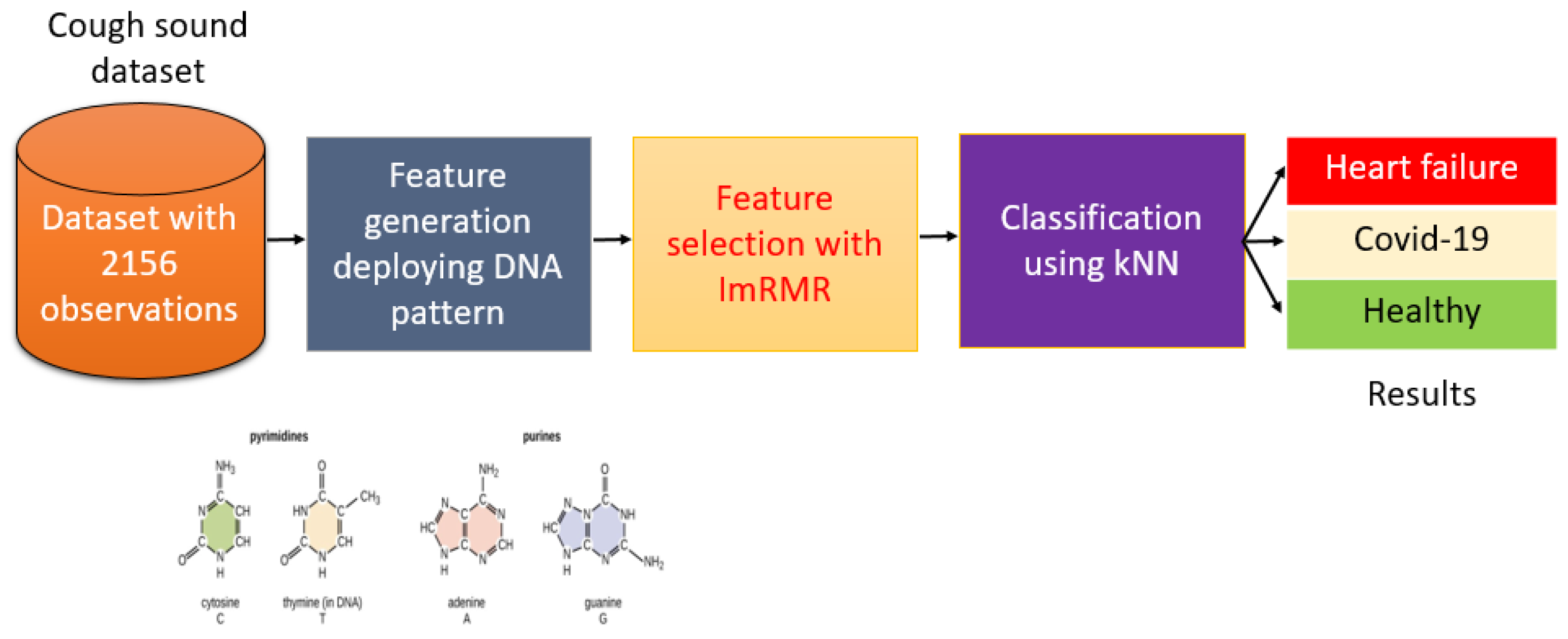
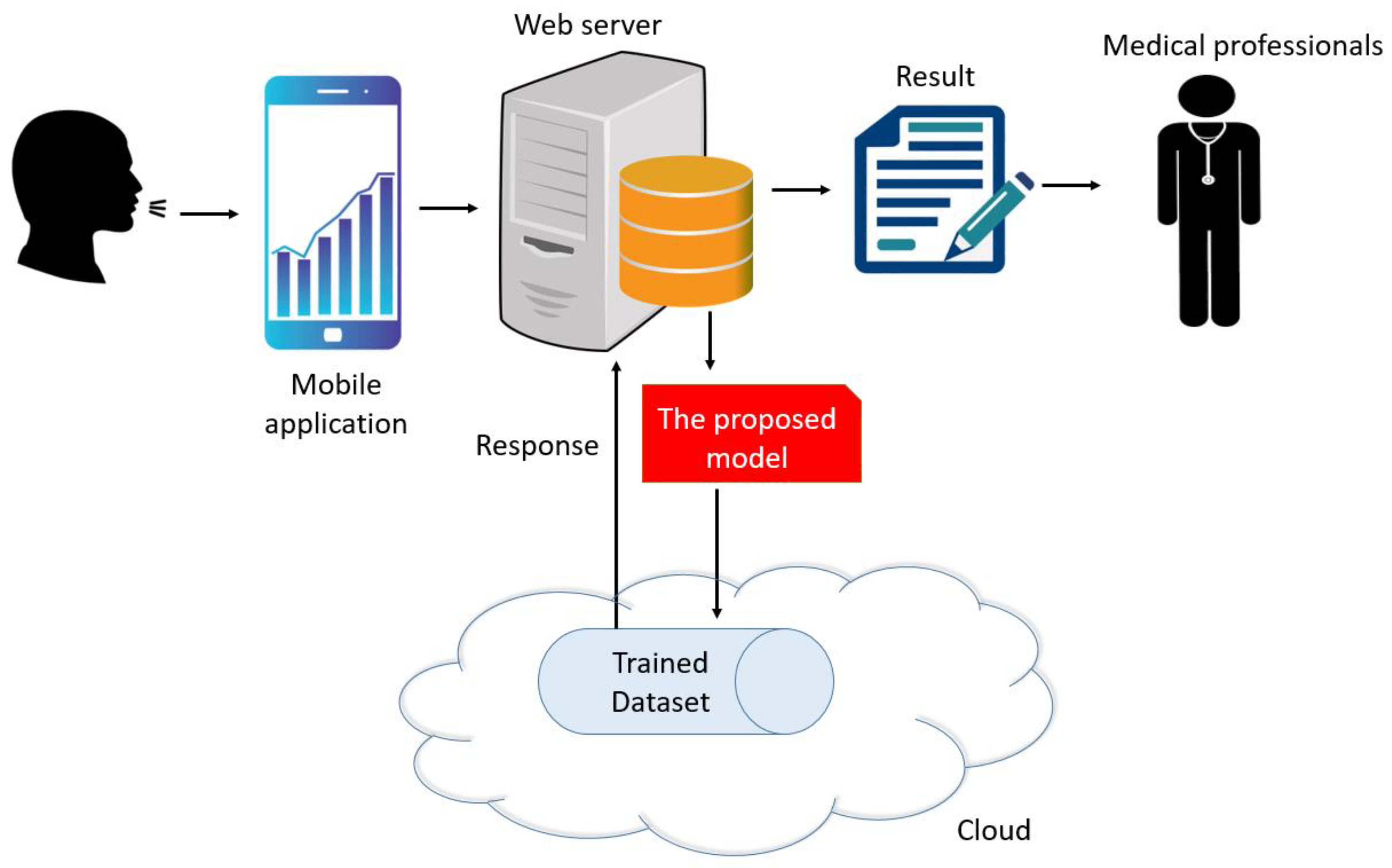
2. Material and Method
2.1. Material
2.2. Method
| Algorithm 1. Proposed algorithm cough sound-based automatic COVID-19 and HF detection |
| Input: Cough dataset (CD) with a size of 2156 × 44,100 (2156 is the total number of observations and 44,100 is the length of each observation. The sampling rate of the sound signal is 44.1 kHz), labels (y) with a length of 2156. Output: Results |
| 01: for c = 1 to 2156 do 02: Read each cough sound. 03: Extract 1024 features deploying DNA patterns. 04: end for c 05: Apply ImRMR to features generated. 06: Classify the features selected using kNN. 07: Obtain results. |
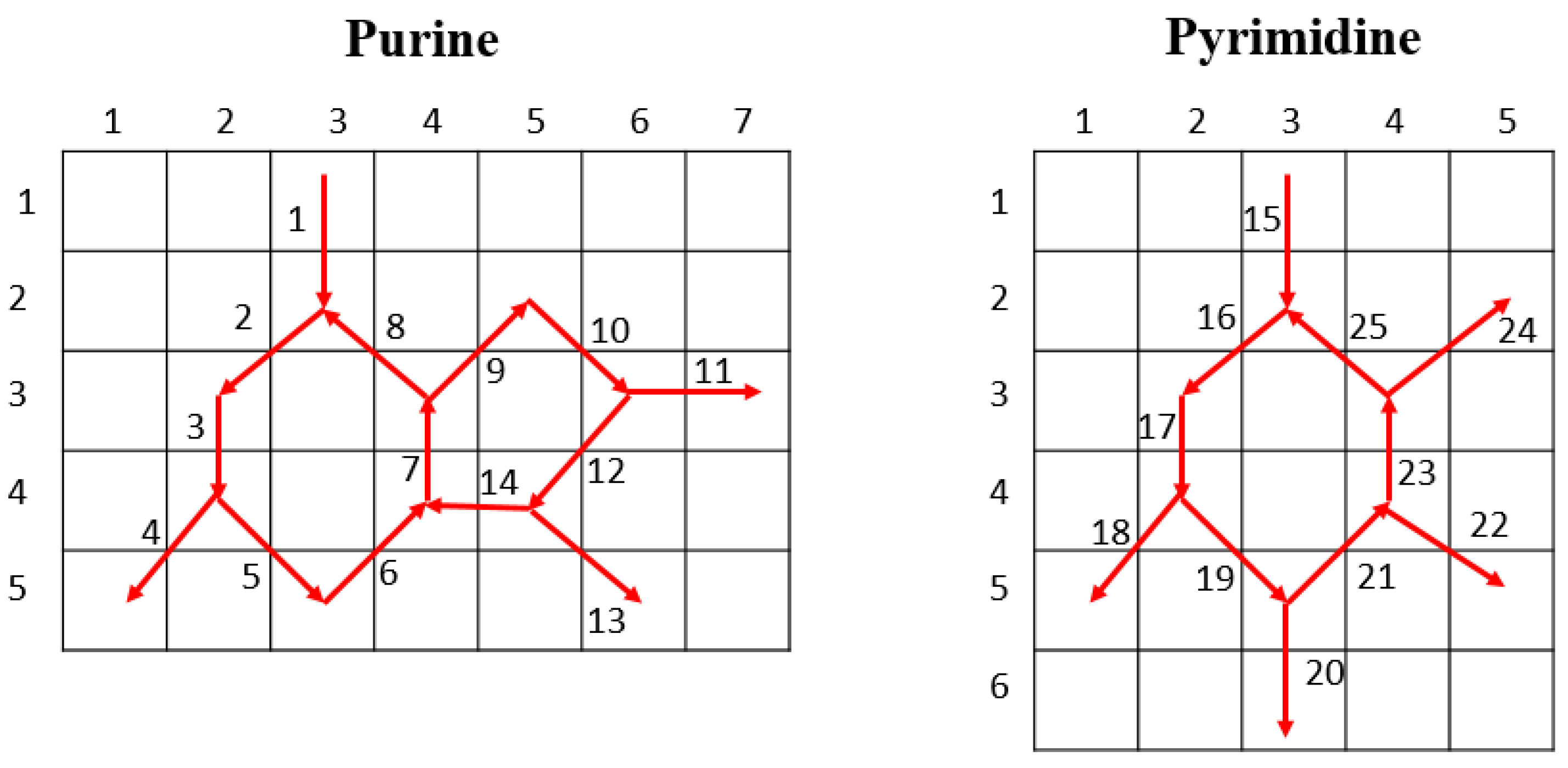
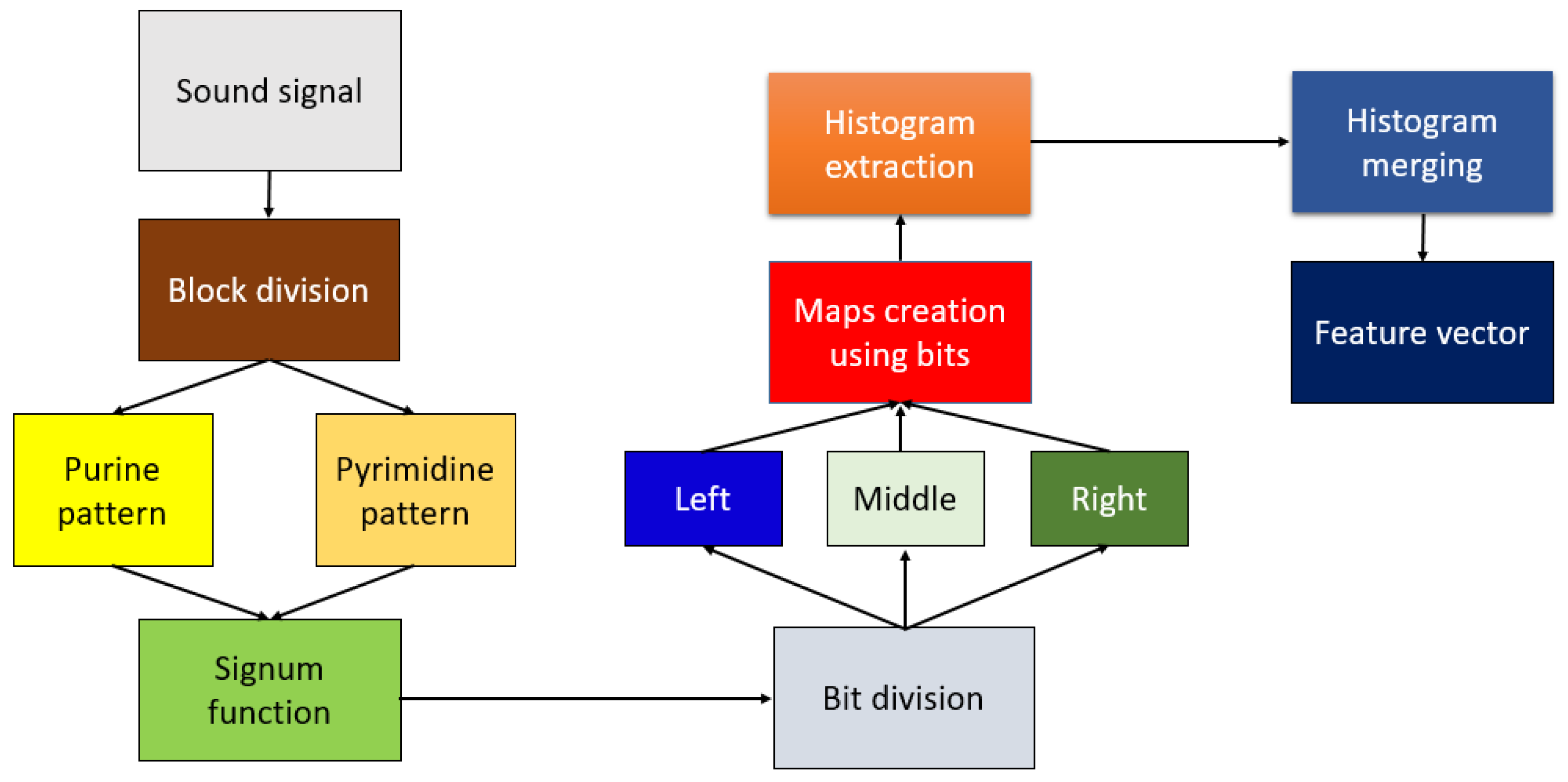
2.2.1. DNA Pattern
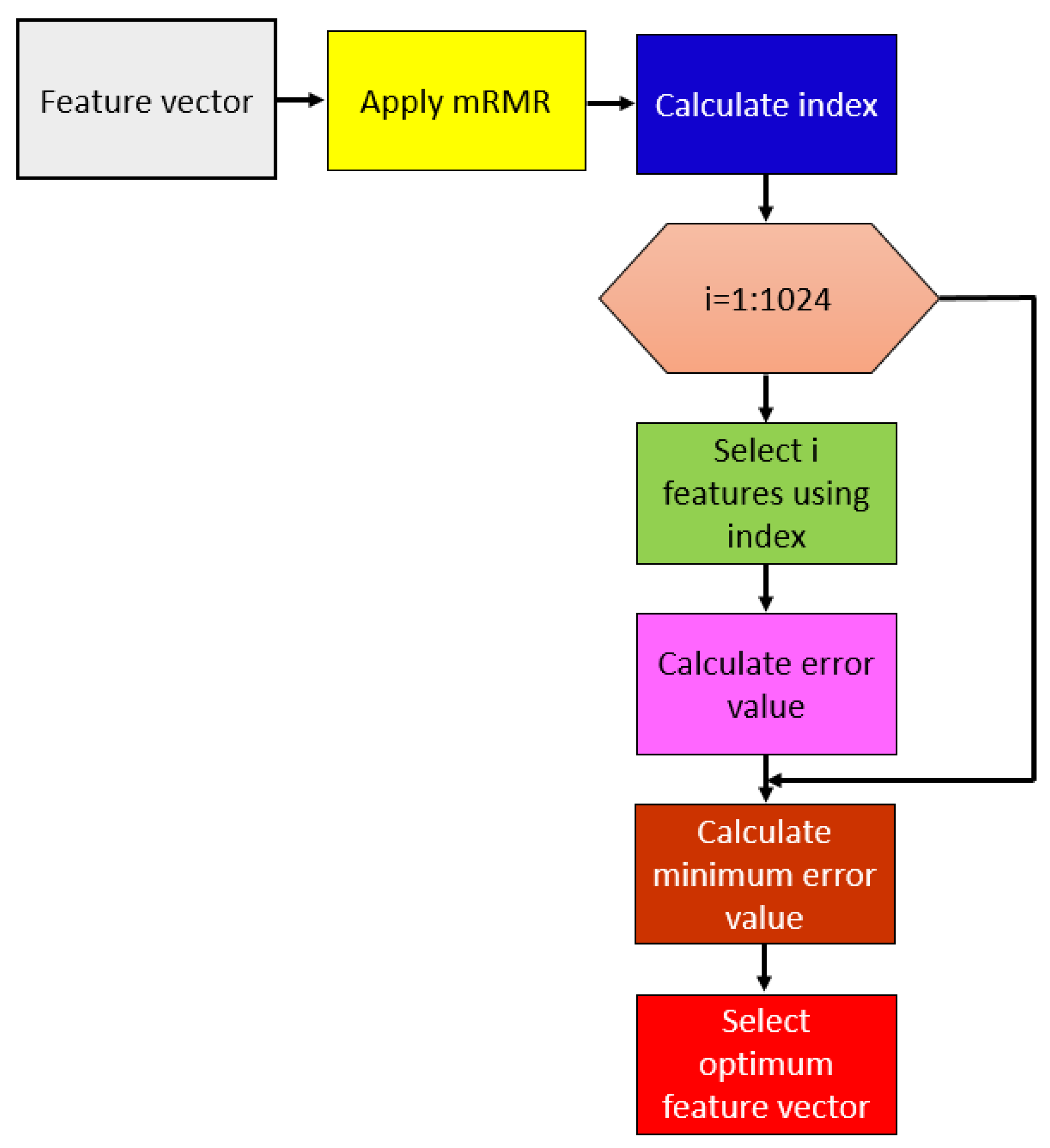
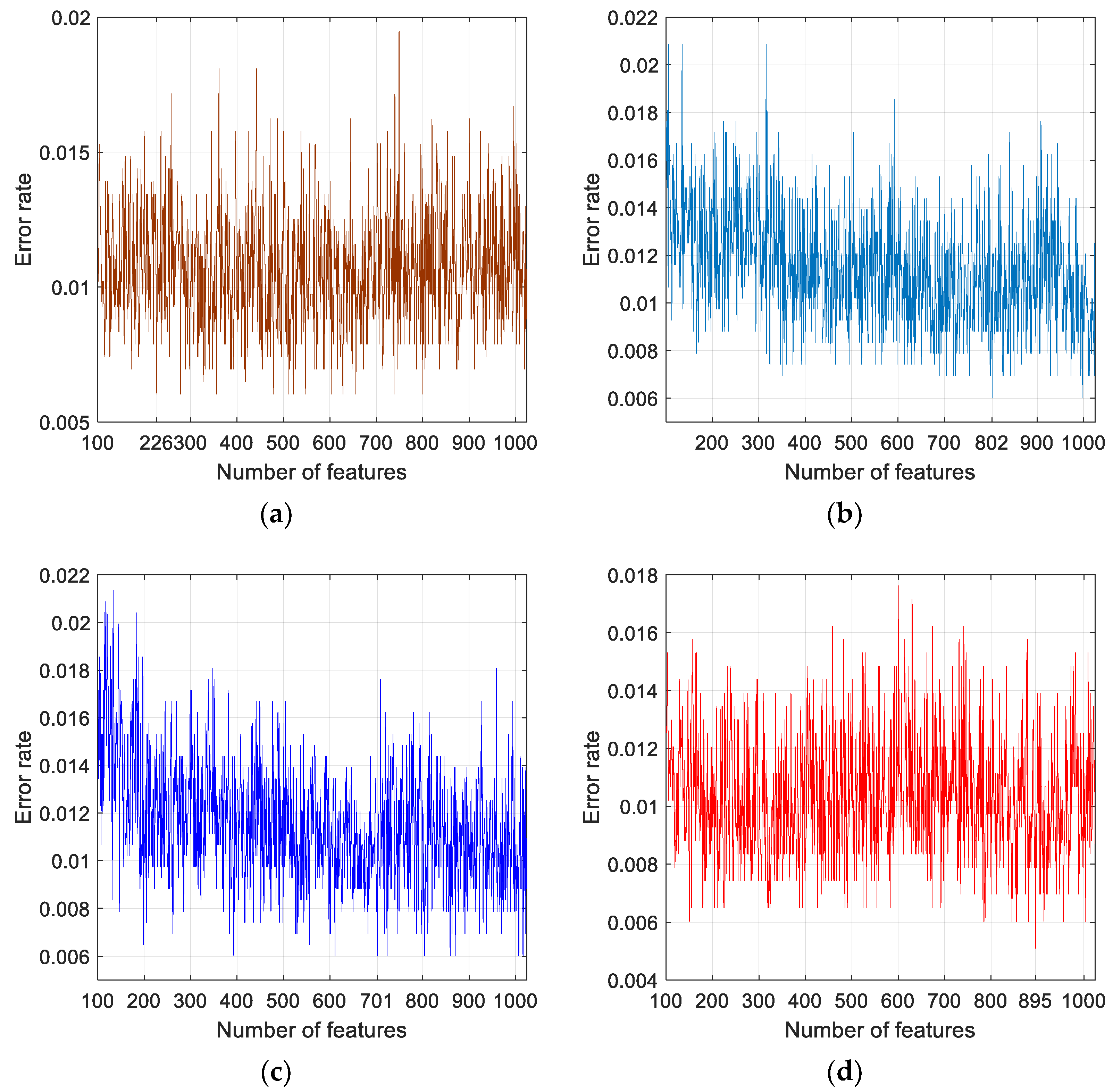
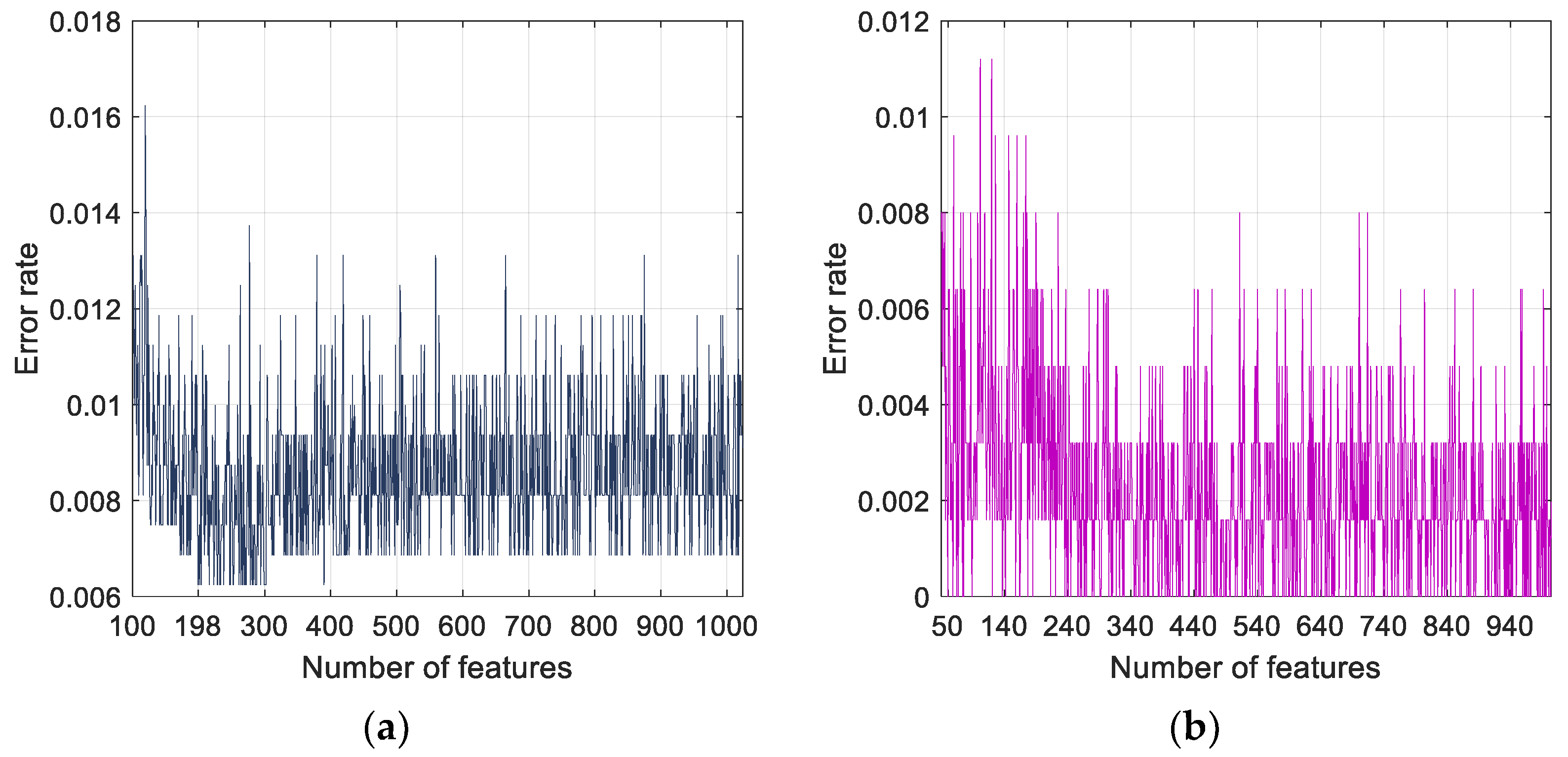
2.2.2. Feature Selection
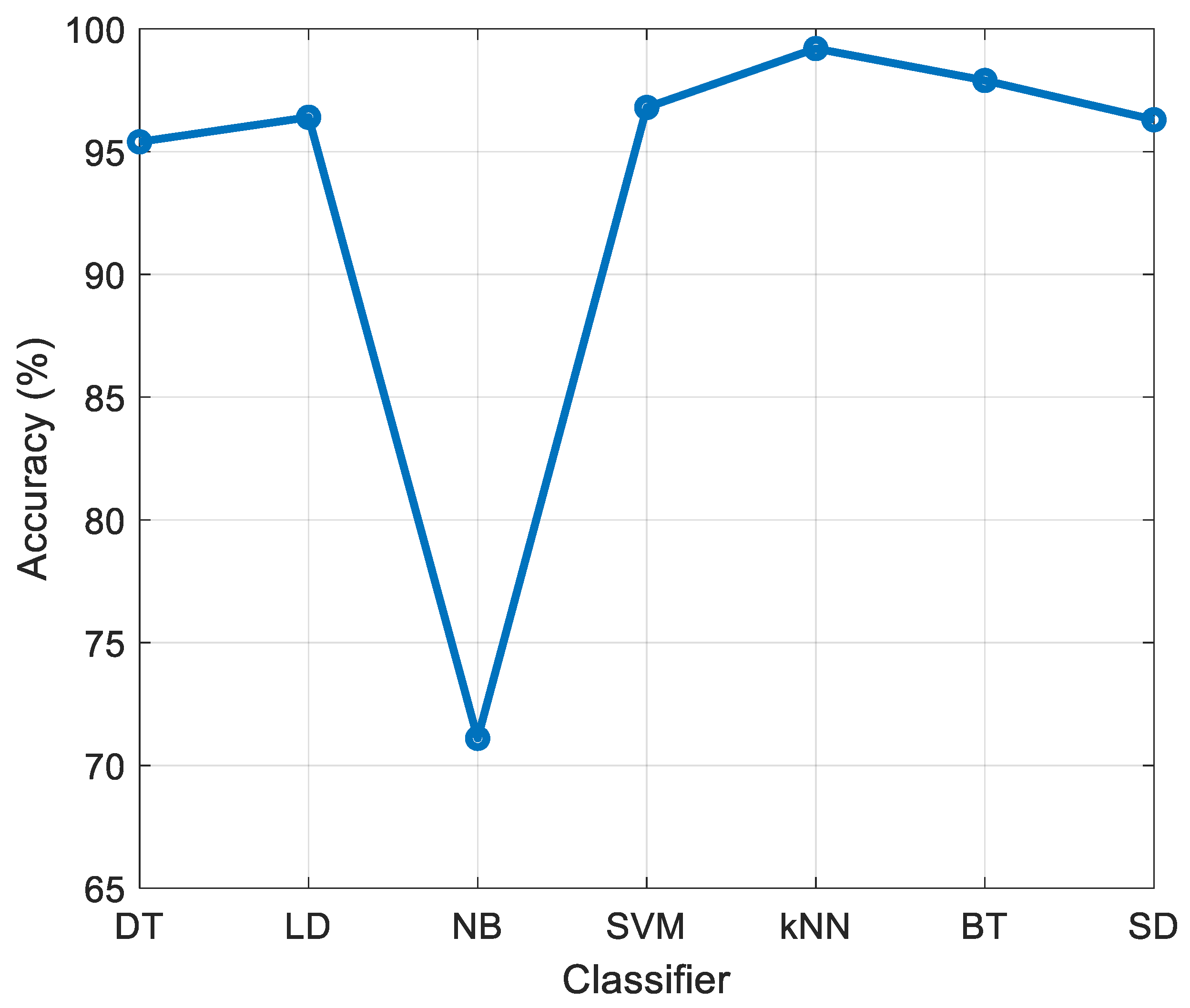
2.2.3. Classification
3. Results
3.1. Experimental Setup
3.2. Cases
3.3. Results
4. Discussion
- Developed a new cough sound dataset, which was collected from healthy subjects, and COVID-19 and HF patients.
- Presented a novel histogram-based feature generator inspired by DNA patterns. To the best our knowledge, this is the first work to automatically classify healthy subjects, HF and COVID-19 patients using cough sounds signals.
- Proposed a DNA pattern- and ImRMR-based model which attained greater than 99% accuracy for all (binary and multiclass) defined classification problems.
- Generated an automated model based on cough sounds that is accurate, economical, rapid, and computationally lightweight.
- The limitations of this work are given below:
- The system should be validated with a larger dataset prior to clinical application.
- Only a three-class system was used (normal, COVID-19 and HF).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hussain, E.; Hasan, M.; Rahman, M.A.; Lee, I.; Tamanna, T.; Parvez, M.Z. CoroDet: A deep learning based classification for COVID-19 detection using chest X-ray images. Chaos Solitons Fractals 2021, 142, 110495. [Google Scholar] [CrossRef]
- Okoshi, H.; Suzuki, H.; Nakano, A.; Hamada, A.; Miyamoto, T.; Yamasawa, F. A Guide to Novel Coronavirus (COVID-19) Infection Control for Businesses. J. Occup. Health 2020, e12225. [Google Scholar] [CrossRef]
- Sheffi, Y. The New (Ab) Normal: Reshaping Business and Supply Chain Strategy Beyond COVID-19; MIT CTL Media: Cambridge, MA, USA, 2020. [Google Scholar]
- Kanne, J.P.; Bai, H.; Bernheim, A.; Chung, M.; Haramati, L.B.; Kallmes, D.F.; Little, B.P.; Rubin, G.D.; Sverzellati, N. COVID-19 imaging: What we know now and what remains unknown. Radiology 2021, 299, E262–E279. [Google Scholar] [CrossRef]
- Hall, G.; Laddu, D.R.; Phillips, S.A.; Lavie, C.J.; Arena, R. A tale of two pandemics: How will COVID-19 and global trends in physical inactivity and sedentary behavior affect one another? Prog. Cardiovasc. Dis. 2020, 64, 108. [Google Scholar] [CrossRef] [PubMed]
- Megahed, N.A.; Ghoneim, E.M. Antivirus-built environment: Lessons learned from COVID-19 pandemic. Sustain. Cities Soc. 2020, 61, 102350. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, S.; Punn, N.S.; Sonbhadra, S.K.; Nagabhushan, P.; Pandian, K.; Saxena, P. Unleashing the power of disruptive and emerging technologies amid COVID 2019: A detailed review. arXiv 2020, arXiv:2005.11507. [Google Scholar]
- Shchendrygina, A.; Nagel, E.; Puntmann, V.O.; Valbuena-Lopez, S. COVID-19 myocarditis and prospective heart failure burden. Expert Rev. Cardiovasc. Ther. 2021, 19, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Pahuja, G.; Nagabhushan, T. A comparative study of existing machine learning approaches for parkinson’s disease detection. IETE J. Res. 2021, 67, 4–14. [Google Scholar] [CrossRef]
- Miah, Y.; Prima, C.N.E.; Seema, S.J.; Mahmud, M.; Kaiser, M.S. Performance comparison of machine learning techniques in identifying dementia from open access clinical datasets. In Advances on Smart and Soft Computing; Springer: Singapore, 2021; pp. 79–89. [Google Scholar]
- Aslan, M.F.; Unlersen, M.F.; Sabanci, K.; Durdu, A. CNN-based transfer learning–BiLSTM network: A novel approach for COVID-19 infection detection. Appl. Soft Comput. 2021, 98, 106912. [Google Scholar] [CrossRef]
- Gupta, A.; Gupta, R.; Garg, N. An efficient approach for classifying chest X-ray images using different embedder with different activation functions in CNN. J. Interdiscip. Math. 2021, 24, 285–297. [Google Scholar] [CrossRef]
- Nazari, S.; Fallah, M.; Kazemipoor, H.; Salehipour, A. A fuzzy inference-fuzzy analytic hierarchy process-based clinical decision support system for diagnosis of heart diseases. Expert Syst. Appl. 2018, 95, 261–271. [Google Scholar] [CrossRef]
- Maghdid, H.S.; Asaad, A.T.; Ghafoor, K.Z.; Sadiq, A.S.; Khan, M.K. Diagnosing COVID-19 pneumonia from X-ray and CT images using deep learning and transfer learning algorithms. arXiv 2020, arXiv:2004.00038. [Google Scholar]
- Huang, Q. Occupancy-driven energy-efficient buildings using audio processing with background sound cancellation. Buildings 2018, 8, 78. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Lu, C.; Hao, C.; Chen, D.; Guo, D. Improving the generalization ability of deep neural networks for cross-domain visual recognition. IEEE Trans. Cogn. Dev. Syst. 2020, 13, 607–620. [Google Scholar] [CrossRef]
- Tao, H.; Wu, T.; Aldeghi, M.; Wu, T.C.; Aspuru-Guzik, A.; Kumacheva, E. Nanoparticle synthesis assisted by machine learning. Nat. Rev. Mater. 2021, 6, 701–716. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Tan, R.-S.; Acharya, U.R. Application of Petersen graph pattern technique for automated detection of heart valve diseases with PCG signals. Inf. Sci. 2021, 565, 91–104. [Google Scholar] [CrossRef]
- Maillo, J.; Ramírez, S.; Triguero, I.; Herrera, F. kNN-IS: An Iterative Spark-based design of the k-Nearest Neighbors classifier for big data. Knowl. Based Syst. 2017, 117, 3–15. [Google Scholar] [CrossRef] [Green Version]
- Masetic, Z.; Subasi, A. Congestive heart failure detection using random forest classifier. Comput. Methods Programs Biomed. 2016, 130, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ralf-Dieter, B. The PTB Diagnostic ECG Database. Available online: http://www.physionet.org/physiobank/database/ptbdb/ (accessed on 23 January 2021).
- Baim, D.S.; Colucci, W.S.; Monrad, E.S.; Smith, H.S.; Wright, R.F.; Lanoue, A.; Gauthier, D.F.; Ransil, B.J.; Grossman, W.; Braunwald, E. Survival of patients with severe congestive heart failure treated with oral milrinone. J. Am. Coll. Cardiol. 1986, 7, 661–670. [Google Scholar] [CrossRef] [Green Version]
- Tripathy, R.K.; Paternina, M.R.; Arrieta, J.G.; Zamora-Méndez, A.; Naik, G.R. Automated detection of congestive heart failure from electrocardiogram signal using Stockwell transform and hybrid classification scheme. Comput. Methods Programs Biomed. 2019, 173, 53–65. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Porumb, M.; Iadanza, E.; Massaro, S.; Pecchia, L. A convolutional neural network approach to detect congestive heart failure. Biomed. Signal Process. Control 2020, 55, 101597. [Google Scholar] [CrossRef]
- Abbas, A.; Abdelsamea, M.M.; Gaber, M.M. Classification of COVID-19 in chest X-ray images using DeTraC deep convolutional neural network. Appl. Intell. 2021, 51, 854–864. [Google Scholar] [CrossRef]
- Candemir, S.; Jaeger, S.; Palaniappan, K.; Musco, J.P.; Singh, R.K.; Xue, Z.; Karargyris, A.; Antani, S.; Thoma, G.; McDonald, C.J. Lung segmentation in chest radiographs using anatomical atlases with nonrigid registration. IEEE Trans. Med. Imaging 2013, 33, 577–590. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, S.; Karargyris, A.; Candemir, S.; Folio, L.; Siegelman, J.; Callaghan, F.; Xue, Z.; Palaniappan, K.; Singh, R.K.; Antani, S. Automatic tuberculosis screening using chest radiographs. IEEE Trans. Med. Imaging 2013, 33, 233–245. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, A.; Gianchandani, N.; Singh, D.; Kumar, V.; Kaur, M. Classification of the COVID-19 infected patients using DenseNet201 based deep transfer learning. J. Biomol. Struct. Dyn. 2020, 39, 5682–5689. [Google Scholar] [CrossRef]
- SARS-COV-2 Ct-Scan Dataset. Available online: www.kaggle.com/plameneduardo/sarscov2-ctscan-dataset (accessed on 12 January 2021).
- Singh, D.; Kumar, V.; Kaur, M. Classification of COVID-19 patients from chest CT images using multi-objective differential evolution–based convolutional neural networks. Eur. J. Clin. Microbiol. Infect. Dis. 2020, 39, 1379–1389. [Google Scholar] [CrossRef]
- Horry, M.J.; Chakraborty, S.; Paul, M.; Ulhaq, A.; Pradhan, B.; Saha, M.; Shukla, N. COVID-19 detection through transfer learning using multimodal imaging data. IEEE Access 2020, 8, 149808–149824. [Google Scholar] [CrossRef]
- Cohen, J.P.; Morrison, P.; Dao, L.; Roth, K.; Duong, T.Q.; Ghassemi, M. COVID-19 image data collection: Prospective predictions are the future. arXiv 2020, arXiv:2006.11988. [Google Scholar]
- Wang, X.; Peng, Y.; Lu, L.; Lu, Z.; Bagheri, M.; Summers, R.M. Chestx-ray8: Hospital-scale chest x-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. arXiv 2017, arXiv:1705.02315. [Google Scholar]
- Yang, X.; He, X.; Zhao, J.; Zhang, Y.; Zhang, S.; Xie, P. Covid-ct-dataset: A ct scan dataset about COVID-19. arXiv 2020, arXiv:2003.13865. [Google Scholar]
- Born, J.; Brändle, G.; Cossio, M.; Disdier, M.; Goulet, J.; Roulin, J.; Wiedemann, N. POCOVID-Net: Automatic detection of COVID-19 from a new lung ultrasound imaging dataset (POCUS). arXiv 2020, arXiv:2004.12084. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. arXiv 2017, arXiv:1610.02357. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, inception-resnet and the impact of residual connections on learning. arXiv 2016, arXiv:1602.07261. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. arXiv 2015, arXiv:1512.00567. [Google Scholar]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. arXiv 2018, arXiv:1707.07012. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. arXiv 2018, arXiv:1608.06993. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Zebin, T.; Rezvy, S. COVID-19 detection and disease progression visualization: Deep learning on chest X-rays for classification and coarse localization. Appl. Intell. 2021, 51, 1010–1021. [Google Scholar] [CrossRef]
- Wardhani, N.W.S.; Rochayani, M.Y.; Iriany, A.; Sulistyono, A.D.; Lestantyo, P. Cross-validation metrics for evaluating classification performance on imbalanced data. In Proceedings of the 2019 International Conference on Computer, Control, Informatics and its Applications (IC3INA), Tangerang, Indonesia, 23–24 October 2019; pp. 14–18. [Google Scholar]
- Krithika, L.; Priya, G.L. Graph based feature extraction and hybrid classification approach for facial expression recognition. J. Ambient Intell. Humaniz. Comput. 2021, 12, 2131–2147. [Google Scholar] [CrossRef]
- Yu, X.; Wang, S.-H.; Zhang, Y.-D. CGNet: A graph-knowledge embedded convolutional neural network for detection of pneumonia. Inf. Process. Manag. 2021, 58, 102411. [Google Scholar] [CrossRef]
- Gupta, A.; Matta, P.; Pant, B. Graph neural network: Current state of Art, challenges and applications. Mater. Today Proc. 2021, 46, 10927–10932. [Google Scholar] [CrossRef]
- Unler, A.; Murat, A.; Chinnam, R.B. mr2PSO: A maximum relevance minimum redundancy feature selection method based on swarm intelligence for support vector machine classification. Inf. Sci. 2011, 181, 4625–4641. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Pławiak, P.; Acharya, U.R. Automated arrhythmia detection using novel hexadecimal local pattern and multilevel wavelet transform with ECG signals. Knowl. Based Syst. 2019, 186, 104923. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Chellappa, R.; Nandhakumar, N. Empirical performance analysis of linear discriminant classifiers. In Proceedings of the 1998 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No. 98CB36231), Santa Barbara, CA, USA, 25 June 1998; pp. 164–169. [Google Scholar]
- Rish, I. An empirical study of the naive Bayes classifier. In Proceedings of the IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, Seattle, WA, USA, 4–6 August 2001; pp. 41–46. [Google Scholar]
- Vapnik, V. The nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Mishra, P.K.; Yadav, A.; Pazoki, M. A novel fault classification scheme for series capacitor compensated transmission line based on bagged tree ensemble classifier. IEEE Access 2018, 6, 27373–27382. [Google Scholar] [CrossRef]
- Ashour, A.S.; Guo, Y.; Hawas, A.R.; Xu, G. Ensemble of subspace discriminant classifiers for schistosomal liver fibrosis staging in mice microscopic images. Health Inf. Sci. Syst. 2018, 6, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.; Chauhan, J.; Grammenos, A.; Han, J.; Hasthanasombat, A.; Spathis, D.; Xia, T.; Cicuta, P.; Mascolo, C. Exploring automatic diagnosis of COVID-19 from crowdsourced respiratory sound data. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, San Diego, CA, USA, 6–10 July 2020; ACM: New York, NY, USA; pp. 3474–3484. [Google Scholar]
- Wei, W.; Wang, J.; Ma, J.; Cheng, N.; Xiao, J. A Real-time Robot-based Auxiliary System for Risk Evaluation of COVID-19 Infection. arXiv 2020, arXiv:2008.07695. [Google Scholar]
- Xia, T.; Han, J.; Qendro, L.; Dang, T.; Mascolo, C. Uncertainty-Aware COVID-19 Detection from Imbalanced Sound Data. arXiv 2021, arXiv:2104.02005. [Google Scholar]
- Hassan, A.; Shahin, I.; Alsabek, M.B. COVID-19 detection system using recurrent neural networks. In Proceedings of the 2020 International Conference on Communications, Computing, Cybersecurity, and Informatics (CCCI), Sharjah, United Arab Emirates, 3–5 November 2020; pp. 1–5. [Google Scholar]
- Pahar, M.; Klopper, M.; Warren, R.; Niesler, T. COVID-19 Cough Classification using Machine Learning and Global Smartphone Recordings. arXiv 2020, arXiv:2012.01926. [Google Scholar]
- Sharma, N.; Krishnan, P.; Kumar, R.; Ramoji, S.; Chetupalli, S.R.; Ghosh, P.K.; Ganapathy, S. Coswara—A Database of Breathing, Cough, and Voice Sounds for COVID-19 Diagnosis. arXiv 2020, arXiv:2005.10548. [Google Scholar]
- Sarcos. Available online: https://coughtest.online (accessed on 3 March 2021).
- Schuller, B.W.; Batliner, A.; Bergler, C.; Mascolo, C.; Han, J.; Lefter, I.; Kaya, H.; Amiriparian, S.; Baird, A.; Stappen, L. The INTERSPEECH 2021 Computational Paralinguistics Challenge: COVID-19 cough, COVID-19 speech, escalation & primates. arXiv 2021, arXiv:2102.13468. [Google Scholar]
- Han, J.; Brown, C.; Chauhan, J.; Grammenos, A.; Hasthanasombat, A.; Spathis, D.; Xia, T.; Cicuta, P.; Mascolo, C. Exploring Automatic COVID-19 Diagnosis via voice and symptoms from Crowdsourced Data. arXiv 2021, arXiv:2102.05225. [Google Scholar]
- Andreu-Perez, J.; Pérez-Espinosa, H.; Timonet, E.; Kiani, M.; Giron-Perez, M.I.; Benitez-Trinidad, A.B.; Jarchi, D.; Rosales, A.; Gkatzoulis, N.; Reyes-Galaviz, O.F. A Generic Deep Learning Based Cough Analysis System from Clinically Validated Samples for Point-of-Need COVID-19 Test and Severity Levels. IEEE Trans. Serv. Comput. 2021, 1–13. [Google Scholar] [CrossRef]
- Chowdhury, M.E.; Ibtehaz, N.; Rahman, T.; Mekki, Y.M.S.; Qibalwey, Y.; Mahmud, S.; Ezeddin, M.; Zughaier, S.; Al-Maadeed, S.A.S. QUCoughScope: An Artificially Intelligent Mobile Application to Detect Asymptomatic COVID-19 Patients using Cough and Breathing Sounds. arXiv 2021, arXiv:2103.12063. [Google Scholar]
- Orlandic, L.; Teijeiro, T.; Atienza, D. The COUGHVID crowdsourcing dataset: A corpus for the study of large-scale cough analysis algorithms. arXiv 2020, arXiv:2009.11644. [Google Scholar]
- Maleki, M. Diagnosis of COVID-19 and Non-COVID-19 Patients by Classifying Only a Single Cough Sound. arXiv 2021, arXiv:2102.04880. [Google Scholar]
- Chaudhari, G.; Jiang, X.; Fakhry, A.; Han, A.; Xiao, J.; Shen, S.; Khanzada, A. Virufy: Global Applicability of Crowdsourced and Clinical Datasets for AI Detection of COVID-19 from Cough. arXiv 2020, arXiv:2011.13320. [Google Scholar]
- Cohen-McFarlane, M.; Goubran, R.; Knoefel, F. Novel coronavirus cough database: Nococoda. IEEE Access 2020, 8, 154087–154094. [Google Scholar] [CrossRef]
- Mouawad, P.; Dubnov, T.; Dubnov, S. Robust Detection of COVID-19 in Cough Sounds: Using Recurrence Dynamics and Variable Markov Model. SN Comput. Sci. 2021, 2, 1–13. [Google Scholar] [CrossRef] [PubMed]
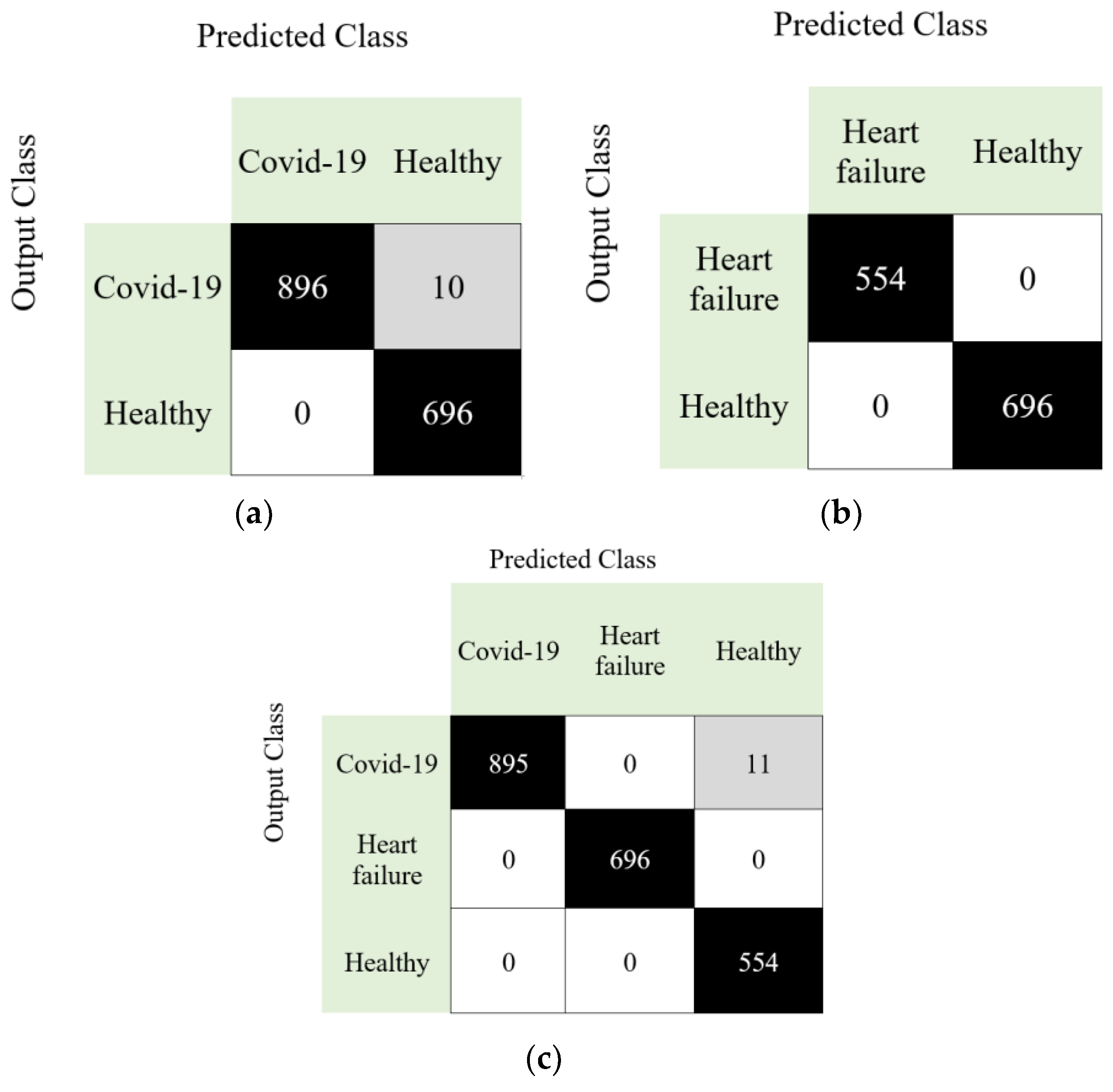
| Case | Accuracy (%) | Sensitivity (%) | Precision (%) | F1-Score (%) | Geometric Mean (%) |
|---|---|---|---|---|---|
| Case 1 | 99.38 | 98.90 | 100 | 99.45 | 99.45 |
| Case 2 | 100 | 100 | 100 | 100 | 100 |
| Case 3 | 99.49 | 99.60 | 99.35 | 99.47 | 99.59 |
| Study | Method | Classifier | Dataset | Subjects/Samples | Results (%) |
|---|---|---|---|---|---|
| Brown et al. [58] | Mel-Frequency Cepstral Coefficients | Support vector machine | Collected data | 23 COVID-19 with cough 29 No-covid19 with cough | AUC: 82.00 Pre: 80.00 Rec: 72.00 |
| Wei et al. [59] | Convolution neural networks, Mel-frequency cepstral coefficients | Support vector machine | Collected data | 64 COVID-19 40 Healthy 20 Bronchitis 20 Chronic pharyngitis 10 children with pertussis 39 Smoking subject | Sen: 98.70 Spe: 94.70 for COVID-19 |
| Xia et al. [60] | Convolutional neural networks | Softmax | Collected data | 330 COVID-19 688 Healthy | AUC: 74.00 Sen: 68.00 Spe: 69.00 |
| Hassan et al. [61] | Recurrent neural network, long-short term memory | Recurrent neural network | Collected data | 60 Healthy 20 COVID-19 | Acc: 97.00 AUC: 97.40 F1: 97.90 Rec: 96.40 Pre:99.30 |
| Pahar et al. [62] | Mel frequency cepstral coefficients, log energies, zero-crossing rate, kurtosis | Long short-term memory, sequential forward search | 1. Coswara [63], 2. Sarcos [64] dataset | 1. 1079 healthy 92 COVID-19 2. 13 COVID-19 negative 8 COVID-19 positive | Spe: 96.00 Sen: 91.00 Acc: 92.91 AUC: 93.75 for combined dataset |
| Schuller et al. [65] | Deep spectrum, autoencoders | Convolutional neural networks | Cambridge COVID-19 sound database [58,66] | 119 COVID-19 606 No-COVID-19 | UAR: 73.90 |
| Andreu-Perez et al. [67] | Empirical mode decomposition, convolutional neural networks | Artificial neural network | Collected data | 2339 COVID-19 positive 6041 COVID-19 negative | AUC: 66.41 Pre: 76.04 Sen: 76.64 Spe: 67.00 |
| Chowdhury et al. [68] | Convolutional neural networks | Convolutional neural networks | Coswara [63], Cambridge [58], CoughVid [69] dataset. | 582 healthy 141 COVID-19 patients | Acc: 95.86 Pre: 95.84 Sen: 95.86 F1: 95.84 Spe: 93.43 |
| Maleki [70] | Mel frequency cepstral coefficients, Sequential forward selection | Euclidean k-nearest neighbors | Combined dataset (Virufy COVID-19 open cough data set [71], NoCoCoDa [72]) | 48 COVID-19 positive 73 COVID-19 negative | Acc: 98.33 F1: 97.99 AUC: 98.60 Sen: 100.0 for Non-COVID-19 Sen: 97.20 for COVID-19 |
| Mouawad et al. [73] | Mel frequency cepstral coefficients, recurrence quantification analysis | Weighted XGBoost | Collected data | 1895 healthy 32 sick samples | Acc: 97.00 F1: 62.00 AUC: 84.00 |
| Our method | DNA pattern | k-nearest neighbors | Collected data | 247 healthy 241 COVID-19 244 heart failure | Acc: 99.38 Sen: 98.90 Pre: 100.0 F1: 99.45 Gm: 99.45 for Case 1 |
| Acc: 100.0 Sen: 100.0 Pre: 100.0 F1: 100.0 Gm: 100.0 for Case 2 | |||||
| Acc: 99.49 Sen: 99.60 Pre: 99.35 F1: 99.47 Gm: 99.59 for Case 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobat, M.A.; Kivrak, T.; Barua, P.D.; Tuncer, T.; Dogan, S.; Tan, R.-S.; Ciaccio, E.J.; Acharya, U.R. Automated COVID-19 and Heart Failure Detection Using DNA Pattern Technique with Cough Sounds. Diagnostics 2021, 11, 1962. https://doi.org/10.3390/diagnostics11111962
Kobat MA, Kivrak T, Barua PD, Tuncer T, Dogan S, Tan R-S, Ciaccio EJ, Acharya UR. Automated COVID-19 and Heart Failure Detection Using DNA Pattern Technique with Cough Sounds. Diagnostics. 2021; 11(11):1962. https://doi.org/10.3390/diagnostics11111962
Chicago/Turabian StyleKobat, Mehmet Ali, Tarik Kivrak, Prabal Datta Barua, Turker Tuncer, Sengul Dogan, Ru-San Tan, Edward J. Ciaccio, and U. Rajendra Acharya. 2021. "Automated COVID-19 and Heart Failure Detection Using DNA Pattern Technique with Cough Sounds" Diagnostics 11, no. 11: 1962. https://doi.org/10.3390/diagnostics11111962
APA StyleKobat, M. A., Kivrak, T., Barua, P. D., Tuncer, T., Dogan, S., Tan, R.-S., Ciaccio, E. J., & Acharya, U. R. (2021). Automated COVID-19 and Heart Failure Detection Using DNA Pattern Technique with Cough Sounds. Diagnostics, 11(11), 1962. https://doi.org/10.3390/diagnostics11111962










