Survival of Self-Replicating Molecules under Transient Compartmentalization with Natural Selection
Abstract
1. Introduction
2. Materials and Methods
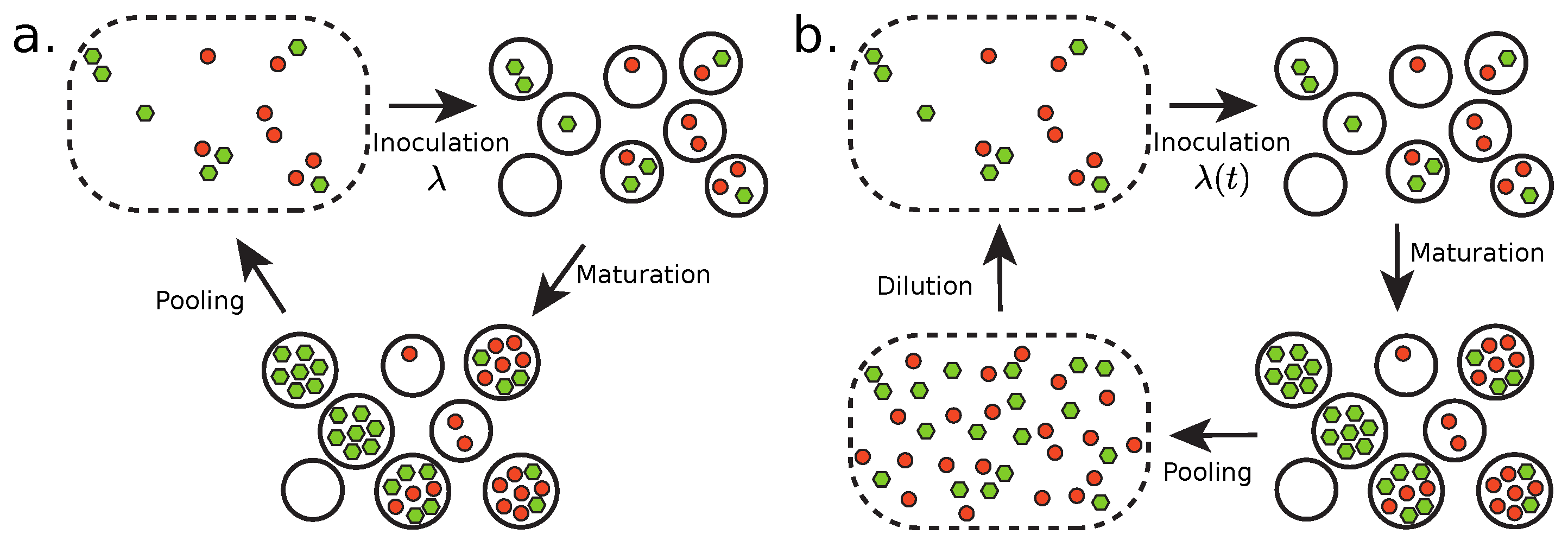
2.1. Transient Compartmentalization with a Fixed Inoculum Size
- Inoculate the compartments.
- Maturate the compartments.
- Pool compartment contents.
2.2. Transient Compartmentalization with Variable Inoculum Size
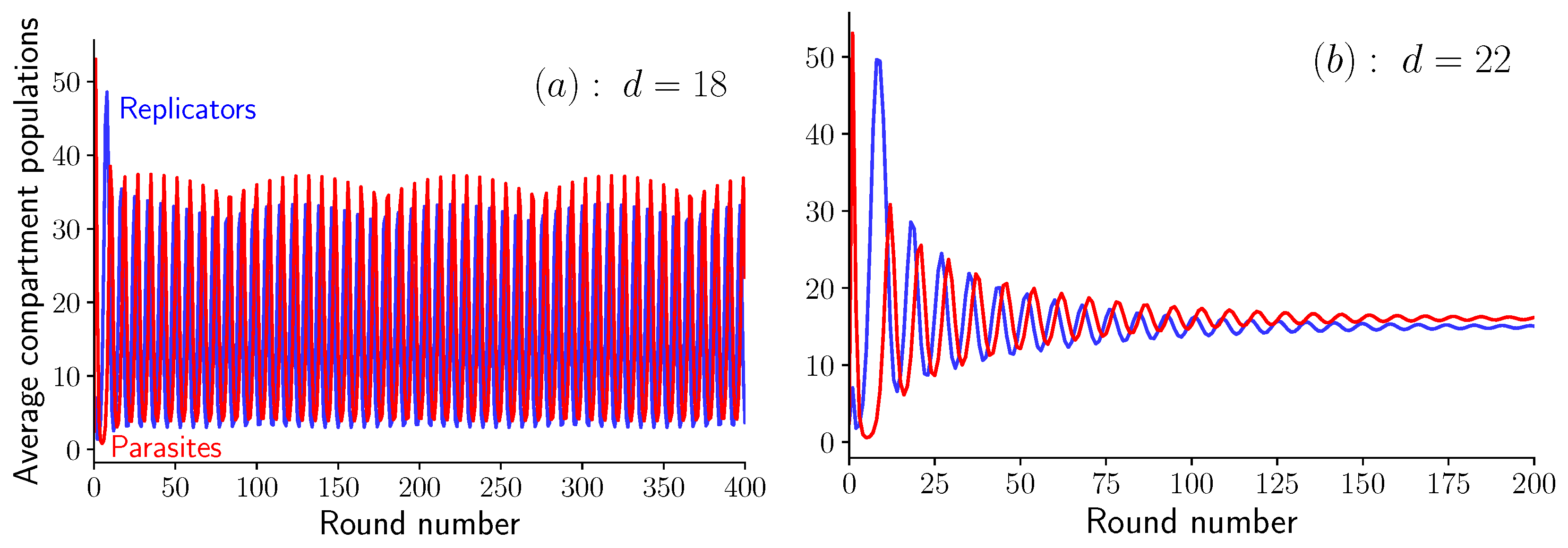
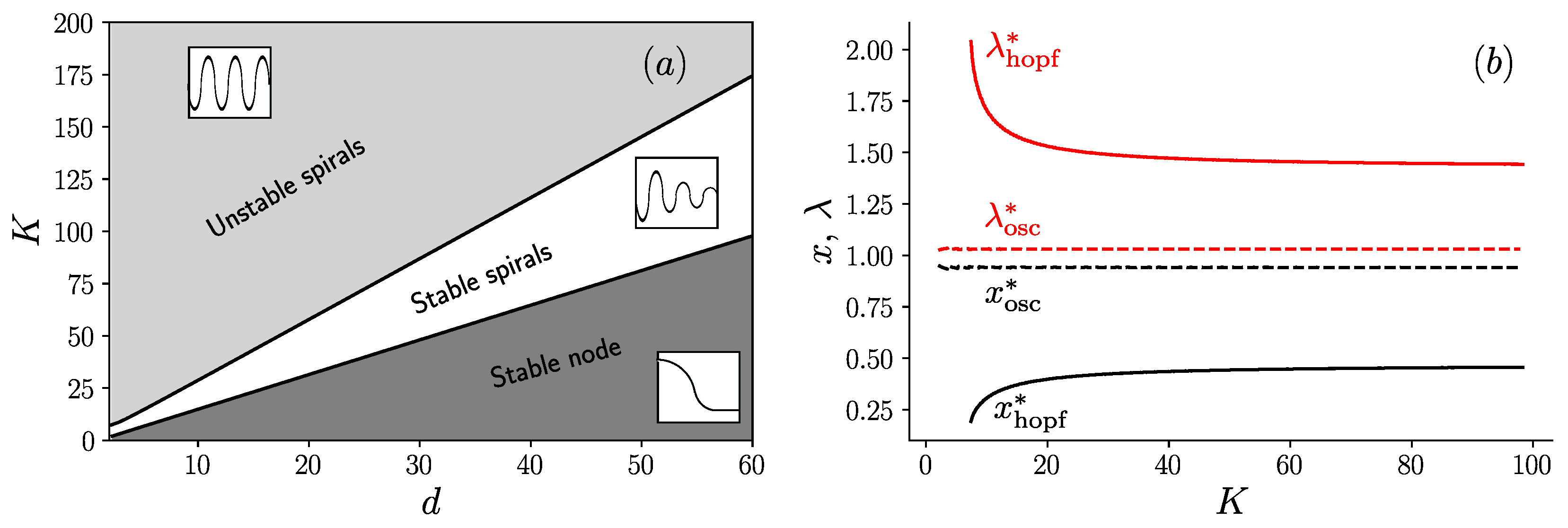
3. Results
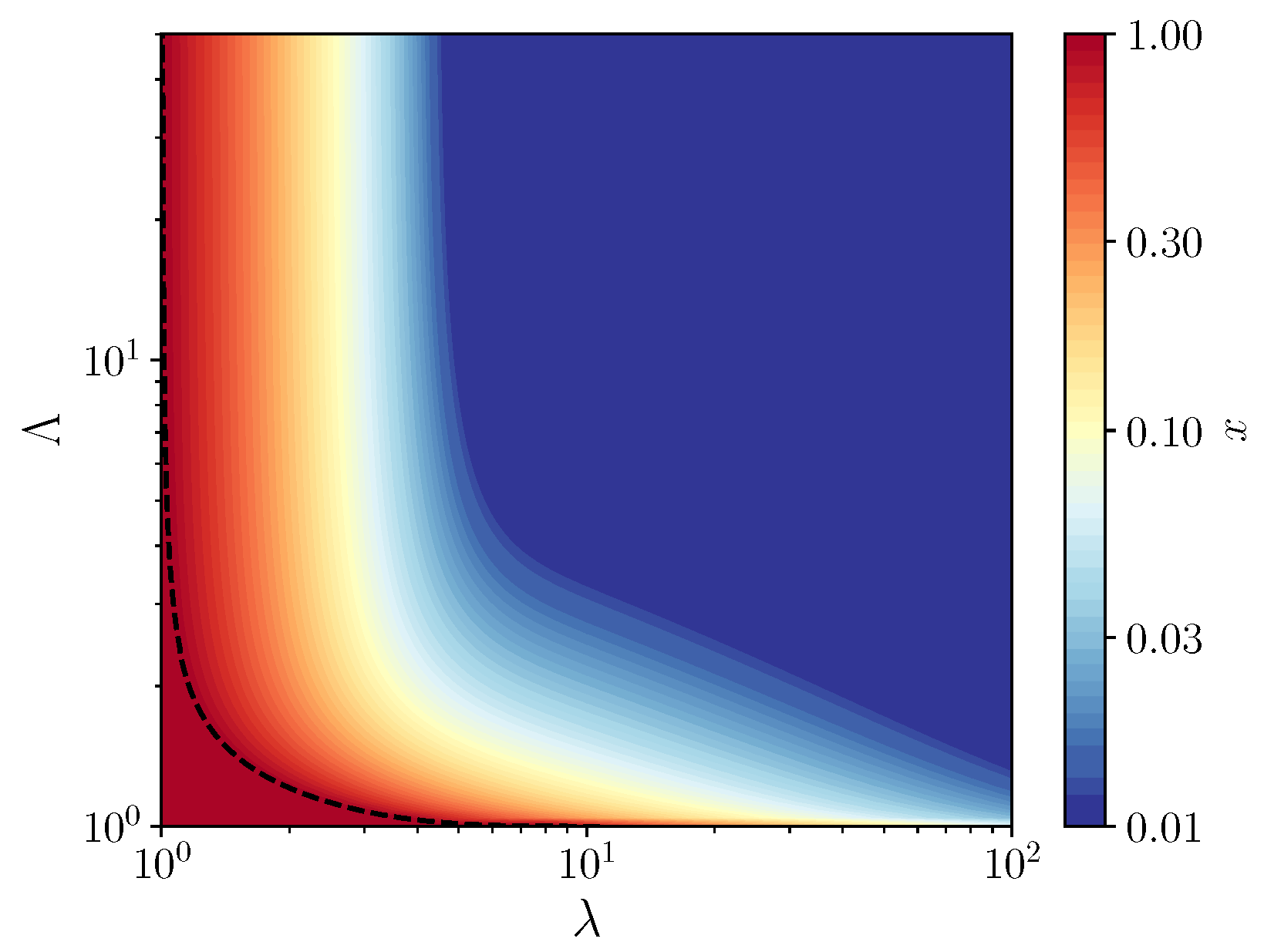
3.1. Fixed Inoculum Size
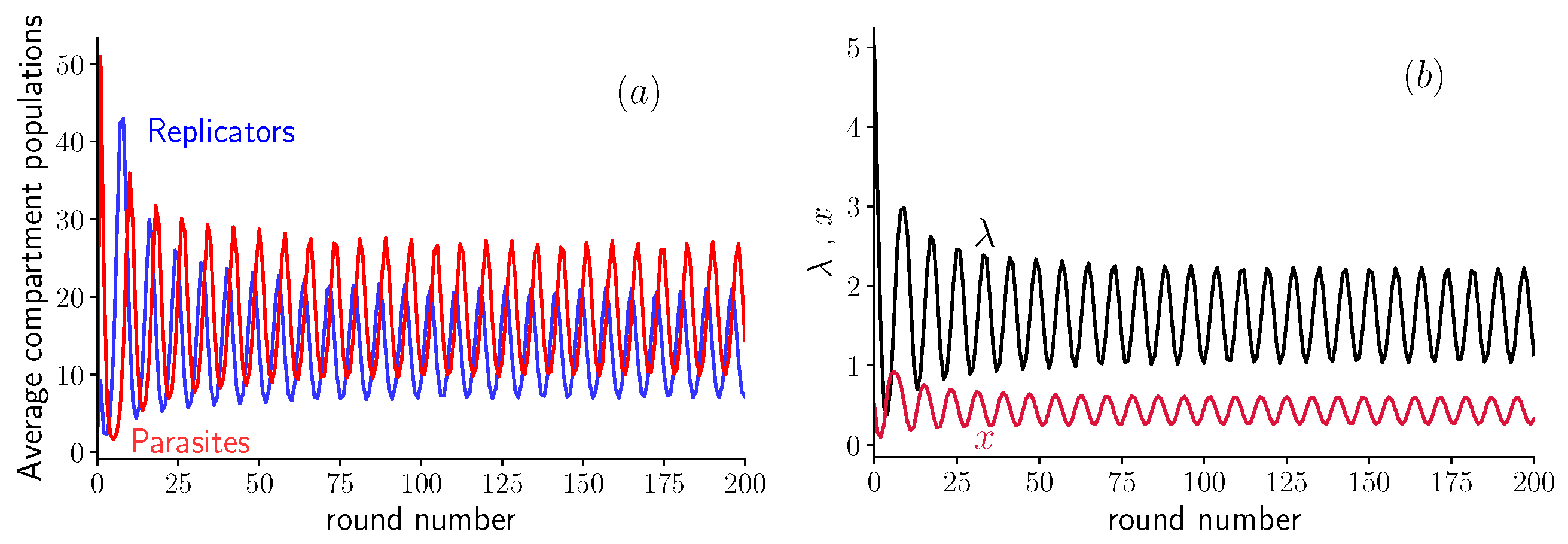
3.2. Variable Inoculum Size
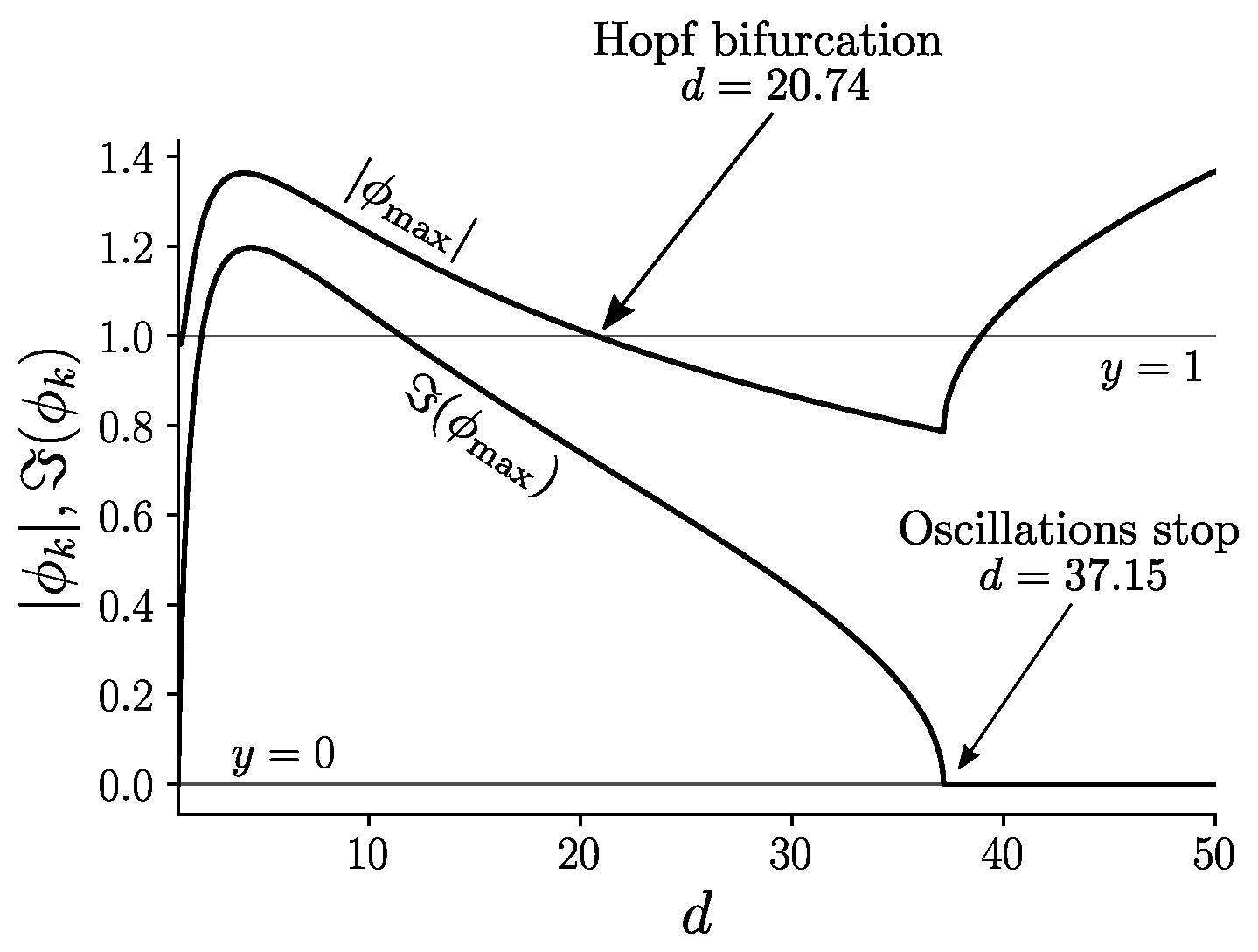
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Exact Solution of the Maturation Equations
Appendix B. Derivation of the Equations in the Λ ≫ 1 Limit
Appendix C. Analysis of The Bifurcation
References
- Dyson, F. Origins of Life; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Spiegelman, S.; Haruna, I.; Holland, I.B.; Beaudreau, G.; Mills, D. The synthesis of a self-propagating infectious nucleic acid with a purified enzyme. Proc. Natl. Acad. Sci. USA 1965, 54, 919–927. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M. Self-organization of matter and the evolution of biological macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef] [PubMed]
- Tupper, A.S.; Higgs, P.G. Error tresholds for RNA replication in the presence of both point mutations and premature termination errors. J. Theor. Biol. 2017, 428, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Grey, D.; Hutson, V.; Szathmáry, E. A re-examination of the stochastic corrector model. Proc. R. Soc. Lond. B 1995, 262, 29–35. [Google Scholar]
- Szathmáry, E.; Demeter, L. Group selection of early replicators and the origin of life. J. Theor. Biol. 1987, 128, 463–486. [Google Scholar] [CrossRef]
- Matsumura, S.; Kun, A.; Ryckelynck, M.; Coldren, F.; Szilágyi, A.; Jossinet, F.; Rick, C.; Nghe, P.; Szathmáry, E.; Griffiths, A.D. Transient compartmentalization of RNA replicators prevents extinction due to parasites. Science 2016, 354, 1293–1296. [Google Scholar] [CrossRef] [PubMed]
- Bansho, Y.; Furubayashi, T.; Ichihashi, N.; Yomo, T. Host–parasite oscillation dynamics and evolution in a compartmentalized RNA replication system. Proc. Natl. Acad. Sci. USA 2016, 113, 4045–4050. [Google Scholar] [CrossRef]
- Blokhuis, A.; Nghe, P.; Peliti, L.; Lacoste, D. The generality of transient compartmentalization and its associated error thresholds. BioRxiv 2019. submitted. [Google Scholar]
- Blokhuis, A.; Lacoste, D.; Nghe, P.; Peliti, L. Selection dynamics in transient compartmentalization. Phys. Rev. Lett. 2018, 120, 158101. [Google Scholar] [CrossRef]
- Tkachenko, A.V.; Maslov, S. Spontaneous emergence of autocatalytic information-coding polymers. J. Chem. Phys. 2015, 143, 045102. [Google Scholar] [CrossRef]
- Geyrhofer, L.; Brenner, N. Coexistence and cooperation in structured habitats. bioRxiv 2018, 1–23. [Google Scholar] [CrossRef]
- Baaske, P.; Weinert, F.M.; Duhr, S.; Lemke, K.H.; Russell, M.J.; Braun, D. Extreme accumulation of nucleotides in simulated hydrothermal pore systems. Proc. Natl. Acad. Sci. USA 2007, 104, 9346–9351. [Google Scholar] [CrossRef]
- Zadorin, A.S.; Rondelez, Y. Selection strategies for randomly partitioned genetic replicators. Phys. Rev. E 2019, 99, 062416. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, N.; Hogeweg, P. Evolutionary dynamics of RNA-like replicator systems: A bioinformatic approach to the origin of life. Phys. Life Rev. 2012, 9, 219–263. [Google Scholar] [CrossRef] [PubMed]
- Furubayashi, T.; Ichihashi, N. Sustainability of a compartmentalized host-parasite replicator system under periodic washout-mixing cycles. Life 2018, 8, 3. [Google Scholar] [CrossRef]
- Blokhuis, A.; Lacoste, D.; Gaspard, P. Reaction Kinetics in open reactors and serial transfers between closed reactors. J. Chem. Phys. 2018, 148, 144902. [Google Scholar] [CrossRef]
- Fujii, T.; Rondelez, Y. Prey Molecular Ecosystems. ACS Nano 2013, 7, 27–34. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos; Perseus Books Publishing: New York, NY, USA, 1994. [Google Scholar]
- Kaneko, K.; Yomo, T. On a kinetic origin of heredity: Minority control in a replicating system with mutually catalytic molecules. J. Theor. Biol. 2002, 214, 563–576. [Google Scholar] [CrossRef]
- Nghe, P.; Hordijk, W.; Kauffman, S.A.; Walker, S.I.; Schmidt, F.J.; Kemble, H.; Yeates, J.A.; Lehman, N. Prebiotic network evolution: Six key parameters. Mol. Biosyst. 2015, 11, 3206–3217. [Google Scholar] [CrossRef]
- Furubayashi, T.; Ueda, K.; Bansho, Y.; Motooka, D.; Nakamura, S.; Ichihashi, N. Evolutionary arms-races between host and parasitic RNA replicators in an artificial cell-like system. bioRxiv 2019, 728659. [Google Scholar] [CrossRef]
- Goldenfeld, N.; Woese, C. Life is physics: Evolution as a collective phenomenon far from equilibrium. Annu. Rev. Condens. Matter Phys. 2011, 2, 375–399. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. The Hypercycle. Naturwissenschaften 1978, 65, 7–41. [Google Scholar] [CrossRef]
- Lancet, D.; Zidovetzki, R.; Markovitch, O. Systems protobiology: origin of life in lipid catalytic networks. J. R. Soc. Interface 2018, 15, 20180159. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.; Esposito, M. Nonequilibrium thermodynamics of chemical reaction networks: wisdom from stochastic thermodynamics. Phys. Rev. X 2016, 6, 041064. [Google Scholar] [CrossRef]
- Polettini, M.; Esposito, M. Irreversible thermodynamics of open chemical networks. I. Emergent cycles and broken conservation laws. J. Chem. Phys. 2014, 141, 024117. [Google Scholar] [CrossRef]
- Kamimura, A.; Matsubara, Y.J.; Kaneko, K.; Takeuchi, N. Horizontal transfer between loose compartments stabilizes replication of fragmented ribozymes. PLoS Comput. Biol. 2019, 15, e1007094. [Google Scholar] [CrossRef]
- Yoshiyama, T.; Ichii, T.; Yomo, T.; Ichihashi, N. Automated in vitro evolution of a translation-coupled RNA replication system in a droplet flow reactor. Sci. Rep. 2018, 8, 11867. [Google Scholar] [CrossRef]
- Beneyton, T.; Krafft, D.; Bednarz, C.; Kleineberg, C.; Woelfer, C.; Ivanov, I.; Vidaković-Koch, T.; Sundmacher, K.; Baret, J.C. Out-of-equilibrium microcompartments for the bottom-up integration of metabolic functions. Nat. Commun. 2018, 9, 2391. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laurent, G.; Peliti, L.; Lacoste, D. Survival of Self-Replicating Molecules under Transient Compartmentalization with Natural Selection. Life 2019, 9, 78. https://doi.org/10.3390/life9040078
Laurent G, Peliti L, Lacoste D. Survival of Self-Replicating Molecules under Transient Compartmentalization with Natural Selection. Life. 2019; 9(4):78. https://doi.org/10.3390/life9040078
Chicago/Turabian StyleLaurent, Gabin, Luca Peliti, and David Lacoste. 2019. "Survival of Self-Replicating Molecules under Transient Compartmentalization with Natural Selection" Life 9, no. 4: 78. https://doi.org/10.3390/life9040078
APA StyleLaurent, G., Peliti, L., & Lacoste, D. (2019). Survival of Self-Replicating Molecules under Transient Compartmentalization with Natural Selection. Life, 9(4), 78. https://doi.org/10.3390/life9040078




