Modelling Bacteria-Inspired Dynamics with Networks of Interacting Chemicals
Abstract
1. Introduction
2. Methods
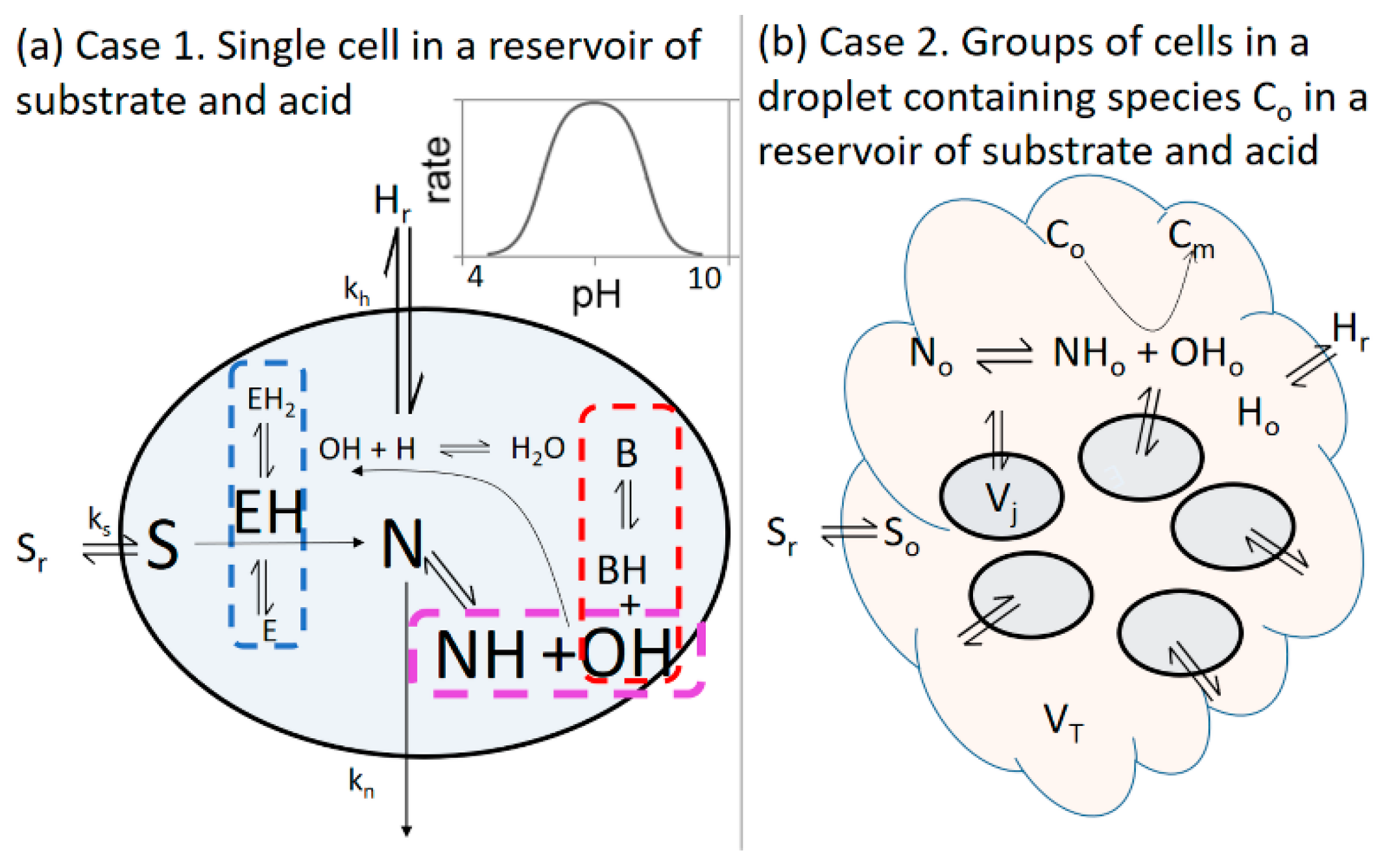
2.1. Case 1: Cell in a Reservoir
2.2. Case 2: Group of Identical Cells in a Fixed Volume of Solution
3. Results
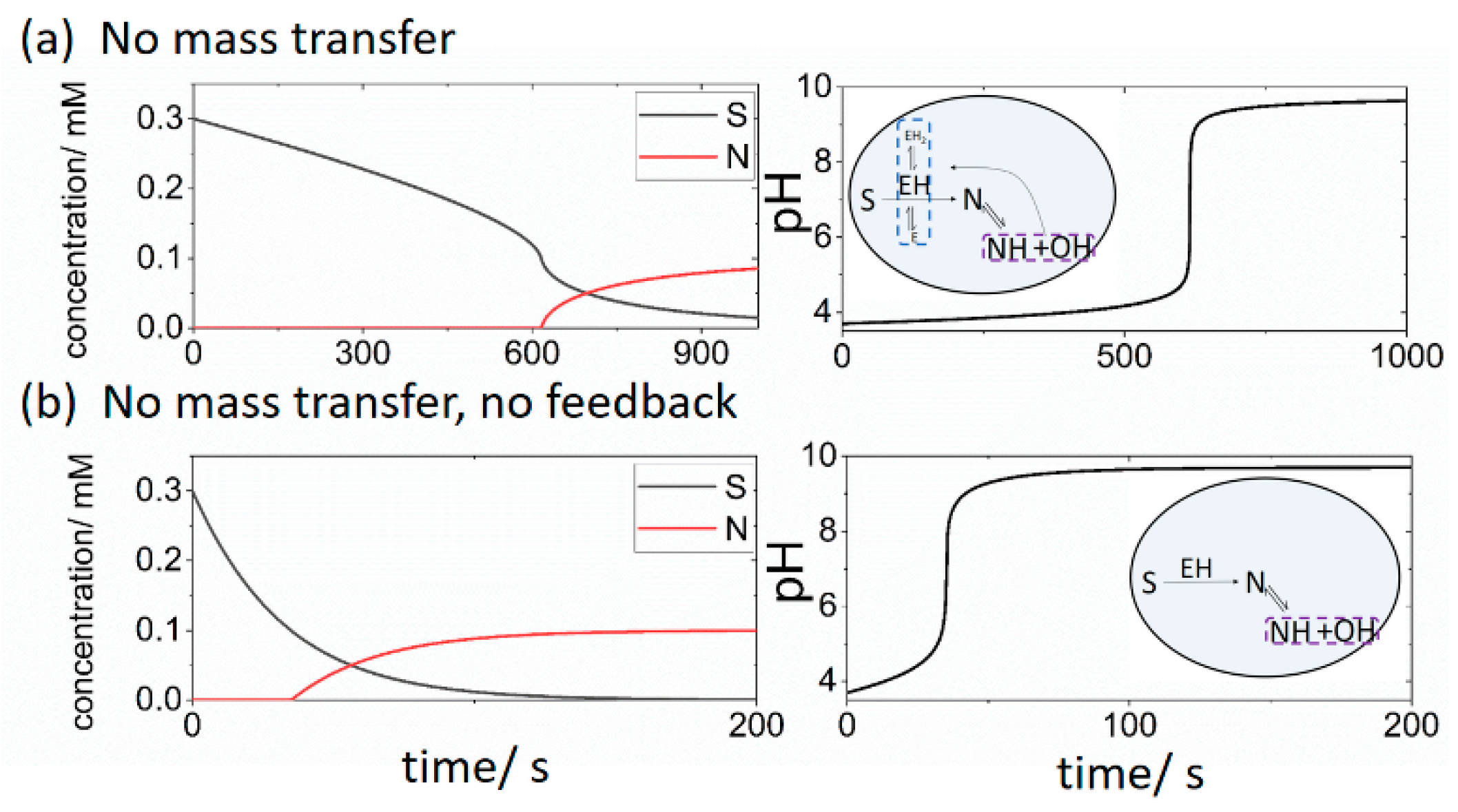
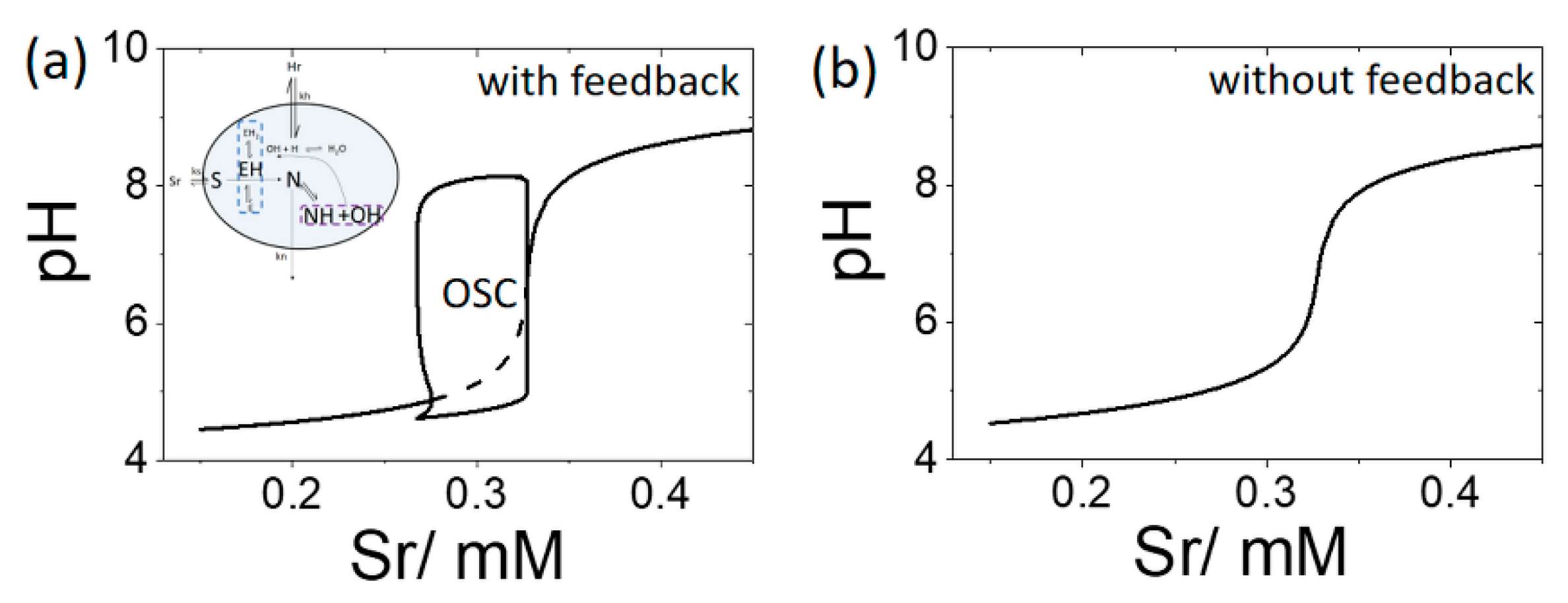
3.1. Case 1: Cell in a Reservoir
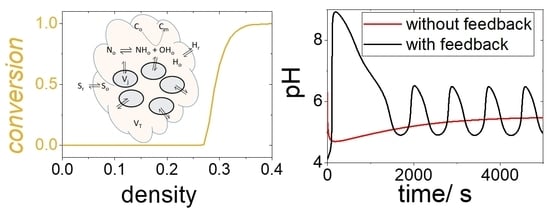
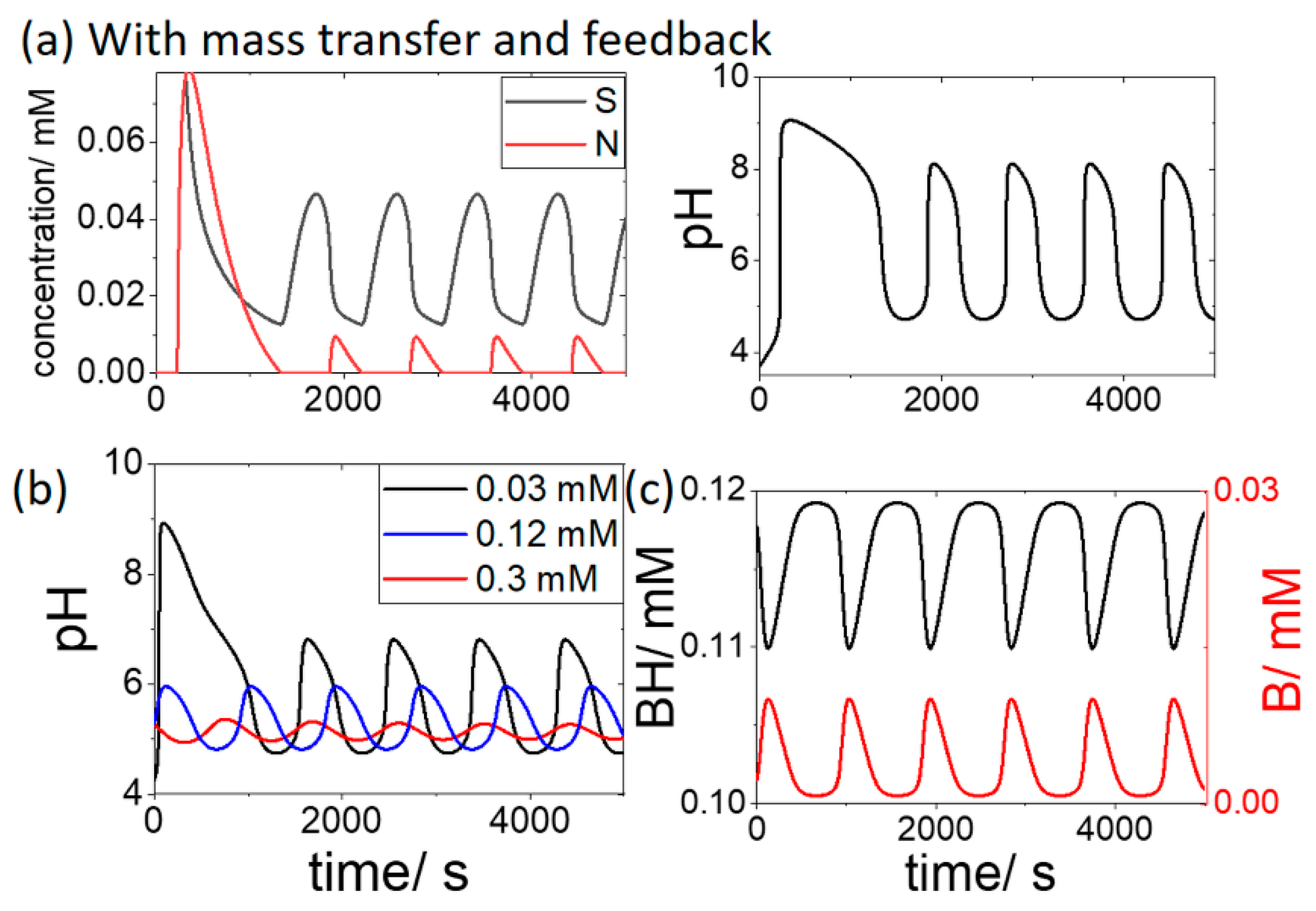
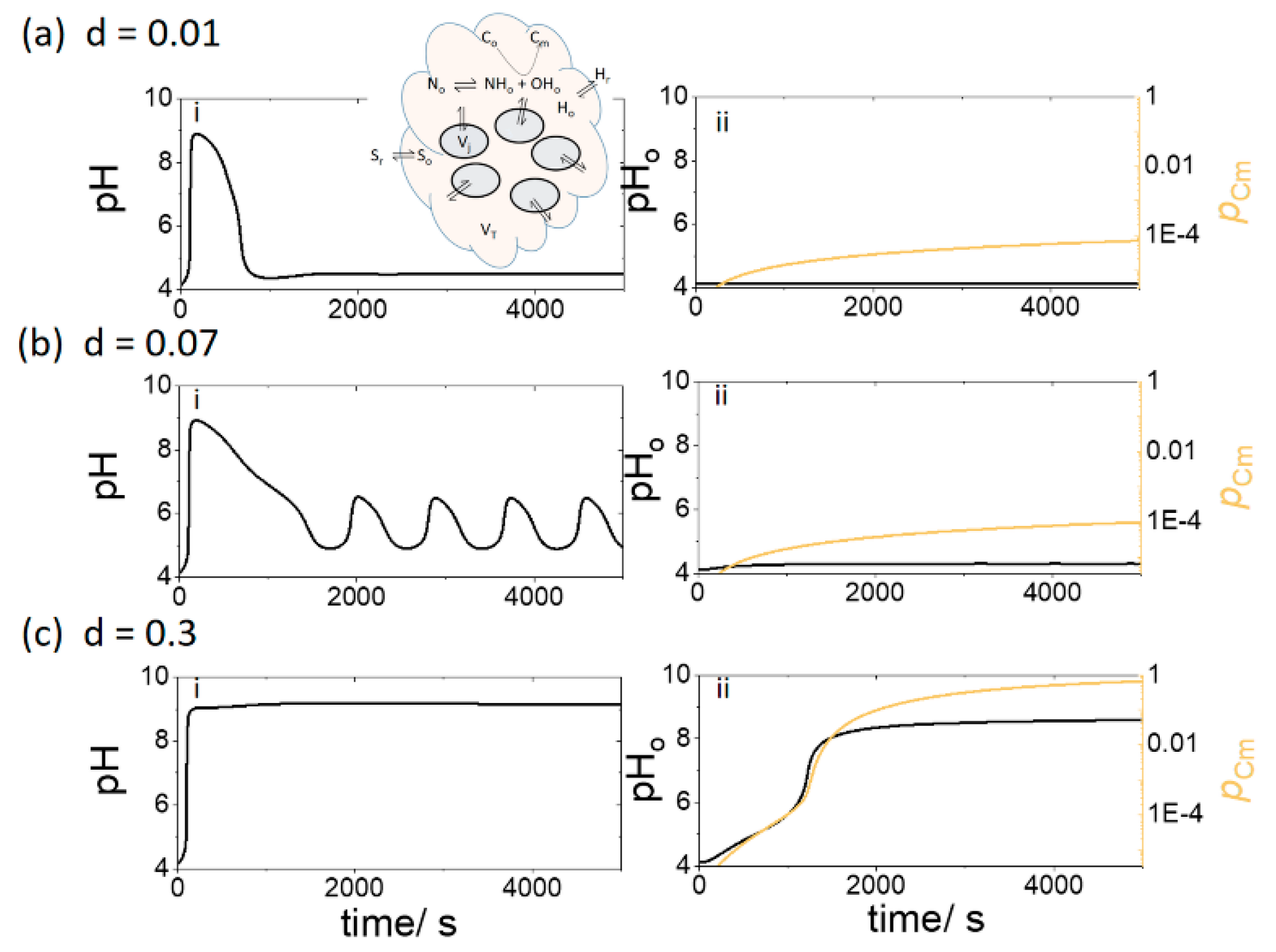
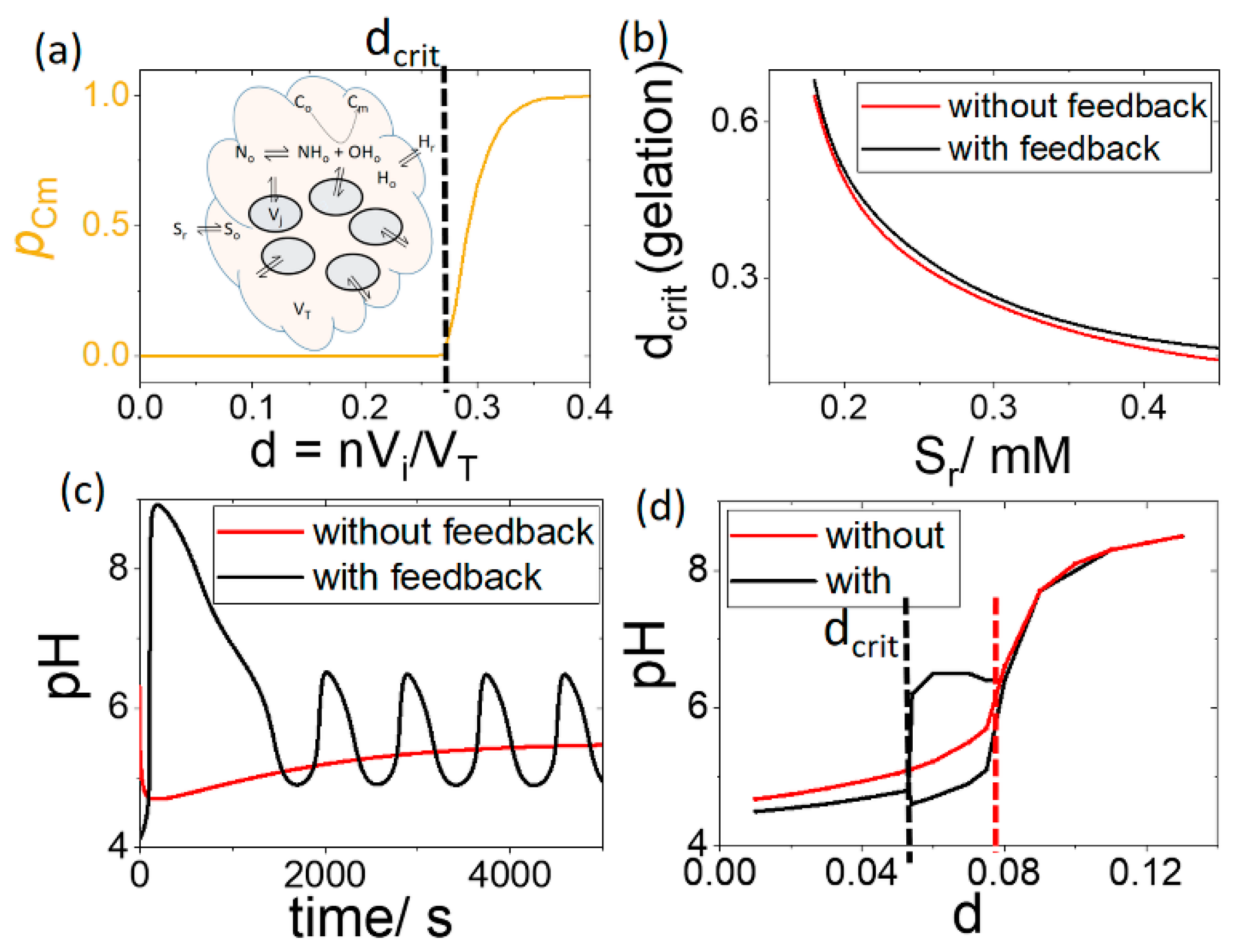
3.2. Case 2. Group of Cells in a Fixed Volume of Solution
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Tyson, J.J.; Chen, K.C.; Novak, B. Sniffers, buzzers, toggles and blinkers: Dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003, 15, 221–231. [Google Scholar] [CrossRef]
- Waters, C.M.; Bassler, B.L. Quorum sensing: Cell-to-cell communication in bacteria. Annu. Rev. Cell Dev. Biol. 2005, 21, 319–346. [Google Scholar] [CrossRef] [PubMed]
- Davies, D.G.; Parsek, M.R.; Pearson, J.P.; Iglewski, B.H.; Costerton, J.W.; Greenberg, E.P. The involvement of cell-to-cell signals in the development of a bacterial biofilm. Science 1998, 280, 295–298. [Google Scholar] [CrossRef] [PubMed]
- Semenov, S.N.; Kraft, L.J.; Ainla, A.; Zhao, M.; Baghbanzadeh, M.; Campbell, V.E.; Kang, K.; Fox, J.M.; Whitesides, G.M. Autocatalytic, bistable, oscillatory networks of biologically relevant organic reactions. Nature 2016, 537, 656–660. [Google Scholar] [CrossRef] [PubMed]
- Niederholtmeyer, H.; Chaggan, C.; Devaraj, N.K. Communication and quorum sensing in non-living mimics of eukaryotic cells. Nat. Commun. 2018, 9, 5027. [Google Scholar] [CrossRef] [PubMed]
- Danino, T.; Mondragón-Palomino, O.; Tsimring, L.; Hasty, J. A synchronized quorum of genetic clocks. Nature 2010, 463, 326–330. [Google Scholar] [CrossRef] [PubMed]
- Ashkenasy, G.; Hermans, T.M.; Otto, S.; Taylor, A.F. Systems chemistry. Chem. Soc. Rev. 2017, 46, 2543–2554. [Google Scholar] [CrossRef]
- Padirac, A.; Fujii, T.; Estévez-Torres, A.; Rondelez, Y.J. Spatial waves in synthetic biochemical networks. Am. Chem. Soc. 2013, 135, 14586–14592. [Google Scholar] [CrossRef]
- Mukherjee, R.; Cohen-Luria, R.; Wagner, N.; Ashkenasy, G. A Bistable Switch in Dynamic Thiodepsipeptide Folding and Template-Directed Ligation. Angew. Chem. Int. Ed. 2015, 54, 12452–12456. [Google Scholar] [CrossRef]
- Míguez, D.G.; Vanag, V.K.; Epstein, I.R. Fronts and pulses in an enzymatic reaction catalyzed by glucose oxidase. Proc. Natl. Acad. Sci. USA 2007, 104, 6992–6997. [Google Scholar] [CrossRef]
- Bodó, G.; Branca, R.M.M.; Tóth, Á.; Horváth, D.; Bagyinka, C. Concentration-dependent front velocity of the autocatalytic hydrogenase reaction. Biophys. J. 2009, 96, 4976–4983. [Google Scholar] [CrossRef]
- Taylor, A.F.; Tinsley, M.R.; Wang, F.; Huang, Z.; Showalter, K. Dynamical quorum sensing and synchronization in large populations of chemical oscillators. Science 2009, 323, 614–617. [Google Scholar] [CrossRef]
- Epstein, I.R.; Xu, B. Reaction–diffusion processes at the nano-and microscales. Nat. Nanotechnol. 2016, 11, 312–319. [Google Scholar] [CrossRef]
- Krajewska, B. Ureases I. Functional, catalytic and kinetic properties: A review. J. Mol. Catal. B Enzym. 2009, 59, 9–21. [Google Scholar] [CrossRef]
- Phillips, A.J.; Gerlach, R.; Lauchnor, E.; Mitchell, A.C.; Cunningham, A.B.; Spangler, L. Engineered applications of ureolytic biomineralization: A review. Biofouling 2013, 29, 715–733. [Google Scholar] [CrossRef]
- Hu, G.; Pojman, J.A.; Scott, S.K.; Wrobel, M.M.; Taylor, A.F.J. Base-Catalyzed Feedback in the Urea− Urease Reaction. Phys. Chem. B 2010, 114, 14059–14063. [Google Scholar] [CrossRef]
- Bánsági, T., Jr.; Taylor, A.F. Switches induced by quorum sensing in a model of enzyme-loaded microparticles. J. R. Soc. Interface 2018, 15, 20170945. [Google Scholar] [CrossRef]
- Keil, L.M.R.; Möller, F.M.; Kieß, M.; Kudella, P.W.; Mast, C.B. Proton gradients and pH oscillations emerge from heat flow at the microscale. Nat. Commun. 2017, 8, 1897. [Google Scholar] [CrossRef]
- Ball, R.; Brindley, J. The life story of hydrogen peroxide II: A periodic pH and thermochemical drive for the RNA world. J. R. Soc. Interface 2015, 12, 20150366. [Google Scholar] [CrossRef]
- Stano, P. Is Research on “Synthetic Cells” Moving to the Next Level? Life 2019, 9, 3. [Google Scholar] [CrossRef]
- Küchler, A.; Yoshimoto, M.; Luginbühl, S.; Mavelli, F.; Walde, P. Enzymatic reactions in confined environments. Nat. Nanotechnol. 2016, 11, 409–420. [Google Scholar] [CrossRef]
- Bánsági, T.; Taylor, A.F.J. Role of differential transport in an oscillatory enzyme reaction. Phys. Chem. B 2014, 118, 6092–6097. [Google Scholar] [CrossRef]
- Ermentrout, B. Simulating, Analyzing, and Animating Dynamical Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Miller, M.B.; Bassler, B.L. Quorum sensing in bacteria. Annu. Rev. Microbiol. 2001, 55, 165–199. [Google Scholar] [CrossRef]
- Horváth, A.K.; Nagypál, I. Classification of clock reactions. ChemPhysChem 2015, 16, 588–594. [Google Scholar] [CrossRef]
- Caplan, S.R.; Naparstek, A.; Zabusky, N.J. Chemical oscillations in a membrane. Nature 1973, 245, 364–366. [Google Scholar] [CrossRef]
- Miele, Y.; Bánsági, T., Jr.; Taylor, A.F.; Stano, P.; Rossi, F. Advances in Artificial Life, Evolutionary Computation and Systems Chemistry: 10th Italian Workshop, WIVACE 2015, Bari, Italy, 22–25 September 2015; Communications in Computer and Information Science; Springer International Publishing: Basel, Switzerland, 2016; Volume 587, pp. 197–208. [Google Scholar]
- Vanag, V.K.; Míguez, D.G.; Epstein, I.R. Designing an enzymatic oscillator: bistability and feedback controlled oscillations with glucose oxidase in a continuous flow stirred tank reactor. J. Chem. Phys. 2006, 125, 194515. [Google Scholar] [CrossRef]
- Horváth, J.; Szalai, I.; De Kepper, P. An experimental design method leading to chemical Turing patterns. Science 2009, 324, 772–775. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. Ser. B 1952, 237, 37–72. [Google Scholar]
- Paula, S.; Volkov, A.G.; Van Hoek, A.N.; Haines, T.H.; Deamer, D.W. Permeation of protons, potassium ions, and small polar molecules through phospholipid bilayers as a function of membrane thickness. Biophys. J. 1996, 70, 339–348. [Google Scholar] [CrossRef]
- Fyles, T.M. Synthetic ion channels in bilayer membranes. Chem. Soc. Rev. 2007, 36, 335–347. [Google Scholar] [CrossRef]
- Garcia-Ojalvo, J.; Elowitz, M.B.; Strogatz, S.H. Modeling a synthetic multicellular clock: Repressilators coupled by quorum sensing. Proc. Natl. Acad. Sci. USA 2004, 101, 10955–10960. [Google Scholar] [CrossRef]
- Shum, H.; Balazs, A.C. Synthetic quorum sensing in model microcapsule colonies. Proc. Natl. Acad. Sci. USA 2017, 114, 8475–8480. [Google Scholar] [CrossRef]
- Singh, H.; Parmananda, P. Quorum sensing via static coupling demonstrated by Chua’s circuits. Phys. Rev. E 2013, 88, 040903. [Google Scholar] [CrossRef]
- Szabo, E. Oregonator generalization as a minimal model of quorum sensing in Belousov–Zhabotinsky reaction with catalyst confinement in large populations of particles. RSC Adv. 2015, 5, 99547–99554. [Google Scholar] [CrossRef]
- Zamora-Munt, J.; Masoller, C.; Garcia-Ojalvo, J.; Roy, R. Crowd synchrony and quorum sensing in delay-coupled lasers. Phys. Rev. Lett. 2010, 105, 264101. [Google Scholar] [CrossRef]
- Din, M.O.; Danino, T.; Prindle, A.; Skalak, M.; Selimkhanov, J.; Allen, K.; Julio, E.; Atolia, E.; Tsimring, L.S.; Bhatia, S.N.; et al. Synchronized cycles of bacterial lysis for in vivo delivery. Nature 2016, 536, 81–85. [Google Scholar] [CrossRef]
- Tóth-Szeles, E.; Horváth, J.; Holló, G.; Szűcs, R.; Nakanishi, H.; Lagzi, I. Chemically coded time-programmed self-assembly. Mol. Syst. Des. Eng. 2017, 2, 274–282. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bánsági, T.; Taylor, A.F. Modelling Bacteria-Inspired Dynamics with Networks of Interacting Chemicals. Life 2019, 9, 63. https://doi.org/10.3390/life9030063
Bánsági T, Taylor AF. Modelling Bacteria-Inspired Dynamics with Networks of Interacting Chemicals. Life. 2019; 9(3):63. https://doi.org/10.3390/life9030063
Chicago/Turabian StyleBánsági, Tamás, and Annette F. Taylor. 2019. "Modelling Bacteria-Inspired Dynamics with Networks of Interacting Chemicals" Life 9, no. 3: 63. https://doi.org/10.3390/life9030063
APA StyleBánsági, T., & Taylor, A. F. (2019). Modelling Bacteria-Inspired Dynamics with Networks of Interacting Chemicals. Life, 9(3), 63. https://doi.org/10.3390/life9030063