Protobiotic Systems Chemistry Analyzed by Molecular Dynamics
Abstract
1. Systems Chemistry in Life’s Origin
2. Molecular Dynamics for Systems Chemistry
3. GARD: A Lipid-Based Systems Chemistry Model for Life’s Origin
4. Molecular Dynamics of Micelles and Mixed Micelles
5. Roadmap for GARD Evidence via Molecular Dynamics
- With the environment being equimolar in the different lipid types (Table 1), we will look for statistically significant deviations from randomly disposed within-micelle equimolarity. It will be necessary to distinguish the contributions of equilibrium-related statistical deviations stemming from kinetic (rate-enhancement) effects, as expected in the GARD model [11]. One possible test for the relative contribution of kinetics and thermodynamics to compositional biases would be a comparison along the accretion process to asymptotically long simulation times, whereby the micellar composition is likely to be governed purely by thermodynamic equilibrium constants. Spatial deviations from randomity (akin to lipid rafts and caveoli in living cells [91,96]) would also point to thermodynamic effects.
- We will examine whether compositional fluctuations are amplified by the anticipated mutually catalytic effects, portraying attractor phenomenology (Figure 1). Such attractor behavior is manifested in a progression whereby random initial fluctuations are augmented by the acting mutually catalytic network towards the emergence of a reproducing composome [8]. We are currently studying such behavior by standard kinetic Monte Carlo simulations to pave the way for future molecular dynamics scrutiny.
- We will examine the net incoming time-dependent amphiphile fluxes for a correlation of their compositional direction to that of the initial premicelles. Such correlation will provide evidence of compositional preservation, the hallmark of homeostatic growth, and an equivalent to compositional replication/reproduction [8].
- We will seek simulated fission events affecting the biasedly grown micelles [80], showing better-than-random similarity between the parental micelle and its progeny.
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Oparin, A.; Gladilin, K. Evolution of self-assembly of probionts. BioSystems 1980, 12, 133–145. [Google Scholar] [CrossRef]
- Joyce, G.F. Foreword. In Origins of Life: The Central Concepts; Deamer, D.W., Fleischaker, G.R., Eds.; Jones and Bartlett: Boston, MA, USA, 1994; pp. xi–xii. [Google Scholar]
- Dyson, F. Origins of Life; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Sadownik, J.W.; Otto, S. Systems Chemistry. In Encyclopedia of Astrobiology; Gargaud, M., Irvine, W.M., Amils, R., Cleaves, H.J., Pinti, D., Quintanilla, J.C., Viso, M., Eds.; Springer Link: Berlin/Heidelberg, Germany, 2015; pp. 1–3. [Google Scholar]
- von Kiedrowski, G.; Otto, S.; Herdewijn, P. Welcome home, systems chemists! J. Syst. Chem. 2010, 1, 1. [Google Scholar] [CrossRef]
- Strazewski, P. The Beginning of Systems Chemistry. Life 2019, 9, 11. [Google Scholar] [CrossRef] [PubMed]
- Grzelczak, M. Colloidal systems chemistry. Replication, reproduction and selection at nanoscale. J. Colloid Interface Sci. 2019, 537, 269–279. [Google Scholar] [CrossRef]
- Lancet, D.; Zidovetzki, R.; Markovitch, O. Systems protobiology: Origin of life in lipid catalytic networks. J. R. Soc. Interface 2018, 15, 20180159. [Google Scholar] [CrossRef] [PubMed]
- Dyson, F.J. A model for the origin of life. J. Mol. Evol. 1982, 18, 344–350. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Segré, D.; Ben-Eli, D.; Lancet, D. Compositional genomes: Prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc. Natl. Acad. Sci. USA 2000, 97, 4112–4117. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Hein, J.; Steel, M. Autocatalytic Sets and the Origin of Life. Entropy 2010, 12, 1733–1742. [Google Scholar] [CrossRef]
- Hayden, E.J.; von Kiedrowski, G.; Lehman, N. Systems chemistry on ribozyme self-construction: Evidence for anabolic autocatalysis in a recombination network. Angew. Chem. 2008, 120, 8552–8556. [Google Scholar] [CrossRef]
- Dadon, Z.; Wagner, N.; Ashkenasy, G. The road to non-enzymatic molecular networks. Angew. Chem. Int. Ed. 2008, 47, 6128–6136. [Google Scholar] [CrossRef]
- Ruiz-Mirazo, K.; Briones, C.; de la Escosura, A. Prebiotic systems chemistry: New perspectives for the origins of life. Chem. Rev. 2014, 114, 285–366. [Google Scholar] [CrossRef]
- Ashkenasy, G.; Hermans, T.M.; Otto, S.; Taylor, A.F. Systems chemistry. Chem. Soc. Rev. 2017, 46, 2543–2554. [Google Scholar] [CrossRef]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- McCammon, J.A.; Gelin, B.R.; Karplus, M. Dynamics of folded proteins. Nature 1977, 267, 585. [Google Scholar] [CrossRef]
- Hodak, H. The Nobel Prize in chemistry 2013 for the development of multiscale models of complex chemical systems: A tribute to Martin Karplus, Michael Levitt and Arieh Warshel. J. Mol. Biol. 2014, 1, 1–3. [Google Scholar] [CrossRef][Green Version]
- van Gunsteren, W.F.; Weiner, P.K.; Wilkinson, A.J. Computer Simulation of Biomolecular Systems: Theoretical and Experimental Applications; Springer Science & Business Media: Dordrecht, The Netherlands, 2013; Volume 3. [Google Scholar]
- Vlachakis, D.; Bencurova, E.; Papangelopoulos, N.; Kossida, S. Current state-of-the-art molecular dynamics methods and applications. In Advances in Protein Chemistry and Structural Biology; Elsevier: Amsterdam, The Netherlands, 2014; Volume 94, pp. 269–313. [Google Scholar]
- Hospital, A.; Goñi, J.R.; Orozco, M.; Gelpí, J.L. Molecular dynamics simulations: Advances and applications. Adv. Appl. Bioinform. Chem. 2015, 8, 37–47. [Google Scholar]
- Silva, D.-A.; Weiss, D.R.; Avila, F.P.; Da, L.-T.; Levitt, M.; Wang, D.; Huang, X. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proc. Natl. Acad. Sci. USA 2014, 111, 7665–7670. [Google Scholar] [CrossRef]
- Sharma, S.; Ding, F.; Dokholyan, N.V. Multiscale modeling of nucleosome dynamics. Biophys. J. 2007, 92, 1457–1470. [Google Scholar] [CrossRef]
- Roccatano, D.; Barthel, A.; Zacharias, M. Structural flexibility of the nucleosome core particle at atomic resolution studied by molecular dynamics simulation. Biopolym. Orig. Res. Biomol. 2007, 85, 407–421. [Google Scholar] [CrossRef]
- Brandman, R.; Brandman, Y.; Pande, V.S. A-site residues move independently from P-site residues in all-atom molecular dynamics simulations of the 70S bacterial ribosome. PLoS ONE 2012, 7, e29377. [Google Scholar] [CrossRef]
- Tinoco, I., Jr.; Wen, J.-D. Simulation and analysis of single-ribosome translation. Phys. Biol. 2009, 6, 025006. [Google Scholar] [CrossRef]
- Dieckmann, A.; Beniken, S.; Lorenz, C.; Doltsinis, N.L.; von Kiedrowski, G. Unravelling a fulvene based Replicator: Experiment and Theory in Interplay. J. Syst. Chem. 2010, 1, 10. [Google Scholar] [CrossRef]
- Orozco, M.; Orellana, L.; Hospital, A.; Naganathan, A.N.; Emperador, A.; Carrillo, O.; Gelpi, J. Coarse-grained representation of protein flexibility. Foundations, successes, and shortcomings. In Advances in Protein Chemistry and Structural Biology; Elsevier: Amsterdam, The Netherlands, 2011; Volume 85, pp. 183–215. [Google Scholar]
- Roussel, G.; Michaux, C.; Perpète, E.A. Multiscale molecular dynamics simulations of sodium dodecyl sulfate micelles: From coarse-grained to all-atom resolution. J. Mol. Model. 2014, 20, 2469. [Google Scholar] [CrossRef]
- Ganesan, A.; Coote, M.L.; Barakat, K. Molecular dynamics-driven drug discovery: Leaping forward with confidence. Drug Discov. Today 2017, 22, 249–269. [Google Scholar] [CrossRef]
- Piana, S.; Klepeis, J.L.; Shaw, D.E. Assessing the accuracy of physical models used in protein-folding simulations: Quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol. 2014, 24, 98–105. [Google Scholar] [CrossRef]
- Mendieta-Wejebe, J.E.; Correa-Basurto, J.; Garcia-Segovia, E.M.; Ceballos-Cancino, G.; Rosales-Hernandez, M.C. Molecular modeling used to evaluate CYP2C9-dependent metabolism: Homology modeling, molecular dynamics and docking simulations. Curr. Drug Metab. 2011, 12, 533–548. [Google Scholar] [CrossRef]
- Marrink, S.; Tieleman, D.; Mark, A. Molecular dynamics simulation of the kinetics of spontaneous micelle formation. J. Phys. Chem. B 2000, 104, 12165–12173. [Google Scholar] [CrossRef]
- DeLisi, C. Computers in molecular biology: Current applications and emerging trends. Science 1988, 240, 47–52. [Google Scholar] [CrossRef]
- Zwier, M.C.; Chong, L.T. Reaching biological timescales with all-atom molecular dynamics simulations. Curr. Opin. Pharmacol. 2010, 10, 745–752. [Google Scholar] [CrossRef]
- Frederix, P.W.; Idé, J.; Altay, Y.; Schaeffer, G.L.; Surin, M.; Beljonne, D.; Bondarenko, A.S.; Jansen, T.L.; Otto, S.; Marrink, S.J. Structural and spectroscopic properties of assemblies of self-replicating peptide macrocycles. ACS Nano 2017, 11, 7858–7868. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Nowak, P.; Otto, S. An allosteric receptor by simultaneous “casting” and “molding” in a dynamic combinatorial library. Angew. Chem. 2015, 127, 847–851. [Google Scholar] [CrossRef]
- Lancet, D.; Shenhav, B. Compositional lipid protocells: Reproduction without polynucleotides. In Protocells: Bridging Nonliving and Living Matter; Rasmussen, S., Bedau, M., Chen, L., Deamer, D., Krakauer, D., Packard, N., Stadler, P., Eds.; MIT Press: Cambridge, MA, USA, 2009; pp. 233–252. [Google Scholar]
- Segré, D.; Ben-Eli, D.; Deamer, D.W.; Lancet, D. The lipid world. Orig. Life Evol. Biosph. 2001, 31, 119–145. [Google Scholar] [CrossRef] [PubMed]
- Markovitch, O.; Lancet, D. Multispecies population dynamics of prebiotic compositional assemblies. J. Theor. Biol. 2014, 357, 26–34. [Google Scholar] [CrossRef] [PubMed]
- Maurer, S.E.; Deamer, D.W.; Boncella, J.M.; Monnard, P.-A. Chemical evolution of amphiphiles: Glycerol monoacyl derivatives stabilize plausible prebiotic membranes. Astrobiology 2009, 9, 979–987. [Google Scholar] [CrossRef]
- Vequi-Suplicy, C.C.; Riske, K.A.; Knorr, R.L.; Dimova, R. Vesicles with charged domains. Biochim. Biophys. Acta 2010, 1798, 1338–1347. [Google Scholar] [CrossRef]
- Bukhryakov, K.V.; Almahdali, S.; Rodionov, V.O. Amplification of Chirality through Self-Replication of Micellar Aggregates in Water. Langmuir 2015, 31, 2931–2935. [Google Scholar] [CrossRef] [PubMed]
- Devaraj, N.K. In Situ Synthesis of Phospholipid Membranes. J. Org. Chem. 2017, 82, 5997–6005. [Google Scholar] [CrossRef]
- Segré, D.; Lancet, D. Composing life. EMBO Rep. 2000, 1, 217–222. [Google Scholar] [CrossRef]
- Wendoloski, J.; Kimatian, S.; Schutt, C.; Salemme, F. Molecular dynamics simulation of a phospholipid micelle. Science 1989, 243, 636–638. [Google Scholar] [CrossRef]
- Jönsson, B.; Edholm, O.; Teleman, O. Molecular dynamics simulations of a sodium octanoate micelle in aqueous solution. J. Chem. Phys. 1986, 85, 2259–2271. [Google Scholar] [CrossRef]
- Watanabe, K.; Ferrario, M.; Klein, M.L. Molecular dynamics study of a sodium octanoate micelle in aqueous solution. J. Phys. Chem. 1988, 92, 819–821. [Google Scholar] [CrossRef]
- Wymore, T.; Gao, X.; Wong, T. Molecular dynamics simulation of the structure and dynamics of a dodecylphosphocholine micelle in aqueous solution. J. Mol. Struct. 1999, 485, 195–210. [Google Scholar] [CrossRef]
- Shelley, J.C.; Sprik, M.; Klein, M.L. Molecular dynamics simulation of an aqueous sodium octanoate micelle using polarizable surfactant molecules. Langmuir 1993, 9, 916–926. [Google Scholar] [CrossRef]
- Boecker, J.; Brickmann, J.; Bopp, P. Molecular dynamics simulation study of an n-decyltrimethylammonium chloride micelle in water. J. Phys. Chem. 1994, 98, 712–717. [Google Scholar] [CrossRef]
- Bogusz, S.; Venable, R.M.; Pastor, R.W. Molecular dynamics simulations of octyl glucoside micelles: Dynamic properties. J. Phys. Chem. B 2001, 105, 8312–8321. [Google Scholar] [CrossRef]
- Bruce, C.D.; Berkowitz, M.L.; Perera, L.; Forbes, M.D. Molecular dynamics simulation of sodium dodecyl sulfate micelle in water: Micellar structural characteristics and counterion distribution. J. Phys. Chem. B 2002, 106, 3788–3793. [Google Scholar] [CrossRef]
- Rakitin, A.R.; Pack, G.R. Molecular dynamics simulations of ionic interactions with dodecyl sulfate micelles. J. Phys. Chem. B 2004, 108, 2712–2716. [Google Scholar] [CrossRef]
- Zhai, Z.; Yan, X.; Song, Z.; Shang, S.; Rao, X. Wormlike micelles constructed by a highly water-soluble carboxylate surfactant containing a phenoxy and nonionic surfactant. J. Mol. Liq. 2017, 248, 595–601. [Google Scholar] [CrossRef]
- Honegger, P.; Schmollngruber, M.; Hagn, G.; Baig, O.; von Baeckmann, C.; Steinhauser, O.; Schröder, C. Molecular dynamics simulation of aqueous 1-dodecyl-3-methylimidazolium chloride: Emerging micelles. J. Mol. Liq. 2018, 272, 766–777. [Google Scholar] [CrossRef]
- Ghaed-Sharaf, T.; Yang, D.-S.; Baldelli, S.; Ghatee, M.H. From Micelles to Vesicle and Membrane Structures of Double Strand Ionic Liquids in Water: Molecular Dynamics Simulation. Langmuir 2019, 35, 2780–2791. [Google Scholar] [CrossRef]
- Posocco, P.; Perazzo, A.; Preziosi, V.; Laurini, E.; Pricl, S.; Guido, S.J.R.A. Interfacial tension of oil/water emulsions with mixed non-ionic surfactants: Comparison between experiments and molecular simulations. RSC Adv. 2016, 6, 4723–4729. [Google Scholar] [CrossRef]
- Indelicato, S.; Bongiorno, D.; Calabrese, V.; Perricone, U.; Almerico, A.M.; Ceraulo, L.; Piazzese, D.; Tutone, M. Micelles, Rods, Liposomes, and Other Supramolecular Surfactant Aggregates: Computational Approaches. Interdiscip. Sci. Comput. Life Sci. 2017, 9, 392–405. [Google Scholar] [CrossRef][Green Version]
- Ritter, E.; Yordanova, D.; Gerlach, T.; Smirnova, I.; Jakobtorweihen, S. Molecular dynamics simulations of various micelles to predict micelle water partition equilibria with COSMOmic: Influence of micelle size and structure. Fluid Phase Equilibria 2016, 422, 43–55. [Google Scholar] [CrossRef]
- Chun, B.J.; Choi, J.I.; Jang, S.S. Molecular dynamics simulation study of sodium dodecyl sulfate micelle: Water penetration and sodium dodecyl sulfate dissociation. Colloids Surf. A Physicochem. Eng. Asp. 2015, 474, 36–43. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, S.; Larson, R.G. Potentials of mean force and escape times of surfactants from micelles and hydrophobic surfaces using molecular dynamics simulations. Langmuir 2015, 31, 1336–1343. [Google Scholar] [CrossRef]
- Yordanova, D.; Ritter, E.; Gerlach, T.; Jensen, J.; Smirnova, I.; Jakobtorweihen, S. Solute partitioning in micelles: Combining molecular dynamics simulations, COSMOmic, and experiments. J. Phys. Chem. B 2017, 121, 5794–5809. [Google Scholar] [CrossRef]
- Gujt, J.; Bešter-Rogač, M.; Spohr, E. Structure and Stability of Long Rod-like Dodecyltrimethylammonium Chloride Micelles in Solutions of Hydroxybenzoates: A Molecular Dynamics Simulation Study. Langmuir 2016, 32, 8275–8286. [Google Scholar] [CrossRef]
- Wang, L.; Fujimoto, K.; Yoshii, N.; Okazaki, S. A molecular dynamics study of the breathing and deforming modes of the spherical ionic SDS and nonionic C12E8 micelles. J. Chem. Phys. 2016, 144, 034903. [Google Scholar] [CrossRef]
- Wang, P.; Pei, S.; Wang, M.; Yan, Y.; Sun, X.; Zhang, J. Study on the transformation from linear to branched wormlike micelles: An insight from molecular dynamics simulation. J. Colloid Interface Sci. 2017, 494, 47–53. [Google Scholar] [CrossRef]
- Faramarzi, S.; Bonnett, B.; Scaggs, C.A.; Hoffmaster, A.; Grodi, D.; Harvey, E.; Mertz, B. Molecular dynamics simulations as a tool for accurate determination of surfactant micelle properties. Langmuir 2017, 33, 9934–9943. [Google Scholar] [CrossRef]
- Levine, B.G.; LeBard, D.N.; DeVane, R.; Shinoda, W.; Kohlmeyer, A.; Klein, M.L. Micellization studied by GPU-accelerated coarse-grained molecular dynamics. J. Chem.Theory Comput. 2011, 7, 4135–4145. [Google Scholar] [CrossRef]
- Liu, G.; Wei, Y.; Gao, F.; Yuan, S.; Liu, C. Origins of entropy change for the amphiphilic molecule in micellization: A molecular dynamics study. Phys. Chem. Chem. Phys. 2016, 18, 11357–11361. [Google Scholar] [CrossRef]
- Johnston, M.A.; Swope, W.C.; Jordan, K.E.; Warren, P.B.; Noro, M.G.; Bray, D.J.; Anderson, R.L. Toward a standard protocol for micelle simulation. J. Phys. Chem. B 2016, 120, 6337–6351. [Google Scholar] [CrossRef]
- Messina, P.V.; Besada-Porto, J.M.; Rial, R.; González-Díaz, H.; Ruso, J.M. Computational modeling and experimental facts of mixed self-assembly systems. Curr. Pharm. Des. 2016, 22, 5249–5256. [Google Scholar] [CrossRef]
- Storm, S.; Jakobtorweihen, S.; Smirnova, I. Solubilization in mixed micelles studied by molecular dynamics simulations and COSMOmic. J. Phys. Chem. B 2014, 118, 3593–3604. [Google Scholar] [CrossRef]
- Pohorille, A.; Wilson, M.A. Molecular dynamics studies of simple membrane—Water interfaces: Structure and functions in the beginnings of cellular life. Orig. Life Evol. Biosph. 1995, 25, 21–46. [Google Scholar] [CrossRef]
- Arai, N.; Yoshimoto, Y.; Yasuoka, K.; Ebisuzaki, T. Self-assembly behaviours of primitive and modern lipid membrane solutions: A coarse-grained molecular simulation study. Phys. Chem. Chem. Phys. 2016, 18, 19426–19432. [Google Scholar] [CrossRef]
- van Hoof, B.; Markvoort, A.J.; van Santen, R.A.; Hilbers, P.A. On protein crowding and bilayer bulging in spontaneous vesicle formation. J. Phys. Chem. B 2012, 116, 12677–12683. [Google Scholar] [CrossRef]
- Bachmann, P.A.; Luisi, P.L.; Lang, J. Autocatalytic self-replicating micelles as models for prebiotic structures. Nature 1992, 357, 57–59. [Google Scholar] [CrossRef]
- Bissette, A.J.; Odell, B.; Fletcher, S.P. Physical autocatalysis driven by a bond-forming thiol–ene reaction. Nat. Commun. 2014, 5, 4607. [Google Scholar] [CrossRef]
- Kraft, J.F.; Vestergaard, M.; Schiøtt, B.; Thøgersen, L. Modeling the self-assembly and stability of DHPC micelles using atomic resolution and coarse grained MD simulations. J. Chem. Theory Comput. 2012, 8, 1556–1569. [Google Scholar] [CrossRef]
- Sammalkorpi, M.; Karttunen, M.; Haataja, M. Micelle fission through surface instability and formation of an interdigitating stalk. J. Am. Chem. Soc. 2008, 130, 17977–17980. [Google Scholar] [CrossRef]
- Pool, R.; Bolhuis, P.G. Sampling the kinetic pathways of a micelle fusion and fission transition. J. Chem. Phys. 2007, 126, 244703. [Google Scholar] [CrossRef]
- Liu, F.; Liu, D.; Zhou, W.; Chen, F.; Wei, J.J.I.; Research, E.C. Coarse-grained molecular dynamics simulations of the breakage and recombination behaviors of surfactant micelles. Ind. Eng. Chem. Res. 2018, 57, 9018–9027. [Google Scholar] [CrossRef]
- Yakovlev, D.S.; Boek, E.S. Molecular dynamics simulations of mixed cationic/anionic wormlike micelles. Langmuir 2007, 23, 6588–6597. [Google Scholar] [CrossRef]
- Shenhav, B.; Bar-Even, A.; Kafri, R.; Lancet, D. Polymer GARD: Computer simulation of covalent bond formation in reproducing molecular assemblies. Orig. Life Evol. Biosph. 2005, 35, 111–133. [Google Scholar] [CrossRef]
- Shenhav, B.; Lancet, D. Prospects of a computational origin of life endeavor. Orig. Life Evol. Biosph. 2004, 34, 181–194. [Google Scholar] [CrossRef]
- Gánti, T. Biogenesis itself. J. Theor. Biol. 1997, 187, 583–593. [Google Scholar] [CrossRef]
- Brogioli, D. Marginally stable chemical systems as precursors of life. Phys. Rev. Lett. 2010, 105, 058102. [Google Scholar] [CrossRef]
- Cui, X.; Mao, S.; Liu, M.; Yuan, H.; Du, Y. Mechanism of surfactant micelle formation. Langmuir 2008, 24, 10771–10775. [Google Scholar] [CrossRef]
- Bhoutekar, A.; Ghosh, S.; Bhattacharya, S.; Chatterjee, A. A new class of enhanced kinetic sampling methods for building Markov state models. J. Chem. Phys. 2017, 147, 152702. [Google Scholar] [CrossRef]
- Zimmerman, M.I.; Porter, J.R.; Sun, X.; Silva, R.R.; Bowman, G.R. Choice of adaptive sampling strategy impacts state discovery, transition probabilities, and the apparent mechanism of conformational changes. arXiv 2018, arXiv:1805.04616. [Google Scholar] [CrossRef]
- Shenhav, B.; Segrè, D.; Lancet, D. Mesobiotic emergence: Molecular and ensemble complexity in early evolution. Adv. Complex Syst. 2003, 6, 15–35. [Google Scholar] [CrossRef]
- Lancet, D.; Sadovsky, E.; Seidemann, E. Probability model for molecular recognition in biological receptor repertoires: Significance to the olfactory system. Proc. Natl. Acad. Sci. USA 1993, 90, 3715–3719. [Google Scholar] [CrossRef]
- Andoh, Y.; Yoshii, N.; Fujimoto, K.; Mizutani, K.; Kojima, H.; Yamada, A.; Okazaki, S.; Kawaguchi, K.; Nagao, H.; Iwahashi, K. MODYLAS: A highly parallelized general-purpose molecular dynamics simulation program for large-scale systems with long-range forces calculated by fast multipole method (FMM) and highly scalable fine-grained new parallel processing algorithms. J. Chem. Theory Comput. 2013, 9, 3201–3209. [Google Scholar] [CrossRef]
- Kawada, S.; Komori, M.; Fujimoto, K.; Yoshii, N.; Okazaki, S. Molecular dynamics study of the formation mechanisms of ionic SDS and nonionic C12E8 micelles and n-dodecane droplets. Chem. Phys. Lett. 2016, 646, 36–40. [Google Scholar] [CrossRef]
- Snow, C.D.; Nguyen, H.; Pande, V.S.; Gruebele, M. Absolute comparison of simulated and experimental protein-folding dynamics. Nature 2002, 420, 102–106. [Google Scholar] [CrossRef]
- Lu, S.M.; Fairn, G.D. Mesoscale organization of domains in the plasma membrane–beyond the lipid raft. Crit. Rev. Biochem. Mol. Biol. 2018, 53, 192–207. [Google Scholar] [CrossRef]
- Lancet, D.; Zidovetzki, R.; Shenhav, B.; Markovitch, O. Metabolic GARD: Replicating catalytic network of lipid-anchored metabolites. In Proceedings of the XVIIIth Intl Conf on Origin of Life, San Diego, CA, USA, 16–21 July 2017; Available online: http://www.hou.usra.edu/meetings/issol2017/pdf/4061.pdf (accessed on 9 May 2019).
- Borhani, D.W.; Shaw, D.E. The future of molecular dynamics simulations in drug discovery. J. Comput.-Aided Mol. Des. 2012, 26, 15–26. [Google Scholar] [CrossRef]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. Modeling chemical reactions in classical molecular dynamics simulations. Polymer 2017, 128, 211–217. [Google Scholar] [CrossRef]
- Kahana, A.; Lancet, D. Enceladus: First observed primordial soup could arbitrate origin of life debate. Astrobiology 2019. in revision. [Google Scholar]
- Sornborger, A.T.; Stancil, P.; Geller, M.R. Toward prethreshold gate-based quantum simulation of chemical dynamics: Using potential energy surfaces to simulate few-channel molecular collisions. Quantum Inf. Process. 2018, 17, 106. [Google Scholar] [CrossRef]
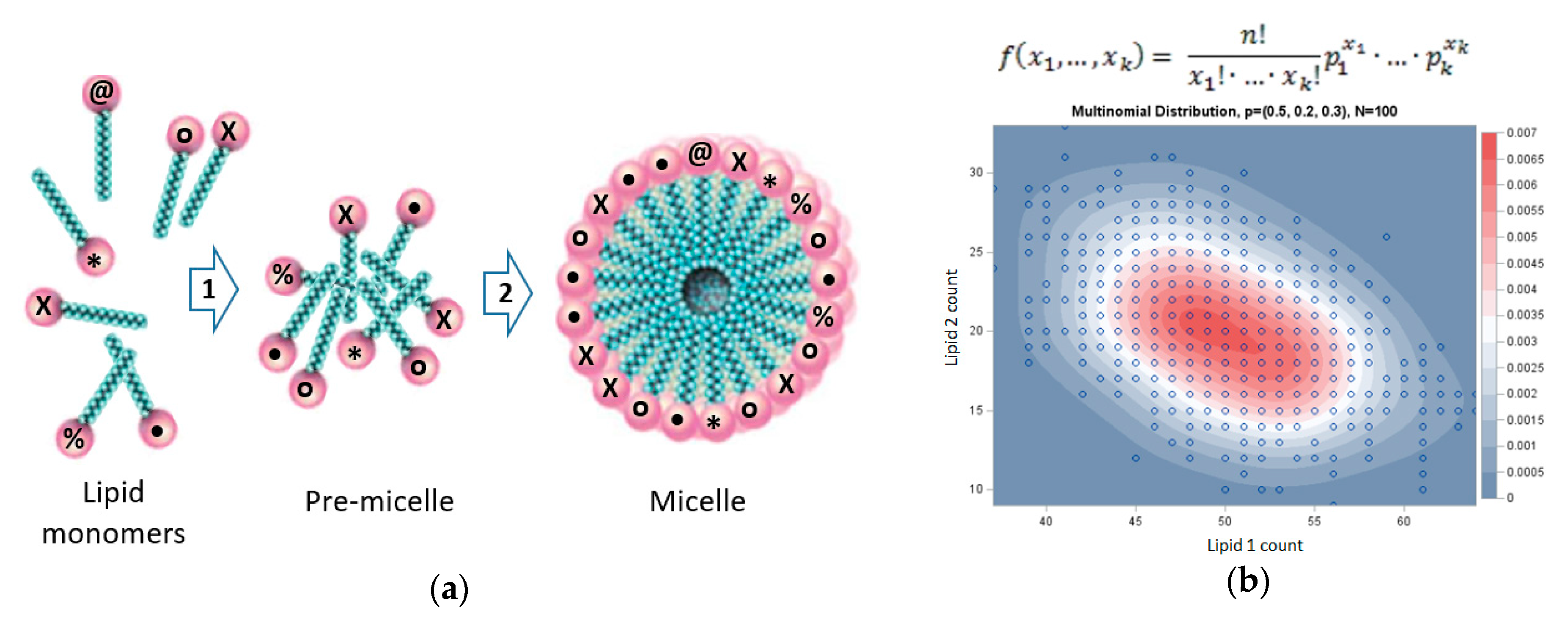
| Lipid Type | % | • | X | * | @ | o | |
|---|---|---|---|---|---|---|---|
| Xi | X1 | X2 | X3 | X4 | X5 | X6 | n |
| Pi | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 | |
| Premicelle Xi | 1 | 2 | 2 | 1 | 0 | 2 | 8 |
| Micelle Xi | 2 | 6 | 5 | 2 | 1 | 5 | 21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahana, A.; Lancet, D. Protobiotic Systems Chemistry Analyzed by Molecular Dynamics. Life 2019, 9, 38. https://doi.org/10.3390/life9020038
Kahana A, Lancet D. Protobiotic Systems Chemistry Analyzed by Molecular Dynamics. Life. 2019; 9(2):38. https://doi.org/10.3390/life9020038
Chicago/Turabian StyleKahana, Amit, and Doron Lancet. 2019. "Protobiotic Systems Chemistry Analyzed by Molecular Dynamics" Life 9, no. 2: 38. https://doi.org/10.3390/life9020038
APA StyleKahana, A., & Lancet, D. (2019). Protobiotic Systems Chemistry Analyzed by Molecular Dynamics. Life, 9(2), 38. https://doi.org/10.3390/life9020038





