Role of Mineral Surfaces in Prebiotic Chemical Evolution. In Silico Quantum Mechanical Studies
Abstract
1. Introduction
2. Quantum Mechanical Methods
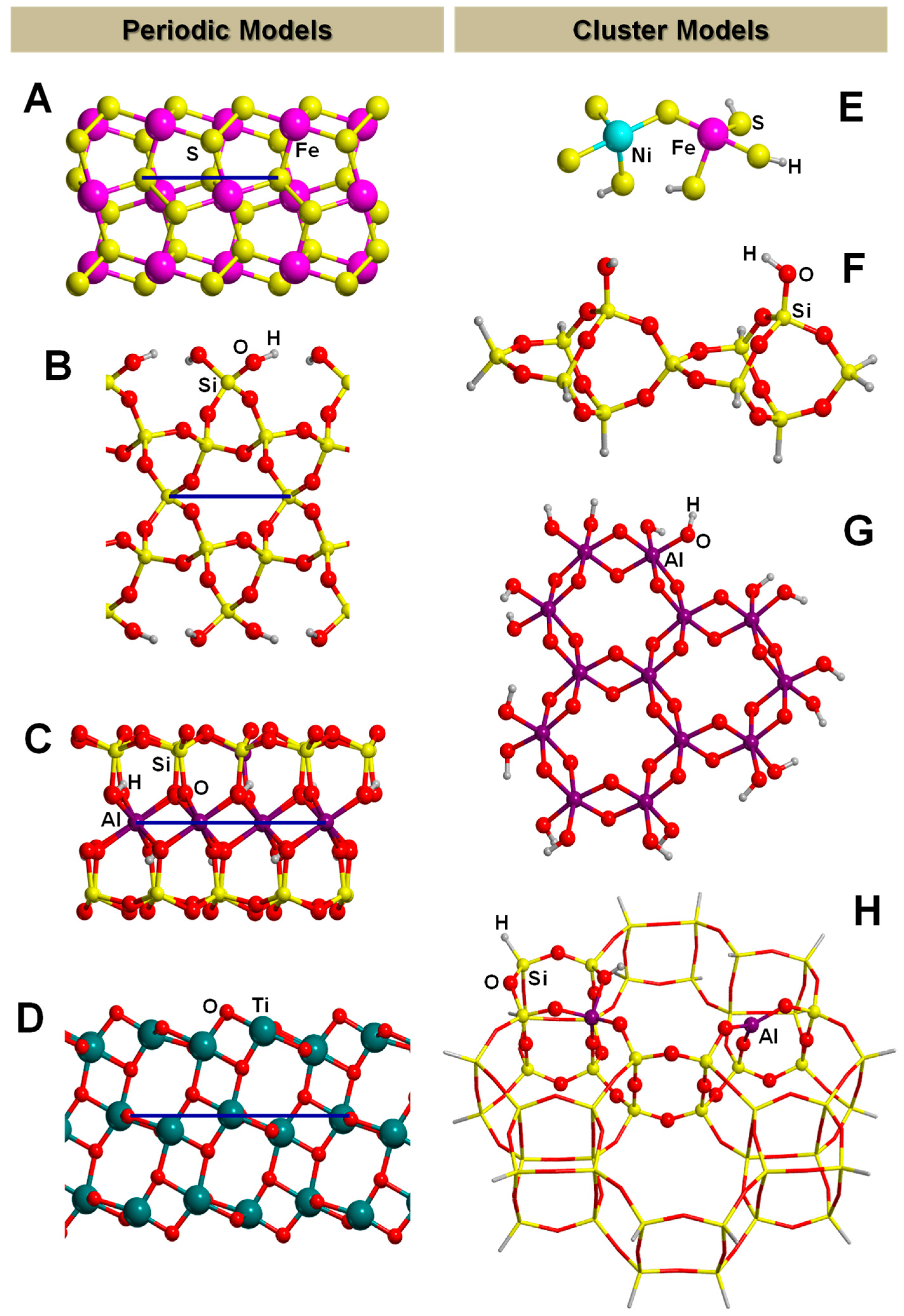
3. Structural Surface Models
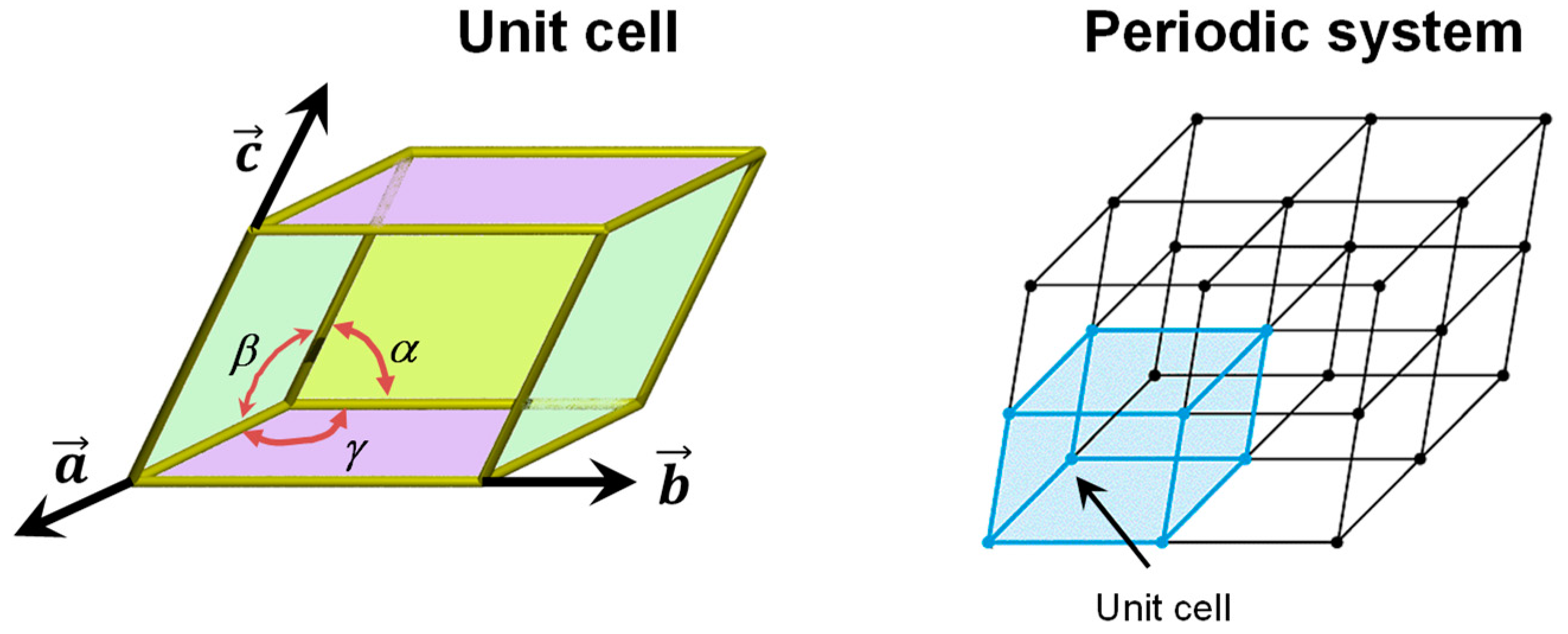
3.1. The Periodic Boundary Conditions Approach
3.2. The Finite Cluster Approach
4. In Silico Prebiotic Studies on Mineral–Organic Interactions
4.1. Clays
4.2. Iron Sulphides
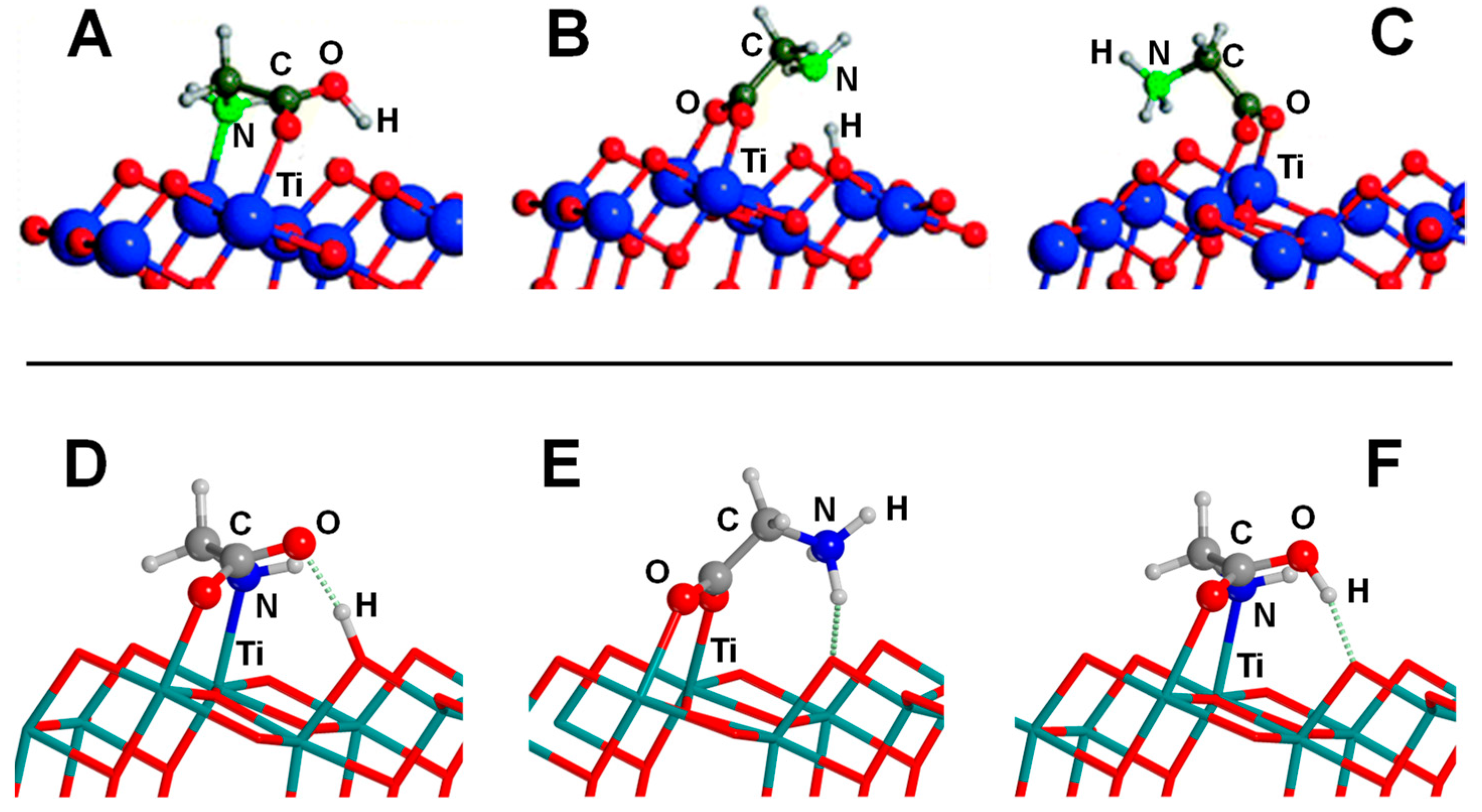
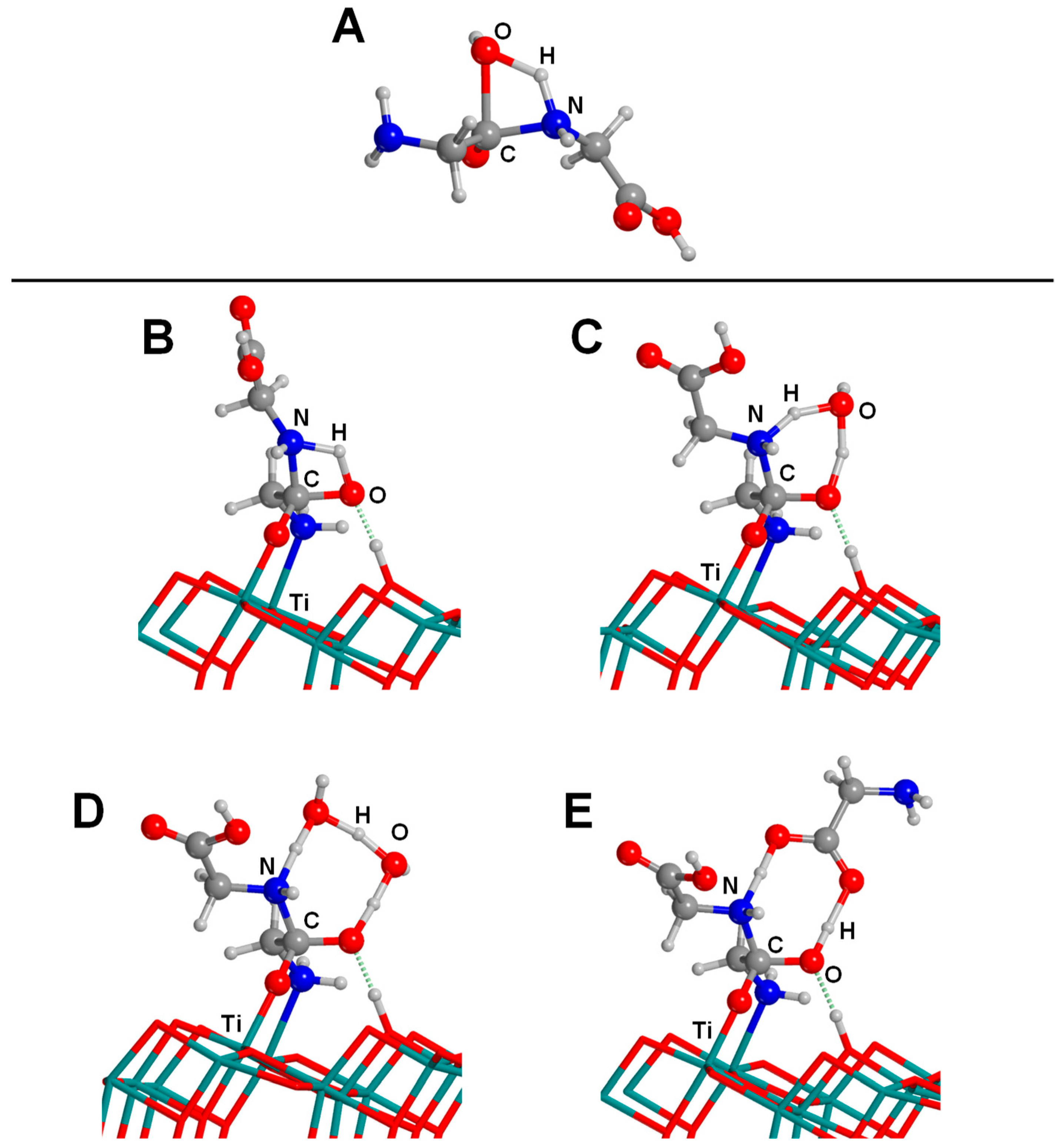
4.3. Titanium Dioxide
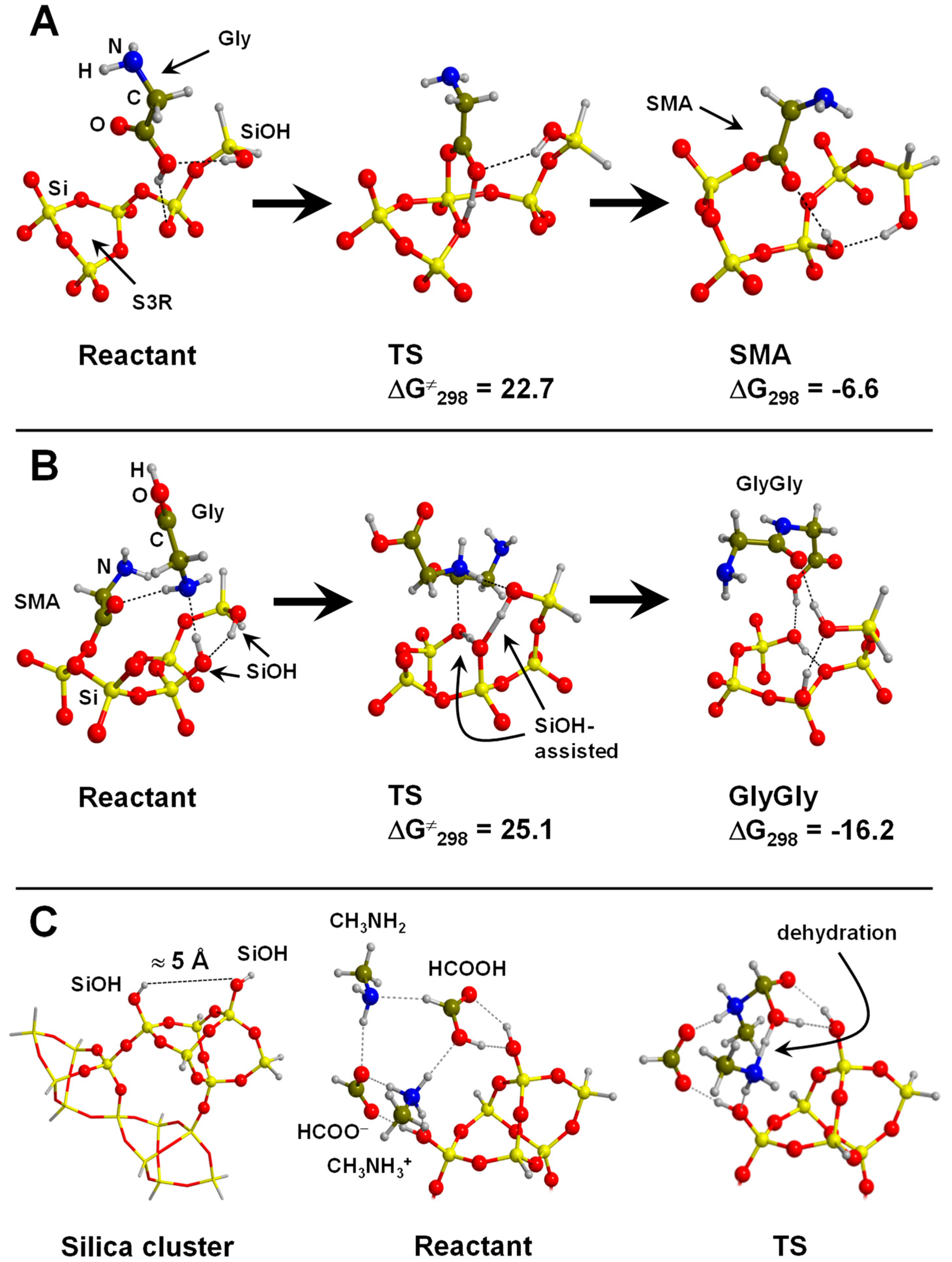
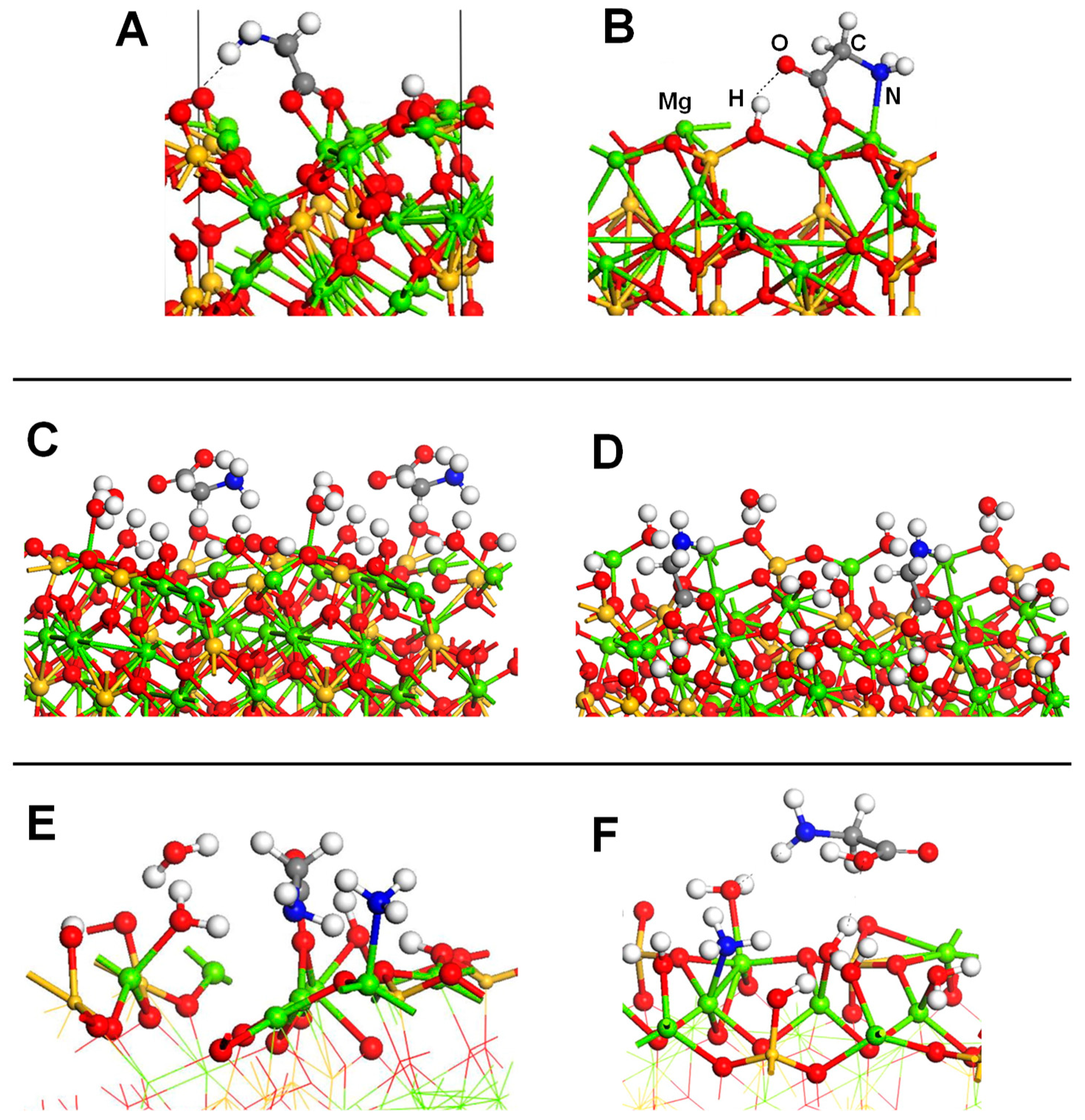
4.4. Silica and Silicates
5. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hazen, R.M. Genesis: The Scientific Quest for Lifes Origin; The National Academies Press: Washington, DC, USA, 2005; p. 368. [Google Scholar]
- Stano, P.; Luisi, P.L. Basic Questions About the Origins of Life: Proceedings of the Erice International School of Complexity (Fourth Course). Orig. Life Evol. Biosph. 2007, 37, 303–307. [Google Scholar] [CrossRef] [PubMed]
- Raine, D.; Luisi, P.L. Open Questions on the Origin of Life (OQOL). Orig. Life Evol. Biosph. 2012, 42, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Brack, A. From Interstellar Amino Acids to Prebiotic Catalytic Peptides: A Review. Chem. Biodivers. 2007, 4, 665–679. [Google Scholar] [CrossRef] [PubMed]
- Orgel, L.E. The origin of life—A review of facts and speculations. Trends Biochem. Sci. 1998, 23, 491–495. [Google Scholar] [CrossRef]
- Orgel, L.E. Prebiotic Chemistry and the Origin of the RNA World. Crit. Rev. Biochem. Mol. Biol. 2004, 39, 99–123. [Google Scholar]
- Ruiz-Mirazo, K.; Briones, C.; de la Escosura, A. Prebiotic Systems Chemistry: New Perspectives for the Origins of Life. Chem. Rev. 2014, 114, 285–366. [Google Scholar] [CrossRef]
- Lehn, J.-M. Perspectives in Chemistry-Steps towards Complex Matter. Angew. Chem. Int. Ed. 2013, 52, 2836–2850. [Google Scholar] [CrossRef]
- Lehn, J.-M. Perspectives in Chemistry—Aspects of Adaptive Chemistry and Materials. Angew. Chem. Int. Ed. 2015, 54, 3276–3289. [Google Scholar] [CrossRef]
- Pross, A. What Is Life? How Chemistry Becomes Biology, 1st ed.; Oxford University Press: Oxford, UK, 2012; p. 200. [Google Scholar]
- Pascal, R.; Boiteau, L. Energy flows, metabolism and translation. Philos. Trans. R. Soc. B 2011, 366, 2949–2958. [Google Scholar] [CrossRef]
- Pross, A. Toward a general theory of evolution: Extending Darwinian theory to inanimate matter. J. Syst. Chem. 2011, 2, 1. [Google Scholar] [CrossRef]
- Hazen, R.M. Presidential Address to the Mineralogical Society of America, Salt Lake City, October 18, 2005: Mineral surfaces and the prebiotic selection and organization of biomolecules. Am. Mineral. 2006, 91, 1715–1729. [Google Scholar] [CrossRef]
- Tielens, A.G.G.M. The molecular universe. Rev. Mod. Phys. 2013, 85, 1021–1081. [Google Scholar] [CrossRef]
- Van Dishoeck, E.F. Astrochemistry of dust, ice and gas: Introduction and overview. Faraday Discuss. 2014, 168, 9–47. [Google Scholar] [CrossRef] [PubMed]
- Herbst, E. Three milieux for interstellar chemistry: Gas, dust, and ice. Phys. Chem. Chem. Phys. 2014, 16, 3344–3359. [Google Scholar] [CrossRef] [PubMed]
- Herbst, E.; Yates, J.T. Introduction: Astrochemistry. Chem. Rev. 2013, 113, 8707–8709. [Google Scholar] [CrossRef] [PubMed]
- Kwok, S. Complex organics in space from Solar System to distant galaxies. Astron. Astrophys. Rev. 2016, 24, 8. [Google Scholar] [CrossRef]
- The Cologne Database for Molecular Spectroscopy (CDMS). Available online: https://cdms.ph1.uni-koeln.de/cdms/portal/ (accessed on 10 December 2018).
- Caselli, P.; Ceccarelli, C. Our astrochemical heritage. Astron. Astrophys. Rev. 2012, 20, 56. [Google Scholar] [CrossRef]
- Henning, T. Cosmic Silicates. Anun. Rev. Astron. Astrophys. 2010, 48, 21–46. [Google Scholar] [CrossRef]
- Ehrenfreund, P.; Charnley, S.B. Organic Molecules in the Interstellar Medium, Comets, and Meteorites: A Voyage from Dark Clouds to the Early Earth. Annu. Rev. Astron. Astrophys. 2000, 38, 427–483. [Google Scholar] [CrossRef]
- Boogert, A.C.A.; Gerakines, P.A.; Whittet, D.C.B. Observations of the Icy Universe. Annu. Rev. Astron. Astrophys. 2015, 53, 541–581. [Google Scholar] [CrossRef]
- Vidali, G. H2 Formation on Interstellar Grains. Chem. Rev. 2013, 113, 8762–8782. [Google Scholar] [CrossRef] [PubMed]
- Van Dishoeck, E.F.; Herbst, E.; Neufeld, D.A. Interstellar Water Chemistry: From Laboratory to Observations. Chem. Rev. 2013, 113, 9043–9085. [Google Scholar] [CrossRef] [PubMed]
- Hama, T.; Watanabe, N. Surface Processes on Interstellar Amorphous Solid Water: Adsorption, Diffusion, Tunneling Reactions, and Nuclear-Spin Conversion. Chem. Rev. 2013, 113, 8783–8839. [Google Scholar] [CrossRef] [PubMed]
- Martins, Z.; Septhon, M. Extraterrestrial amino acids. In Amino Acids, Peptides, Proteins in Organic Chemistry; Hughes, A.B., Ed.; Wiley VCH: Weinheim, Germany, 2009; Volume 1, pp. 3–42. [Google Scholar]
- Martins, Z. Organic Chemistry of Carbonaceous Meteorites. Elements 2011, 7, 35–40. [Google Scholar] [CrossRef]
- Glavin, D.P.; Callahan, M.P.; Dworkin, J.P.; Elsila, J.E. The effects of parent body processes on amino acids in carbonaceous chondrites. Meteorit. Planet. Sci. 2010, 45, 1948–1972. [Google Scholar] [CrossRef]
- Mumma, M.J.; Charnley, S.B. The Chemical Composition of Comets—Emerging Taxonomies and Natal Heritage. Annu. Rev. Astron. Astrophys. 2011, 49, 471–524. [Google Scholar] [CrossRef]
- Rotelli, L.; Trigo-Rodríguez, J.M.; Moyano-Cambero, C.E.; Carota, E.; Botta, L.; Di Mauro, E.; Saladino, R. The key role of meteorites in the formation of relevant prebiotic molecules in a formamide/water environment. Sci. Rep. 2016, 6, 38888. [Google Scholar] [CrossRef] [PubMed]
- Melissa, G.T. Atmospheric Prebiotic Chemistry and Organic Hazes. Curr. Org. Chem. 2013, 17, 1710–1723. [Google Scholar]
- Miller, S.L. A Production of Amino Acids Under Possible Primitive Earth Conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.L. Production of Some Organic Compounds under Possible Primitive Earth Conditions. J. Am. Chem. Soc. 1955, 77, 2351–2361. [Google Scholar] [CrossRef]
- Oró, J. Mechanism of Synthesis of Adenine from Hydrogen Cyanide under Possible Primitive Earth Conditions. Nature 1961, 191, 1193–1194. [Google Scholar] [CrossRef] [PubMed]
- Hazen, R.M. Paleomineralogy of the Hadean Eon: A preliminary species list. Am. J. Sci. 2013, 313, 807–843. [Google Scholar] [CrossRef]
- Costanzo, G.; Saladino, R.; Crestini, C.; Ciciriello, F.; Di Mauro, E. Formamide as the main building block in the origin of nucleic acids. BMC Evol. Biol. 2007, 7, S1. [Google Scholar] [CrossRef]
- Saladino, R.; Crestini, C.; Ciciriello, F.; Costanzo, G.; Di Mauro, E. Formamide Chemistry and the Origin of Informational Polymers. Chem. Biodivers. 2007, 4, 694–720. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Botta, G.; Pino, S.; Costanzo, G.; Di Mauro, E. Genetics first or metabolism first? The formamide clue. Chem. Soc. Rev. 2012, 41, 5526–5565. [Google Scholar] [CrossRef] [PubMed]
- Wächtershäuer, G. Before Enzymes and Templates: Theory of Surface Metabolism. Microbiol. Rev. 1988, 52, 452–484. [Google Scholar]
- Martin, W.; Baross, J.; Kelley, D.; Russell, M.J. Hydrothermal vents and the origin of life. Nat. Rev. Microbiol. 2008, 6, 805–814. [Google Scholar] [CrossRef] [PubMed]
- Cody, G.D.; Boctor, N.Z.; Filley, T.R.; Hazen, R.M.; Scott, J.H.; Sharma, A.; Yoder, H.S., Jr. Primordial Carbonylated Iron-Sulfur Compounds and the Synthesis of Pyruvate. Science 2000, 289, 1337–1340. [Google Scholar] [CrossRef]
- Cody, G.D.; Boctor, N.Z.; Hazen, R.M.; Brandes, J.A.; Morowitz, H.J.; Yoder, H.S. Geochemical roots of autotrophic carbon fixation: Hydrothermal experiments in the system citric acid, H2O-(±FeS)–(±NiS). Geochim. Cosmochim. Acta 2001, 65, 3557–3576. [Google Scholar] [CrossRef]
- Shock, E.L.; Schulte, M.D. Organic synthesis during fluid mixing in hydrothermal systems. J. Geophys. Res. 1998, 103, 28513–28527. [Google Scholar] [CrossRef]
- Shock, E.; Canovas, P. The potential for abiotic organic synthesis and biosynthesis at seafloor hydrothermal systems. Geofluids 2010, 10, 161–192. [Google Scholar]
- Shock, E.L.; Boyd, E.S. Principles of Geobiochemistry. Elements 2015, 11, 395–401. [Google Scholar] [CrossRef]
- Benner, S.A. Paradoxes in the Origin of Life. Orig. Life Evol. Biosph. 2014, 44, 339–343. [Google Scholar] [CrossRef] [PubMed]
- Westall, F.; Brack, A. The Importance of Water for Life. Space Sci. Rev. 2018, 214, 50. [Google Scholar] [CrossRef]
- Pólya, G. Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Straßennetz. Math. Ann. 1921, 84, 149–160. [Google Scholar] [CrossRef]
- Bernal, J.D. The Physical Basis of Life. Proc. Phys. Soc. 1949, 62, 597–618. [Google Scholar] [CrossRef]
- Orgel, L.E. Polymerization on the Rocks: Theoretical Introduction. Orig. Life Evol. Biosph. 1998, 28, 227–234. [Google Scholar] [CrossRef]
- Smith, J.V. Biochemical evolution. I. Polymerization on internal, organophilic silica surfaces of dealuminated zeolites and feldspars. Proc. Natl. Acad. Sci. USA 1998, 95, 3370–3375. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Glycine oligomerization on silica and alumina. React. Kinet. Mech. Catal. Lett. 1997, 62, 281–286. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Silica, Alumina, and Clay-Catalyzed Alanine Peptide Bond Formation. J. Mol. Evol. 1997, 45, 457–466. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Silica, Alumina and Clay Catalyzed Peptide Bond Formation: Enhanced Efficiency of Alumina Catalyst. Orig. Life Evol. Biosph. 1999, 29, 451–461. [Google Scholar] [CrossRef] [PubMed]
- Lambert, J.-F.; Jaber, M.; Georgelin, T.; Stievano, L. A Comparative Study of the Catalysis of Peptide Bond Formation by Oxide Surfaces. Phys. Chem. Chem. Phys. 2013, 15, 13371–13380. [Google Scholar] [CrossRef] [PubMed]
- Martra, G.; Deiana, C.; Sakhno, Y.; Barberis, I.; Fabbiani, M.; Pazzi, M.; Vincenti, M. The Formation and Self-Assembly of Long Prebiotic Oligomers Produced by the Condensation of Unactivated Amino Acids on Oxide Surfaces. Angew. Chem. Int. Ed. 2014, 53, 4671–4674. [Google Scholar] [CrossRef] [PubMed]
- Rimola, A.; Fabbiani, M.; Sodupe, M.; Ugliengo, P.; Martra, G. How Does Silica Catalyze the Amide Bond Formation under Dry Conditions? Role of Specific Surface Silanol Pairs. ACS Catal. 2018, 8, 4558–4568. [Google Scholar] [CrossRef]
- Ferris, J.P.; Hill, A.R.; Liu, R.; Orgel, L.E. Synthesis of Long Prebiotic Oligomers on Mineral Surfaces. Nature 1996, 381, 59–61. [Google Scholar] [CrossRef] [PubMed]
- Lahav, N.; White, D.; Chang, S. Peptide formation in the prebiotic era: Thermal condensation of glycine in fluctuating clay environments. Science 1978, 201, 67–69. [Google Scholar] [CrossRef] [PubMed]
- Bujdák, J.; Rode, B.M. Activated alumina as an energy source for peptide bond formation: Consequences for mineral-mediated prebiotic processes. Amino Acids 2001, 21, 281–291. [Google Scholar] [CrossRef] [PubMed]
- Bujdák, J.; Rode, B.M. Preferential amino acid sequences in alumina-catalyzed peptide bond formation. J. Inorg. Biochem. 2002, 90, 1–7. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Peptide Bond Formation on the Surface of Activated Alumina: Peptide Chain Elongation. Catal. Lett. 2003, 91, 149–154. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Alumina catalyzed reactions of amino acids. J. Therm. Anal. Calorim. 2003, 73, 797–805. [Google Scholar] [CrossRef]
- Iqubal, M.A.; Sharma, R.; Jheeta, S.; Kamaluddin. Thermal Condensation of Glycine and Alanine on Metal Ferrite Surface: Primitive Peptide Bond. Life 2017, 7, 15. [Google Scholar] [CrossRef]
- Matrajt, G.; Blanot, D. Properties of synthetic ferrihydrite as an amino acid adsorbent and a promoter of peptide bond formation. Amino Acids 2004, 26, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Deiana, C.; Sakhno, Y.; Fabbiani, M.; Pazzi, M.; Vincenti, M.; Martra, G. Direct Synthesis of Amides from Carboxylic Acids and Amines by Using Heterogeneous Catalysts: Evidence of Surface Carboxylates as Activated Electrophilic Species. ChemCatChem 2013, 5, 2832–2834. [Google Scholar] [CrossRef]
- Leyton, P.; Saladino, R.; Crestini, C.; Campos-Vallette, M.; Paipa, C.; Berríos, A.; Fuentes, S.; Zárate, R.A. Influence of TiO2 on prebiotic thermal synthesis of the Gly-Gln polymer. Amino Acids 2012, 42, 2079–2088. [Google Scholar] [CrossRef] [PubMed]
- Muller, A.W.J.; Schulze-Makuch, D. Sorption heat engines: Simple inanimate negative entropy generators. Phys. A Stat. Mech. Appl. 2006, 362, 369–381. [Google Scholar] [CrossRef]
- Rode, B.M. Peptides and the origin of life. Peptides 1999, 20, 773–786. [Google Scholar] [CrossRef]
- Schwendinger, M.G.; Rode, B.M. Salt-induced formation of mixed peptides under possible prebiotic conditions. Inorg. Chim. Acta 1991, 186, 247–251. [Google Scholar] [CrossRef]
- Rode, B.M.; Son, H.L.; Suwannachot, Y.; Bujdak, J. The Combination of Salt Induced Peptide Formation Reaction and Clay Catalysis: A Way to Higher Peptides under Primitive Earth Conditions. Orig. Life Evol. Biosph. 1999, 29, 273–286. [Google Scholar] [CrossRef]
- Imai, E.-i.; Honda, H.; Hatori, K.; Brack, A.; Matsuno, K. Elongation of Oligopeptides in a Simulated Submarine Hydrothermal System. Science 1999, 283, 831–833. [Google Scholar] [CrossRef]
- Tsukahara, H.; Imai, E.-I.; Honda, H.; Hatori, K.; Matsuno, K. Prebiotic Oligomerization on or Inside Lipid Vesicles in Hydrothermal Environments. Orig. Life Evol. Biosph. 2002, 32, 13–21. [Google Scholar] [CrossRef]
- Sugahara, H.; Mimura, K. Peptide synthesis triggered by comet impacts: A possible method for peptide delivery to the early Earth and icy satellites. Icarus 2015, 257, 103–112. [Google Scholar] [CrossRef]
- Blank, J.G.; Miller, G.H.; Ahrens, M.J.; Winans, R.E. Experimental Shock Chemistry of Aqueous Amino Acid Solutions and the Cometary Delivery of Prebiotic Compounds. Orig. Life Evol. Biosph. 2001, 31, 15–51. [Google Scholar] [CrossRef] [PubMed]
- Yamagata, Y.; Inomata, K. Condensation of glycylglycine to oligoglycines with trimetaphosphate in aqueous solution. II: Catalytic effect of Magnesium ion. Orig. Life Evol. Biosph. 1997, 27, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Gibard, C.; Bhowmik, S.; Karki, M.; Kim, E.-K.; Krishnamurthy, R. Phosphorylation, oligomerization and self-assembly in water under potential prebiotic conditions. Nat. Chem. 2017, 10, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Kitadai, N.; Maruyama, S. Origins of building blocks of life: A review. Geosci. Front. 2018, 9, 1117–1153. [Google Scholar] [CrossRef]
- Lambert, J.-F. Adsorption and Polymerization of Amino Acids on Mineral Surfaces: A Review. Orig. Life Evol. Biosph. 2008, 38, 211–242. [Google Scholar] [CrossRef] [PubMed]
- James Cleaves, H., II; Michalkova Scott, A.; Hill, F.C.; Leszczynski, J.; Sahai, N.; Hazen, R. Mineral–organic interfacial processes: Potential roles in the origins of life. Chem. Soc. Rev. 2012, 41, 5502–5525. [Google Scholar] [CrossRef] [PubMed]
- Rimola, A.; Costa, D.; Sodupe, M.; Lambert, J.-F.; Ugliengo, P. Silica Surface Features and Their Role in the Adsorption of Biomolecules: Computational Modeling and Experiments. Chem. Rev. 2013, 113, 4216–4313. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Villa, A.; Pietrucci, F.; Saitta, A.M. Prebiotic chemistry and origins of life research with atomistic computer simulations. Phys. Life Rev. 2018. [Google Scholar] [CrossRef]
- Van Duin, A.C.T.; Strachan, A.; Stewman, S.; Zhang, Q.; Xu, X.; Goddard, W.A. ReaxFFSiO Reactive Force Field for Silicon and Silicon Oxide Systems. J. Phys. Chem. A 2003, 107, 3803–3811. [Google Scholar] [CrossRef]
- Coveney, P.V.; Swadling, J.B.; Wattis, J.A.D.; Greenwell, H.C. Theory, modelling and simulation in origins of life studies. Chem. Soc. Rev. 2012, 41, 5430–5446. [Google Scholar] [CrossRef] [PubMed]
- Swadling, J.B.; Suter, J.L.; Greenwell, H.C.; Coveney, P.V. Influence of Surface Chemistry and Charge on Mineral–RNA Interactions. Langmuir 2013, 29, 1573–1583. [Google Scholar] [CrossRef] [PubMed]
- Swadling, J.B.; Coveney, P.V.; Christopher Greenwell, H. Stability of free and mineral-protected nucleic acids: Implications for the RNA world. Geochim. Cosmochim. Acta 2012, 83, 360–378. [Google Scholar] [CrossRef]
- Erastova, V.; Degiacomi, M.T.; Fraser, D.G.; Greenwell, H.C. Mineral surface chemistry control for origin of prebiotic peptides. Nat. Commun. 2017, 8, 2033. [Google Scholar] [CrossRef] [PubMed]
- Paldus, J.; Čížek, J.; Shavitt, I. Correlation Problems in Atomic and Molecular Systems. IV. Extended Coupled-Pair Many-Electron Theory and Its Application to the BH3 Molecule. Phys. Rev. A 1972, 5, 50–67. [Google Scholar] [CrossRef]
- Sherrill, C.D. Frontiers in electronic structure theory. J. Chem. Phys. 2010, 132, 110902. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Cheng, L.; Harding, M.E.; Matthews, D.A.; Szalay, P.G. CFOUR, Coupled-Cluster Techniques for Computational Chemistry, a Quantum-Chemical Program Package, 2.00; Institut für Physikalische Chemie: Stuttgart, Germany, 2010. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Hobza, P.; Šponer, J.; Reschel, T. Density functional theory and molecular clusters. J. Comput. Chem. 1995, 16, 1315–1325. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Branduardi, D.; Gervasio, F.L.; Parrinello, M. From A to B in free energy space. J. Chem. Phys. 2007, 126, 054103. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-P.; Titov, A.; McGibbon, R.; Liu, F.; Pande, V.S.; Martínez, T.J. Discovering chemistry with an ab initio nanoreactor. Nat. Chem. 2014, 6, 1044–1048. [Google Scholar] [CrossRef]
- Saitta, A.M.; Saija, F. Miller experiments in atomistic computer simulations. Proc. Natl. Acad. Sci. USA 2014, 111, 13768–13773. [Google Scholar] [CrossRef]
- Pietrucci, F.; Saitta, A.M. Formamide reaction network in gas phase and solution via a unified theoretical approach: Toward a reconciliation of different prebiotic scenarios. Proc. Natl. Acad. Sci. USA 2015, 112, 15030–15035. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Pisani, C.; Schütz, M.; Casassa, S.; Usvyat, D.; Maschio, L.; Lorenz, M.; Erba, A. CRYSCOR: A program for the post-Hartree–Fock treatment of periodic systems. Phys. Chem. Chem. Phys. 2012, 14, 7615–7628. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Svensson, M.; Humbel, S.; Froese, R.D.J.; Matsubara, T.; Sieber, S.; Morokuma, K. ONIOM: A Multilayered Integrated MO + MM Method for Geometry Optimizations and Single Point Energy Predictions. A Test for Diels−Alder Reactions and Pt(P(t-Bu)3)2 + H2 Oxidative Addition. J. Phys. Chem. 1996, 100, 19357–19363. [Google Scholar] [CrossRef]
- Michalková, A.; Tunega, D.; Nagy, L.T. Theoretical study of interactions of dickite and kaolinite with small organic molecules. J. Mol. Struct. THEOCHEM 2002, 581, 37–49. [Google Scholar] [CrossRef]
- Rutkai, G.; Kristóf, T. Molecular simulation study of intercalation of small molecules in kaolinite. Chem. Phys. Lett. 2008, 462, 269–274. [Google Scholar] [CrossRef]
- Michalkova Scott, A.; Dawley, M.M.; Orlando, T.M.; Hill, F.C.; Leszczynski, J. Theoretical Study of the Roles of Na+ and Water on the Adsorption of Formamide on Kaolinite Surfaces. J. Phys. Chem. C 2012, 116, 23992–24005. [Google Scholar] [CrossRef]
- Dawley, M.M.; Scott, A.M.; Hill, F.C.; Leszczynski, J.; Orlando, T.M. Adsorption of Formamide on Kaolinite Surfaces: A Combined Infrared Experimental and Theoretical Study. J. Phys. Chem. C 2012, 116, 23981–23991. [Google Scholar] [CrossRef]
- Aquino, A.J.A.; Tunega, D.; Haberhauer, G.; Gerzabek, M.H.; Lischka, H. Adsorption of organic substances on broken clay surfaces: A quantum chemical study. J. Comput. Chem. 2003, 24, 1853–1863. [Google Scholar] [CrossRef] [PubMed]
- Robinson, T.L.; Michalkova, A.; Gorb, L.; Leszczynski, J. Hydrogen bonding of thymine and uracil with surface of dickite: An ab initio study. J. Mol. Struct. 2007, 844–845, 48–58. [Google Scholar] [CrossRef]
- Michalkova, A.; Robinson, T.L.; Leszczynski, J. Adsorption of thymine and uracil on 1:1 clay mineral surfaces: Comprehensive ab initio study on influence of sodium cation and water. Phys. Chem. Chem. Phys. 2011, 13, 7862–7881. [Google Scholar] [CrossRef]
- Mignon, P.; Ugliengo, P.; Sodupe, M. Theoretical Study of the Adsorption of RNA/DNA Bases on the External Surfaces of Na+-Montmorillonite. J. Phys. Chem. C 2009, 113, 13741–13749. [Google Scholar] [CrossRef]
- Mignon, P.; Sodupe, M. Structural Behaviors of Cytosine into the Hydrated Interlayer of Na+-Montmorillonite Clay. An ab Initio Molecular Dynamics Study. J. Phys. Chem. C 2013, 117, 26179–26189. [Google Scholar] [CrossRef]
- Mignon, P.; Sodupe, M. Theoretical study of the adsorption of DNA bases on the acidic external surface of montmorillonite. Phys. Chem. Chem. Phys. 2012, 14, 945–954. [Google Scholar] [CrossRef]
- Mignon, P.; Ugliengo, P.; Sodupe, M.; Hernandez, E.R. Ab initio molecular dynamics study of the hydration of Li+, Na+ and K+ in a montmorillonite model. Influence of isomorphic substitution. Phys. Chem. Chem. Phys. 2010, 12, 688–697. [Google Scholar] [CrossRef]
- Escamilla-Roa, E.; Huertas, F.J.; Hernández-Laguna, A.; Sainz-Díaz, C.I. A DFT study of the adsorption of glycine in the interlayer space of montmorillonite. Phys. Chem. Chem. Phys. 2017, 19, 14961–14971. [Google Scholar] [CrossRef] [PubMed]
- Ramos, M.E.; Huertas, F.J. Adsorption of glycine on montmorillonite in aqueous solutions. Appl. Clay Sci. 2013, 80–81, 10–17. [Google Scholar] [CrossRef]
- Russell, M.J.; Hall, A.J.; Cairns-Smith, A.G.; Braterman, P.S. Submarine hot springs and the origin of life. Nature 1988, 336, 117. [Google Scholar] [CrossRef]
- Dörr, M.; Alpermann, T.; Weigand, W. Question 1: The FeS/H2S System as a Possible Primordial Source of Redox Energy. Orig. Life Evol. Biosph. 2007, 37, 329–333. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; Wächtershäuser, G. Activated Acetic Acid by Carbon Fixation on (Fe,Ni)S Under Primordial Conditions. Science 1997, 276, 245–247. [Google Scholar] [CrossRef]
- Dörr, M.; Käßbohrer, J.; Grunert, R.; Kreisel, G.; Brand, W.A.; Werner, R.A.; Geilmann, H.; Apfel, C.; Robl, C.; Weigand, W. A Possible Prebiotic Formation of Ammonia from Dinitrogen on Iron Sulfide Surfaces. Angew. Chem. Int. Ed. 2003, 42, 1540–1543. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; Wächtershäuser, G. Primordial reductive amination revisited. Tetrahedron Lett. 2003, 44, 1695–1697. [Google Scholar] [CrossRef]
- Huber, C.; Wächtershäuser, G. α-Hydroxy and α-Amino Acids Under Possible Hadean, Volcanic Origin-of-Life Conditions. Science 2006, 314, 630–632. [Google Scholar] [CrossRef]
- Huber, C.; Wächtershäuser, G. Peptides by Activation of Amino Acids with CO on (Ni,Fe)S Surfaces: Implications for the Origin of Life. Science 1998, 281, 670–672. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; Eisenreich, W.; Hecht, S.; Wächtershäuser, G. A Possible Primordial Peptide Cycle. Science 2003, 301, 938–940. [Google Scholar] [CrossRef] [PubMed]
- Michalkova, A.; Kholod, Y.; Kosenkov, D.; Gorb, L.; Leszczynski, J. Viability of pyrite pulled metabolism in the ‘iron-sulfur world’ theory: Quantum chemical assessment. Geochim. Cosmochim. Acta 2011, 75, 1933–1941. [Google Scholar] [CrossRef]
- Stirling, A.; Rozgonyi, T.; Krack, M.; Bernasconi, M. Prebiotic NH3 Formation: Insights from Simulations. Inorg. Chem. 2016, 55, 1934–1939. [Google Scholar] [CrossRef] [PubMed]
- Pollet, R.; Boehme, C.; Marx, D. AB INITIO Simulations of Desorption and Reactivity of Glycine at a Water-Pyrite Interface at “Iron-Sulfur World” Prebiotic Conditions. Orig. Life Evol. Biosph. 2006, 36, 363–379. [Google Scholar] [CrossRef]
- Boehme, C.; Marx, D. Glycine on a Wet Pyrite Surface at Extreme Conditions. J. Am. Chem. Soc. 2003, 125, 13362–13363. [Google Scholar] [CrossRef]
- Nair, N.N.; Schreiner, E.; Marx, D. Glycine at the Pyrite–Water Interface: The Role of Surface Defects. J. Am. Chem. Soc. 2006, 128, 13815–13826. [Google Scholar] [CrossRef]
- Schreiner, E.; Nair, N.N.; Marx, D. Influence of Extreme Thermodynamic Conditions and Pyrite Surfaces on Peptide Synthesis in Aqueous Media. J. Am. Chem. Soc. 2008, 130, 2768–2770. [Google Scholar] [CrossRef]
- Nair, N.N.; Schreiner, E.; Marx, D. Peptide Synthesis in Aqueous Environments: The Role of Extreme Conditions on Amino Acid Activation. J. Am. Chem. Soc. 2008, 130, 14148–14160. [Google Scholar] [CrossRef]
- Kricheldorf, H.R. Polypeptides and 100 Years of Chemistry of α-Amino Acid N-Carboxyanhydrides. Angew. Chem. Int. Ed. 2006, 45, 5752–5784. [Google Scholar] [CrossRef]
- Leman, L.; Orgel, L.; Ghadiri, M.R. Carbonyl Sulfide-Mediated Prebiotic Formation of Peptides. Science 2004, 306, 283–286. [Google Scholar] [CrossRef] [PubMed]
- Pascal, R.; Boiteau, L.; Commeyras, A. From the Prebiotic Synthesis of α-Amino Acids Towards a PrimitiveTranslation Apparatus for the Synthesis of Peptides. In Prebiotic Chemistry; Walde, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 69–122. [Google Scholar]
- Weingärtner, H.; Franck, E.U. Supercritical Water as a Solvent. Angew. Chem. Int. Ed. 2005, 44, 2672–2692. [Google Scholar] [CrossRef] [PubMed]
- Schreiner, E.; Nair, N.N.; Wittekindt, C.; Marx, D. Peptide Synthesis in Aqueous Environments: The Role of Extreme Conditions and Pyrite Mineral Surfaces on Formation and Hydrolysis of Peptides. J. Am. Chem. Soc. 2011, 133, 8216–8226. [Google Scholar] [CrossRef] [PubMed]
- Wittekindt, C.; Marx, D. Water confined between sheets of mackinawite FeS minerals. J. Chem. Phys. 2012, 137, 054710. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Santiburcio, D.; Wittekindt, C.; Marx, D. Nanoconfinement effects on hydrated excess protons in layered materials. Nat. Commun. 2013, 4, 2349. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Santiburcio, D.; Marx, D. Chemistry in nanoconfined water. Chem. Sci. 2017, 8, 3444–3452. [Google Scholar] [CrossRef] [PubMed]
- Hazen, R.M.; Papineau, D.; Bleeker, W.; Downs, R.T.; Ferry, J.M.; McCoy, T.J.; Sverjensky, D.A.; Yang, H. Mineral evolution. Am. Mineral. 2008, 93, 1693–1720. [Google Scholar] [CrossRef]
- Hazen, R.M.; Bekker, A.; Bish, D.L.; Bleeker, W.; Downs, R.T.; Farquhar, J.; Ferry, J.M.; Grew, E.S.; Knoll, A.H.; Papineau, D.; et al. Needs and opportunities in mineral evolution research. Am. Mineral. 2011, 96, 953–963. [Google Scholar] [CrossRef]
- Han, J.; Brearley, A.J. Formation of TiO2 Nanoparticles in a CAI-Like Object from an AOA in the ALHA 77307 CO3.0 Carbonaceous Chondrite. Meteorit. Planet. Sci. 2011, 46, 5190. [Google Scholar]
- Wang, A.; Kuebler, K.; Jolliff, B.; Haskin, L.A. Mineralogy of a Martian meteorite as determined by Raman spectroscopy. J. Raman Spectrosc. 2004, 35, 504–514. [Google Scholar] [CrossRef]
- Zürcher, L.; Kring, D.A. Hydrothermal alteration in the core of the Yaxcopoil-1 borehole, Chicxulub impact structure, Mexico. Meteorit. Planet. Sci. 2010, 39, 1199–1221. [Google Scholar] [CrossRef]
- Sang, L.; Zhao, Y.; Burda, C. TiO2 Nanoparticles as Functional Building Blocks. Chem. Rev. 2014, 114, 9283–9318. [Google Scholar] [CrossRef]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Ojamäe, L.; Aulin, C.; Pedersen, H.; Käll, P.-O. IR and quantum-chemical studies of carboxylic acid and glycine adsorption on rutile TiO2 nanoparticles. J. Colloid Interface Sci. 2006, 296, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Langel, W.; Menken, L. Simulation of the interface between titanium oxide and amino acids in solution by first principles MD. Surf. Sci. 2003, 538, 1–9. [Google Scholar] [CrossRef]
- Tonner, R. Adsorption of Proline and Glycine on the TiO2(110) Surface: A Density Functional Theory Study. ChemPhysChem 2010, 11, 1053–1061. [Google Scholar] [CrossRef] [PubMed]
- Qiu, T.; Barteau, M.A. STM study of glycine on TiO2(110) single crystal surfaces. J. Colloid Interface Sci. 2006, 303, 229–235. [Google Scholar] [CrossRef]
- Lerotholi, T.J.; Kröger, E.A.; Knight, M.J.; Unterberger, W.; Hogan, K.; Jackson, D.C.; Lamont, C.L.A.; Woodruff, D.P. Adsorption structure of glycine on TiO2(110): A photoelectron diffraction determination. Surf. Sci. 2009, 603, 2305–2311. [Google Scholar] [CrossRef]
- Thomas, A.G.; Flavell, W.R.; Chatwin, C.P.; Kumarasinghe, A.R.; Rayner, S.M.; Kirkham, P.F.; Tsoutsou, D.; Johal, T.K.; Patel, S. Adsorption of phenylalanine on single crystal rutile TiO2(110) surface. Surf. Sci. 2007, 601, 3828–3832. [Google Scholar] [CrossRef]
- Muir, J.M.R.; Idriss, H. Computational study of cysteine interaction with the rutile TiO2 (110) surface. Surf. Sci. 2013, 617, 60–67. [Google Scholar] [CrossRef]
- Jonsson, C.M.; Jonsson, C.L.; Estrada, C.; Sverjensky, D.A.; Cleaves, H.J.; Hazen, R.M. Adsorption of l-aspartate to rutile (α-TiO2): Experimental and theoretical surface complexation studies. Geochim. Cosmochim. Acta 2010, 74, 2356–2367. [Google Scholar] [CrossRef]
- Szieberth, D.; Maria Ferrari, A.; Dong, X. Adsorption of glycine on the anatase (101) surface: An ab initio study. Phys. Chem. Chem. Phys. 2010, 12, 11033–11040. [Google Scholar] [CrossRef] [PubMed]
- Pantaleone, S.; Rimola, A.; Sodupe, M. Canonical, Deprotonated, or Zwitterionic? A Computational Study on Amino Acid Interaction with the TiO2 (101) Anatase Surface. J. Phys. Chem. C 2017, 121, 14156–14165. [Google Scholar] [CrossRef]
- Li, W.; Kotsis, K.; Manzhos, S. Comparative density functional theory and density functional tight binding study of arginine and arginine-rich cell penetrating peptide TAT adsorption on anatase TiO2. Phys. Chem. Chem. Phys. 2016, 18, 19902–19917. [Google Scholar] [CrossRef] [PubMed]
- Civiš, S.; Szabla, R.; Szyja, B.M.; Smykowski, D.; Ivanek, O.; Knížek, A.; Kubelík, P.; Šponer, J.; Ferus, M.; Šponer, J.E. TiO2-catalyzed synthesis of sugars from formaldehyde in extraterrestrial impacts on the early Earth. Sci. Rep. 2016, 6, 23199. [Google Scholar] [CrossRef] [PubMed]
- Pantaleone, S.; Ugliengo, P.; Sodupe, M.; Rimola, A. When the Surface Matters: Prebiotic Peptide-Bond Formation on the TiO2 (101) Anatase Surface through Periodic DFT-D2 Simulations. Chem. Eur. J. 2018, 24, 16292–16301. [Google Scholar] [CrossRef]
- Rimola, A.; Tosoni, S.; Sodupe, M.; Ugliengo, P. Peptide bond formation activated by the interplay of Lewis and Brønsted catalysts. Chem. Phys. Lett. 2005, 408, 295–301. [Google Scholar] [CrossRef]
- Rimola, A.; Tosoni, S.; Sodupe, M.; Ugliengo, P. Does Silica Surface Catalyse Peptide Bond Formation? New Insights from First-Principles Calculations. ChemPhysChem 2006, 7, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Aluminosilicate Surfaces as Promoters for Peptide Bond Formation: An Assessment of Bernal’s Hypothesis by ab Initio Methods. J. Am. Chem. Soc. 2007, 129, 8333–8344. [Google Scholar] [CrossRef]
- Rimola, A.; Ugliengo, P.; Sodupe, M. Formation versus Hydrolysis of the Peptide Bond from a Quantum-mechanical Viewpoint: The Role of Mineral Surfaces and Implications for the Origin of Life. Int. J. Mol. Sci. 2009, 10, 746–760. [Google Scholar] [CrossRef] [PubMed]
- Signorile, M.; Salvini, C.; Zamirri, L.; Bonino, F.; Martra, G.; Sodupe, M.; Ugliengo, P. Formamide Adsorption at the Amorphous Silica Surface: A Combined Experimental and Computational Approach. Life 2018, 8, 42. [Google Scholar] [CrossRef]
- Ugliengo, P.; Sodupe, M.; Musso, F.; Bush, I.J.; Orlando, R.; Dovesi, R. Realistic Models of Hydroxylated Amorphous Silica Surfaces and MCM-41 Mesoporous Material Simulated by Large-scale Periodic B3LYP Calculations. Adv. Mater. 2008, 20, 4579–4583. [Google Scholar] [CrossRef]
- Erba, A.; Baima, J.; Bush, I.; Orlando, R.; Dovesi, R. Large-Scale Condensed Matter DFT Simulations: Performance and Capabilities of the CRYSTAL Code. J. Chem. Theory Comput. 2017, 13, 5019–5027. [Google Scholar] [CrossRef] [PubMed]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Tsendra, O.; Scott, A.M.; Gorb, L.; Boese, A.D.; Hill, F.C.; Ilchenko, M.M.; Leszczynska, D.; Leszczynski, J. Adsorption of Nitrogen-Containing Compounds on the (100) α-Quartz Surface: Ab Initio Cluster Approach. J. Phys. Chem. C 2014, 118, 3023–3034. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Gromovoy, T.Y.; Golovaty, V.G.; Glukhoy, A.M. Mechanisms of amino acid polycondensation on silica and alumina surfaces. Orig. Life Evol. Biosph. 1990, 20, 483–498. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Amide and Peptide Bond Formation: Interplay between Strained Ring Defects and Silanol Groups at Amorphous Silica Surfaces. J. Phys. Chem. C 2016, 120, 24817–24826. [Google Scholar] [CrossRef]
- Rimola, A.; Ugliengo, P.; Sodupe, M. Strained ring motif at silica surfaces: A quantum mechanical study of their reactivity towards protic molecules. Comput. Theor. Chem. 2015, 1074, 168–177. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Ugliengo, P.; Rimola, A.; Sodupe, M. B3LYP Periodic Study of the Physicochemical Properties of the Nonpolar (010) Mg-Pure and Fe-Containing Olivine Surfaces. J. Phys. Chem. A 2014, 118, 5866–5875. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Sodupe, M.; Ugliengo, P.; Rimola, A. Interstellar H adsorption and H2 formation on the crystalline (010) forsterite surface: A B3LYP-D2* periodic study. Phys. Chem. Chem. Phys. 2014, 16, 17447–17457. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Martínez-González, J.Á.; Sodupe, M.; Ugliengo, P.; Rimola, A. Relevance of silicate surface morphology in interstellar H2 formation. Insights from quantum chemical calculations. Mon. Not. R. Astron. Soc. 2015, 453, 914–924. [Google Scholar] [CrossRef]
- Escamilla-Roa, E.; Moreno, F. Adsorption of glycine by cometary dust: Astrobiological implications. Planet. Space Sci. 2012, 70, 1–9. [Google Scholar] [CrossRef]
- Escamilla-Roa, E.; Moreno, F. Adsorption of glycine on cometary dust grains: II—Effect of amorphous water ice. Planet. Space Sci. 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Escamilla-Roa, E.; Sainz-Díaz, C.I. Effect of Amorphous Ammonia–Water Ice onto Adsorption of Glycine on Cometary Dust Grain and IR Spectroscopy. J. Phys. Chem. C 2014, 118, 26080–26090. [Google Scholar] [CrossRef]
- Rimola, A.; Trigo-Rodríguez, J.M.; Martins, Z. Interaction of organic compounds with chondritic silicate surfaces. Atomistic insights from quantum chemical periodic simulations. Phys. Chem. Chem. Phys. 2017, 19, 18217–18231. [Google Scholar] [CrossRef] [PubMed]
- Fornaro, T.; Brucato, J.R.; Feuillie, C.; Sverjensky, D.A.; Hazen, R.M.; Brunetto, R.; D’Amore, M.; Barone, V. Binding of Nucleic Acid Components to the Serpentinite-Hosted Hydrothermal Mineral Brucite. Astrobiology 2018, 18, 989–1007. [Google Scholar] [CrossRef]
- Phuakkong, O.; Bobuatong, K.; Pantu, P.; Boekfa, B.; Probst, M.; Limtrakul, J. Glycine Peptide Bond Formation Catalyzed by Faujasite. ChemPhysChem 2011, 12, 2160–2168. [Google Scholar] [CrossRef]
- Rios-Font, R.; Rodríguez-Santiago, L.; Bertran, J.; Sodupe, M. Influence of N7 Protonation on the Mechanism of the N-Glycosidic Bond Hydrolysis in 2′-Deoxyguanosine. A Theoretical Study. J. Phys. Chem. B 2007, 111, 6071–6077. [Google Scholar] [CrossRef]
- Wang, J.; Gu, J.; Nguyen, M.T.; Springsteen, G.; Leszczynski, J. From Formamide to Purine: A Self-Catalyzed Reaction Pathway Provides a Feasible Mechanism for the Entire Process. J. Phys. Chem. B 2013, 117, 9333–9342. [Google Scholar] [CrossRef]
- Ferus, M.; Michalčíková, R.; Shestivská, V.; Šponer, J.; Šponer, J.E.; Civiš, S. High-Energy Chemistry of Formamide: A Simpler Way for Nucleobase Formation. J. Phys. Chem. A 2014, 118, 719–736. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Affinity Scale for the Interaction of Amino Acids with Silica Surfaces. J. Phys. Chem. C 2009, 113, 5741–5750. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Ugliengo, P.; Sodupe, M.; Rimola, A. Does Fe2+ in olivine-based interstellar grains play any role in the formation of H2? Atomistic insights from DFT periodic simulations. Chem. Commun. 2016, 52, 6873–6876. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Tilocca, A.; Dulub, O.; Selloni, A.; Diebold, U. Local ordering and electronic signatures of submonolayer water on anatase TiO2(101). Nat. Mater. 2009, 8, 585–589. [Google Scholar] [CrossRef] [PubMed]
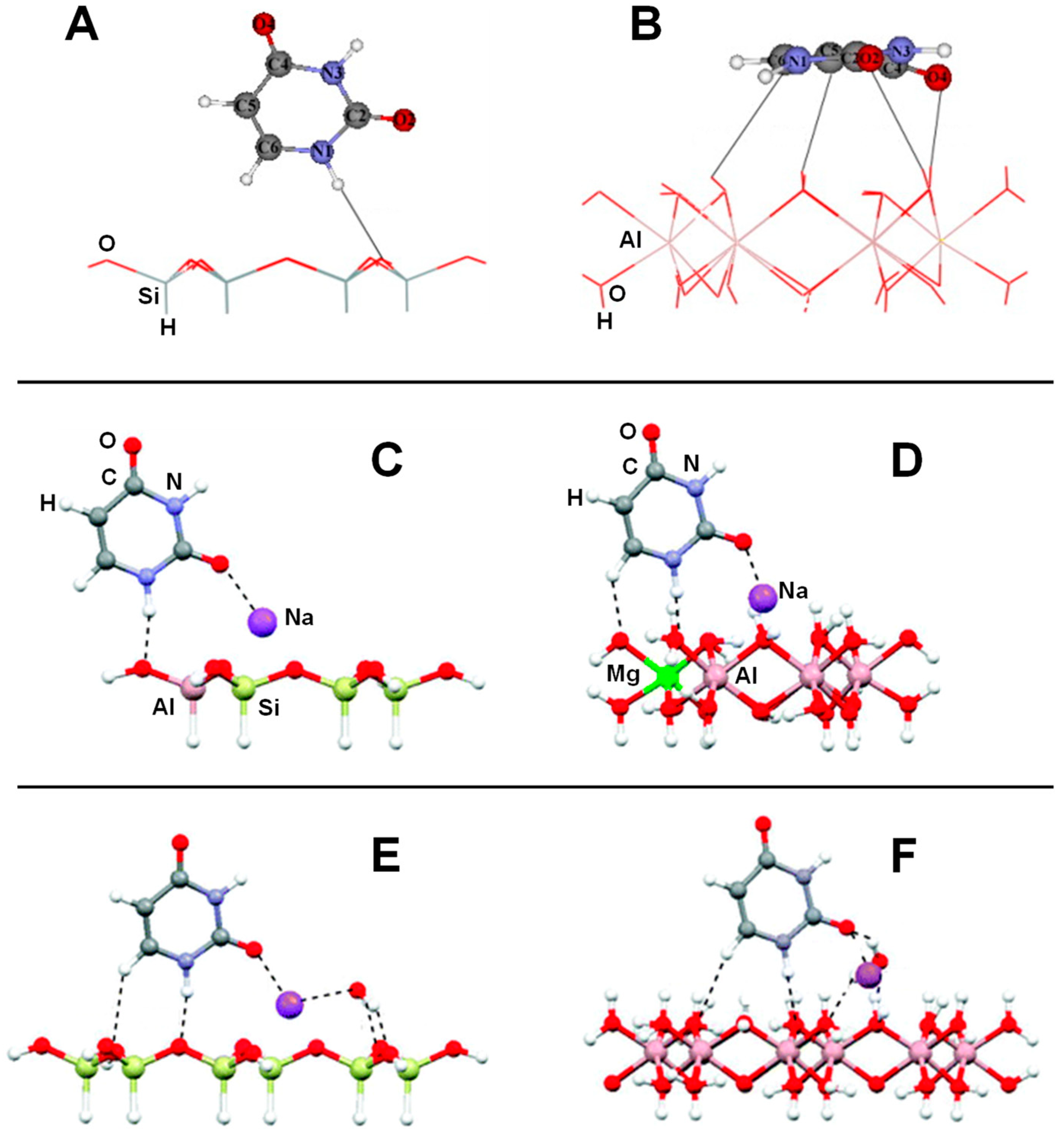
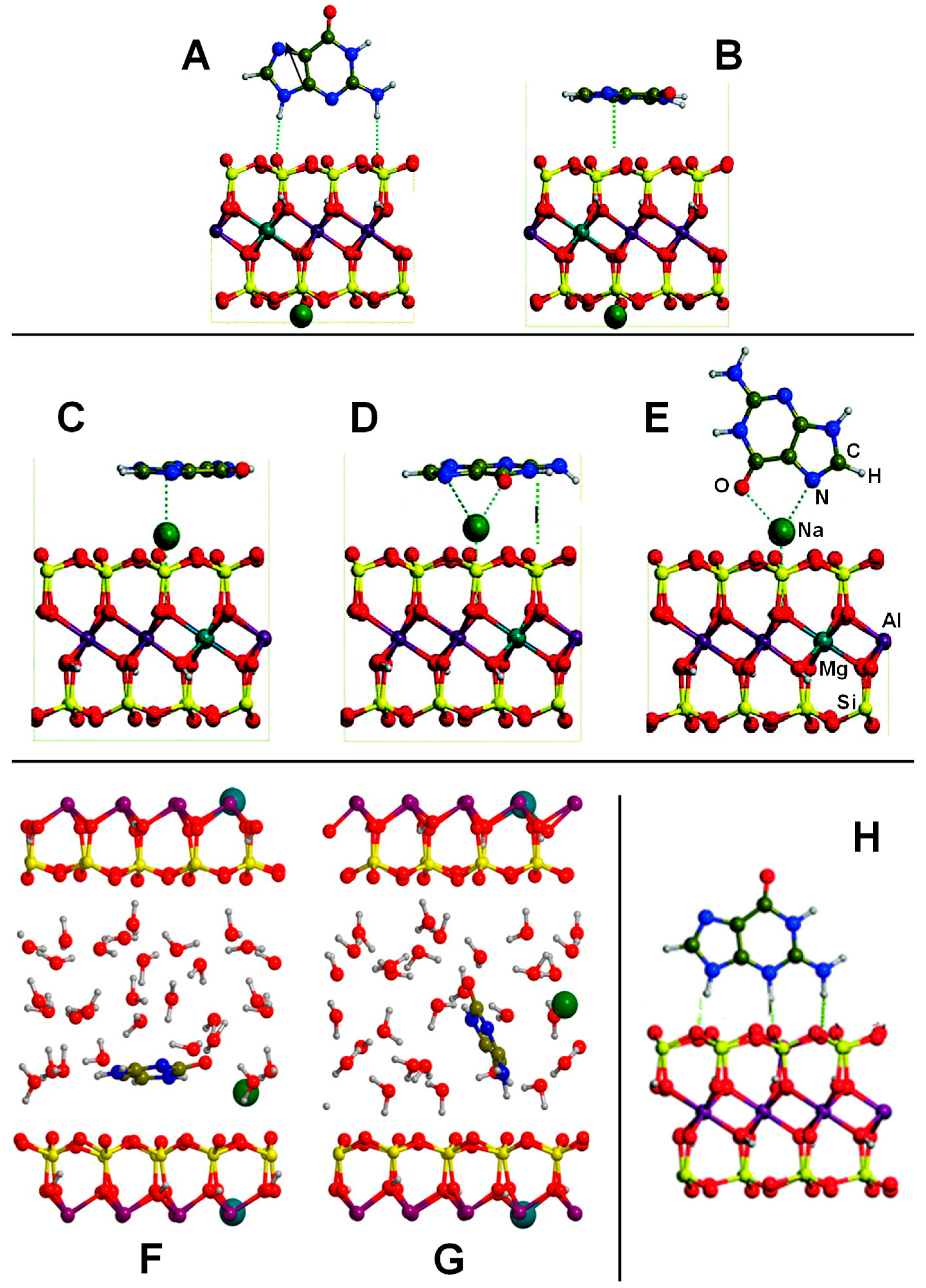
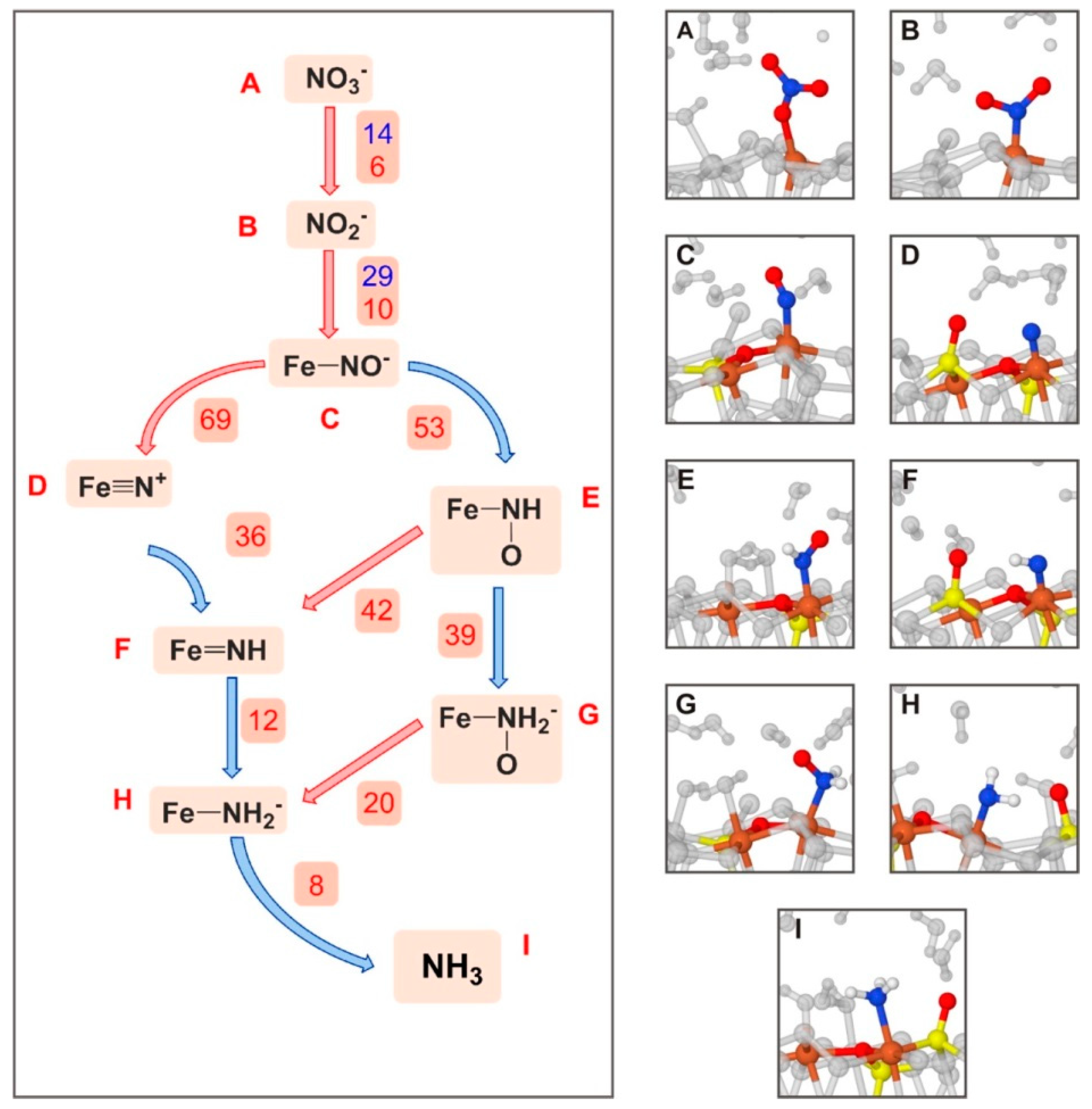
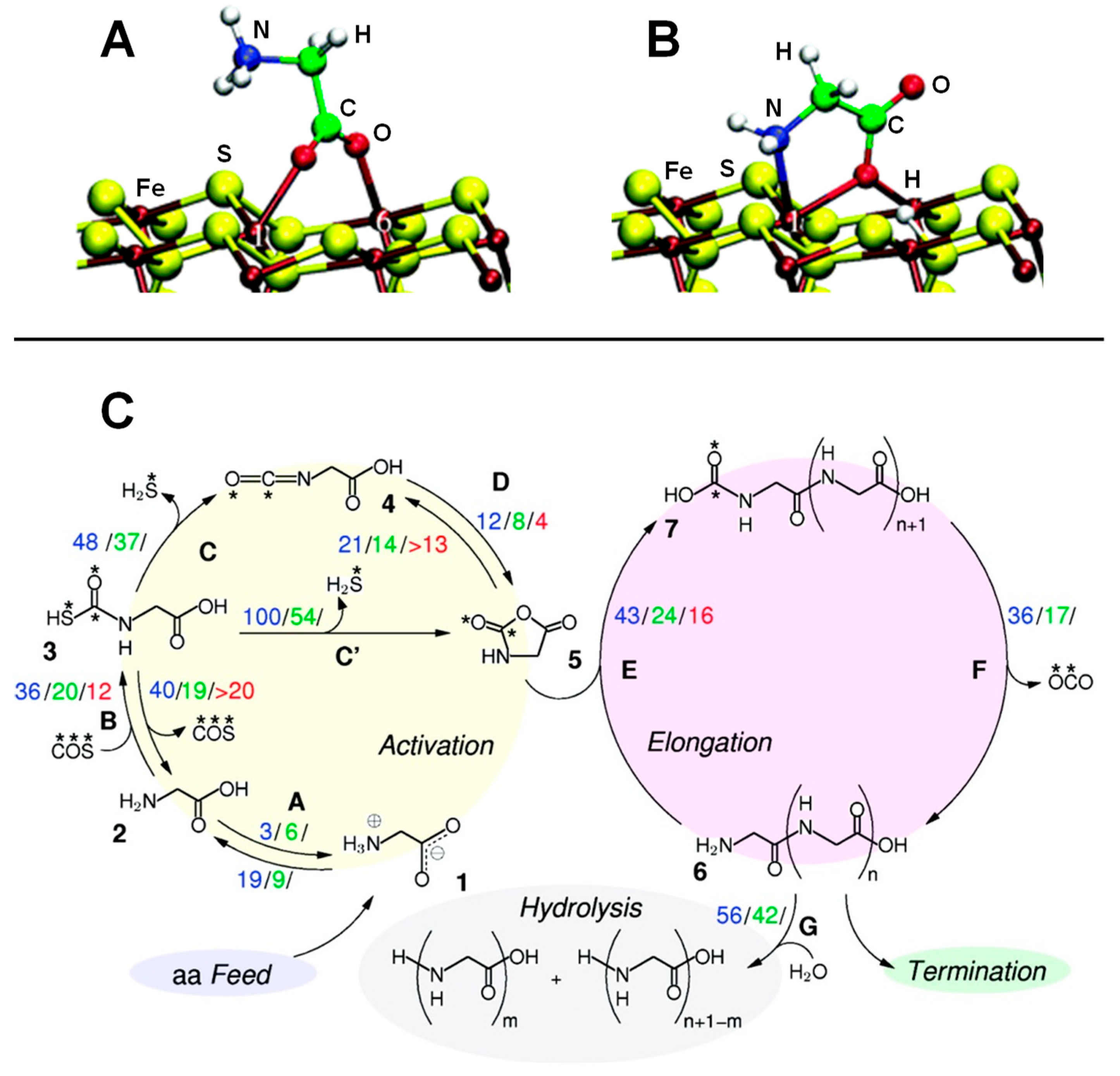
| Surface | Sheet | Level of Theory | ΔECads | Ref. |
|---|---|---|---|---|
| Dickite | Octahedral–adsorption | B3LYP/3-21G(d) | −14.5 | [117] |
| Octahedral–intercalation | B3LYP/3-21G(d) | −20.2 | [117] | |
| Kaolinite | Octahedral | M05-2X/6-31G(d) | −14.8 | [119,120] |
| Tetrahedral | M05-2X/6-31G(d) | −13.7 | [119,120] | |
| Octahedral–water | M05-2X/6-31G(d) | −9.2 | [119] | |
| Tetrahedral–water | M05-2X/6-31G(d) | −5.9 | [119] | |
| Na+-kaolinite | Octahedral | M05-2X/6-31G(d) | −108.2 | [119] |
| Tetrahedral | M05-2X/6-31G(d) | −20.3 | [119] | |
| Octahedral–water | M05-2X/6-31G(d) | −21.7 | [119] | |
| Tetrahedral–water | M05-2X/6-31G(d) | −17.8 | [119] |
| Surface | Sheet | Molecule | Level of Theory | ΔECads |
|---|---|---|---|---|
| Dickite | Octahedral | Uracil | B3LYP/6-31G(d) | −30.3 |
| Dickite | Tetrahedral | Uracil | B3LYP/6-31G(d) | −3.6 |
| Dickite | Octahedral | Thymine | B3LYP/6-31G(d) | −21.1 |
| Dickite | Tetrahedral | Thymine | B3LYP/6-31G(d) | −1.4 |
| Dickite | Octahedral–water | Uracil | B3LYP/6-31G(d) | −47.8 |
| Dickite | Tetrahedral–water | Uracil | B3LYP/6-31G(d) | −8.6 |
| Dickite | Octahedral–water | Thymine | B3LYP/6-31G(d) | -45.7 |
| Dickite | Tetrahedral–water | Thymine | B3LYP/6-31G(d) | −8.2 |
| Na+-kaolinite | Octahedral | Uracil | M05-2X/6-31G(d)a | −46.1 |
| Na+-kaolinite | Tetrahedral | Uracil | M05-2X/6-31G(d)a | −31.0 |
| Na+-kaolinite | Octahedral | Thymine | M05-2X/6-31G(d)a | −44.4 |
| Na+-kaolinite | Tetrahedral | Thymine | M05-2X/6-31G(d)a | −29.9 |
| Na+-kaolinite | Octahedral–water | Uracil | M05-2X/6-31G(d)a | −43.7 |
| Na+-kaolinite | Tetrahedral–water | Uracil | M05-2X/6-31G(d)a | −28.5 |
| Na+-kaolinite | Octahedral–water | Thymine | M05-2X/6-31G(d)a | −43.4 |
| Na+-kaolinite | Tetrahedral–water | Thymine | M05-2X/6-31G(d)a | −27.0 |
| External Surface | Nucleobase | Adsorption Type | ΔEads |
|---|---|---|---|
| Na+-free side | Adenine | ┴ | −3.7 |
| ║ | −10.8 | ||
| Cytosine | ┴ | −6.6 | |
| ║ | −9.1 | ||
| Guanine | ┴ | −11.3 | |
| ║ | −10.9 | ||
| Thymine | ┴ | −7.3 | |
| ║ | −10.7 | ||
| Uracil | ┴ | −5.7 | |
| ║ | −8.5 | ||
| Na+-containing side | Adenine | Cation–π/ring | −11.6 |
| Cation–π/displaced | −17.0 | ||
| Cation–heteroatom | −20.2 | ||
| Cytosine | Cation–π/ring | −10.2 | |
| Cation–π/displaced | −26.6 | ||
| Cation–heteroatom | −27.0 | ||
| Guanine | Cation–π/ring | −13.1 | |
| Cation–π/displaced | −26.1 | ||
| Cation-heteroatom | −27.6 | ||
| Thymine | Cation–π/ring | −7.6 | |
| Cation–π/displaced | −21.7 | ||
| Cation–heteroatom | −19.1 | ||
| Uracil | Cation–π/ring | −5.7 | |
| Cation–π/displaced | −21.2 | ||
| Cation–heteroatom | −18.8 | ||
| H+-montmorillonite | Adenine | ║ on tetrahedral substituted | −37.7 |
| ║ on octahedral substituted | −49.1 | ||
| ┴ on tetrahedral substituted | −39.0 | ||
| ┴ on octahedral substituted | −49.4 | ||
| Guanine | ║ on tetrahedral substituted | −39.8 | |
| ║ on octahedral substituted | −48.4 | ||
| ┴ on tetrahedral substituted | −40.7 | ||
| ┴ on octahedral substituted | −50.0 | ||
| Cytosine | ║ on tetrahedral substituted | −42.4 | |
| ║ on octahedral substituted | −44.0 | ||
| ┴ on tetrahedral substituted | −32.3 | ||
| ┴ on octahedral substituted | −41.8 |
| Surface | Amino Acid | Amino Acid State | Method | ΔEads | Ref. |
|---|---|---|---|---|---|
| Rutile (110) | Glycine | Deprotonated | PW91/PWs | −48.5 | [160] |
| Glycine | Zwitterionic | PW91/PWs | −47.1 | [160] | |
| Glycine | Deprotonated | PBE/PWs | −31.3 | [162] | |
| Glycine | Zwitterionic | PBE/PWs | −29.2 | [162] | |
| Proline | Deprotonated | PBE/PWs | −30.6 | [162] | |
| Proline | Zwitterionic | PBE/PWs | −26.1 | [162] | |
| Cysteine | Deprotonated | PBE/PWs | −33.9 | [166] | |
| Cysteine | Zwitterionic | PBE/PWs | −31.1 | [166] | |
| Anatase (101) | Glycine | Deprotonated | PBE0/GTO | −25.6 | [168] |
| Glycine | Zwitterionic | PBE0/GTO | −17.6 | [168] | |
| Glycine | Canonical | PBE0/GTO | −26.7 | [168] | |
| Glycine | Deprotonated | PBE/PWs | −25.9 | [169] | |
| Glycine | Zwitterionic | PBE/PWs | −24.0 | [169] | |
| Glycine | Canonical | PBE/PWs | −23.4 | [169] |
| CLAYS (Section 4.1) | QM Method | SA | Obs. | Reference |
|---|---|---|---|---|
| Dickite/FA (adsorption/intercalation) | B3LYP/3-21G(d) | CLU | S, E | Table 1 |
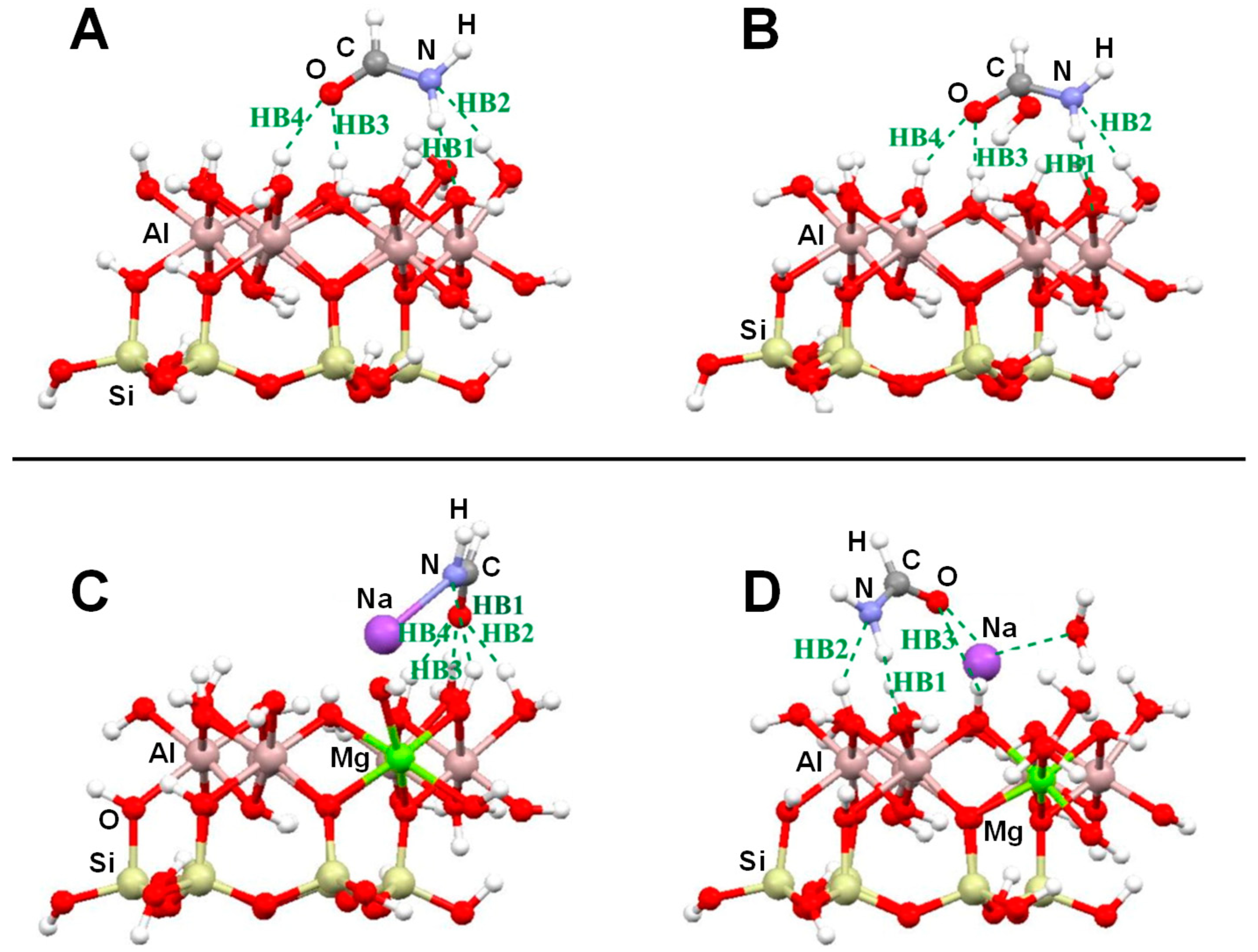
| Dickite/U; Dickite/U-H2O | B3LYP/6-31G(d) | CLU | S, E | Table 2, Figure 4A,B |
| Dickite/T; Dickite/T-H2O | B3LYP/6-31G(d) | CLU | S, E | Table 2 |
| Na+-Kaolinite/FA | MO5-2X/6-31G(d) | CLU | S, E | Table 1 |
| Na+-Kaolinite/U; Na+-Kaolinite/U-H2O | MO5-2X/6-31G(d) | CLU | S, E | Table 2, Figure 4C–F |
| Kaolinite/FA; Kaolinite/FA/H2O | M05-2X/6-31G(d) | CLU | S, E, V | Table 1, Figure 3 |
| Kaolinite/N-methylacetamide | BLYP/SVP + sp | CLU | S, E, V | Ref. [121] |
| Na+-free side: Montmorillonite/A; C; G; T; U Na+-containing side: Montmorillonite/A; C; G: T; U Na+-Montmorillonite/C-H2O H+-Montmorillonite/A; G; C | PBE-D2/PWs | PBC | S, E | Table 3, Figure 5 |
| K+-Montmorillonite/GLY GLY+-Montmorillonite/GLY | PBE-D2/PWs-Num | PBC | S, E | Ref. [128,129] |
| IRON SULPHIDES (Section 4.2) | QM Method | SA | Obs. | Reference |
| Violarite (Fe,Ni)S + CH3SH + CO + H2O→CH3COOH + H2S | B3LYP/TZVP | CLU | S, RE | Figure 2E |
| FeS2-defective (100)+NO3−→NH3 | AIMD/PBE-D2/PWs + GTO | PBC | S, FRE | Figure 6 |
| FeS2 (100)/GLY FeS2-defective (100)/GLY | AIMD/PBE/PWs | PBC | S, FRE | Figure 7A,B |
| FeS2-defective (100) + GLY + COS→(GLY)n + H2S | AIMD/PBE/PWs | PBC | S, FRE | Figure 7C |
| FeS+nGLY→(GLY)n | AIMD/PBE/PWs | PBC | S, FRE | Ref. [152] |
| TITANIUM DIOXIDE (Section 4.3) | QM Method | SA | Obs. | Reference |
|---|---|---|---|---|
| Rutile (110)/GLY | PW91/PWs | PBC | S, E | Table 4 |
| Rutile (110)/GLY/CYS/PRO | PBE/PWs | PBC | S, E | Table 4 |
| Rutile(OH) (100)-(110)-H2O/GLY/MET/SER/CYS | AIMD/PWs | PBC | S, E | Ref. [161] |
| Anatase (101)/GLY | PBE/PWs | PBC | S, E | Table 4, Figure 8 |
| Anatase (101)/LEU/MET/PHE/SER/CYS/GLU/GLN/LYS/HIS/ARG | PBE/PWs | PBC | S, E | Ref. [169] |
| Anatase (101)/GLY | PBE0/GTO, PBE/PWs | PBC | S, E | Table 4, Figure 8 |
| Anatase (101)/2GLY→GLY2 | PBE/PWs | PBC | S, E | Figure 9 |
| Anatase-O-defective (001)/2H2CO→HOCH2CHO | PBE/PW | PBC | S, E | Ref. [171] |
| SILICA & SILICATES (Section 4.4) | QM Method | SA | Obs. | Reference |
| a-SiO2/FA-(FA)2 | PBE-D2/GTO | PBC | S, E, V | Ref. [177] |
| α-quartz (100)/aromatic N-containing molecules | DFT/MP2/GTO | CLU | S, E | Ref. [181] |
| a-SiO2(defective)/Gly→surface mixed anydride | B3LYP/GTO | CLU | S, RE, V | Figure 10A,B |
| a-SiO2/CH3NH2+HCOOH→GLY+H2O | B3LYP/GTO | CLU | S, RE, V | Figure 10C |
| Mg2SiO4(100)/GLY/H2O/NH3 | PBE/PWs | PBC | S, E | Figure 11 |
| Mg2SiO4(101)/14 organic compounds | B3LYP-D2/GTO | PBC | S, E | Ref. [191] |
| Mg(OH)2 (110)/U/UD/UPM/AMP | B3LYP-D2/GTO | PBC | S, E | Ref. [192] |
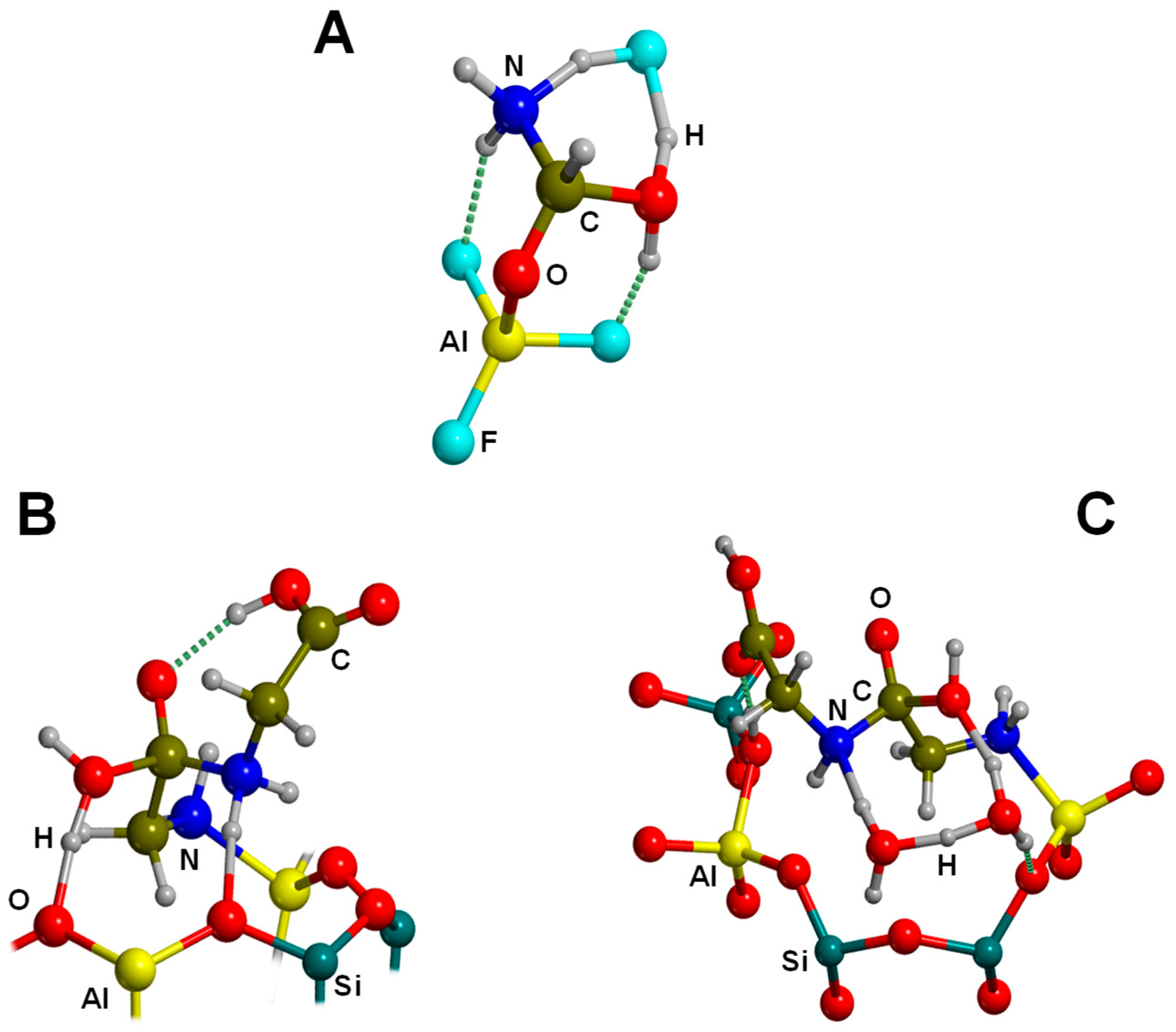
| AlF3/HF+NH3+HCOOH→GLY+H2O | B3LYP/GTO CCSD(T)/GTO | CLU | S, RE | Figure 12A |
| Feldspar (SiOHAl)+2GLY→GLY2+H2O | ONIOM(B3LYP//MNDO) | CLU | S, RE | Figure 12B |
| Feldspar (SiOHAl)-GLY-GLY+3H2O | ONIOM(B3LYP//MNDO) | CLU | S, RE | Figure 12C |
| Faujasite+2GLY→GLY2+H2O | M08-HX/GTO | CLU | S, RE | Ref. [193] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rimola, A.; Sodupe, M.; Ugliengo, P. Role of Mineral Surfaces in Prebiotic Chemical Evolution. In Silico Quantum Mechanical Studies. Life 2019, 9, 10. https://doi.org/10.3390/life9010010
Rimola A, Sodupe M, Ugliengo P. Role of Mineral Surfaces in Prebiotic Chemical Evolution. In Silico Quantum Mechanical Studies. Life. 2019; 9(1):10. https://doi.org/10.3390/life9010010
Chicago/Turabian StyleRimola, Albert, Mariona Sodupe, and Piero Ugliengo. 2019. "Role of Mineral Surfaces in Prebiotic Chemical Evolution. In Silico Quantum Mechanical Studies" Life 9, no. 1: 10. https://doi.org/10.3390/life9010010
APA StyleRimola, A., Sodupe, M., & Ugliengo, P. (2019). Role of Mineral Surfaces in Prebiotic Chemical Evolution. In Silico Quantum Mechanical Studies. Life, 9(1), 10. https://doi.org/10.3390/life9010010