Regulation of Expression and Evolution of Genes in Plastids of Rhodophytic Branch
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
| Locus | Species | P | C | S | Locus | Species | P | C | S |
|---|---|---|---|---|---|---|---|---|---|
| NC_024079.1 | Asterionella formosa | 134 | 129 | 0 | NC_024084.1 | Leptocylindrus danicus | 132 | 130 | 0 |
| NC_024080.1 | Asterionellopsis glacialis | 145 | 138 | 1 | NC_022667.1 | Leucocytozoon caulleryi | 30 | 30 | 0 |
| NC_012898.1 | Aureococcus anophagefferens | 105 | 105 | 0 | NC_024085.1 | Lithodesmium undulatum | 138 | 129 | 0 |
| NC_012903.1 | Aureoumbra lagunensis | 110 | 110 | 0 | NC_020014.1 | Nannochloropsis gaditana | 119 | 116 | 3 |
| NC_011395.1 | Babesia bovis | 32 | 26 | 3 | NC_022259.1 | N. granulata | 125 | 123 | 0 |
| LK028575.1 | B. microti | 31 | 22 | 7 | NC_022262.1 | N. limnetica | 124 | 123 | 0 |
| NC_028029.1 | B. orientalis | 38 | 28 | 7 | NC_022263.1 | N. oceanica | 126 | 123 | 1 |
| NC_021075.1 | Calliarthron tuberculosum | 201 | 200 | 1 | NC_022260.1 | N. oculata | 126 | 123 | 0 |
| NC_025313.1 | Cerataulina daemon | 132 | 130 | 0 | NC_022261.1 | N. salina | 123 | 123 | 0 |
| NC_025310.1 | Chaetoceros simplex | 131 | 128 | 0 | NC_001713.1 | Odontella sinensis | 140 | 128 | 9 |
| NC_020795.1 | Chondrus crispus | 204 | 204 | 0 | NC_020371.1 | Pavlova lutheri | 111 | 103 | 8 |
| NC_026522.1 | Choreocolax polysiphoniae | 71 | 71 | 0 | NC_016703.2 | Phaeocystis antarctica | 108 | 108 | 0 |
| NC_014340.2 | Chromera velia | 78 | 51 | 24 | NC_021637.1 | P. globosa | 108 | 108 | 0 |
| NC_014345.1 | Chromerida sp. RM11 | 81 | 69 | 5 | NC_008588.1 | Phaeodactylum tricornutum | 132 | 130 | 0 |
| NC_024081.1 | Coscinodiscus radiatus | 139 | 130 | 0 | NC_023293.1 | Plasmodium chabaudi | 31 | 31 | 0 |
| NC_013703.1 | Cryptomonas paramecium | 82 | 79 | 3 | NC_017932.1 | P. vivax | 31 | 31 | 0 |
| NC_004799.1 | Cyanidioschyzon merolae | 207 | 189 | 18 | NC_000925.1 | Porphyra purpurea | 209 | 209 | 0 |
| NC_001840.1 | Cyanidium caldarium | 197 | 186 | 11 | NC_023133.1 | Porphyridium purpureum | 224 | 183 | 40 |
| KP866208.1 | Cyclospora cayetanensis | 28 | 27 | 1 | NC_027721.1 | Pseudo-nitzschia multiseries | 104 | 103 | 1 |
| NC_024082.1 | Cylindrotheca closterium | 161 | 142 | 12 | NC_021189.1 | Pyropia haitanensis | 211 | 210 | 1 |
| NC_024083.1 | Didymosphenia geminata | 130 | 128 | 0 | NC_024050.1 | P. perforata | 209 | 207 | 2 |
| NC_014287.1 | Durinskia baltica | 129 | 127 | 0 | NC_007932.1 | P. yezoensis | 209 | 206 | 3 |
| NC_013498.1 | Ectocarpus siliculosus | 148 | 143 | 1 | NC_025311.1 | Rhizosolenia imbricata | 135 | 123 | 1 |
| NC_004823.1 | Eimeria tenella | 28 | 26 | 2 | NC_009573.1 | Rhodomonas salina | 146 | 145 | 1 |
| NC_007288.1 | Emiliania huxleyi | 119 | 112 | 7 | NC_025312.1 | Roundia cardiophora | 140 | 126 | 0 |
| NC_024928.1 | Eunotia naegelii | 160 | 136 | 2 | NC_018523.1 | Saccharina japonica | 139 | 139 | 0 |
| NC_015403.1 | Fistulifera solaris | 135 | 130 | 1 | NC_027589.1 | Teleaulax amphioxeia | 143 | 143 | 0 |
| NC_016735.1 | Fucus vesiculosus | 139 | 139 | 0 | NC_014808.1 | Thalassiosira oceanica | 142 | 126 | 1 |
| NC_024665.1 | Galdieria sulphuraria | 182 | 181 | 1 | NC_008589.1 | T. pseudonana | 141 | 127 | 0 |
| NC_023785.1 | Gracilaria salicornia | 202 | 200 | 2 | NC_025314.1 | T. weissflogii | 141 | 127 | 0 |
| NC_006137.1 | G. tenuistipitata | 203 | 201 | 2 | NC_007758.1 | Theileria parva | 44 | 27 | 12 |
| NC_021618.1 | Grateloupia taiwanensis | 233 | 201 | 32 | NC_001799.1 | Toxoplasma gondii | 26 | 21 | 5 |
| NC_000926.1 | Guillardia theta | 147 | 142 | 5 | NC_026851.1 | Trachydiscus minutus | 137 | 124 | 8 |
| NC_010772.1 | Heterosigma akashiwo | 156 | 139 | 3 | NC_027746.1 | Triparma laevis | 141 | 135 | 4 |
| NC_014267.1 | Kryptoperidinium foliaceum | 139 | 132 | 6 | NC_016731.1 | Ulnaria acus | 130 | 128 | 0 |
| NC_027093.1 | Lepidodinium chlorophorum | 62 | 52 | 7 | NC_026523.1 | Vertebrata lanosa | 192 | 191 | 1 |
2.2. Methods
2.3. Description of the Clustering Algorithm
3. Results
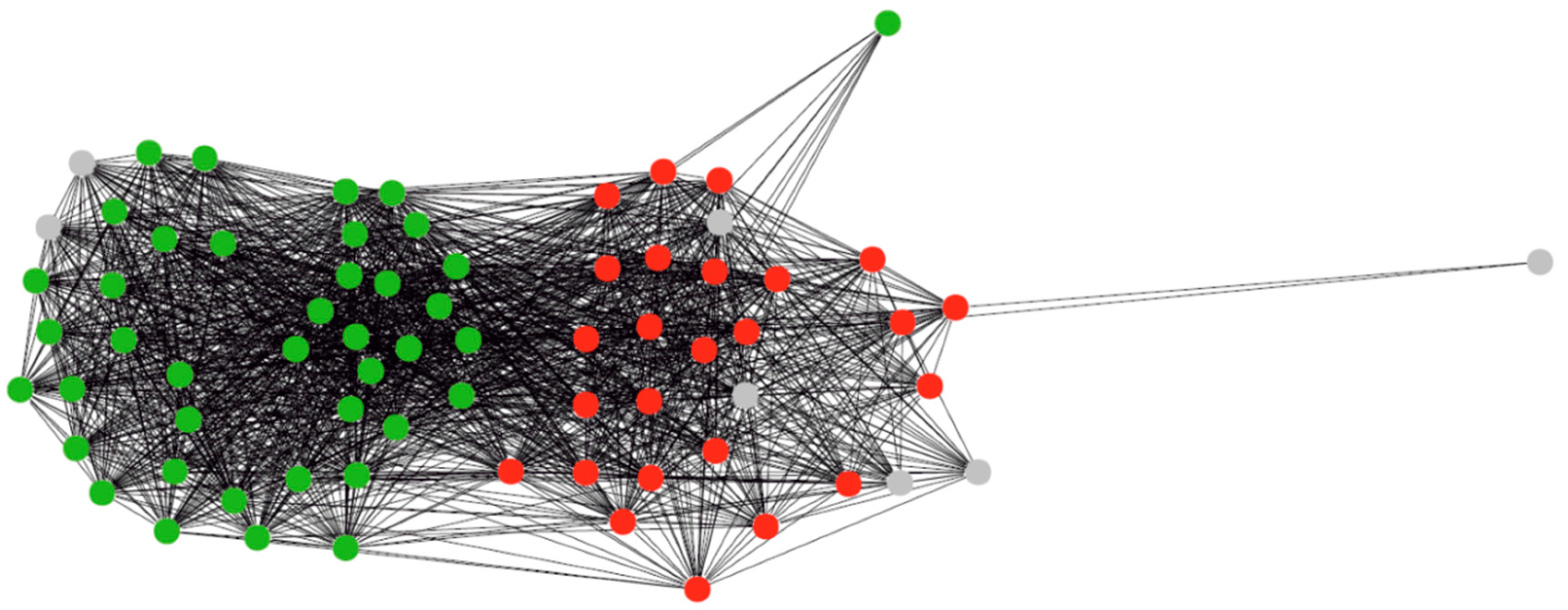
3.1. Clustering of Proteins
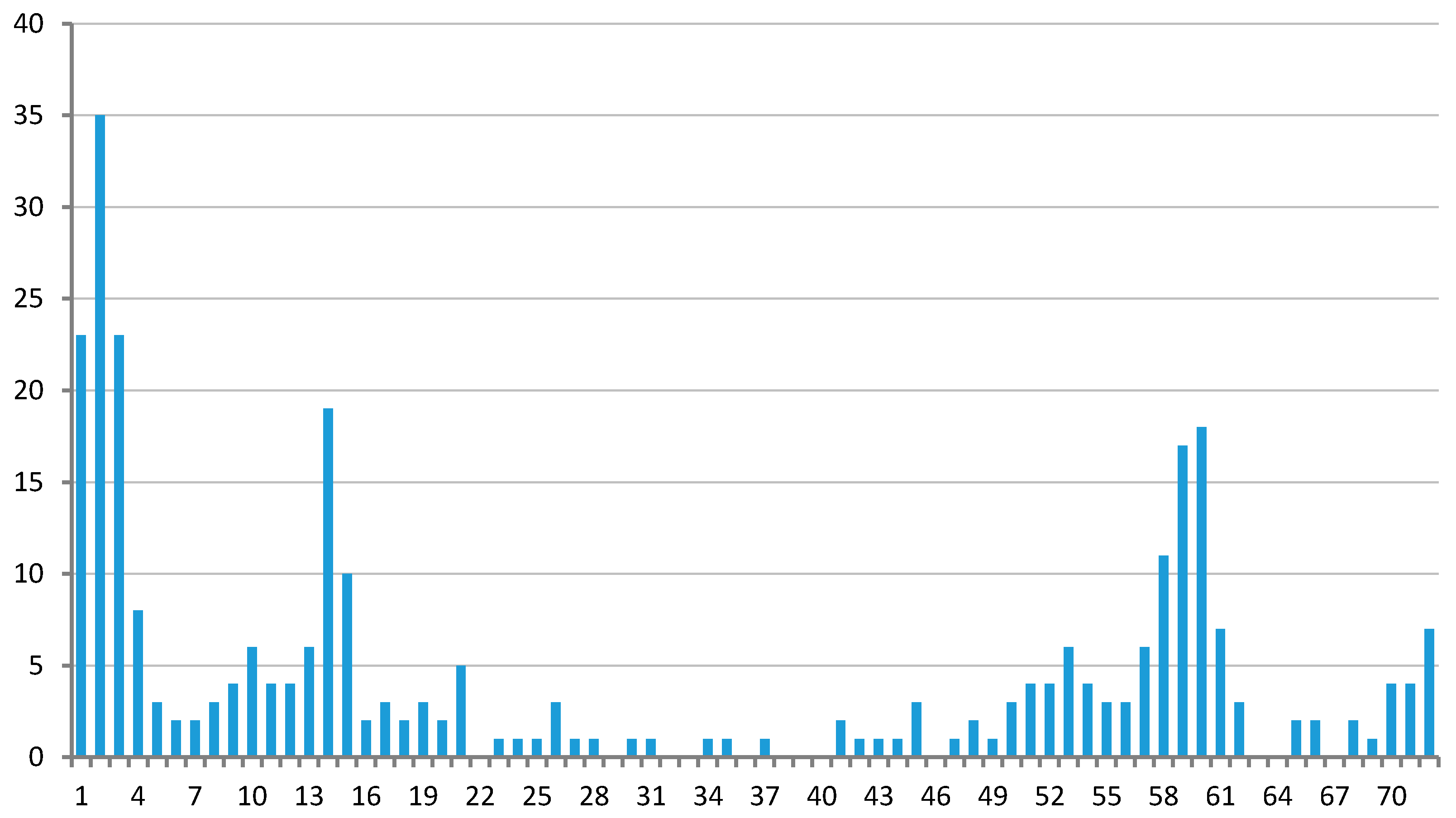


3.2. Regulons of Transcription Factors Encoded by Plastids
| Accession | Source | Protein Description |
|---|---|---|
| YP_007878178.1 | Calliarthron tuberculosum | conserved hypothetical plastid protein |
| YP_007627336.1 | Chondrus crispus | conserved hypothetical plastid protein |
| YP_009122074.1 | Choreocolax polysiphoniae | hypothetical protein |
| YP_003359295.1 | Cryptomonas paramecium | TctD-like protein |
| NP_849011.1 | Cyanidioschyzon merolae | ompR-like transcriptional regulator |
| NP_045122.1 | Cyanidium caldarium | regulatory component of sensory transduction system |
| YP_009051025.1 | Galdieria sulphuraria | putative transcriptional regulator LuxR |
| YP_009019567.1 | Gracilaria salicornia | tctD transcriptional regulator |
| YP_063559.1 | Gracilaria tenuistipitata | tctD transcriptional regulator |
| YP_008144796.1 | Grateloupia taiwanensis | putative transcriptional regulator Ycf29 |
| NP_050668.1 | Guillardia theta | tctD homolog |
| NP_053953.1 | Porphyra purpurea | ORF29 |
| YP_007947873.1 | Pyropia haitanensis | hypothetical chloroplast protein 29 |
| YP_009027627.1 | Pyropia perforata | hypothetical chloroplast protein 29 |
| YP_537024.1 | Pyropia yezoensis | hypothetical chloroplast protein 29 |
| YP_001293481.1 | Rhodomonas salina | TctD-like protein |
| YP_009159161.1 | Teleaulax amphioxeia | TctD-like protein |
| YP_009122313.1 | Vertebrata lanosa | hypothetical protein |
3.3. Regulation of Ycf24 (SufB) Translation Initiation

3.4. Regulation of Translation Initiation in Babesia spp. and Theileria parva

| Accession | Source | Protein Description |
|---|---|---|
| YP_002290869.1 | Babesia bovis | hypothetical protein |
| CDR32594.1 | Babesia microti | ribosomal protein L5 |
| YP_009170371.1 | Babesia orientalis | ribosomal protein L5 |
| XP_762679.1 | Theileria parva | hypothetical protein |
4. Discussion
4.1. Protein Clustering
4.2. Regulons of Plastid-Encoded Transcription Factors Ycf28, Ycf29, and Ycf30
4.3. Regulation of Ycf24 (SufB) Translation Initiation
4.4. Regulation of Translation Initiation in Babesia spp. and Theileria parva
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aboulaila, M.; Munkhjargal, T.; Sivakumar, T.; Ueno, A.; Nakano, Y.; Yokoyama, M.; Yoshinari, T.; Nagano, D.; Katayama, K.; El-Bahy, N.; et al. Apicoplast-targeting antibacterials inhibit the growth of Babesia parasites. Antimicrob. Agents Chemother. 2012, 56, 3196–3206. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Lopes, J.S.; Foster, P.G.; Embley, T.M.; Cox, C.J. Compositional Biases among Synonymous Substitutions Cause Conflict between Gene and Protein Trees for Plastid Origins. Mol. Biol. Evol. 2014, 31, 1697–1709. [Google Scholar] [CrossRef] [PubMed]
- Sadovskaya, T.A.; Seliverstov, A.V. Analysis of the 5′-leader regions of several plastid genes in Protozoa of the phylum Apicomplexa and red algae. Mol. Biol. 2009, 43, 552–556. [Google Scholar] [CrossRef]
- Janouškovec, J.; Horak, A.; Oborník, M.; Lukeš, J.; Keeling, P.J. A common red algal origin of the apicomplexan, dinoflagellate, and heterokont plastids. Proc. Natl. Acad. Sci. USA 2010, 107, 10949–10954. [Google Scholar] [CrossRef] [PubMed]
- Imanian, B.; Pombert, J.F.; Keeling, P.J. The complete plastid genomes of the two “dinotoms” Durinskia baltica and Kryptoperidinium foliaceum. PLoS ONE 2010, 5, e10711. [Google Scholar] [CrossRef] [PubMed]
- Kohler, S.; Delwiche, C.F.; Denny, P.W.; Tilney, L.G.; Webster, P.; Wilson, R.J.; Palmer, J.D.; Roos, D.S. A plastid of probable green algal origin in Apicomplexan parasites. Science 1997, 275, 1485–1489. [Google Scholar] [CrossRef] [PubMed]
- Lau, A.O.; McElwain, T.F.; Brayton, K.A.; Knowles, D.P.; Roalson, E.H. Babesia bovis: A comprehensive phylogenetic analysis of plastid-encoded genes supports green algal origin of apicoplasts. Exp. Parasitol. 2009, 123, 236–243. [Google Scholar] [CrossRef] [PubMed]
- Oborník, M.; Lukeš, J. The Organellar Genomes of Chromera and Vitrella, the Phototrophic Relatives of Apicomplexan Parasites. Annu. Rev. Microbiol. 2015, 69, 129–144. [Google Scholar] [CrossRef] [PubMed]
- Salomaki, E.D.; Nickles, K.R.; Lane, C.E. The ghost plastid of Choreocolax polysiphoniae. J. Phycoly 2015, 51, 217–221. [Google Scholar] [CrossRef]
- Zhu, G.; Marchewka, M.J.; Keithly, J.S. Cryptosporidium parvum appears to lack a plastid genome. Microbiology 2000, 146, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Toso, M.A.; Omoto, C.K. Gregarina niphandrodes may lack both a plastid genome and organelle. J. Eukaryot. Microbiol. 2007, 54, 66–72. [Google Scholar] [CrossRef] [PubMed]
- Simdyanov, T.G.; Diakin, A.Y.; Aleoshin, V.V. Ultrastructure and 28S rDNA phylogeny of two gregarines: Cephaloidophora cf. communis and Heliospora cf. longissima with remarks on gregarine morphology and phylogenetic analysis. Acta Protozool. 2015, 54, 241–263. [Google Scholar]
- Huang, Y.; He, L.; Wu, W.; He, P.; He, W.J.; Yu, L.; Malobi, N.; Zhou, Q.Y.; Shen, B.; Zhao, L.J. Characterization and annotation of Babesia orientalis apicoplast genome. Parasit. Vectors 2015, 8. [Google Scholar] [CrossRef] [PubMed]
- Garg, A.; Stein, A.; Zhao, W.; Dwivedi, A.; Frutos, R.; Cornillot, E.; ben Mamoun, C. Sequence and annotation of the apicoplast genome of the human pathogen Babesia microti. PLoS ONE 2014, 9. [Google Scholar] [CrossRef]
- Brayton, K.A.; Lau, A.O.; Herndon, D.R.; Hannick, L.; Kappmeyer, L.S.; Berens, S.J.; Bidwell, S.L.; Brown, W.C.; Crabtree, J.; Fadrosh, D.; et al. Genome sequence of Babesia bovis and comparative analysis of apicomplexan hemoprotozoa. PLoS Pathog. 2007, 3, 1401–1413. [Google Scholar] [CrossRef] [PubMed]
- Gardner, M.J.; Bishop, R.; Shah, T.; de Villiers, E.P.; Carlton, J.M.; Hall, N.; Ren, Q.; Paulsen, I.T.; Pain, A.; Berriman, M.; et al. Genome sequence of Theileria parva, a bovine pathogen that transforms lymphocytes. Science 2005, 309, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Fuller, A.L.; McDougald, L.R.; Zhu, G. Apicoplast genome of the coccidian Eimeria tenella. Gene 2003, 321, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.; Guo, Y.; Zhang, L.; Rowe, L.A.; Roellig, D.M.; Frace, M.A.; Li, N.; Liu, S.; Feng, Y.; Xiao, L. Genetic similarities between Cyclospora cayetanensis and cecum-infecting avian Eimeria spp. in apicoplast and mitochondrial genomes. Parasit. Vectors 2015, 8. [Google Scholar] [CrossRef] [PubMed]
- Imura, T.; Sato, S.; Sato, Y.; Sakamoto, D.; Isobe, T.; Murata, K.; Holder, A.A.; Yukawa, M. The apicoplast genome of Leucocytozoon caulleryi, a pathogenic apicomplexan parasite of the chicken. Parasitol. Res. 2014, 113, 823–828. [Google Scholar] [CrossRef] [PubMed]
- Sato, S.; Sesay, A.K.; Holder, A.A. The unique structure of the apicoplast genome of the rodent malaria parasite Plasmodium chabaudi chabaudi. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Reith, M.E.; Munholland, J. Complete nucleotide sequence of the Porphyra purpurea chloroplast. Plant Mol. Biol. Rep. 1995, 13, 333–335. [Google Scholar] [CrossRef]
- Seliverstov, A.V.; Lysenko, E.A.; Lyubetsky, V.A. Rapid evolution of promoters for the plastome gene ndhF in flowering plants. Russ. J. Plant Physiol. 2009, 56, 838–845. [Google Scholar] [CrossRef]
- Lyubetsky, V.A.; Rubanov, L.I.; Seliverstov, A.V. Lack of conservation of bacterial type promoters in plastids of Streptophyta. Biol. Direct. 2010, 5. [Google Scholar] [CrossRef] [PubMed]
- Homann, A.; Link, G. DNA-binding and transcription characteristics of three cloned sigma factors from mustard (Sinapis alba L.) suggest overlapping and distinct roles in plastid gene expression. Eur. J. Biochem. 2003, 270, 1288–1300. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y. Efficient high-quality force-directed graph drawing. Math. J. 2006, 10, 37–71. [Google Scholar]
- Crooks, G.E.; Hon, G.; Chandonia, J.M.; Brenner, S.E. WebLogo: A sequence logo generator. Genome Res. 2004, 14, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Stecher, G.; Peterson, D.; Filipski, A.; Kumar, S. MEGA6: Molecular Evolutionary Genetics Analysis Version 6.0. Mol. Bio.l Evol. 2013, 30, 2725–2729. [Google Scholar] [CrossRef] [PubMed]
- Page, R.D.M. TreeView: An application to display phylogenetic trees on personal computers. Comput. Appl. Biosci. 1996, 12, 357–358. [Google Scholar] [PubMed]
- Finn, R.D.; Bateman, A.; Clements, J.; Coggill, P.; Eberhardt, R.Y.; Eddy, S.R.; Heger, A.; Hetherington, K.; Holm, L.; Mistry, J.; et al. The Pfam protein families database. Nucleic Acids Res. 2014, 42, D222–D230. [Google Scholar] [CrossRef] [PubMed]
- Edgar, R.C. MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2014, 32, 1792–1797. [Google Scholar] [CrossRef] [PubMed]
- Stamatakis, A. RAxML version 8: A tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 2014, 30, 1312–1313. [Google Scholar] [CrossRef] [PubMed]
- Lyubetsky, V.A.; Seliverstov, A.V.; Zverkov, O.A. Elaboration of the homologous plastid-encoded protein families that separate paralogs in Magnoliophytes. Math. Biol. Bioinform. 2013, 8, 225–233. (in Russian). [Google Scholar] [CrossRef]
- Zverkov, O.A.; Seliverstov, A.V.; Lyubetsky, V.A. Plastid-encoded protein families specific for narrow taxonomic groups of algae and protozoa. Mol. Biol. 2012, 46, 717–726. [Google Scholar] [CrossRef]
- Lyubetsky, V.; Seliverstov, A.; Zverkov, O. Transcription regulation of plastid genes involved in sulfate transport in Viridiplantae. BioMed Res. Int. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Zverkov, O.A.; Seliverstov, A.V.; Lyubetsky, V.A. A database of plastid protein families from red algae and Apicomplexa and expression regulation of the moeB gene. BioMed Res. Int. 2015, 2015. [Google Scholar] [CrossRef] [PubMed]
- Van Dongen, S. Graph clustering via a discrete uncoupling process. SIAM J. Matrix Anal. Appl. 2008, 30, 121–141. [Google Scholar] [CrossRef]
- Galashov, A.E.; Kel’manov, A.V. A 2-approximate algorithm to solve one problem of the family of disjoint vector subsets. Autom. Remote Control. 2014, 75, 595–606. [Google Scholar] [CrossRef]
- Kel'manov, A.V.; Khamidullin, S.A. An approximation polynomial-time algorithm for a sequence bi-clustering problem. Comp. Math. Math. Phys. 2015, 55, 1068–1076. [Google Scholar] [CrossRef]
- Kel'manov, A.V.; Khandeev, V.I. A randomized algorithm for two-cluster partition of a set of vectors. Comp. Math. Math. Phys. 2015, 55, 330–339. [Google Scholar] [CrossRef]
- Kel’manov, A.V.; Romanchenko, S.M. An FPTAS for a vector subset search problem. J. Appl. Ind. Math. 2014, 8, 329–336. [Google Scholar] [CrossRef]
- Kel’manov, A.V.; Khamidullin, S.A. An approximating polynomial algorithm for a sequence partitioning problem. J. Appl. Ind. Math. 2014, 8, 236–244. [Google Scholar] [CrossRef]
- Kruskal, J.B. On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Katoh, A.; Lee, K.S.; Fukuzawa, H.; Ohyama, K.; Ogawa, T. cemA homologue essential to CO2 transport in the cyanobacterium Synechocystis PCC6803. Proc. Natl. Acad. Sci. USA 1996, 93, 4006–4010. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, D.; Price, D.C.; Chan, C.X.; Qiu, H.; Rose, N.; Ball, S.; Weber, A.P.; Arias, M.C.; Henrissat, B.; Coutinho, P.M.; et al. Genome of the red alga Porphyridium purpureum. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Lopatovskaya, K.V.; Seliverstov, A.V.; Lyubetsky, V.A. NtcA and NtcB regulons in cyanobacteria and rhodophyta chloroplasts. Mol. Biol. 2011, 45, 522–526. [Google Scholar] [CrossRef]
- Minoda, A.; Weber, A.P.; Tanaka, K.; Miyagishima, S.Y. Nucleus-independent control of the rubisco operon by the plastid-encoded transcription factor Ycf30 in the red alga Cyanidioschyzon merolae. Plant Physiol. 2010, 154, 1532–1540. [Google Scholar] [CrossRef] [PubMed]
- Kozobay-Avraham, L.; Hosid, S.; Bolshoy, A. Involvement of DNA curvature in intergenic regions of prokaryotes. Nucleic Acids Res. 2006, 34, 2316–2327. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kamzolova, S.G.; Sorokin, A.A.; Dzhelyadin, T.R.; Beskaravainy, P.M.; Osypov, A.A. Electrostatic potentials of E. coli genome DNA. J. Biomol. Struct. Dyn. 2005, 23, 341–346. [Google Scholar] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zverkov, O.A.; Seliverstov, A.V.; Lyubetsky, V.A. Regulation of Expression and Evolution of Genes in Plastids of Rhodophytic Branch. Life 2016, 6, 7. https://doi.org/10.3390/life6010007
Zverkov OA, Seliverstov AV, Lyubetsky VA. Regulation of Expression and Evolution of Genes in Plastids of Rhodophytic Branch. Life. 2016; 6(1):7. https://doi.org/10.3390/life6010007
Chicago/Turabian StyleZverkov, Oleg Anatolyevich, Alexandr Vladislavovich Seliverstov, and Vassily Alexandrovich Lyubetsky. 2016. "Regulation of Expression and Evolution of Genes in Plastids of Rhodophytic Branch" Life 6, no. 1: 7. https://doi.org/10.3390/life6010007
APA StyleZverkov, O. A., Seliverstov, A. V., & Lyubetsky, V. A. (2016). Regulation of Expression and Evolution of Genes in Plastids of Rhodophytic Branch. Life, 6(1), 7. https://doi.org/10.3390/life6010007









