Integrated in silico Analyses of Regulatory and Metabolic Networks of Synechococcus sp. PCC 7002 Reveal Relationships between Gene Centrality and Essentiality
Abstract
:1. Introduction
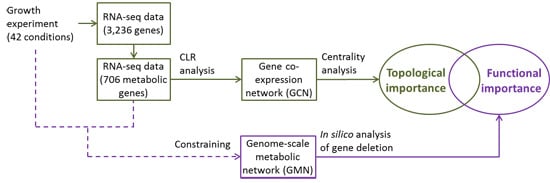
2. Materials and Methods
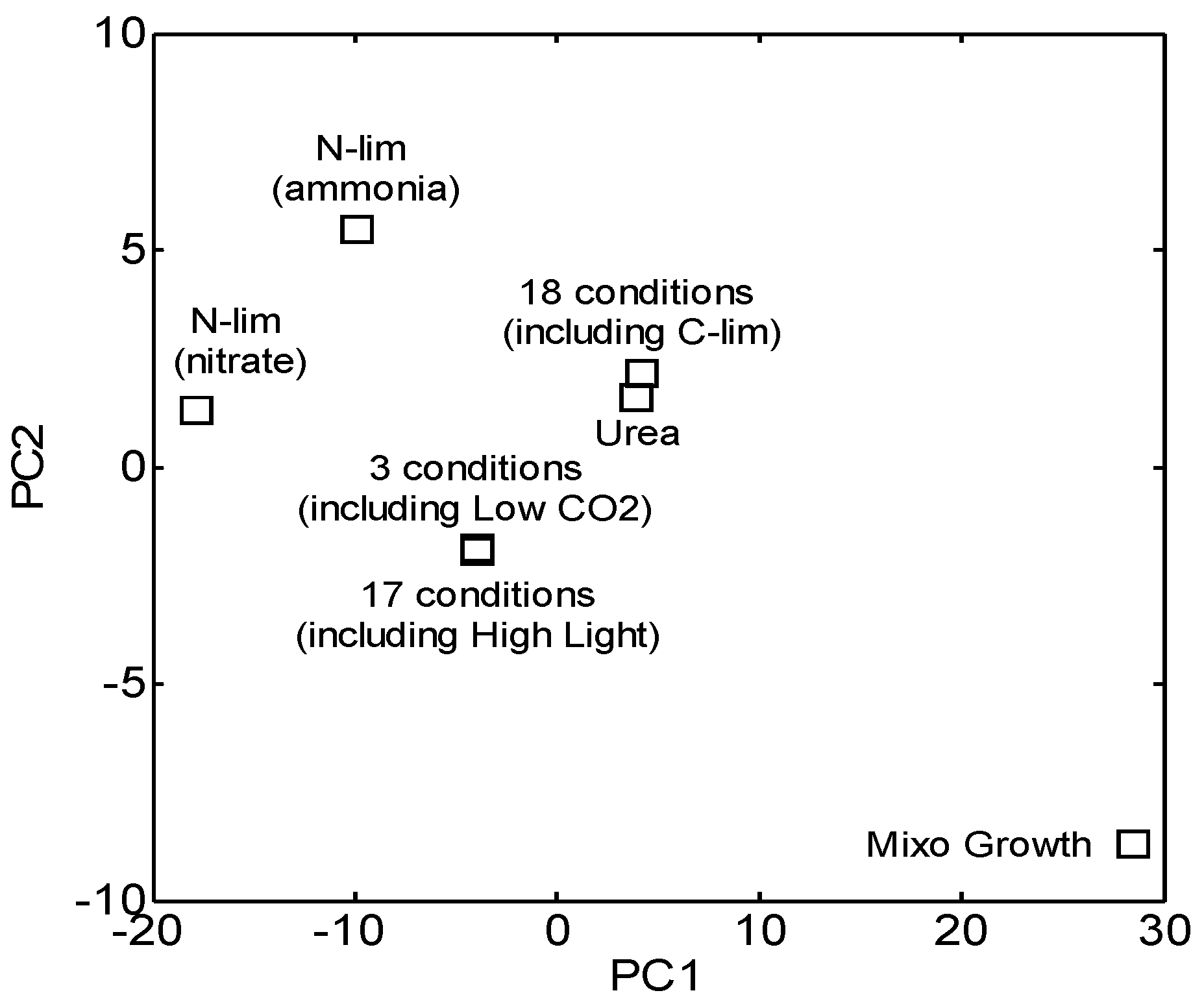
2.1. Experimental Conditions and Measurements
2.2. Metabolic Network Analysis of Wild-Type and Knock-Out Strains
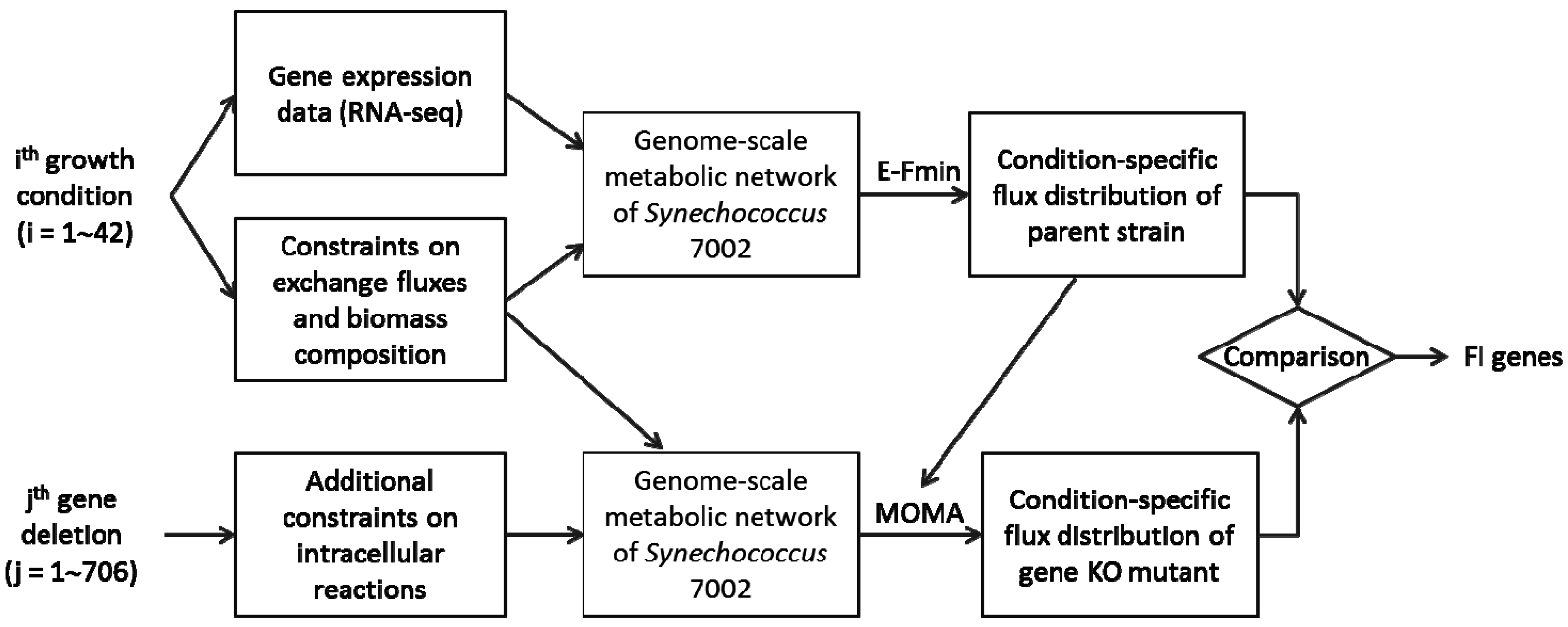
2.3. Reconstruction of Gene Co-Expression Network (GCN)
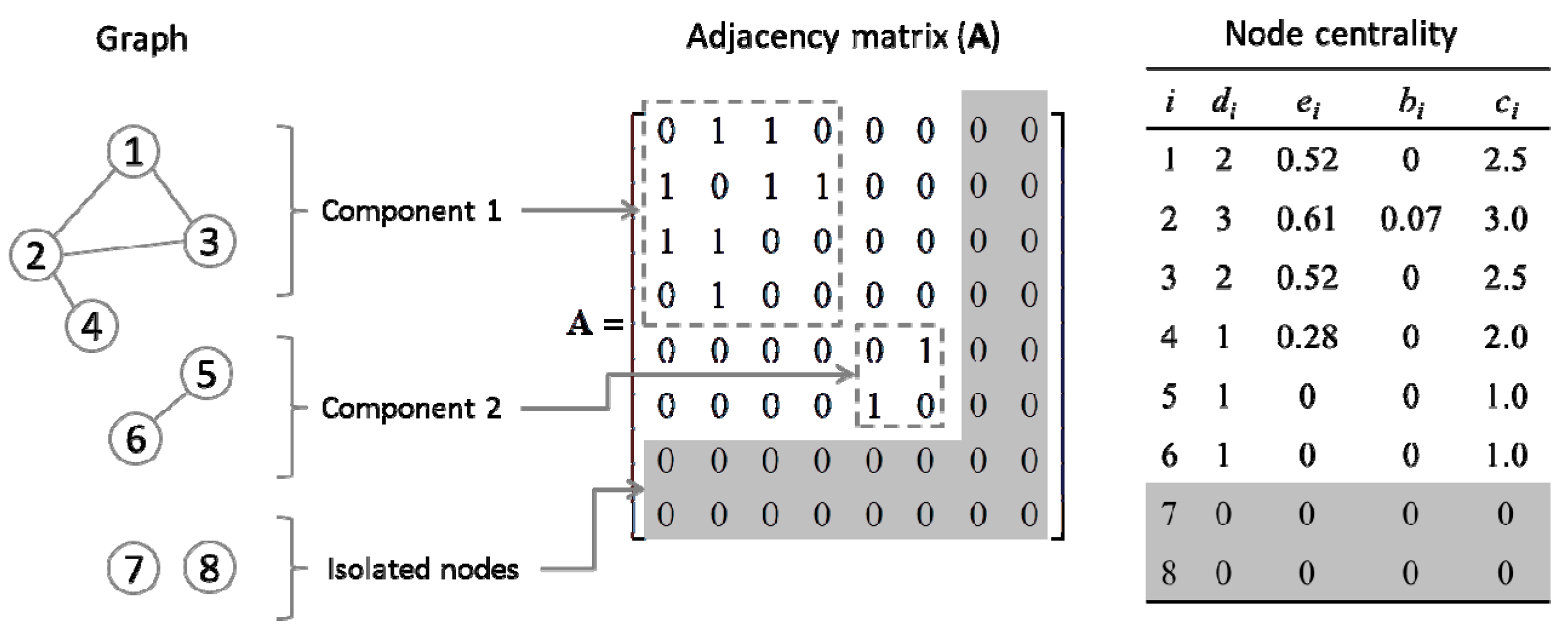
2.4. Quantification of Gene Centrality
3. Results and Discussion
3.1. Reconstruction and Topological Analysis of GCN
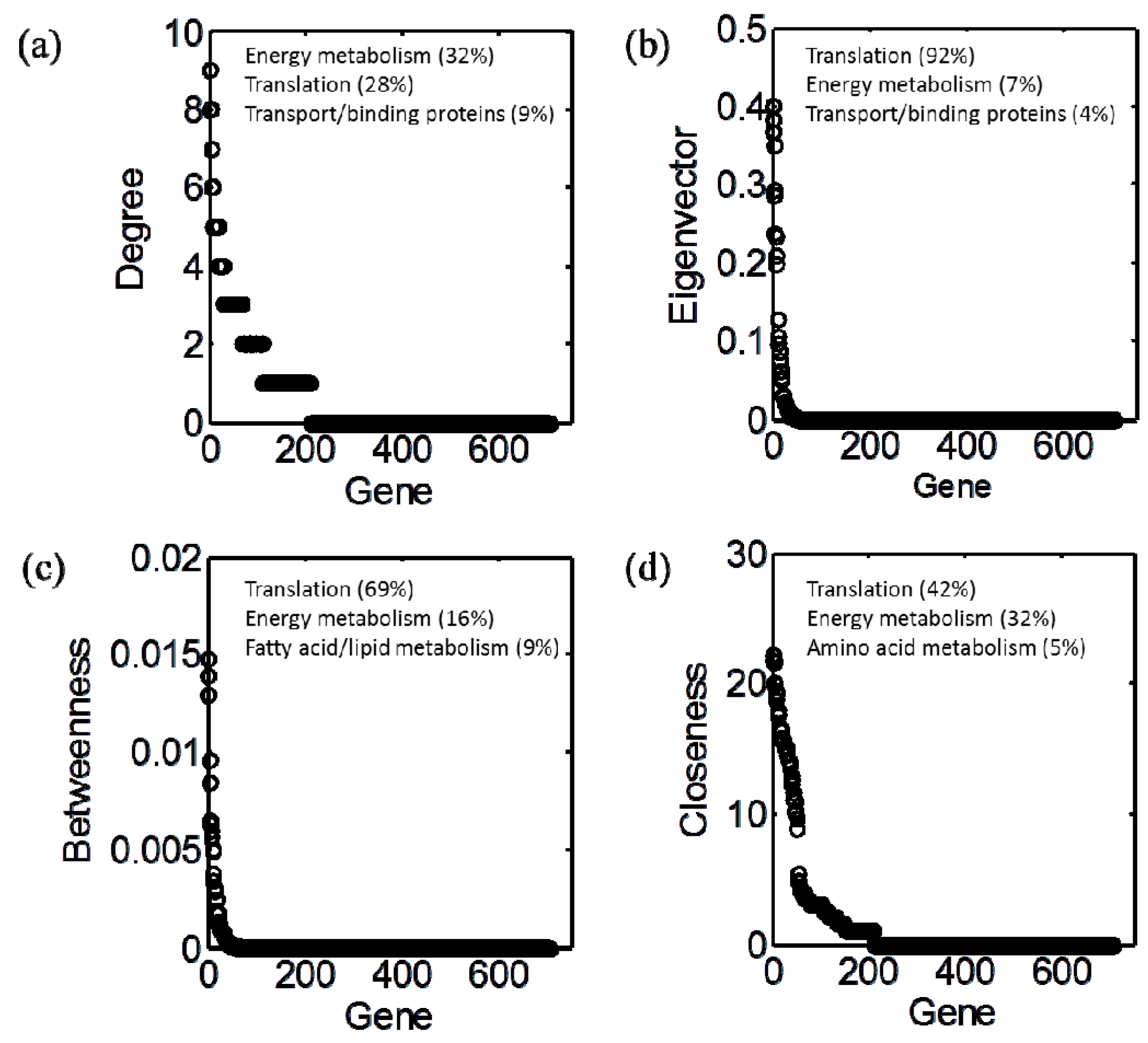
3.2. Centrality Analyses
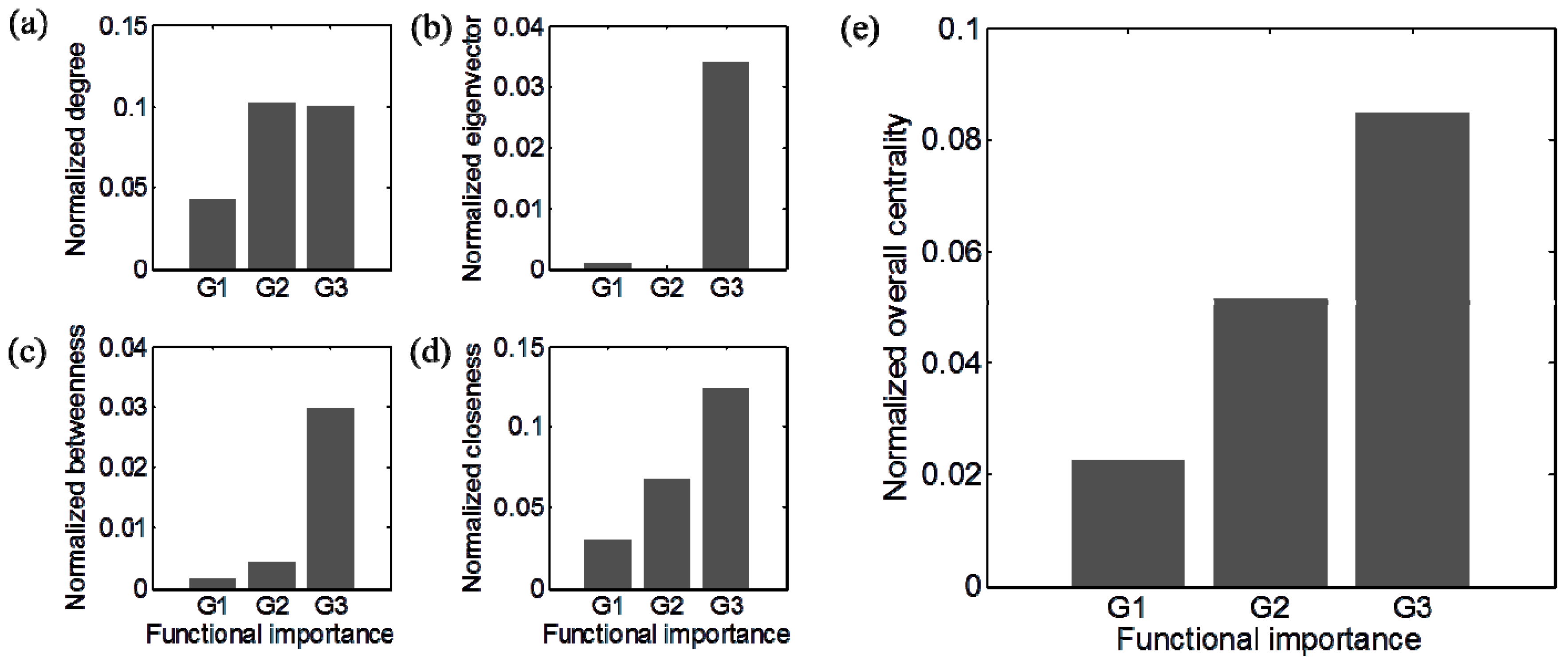
3.3. Identification of Functionally Important (FI) Genes
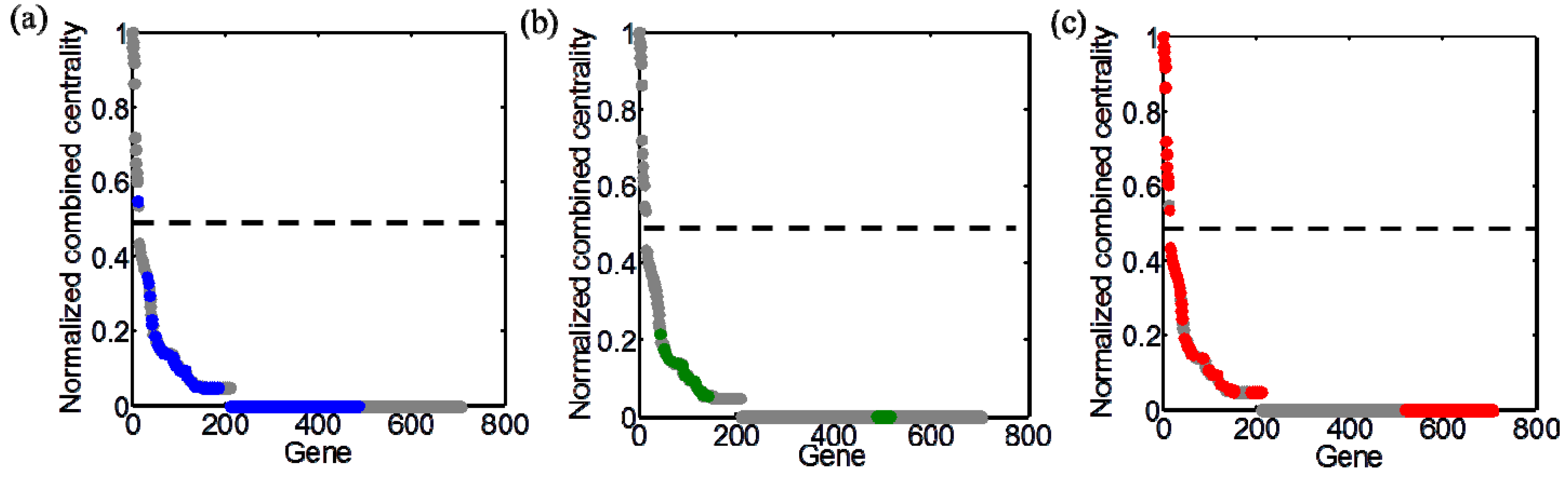
3.4. Integration of Topological and Functional Analyses
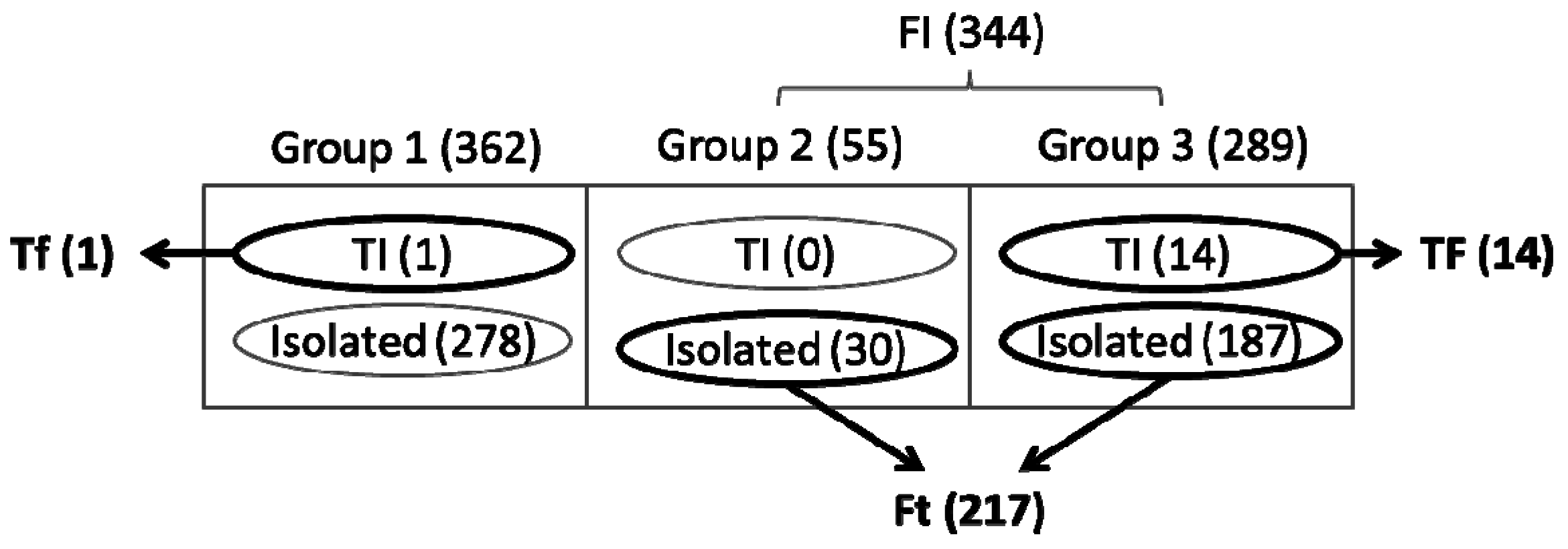
4. Concluding Remarks
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bernstein, H.C.; Konopka, A.; Melnicki, M.R.; Hill, E.A.; Kucek, L.A.; Zhang, S.Y.; Shen, G.Z.; Bryant, D.A.; Beliaev, A.S. Effect of mono- and dichromatic light quality on growth rates and photosynthetic performance of synechococcus sp pcc 7002. Front. Microbiol. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Grossman, A.R.; Schaefer, M.R.; Chiang, G.G.; Collier, J.L. The phycobilisome, a light-harvesting complex responsive to environmental-conditions. Microbiol. Rev. 1993, 57, 725–749. [Google Scholar] [PubMed]
- Grossman, A.R.; Schaefer, M.R.; Chiang, G.G.; Collier, J.L. The responses of cyanobacteria to environmental conditions: Light and nutrients. In The Molecular Biology of Cyanobacteria; Springer: Berlin/Heidelberg, Germany, 2004; pp. 641–675. [Google Scholar]
- Hernández-Prieto, M.A.; Semeniuk, T.A.; Futschik, M.E. Toward a systems-level understanding of gene regulatory, protein interaction, and metabolic networks in cyanobacteria. Front. Genet. 2014, 5. [Google Scholar] [CrossRef]
- Strauss, E.J.; Falkow, S. Microbial pathogenesis: Genomics and beyond. Science 1997, 276, 707–712. [Google Scholar] [CrossRef] [PubMed]
- Itoh, T.; Takemoto, K.; Mori, H.; Gojobori, T. Evolutionary instability of operon structures disclosed by sequence comparisons of complete microbial genomes. Mol. Biol. Evol. 1999, 16, 332–346. [Google Scholar] [CrossRef] [PubMed]
- Henry, C.S.; DeJongh, M.; Best, A.A.; Frybarger, P.M.; Linsay, B.; Stevens, R.L. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 2010, 28, 977–922. [Google Scholar] [CrossRef] [PubMed]
- Thiele, I.; Palsson, B.O. A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat. Protocols 2010, 5, 93–121. [Google Scholar] [CrossRef]
- Moxley, J.F.; Jewett, M.C.; Antoniewicz, M.R.; Villas-Boas, S.G.; Alper, H.; Wheeler, R.T.; Tong, L.; Hinnebusch, A.G.; Ideker, T.; Nielsen, J.; et al. Linking high-resolution metabolic flux phenotypes and transcriptional regulation in yeast modulated by the global regulator gcn4p. Proc. Natl. Acad. Sci. USA 2009, 106, 6477–6482. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Palsson, B.O. The growing scope of applications of genome-scale metabolic reconstructions using escherichia coli. Nat. Biotechnol. 2008, 26, 659–667. [Google Scholar] [CrossRef] [PubMed]
- Oberhardt, M.A.; Palsson, B.O.; Papin, J.A. Applications of genome-scale metabolic reconstructions. Mol. Syst. Biol. 2009, 5. [Google Scholar] [CrossRef]
- McDermott, J.E.; Taylor, R.C.; Yoon, H.J.; Heffron, F. Bottlenecks and hubs in inferred networks are important for virulence in salmonella typhimurium. J. Comput. Biol. 2009, 16, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Ishchukov, I.; Wu, Y.; Van Puyvelde, S.; Vanderleyden, J.; Marchal, K. Inferring the relation between transcriptional and posttranscriptional regulation from expression compendia. BMC Microbiol. 2014, 14. [Google Scholar] [CrossRef] [PubMed]
- Faith, J.J.; Hayete, B.; Thaden, J.T.; Mogno, I.; Wierzbowski, J.; Cottarel, G.; Kasif, S.; Collins, J.J.; Gardner, T.S. Large-scale mapping and validation of escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007, 5, 54–66. [Google Scholar] [CrossRef]
- Gibson, S.M.; Ficklin, S.P.; Isaacson, S.; Luo, F.; Feltus, F.A.; Smith, M.C. Massive-scale gene co-expression network construction and robustness testing using random matrix theory. PLoS One 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Wunderlich, Z.; Mimy, L.A. Using the topology of metabolic networks to predict viability of mutant strains. Biophys. J. 2006, 91, 2304–2311. [Google Scholar] [CrossRef] [PubMed]
- Palumbo, M.C.; Colosimo, A.; Giuliani, A.; Farina, L. Functional essentiality from topology features in metabolic networks: A case study in yeast. Febs Lett. 2005, 579, 4642–4646. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, R.; Palsson, B.O. Properties of metabolic networks: Structure versus function. Biophys. J. 2005, 88, L7–L9. [Google Scholar]
- Del Rio, G.; Koschutzki, D.; Coello, G. How to identify essential genes from molecular networks? BMC Syst. Biol. 2009, 3. [Google Scholar] [CrossRef]
- Liu, H.B.; Jing, H.M.; Wong, T.H.C.; Chen, B.Z. Co-occurrence of phycocyanin- and phycoerythrin-rich Synechococcus in subtropical estuarine and coastal waters of Hong Kong. Environ. Microbiol. Rep. 2014, 6, 90–99. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Wommack, K.E.; Chen, F. Abundance and distribution of Synechococcus spp. And cyanophages in the chesapeake bay. Appl. Environ. Microbiol. 2011, 77, 7459–7468. [Google Scholar] [CrossRef] [PubMed]
- Van Baalen, C. Studies on marine blue-green algae. Bot. Mar. 1962, 4, 129–139. [Google Scholar]
- Ludwig, M.; Bryant, D.A. Transcription profiling of the model cyanobacterium Synechococcus sp. strain pcc 7002 by next-gen (SOLiDTM) sequencing of cDNA. Front. Microbiol. 2011, 2. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, M.; Bryant, D.A. Synechococcus sp strain pcc 7002 transcriptome: Acclimation to temperature, salinity, oxidative stress, and mixotrophic growth conditions. Front. Microbiol. 2012, 3. [Google Scholar] [CrossRef]
- Beliaev, A.S.; Romine, M.F.; Serres, M.; Bernstein, H.C.; Linggi, B.E.; Markillie, L.M.; Isern, N.G.; Chrisler, W.B.; Kucek, L.A.; Hill, E.A.; et al. Inference of interactions in cyanobacterial-heterotrophic co-cultures via transcriptome sequencing. ISME J. 2014, 8, 2243–2255. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, M.; Bryant, D.A. Acclimation of the global transcriptome of the cyanobacterium Synechococcus sp strain pcc 7002 to nutrient limitations and different nitrogen sources. Front. Microbiol. 2012, 3. [Google Scholar] [CrossRef]
- Melnicki, M.R.; Pinchuk, G.E.; Hill, E.A.; Kucek, L.A.; Stolyar, S.M.; Fredrickson, J.K.; Konopka, A.E.; Beliaev, A.S. Feedback-controlled led photobioreactor for photophysiological studies of cyanobacteria. Bioresource Technol. 2013, 134, 127–133. [Google Scholar] [CrossRef]
- McClure, R.; Balasubramanian, D.; Sun, Y.; Bobrovskyy, M.; Sumby, P.; Genco, C.A.; Vanderpool, C.K.; Tjaden, B. Computational analysis of bacterial rna-seq data. Nucleic Acids Res. 2013, 41. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, J.J.; Reed, J.L. Identification of functional differences in metabolic networks using comparative genomics and constraint-based models. PLoS One 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Song, H.S.; Reifman, J.; Wallqvist, A. Prediction of metabolic flux distribution from gene expression data based on the flux minimization principle. PLoS One 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Segre, D.; Vitkup, D.; Church, G.M. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. USA 2002, 99, 15112–15117. [Google Scholar] [CrossRef] [PubMed]
- Opsahl, T.; Agneessens, F.; Skvoretz, J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Netw. 2010, 32, 245–251. [Google Scholar] [CrossRef]
- Bounova, G.; de Weck, O. Overview of metrics and their correlation patterns for multiple- metric topology analysis on heterogeneous graph ensembles. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Octave Networks Toolbox First Release. Available online: https://zenodo.Org/record/10778 (accessed on 18 March 2015).
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.-S.; McClure, R.S.; Bernstein, H.C.; Overall, C.C.; Hill, E.A.; Beliaev, A.S. Integrated in silico Analyses of Regulatory and Metabolic Networks of Synechococcus sp. PCC 7002 Reveal Relationships between Gene Centrality and Essentiality. Life 2015, 5, 1127-1140. https://doi.org/10.3390/life5021127
Song H-S, McClure RS, Bernstein HC, Overall CC, Hill EA, Beliaev AS. Integrated in silico Analyses of Regulatory and Metabolic Networks of Synechococcus sp. PCC 7002 Reveal Relationships between Gene Centrality and Essentiality. Life. 2015; 5(2):1127-1140. https://doi.org/10.3390/life5021127
Chicago/Turabian StyleSong, Hyun-Seob, Ryan S. McClure, Hans C. Bernstein, Christopher C. Overall, Eric A. Hill, and Alexander S. Beliaev. 2015. "Integrated in silico Analyses of Regulatory and Metabolic Networks of Synechococcus sp. PCC 7002 Reveal Relationships between Gene Centrality and Essentiality" Life 5, no. 2: 1127-1140. https://doi.org/10.3390/life5021127
APA StyleSong, H.-S., McClure, R. S., Bernstein, H. C., Overall, C. C., Hill, E. A., & Beliaev, A. S. (2015). Integrated in silico Analyses of Regulatory and Metabolic Networks of Synechococcus sp. PCC 7002 Reveal Relationships between Gene Centrality and Essentiality. Life, 5(2), 1127-1140. https://doi.org/10.3390/life5021127