Optimization of the Non-Local Means Algorithm for Breast Diffusion-Weighted Magnetic Resonance Imaging Using a 3D-Printed Breast-Mimicking Phantom
Abstract
1. Introduction
2. Materials and Methods
2.1. Phantom Production
2.2. MRI Equipment and DWMR Image Acquisition
2.3. NLM Algorithm
2.4. Quantitative Evaluation
3. Results
3.1. Quantitative Evaluation Results of DWMR Images
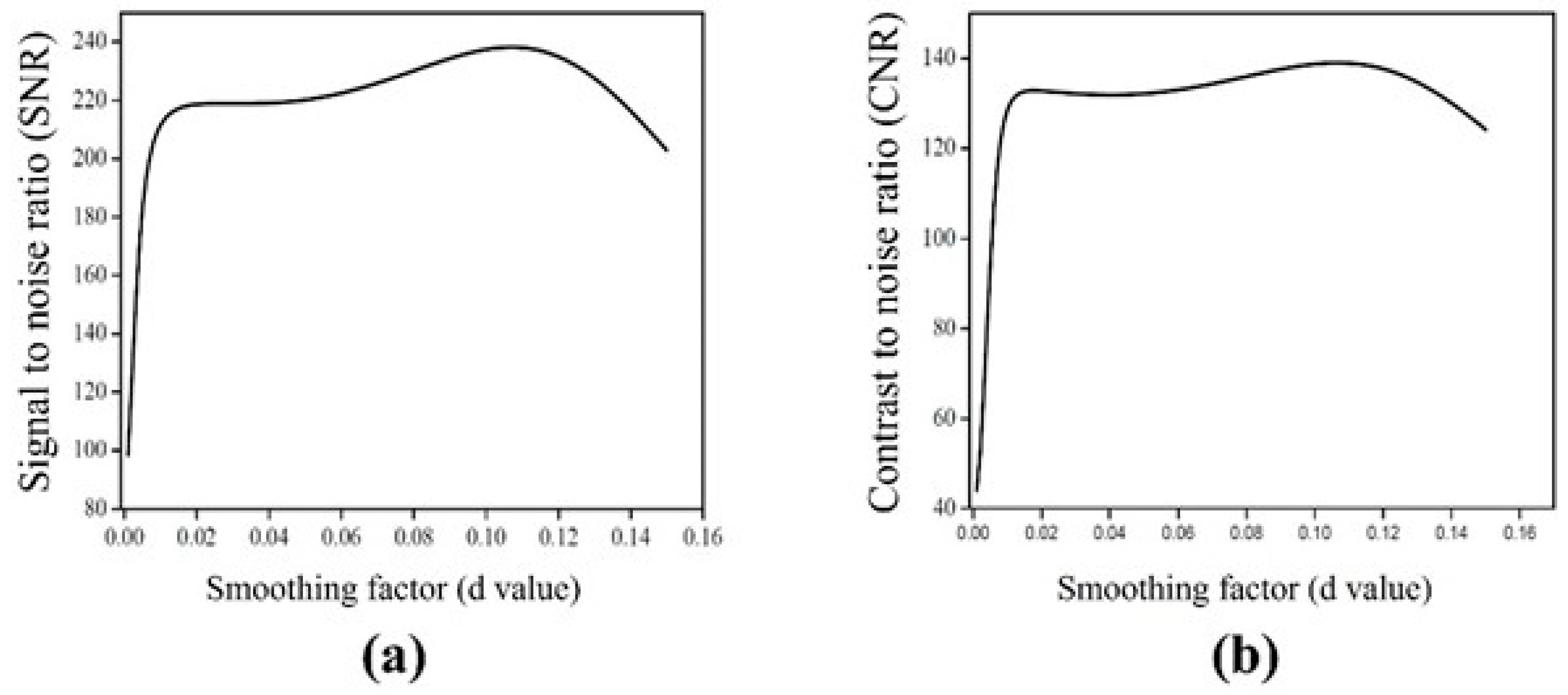
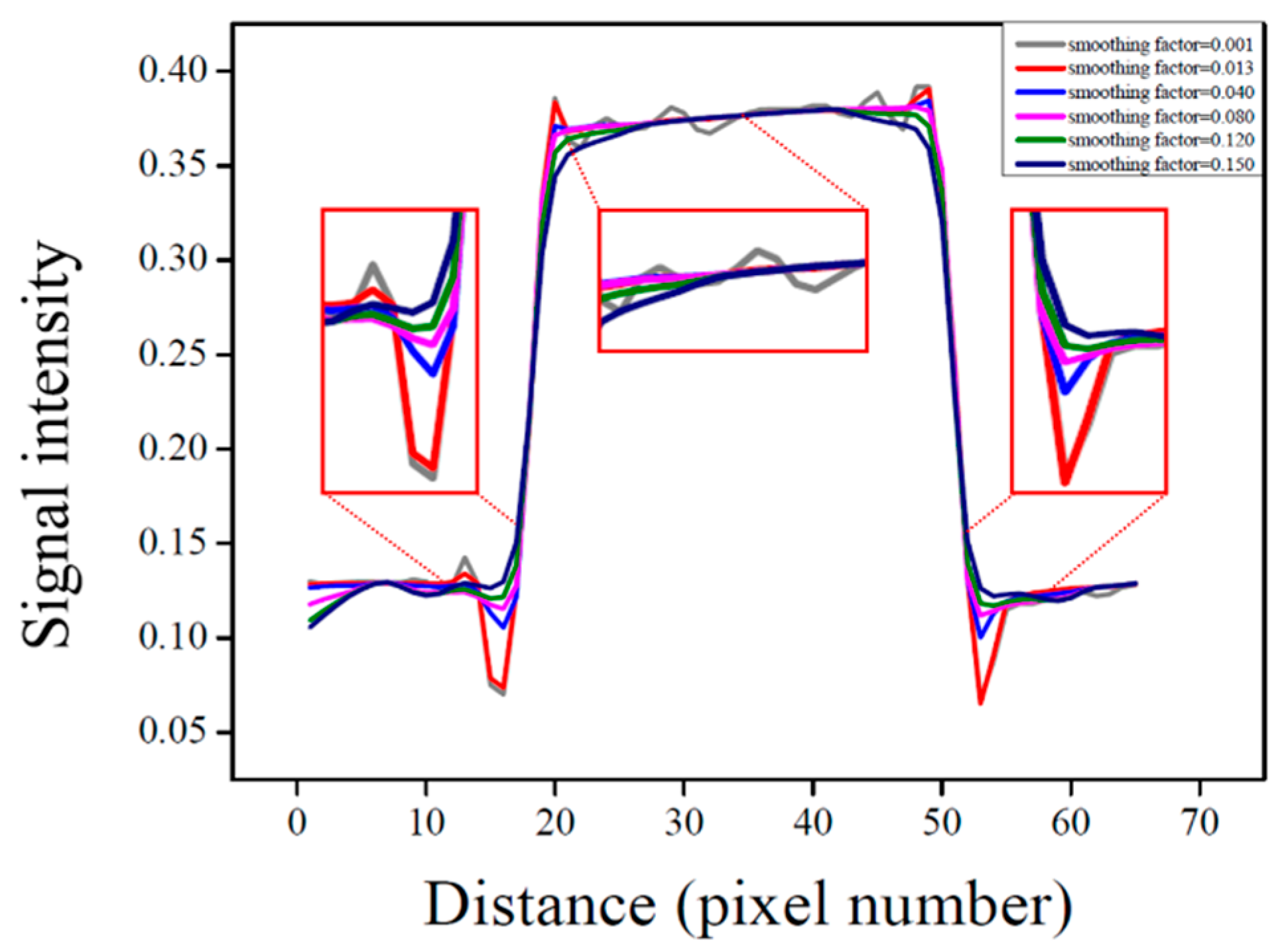
3.2. Quantitative Evaluation Results of NLM-Optimized Images
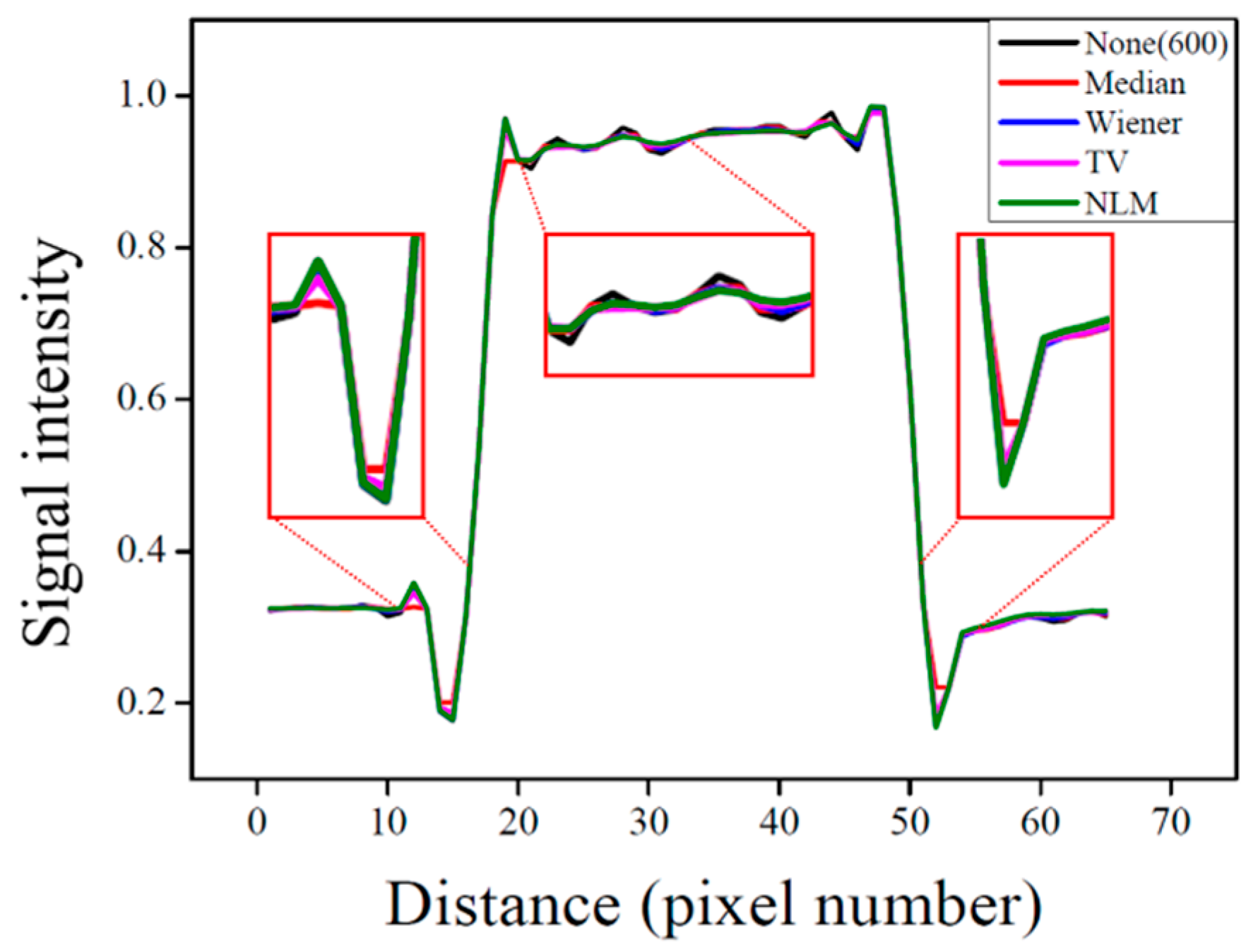
3.3. Comparison with Conventional Noise Reduction Algorithms
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y.; Gong, M.; Wang, Y.; Yang, Y.; Liu, S.; Zeng, Q. Global trends and forecasts of breast cancer incidence and deaths. Sci. Data 2023, 10, 334. [Google Scholar] [CrossRef] [PubMed]
- Amornsiripanitch, N.; Bickelhaupt, S.; Shin, H.J.; Dang, M.; Rahbar, H.; Pinker, K.; Partridge, S.C. Diffusion-weighted MRI for unenhanced breast cancer screening. Radiology 2019, 293, 504–520. [Google Scholar] [CrossRef]
- Tian, M.; Song, K. Boosting magnetic resonance image denoising with generative adversarial networks. IEEE Access 2021, 9, 62266–62275. [Google Scholar] [CrossRef]
- Dikaios, N.; Punwani, S.; Hamy, V.; Purpura, P.; Rice, S.; Forster, M.; Mendes, R.; Taylor, S.; Atkinson, D. Noise estimation from averaged diffusion weighted images: Can unbiased quantitative decay parameters assist cancer evaluation? Magn. Reson. Med. 2014, 71, 2105–2117. [Google Scholar] [CrossRef]
- Srinivasan, A.; Dvorak, R.; Perni, K.; Rohrer, S.; Mukherji, S.K. Differentiation of benign and malignant pathology in the head and neck using 3T apparent diffusion coefficient values: Early experience. Am. J. Neuroradiol. 2008, 29, 40–44. [Google Scholar] [CrossRef] [PubMed]
- Gudbjartsson, H.; Patz, S. The Rician distribution of noisy MRI data. Magn. Reson. Med. 1995, 34, 910–914. [Google Scholar] [CrossRef]
- Eichner, C.; Paquette, M.; Mildner, T.; Schlumm, T.; Pléh, K.; Samuni, L.; Crockford, C.; Wittig, R.M.; Jäger, C.; Möller, H.E.; et al. Increased sensitivity and signal-to-noise ratio in diffusion-weighted MRI using multi-echo acquisitions. Neuroimage 2020, 221, 117172. [Google Scholar] [CrossRef] [PubMed]
- Karki, K.; Hugo, G.D.; Ford, J.C.; Olsen, K.M.; Saraiya, S.; Groves, R.; Weiss, E. Estimation of optimal b-value sets for obtaining apparent diffusion coefficient free from perfusion in non-small cell lung cancer. Phys. Med. Biol. 2015, 60, 7877. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, F.; Fan, H.; Zhang, C. Brief review of image denoising techniques. Vis. Comput. Ind. Biomed. Art 2019, 2, 7. [Google Scholar] [CrossRef]
- Gruber, B.; Froeling, M.; Leiner, T.; Klomp, D.W.J. RF coils: A practical guide for nonphysicists. J. Magn. Reson. Imaging 2018, 48, 590–604. [Google Scholar] [CrossRef]
- Heo, Y.C.; Kim, K.; Lee, Y. Image denoising using non-local means (NLM) approach in magnetic resonance (MR) imaging: A systematic review. Appl. Sci. 2020, 10, 7028. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, W.-J.; Wan, F.-N.; Chen, Z.-Z.; Kong, Y.-Y.; Liu, X.-H.; Ye, D.-W.; Dai, B. Deep learning network enhances imaging quality of low-b-value diffusion–weighted imaging and improves lesion detection in prostate cancer. BMC Cancer 2025, 25, 953. [Google Scholar] [CrossRef]
- Liu, R.; Xiao, S.; Liu, T.; Jiang, F.; Yuan, C.; Chen, J. Dual stage MRI image restoration based on blind spot denoising and hybrid attention. BMC Med. Imaging 2024, 24, 259. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Li, J.; Zhang, H.; Zhao, D.; Wei, B.; Xu, Y. Restore-rwkv: Efficient and effective medical image restoration with rwkv. IEEE J. Biomed. Health Inform. 2025, 1–14. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, M.X.; Wang, W.; Li, Y.; Zhang, F. A self-guided deep learning technique for MRI image noise reduction. J. Theory Pract. Eng. Sci. 2024, 4, 109–117. [Google Scholar]
- Tran, A.T.; Zeevi, T.; Payabvash, S. Strategies to Improve the Robustness and Generalizability of Deep Learning Segmentation and Classification in Neuroimaging. BioMedInformatics 2025, 5, 20. [Google Scholar] [CrossRef]
- Gal, Y.; Mehnert, A.; Bradley, A.; McMahon, K.; Kennedy, D.; Crozier, S. Denoising of dynamic contrast-enhanced MR images using dynamic nonlocal means. IEEE Trans. Med. Imaging 2010, 29, 302–310. [Google Scholar] [CrossRef]
- Hargreaves, B.A.; Worters, P.W.; Pauly, K.B.; Pauly, J.M.; Koch, K.M.; Gold, G.E. Metal-induced artifacts in MRI. Am. J. Roentgenol. 2011, 197, 547–555. [Google Scholar] [CrossRef]
- Pullens, P.; Bladt, P.; Sijbers, J.; Maas, A.I.R.; Parizel, P.M. A safe, cheap, and easy-to-use isotropic diffusion MRI phantom for clinical and multicenter studies. Med. Phys. 2017, 44, 1063–1070. [Google Scholar] [CrossRef]
- Keenan, K.E.; Wilmes, L.J.; Aliu, S.O.; Newitt, D.C.; Jones, E.F.; Boss, M.A.; Stupic, K.F.; Russek, S.E.; Hylton, N.M. Design of a breast phantom for quantitative MRI. J. Magn. Reson. Imaging 2016, 44, 610–619. [Google Scholar] [CrossRef] [PubMed]
- Thomassin-Naggara, I.; De Bazelaire, C.; Chopier, J.; Bazot, M.; Marsault, C.; Trop, I. Diffusion-weighted MR imaging of the breast: Advantages and pitfalls. Eur. J. Radiol. 2013, 82, 435–443. [Google Scholar] [CrossRef]
- Shokeir, F.A.; Soliman, N.; Khater, A.; Bayoumi, D. Evaluation of molecular subtypes of breast cancer using MRI BI-RADS Lexicon. Egypt. J. Radiol. Nucl. Med. 2024, 55, 52. [Google Scholar] [CrossRef]
- Surov, A.; Meyer, H.J.; Wienke, A. Can apparent diffusion coefficient (ADC) distinguish breast cancer from benign breast findings? A meta-analysis based on 13,847 lesions. BMC Cancer 2019, 19, 955. [Google Scholar] [CrossRef]
- Sun, Y.S.; Zhao, Z.; Yang, Z.N.; Xu, F.; Lu, H.J.; Zhu, Z.Y.; Shi, W.; Jiang, J.; Yao, P.P.; Zhu, H.P. Risk factors and preventions of breast cancer. Int. J. Biol. Sci. 2017, 13, 1387. [Google Scholar] [CrossRef]
- Yılmaz, E.; Güldoğan, N.; Ulus, S.; Türk, E.B.; Mısır, M.E.; Arslan, A.; Arıbal, M.E. Diagnostic value of synthetic diffusion-weighted imaging on breast magnetic resonance imaging assessment: Comparison with conventional diffusion-weighted imaging. Diagn. Interv. Radiol. 2024, 30, 91. [Google Scholar] [CrossRef] [PubMed]
- Le Bihan, D.; Iima, M.; Partridge, S.C. Fat-signal suppression in breast diffusion-weighted imaging: The Good, the Bad, and the Ugly. Eur. Radiol. 2025, 35, 733–741. [Google Scholar] [CrossRef] [PubMed]
- Camps-Herrero, J. Diffusion-weighted imaging of the breast: Current status as an imaging biomarker and future role. BJR Open 2019, 1, 20180049. [Google Scholar] [CrossRef] [PubMed]
- Kang, B.J.; Kim, M.J.; Shin, H.J.; Moon, W.K. Acquisition and interpretation guidelines of breast diffusion-weighted MRI (DW-MRI): Breast imaging study group of Korean Society of Magnetic Resonance in Medicine recommendations. Investig. Magn. Reson. Imaging 2022, 26, 83–95. [Google Scholar] [CrossRef]
- Mendez, A.M.; Fang, L.K.; Meriwether, C.H.; Batasin, S.J.; Loubrie, S.; Rodríguez-Soto, A.E.; Rakow-Penner, R.A. Diffusion breast MRI: Current standard and emerging techniques. Front. Oncol. 2022, 12, 844790. [Google Scholar] [CrossRef]
- Mann, R.M.; Cho, N.; Moy, L. Breast MRI: State of the art. Radiology 2019, 292, 520–536. [Google Scholar] [CrossRef]
- Lin, C.X.; Tian, Y.; Li, J.M.; Liao, S.T.; Liu, Y.T.; Zhan, R.G.; Du, Z.L.; Yu, X.R. Diagnostic value of multiple b-value diffusion-weighted imaging in discriminating the malignant from benign breast lesions. BMC Med. Imaging 2023, 23, 10. [Google Scholar] [CrossRef]
- Arponen, O.; Sudah, M.; Sutela, A.; Taina, M.; Masarwah, A.; Liimatainen, T.; Vanninen, R. Gadoterate meglumine decreases ADC values of breast lesions depending on the b value combination. Sci. Rep. 2018, 8, 87. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Wiest-Daesslé, N.; Prima, S.; Coupé, P.; Morrissey, S.P.; Barillot, C. Rician noise removal by non-local means filtering for low signal-to-noise ratio MRI: Applications to DT-MRI. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, New York, NY, USA, 6–10 September 2008; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2008; pp. 171–179. [Google Scholar]
- Seo, K.H.; Kang, S.H.; Shim, J.; Lee, Y. Optimization of smoothing factor for fast non-local means algorithm in high pitch based low-dose computed tomography images with tin-filter. Radiat. Phys. Chem. 2023, 206, 110762. [Google Scholar] [CrossRef]
- Kang, S.H.; Kim, J.Y. Application of fast non-local means algorithm for noise reduction using separable color channels in light microscopy images. Int. J. Environ. Res. Public Health 2021, 18, 2903. [Google Scholar] [CrossRef]
- Hernández-Gutiérrez, I.V.; Gallegos-Funes, F.J.; Rosales-Silva, A.J. Improved preclassification non local-means (IPNLM) for filtering of grayscale images degraded with additive white Gaussian noise. EURASIP J. Image Video Process. 2018, 2018, 104. [Google Scholar] [CrossRef]
- Magnotta, V.A.; Friedman, L. Measurement of signal-to-noise and contrast-to-noise in the fBIRN multicenter imaging study. J. Digit. Imaging 2006, 19, 140–147. [Google Scholar] [CrossRef]
- Rodríguez-Molares, A.; Marius, O.; Rindal, O.M.; D’Hooge, J.; Måsøy, S.-E.; Austeng, A.; Torp, H. The generalized contrast-to-noise ratio. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018. [Google Scholar] [CrossRef]
- Kastryulin, S.; Zakirov, J.; Pezzotti, N.; Dylov, D.V. Image quality assessment for magnetic resonance imaging. IEEE Access 2023, 11, 14154–14168. [Google Scholar] [CrossRef]
- Du, J.; Wang, L.; Liu, Y.; Zhou, Z.; He, Z.; Jia, Y. Brain MRI super-resolution using 3D dilated convolutional encoder–decoder network. IEEE Access 2020, 8, 18938–18950. [Google Scholar] [CrossRef]
- Hussain, S.; Mubeen, I.; Ullah, N.; Shah, S.S.U.D.; Khan, B.A.; Zahoor, M.; Ullah, R.; Khan, F.A.; Sultan, M.A. Modern diagnostic imaging technique applications and risk factors in the medical field: A review. BioMed Res. Int. 2022, 2022, 5164970. [Google Scholar] [CrossRef] [PubMed]
- Durur-Subasi, I. DW-MRI of the breast: A pictorial review. Insights Imaging 2019, 10, 61. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, J.; Wu, X. Non-local MRI denoising using random sampling. Magn. Reson. Imaging 2016, 34, 990–999. [Google Scholar] [CrossRef]
- Dresen, R.C.; De Vuysere, S.; De Keyzer, F.; Van Cutsem, E.; Prenen, H.; Vanslembrouck, R.; De Hertogh, G.; Wolthuis, A.; D’Hoore, A.; Vandecaveye, V. Whole-body diffusion-weighted MRI for operability assessment in patients with colorectal cancer and peritoneal metastases. Cancer Imaging 2019, 19, 1. [Google Scholar] [CrossRef]
- Chen, G.; Wu, Y.; Shen, D.; Yap, P.-T. Noise reduction in diffusion MRI using non-local self-similar information in joint x−q space. Med. Image Anal. 2019, 53, 79–94. [Google Scholar] [CrossRef]
- Bento, M.; Fantini, I.; Park, J.; Rittner, L.; Frayne, R. Deep Learning in Large and Multi-Site Structural Brain MR Imaging Datasets. Front. Neuroinform. 2022, 15, 805669. [Google Scholar] [CrossRef]
- Mårtensson, G.; Ferreira, D.; Granberg, T.; Cavallin, L.; Oppedal, K.; Padovani, A.; Rektorova, I.; Bonanni, L.; Pardini, M.; Kramberger, M.G.; et al. The reliability of a deep learning model in clinical out-of-distribution MRI data: A multicohort study. Med. Image Anal. 2020, 66, 101714. [Google Scholar] [CrossRef]
- Sharma, M.; Dogra, A.; Goyal, B.; Gupta, A.; Saikia, M.J. Detail-preserving denoising of CT and MRI images via adaptive clustering and non-local means algorithm. Sci. Rep. 2025, 15, 23859. [Google Scholar] [CrossRef] [PubMed]
- Werner, S.; Zinsser, D.; Esser, M.; Nickel, D.; Nikolaou, K.; Othman, A.E. Enhanced Image Processing Using Complex Averaging in Diffusion-Weighted Imaging of the Prostate: The Impact on Image Quality and Lesion Detectability. Diagnostics 2023, 13, 2325. [Google Scholar] [CrossRef] [PubMed]
- Biagini, C.; Michele, M.; Pratesi, A.; Mungai, F.; Betti, M.; Izzo, G.; Biagini, C.; Natale, L. Signal-to-noise ratio importance in apparent diffusion coefficient measurements using diffusion-weighted echo-planar-imaging scans. J. Adv. Phys. 2014, 4, 517–525. [Google Scholar] [CrossRef]
- Lemainque, T.; Yoneyama, M.; Morsch, C.; Iordanishvili, E.; Barabasch, A.; Schulze-Hagen, M.; Peeters, J.M.; Kuhl, C.; Zhang, S. Reduction of ADC bias in diffusion MRI with deep learning-based acceleration: A phantom validation study at 3.0 T. Magn. Reson. Imaging 2024, 110, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Kishimoto, A.O.; Kataoka, M.; Iima, M.; Honda, M.; Miyake, K.K.; Ohashi, A.; Ota, R.; Kataoka, T.; Sakurai, T.; Toi, M.; et al. Evaluation of Malignant Breast Lesions Using High-resolution Readout-segmented Diffusion-weighted Echo-planar Imaging: Comparison with Pathology. Magn. Reson. Med. Sci. 2021, 20, 204–215. [Google Scholar] [CrossRef]
- Min, Q.; Shao, K.; Zhai, L.; Liu, W.; Zhu, C.; Yuan, L.; Yang, J. Differential diagnosis of benign and malignant breast masses using diffusion-weighted magnetic resonance imaging. World J. Surg. Oncol. 2015, 13, 32. [Google Scholar] [CrossRef]
- Maric, J.; Boban, J.; Ivkovic-Kapicl, T.; Djilas, D.; Vucaj-Cirilovic, V.; Bogdanovic-Stojanovic, D. Differentiation of breast lesions and distinguishing their histological subtypes using diffusion-weighted imaging and ADC values. Front. Oncol. 2020, 10, 332. [Google Scholar] [CrossRef]
- Choi, S.J.; Kim, K.W.; Ko, Y.; Cho, Y.C.; Jang, J.S.; Ahn, H.; Kim, D.W.; Kim, M.Y. Whole Process of Standardization of Diffusion-Weighted Imaging: Phantom Validation and Clinical Application According to the QIBA Profile. Diagnostics 2024, 14, 583. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Huang, W.; Rooney, W.D. Signal-to-noise ratio, contrast-to-noise ratio and pharmacokinetic modeling considerations in dynamic contrast-enhanced magnetic resonance imaging. Magn. Reson. Imaging 2012, 30, 1313–1322. [Google Scholar] [CrossRef] [PubMed]
- Welvaert, M.; Rosseel, Y. On the definition of signal-to-noise ratio and contrast-to-noise ratio for fMRI data. PLoS ONE 2013, 8, e77089. [Google Scholar] [CrossRef] [PubMed]




| b-Value | Signal Intensity | Standard Deviation | SNR | CNR |
|---|---|---|---|---|
| 0 | 925.93 | 10.04 | 92.26 | 0.85 |
| 200 | 759.45 | 7.73 | 98.27 | 18.14 |
| 400 | 617.34 | 5.23 | 117.98 | 33.02 |
| 600 | 501.89 | 4.07 | 123.30 | 38.60 |
| 800 | 409.45 | 3.76 | 108.85 | 43.37 |
| 1000 | 332.54 | 3.43 | 96.87 | 43.63 |
| 1200 | 271.42 | 2.95 | 92.02 | 37.78 |
| 1400 | 221.70 | 2.87 | 77.36 | 35.14 |
| 1600 | 181.40 | 3.01 | 60.26 | 30.33 |
| 1800 | 148.13 | 3.00 | 49.31 | 25.76 |
| 2000 | 120.16 | 2.69 | 44.70 | 25.96 |
|
Smoothing
Factor |
Signal
Intensity |
Standard
Deviation | SNR | CNR |
|---|---|---|---|---|
| 0.010 | 332.54 | 3.38 | 98.52 | 44.02 |
| 0.011 | 332.57 | 1.57 | 211.52 | 128.57 |
| 0.012 | 332.56 | 1.56 | 213.38 | 130.25 |
| 0.013 | 332.55 | 1.55 | 214.77 | 131.32 |
| 0.014 | 332.55 | 1.54 | 215.81 | 131.98 |
| 0.015 | 332.55 | 1.54 | 216.60 | 132.39 |
| 0.02 | 332.56 | 1.53 | 217.20 | 132.63 |
| 0.03 | 332.59 | 1.52 | 218.63 | 132.77 |
| 0.04 | 332.61 | 1.52 | 218.92 | 132.15 |
| 0.05 | 332.61 | 1.52 | 219.07 | 131.87 |
| 0.06 | 332.59 | 1.51 | 220.15 | 132.15 |
| 0.07 | 332.55 | 1.50 | 222.47 | 133.00 |
| 0.08 | 332.50 | 1.47 | 225.92 | 134.34 |
| 0.09 | 332.43 | 1.44 | 230.11 | 135.96 |
| 0.10 | 332.34 | 1.42 | 234.31 | 137.56 |
| 0.11 | 332.25 | 1.40 | 237.41 | 138.71 |
| 0.12 | 332.15 | 1.40 | 238.03 | 138.91 |
| 0.13 | 332.04 | 1.41 | 234.90 | 137.66 |
| 0.14 | 331.94 | 1.46 | 227.47 | 134.68 |
| 0.15 | 331.83 | 1.53 | 216.28 | 130.06 |
| Algorithm | SNR | CNR |
|---|---|---|
| None (600) | 123.30 | 38.60 |
| None (1000) | 96.87 | 43.63 |
| median | 150.36 | 57.67 |
| Wiener | 185.38 | 76.84 |
| TV | 138.14 | 53.53 |
| NLM (1000) | 215.81 | 131.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Kang, S.-H.; Lee, Y. Optimization of the Non-Local Means Algorithm for Breast Diffusion-Weighted Magnetic Resonance Imaging Using a 3D-Printed Breast-Mimicking Phantom. Life 2025, 15, 1373. https://doi.org/10.3390/life15091373
Park S, Kang S-H, Lee Y. Optimization of the Non-Local Means Algorithm for Breast Diffusion-Weighted Magnetic Resonance Imaging Using a 3D-Printed Breast-Mimicking Phantom. Life. 2025; 15(9):1373. https://doi.org/10.3390/life15091373
Chicago/Turabian StylePark, Soungmo, Seong-Hyeon Kang, and Youngjin Lee. 2025. "Optimization of the Non-Local Means Algorithm for Breast Diffusion-Weighted Magnetic Resonance Imaging Using a 3D-Printed Breast-Mimicking Phantom" Life 15, no. 9: 1373. https://doi.org/10.3390/life15091373
APA StylePark, S., Kang, S.-H., & Lee, Y. (2025). Optimization of the Non-Local Means Algorithm for Breast Diffusion-Weighted Magnetic Resonance Imaging Using a 3D-Printed Breast-Mimicking Phantom. Life, 15(9), 1373. https://doi.org/10.3390/life15091373






