Binary and Multi-Class Classification of Colorectal Polyps Using CRP-ViT: A Comparative Study Between CNNs and QNNs
Abstract
1. Introduction
1.1. CNN
1.2. QNN
1.3. Survey of Literature
1.4. Problem Identified from the Literature
1.5. Aim and Objective of This Article
1.6. Contribution of This Article
- A diverse CRP image dataset is aggregated by combining publicly available sources with self-curated real-time clinical colonoscopy images to enhance the dataset’s variability in training and evaluating DL models in the detection of CRP.
- A novel architectural modification is proposed by replacing classical convolutional layers in the original CRPCNN-ViT model with Quanvolutional layers, resulting in a hybrid quantum model named CRPQNN-ViT. This integration aims to deploy quantum computational advantages such as parallelism and entanglement for improved feature representation and classification performance.
- Both the classical (CRPCNN-ViT) and quantum (CRPQNN-ViT) models are employed for binary (polyp or normal) and multi-class classification (hyperplastic or adenoma or serrated or normal).
- A detailed comparative analysis is conducted between the CRPCNN-ViT and CRPQNN-ViT models. Performance is evaluated using standard classification metric, as well as computational complexity parameters to highlight the trade-offs between classical and quantum-enhanced models in practical deployment scenarios.
- An ablation study is performed on the CRPQNN-ViT model to systematically evaluate the impact of quantum components on CRP-ViT architectures.
1.7. Outline of This Article
2. Materials and Methods
2.1. Phase 1: Binary Classification
2.2. Phase 2: Multi-Classification
2.3. Proposed Architecture
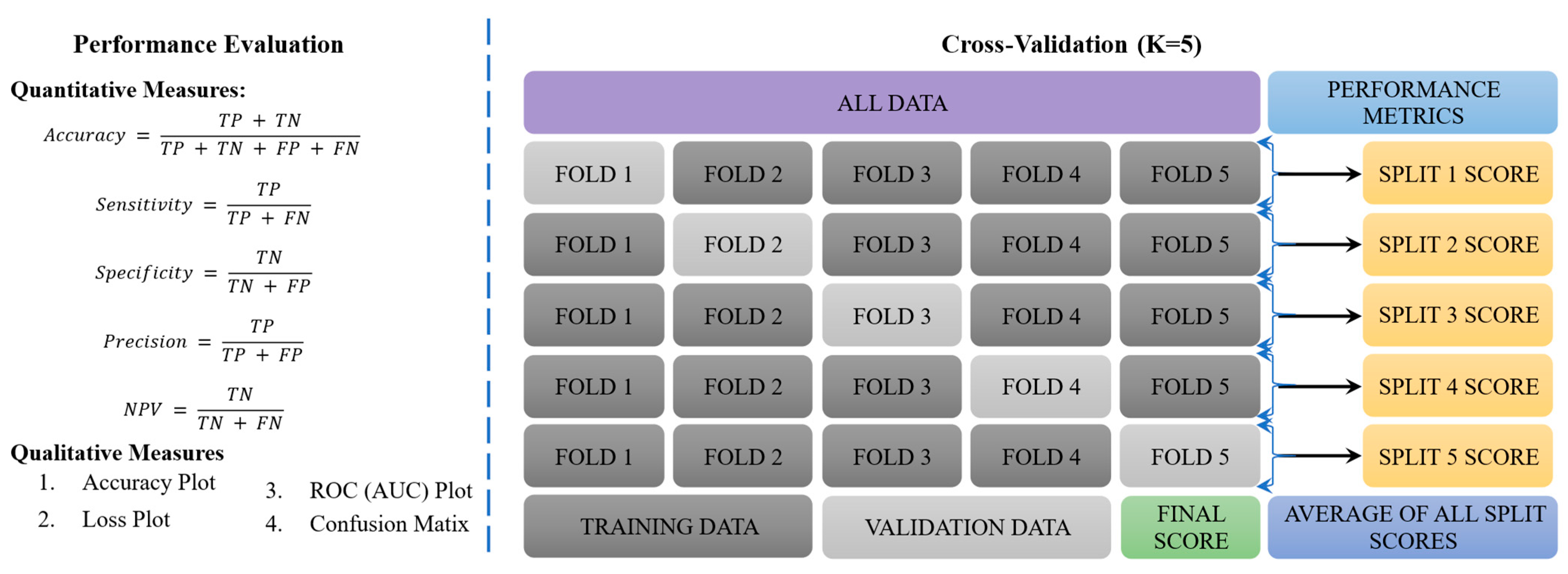
2.4. Performance Evaluation and Cross-Validation
2.5. Comparative Analysis Between CNN and QNN
3. Results
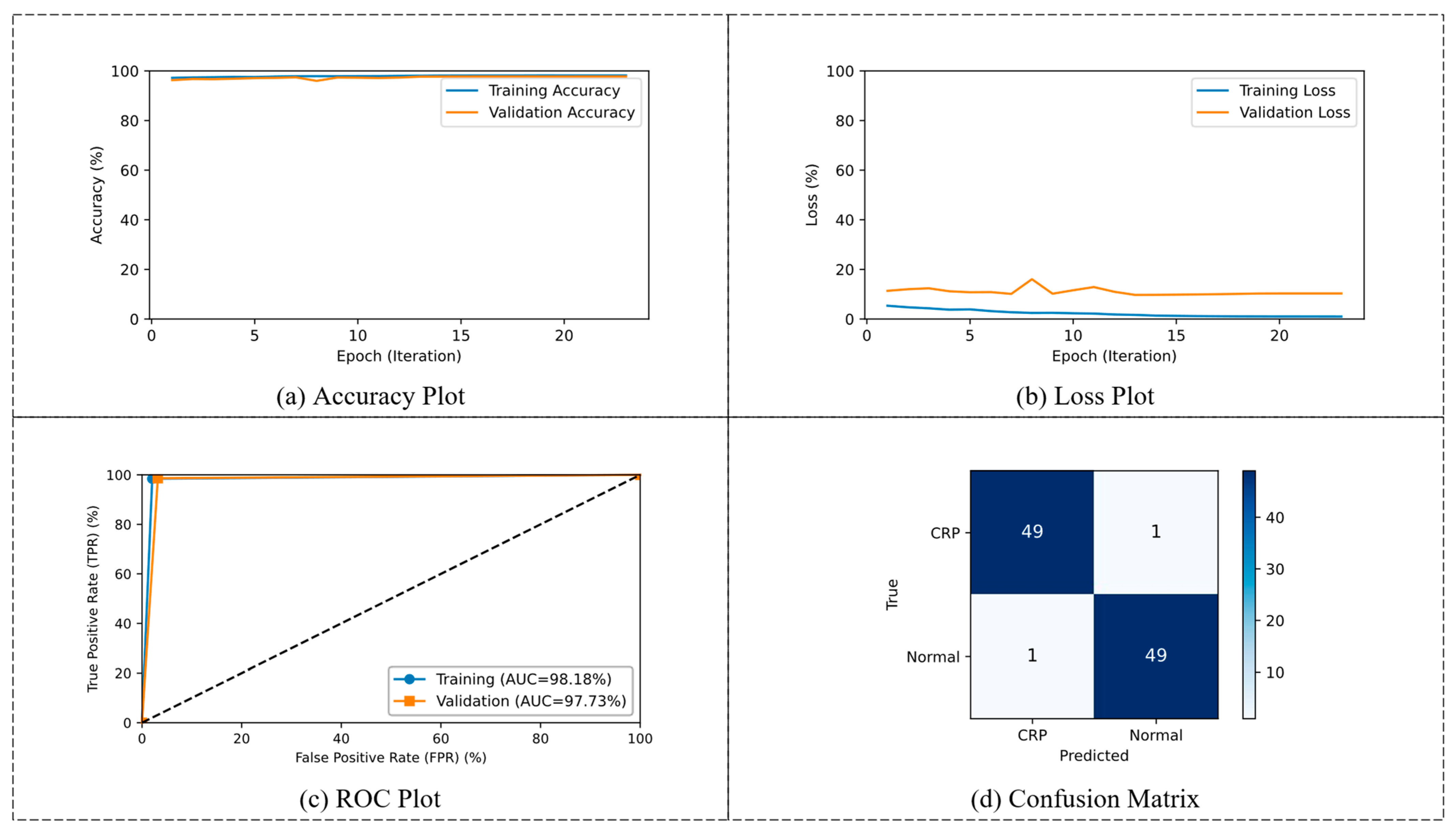
3.1. Phase 1: Binary Classification
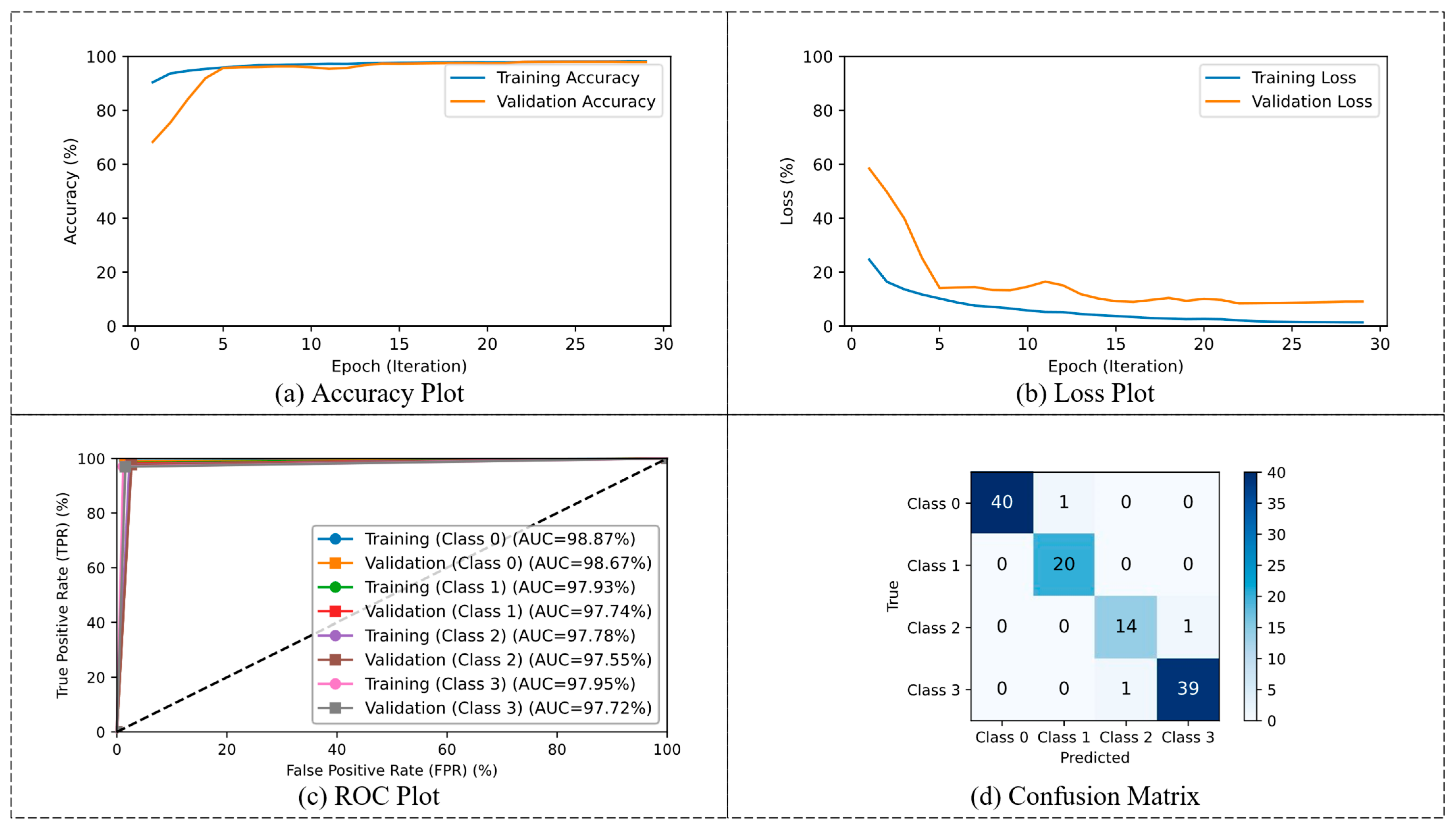
3.2. Phase 2: Multi-Classification
4. Discussion
4.1. Phase 1: Binary Classification
4.2. Phase 2: Multi-Classification
4.3. Challenges and Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marabotto, E.; Kayali, S.; Buccilli, S.; Levo, F.; Bodini, G.; Giannini, E.G.; Savarino, V.; Savarino, E.V. Colorectal cancer in inflammatory bowel diseases: Epidemiology and prevention: A review. Cancers 2022, 14, 4254. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, B.A.; Noujaim, M.; Roper, J. Cause, epidemiology, and histology of polyps and pathways to colorectal cancer. Gastrointest. Endosc. Clin. 2022, 32, 177–194. [Google Scholar] [CrossRef] [PubMed]
- Kanth, P.; Inadomi, J.M. Screening and prevention of colorectal cancer. BMJ 2021, 374, n1855. [Google Scholar] [CrossRef] [PubMed]
- Selvaraj, J.; Umapathy, S. CRPU-NET: A deep learning model based semantic segmentation for the detection of colorectal polyp in lower gastrointestinal tract. Biomed. Phys. Eng. Express 2023, 10, 015018. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wei, X.; Feng, X.; Liu, Y.; Feng, G.; Du, Y. Repeatability of radiomics studies in colorectal cancer: A systematic review. BMC Gastroenterol. 2023, 23, 125. [Google Scholar] [CrossRef] [PubMed]
- Porter, R.J.; Din, S.; Bankhead, P.; Oniscu, A.; Arends, M.J. QuPath algorithm accurately identifies MLH1-deficient inflammatory bowel disease-associated colorectal cancers in a tissue microarray. Diagnostics 2023, 13, 1890. [Google Scholar] [CrossRef] [PubMed]
- Karalis, V.D. The integration of artificial intelligence into clinical practice. Appl. Biosci. 2024, 3, 14–44. [Google Scholar] [CrossRef]
- Sharma, N.; Kaushik, P. Integration of AI in Healthcare Systems—A Discussion of the Challenges and Opportunities of Integrating AI in Healthcare Systems for Disease Detection and Diagnosis. In AI in Disease Detection: Advancements and Applications; Wiley: Hoboken, NJ, USA, 2025; pp. 239–263. [Google Scholar] [CrossRef]
- Uddin, K.M.M.; Bhuiyan, M.T.A.; Saad, M.N.; Islam, A.; Islam, M.M. Ensemble Machine Learning-Based Approach to Predict Cervical Cancer with Hyperparameter Tuning and Model Explainability. Biomed. Mater. Devices 2025, 3, 1463–1490. [Google Scholar] [CrossRef]
- Ilmi, H.R.; Khalaf, E.T. Blaze Pose Graph Neural Networks and Long Short-Term Memory for Yoga Posture Recognition. IJACI Int. J. Adv. Comput. Inform. 2025, 1, 79–88. [Google Scholar] [CrossRef]
- Yu, H.; Yang, L.T.; Zhang, Q.; Armstrong, D.; Deen, M.J. Convolutional neural networks for medical image analysis: State-of-the-art, comparisons, improvement and perspectives. Neurocomputing 2021, 444, 92–110. [Google Scholar] [CrossRef]
- Taye, M.M. Theoretical understanding of convolutional neural network: Concepts, architectures, applications, future directions. Computation 2023, 11, 52. [Google Scholar] [CrossRef]
- Wei, H.; Yi, D.; Hu, S.; Zhu, G.; Ding, Y.; Pang, M. Multi-granularity classification of upper gastrointestinal endoscopic images. Neurocomputing 2025, 626, 129564. [Google Scholar] [CrossRef]
- Hassija, V.; Palanisamy, B.; Chatterjee, A.; Mandal, A.; Chakraborty, D.; Pandey, A.; Chalapathi, G.; Kumar, D. Transformers for Vision: A Survey on Innovative Methods for Computer Vision. IEEE Access 2025, 13, 95496–95523. [Google Scholar] [CrossRef]
- Ali, A.M.; Benjdira, B.; Koubaa, A.; El-Shafai, W.; Khan, Z.; Boulila, W. Vision transformers in image restoration: A survey. Sensors 2023, 23, 2385. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN variants for computer vision: History, architecture, application, challenges and future scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
- Davoodi, P.; Ezoji, M.; Sadeghnejad, N. Classification of natural images inspired by the human visual system. Neurocomputing 2023, 518, 60–69. [Google Scholar] [CrossRef]
- Chen, L.; Li, S.; Bai, Q.; Yang, J.; Jiang, S.; Miao, Y. Review of image classification algorithms based on convolutional neural networks. Remote Sens. 2021, 13, 4712. [Google Scholar] [CrossRef]
- Cong, S.; Zhou, Y. A review of convolutional neural network architectures and their optimizations. Artif. Intell. Rev. 2023, 56, 1905–1969. [Google Scholar] [CrossRef]
- Elharrouss, O.; Akbari, Y.; Almadeed, N.; Al-Maadeed, S. Backbones-review: Feature extractor networks for deep learning and deep reinforcement learning approaches in computer vision. Comput. Sci. Rev. 2024, 53, 100645. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Zafar, A.; Aamir, M.; Mohd Nawi, N.; Arshad, A.; Riaz, S.; Alruban, A.; Dutta, A.K.; Almotairi, S. A comparison of pooling methods for convolutional neural networks. Appl. Sci. 2022, 12, 8643. [Google Scholar] [CrossRef]
- He, L.; Wang, M. SliceSamp: A Promising Downsampling Alternative for Retaining Information in a Neural Network. Appl. Sci. 2023, 13, 11657. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhang, Y.; Han, X.; Deveci, M.; Parmar, M. A review of convolutional neural networks in computer vision. Artif. Intell. Rev. 2024, 57, 99. [Google Scholar] [CrossRef]
- Ahmed, S.F.; Alam, M.S.B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Mofijur, M.; Shawkat Ali, A.; Gandomi, A.H. Deep learning modelling techniques: Current progress, applications, advantages, and challenges. Artif. Intell. Rev. 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
- Vakalopoulou, M.; Christodoulidis, S.; Burgos, N.; Colliot, O.; Lepetit, V. Deep learning: Basics and convolutional neural networks (CNNs). In Machine Learning for Brain Disorders; Springer Nature: New York, NY, USA, 2023; pp. 77–115. [Google Scholar]
- Reyad, M.; Sarhan, A.M.; Arafa, M. A modified Adam algorithm for deep neural network optimization. Neural Comput. Appl. 2023, 35, 17095–17112. [Google Scholar] [CrossRef]
- Hassan, E.; Shams, M.Y.; Hikal, N.A.; Elmougy, S. The effect of choosing optimizer algorithms to improve computer vision tasks: A comparative study. Multimed. Tools Appl. 2023, 82, 16591–16633. [Google Scholar] [CrossRef] [PubMed]
- Seetohul, V.; Jahankhani, H.; Kendzierskyj, S.; Will Arachchige, I.S. Quantum Reinforcement Learning: Advancing AI Agents Through Quantum Computing. In Space Law Principles and Sustainable Measures; Springer Nature: Berlin/Heidelberg, Germany, 2024; pp. 55–73. [Google Scholar]
- Barreto, A.G.; Fanchini, F.F.; Papa, J.P.; de Albuquerque, V.H.C. Why consider quantum instead classical pattern recognition techniques? Appl. Soft Comput. 2024, 165, 112096. [Google Scholar] [CrossRef]
- Innan, N.; Behera, B.K.; Al-Kuwari, S.; Farouk, A. QNN-VRCS: A Quantum Neural Network for Vehicle Road Cooperation Systems. IEEE Trans. Intell. Transp. Syst. 2025, 1–10. [Google Scholar] [CrossRef]
- Meghanath, A.; Das, S.; Behera, B.K.; Khan, M.A.; Al-Kuwari, S.; Farouk, A. QDCNN: Quantum Deep Learning for Enhancing Safety and Reliability in Autonomous Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2025, 1–11. [Google Scholar] [CrossRef]
- Acampora, G.; Schiattarella, R. Deep neural networks for quantum circuit mapping. Neural Comput. Appl. 2021, 33, 13723–13743. [Google Scholar] [CrossRef]
- Khrennikov, A. Roots of quantum computing supremacy: Superposition, entanglement, or complementarity? Eur. Phys. J. Spec. Top. 2021, 230, 1053–1057. [Google Scholar] [CrossRef]
- González, F.A.; Vargas-Calderón, V.; Vinck-Posada, H. Classification with quantum measurements. J. Phys. Soc. Jpn. 2021, 90, 044002. [Google Scholar] [CrossRef]
- Guarasci, R.; De Pietro, G.; Esposito, M. Quantum natural language processing: Challenges and opportunities. Appl. Sci. 2022, 12, 5651. [Google Scholar] [CrossRef]
- Hur, T.; Kim, L.; Park, D.K. Quantum convolutional neural network for classical data classification. Quantum Mach. Intell. 2022, 4, 3. [Google Scholar] [CrossRef]
- Hermans, S.; Pompili, M.; Beukers, H.; Baier, S.; Borregaard, J.; Hanson, R. Qubit teleportation between non-neighbouring nodes in a quantum network. Nature 2022, 605, 663–668. [Google Scholar] [CrossRef] [PubMed]
- Hughes, C.; Isaacson, J.; Perry, A.; Sun, R.F.; Turner, J.; Hughes, C.; Isaacson, J.; Perry, A.; Sun, R.F.; Turner, J. What is a qubit? In Quantum Computing for the Quantum Curious; Springer Nature: Berlin/Heidelberg, Germany, 2021; pp. 7–16. [Google Scholar]
- Ovalle-Magallanes, E.; Alvarado-Carrillo, D.E.; Avina-Cervantes, J.G.; Cruz-Aceves, I.; Ruiz-Pinales, J. Quantum angle encoding with learnable rotation applied to quantum–classical convolutional neural networks. Appl. Soft Comput. 2023, 141, 110307. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Chen, C.; Jiang, R.; Huang, W. Development of variational quantum deep neural networks for image recognition. Neurocomputing 2022, 501, 566–582. [Google Scholar] [CrossRef]
- Fasulo, E.; D’Amico, F.; Zilli, A.; Furfaro, F.; Cicerone, C.; Parigi, T.L.; Peyrin-Biroulet, L.; Danese, S.; Allocca, M. Advancing Colorectal Cancer Prevention in Inflammatory Bowel Disease (IBD): Challenges and Innovations in Endoscopic Surveillance. Cancers 2024, 17, 60. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.; Muzammil, M.A.; Dahiya, D.S.; Ali, F.; Yasin, S.; Hanif, W.; Gangwani, M.K.; Aziz, M.; Khalaf, M.; Basuli, D. Artificial intelligence in gastrointestinal endoscopy: A comprehensive review. Ann. Gastroenterol. 2024, 37, 133. [Google Scholar] [CrossRef] [PubMed]
- Tontini, G.E.; Rimondi, A.; Vernero, M.; Neumann, H.; Vecchi, M.; Bezzio, C.; Cavallaro, F. Artificial intelligence in gastrointestinal endoscopy for inflammatory bowel disease: A systematic review and new horizons. Ther. Adv. Gastroenterol. 2021, 14, 17562848211017730. [Google Scholar] [CrossRef] [PubMed]
- Urban, G.; Tripathi, P.; Alkayali, T.; Mittal, M.; Jalali, F.; Karnes, W.; Baldi, P. Deep learning localizes and identifies polyps in real time with 96% accuracy in screening colonoscopy. Gastroenterology 2018, 155, 1069–1078.e8. [Google Scholar] [CrossRef] [PubMed]
- Krenzer, A.; Heil, S.; Fitting, D.; Matti, S.; Zoller, W.G.; Hann, A.; Puppe, F. Automated classification of polyps using deep learning architectures and few-shot learning. BMC Med. Imaging 2023, 23, 59. [Google Scholar] [CrossRef] [PubMed]
- Balasubramani, S.; Renjith, P.; Kavisankar, L.; Rajavel, R.; Malarvel, M.; Shankar, A. A Quantum-Enhanced Artificial Neural Network Model for Efficient Medical Image Compression. IEEE Access 2025, 13, 31809–31828. [Google Scholar] [CrossRef]
- Yengec-Tasdemir, S.B.; Aydin, Z.; Akay, E.; Dogan, S.; Yilmaz, B. An effective colorectal polyp classification for histopathological images based on supervised contrastive learning. Comput. Biol. Med. 2024, 172, 108267. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, P.; Sharma, V.; Prakash, A.J.; Bhuyan, M.K.; Patro, K.K.; Samee, N.A.; Alamro, H.; Iwahori, Y.; Tadeusiewicz, R.; Acharya, U.R. Semi-supervised generative adversarial networks for improved colorectal polyp classification using histopathological images. Inf. Sci. 2024, 658, 120033. [Google Scholar] [CrossRef]
- De Carvalho, T.; Kader, R.; Brandao, P.; Lovat, L.B.; Mountney, P.; Stoyanov, D. NICE polyp feature classification for colonoscopy screening. Int. J. Comput. Assist. Radiol. Surg. 2025, 20, 1015–1024. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Haq, E.U.; Yong, Q.; Yuan, Z.; Jianjun, H.; Haq, R.U.; Qin, X. Accurate multiclassification and segmentation of gastric cancer based on a hybrid cascaded deep learning model with a vision transformer from endoscopic images. Inf. Sci. 2024, 670, 120568. [Google Scholar] [CrossRef]
- Awujoola, J.O.; Enem, T.A.; Owolabi, J.A.; Akusu, O.C.; Abioye, O.; AbidemiAwujoola, E.; OlayinkaAdelegan, R. Exploring the Intersection of Quantum Neural Networks and Classical Neural Networks for Early Cancer Identification. In Quantum Computing; Auerbach Publications: Abingdon-on-Thames, UK, 2025; pp. 147–169. [Google Scholar]
- Khan, M.A.; Aman, M.N.; Sikdar, B. Beyond bits: A review of quantum embedding techniques for efficient information processing. IEEE Access 2024, 12, 46118–46137. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Is quantum advantage the right goal for quantum machine learning? Prx Quantum 2022, 3, 030101. [Google Scholar] [CrossRef]
- Selvaraj, J.; Umapathy, S.; Rajesh, N.A. Artificial intelligence based real time colorectal cancer screening study: Polyp segmentation and classification using multi-house database. Biomed. Signal Process. Control 2025, 99, 106928. [Google Scholar] [CrossRef]
- Selvaraj, J.; Sadaf, K.; Aslam, S.M.; Umapathy, S. Multiclassification of Colorectal Polyps from Colonoscopy Images Using AI for Early Diagnosis. Diagnostics 2025, 15, 1285. [Google Scholar] [CrossRef] [PubMed]
- Bernal, J.; Sánchez, J.; Vilarino, F. Towards automatic polyp detection with a polyp appearance model. Pattern Recognit. 2012, 45, 3166–3182. [Google Scholar] [CrossRef]
- Bernal, J.; Sánchez, F.J.; Fernández-Esparrach, G.; Gil, D.; Rodríguez, C.; Vilariño, F. WM-DOVA maps for accurate polyp highlighting in colonoscopy: Validation vs. saliency maps from physicians. Comput. Med. Imaging Graph. 2015, 43, 99–111. [Google Scholar] [CrossRef] [PubMed]
- Mesejo, P.; Pizarro, D.; Abergel, A.; Rouquette, O.; Beorchia, S.; Poincloux, L.; Bartoli, A. Computer-aided classification of gastrointestinal lesions in regular colonoscopy. IEEE Trans. Med. Imaging 2016, 35, 2051–2063. [Google Scholar] [CrossRef] [PubMed]
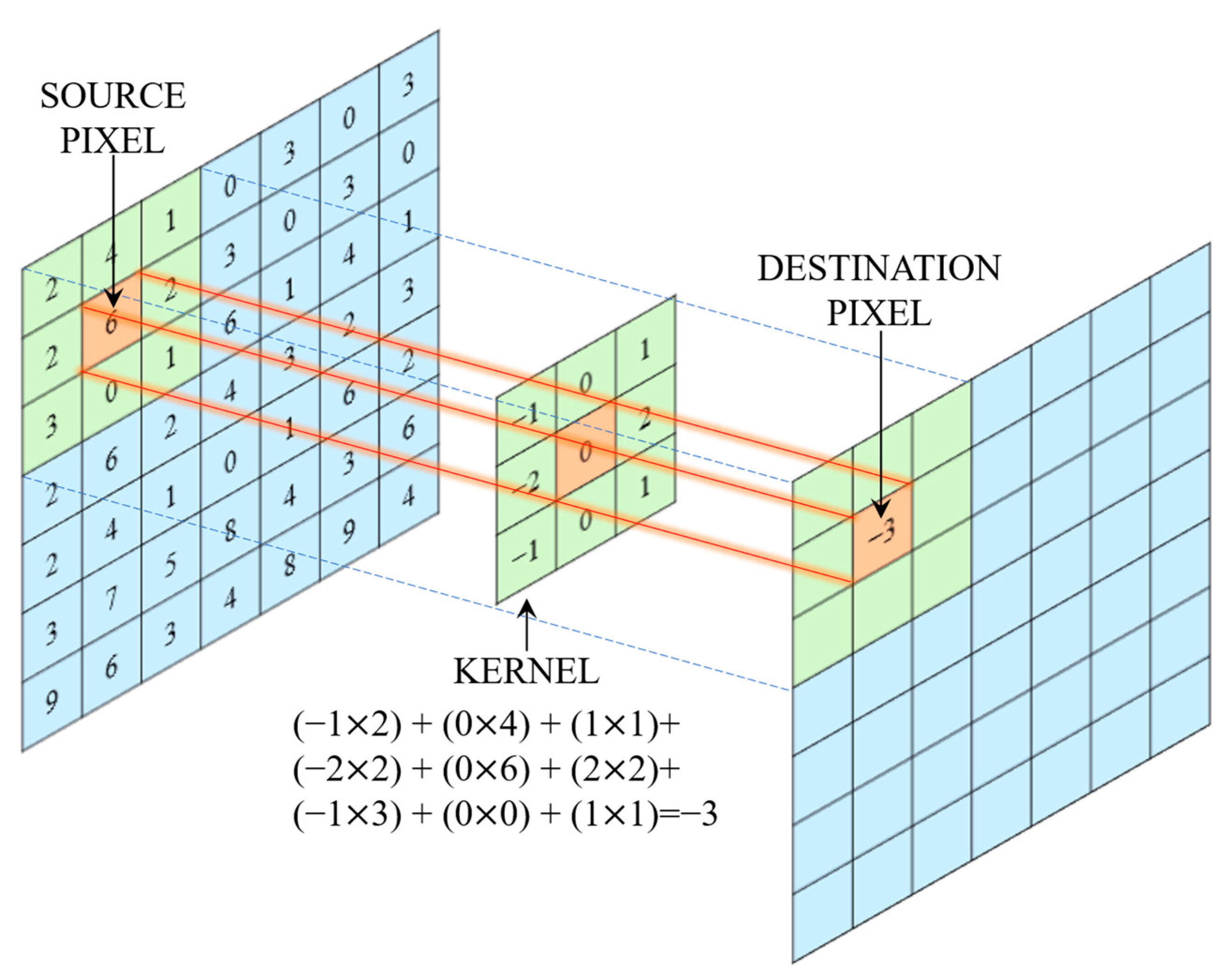
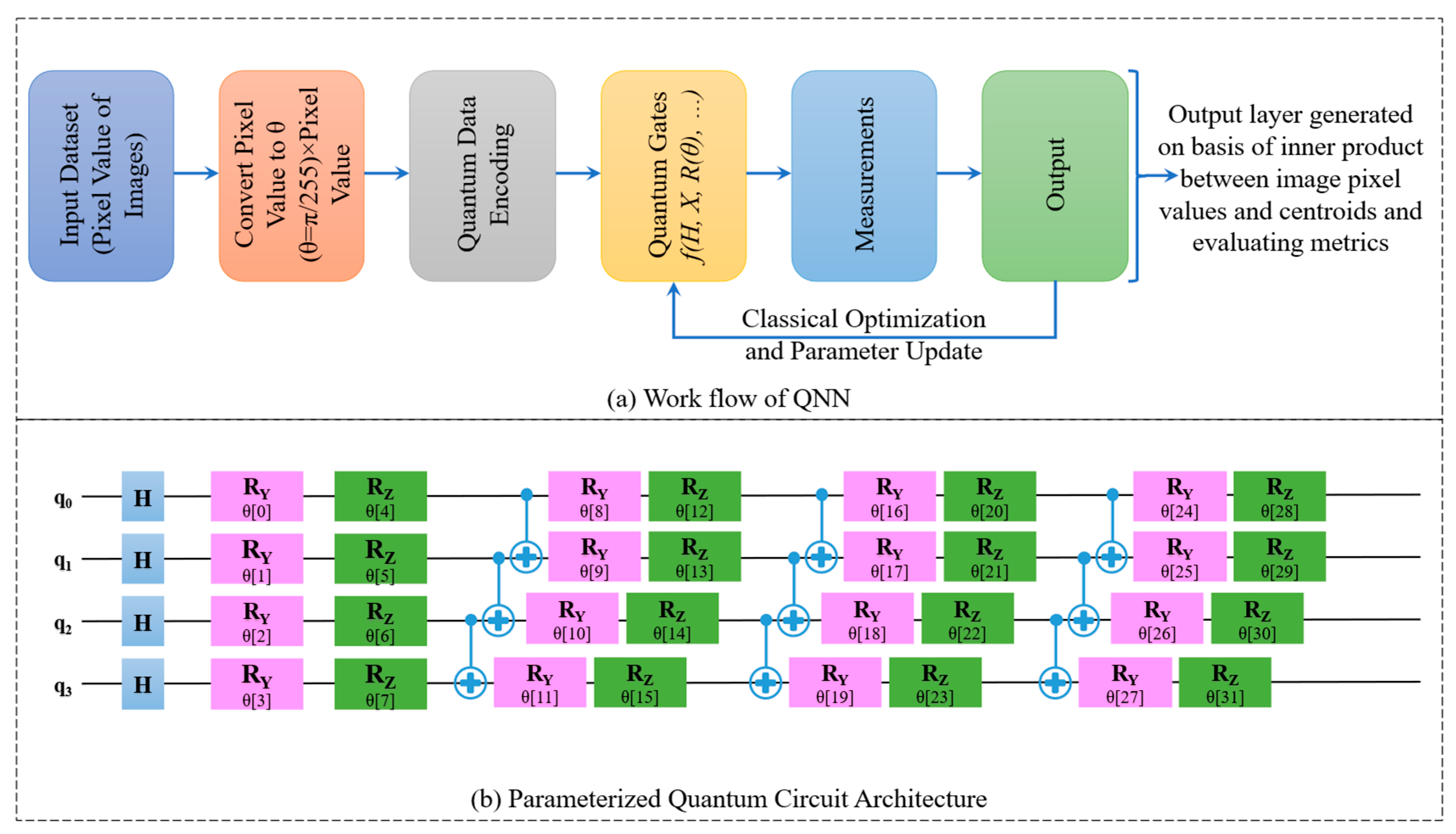

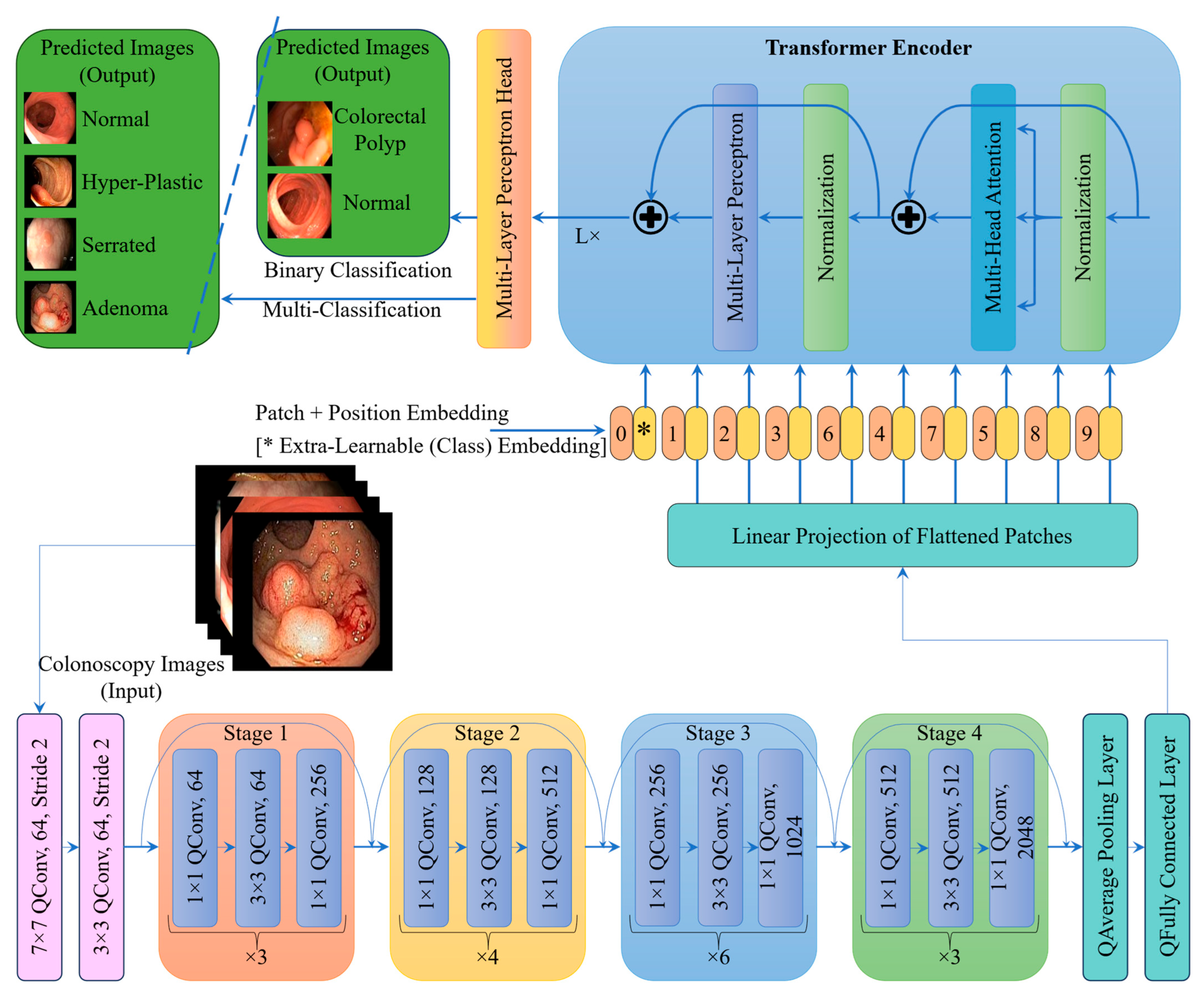
| Stage | Layer Type | Details/Description | No. of Layers | Output Size |
|---|---|---|---|---|
| Input | Quantum-Encoded Input Image | 256 × 256 × 3 | – | 256 × 256 × 3 |
| Stage 0 | Quantum Conv + Quantum Pooling | 7 × 7 QConv, 64 filters, stride 2 + 3 × 3 QPool | 2 | 56 × 56 × 64 |
| Stage 1 | Quantum Conv Block + 2 Identity QBlocks | [1 × 1, 64] → [3 × 3, 64] → [1 × 1, 256] | 3 blocks (9 layers) | 56 × 56 × 256 |
| Stage 2 | Quantum Conv Block + 3 Identity QBlocks | [1 × 1, 128] → [3 × 3, 128] → [1 × 1, 512] | 4 blocks (12 layers) | 28 × 28 × 512 |
| Stage 3 | Quantum Conv Block + 5 Identity QBlocks | [1 × 1, 256] → [3 × 3, 256] → [1 × 1, 1024] | 6 blocks (18 layers) | 14 × 14 × 1024 |
| Stage 4 | Quantum Conv Block + 2 Identity QBlocks | [1 × 1, 512] → [3 × 3, 512] → [1 × 1, 2048] | 3 blocks (9 layers) | 7 × 7 × 2048 |
| Pooling | Quantum Global Average Pooling | Reduces feature map to 1 × 1 × 2048 | 1 | 1 × 1 × 2048 |
| FC Layer | Quantum Fully Connected + QSigmoid/QSoftmax | Dense layer with QSigmoid/QSoftmax (intermediate feature vector) | 1 | 2048 or custom size |
| Patch Embedding | Patchify + Linear Projection | Convert 2D features to patch tokens (e.g., 16 × 16 patches) | 1 | N × D (e.g., 196 × 768) |
| Transformer Encoder | Multi-Head Self-Attention + MLP | Multiple transformer blocks with LayerNorm and MLP | 12 blocks typical | N × D (e.g., 196 × 768) |
| Classification Head | MLP Head + Sigmoid for Binary/ MLP Head + Softmax for Multi-Class | Final classification from [CLS] token | 1 | 2 for binary/ 4 for multi-class |
| Task | Epoch | Accuracy | Sensitivity | Specificity | Precision | NPV |
|---|---|---|---|---|---|---|
| Training | 23 | 98.18 | 98.41 | 97.95 | 97.96 | 98.4 |
| Validation | 97.73 | 98.64 | 96.82 | 96.88 | 98.61 |
| K-Fold | Accuracy | Sensitivity | Specificity | Precision | NPV |
|---|---|---|---|---|---|
| K = 1 | 98.18 | 99.09 | 97.27 | 97.27 | 99.07 |
| K = 2 | 97.95 | 99.09 | 96.82 | 96.82 | 99.07 |
| K = 3 | 97.27 | 98.18 | 96.36 | 96.36 | 98.15 |
| K = 4 | 97.5 | 98.64 | 96.36 | 96.36 | 98.6 |
| K = 5 | 97.73 | 98.64 | 96.82 | 96.82 | 98.61 |
| Mean ± SD | 97.73 ± 0.31 | 98.73 ± 0.38 | 96.73 ± 0.33 | 96.73 ± 0.33 | 98.70 ± 0.36 |
| K-Fold | Accuracy | Sensitivity | Specificity | Precision | NPV |
|---|---|---|---|---|---|
| 80:20 Split (A) | 97.73 | 98.64 | 96.82 | 96.88 | 98.61 |
| 5-Fold (B) | 97.73 | 98.73 | 96.73 | 96.73 | 98.7 |
| Difference Between (A and B) | 00.00 | 0.09 | 0.09 | 0.15 | 0.09 |
| Optimizers | Epoch | Class | Accuracy | Sensitivity | Specificity | Precision | NPV | Overall Accuracy |
|---|---|---|---|---|---|---|---|---|
| Training | 29/50 | 0 | 99.15 | 98.59 | 99.72 | 99.15 | 99.53 | 98.13 |
| 1 | 98.48 | 97.38 | 99.49 | 98.48 | 99.11 | |||
| 2 | 97.82 | 97.73 | 99.27 | 97.82 | 99.24 | |||
| 3 | 97.06 | 98.84 | 99.03 | 97.06 | 99.62 | |||
| Validation | 0 | 98.86 | 98.49 | 99.62 | 98.87 | 98.86 | 97.92 | |
| 1 | 98.11 | 97.37 | 98.49 | 98.11 | 98.11 | |||
| 2 | 97.73 | 97.36 | 98.11 | 97.73 | 97.73 | |||
| 3 | 96.97 | 98.46 | 95.09 | 96.97 | 96.97 |
| K-Fold | Class | Accuracy | Sensitivity | Specificity | Precision | NPV | Overall Accuracy |
|---|---|---|---|---|---|---|---|
| K = 1 | 0 | 98.48 | 98.48 | 99.15 | 98.48 | 99.15 | 97.54 |
| 1 | 96.64 | 96.64 | 99.05 | 96.64 | 99.05 | ||
| 2 | 96.98 | 96.98 | 98.86 | 97.36 | 98.84 | ||
| 3 | 98.07 | 98.07 | 97.59 | 96.21 | 98.86 | ||
| K = 2 | 0 | 98.5 | 98.5 | 99.62 | 99.62 | 98.5 | 98.39 |
| 1 | 97.75 | 97.75 | 98.86 | 98.49 | 98.12 | ||
| 2 | 98.11 | 98.11 | 98.11 | 98.11 | 98.11 | ||
| 3 | 99.22 | 99.22 | 98.42 | 96.97 | 99.36 | ||
| K = 3 | 0 | 98.49 | 98.49 | 98.86 | 98.49 | 98.86 | 97.82 |
| 1 | 97.74 | 97.74 | 98.11 | 98.11 | 97.74 | ||
| 2 | 96.98 | 96.98 | 97.35 | 97.35 | 96.98 | ||
| 3 | 98.08 | 98.08 | 96.97 | 96.97 | 98.08 | ||
| K = 4 | 0 | 98.5 | 98.5 | 99.24 | 99.24 | 98.5 | 98.2 |
| 1 | 98.11 | 98.11 | 98.48 | 98.48 | 98.11 | ||
| 2 | 97.73 | 97.73 | 97.73 | 97.73 | 97.73 | ||
| 3 | 98.47 | 98.47 | 97.35 | 97.35 | 98.47 | ||
| K = 5 | 0 | 98.12 | 98.12 | 98.86 | 98.86 | 98.12 | 97.73 |
| 1 | 97.36 | 97.36 | 97.73 | 97.73 | 97.36 | ||
| 2 | 97.35 | 97.35 | 97.35 | 97.35 | 97.35 | ||
| 3 | 98.08 | 98.08 | 96.97 | 96.97 | 98.08 | ||
| Mean ± SD | 0 | 98.42 ± 0.17 | 98.42 ± 0.17 | 99.15 ± 0.32 | 98.94 ± 0.49 | 98.63 ± 0.39 | 97.94 ± 0.35 |
| 1 | 97.52 ± 0.56 | 97.52 ± 0.56 | 98.45 ± 0.54 | 97.89 ± 0.77 | 98.08 ± 0.63 | ||
| 2 | 97.43 ± 0.49 | 97.43 ± 0.49 | 97.88 ± 0.63 | 97.58 ± 0.34 | 97.80 ± 0.72 | ||
| 3 | 98.38 ± 0.50 | 98.38 ± 0.50 | 97.46 ± 0.60 | 96.89 ± 0.42 | 98.57 ± 0.55 |
| Method | Class | Accuracy | Sensitivity | Specificity | Precision | NPV | Overall Accuracy |
|---|---|---|---|---|---|---|---|
| 80:20 Split (A) | 0 | 98.86 | 98.49 | 99.62 | 98.87 | 98.86 | 97.92 |
| 1 | 98.11 | 97.74 | 98.49 | 98.11 | 98.11 | ||
| 2 | 97.73 | 97.36 | 98.11 | 97.73 | 97.73 | ||
| 3 | 96.97 | 98.08 | 95.85 | 96.97 | 96.97 | ||
| 5-Fold (B) | 0 | 98.42 | 98.42 | 99.15 | 98.94 | 98.63 | 97.94 |
| 1 | 97.52 | 97.52 | 98.45 | 97.89 | 98.08 | ||
| 2 | 97.43 | 97.43 | 97.88 | 97.58 | 97.80 | ||
| 3 | 98.38 | 98.38 | 97.46 | 96.89 | 98.57 | ||
| Difference Between (A and B) | 0 | 0.44 | 0.07 | 0.47 | −0.07 | 0.23 | −0.02 |
| 1 | 0.59 | 0.22 | 0.04 | 0.22 | 0.03 | ||
| 2 | 0.3 | −0.07 | 0.23 | 0.15 | −0.07 | ||
| 3 | −1.41 | −0.30 | −1.61 | 0.08 | −1.60 |
| Method | Model | Computational Complexity/Load | Time | |||
|---|---|---|---|---|---|---|
| Total Parameters (Million) | MACs (Giga) | FLOPs (Giga) | Training and Validation Per Image (Milliseconds) | Testing Per Image (Milliseconds) | ||
| CRPCNN-ViT [56] | CNN | 132 | 11.6 | 23.2 | 17.69 | 3.58 |
| CRPQNN-ViT | QNN | 86 | 8.5 | 17 | 10.61 | 1.79 |
| Method | Epoch | Training | Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Sensitivity | Specificity | Precision | NPV | Accuracy | Sensitivity | Specificity | Precision | NPV | ||
| CRPCNN-ViT [56] | 20 | 97.44 | 97.61 | 97.28 | 97.27 | 97.61 | 96.59 | 96.38 | 96.80 | 96.82 | 96.36 |
| CRPQNN-ViT | 23 | 98.18 | 98.41 | 97.95 | 97.96 | 98.4 | 97.73 | 98.64 | 96.82 | 96.88 | 98.61 |
| Difference | 3 | 0.74 | 0.8 | 0.67 | 0.69 | 0.79 | 1.14 | 2.26 | 0.02 | 0.06 | 2.25 |
| Method | Accuracy | Sensitivity | Specificity | Precision | NPV |
|---|---|---|---|---|---|
| CRPCNN-ViT (A) [56] | 96.60 ± 0.03 | 96.41 ± 0.03 | 96.81 ± 0.02 | 96.83 ± 0.02 | 96.37 ± 0.02 |
| CRPQNN-ViT (B) | 97.73 ± 0.31 | 98.73 ± 0.38 | 96.73 ± 0.33 | 96.73 ± 0.33 | 98.70 ± 0.36 |
| Difference Between (A and B) | +1.13 ± 0.31 | +2.32 ± 0.38 | −0.08 ± 0.33 | −0.10 ± 0.33 | +2.33 ± 0.36 |
| Method | Model | Computational Complexity/Load | Time | |||
|---|---|---|---|---|---|---|
| Total Parameters (Million) | MACs (Giga) | FLOPs (Giga) | Training and Validation Per Image (Milliseconds) | Testing Per Image (Milliseconds) | ||
| CRPCNN-ViT [57] | CNN | 132 | 11.6 | 23.2 | 18.93 | 4.20 |
| CRPQNN-ViT | QNN | 86 | 8.5 | 17 | 11.36 | 2.11 |
| Model | Epoch | Class | Training | Validation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Sensitivity | Specificity | Precision | NPV | Overall Accuracy | Accuracy | Sensitivity | Specificity | Precision | NPV | Overall Accuracy | |||
| CRPCNN-ViT [57] | 22/50 | 0 | 97.92 | 97.55 | 99.31 | 97.44 | 98.9 | 97.28 | 98.01 | 97.75 | 98.29 | 98.86 | 98.51 | 96.02 |
| 1 | 96.44 | 96.44 | 99.13 | 97.25 | 98.5 | 95.93 | 93.8 | 97.97 | 97.35 | 96.2 | ||||
| 2 | 97.16 | 97.16 | 99.15 | 96.5 | 98.75 | 96.57 | 95.08 | 96.68 | 95.08 | 97.04 | ||||
| 3 | 97.98 | 97.98 | 99.43 | 97.98 | 99 | 96.97 | 97.61 | 96.8 | 92.8 | 99.02 | ||||
| CRPQNN -ViT | 29/50 | 0 | 99.15 | 98.59 | 99.72 | 99.15 | 99.53 | 98.13 | 98.86 | 98.49 | 99.62 | 98.87 | 98.86 | 97.92 |
| 1 | 98.48 | 97.38 | 99.49 | 98.48 | 99.11 | 98.11 | 97.37 | 98.49 | 98.11 | 98.11 | ||||
| 2 | 97.82 | 97.73 | 99.27 | 97.82 | 99.24 | 97.73 | 97.36 | 98.11 | 97.73 | 97.73 | ||||
| 3 | 97.06 | 98.84 | 99.03 | 97.06 | 99.62 | 96.97 | 98.46 | 95.09 | 96.97 | 96.97 | ||||
| Difference | 7 | 0 | 1.23 | 1.04 | 0.41 | 1.71 | 0.63 | 0.85 | 0.85 | 0.74 | 1.33 | −0.01 | 0.35 | 1.9 |
| 1 | 2.04 | 0.94 | 0.36 | 1.23 | 0.61 | 2.18 | 3.57 | 0.52 | 0.76 | 1.91 | ||||
| 2 | 0.66 | 0.57 | 0.12 | 1.32 | 0.49 | 1.16 | 2.28 | 1.43 | 2.65 | 0.69 | ||||
| 3 | −0.92 | 0.86 | −0.40 | −0.92 | 0.62 | 0 | 0.85 | −1.71 | 4.17 | −2.05 | ||||
| Method | Class | Accuracy | Sensitivity | Specificity | Precision | NPV | Overall Accuracy |
|---|---|---|---|---|---|---|---|
| CRPCNN-ViT (A) [57] | 0 | 98.22 ± 0.94 | 96.87 ± 0.86 | 98.64 ± 0.85 | 97.88 ± 1.24 | 98.19 ± 0.95 | 96.27 ± 1.06 |
| 1 | 97.07 ± 1.02 | 95.24 ± 1.22 | 97.70 ± 1.21 | 96.29 ± 1.65 | 97.42 ± 0.81 | ||
| 2 | 96.77 ± 1.06 | 95.61 ± 1.04 | 97.15 ± 1.33 | 95.00 ± 1.61 | 97.94 ± 0.98 | ||
| 3 | 96.89 ± 1.55 | 97.42 ± 1.45 | 96.43 ± 1.68 | 94.09 ± 1.19 | 98.99 ± 0.69 | ||
| CRPQNN-ViT (B) | 0 | 98.42 ± 0.17 | 98.42 ± 0.17 | 99.15 ± 0.32 | 98.94 ± 0.49 | 98.63 ± 0.39 | 97.94 ± 0.35 |
| 1 | 97.52 ± 0.56 | 97.52 ± 0.56 | 98.45 ± 0.54 | 97.89 ± 0.77 | 98.08 ± 0.63 | ||
| 2 | 97.43 ± 0.49 | 97.43 ± 0.49 | 97.88 ± 0.63 | 97.58 ± 0.34 | 97.80 ± 0.72 | ||
| 3 | 98.38 ± 0.50 | 98.38 ± 0.50 | 97.46 ± 0.60 | 96.89 ± 0.42 | 98.57 ± 0.55 | ||
| Difference Between (A and B) | 0 | +0.20 ± 0.96 | +1.55 ± 0.88 | +0.51 ± 0.91 | +1.06 ± 1.34 | +0.44 ± 1.03 | +1.67 ± 1.11 |
| 1 | +0.45 ± 1.16 | +2.28 ± 1.35 | +0.75 ± 1.33 | +1.60 ± 1.83 | +0.66 ± 1.03 | ||
| 2 | +0.66 ± 1.17 | +1.82 ± 1.14 | +0.73 ± 1.47 | +2.58 ± 1.65 | −0.14 ± 1.23 | ||
| 3 | +1.49 ± 1.63 | +0.96 ± 1.55 | +1.03 ± 1.78 | +2.80 ± 1.26 | −0.42 ± 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvaraj, J.; Almutairi, F.; Aslam, S.M.; Umapathy, S. Binary and Multi-Class Classification of Colorectal Polyps Using CRP-ViT: A Comparative Study Between CNNs and QNNs. Life 2025, 15, 1124. https://doi.org/10.3390/life15071124
Selvaraj J, Almutairi F, Aslam SM, Umapathy S. Binary and Multi-Class Classification of Colorectal Polyps Using CRP-ViT: A Comparative Study Between CNNs and QNNs. Life. 2025; 15(7):1124. https://doi.org/10.3390/life15071124
Chicago/Turabian StyleSelvaraj, Jothiraj, Fadhiyah Almutairi, Shabnam M. Aslam, and Snekhalatha Umapathy. 2025. "Binary and Multi-Class Classification of Colorectal Polyps Using CRP-ViT: A Comparative Study Between CNNs and QNNs" Life 15, no. 7: 1124. https://doi.org/10.3390/life15071124
APA StyleSelvaraj, J., Almutairi, F., Aslam, S. M., & Umapathy, S. (2025). Binary and Multi-Class Classification of Colorectal Polyps Using CRP-ViT: A Comparative Study Between CNNs and QNNs. Life, 15(7), 1124. https://doi.org/10.3390/life15071124






