Learning Effects in Air Displacement Plethysmography
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. ADP Measurements
2.3. Statistical Analyses
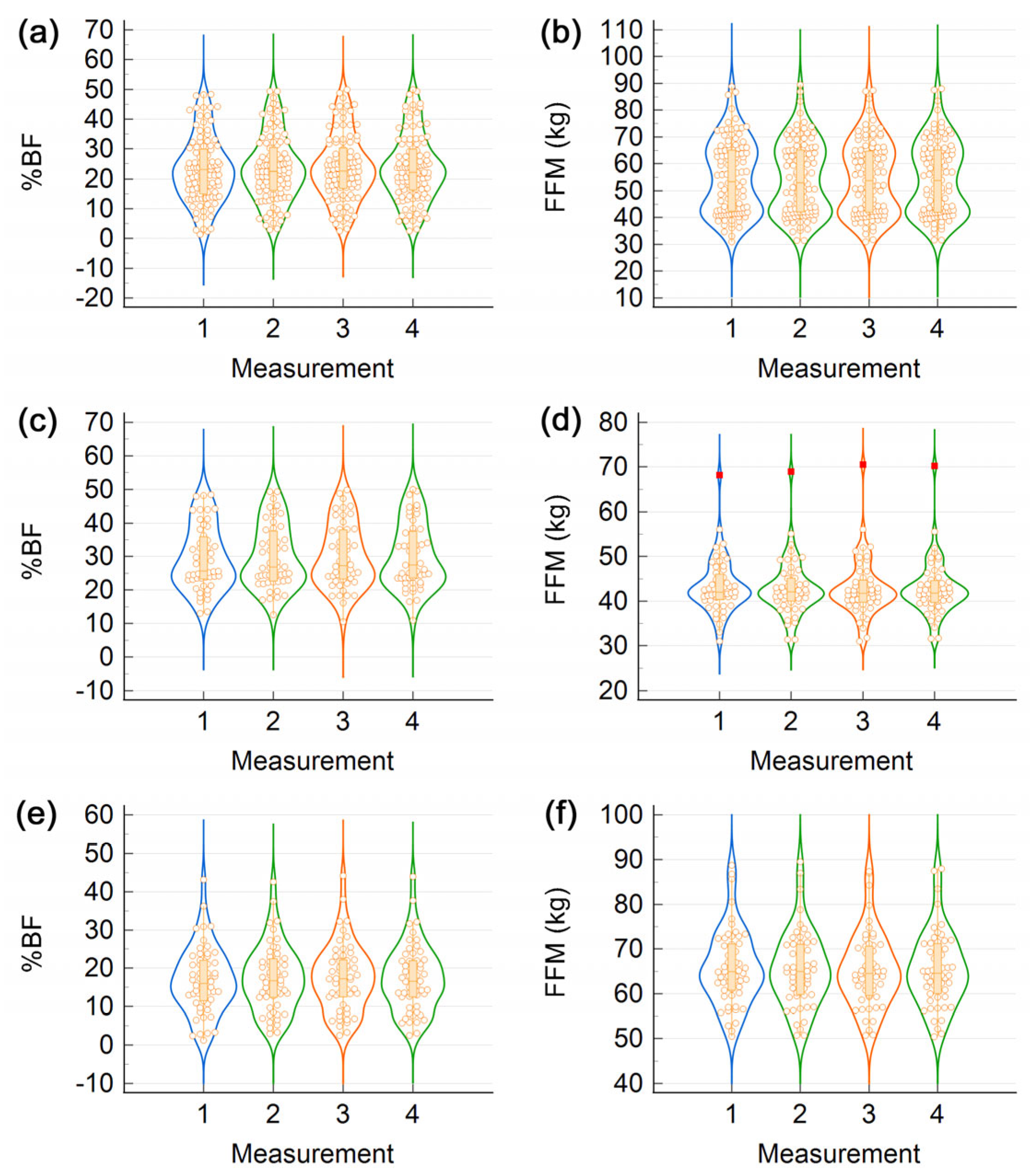
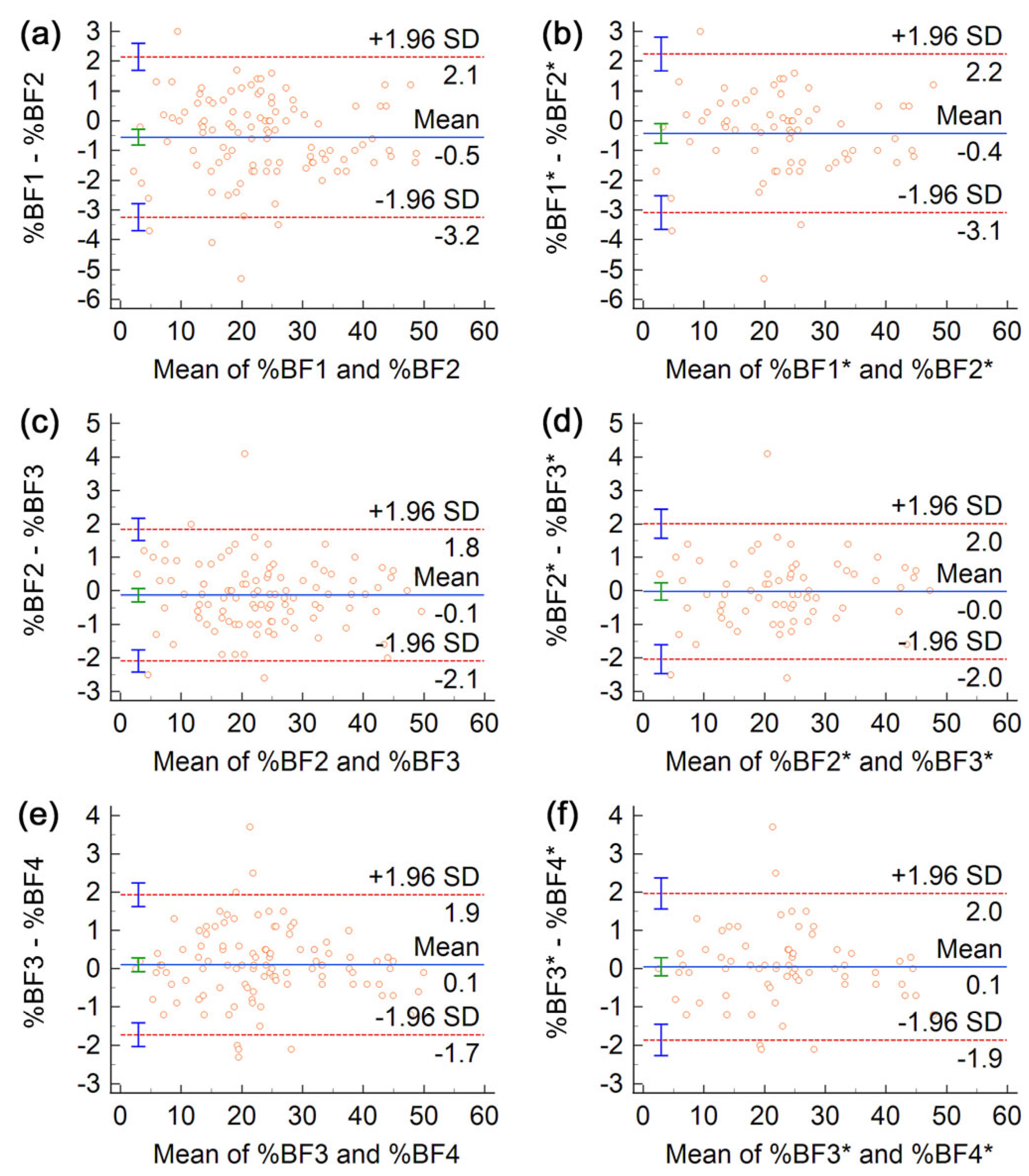
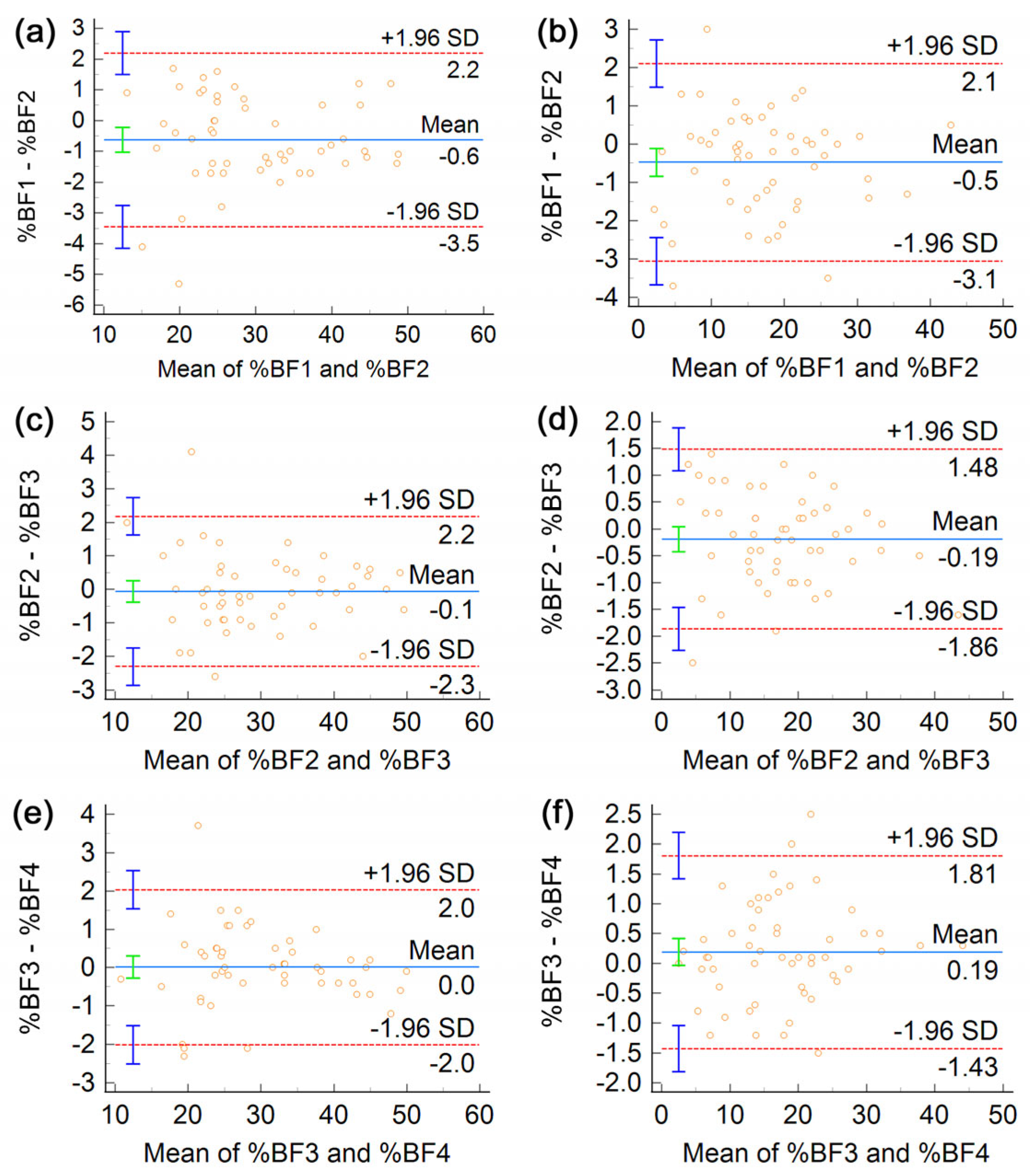
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muller, M.J.; Braun, W.; Enderle, J.; Bosy-Westphal, A. Beyond BMI: Conceptual Issues Related to Overweight and Obese Patients. Obes Facts 2016, 9, 193–205. [Google Scholar] [CrossRef]
- Heymsfield, S.; Lohman, T.G.; Wang, Z.-M.; Going, S. Human Body Composition, 2nd ed.; Human Kinetics: Chapmaign, IL, USA, 2005. [Google Scholar]
- Lohman, T.G. Skinfolds and body density and their relation to body fatness: A review. Hum. Biol. 1981, 53, 181–225. [Google Scholar]
- Müller, M.; Enderle, J.; Pourhassan, M.; Braun, W.; Eggeling, B.; Lagerpusch, M.; Glüer, C.-C.; J Kehayias, J.; Kiosz, D.; Bosy-Westphal, A. Metabolic adaptation to caloric restriction and subsequent refeeding: The Minnesota Starvation Experiment revisited. Am. J. Clin. Nutr. 2015, 102, 807–819. [Google Scholar] [CrossRef]
- Ackland, T.R.; Lohman, T.G.; Sundgot-Borgen, J.; Maughan, R.J.; Meyer, N.L.; Stewart, A.D.; Müller, W. Current status of body composition assessment in sport. Sports Med. 2012, 42, 227–249. [Google Scholar] [CrossRef]
- Blue, M.N.M.; Tinsley, G.M.; Ryan, E.D.; Smith-Ryan, A.E. Validity of Body-Composition Methods across Racial and Ethnic Populations. Adv. Nutr. 2021, 12, 1854–1862. [Google Scholar] [CrossRef] [PubMed]
- Behnke, A.R., Jr.; Feen, B.G.; Welham, W.C. The specific gravity of healthy men: Body weight ÷ volume as an index of obesity. J. Am. Med. Assoc. 1942, 118, 495–498. [Google Scholar] [CrossRef]
- Dempster, P.; Aitkens, S. A new air displacement method for the determination of human body composition. Med. Sci. Sports Exerc. 1995, 27, 1692–1697. [Google Scholar] [CrossRef]
- McCrory, M.A.; Gomez, T.D.; Bernauer, E.M.; Mole, P.A. Evaluation of a new air displacement plethysmograph for measuring human body composition. Med. Sci. Sports Exerc. 1995, 27, 1686–1691. [Google Scholar] [CrossRef]
- Fields, D.A.; Goran, M.I.; McCrory, M.A. Body-composition assessment via air-displacement plethysmography in adults and children: A review. Am. J. Clin. Nutr. 2002, 75, 453–467. [Google Scholar] [CrossRef]
- Yee, A.J.; Fuerst, T.; Salamone, L.; Visser, M.; Dockrell, M.; Van Loan, M.; Kern, M. Calibration and validation of an air-displacement plethysmography method for estimating percentage body fat in an elderly population: A comparison among compartmental models. Am. J. Clin. Nutr. 2001, 74, 637–642. [Google Scholar] [CrossRef] [PubMed]
- Biaggi, R.R.; Vollman, M.W.; Nies, M.A.; Brener, C.E.; Flakoll, P.J.; Levenhagen, D.K.; Sun, M.; Karabulut, Z.; Chen, K.Y. Comparison of air-displacement plethysmography with hydrostatic weighing and bioelectrical impedance analysis for the assessment of body composition in healthy adults. Am. J. Clin. Nutr. 1999, 69, 898–903. [Google Scholar] [CrossRef]
- Wang, Z.; Pi-Sunyer, F.X.; Kotler, D.P.; Wielopolski, L.; Withers, R.T.; Pierson, R.N., Jr.; Heymsfield, S.B. Multicomponent methods: Evaluation of new and traditional soft tissue mineral models by in vivo neutron activation analysis. Am. J. Clin. Nutr. 2002, 76, 968–974. [Google Scholar] [CrossRef] [PubMed]
- Fields, D.A.; Gunatilake, R.; Kalaitzoglou, E. Air displacement plethysmography: Cradle to grave. Nutr. Clin. Pract. 2015, 30, 219–226. [Google Scholar] [CrossRef]
- Fields, D.A.; Higgins, P.B.; Radley, D. Air-displacement plethysmography: Here to stay. Curr. Opin. Clin. Nutr. Metab. Care 2005, 8, 624–629. [Google Scholar] [CrossRef] [PubMed]
- Blue, M.N.M.; Hirsch, K.R.; Brewer, G.J.; Cabre, H.E.; Gould, L.M.; Tinsley, G.M.; Ng, B.K.; Ryan, E.D.; Padua, D.; Smith-Ryan, A.E. The validation of contemporary body composition methods in various races and ethnicities. Br. J. Nutr. 2022, 128, 2387–2397. [Google Scholar] [CrossRef] [PubMed]
- Tinsley, G.M. Five-component model validation of reference, laboratory and field methods of body composition assessment. Br. J. Nutr. 2020, 125, 1246–1259. [Google Scholar] [CrossRef] [PubMed]
- Nickerson, B.S.; McLester, C.N.; McLester, J.R.; Kliszczewicz, B.M. Agreement Between 2 Segmental Bioimpedance Devices, BOD POD, and DXA in Obese Adults. J. Clin. Densitom. 2020, 23, 138–148. [Google Scholar] [CrossRef]
- Nickerson, B.S.; Tinsley, G.M.; Esco, M.R. Validity of Field and Laboratory Three-Compartment Models in Healthy Adults. Med. Sci. Sports Exerc. 2019, 51, 1032–1039. [Google Scholar] [CrossRef]
- Minderico, C.S.; Silva, A.M.; Teixeira, P.J.; Sardinha, L.B.; Hull, H.R.; Fields, D.A. Validity of air-displacement plethysmography in the assessment of body composition changes in a 16-month weight loss program. Nutr. Metab. 2006, 3, 32. [Google Scholar] [CrossRef]
- Anderson, D.E. Reliability of air displacement plethysmography. J. Strength Cond. Res. 2007, 21, 169–172. [Google Scholar] [CrossRef]
- Ball, S.D. Interdevice variability in percent fat estimates using the BOD POD. Eur. J. Clin. Nutr. 2005, 59, 996–1001. [Google Scholar] [CrossRef]
- Collins, A.L.; McCarthy, H.D. Evaluation of factors determining the precision of body composition measurements by air displacement plethysmography. Eur. J. Clin. Nutr. 2003, 57, 770–776. [Google Scholar] [CrossRef] [PubMed]
- Collins, A.L.; Saunders, S.; McCarthy, H.D.; Williams, J.E.; Fuller, N.J. Within- and between-laboratory precision in the measurement of body volume using air displacement plethysmography and its effect on body composition assessment. Int. J. Obes. Relat. Metab. Disord. 2004, 28, 80–90. [Google Scholar] [CrossRef] [PubMed]
- Levenhagen, D.K.; Borel, M.J.; Welch, D.C.; Piasecki, J.H.; Piasecki, D.P.; Chen, K.Y.; Flakoll, P.J. A comparison of air displacement plethysmography with three other techniques to determine body fat in healthy adults. J. Parenter. Enter. Nutr. 1999, 23, 293–299. [Google Scholar] [CrossRef] [PubMed]
- Miyatake, N.; Nonaka, K.; Fujii, M. A new air displacement plethysmograph for the determination of Japanese body composition. Diabetes Obes. Metab. 1999, 1, 347–351. [Google Scholar] [CrossRef] [PubMed]
- Noreen, E.E.; Lemon, P.W.R. Reliability of air displacement plethysmography in a large, heterogeneous sample. Med. Sci. Sports Exerc. 2006, 38, 1505–1509. [Google Scholar] [CrossRef]
- Nuñez, C.; Kovera, A.J.; Pietrobelli, A.; Heshka, S.; Horlick, M.; Kehayias, J.J.; Wang, Z.; Heymsfield, S.B. Body composition in children and adults by air displacement plethysmography. Eur. J. Clin. Nutr. 1999, 53, 382–387. [Google Scholar] [CrossRef]
- Sardinha, L.B.; Lohman, T.G.; Teixeira, P.J.; Guedes, D.P.; Going, S.B. Comparison of air displacement plethysmography with dual-energy X-ray absorptiometry and 3 field methods for estimating body composition in middle-aged men. Am. J. Clin. Nutr. 1998, 68, 786–793. [Google Scholar] [CrossRef]
- Vescovi, J.D.; Zimmerman, S.L.; Miller, W.C.; Fernhall, B. Effects of clothing on accuracy and reliability of air displacement plethysmography. Med. Sci. Sports Exerc. 2002, 34, 282–285. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Schabort, E.J.; Hawley, J.A. Reliability of Power in Physical Performance Tests. Sports Med. 2001, 31, 211–234. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G. Measures of reliability in sports medicine and science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef] [PubMed]
- COSMED. BOD POD Gold Standard Body Composition Tracking System Operator’s Manual-P/N 210-2400 Rev. M-DCO 1765; COSMED USA, Inc.: Concord, CA, USA, 2015. [Google Scholar]
- Horhat, R.; Miclos-Balica, M.; Muntean, P.; Popa, S.; Sima, I.; Glisici, B.; Cîrja, O.; Neagu, A.; Neagu, M. The impact of subject positioning on body composition assessments by air displacement plethysmography evaluated in a heterogeneous sample. PLoS ONE 2022, 17, e0267089. [Google Scholar] [CrossRef] [PubMed]
- Peeters, M.W. Subject positioning in the BOD POD® only marginally affects measurement of body volume and estimation of percent body fat in young adult men. PLoS ONE 2012, 7, e32722. [Google Scholar] [CrossRef]
- Hintze, J.L.; Nelson, R.D. Violin Plots: A Box Plot-Density Trace Synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Bland, M.J.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Giavarina, D. Understanding Bland Altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-Y. Statistical notes for clinical researchers: Evaluation of measurement error 2: Dahlberg’s error, Bland-Altman method, and Kappa coefficient. Restor. Dent. Endod. 2013, 38, 182–185. [Google Scholar] [CrossRef]
- Ulijaszek, S.J.; Kerr, D.A. Anthropometric measurement error and the assessment of nutritional status. Br. J. Nutr. 1999, 82, 165–177. [Google Scholar] [CrossRef]
- Weir, J.P. Quantifying test-retest reliability using the intraclass correlation coefficient and the SEM. J. Strength Cond. Res. 2005, 19, 231–240. [Google Scholar] [CrossRef]
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420–428. [Google Scholar] [CrossRef]
- Lin, L.I. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- Hollman, J.H.; Beckman, B.A.; Brandt, R.A.; Merriwether, E.N.; Williams, R.T.; Nordrum, J.T. Minimum Detectable Change in Gait Velocity during Acute Rehabilitation following Hip Fracture. J. Geriatr. Phys. Ther. 2008, 31, 53–56. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis, 1st ed.; Pearson: London, UK, 1977. [Google Scholar]
- Tucker, L.A.; Lecheminant, J.D.; Bailey, B.W. Test-retest reliability of the Bod Pod: The effect of multiple assessments. Percept. Mot. Skills 2014, 118, 563–570. [Google Scholar] [CrossRef]
- Muntean, P.; Micloș-Balica, M.; Popa, A.; Neagu, A.; Neagu, M. Reliability of Repeated Trials Protocols for Body Composition Assessment by Air Displacement Plethysmography. Int. J. Environ. Res. Public Health 2021, 18, 10693. [Google Scholar] [CrossRef]
- Peeters, M.W.; Claessens, A.L. Effect of deviating clothing schemes on the accuracy of body composition measurements by air-displacement plethysmography. Int. J. Body Compos. Res. 2009, 7, 123–129. [Google Scholar]
- Wells, J.C.; Fuller, N.J. Precision of measurement and body size in whole-body air-displacement plethysmography. Int. J. Obes. Relat. Metab. Disord. 2001, 25, 1161–1167. [Google Scholar] [CrossRef]
- Singh, R.K.; Guru, C.S.; Rastogi, J.; Jaipurkar, R.; Sharma, A.; Apte, V.V. Test-retest reliability of air displacement plethysmography (BOD POD) in the adult healthy Indian male population. Indian J. Physiol. Pharmacol. 2022, 66, 251–266. [Google Scholar] [CrossRef]
- Masaoka, Y.; Homma, I. The effect of anticipatory anxiety on breathing and metabolism in humans. Respir. Physiol. 2001, 128, 171–177. [Google Scholar] [CrossRef]
- Tegenkamp, M.H.; Clark, R.R.; Schoeller, D.A.; Landry, G.L. Effects of Covert Subject Actions on Percent Body Fat by Air-Displacement Plethsymography. J. Strength Cond. Res. 2011, 25, 2010–2017. [Google Scholar] [CrossRef]
| All (n = 105) | Women (n = 51) | Men (n = 54) | |
|---|---|---|---|
| Age (y) | 30.4 ± 10.2 [20.0, 66.5] (25.1) | 31.2 ± 12.6 [20.0, 66.5] (24.6) | 29.6 ± 7.3 [20.3, 54.9] (26.3) |
| Height (m) | 1.71 ± 0.10 [1.49, 1.92] (1.71) | 1.63 ± 0.06 [1.49, 1.77] (1.63) | 1.80 ± 0.06 [1.69, 1.92] (1.80) |
| BM 1 (kg) | 71.7 ± 16.9 [38.0, 156.0] (72.2) | 62.4 ± 12.0 [38.0, 94.4] (59.2) | 80.4 ± 16.2 [57.5, 156.0] (78.2) |
| BMI (kg/m2) | 24.2 ± 4.5 [16.7, 45.1] (23.9) | 23.6 ± 4.5 [16.7, 33.7] (21.9) | 24.9 ± 4.3 [17.7, 45.1] (24.6) |
| All (n = 105) | Women (n = 51) | Men (n = 54) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Pair | TEM 1 | SEM | MDC | TEM | SEM | MDC | TEM | SEM | MDC |
| %BF (%) | (1,2) | 1.04 | 1.04 | 2.88 | 1.10 | 1.10 | 3.04 | 0.98 | 0.98 | 2.71 |
| (2,3) | 0.71 | 0.71 | 1.97 | 0.80 | 0.80 | 2.21 | 0.61 | 0.61 | 1.69 | |
| (3,4) | 0.66 | 0.66 | 1.82 | 0.72 | 0.72 | 1.99 | 0.59 | 0.59 | 1.64 | |
| FFM (kg) | (1,2) | 0.730 | 0.728 | 2.018 | 0.671 | 0.668 | 1.851 | 0.781 | 0.777 | 2.154 |
| (2,3) | 0.511 | 0.510 | 1.412 | 0.500 | 0.498 | 1.380 | 0.521 | 0.518 | 1.436 | |
| (3,4) | 0.452 | 0.451 | 1.249 | 0.422 | 0.420 | 1.165 | 0.478 | 0.476 | 1.319 | |
| BV (L) | (1,2) | 0.146 | 0.145 | 0.403 | 0.134 | 0.133 | 0.369 | 0.156 | 0.155 | 0.431 |
| (2,3) | 0.103 | 0.102 | 0.284 | 0.102 | 0.101 | 0.281 | 0.103 | 0.103 | 0.285 | |
| (3,4) | 0.107 | 0.107 | 0.296 | 0.084 | 0.084 | 0.233 | 0.125 | 0.124 | 0.344 | |
| All (n = 105) | Women (n = 51) | Men (n = 54) | |||||
|---|---|---|---|---|---|---|---|
| Variable | Pair | ICC (2,1) 1 | CCC | ICC (2,1) | CCC | ICC (2,1) | CCC |
| %BF (%) | (1,2) | 0.9910 | 0.9909 | 0.9884 | 0.9862 | 0.9871 | 0.9868 |
| (2,3) | 0.9958 | 0.9958 | 0.9927 | 0.9927 | 0.9950 | 0.9949 | |
| (3,4) | 0.9964 | 0.9964 | 0.9943 | 0.9942 | 0.9953 | 0.9953 | |
| FFM (kg) | (1,2) | 0.9971 | 0.9971 | 0.9881 | 0.9878 | 0.9914 | 0.9913 |
| (2,3) | 0.9986 | 0.9986 | 0.9937 | 0.9935 | 0.9961 | 0.9961 | |
| (3,4) | 0.9989 | 0.9989 | 0.9955 | 0.9954 | 0.9967 | 0.9966 | |
| All (n = 105) | Women (n = 51) | Men (n = 54) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | ICC (2,1) | SEM | MDC | ICC (2,1) | SEM | MDC | ICC (2,1) | SEM | MDC |
| %BF (%) | 0.9960 | 0.70 | 1.93 | 0.9933 | 0.77 | 2.14 | 0.9950 | 0.61 | 1.68 |
| FFM (kg) | 0.9987 | 0.49 | 1.35 | 0.9943 | 0.47 | 1.30 | 0.9963 | 0.50 | 1.39 |
| BV (L) | 1.0000 | 0.107 | 0.297 | 0.9999 | 0.095 | 0.264 | 1.0000 | 0.117 | 0.323 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muntean, P.; Popa, A.; Miclos-Balica, M.; Schick, F.; Munteanu, O.; Pupazan, V.; Neagu, A.; Neagu, M. Learning Effects in Air Displacement Plethysmography. Life 2023, 13, 1315. https://doi.org/10.3390/life13061315
Muntean P, Popa A, Miclos-Balica M, Schick F, Munteanu O, Pupazan V, Neagu A, Neagu M. Learning Effects in Air Displacement Plethysmography. Life. 2023; 13(6):1315. https://doi.org/10.3390/life13061315
Chicago/Turabian StyleMuntean, Paul, Anca Popa, Monica Miclos-Balica, Falk Schick, Oana Munteanu, Vasile Pupazan, Adrian Neagu, and Monica Neagu. 2023. "Learning Effects in Air Displacement Plethysmography" Life 13, no. 6: 1315. https://doi.org/10.3390/life13061315
APA StyleMuntean, P., Popa, A., Miclos-Balica, M., Schick, F., Munteanu, O., Pupazan, V., Neagu, A., & Neagu, M. (2023). Learning Effects in Air Displacement Plethysmography. Life, 13(6), 1315. https://doi.org/10.3390/life13061315