An Integrated Algorithmic MADM Approach for Heart Diseases’ Diagnosis Based on Neutrosophic Hypersoft Set with Possibility Degree-Based Setting
Abstract
:1. Introduction
- The approaches such as the Fs-set, IFs-set, Ns-set, etc., have been extensively utilized in various circumstances to resolve decision-making problems. Nevertheless, under several conditions, these structures demonstrate inadequacies in categorizing the entities according to their possibility grades. In other words, it can be interpreted that in the existing literature, the possibility degree of each element is regarded as one. However, in several realistic applications, different individuals may assign different possibility grades to each entity. To handle such concerns, Alkhazaleh et al. [24] explored the possibility Fs-set (pFs-set), which ensures the allocation of a possibility grade with every approximate element in the fs-set. However, such a model is not compatible with the use of the nonmembership grade. In order to tackle it and address it more appropriately, Bashir et al. [25] introduced the possibility IFs-set (pIFs-set). In the pIFs-set, the ifs numbers are assessed through the use of the possibility grade while computing the ranking analysis, but the degree of indeterminacy is ignored. This shortcoming was addressed by developing the possibility Ns-set (pNs-set) in [26].
- While in real-world observations, we come across various situations when the parameters are not enough to make the right decision, they demand being classified into their respective parametric-valued-based sets. Such situations have been tackled with the development of Hs-sets, which employ a particular mapping maa-function to manage these settings.
- The nHs-set is the generalization of the Fs-set, IFs-set, Ns-set, FHs-set, and IFHs-set. Since these models have limitations such as the degree of indeterminacy and the maa-function being ignored in the fs-set and ifs-set, the maa-function being ignored in the Ns-set, and the degree of indeterminacy being ignored in the FHs-set and IFHs-set, the NHs-set is meant to tackle such limitations.
- The proposed model, the possibility neutrosophic hypersoft set (pNHs-set), is a novel structure, which not only generalizes the existing models, but also makes them adequate with the use of the maa-function. In the pNHs-set, a possibility degree is attached to the neutrosophic numbers of the maa-function of the pNHs-set to judge their uncertain nature. In this sense, it is a more flexible and generalized model to deal with uncertain data diligently.
- Some elementary notions and algebraic operations of the pNHs-set are characterized with the support of explicatory examples.
- In contrast with existing approaches, the attributes and sub-attributive values (real data) of the Cleveland data set for the diagnosis of heart diseases are first analyzed on the basis of their operational and linguistic roles, and then, their linguistic values are transformed into possibility grades by using a suitable algebraic approach.
- Sanchez’s method (a classical approach for medical diagnosis) is modified under the pNHs-set environment to establish a relationship among patients under observation, prescribed attributes, and the decision-makers (medical specialists).
- A modified algorithm is put forward for the medical diagnosis of heart diseases by integrating the theory of pNHs-sets, the prescribed real data of Cleveland data set, and the modified Sanchez’s method.
- The validity of the proposed algorithm is assessed by its implementation in a real-world problem-based scenario.
- The advantageous aspects of the proposed approach are judged through a structural comparison with some relevant existing approaches.
2. Preliminaries
3. Possibility Neutrosophic Hypersoft Set and Set-Theoretic Operations
- The situation that declares the essential classification of the parameters into their related sub-parametric values in the form of different sets.
- The situation that requires the claim of the maa-function that it is proficient to undertake the multi-argument domain in the form of sub-parametric-valued tuples.
- The situation that compels the decision-makers to give their expert judgments in the form of neutrosophic values, which guarantee the three dimensions, i.e., truth (real membership), indeterminacy (neutral value), and falsity (real nonmembership), of the opinion of decision-makers.
- The situation that requires the reflection of the possibility degree to evaluate the approval level of the collected expert judgments for the objects being considered.
- (i)
- is a pNHs-set with , and
- (ii)
- is also a pNHs-set with , and
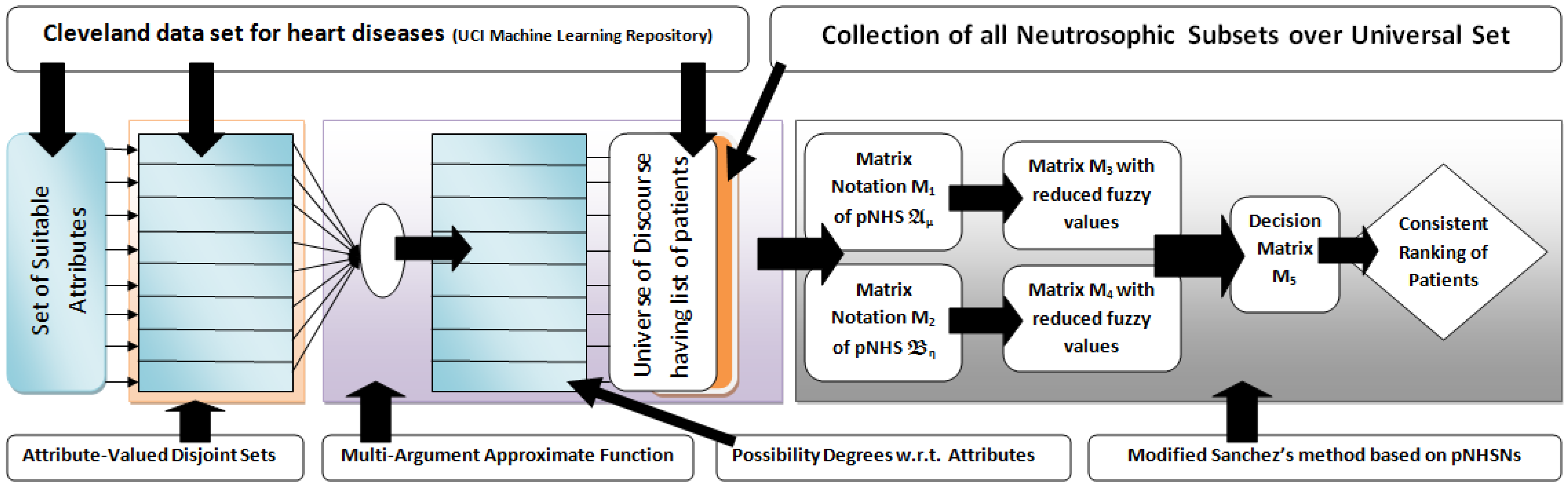
4. Proposed Methodology and Algorithmic Implementation
4.1. Modified Sanchez’s Method
4.2. Cleveland Data Set
4.3. Operational Role of Selected Attributes
- Age: Aging is an independent risk factor for heart diseases. Although the risk of heart disease is higher in older people (60 years or more), with the association of certain other factors, younger people can be at risk. Medical specialists have categorized aging into four categories: up to 20 years, up to 40 years, up to 60 years, and above 60 years.
- Chest pain type: Chest pain is perhaps the most well-known reason that individuals visit the trauma center. It changes relying on the individual. It likewise differs in: quality, force, span, area. It might feel like a sharp, agonizing feeling or a dull pain. It could be an indication of a genuine heart-related issue. Numerous normal causes that are not dangerous may likewise have caused it. Heart-related chest pain can be categorized into typical angina (TA), atypical angina (ATA), non-anginal pain, and asymptomatic (AM). Typical angina consists of (1) substernal chest pain or discomfort that is (2) provoked by exertion or emotional stress and (3) relieved by rest or nitroglycerine (or both). Atypical (probable) angina chest pain applies when two out of three criteria of classic angina are present. Non-anginal pain is applied to hospitalized patients in order to designate that they neither have an acute coronary syndrome nor display evidence of a coronary ischemia. Asymptomatic means there are no symptoms for the disease under consideration.
- Resting blood pressure: Blood pressure is a particular kind of pressure that is exerted by the blood against the artery walls. Such pressure is further categorized as systolic and diastolic. The first one is produced when the heart drains off the blood into the blood vessels, and the second one is produced inside the arteries due to the relaxing state of the heart. Hypertension is the point at which the power of the blood is excessively high during heart compression or relaxing inside the arteries. The arteries may have an increased resistance against the flow of blood. Both pressures are measured in mm Hg. Typical blood pressure is systolic if under 120 and diastolic if under 80 (120/80). Raised blood pressure is systolic if 120 to 129 and diastolic under 80.
- Serum cholesterol: Cholesterol is a sort of fat. It is also known as a lipid. It goes through our bloodstream in small particles wrapped inside proteins. These bundles are known as lipoproteins. LDL is one of the principal kinds of lipoproteins in our blood. The other principal type is high-thickness lipoproteins (HDLs). A third kind of lipid, called a triglyceride, likewise courses in our blood. Estimating our LDL (“bad” cholesterol), HDL (“good” cholesterol), and triglycerides will give us a number called our complete blood cholesterol, or serum cholesterol. Our body needs cholesterol to build healthy cells, but high levels of cholesterol can increase our risk of heart disease. With high cholesterol, we can develop fatty deposits in our blood vessels. Eventually, these deposits grow, making it difficult for enough blood to flow through our arteries. Serum cholesterol levels is calculated by adding HDL and LDL cholesterol levels with 20 percent of triglycerides. It ranges from 126 mg/dL to 564 mg/dL. The ranges of certain cholesterol are given in Table 4.
- Fasting blood sugar: A large number of people who suffer a heart disease have high glucose due to the “stress response”. This means that even people who are not diabetic may have high blood sugar. Its ranges are given in Table 5. Its normal range is 120 mg/dL for a healthy person.
- Maximum heart rate achieved: Heart rate is a major determinant of oxygen consumption in patients with ischemic heart disease. Its maximum value that can be achieved ranges from 71 beats per minute to 195 beats per minute.
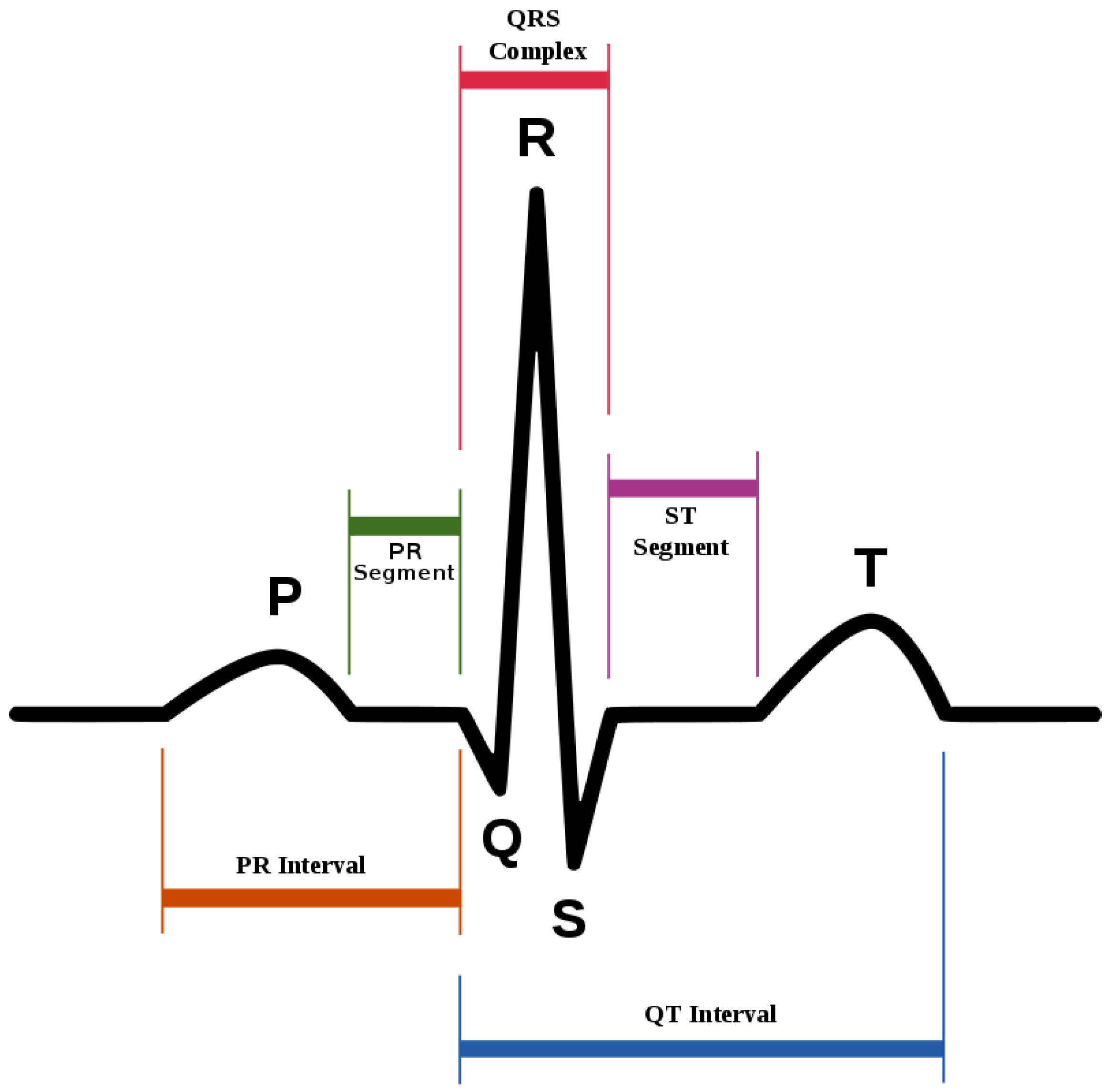
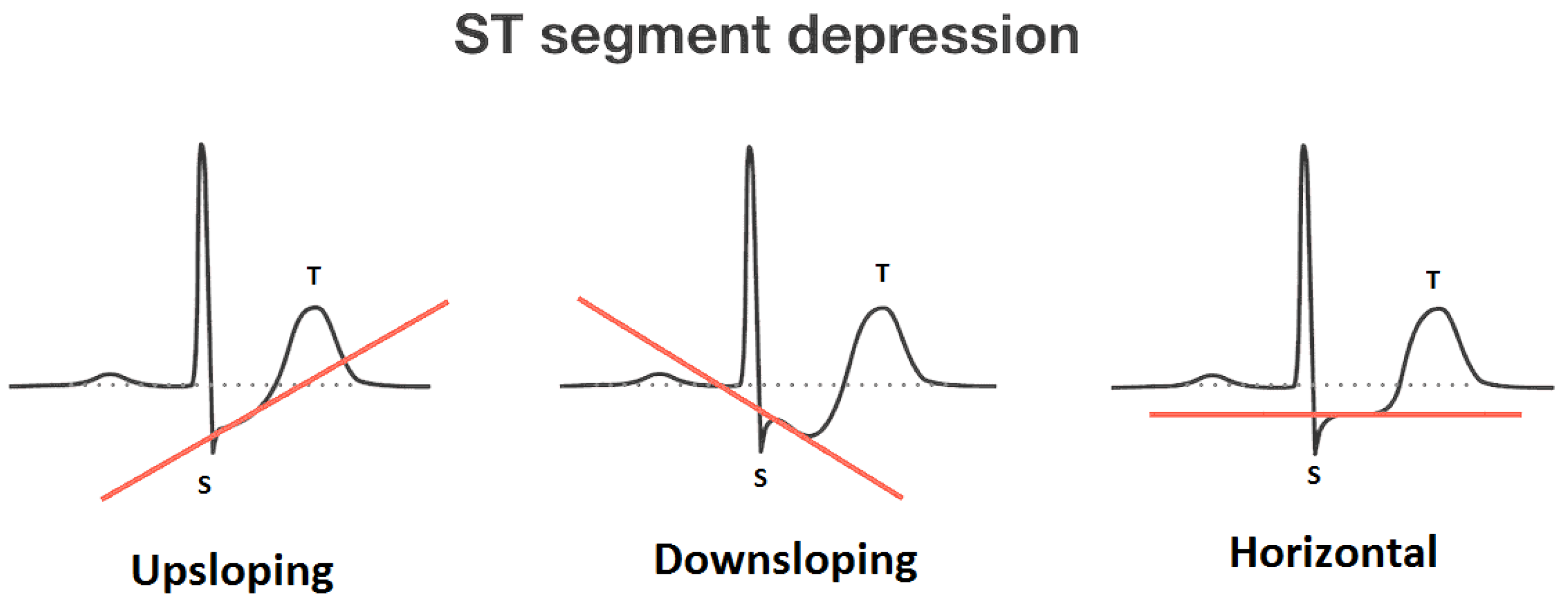
- Oldpeak and slope: Oldpeak: ST (S = shock, T = toxicity) depression induced by exercise relative to rest is considered a reliable electrocardiogram (ECG) finding for the diagnosis of obstructive coronary disorders. It is measured in mm and ranges from 0.0 to 0.5. Its graphical representation is given in Figure 2. The slope of the peak exercise ST-segment has three categories: upsloping, flat (horizontal) and downsloping. The graphical depiction of ST-sloping is provided in Figure 3.
- Thal: This is a blood disorder known as thalassemia. It can be classified as null (value = 0), fixed defect (value = 3, no blood flow in some part of the heart), normal blood flow (value = 6), and reversible defect (value = 7; blood flow is observed, but it is not normal). Usually, the first category is ignored when diagnosing heart diseases.
4.4. Possibility Grades Corresponding to Selected Attributes
4.5. Scenario and Statement of the Problem
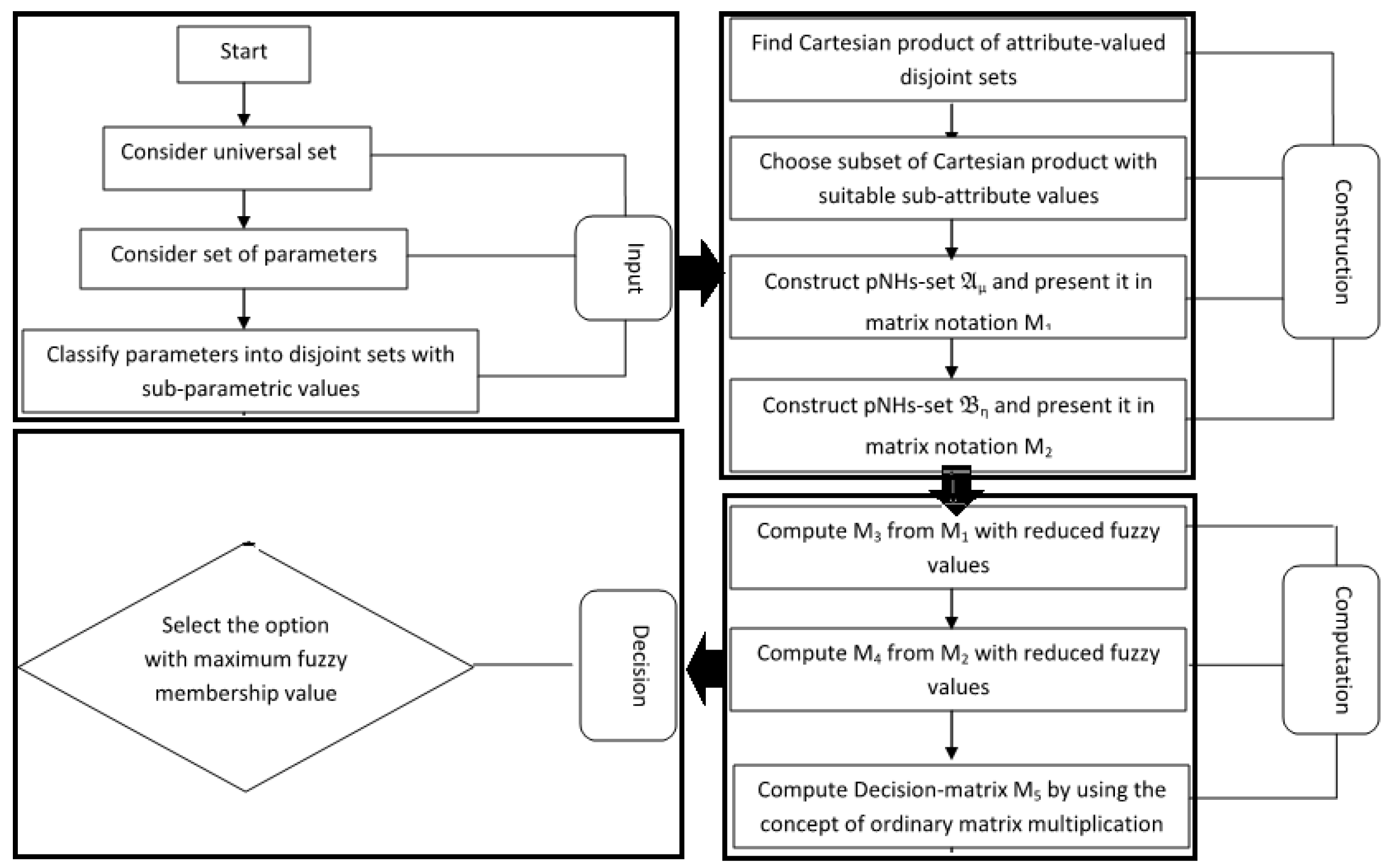
4.6. Proposed Algorithm and Implementation
| Algorithm 1 Diagnosis of heart diseases through aggregation of the pNHs-set. |
▹Start ▹Input: 1. Consider as the universe of discourse consisting of patients under observation. 2. Consider as set of parameters . 3. Classify n parameters into disjoint parametric-valued sets: ▹. Construction: 4. Determine with , where denotes the cardinality of sets . 5. Choose a subset of with in accordance with the priorities of attribute values. 6. Construct pNHs-sets and , and represent in matrix notations and , respectively. ▹Computation: 7. Compute , where 8. Compute , where . 9. Compute . 10. Compute scores by calculating the row-sum of . ▹Output: 11. Choose the Max as final selection. ▹End |
5. Discussion and Comparison Analysis
- The adopted technique took the idea of parameterization together with the pNHs-set to handle the contemporary decision-making concerns. The supposed possibility degree emulates the uncertain attitude of the level of acknowledgment; in this manner, this has incredible prospects for legitimacy within the domain of computations.
- Attributes and their sub-attributive values with real values from the Cleveland data set were transformed to fuzzy memberships with an appropriate transformation criterion.
- As the presented model places emphasis on the comprehensive observation of the parameters and their respective sub-parametric values, it ensures better, reliable, and flexible results from medical physicians as decision-makers.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy, Neutrosophic Probability, Set, and Logic, Analytic Synthesis and Synthetic Analysis; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Molodtsov, D. Soft set theory—First results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Maji, P.; Biswas, R.; Roy, A. Soft set theory. Comput. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.I.; Feng, F.; Liu, X.; Min, W.K.; Shabir, M. On some new operations in soft set theory. Comput. Math. Appl. 2009, 57, 1547–1553. [Google Scholar] [CrossRef] [Green Version]
- Maji, P.K.; Biswas, R.; Roy, A.R. Fuzzy soft sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Maji, P.K.; Biswas, R.; Roy, A.R. Intuitionistic fuzzy soft sets. J. Fuzzy Math. 2001, 9, 677–692. [Google Scholar]
- Maji, P.K. Neutrosophic soft set. Ann. Fuzzy Math. Inform. 2013, 5, 157–168. [Google Scholar]
- Smarandache, F. Extension of soft set of hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst. 2018, 22, 168–170. [Google Scholar] [CrossRef]
- Abbas, F.; Murtaza, G.; Smarandache, F. Basic operations on hypersoft sets and hypersoft points. Neutrosophic Sets Syst. 2020, 35, 407–421. [Google Scholar] [CrossRef]
- Saeed, M.; Rahman, A.U.; Ahsan, M.; Smarandache, F. An inclusive study on fundamentals of hypersoft set. In Theory and Application of Hypersoft Set, 1st ed.; Pons Publishing House: Brussels, Belgium, 2021; pp. 1–23. [Google Scholar]
- Rahman, A.U.; Saeed, M.; Smarandache, F.; Ahmad, M.R. Development of hybrids of hypersoft set with complex fuzzy set, complex intuitionistic fuzzy set and complex neutrosophic set. Neutrosophic Sets Syst. 2020, 38, 335–354. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Smarandache, F. Convex and concave hypersoft sets with some properties. Neutrosophic Sets Syst. 2020, 38, 497–508. [Google Scholar] [CrossRef]
- Debnath, S. Fuzzy hypersoft sets and its weightage operator for decision making. J. Fuzzy Ext. Appl. 2021, 2, 163–170. [Google Scholar] [CrossRef]
- Yolcu, A.; Smarandache, F.; Öztürk, T.Y. Intuitionistic fuzzy hypersoft sets. Commun. Fac. Sci. Univ. Ank. Ser. Math. Stat. 2021, 70, 443–455. [Google Scholar] [CrossRef]
- Saqlain, M.; Saeed, M.; Ahmad, M.R.; Smarandache, F. Generalization of TOPSIS for neutrosophic hypersoft sets using accuracy function and its application. Neutrosophic Sets Syst. 2020, 27, 131–137. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Saeed, M.H.; Mehmood, A.; Abdeljawad, T. An application of neutrosophic hypersoft mapping to diagnose hepatitis and propose appropriate treatment. IEEE Access 2021, 9, 70455–70471. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Rahman, A.U.; Mehmood, A. An application of neutrosophic hypersoft mapping to diagnose brain tumor and propose appropriate treatment. J. Intell. Fuzzy Syst. 2021, 41, 1677–1699. [Google Scholar] [CrossRef]
- Saeed, M.; Rahman, A.U.; Arshad, M.; Dhital, A. A novel approach to neutrosophic hypersoft graphs with properties. Neutrosophic Sets Syst. 2021, 46, 336–355. [Google Scholar] [CrossRef]
- Saeed, M.; Rahman, A.U.; Arshad, M. A study on some operations and products of neutrosophic hypersoft graphs. J. Appl. Math. Comput. 2021, preview. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Dhital, A. Decision making application based on neutrosophic parameterized hypersoft set theory. Neutrosophic Sets Syst. 2021, 41, 1–14. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Alodhaibi, S.S.; Khalifa, H.A.E.W. Decision making algorithmic approaches based on parameterization of neutrosophic set under hypersoft set environment with fuzzy, intuitionistic fuzzy and neutrosophic settings. CMES Comput. Model. Eng. Sci. 2021, 128, 743–777. [Google Scholar] [CrossRef]
- Alkhazaleh, S.; Salleh, A.R.; Hassan, N. Possibility fuzzy soft set. Adv. Decis. Sci. 2011, 2011, 479756. [Google Scholar] [CrossRef]
- Bashir, M.; Salleh, A.R.; Alkhazaleh, S. Possibility intuitionistic fuzzy soft set. Adv. Decis. Sci. 2012, 2012, 404325. [Google Scholar] [CrossRef] [Green Version]
- Karaaslan, F. Similarity measure between possibility neutrosophic soft sets and its applications. Univ. Politeh. Buchar. Sci. Bull. Ser. A Appl. Math. Phys. 2016, 78, 155–162. [Google Scholar]
- Sanchez, E. Inverses of fuzzy relations. Application to possibility distributions and medical diagnosis. Fuzzy Sets Syst. 1979, 2, 75–86. [Google Scholar] [CrossRef]
- UC Irvine Machine Learning Repository, Cleveland Heart Disease Data Details. Dataset. 2010. Available online: https://archive.ics.uci.edu/ml/datasets/heart+Disease (accessed on 3 October 2021).
- Rahman, A.U.; Saeed, M.; Khalifa, H.A.E.-W.; Afifi, W.A. Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Math. 2022, 7, 3866–3895. [Google Scholar] [CrossRef]


| Abbreviation | Stands for | Abbreviation | Stands for | Abbreviation | Stands for |
|---|---|---|---|---|---|
| F-set | Fuzzy set | IF-set | Intuitionistic fuzzy set | N-set | Neutrosophic set |
| S-set | Soft set | Fs-set | Fuzzy soft set | IFs-set | Intuitionistic fuzzy soft set |
| Ns-set | Neutrosophic soft set | Hs-set | Hypersoft set | maa-function | multi-argument function |
| FHs-set | Fuzzy hypersoft set | IFHs-set | Intuitionistic fuzzy hypersoft set | NHs-set | Neutrosophic hypersoft set |
| pFs-set | Possibility fuzzy soft set | pIFs-set | Possibility intuitionistic fuzzy soft set | pNs-set | Possibility neutrosophic soft set |
| pNHs-set | Possibility neutrosophic hypersoft set | Universal set | Power set of | ||
| Family of fuzzy sets | Family of intuitionistic fuzzy sets | Family of neutrosophic sets |
| Sr. No. | Sr. No. | Attributes | Attributes |
|---|---|---|---|
| by Analysis | by Data Set | (Abbreviations) | (Full Names) |
| 1 | 3 | age | Age in years |
| 2 | 4 | sex | Sex (male/female) |
| 3 | 9 | cp | Chest pain type) |
| 4 | 10 | trestpbs | Resting blood pressure (mm Hg) |
| 5 | 12 | chol | Serum cholesterol (mg/dL) |
| 6 | 16 | fbs | Fasting blood sugar (120 mg/dL) |
| 7 | 19 | restecg | Resting electrocardiographic results |
| 8 | 32 | Thalach | Maximum heart rate achieved |
| 9 | 38 | Exang | Exercise-induced angina |
| 10 | 40 | Oldpeak | ST depression induced by exercise relative to rest |
| 11 | 41 | slope | The slope of the peak exercise ST segment |
| 12 | 44 | ca | Number of major vessels (0–3) colored by fluoroscopy |
| 13 | 51 | thal | 3 = normal; 6 = fixed defect; 7 = reversible defect |
| 14 | 58 | num | Diagnosis of heart disease (angiographic disease status) |
| Sr. No. | Sr. No. | Attributes | Attributes | Values Corresponding |
|---|---|---|---|---|
| by Analysis | by Data Set | (Abbreviations) | (Full Names) | to Attributes in Data Set |
| 1 | 3 | age | Age in years | 0–20, 21–40, 41–60, Above 60 |
| 3 | 9 | cp | Chest pain type | 1. Typical angina, 2. atypical angina, 3. non-anginal pain, 4. asymptomatic |
| 4 | 10 | trestpbs | Resting blood pressure (mm Hg) | 90–200mm Hg |
| 5 | 12 | chol | Serum cholesterol (mg/dL) | 126–564 mg/dL |
| 6 | 16 | fbs | Fasting blood sugar (120 mg/dL) | 120 mg/dL |
| 8 | 32 | Thalach | Maximum heart rate achieved | 71–195 |
| 10 | 40 | Oldpeak | ST depression induced by exercise relative to rest | 0.0–5.6 |
| 11 | 41 | slope | The slope of the peak exercise ST segment | 1. upsloping, 2. flat, 3. downsloping |
| 13 | 51 | thal | 3 = normal; 6 = fixed defect; 7 = reversible defect | 1. normal, 2. fixed defect, 3. reversible defect |
| Healthy Serum Cholesterol | Less than 200 mg/dL |
| Healthy HDL Cholesterol | Higher than 55 mg/dL for women and 45 mg/dL for men |
| Healthy LDL Cholesterol | Less than 130 mg/dL |
| Healthy Triglycerides | Less than 150 mg/dL |
| Blood Sugar (mg/dL) | Interpretation |
|---|---|
| Above 250 | Very high |
| 181–250 | High |
| 70–180 | In target range |
| 55–69 | Low |
| Below 55 | Very low |
| Selected Attributes | Prescribed Values in Data Set | Transformed Fuzzy Values |
|---|---|---|
| Age | 0–20, 21–40, 41–60, 61–80 | 0–0.25, 0.2625–0.50, 0.5125–0.75, 0.7625–1.00 |
| Chest pain type) | 1, 2, 3, 4 | 0.25, 0.50, 0.75, 1.00 |
| Resting blood pressure | 90–200 | 0.45–1.00 |
| Serum cholesterol | 126–564 | 0.2234–1.0000 |
| Fasting blood sugar | 0, 120 | 0,1 |
| Maximum heart rate achieved | 71–195 | 0.3641–1.0000 |
| Oldpeak | 0.0–5.6 | 0–1 |
| Slope | 1, 2, 3 | 0.33, 0.66, 1.00 |
| Thal | 3, 6, 7 | 0.4286, 0.8571, 1.0000 |
| 0.2 | 0.1 | 0.05 | 0.15 | 0.4 | 0.2 | 0.3 | 0.25 | |
| 0.1 | 0.2 | 0.25 | 0.3 | 0.2 | 0.25 | 0.35 | 0.3 | |
| 0.45 | 0.4 | 0.65 | 0.3 | 0.2 | 0.2 | 0.25 | 0.3 | |
| 0.25 | 0.5 | 0.05 | 0.15 | 0.25 | 0.35 | 0.05 | 0.15 | |
| 0.4 | 0.5 | 0.65 | 0.25 | 0.2 | 0.25 | 0.15 | 0.25 | |
| 0.05 | 0.4 | 0.15 | 0.15 | 0.3 | 0.2 | 0.15 | 0.1 |
| 0.15 | 0.1 | 0.15 | 0.15 | |
| 0.15 | 0.25 | 0.15 | 0.05 | |
| 0.25 | 0.25 | 0.3 | 0.25 | |
| 0.1 | 0.3 | 0.3 | 0.35 | |
| 0.05 | 0.45 | 0.3 | 0.2 | |
| 0.35 | 0.1 | 0.15 | 0.05 | |
| 0.4 | 0.45 | 0.15 | 0.15 | |
| 0.05 | 0.15 | 0.1 | 0.55 |
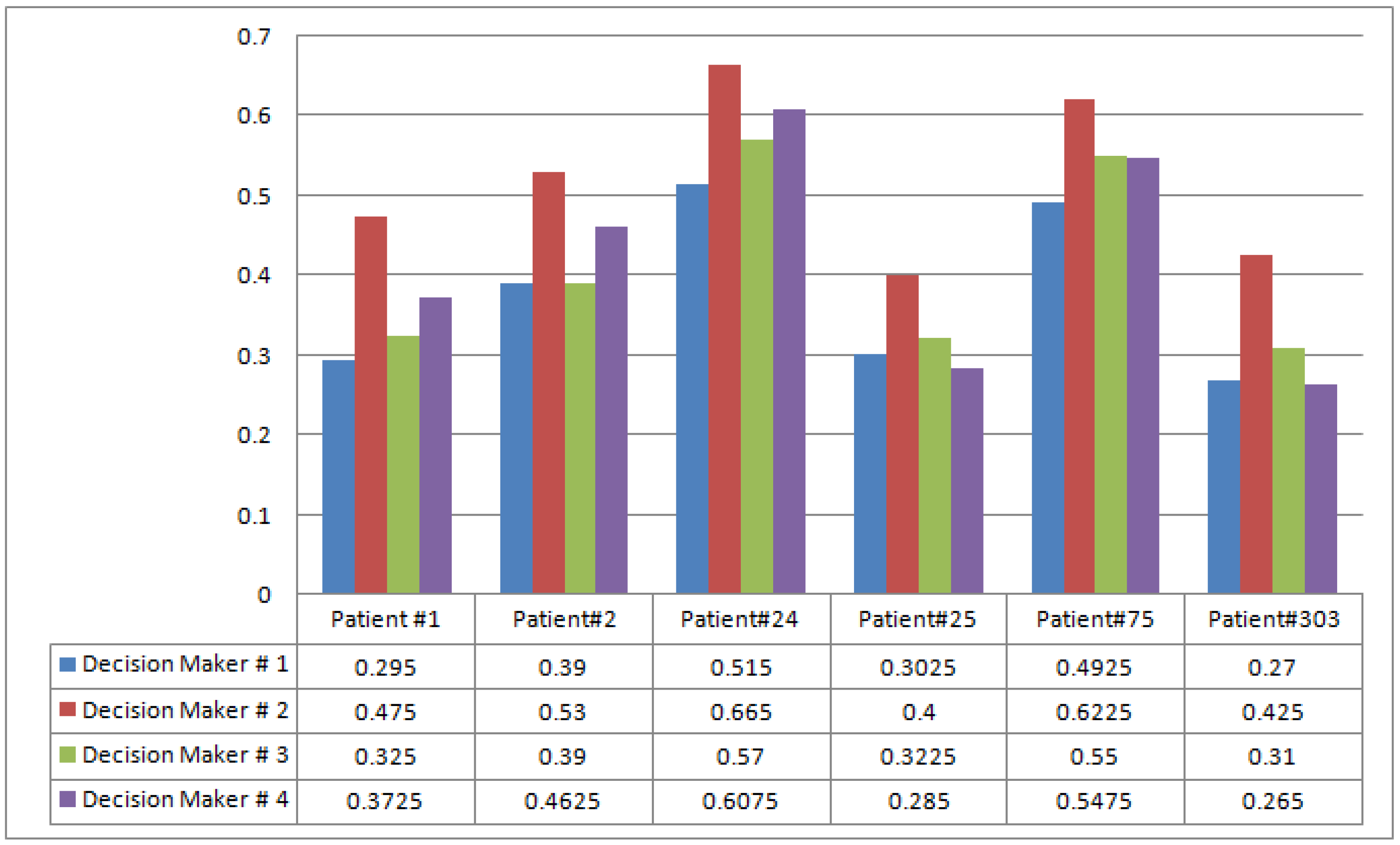
| 0.295 | 0.475 | 0.325 | 0.3725 | |
| 0.39 | 0.53 | 0.39 | 0.4625 | |
| 0.515 | 0.665 | 0.57 | 0.6075 | |
| 0.3025 | 0.4 | 0.3225 | 0.285 | |
| 0.4925 | 0.6225 | 0.55 | 0.5475 | |
| 0.27 | 0.425 | 0.31 | 0.265 |
| 1.4675 | |
| 1.7725 | |
| 2.3575 | |
| 1.3100 | |
| 2.2125 | |
| 1.2700 |
| Authors | Structure | I.G | M.G | N.M.G | G.O.P | S.A.A.F | M.A.A.F |
|---|---|---|---|---|---|---|---|
| Debnath [15] | FHs-set | × | ✓ | × | × | ✓ | ✓ |
| Yolcu et al. [16] | IFHs-set | × | ✓ | ✓ | × | ✓ | ✓ |
| Alkhazaleh et al. [24] | pFs-set | × | ✓ | × | ✓ | ✓ | × |
| Bashir et al. [25] | pIFs-set | × | ✓ | ✓ | ✓ | ✓ | × |
| Karaaslan [26] | pNs-set | ✓ | ✓ | ✓ | ✓ | ✓ | × |
| Rahman et al. [29] | pIFHs-set | × | ✓ | ✓ | ✓ | ✓ | ✓ |
| Proposed Model | pNHs-set | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.U.; Saeed, M.; Mohammed, M.A.; Krishnamoorthy, S.; Kadry, S.; Eid, F. An Integrated Algorithmic MADM Approach for Heart Diseases’ Diagnosis Based on Neutrosophic Hypersoft Set with Possibility Degree-Based Setting. Life 2022, 12, 729. https://doi.org/10.3390/life12050729
Rahman AU, Saeed M, Mohammed MA, Krishnamoorthy S, Kadry S, Eid F. An Integrated Algorithmic MADM Approach for Heart Diseases’ Diagnosis Based on Neutrosophic Hypersoft Set with Possibility Degree-Based Setting. Life. 2022; 12(5):729. https://doi.org/10.3390/life12050729
Chicago/Turabian StyleRahman, Atiqe Ur, Muhammad Saeed, Mazin Abed Mohammed, Sujatha Krishnamoorthy, Seifedine Kadry, and Fatma Eid. 2022. "An Integrated Algorithmic MADM Approach for Heart Diseases’ Diagnosis Based on Neutrosophic Hypersoft Set with Possibility Degree-Based Setting" Life 12, no. 5: 729. https://doi.org/10.3390/life12050729
APA StyleRahman, A. U., Saeed, M., Mohammed, M. A., Krishnamoorthy, S., Kadry, S., & Eid, F. (2022). An Integrated Algorithmic MADM Approach for Heart Diseases’ Diagnosis Based on Neutrosophic Hypersoft Set with Possibility Degree-Based Setting. Life, 12(5), 729. https://doi.org/10.3390/life12050729










