Prediction of Cortical Bone Thickness Variations in the Tibial Diaphysis of Running Rats
Abstract
1. Introduction
2. Experiments
- Sedentary control group: the rats were 26.7 (±1.1) cm long and weighed 492.1 (±34.6) g. They were left to their everyday activity (eating and walking), without any specific running activity, for 8 weeks. At the end of this program, the mean cortical bone thickness of the tibial diaphysis was 957 (±110) µm. This value was normalized to 1 to facilitate comparisons between groups. The mechanical load (body weight) for the bone remodeling was assumed to be constant over time.
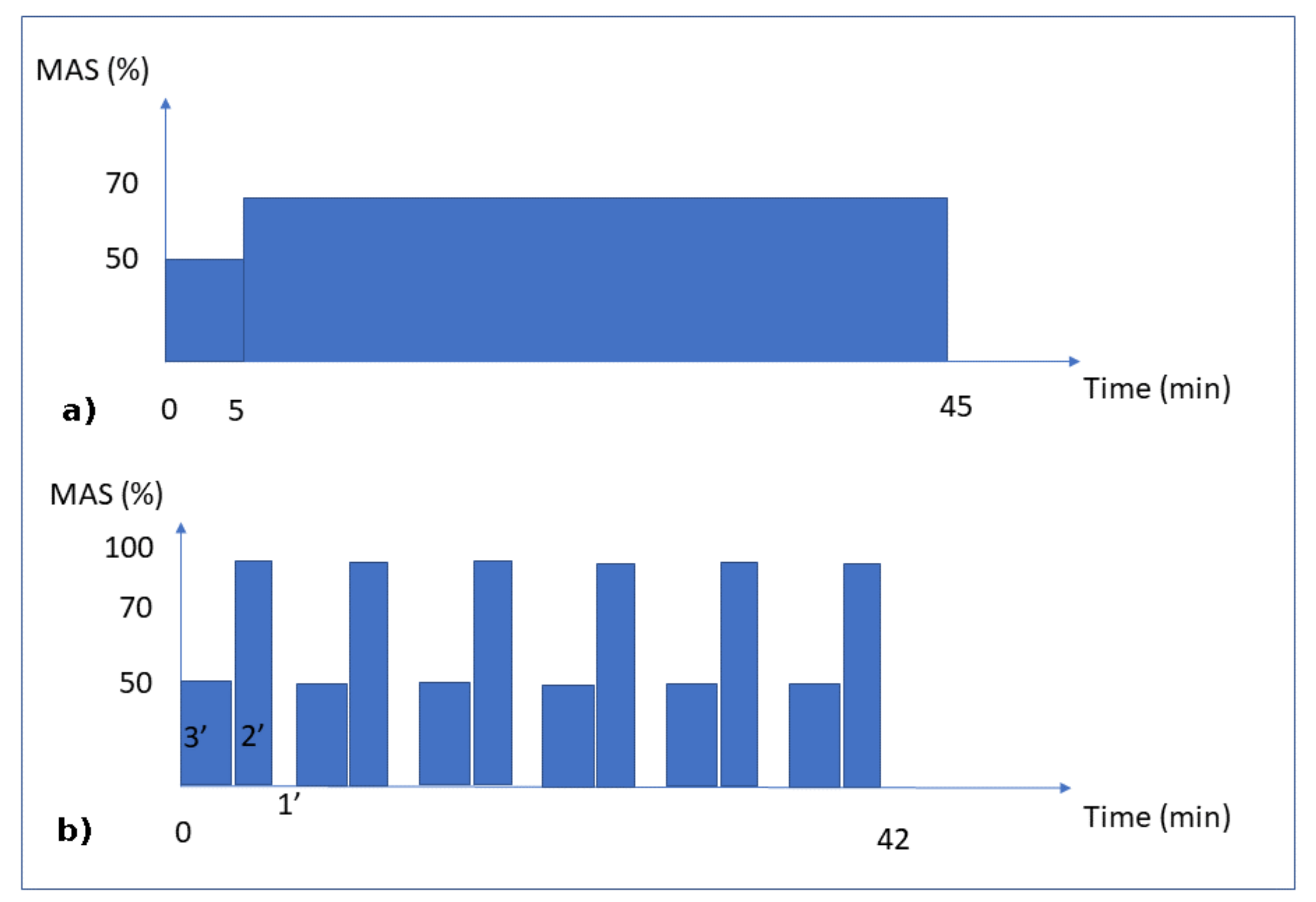
- Continuous running group: the rats were 26.4 (±0.7) cm long and weighed 486.4 (±31.8) g. This group was subjected to 8 weeks of running for 45 min per day at an intensity of 70% of the maximal aerobic speed (MAS) (Figure 1a). At the end of the exercise program, the mean cortical bone thickness of the tibial diaphysis was 708 µm (±65 µm).
- Intermittent running group: the rats were 26.5 (±0.6) cm long and weighed 475.1 (±30.3) g. This group was subjected to an interval-training running activity for 42 min per day for 8 weeks. This protocol consisted in 7 repetitions of blocks of 3 min at 50% of the MAS, followed by 2 min at 100% of the MAS and 1 min of passive rest (Figure 1b). At the end of the exercise program, the mean cortical bone thickness of the tibial diaphysis was 1024 (±112) µm.
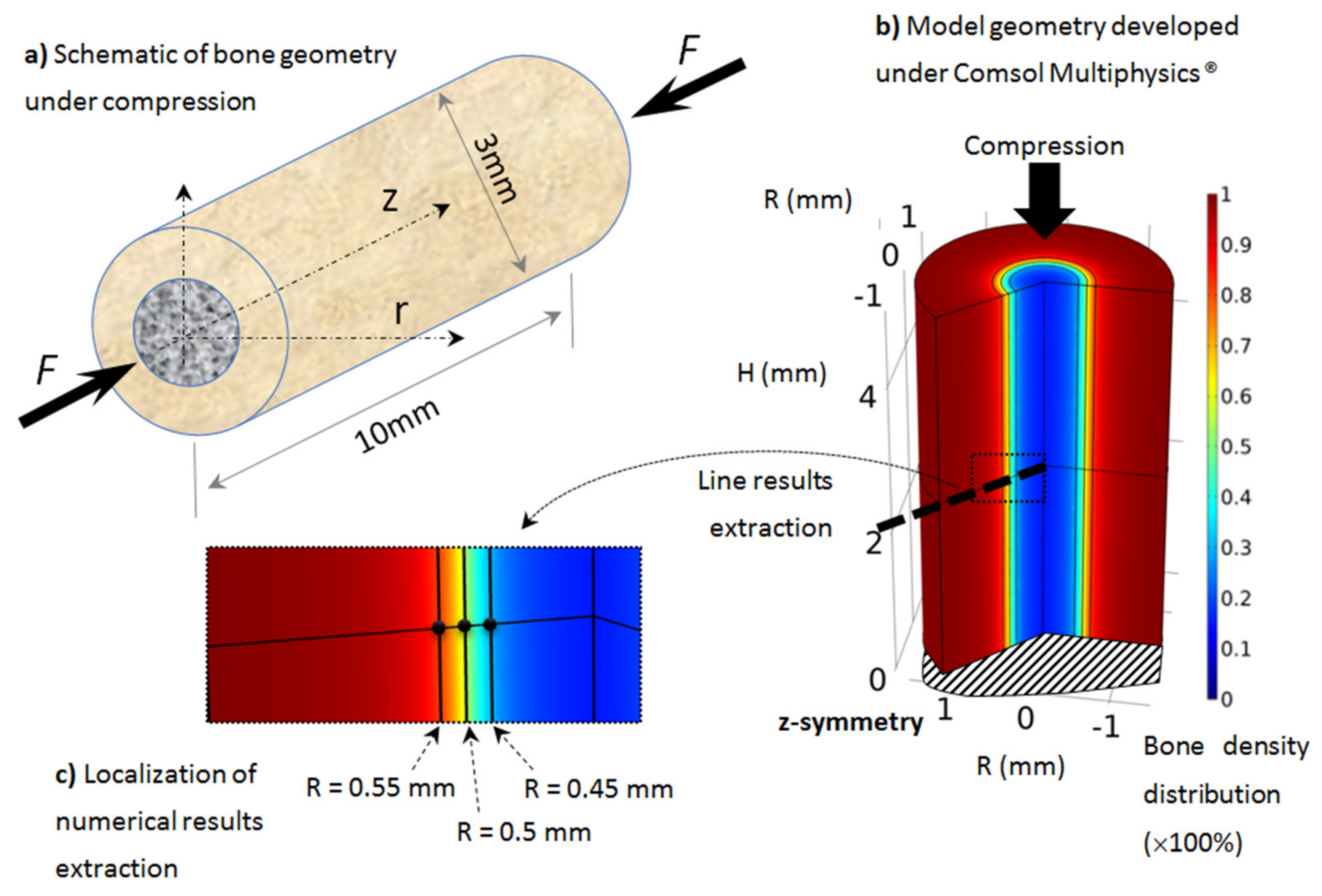
2.1. Post-Mortem Micro-Computed Tomography (µCT) and Computation
2.2. Bone Histology
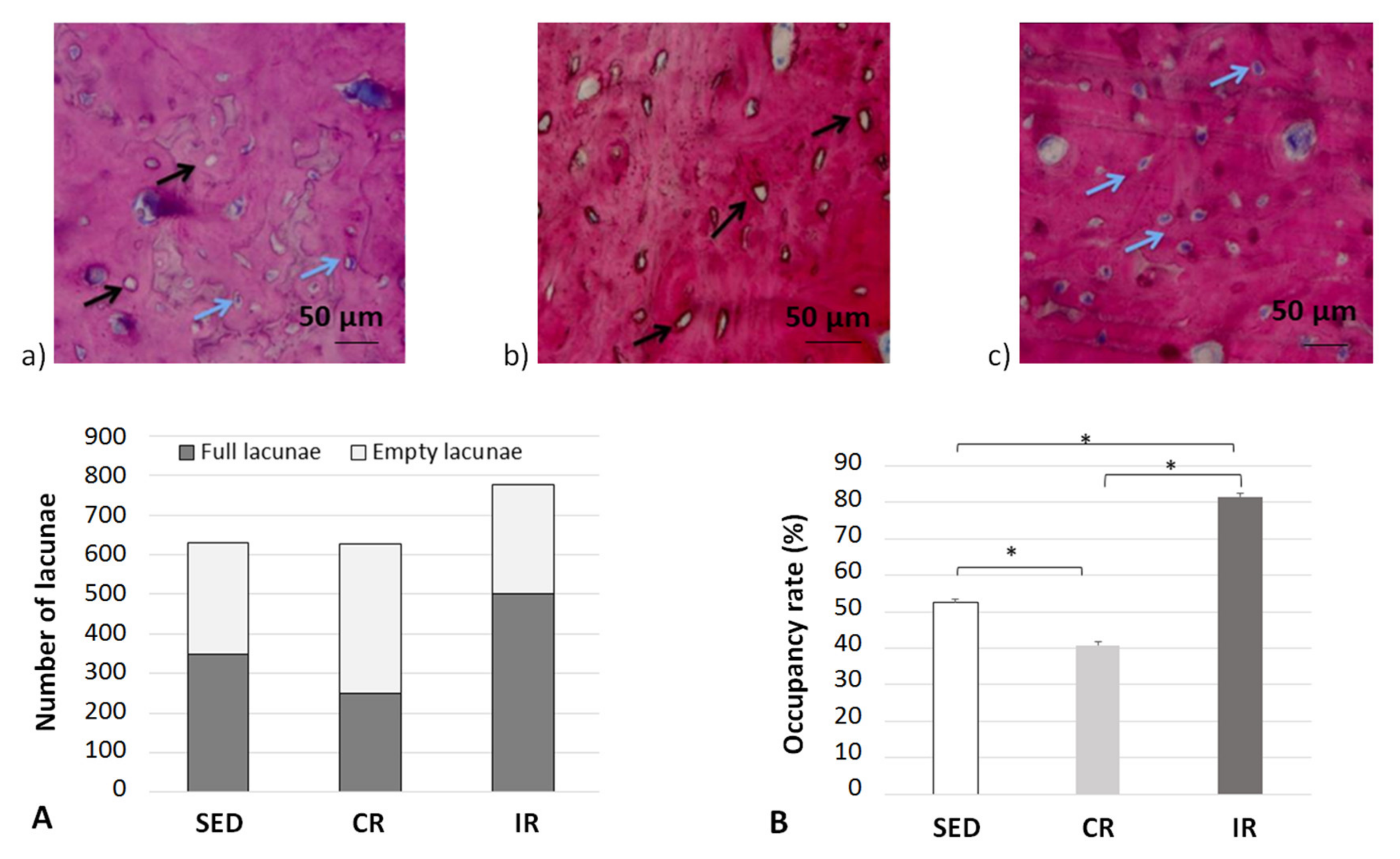
2.3. Occupation Rate of Osteocyte Lacunae
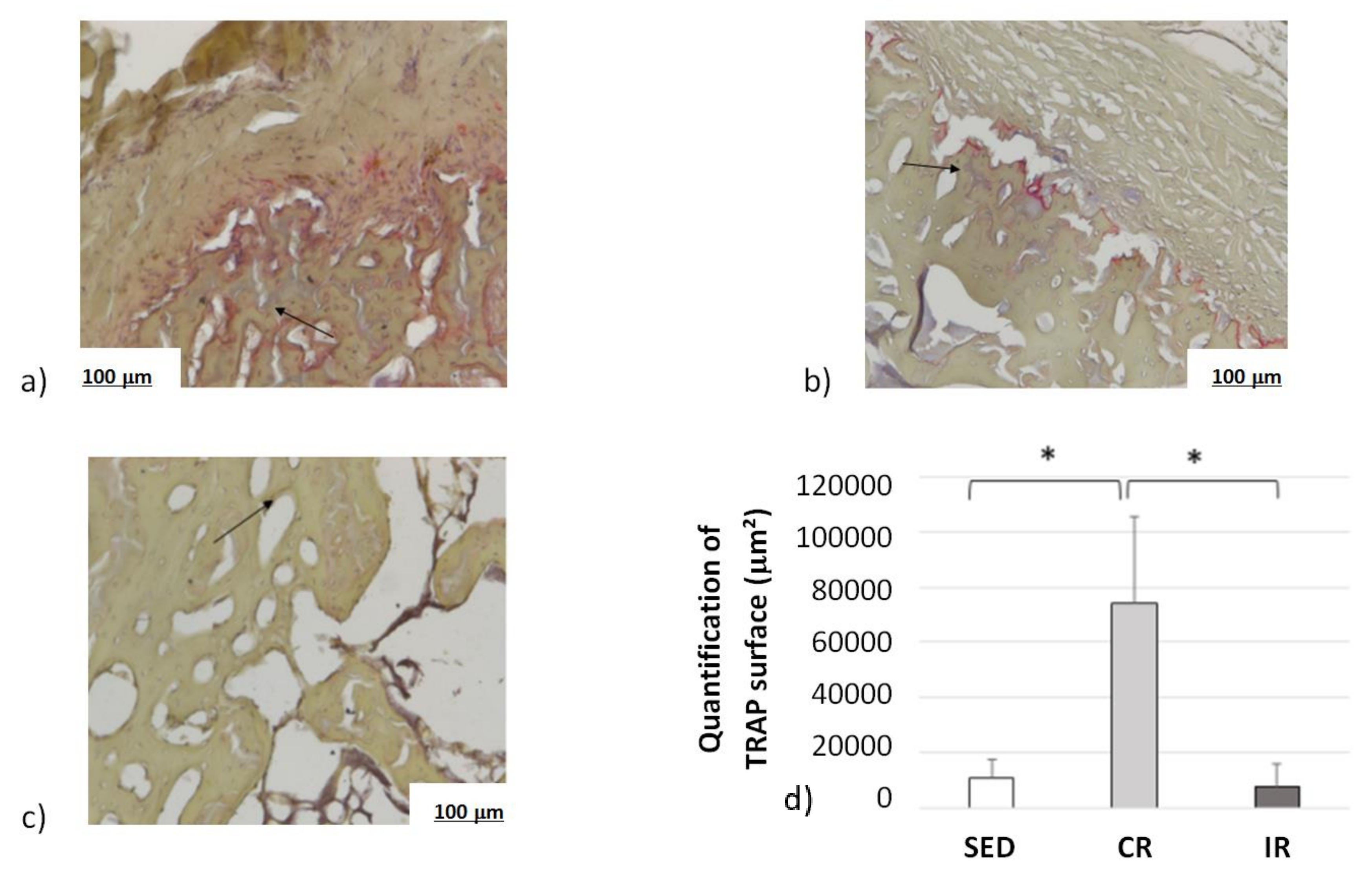
2.4. TRAP Histochemistry
2.5. Statistical Analysis
3. Theoretical Model
3.1. Theory
- -
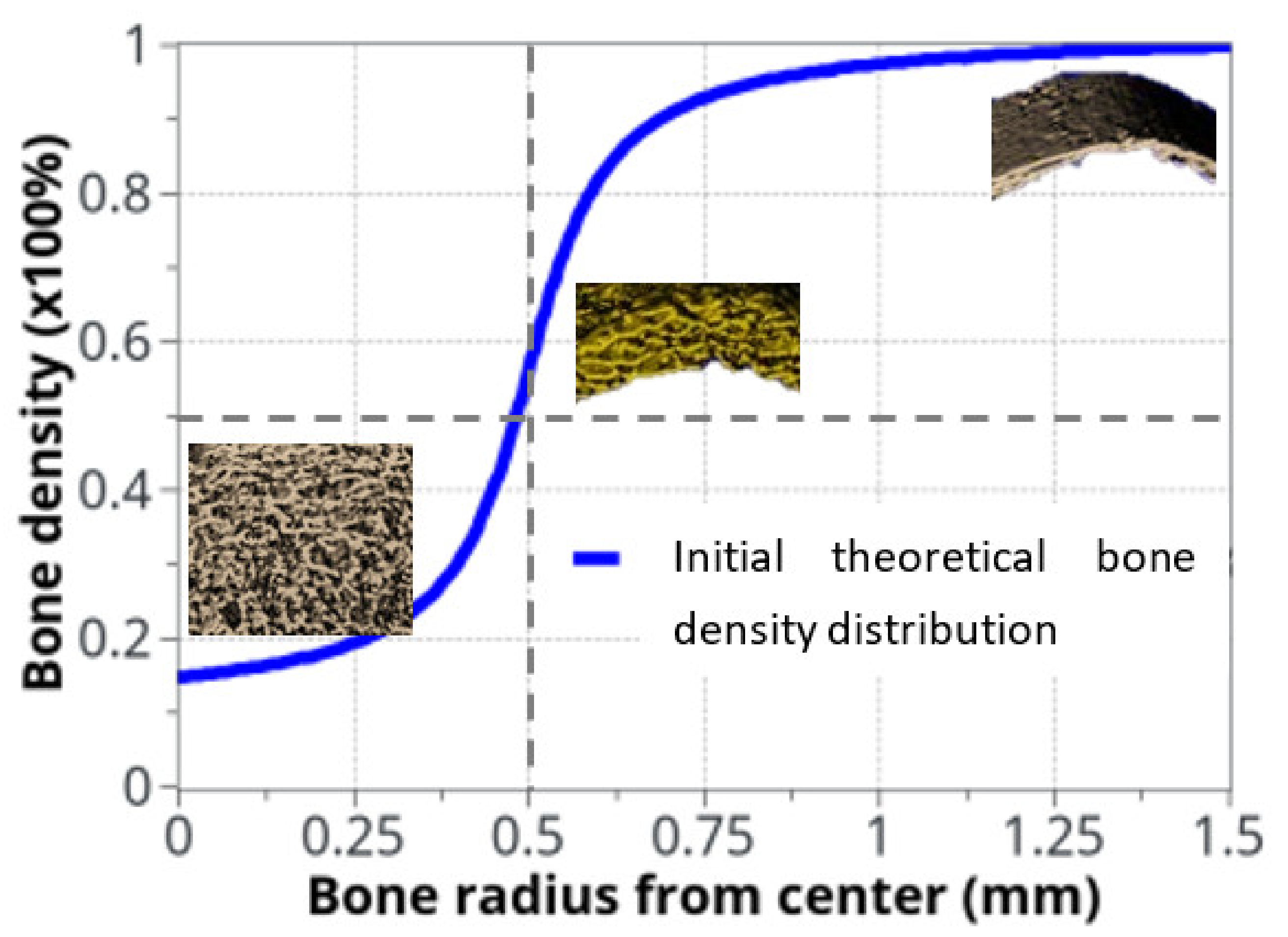
- In the trabecular bone (center part), cells are located in the bone marrow and are ready to be biologically activated. However, they are not very active, as they are far away from the cortical-trabecular interface and the mechanical support of the bone.
- -
- Around the cortical-trabecular interface (on each side) is where the cell activity is at its maximum for the bone remodeling to occur.
- -
- In the cortical bone, mainly osteocytes are present to sense the mechanical load, without osteoblasts and with a minority of osteoclasts; hence almost no bone remodeling occurs.
3.2. Application
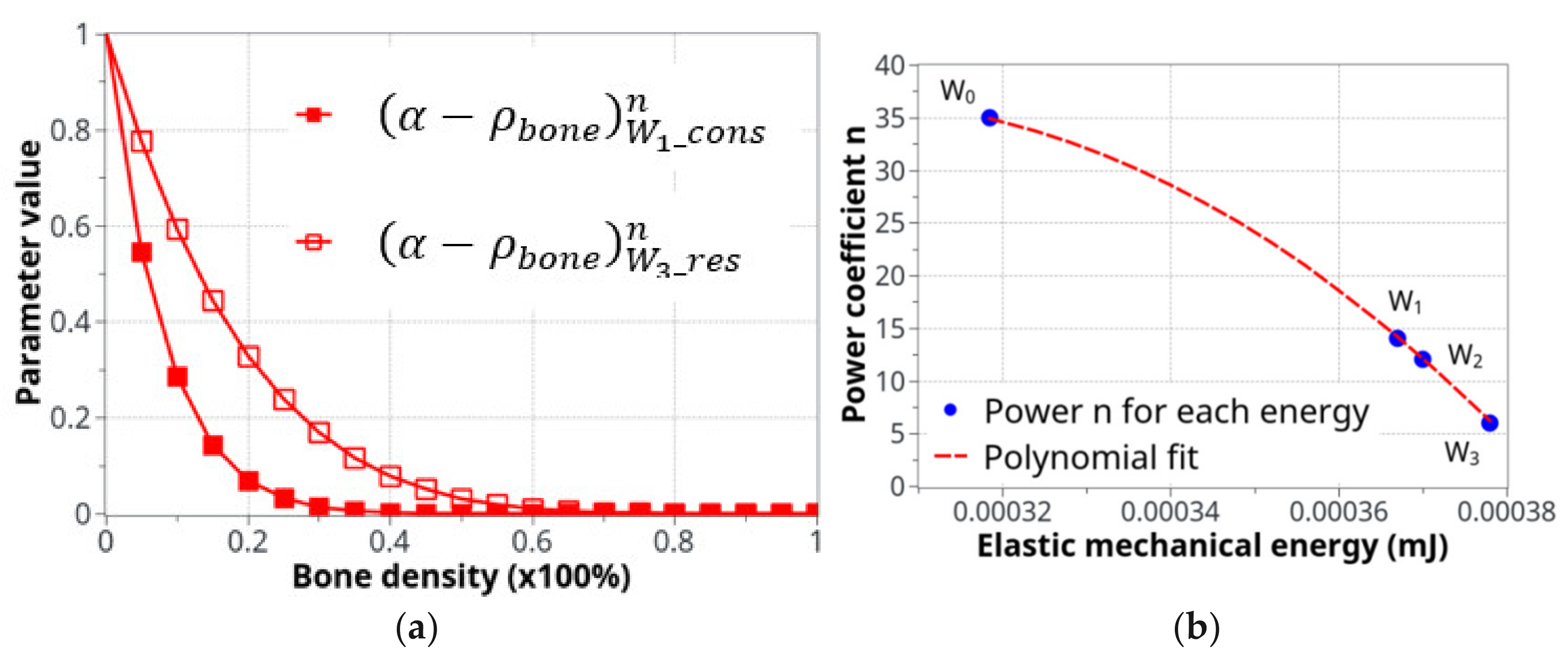
3.3. Parameter Identification
- -
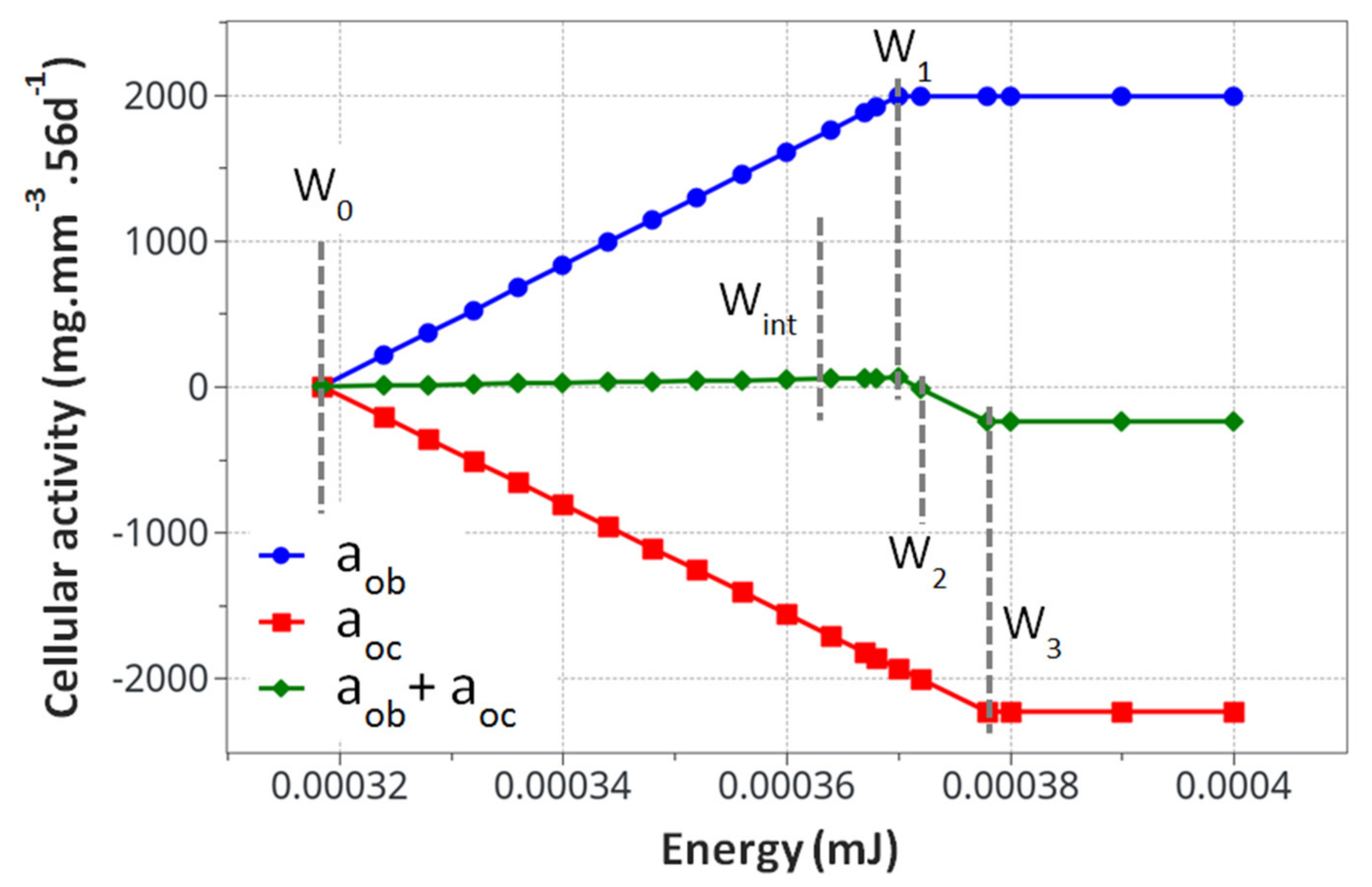
- W0: Homeostasis, where no bone density variation occurs within the sedentary control group. It was evaluated directly from the rat body weight and bone geometry at the beginning of the experiments using the standard mechanics of elasticity.
- -
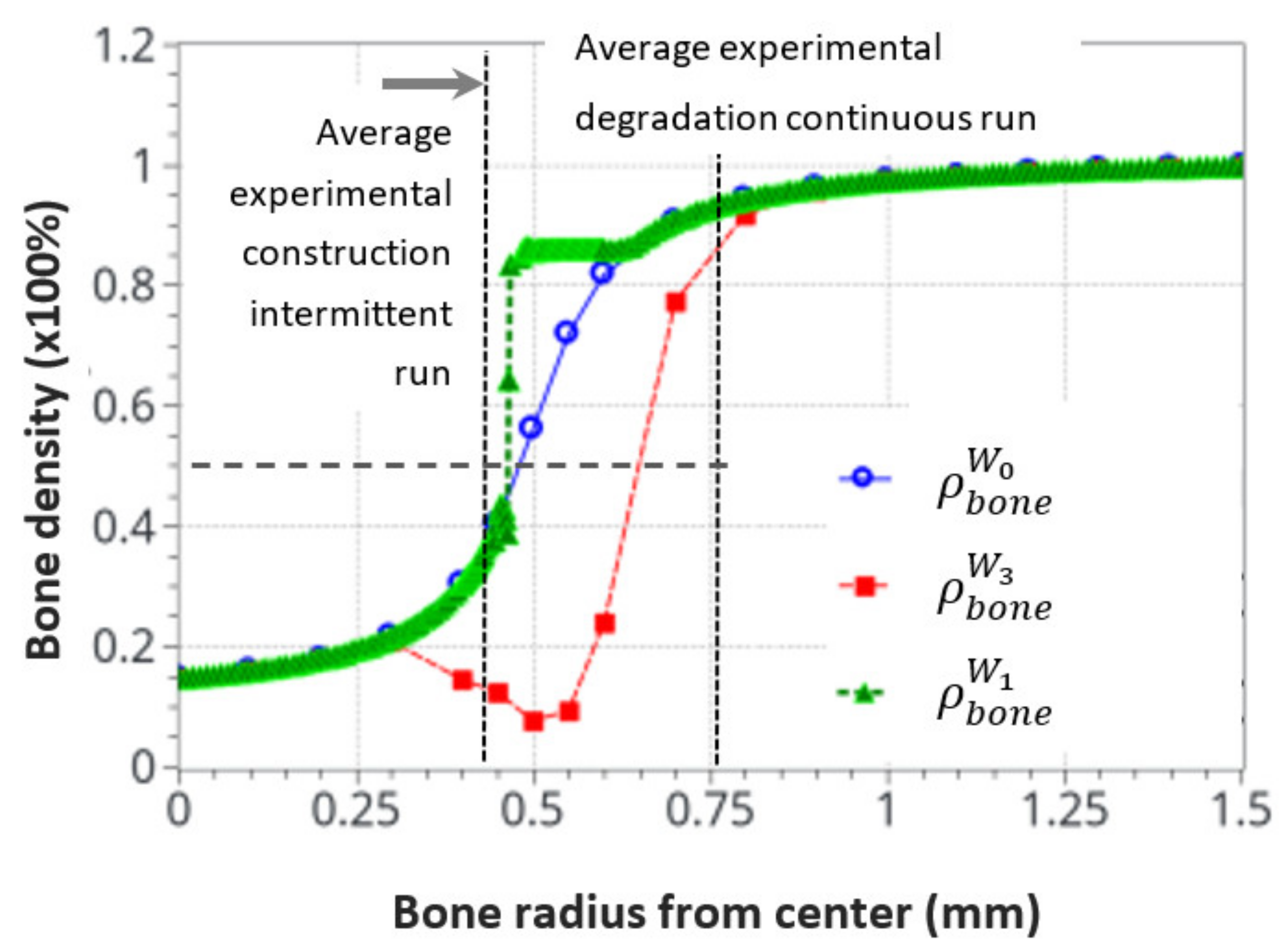
- W1: Energy for the maximum mineral bone density increase, assumed to correspond to the bone density increase after 8 weeks of exercise in the intermittent running group. It was evaluated from the experimental data. This energy was extrapolated from the maximum cortical bone thickness observed experimentally in the intermittent running scenario.
- -
- W3: The energy level corresponding to the maximum resorption rate (depending on cell availability), whatever the extra-increase in the mechanical energy. It was assumed to be the maximum degradation rate observed in the continuous running group after 8 weeks of running with the minimum cortical bone thickness.
- -
- W2: The threshold energy level at which bone density will start to decrease if the energy level increases. It corresponds to the linear interpolation between W1 and W3, where osteoblast and osteoclast activity are considered to be equal.
4. Results and Discussion
4.1. Numerical Model Parameter Identification
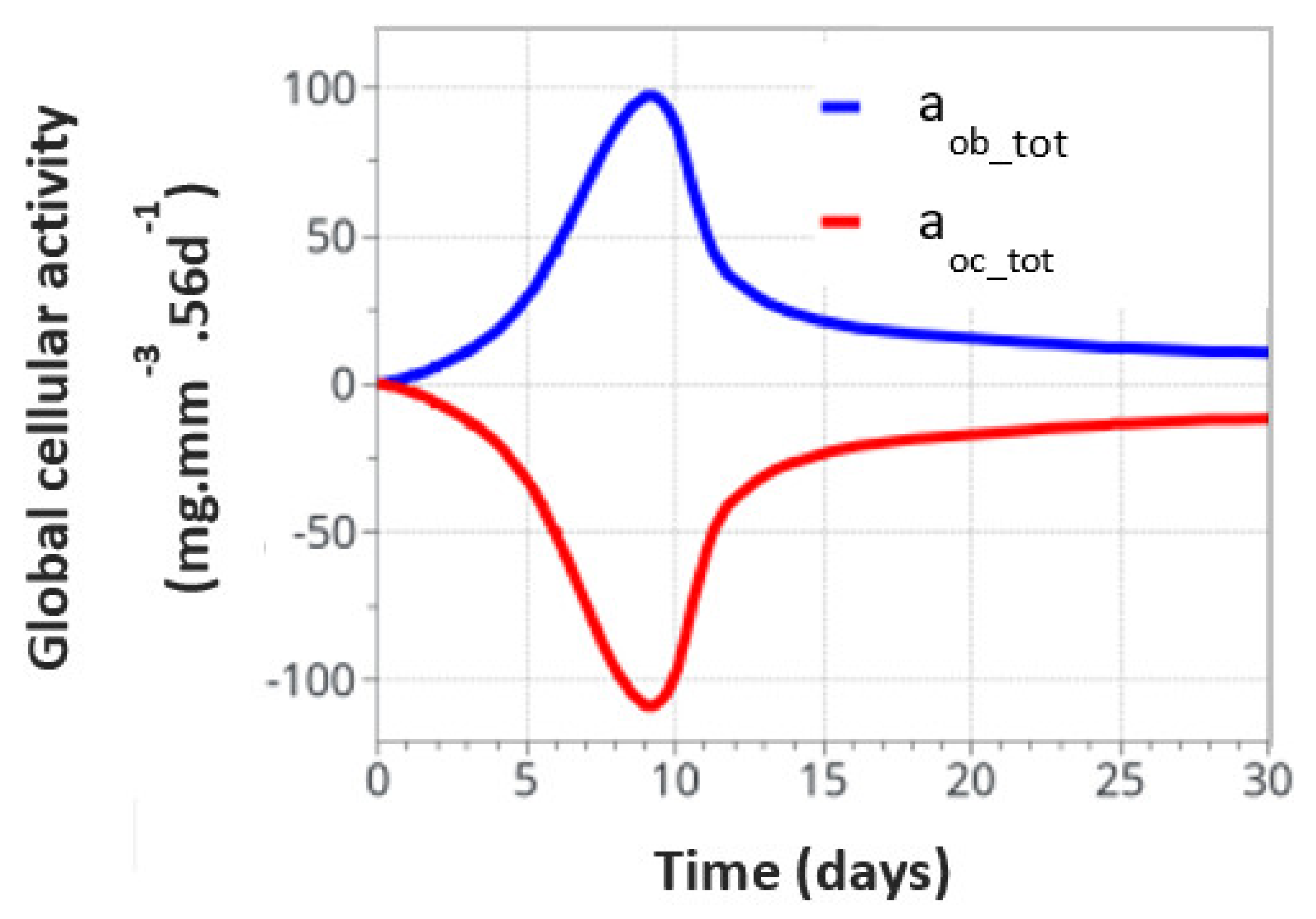
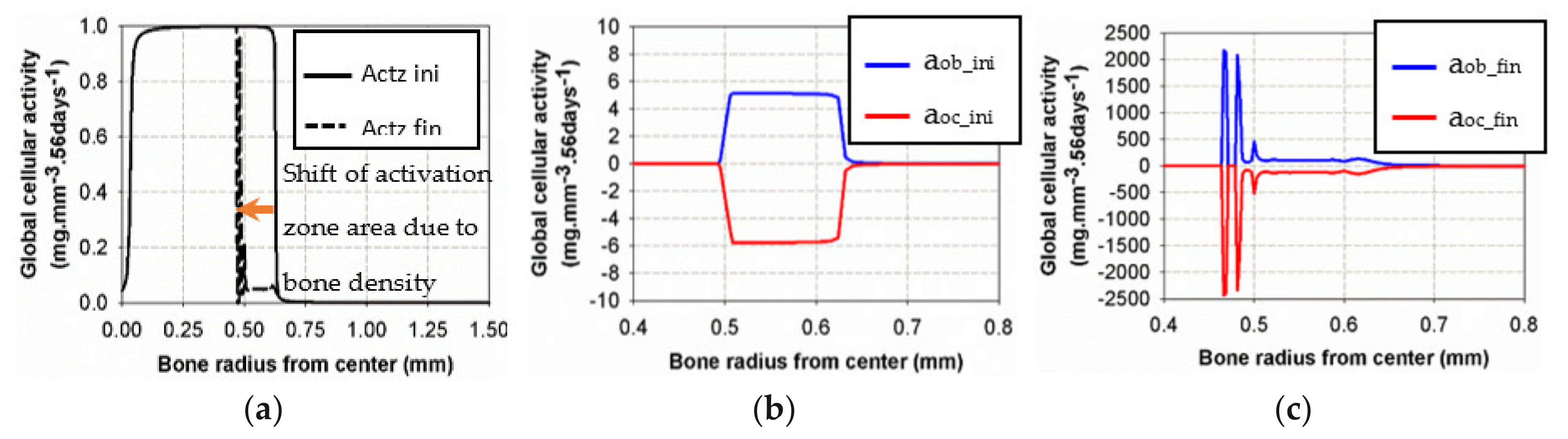
4.2. Theoretical Model Results
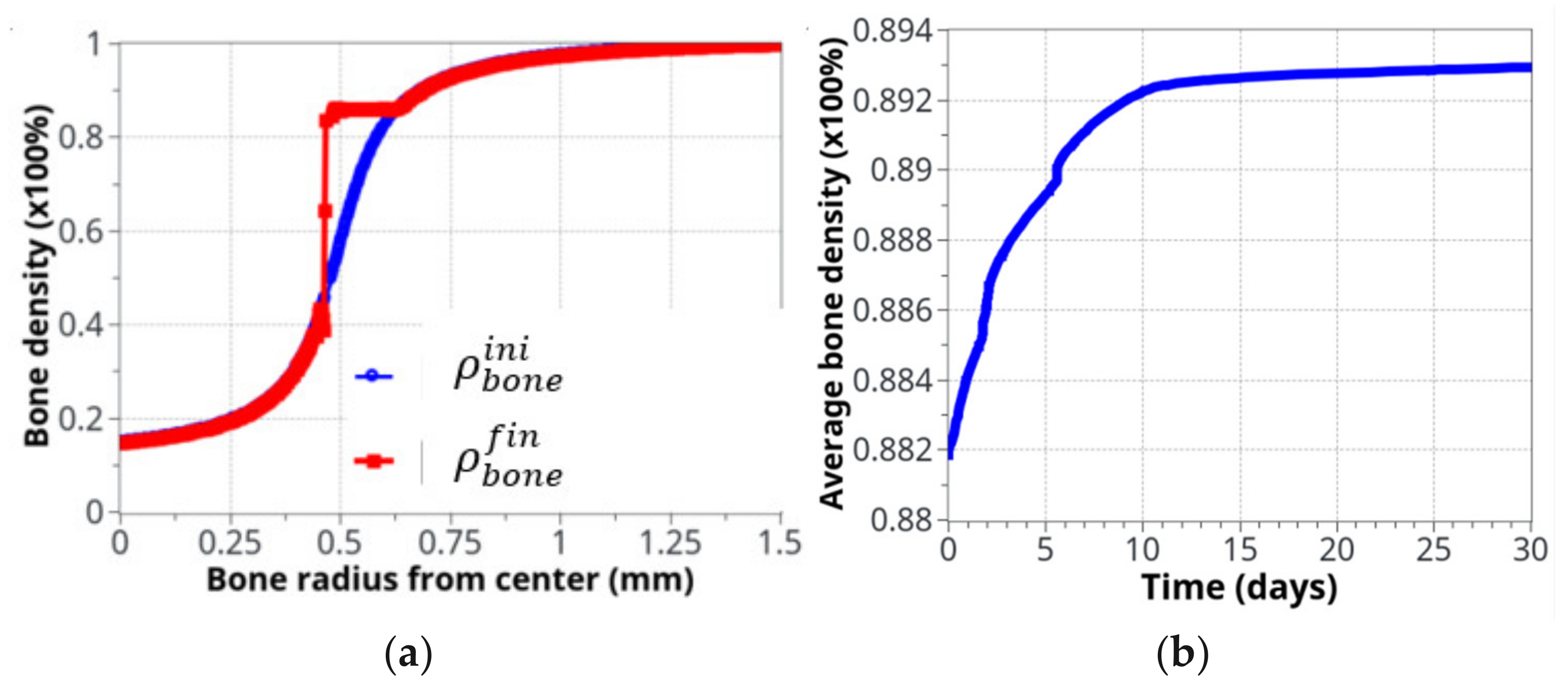
4.3. Bone Density Prediction
4.3.1. Intermittent Running Scenario
4.3.2. Continuous Running Scenario
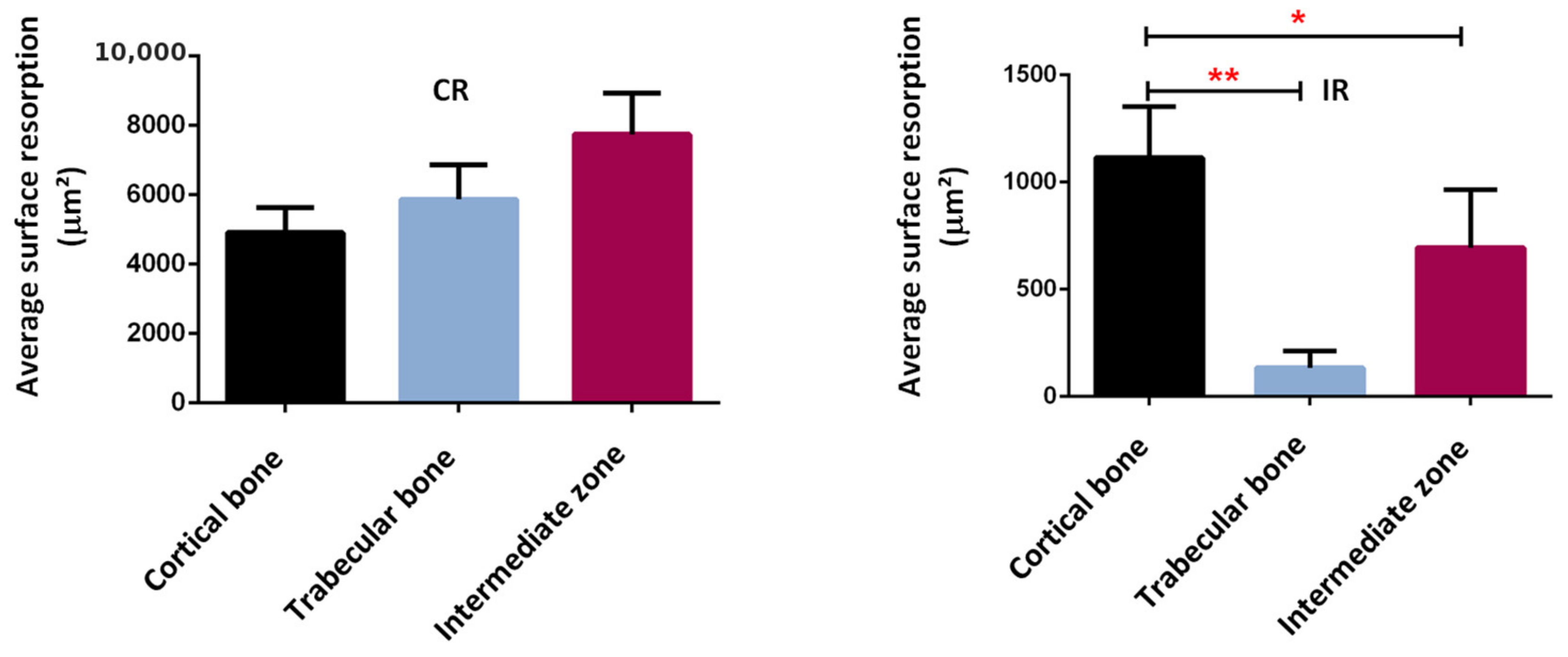
4.4. Correlation between Cell Scale Experimental Results and Bone Scale Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wolff, J. The Law of Bone Remodelling; Springer Science: Berlin, Germany, 2012; 126p, ISBN 364271031X. [Google Scholar]
- Carter, D.R. Mechanical loading histories and cortical bone remodeling. Cal. Tissue Int. 1984, 36, S19–S24. [Google Scholar] [CrossRef]
- Carter, D.R.; Van der Meulen, M.C.H.; Beaupré, G.S. Mechanical factors in bone growth and development. Bone 1996, 18, S5–S10. [Google Scholar] [CrossRef]
- Beaupré, G.S.; Orr, T.E.; Carter, D.R. An approach for time-dependent bone modeling and remodeling—Application: A preliminary remodeling simulation. J. Orthop. Res. 1990, 8, 662–670. [Google Scholar] [CrossRef] [PubMed]
- Ruimerman, R.; Hilbers, P.; van Rietbergen, B.; Huiskes, R. A theoretical framework for strain-related trabecular bone maintenance and adaptation. J. Biomech. 2005, 38, 931–941. [Google Scholar] [CrossRef] [PubMed]
- Pivonka, P.; Zimak, J.; Smith, D.W.; Gardiner, B.S.; Dunstan, C.R.; Sims, N.A. Model structure and control of bone remodeling: A theoretical study. Bone 2008, 43, 249–263. [Google Scholar] [CrossRef] [PubMed]
- Frost, H.M. Bone mass and the mechanostat: A proposal. Anat. Rec. 1987, 219, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Frost, H.M. Bone’s mechanostat: A 2003 update. Anat. Rec. 2003, 275, 1081–1101. [Google Scholar] [CrossRef] [PubMed]
- Pivonka, P.; Komarova, S.V. Mathematical modeling in bone biology: From intracellular signaling to tissue mechanics. Bone 2010, 47, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Klein-Nulend, J.; Baker, A.D.; Bacabac, R.G.; Vatsa, A.; Weinbaum, S. Mechanosensation and transduction in osteocytes. Bone 2013, 54, 182–190. [Google Scholar] [CrossRef]
- Stoltz, J.; Magdalou, J.; George, D.; Li, Y.; de Isla, N.; He, X.; Rémond, Y. Influence of mechanical forces on bone: Introduction to mechanobiology and mechanical adaptation concept. J. Cell. Immunother. 2018, 4, 10–12. [Google Scholar] [CrossRef]
- Burr, D.B.; Allen, M.R. Bone Growth, Modeling and Remodeling. In Basic and Applied Bone Biology, 2nd ed.; Burr, D.B., Allen, M.R., Eds.; Elsevier Academic Press: Cambridge, MA, USA, 2019; pp. 85–100. [Google Scholar]
- Stoltz, J.; Chen, Y.; Magdalou, J.; George, D.; Huselstein, C.; de Isla, N.; Zhang, L.; Mainard, D.; Li, Y.; Rémond, Y. Response of bone cells to mechanical stimulations: An overview. Biomed. Health Res. 2019, 79, 71–76. [Google Scholar]
- Stoltz, J.F.; Rémond, Y.; George, D.; Magdalou, J.; Li, Y.P.; Han, Z.C.; Zhang, L.; de Isla, N.; Chen, Y. The Mechanoadaptation Concept of Cells. In Stem Cells and Regenerative Medicine; George, D., Magdalou, J., François Stoltz, J., Eds.; IOS Press: Amsterdam, The Netherlands, 2021; pp. 47–59. ISBN 978-1-64368-027-9. [Google Scholar]
- Lemaire, T.; Capiez-Lernout, E.; Kaiser, J.; Naili, S.; Sansalone, V. What is the importance of multiphysical phenomena in bone remodelling signals expression? A multiscale perspective. J. Mech. Behav. Biomed. Mater. 2011, 4, 909–920. [Google Scholar] [CrossRef] [PubMed]
- Lemaire, T.; Kaiser, J.; Naili, S.; Sansalone, V. Three-scale multiphysics modeling of transport phenomena within cortical bone. Math. Prob. Eng. 2015, 2015, 398970. [Google Scholar] [CrossRef][Green Version]
- Spingarn, C.; Wagner, D.; Rémond, Y.; George, D. Multiphysics of bone remodeling: A 2D mesoscale activation simulation. Bio-Med. Mater. Eng. 2017, 28, S153–S158. [Google Scholar] [CrossRef] [PubMed]
- Pastrama, M.-I.; Scheiner, S.; Pivonka, P.; Hellmich, C. A mathematical multiscale model of bone remodeling, accounting for pore space-specific mechanosensation. Bone 2018, 107, 208–221. [Google Scholar] [CrossRef] [PubMed]
- Sheidaei, A.; Kazempour, M.; Hasanabadi, A.; Nosouhi, F.; Pithioux, M.; Baniassadi, M.; Rémond, Y.; George, D. Influence of bone microstructure distribution on developed mechanical energy for bone remodeling using a statistical reconstruction method. Math. Mech. Solids 2019, 24, 3027–3041. [Google Scholar] [CrossRef]
- Bagherian, A.; Famouri, S.; Baghani, M.; George, D.; Sheidaei, A.; Baniassadi, M. A new statistical descriptor for the physical characterization and 3D reconstruction of heterogeneous materials. Trans. Porous Med. 2021; in press. [Google Scholar] [CrossRef]
- Famouri, S.; Bagherian, A.; Shahmohammadi, A.; George, D.; Baghani, M.; Baniassadi, M. Refining anticipation of degraded bone microstructures during osteoporosis based on statistical homogenized reconstruction method via quality of connection function. Int. J. Comp. Mater. Sci. Eng. 2020, 9, 2050023. [Google Scholar] [CrossRef]
- Lekszycki, T.; Dell’Isola, F. A mixture model with evolving mass densities for describing synthesis and resorption phenomena in bones reconstructed with bio-resorbable materials. ZAMM 2012, 92, 426–444. [Google Scholar] [CrossRef]
- Madeo, A.; George, D.; Lekszycki, T.; Nierenberger, M.; Rémond, Y. A second gradient continuum model accounting for some effects of micro-structure on reconstructed bone remodeling. C. R. Mécanique 2012, 340, 575–589. [Google Scholar] [CrossRef]
- Andreaus, U.; Giorgio, I.; Lekszycki, T. A 2-D continuum model of a mixture of bone tissue and bio-resorbable material for simulating mass density redistribution under load slowly variable in time. ZAMM 2014, 94, 978–1000. [Google Scholar] [CrossRef]
- Scala, I.; Spingarn, C.; Rémond, Y.; Madeo, A.; George, D. Mechanically-driven bone remodeling simulations: Applications to LIPUS treated rat calvarial defects. Math. Mech. Solids 2016, 22, 1976–1988. [Google Scholar] [CrossRef]
- Giorgio, I.; Andreaus, U.; Scerrato, D.; Dell’Isola, F. A visco-poroelastic model of functional adaptation in bones reconstructed with bio-resorbable materials. Biomech. Model. Mechanobiol. 2016, 15, 1325–1343. [Google Scholar] [CrossRef] [PubMed]
- Giorgio, I.; Andreaus, U.; Dell’Isola, F.; Lekszycki, T. Viscous second gradient porous materials for bones reconstructed with bio-resorbable grafts. Extrem. Mech. Lett. 2017, 13, 141–147. [Google Scholar] [CrossRef]
- Allena, R.; Maini, P.K. Reaction-diffusion finite element model of lateral line primordium migration to explore cell leadership. Bull. Math. Biol. 2014, 76, 3028–3050. [Google Scholar] [CrossRef]
- Schmitt, M.; Allena, R.; Schouman, T.; Frasca, S.; Collombet, J.M.; Holy, X.; Rouch, P. Diffusion model to describe osteogenesis within a porous titanium scaffold. Comp. Meth. Biomech. Biomed. Eng. 2015, 19, 171–179. [Google Scholar] [CrossRef]
- Frame, J.; Rohan, P.Y.; Corté, L.; Allena, R. A mechano-biological model of multi-tissue evolution in bone. Contin. Mech. Thermodyn. 2017, 31, 1–31. [Google Scholar] [CrossRef]
- Frame, J.; Rohan, P.Y.; Corté, L.; Allena, R. Optimal bone structure is dependent on the interplay between mechanics and cellular activities. Mech. Res. Commun. 2018, 92, 43–48. [Google Scholar] [CrossRef]
- George, D.; Allena, R.; Rémond, Y. Cell nutriments and motility for mechanobiological bone remodeling in the context of orthodontic periodontal ligament deformation. J. Cell. Immunother. 2018, 4, 26–29. [Google Scholar] [CrossRef]
- George, D.; Allena, R.; Rémond, Y. A multiphysics stimulus for continuum mechanics bone remodeling. Math. Mech. Comp. Syst. 2018, 6, 307–319. [Google Scholar] [CrossRef]
- George, D.; Allena, R.; Rémond, Y. Integrating molecular and cellular kinetics into a coupled continuum mechanobiological stimulus for bone reconstruction. Contin. Mech. Thermodyn. 2019, 31, 725–740. [Google Scholar] [CrossRef]
- Ehrlich, P.J.; Lanyon, L.E. Mechanical strain and bone cell function: A review. Osteop. Int. 2002, 13, 688–700. [Google Scholar] [CrossRef] [PubMed]
- Ignatius, A.; Blessig, H.; Liedert, A.; Schmidt, C.; Neidlinger-Wilke, C.; Kaspar, D.; Friemert, B.; Clase, L. Tissue engineering of bone: Effects of mechanical strain on osteoblastic cells in type I collagen matrices. Biomaterials 2005, 26, 311–318. [Google Scholar] [CrossRef] [PubMed]
- Lemaire, T.; Naili, S.; Sansalone, V. Multiphysical modelling of fluid transport through osto-articular media. Ann. Braz. Acad. Sci. 2010, 82, 127–144. [Google Scholar] [CrossRef][Green Version]
- Hojo, H.; Ohba, S. Gene regulatory landscape in osteoblast differentiation. Bone 2020, 137, 115458. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Canalis, E. Notch and the regulation of osteoclast differentiation and function. Bone 2020, 138, 115474. [Google Scholar] [CrossRef] [PubMed]
- Ganesh, T.; Laughrey, L.E.; Niroobakhsh, M.; Lara-Castillo, N. Multiscale finite element modeling of mechanical strains and fluid flow in osteocyte lacunocanalicular system. Bone 2020, 137, 115328. [Google Scholar] [CrossRef]
- Sibonga, J.; Matsumoto, T.; Jones, J.; Shapiro, J.; Lang, T.; Shackelford, L.; Smith, S.M.; Young, M.; Keyak, J.; Kohri, K.; et al. Resistive exercise in astronauts on prolonged spaceflights provides partial protection against spaceflight-induced bone loss. Bone 2019, 128, 112037. [Google Scholar] [CrossRef]
- Bagherian, A.; Baghani, M.; George, D.; Rémond, Y.; Chappard, C.; Patlazhan, S.; Baniassadi, M. A novel numerical model for the prediction of patient dependent bone density loss in microgravity based on micro-CT images. Contin. Mech. Thermodyn. 2020, 32, 927–943. [Google Scholar] [CrossRef]
- Singhal, V.; Sanchita, S.; Malhotra, S.; Bose, A.; Flores, L.P.T.; Valera, R.; Stanford, F.C.; Slattery, M.; Rosenblum, J.; Goldstein, M.A.; et al. Suboptimal bone microarchitecture in adolescent girls with obesity compared to normal-weight controls and girls with anorexia nervosa. Bone 2019, 122, 246–253. [Google Scholar] [CrossRef]
- Marin-Puyalto, J.; Mäestu, J.; Gómez-Cabello, A.; Lätt, E.; Remmel, L.; Purge, P.; Vicente-Rodríguez, G.; Jürimäe, J. Frequency and duration of vigorous physical activity bouts are associated with adolescent boys’ bone mineral status: A cross-sectional study. Bone 2019, 120, 141–147. [Google Scholar] [CrossRef] [PubMed]
- O’Leary, T.J.; Izard, R.M.; Walsh, N.P.; Tang, J.C.Y.; Fraser, W.D.; Greeves, J.P. Skeletal macro-and microstructure adaptations in men undergoing arduous military training. Bone 2019, 125, 54–60. [Google Scholar] [CrossRef] [PubMed]
- George, D.; Allena, R.; Bourzac, C.; Pallu, S.; Bensidhoum, M.; Portier, H.; Rémond, Y. A new comprehensive approach for bone remodeling under medium and high mechanical load based on cellular activity. Math. Mech. Complex Syst. 2021, 8, 287–306. [Google Scholar] [CrossRef]
- Bourzac, C.; Bensidhoum, M.; Manassero, M.; Chappard, C.; Michoux, N.; Pallu, S.; Portier, H. Preventive Moderate Continuous Running-Exercise Conditioning Improves the Healing of Non-Critical Size Bone Defects in Male Wistar Rats: A Pilot Study Using µCT. Life 2020, 10, 308. [Google Scholar] [CrossRef] [PubMed]
- Bouxsein, M.L.; Boyd, S.K.; Christiansen, B.A.; Guldberg, R.E.; Jepsen, K.J.; Müller, R. Guidelines for assessment of bone microstructure in rodents using micro-computed tomography. J. Bone Min. Res. 2010, 25, 1468–1486. [Google Scholar] [CrossRef] [PubMed]
- Zeitoun, D.; Caliaperoumal, G.; Bensidhoum, M.; Constans, J.M.; Anagostou, F.; Bousson, V. Microcomputed tomography of the femur of diabetic rats: Alterations of trabecular and cortical bone microarchitecture and vasculature—A feasibility study. Eur. Radiol. Exp. 2019, 3, 17. [Google Scholar] [CrossRef] [PubMed]
- Ballanti, P.; Minisola, S.; Pacitti, M.T.; Scarnecchia, L.; Mazzuoli, G.F.; Bonucci, E. Tartrate-resistant acid phosphate activity as osteoclastic marker: Sensitivity of cytochemical assessment and serum assay in comparison with standardized osteoclast histomorphometry. Osteoporos. Int. 1997, 7, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Delaisse, J.-M.; Andersen, T.L.; Kristensen, H.B.; Jensen, P.R.; Andreasen, C.M.; Soe, K. Re-thinking the bone remodeling cycle mechanism and the origin of bone loss. Bone 2020, 141, 115628. [Google Scholar] [CrossRef]
- Rho, J.Y.; Ho Ba Tho, M.C.; Ashman, R.B. Relations of mechanical properties to density and CT numbers in human bone. Med. Eng. Phys. 1995, 17, 347–355. [Google Scholar] [CrossRef]
- Bernard, S.; Grimal, Q.; Laugier, P. Accurate measurement of cortical bone elasticity tensor with resonant ultrasound spectroscopy. J. Mech. Behav. Biomed. Mater. 2013, 18, 12–19. [Google Scholar] [CrossRef]
- Mow, V.C.; Huiskes, R. Basic Orthopaedic Biomechanics and Mechano-Biology, 3rd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2005; p. 140. [Google Scholar]
- Forwood, M.R.; Parker, A.W. Microdamage in response to repetitive torsional loading in the rat tibia. Calcif. Tissue Int. 1989, 45, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Grimston, S.K.; Engsberg, J.R.; Kloiber, R. Bone mass, external loadsand stress fracture in female runners. Int. J. Sports Biomech. 1991, 7, 293–302. [Google Scholar] [CrossRef]
- Herman, B.C.; Cardoso, L.; Majeska, R.J.; Jepsen, K.J.; Schaffler, M.B. Activation of bone remodeling after fatigue: Differential response to linear microcracks and diffuse damage. NIH Pub. Access 2010, 47, 766–772. [Google Scholar] [CrossRef] [PubMed]
- Hao, L.; Rui-Xin, L.; Bin, Z.; Bao-Hui, H.; Ying-Jie, L.; Xi-Zheng, Z. Effects of athletic fatigue damage and the associated bone targeted remodeling in the rat ulan. BioMed. Eng. Online 2017, 16, 99. [Google Scholar] [CrossRef] [PubMed]
- Joo, Y.-I.; Sone, T.; Fukunaga, M.; Lim, S.-G.; Onodera, S. Effects of endurance exercise on three-dimensional trabecular bone microarchitecture in young growing rats. Bone 2003, 33, 485–493. [Google Scholar] [CrossRef]
- Ebata, H.; Moriyama, K.; Kuboki, T.; Kidoaki, S. General cellular durotaxis induced with cell-scale heterogeneity of matrix-elasticity. Biomaterials 2020, 230, 119647. [Google Scholar] [CrossRef]
- Scerrato, D.; Bersani, A.M.; Giorgio, I. Bio-inspired design of a porous resorbable scaffold for bone reconstruction: A preliminary study. Biomimetics 2021, 6, 18. [Google Scholar] [CrossRef] [PubMed]
- Giorgio, I.; Spagnuolo, M.; Andreaus, U.; Scerrato, D.; Bersani, A.M. In-depth gaze at the astonishing mechanical behavior of bone: A review for designing bio-inspired hierarchical metamaterials. Math. Mech. Sol. 2021, 26, 1074–1103. [Google Scholar] [CrossRef]




| Sedentary Control | Continuous Running | Intermittent Running | |
|---|---|---|---|
| Cortical tibial thickness (µm) | 957 (±110) Normalized = 1 | 708 (±65) Normalized = 0.74 | 1024 (±112) Normalized = 1.07 |
| Loading type | Constant load (body weight) | 1 week for 25 min/day, 8 weeks for 45 min/day, Oxygen = 70% MAS | 1 week for 25 min/day continuous, 8 weeks intermittent for 42 min/day, Oxygen = 50%, 100% MASand rest |
| Sedentary Control | Continuous Running | Intermittent Running | |
|---|---|---|---|
| BMD (g HA/cm3) | 113.11 (± 4.12) | 109.16 (± 4.31) * | 106.13 (± 4.22) * |
| Parameters Determined from Experimental Data (×10−4 mJ) | Parameters Calculated (ki = mg·mJ−1·mm−3·56d−1; Ai = mg·mm−3·56d−1) | ||||||
|---|---|---|---|---|---|---|---|
| W0 | W1 | W2 | W3 | k1 | k2 | A1 | A2 |
| 3.1847 | 3.7 | 3.72 | 3.78 | 386.64 × 105 | −375 × 105 | 1992.36 | −2232.38 |
| Osteoblast Activity Coefficient at W1 | Osteoclast Activity Coefficient at W1 | Osteoblast Activity Coefficient at W3 | Osteoclast Activity Coefficient at W3 | Cellular Activity Power at W1 | Cellular Activity Power at W3 |
|---|---|---|---|---|---|
| α = 1.0009 | α = 1.0 | α = 1.0007 | α = 1.0 | n = 13.6 | n = 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
George, D.; Pallu, S.; Bourzac, C.; Wazzani, R.; Allena, R.; Rémond, Y.; Portier, H. Prediction of Cortical Bone Thickness Variations in the Tibial Diaphysis of Running Rats. Life 2022, 12, 233. https://doi.org/10.3390/life12020233
George D, Pallu S, Bourzac C, Wazzani R, Allena R, Rémond Y, Portier H. Prediction of Cortical Bone Thickness Variations in the Tibial Diaphysis of Running Rats. Life. 2022; 12(2):233. https://doi.org/10.3390/life12020233
Chicago/Turabian StyleGeorge, Daniel, Stéphane Pallu, Céline Bourzac, Rkia Wazzani, Rachele Allena, Yves Rémond, and Hugues Portier. 2022. "Prediction of Cortical Bone Thickness Variations in the Tibial Diaphysis of Running Rats" Life 12, no. 2: 233. https://doi.org/10.3390/life12020233
APA StyleGeorge, D., Pallu, S., Bourzac, C., Wazzani, R., Allena, R., Rémond, Y., & Portier, H. (2022). Prediction of Cortical Bone Thickness Variations in the Tibial Diaphysis of Running Rats. Life, 12(2), 233. https://doi.org/10.3390/life12020233







