Repair Kinetics of DSB-Foci Induced by Proton and α-Particle Microbeams of Different Energies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cell Culture
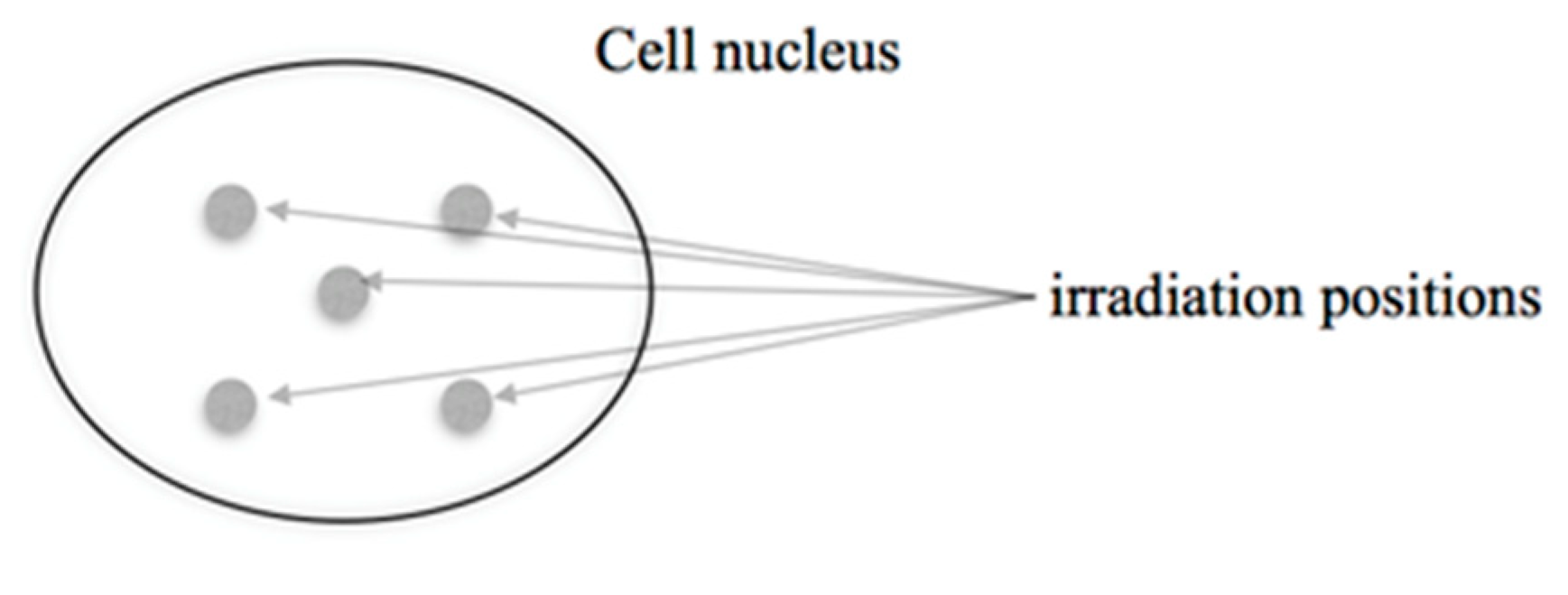
2.2. Microbeam Irradiations
2.3. Immunostaining and Microscopy
2.4. Data Analysis
- The expected number of foci per nucleus and the respective uncertainty for a radiation condition were estimated, respectively, as the mean and the sample standard deviation of the mean values found in the three replicate experiments.
- The possibility of indistinguishable foci in case of tracks passing the nucleus in proximity was taken into account using a development of the approach of Gonon et al. [15]: The mean number of tracks in proximity (leading to indistinguishable foci) were determined by a simulation of the irradiation, separately for each possible number of ions in such a track “cluster”. The positions of the points of ion passage through the image plane as well as the lengths of the main axes and orientation of the ellipse representing a cell nucleus were randomly sampled. (Supplementary Tables S1 and S2).
- In addition, the possibility that several foci are formed within an ion track and are indistinguishable is taken into account. The number of foci formed in an ion track is assumed to be Poisson distributed.
- It is assumed that radiation-induced foci and foci induced by non-radiation causes occur statistically independently.
- Sham irradiated foci are assumed to be always repairable whereas for radiation-induced foci it is possible that foci are persistent.
- The repair of foci is assumed to be below the saturation point and to follow first order kinetics with a repair rate independent of radiation quality. The first assumption seems justified because even at the highest LET values, the dose to the nucleus from the five passing ion tracks is less than 1 Gy.
3. Results
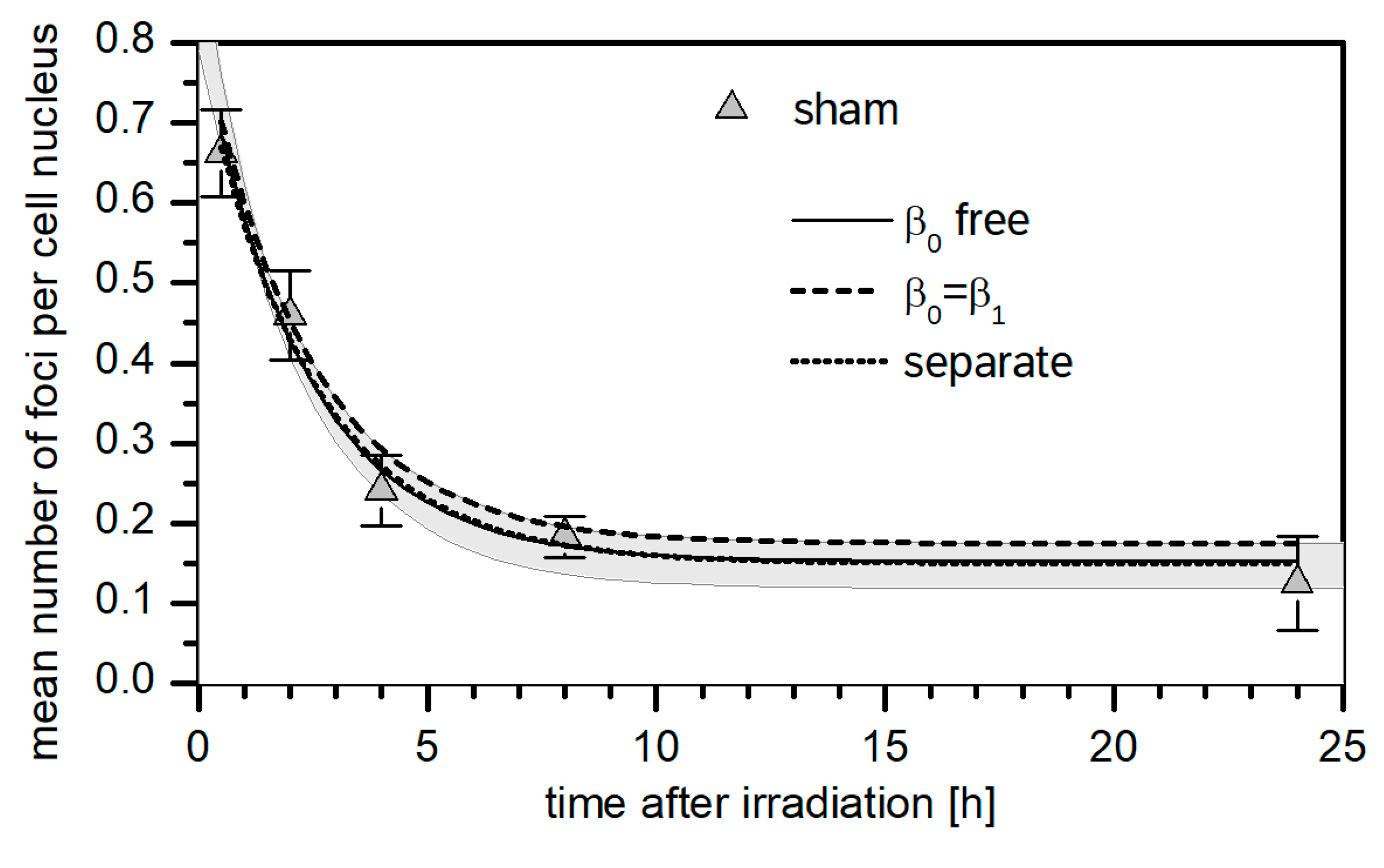
3.1. 53BP1 Foci Background
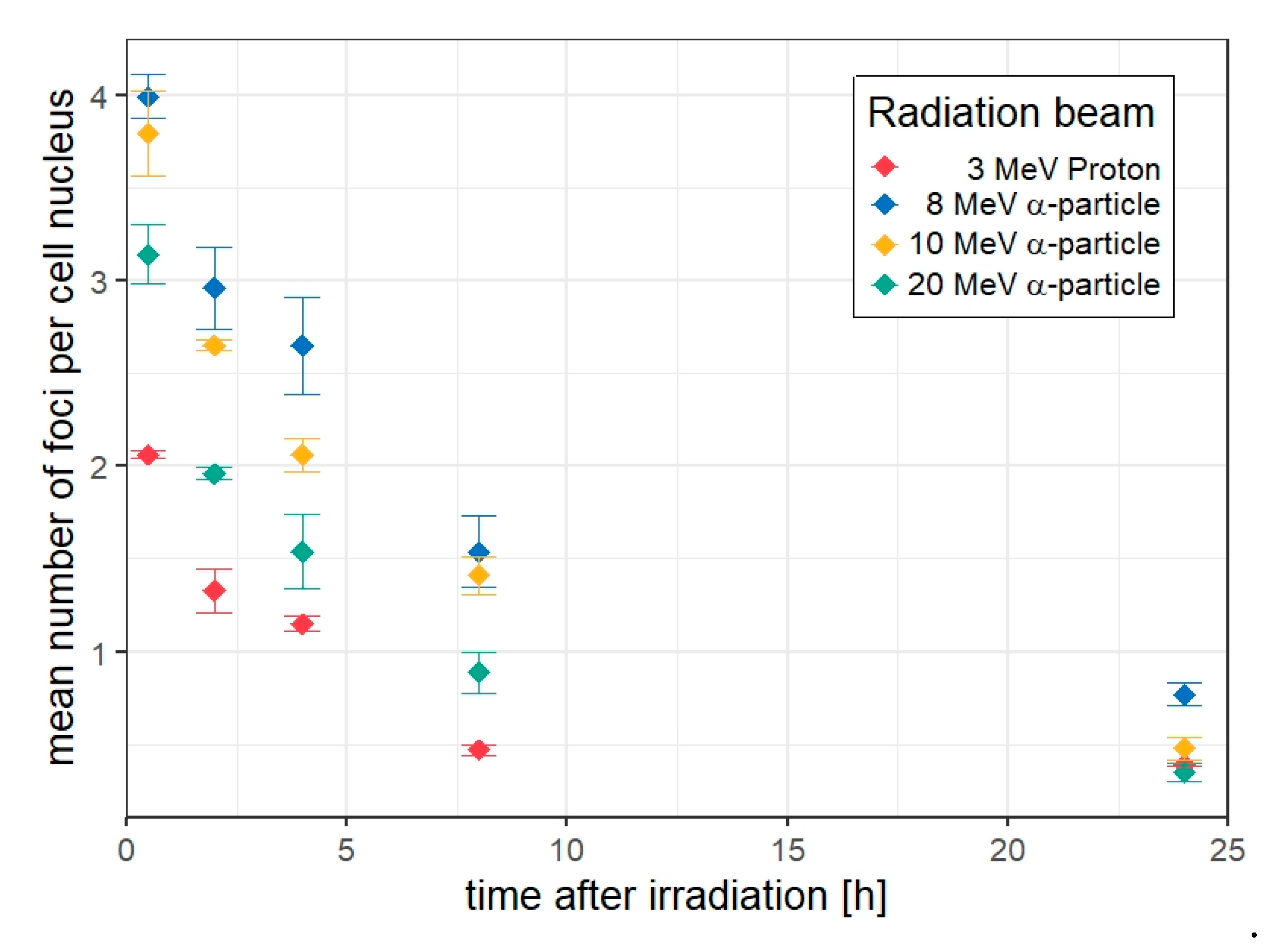
3.2. 53BP1 Foci in HUVEC Cells Targeted with 5 Ions
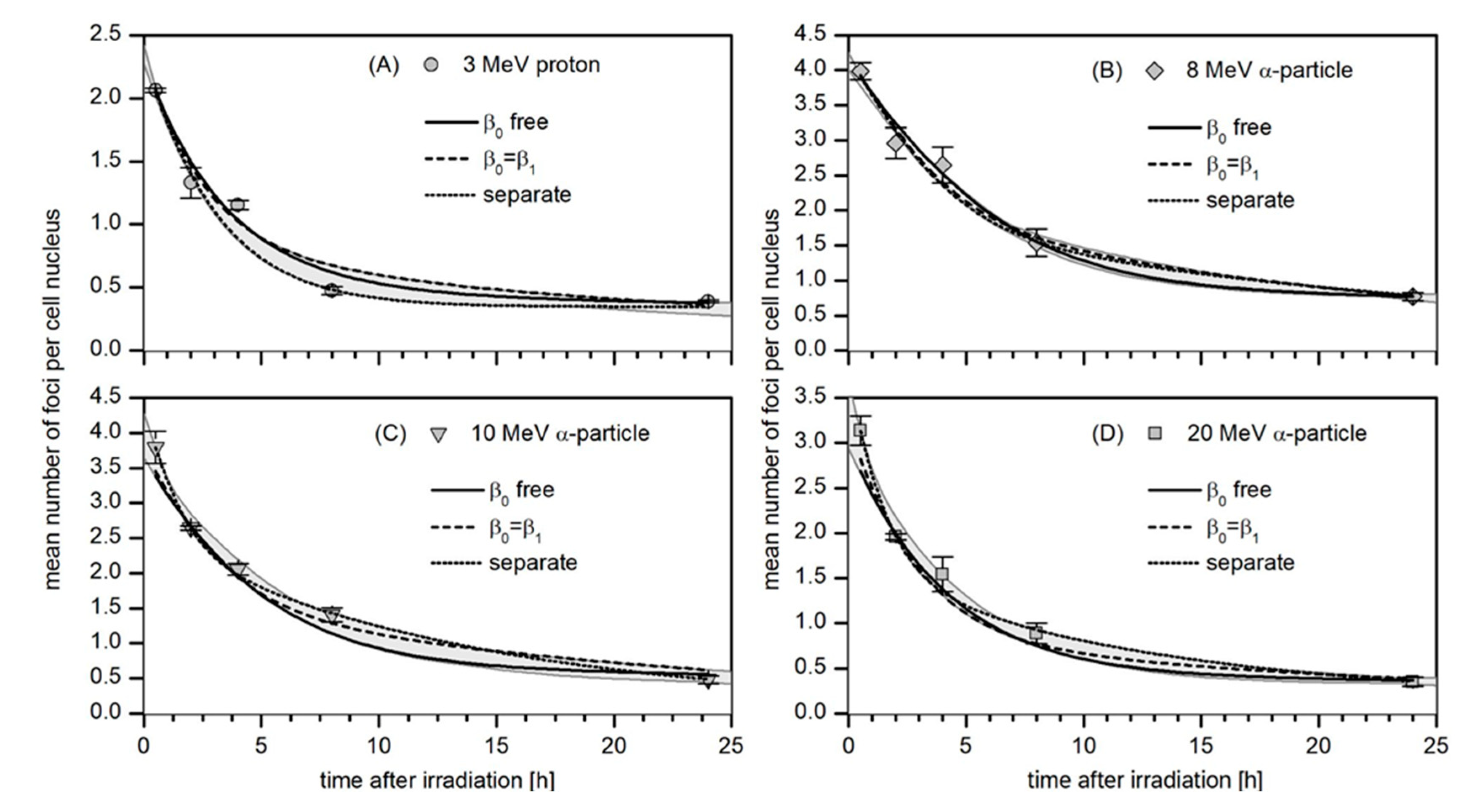
3.3. Kinetics of the Decay of 53BP1 Foci
3.4. Robustness Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ward, J.F. DNA damage produced by ionizing radiation in mammalian cells: Identities, mechanisms of formation, and reparability. Prog. Nucleic Acid Res. Mol. Biol. 1988, 35, 95–125. [Google Scholar] [CrossRef] [PubMed]
- Vilenchik, M.M.; Knudson, A.G. Endogenous DNA double-strand breaks: Production, fidelity of repair, and induction of cancer. Proc. Natl. Acad. Sci. USA 2003, 100, 12871–12876. [Google Scholar] [CrossRef]
- Pastwa, E.; Neumann, R.D.; Mezhevaya, K.; Winters, T.A. Repair of Radiation-Induced DNA Double-Strand Breaks is Dependent upon Radiation Quality and the Structural Complexity of Double-Strand Breaks. Radiat. Res. 2003, 159, 251–261. [Google Scholar] [CrossRef] [PubMed]
- Du, L.-L.; Nakamura, T.M.; Moser, B.A.; Russell, P. Retention but Not Recruitment of Crb2 at Double-Strand Breaks Requires Rad1 and Rad3 Complexes. Mol. Cell. Biol. 2003, 23, 6150–6158. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Capetillo, O.; Chen, H.-T.; Celeste, A.; Ward, I.; Romanienko, P.J.; Morales, J.; Naka, K.; Xia, Z.; Camerini-Otero, R.D.; Motoyama, N.; et al. DNA damage-induced G2–M checkpoint activation by histone H2AX and 53BP1. Nat. Curell Biol. 2002, 4, 993–997. [Google Scholar] [CrossRef]
- Rogakou, E.P.; Pilch, D.R.; Orr, A.H.; Ivanova, V.S.; Bonner, W.M. DNA Double-stranded Breaks Induce Histone H2AX Phosphorylation on Serine 139. J. Biol. Chem. 1998, 273, 5858–5868. [Google Scholar] [CrossRef] [PubMed]
- Anderson, L.; Henderson, C.; Adachi, Y. Phosphorylation and Rapid Relocalization of 53BP1 to Nuclear Foci upon DNA Damage. Mol. Cell. Biol. 2001, 21, 1719–1729. [Google Scholar] [CrossRef]
- Mosconi, M.; Giesen, U.; Langner, F.; Mielke, C.; Rosa, I.D.; Dirks, W.G. 53BP1 and MDC1 foci formation in HT-1080 cells for low- and high-LET microbeam irradiations. Radiat. Environ. Biophys. 2011, 50, 345–352. [Google Scholar] [CrossRef]
- Hable, V.; Drexler, G.; Brüning, T.; Burgdorf, C.; Greubel, C.; Derer, A.; Seel, J.; Strickfaden, H.; Cremer, T.; Friedl, A.; et al. Recruitment Kinetics of DNA Repair Proteins Mdc1 and Rad52 but Not 53BP1 Depend on Damage Complexity. PLoS ONE 2012, 7, e41943. [Google Scholar] [CrossRef]
- Georgakilas, A.G.; O’Neill, P.; Stewart, R.D. Induction and Repair of Clustered DNA Lesions: What Do We Know So Far? Radiat. Res. 2013, 180, 100–109. [Google Scholar] [CrossRef]
- Jezkova, L.; Zadneprianetc, M.; Kulikova, E.; Smirnova, E.; Bulanova, T.; Depes, D.; Falkova, I.; Boreyko, A.; Krasavin, E.; Davidkova, M.; et al. Particles with similar LET values generate DNA breaks of different complexity and reparability: A high-resolution microscopy analysis of γH2AX/53BP1 foci. Nanoscale 2017, 10, 1162–1179. [Google Scholar] [CrossRef]
- Gulliford, S.; Prise, K. Relative Biological Effect/Linear Energy Transfer in Proton Beam Therapy: A Primer. Clin. Oncol. 2019, 31, 809–812. [Google Scholar] [CrossRef]
- Datta, K.; Jaruga, P.; Dizdaroglu, M.; Neumann, R.D.; Winters, T.A. Molecular Analysis of Base Damage Clustering Associated with a Site-Specific Radiation-Induced DNA Double-Strand Break. Radiat. Res. 2006, 166, 767–781. [Google Scholar] [CrossRef]
- Nikjoo, H.; O’Neill, P.; Terrissol, M.; Goodhead, D.T. Quantitative modelling of DNA damage using Monte Carlo track structure method. Radiat. Environ. Biophys. 1999, 38, 31–38. [Google Scholar] [CrossRef]
- Gonon, G.; Villagrasa, C.; Voisin, P.; Meylan, S.; Bueno, M.; Benadjaoud, M.A.; Tang, N.; Langner, F.; Rabus, H.; Barquinero, J.-F.; et al. From Energy Deposition of Ionizing Radiation to Cell Damage Signaling: Benchmarking Simulations by Measured Yields of Initial DNA Damage after Ion Microbeam Irradiation. Radiat. Res. 2019, 191, 566–584. [Google Scholar] [CrossRef]
- Rabus, H.; Palmans, H.; Hilgers, G.; Sharpe, P.; Pinto, M.; Villagrasa, C.; Nettelbeck, H.; Moro, D.; Pola, A.; Pszona, S.; et al. Biologically Weighted Quantities in Radiotherapy: An EMRP Joint Research Project. EPJ Web Conf. 2014, 77, 00021. [Google Scholar] [CrossRef]
- Palmans, H.; Rabus, H.; Belchior, A.L.; Bug, M.U.; Galer, S.; Giesen, U.; Gonon, G.; Gruel, G.; Hilgers, G.; Moro, D.; et al. Future development of biologically relevant dosimetry. Br. J. Radiol. 2015, 88, 20140392. [Google Scholar] [CrossRef]
- Greif, K.-D.; Brede, H.J.; Frankenberg, D.; Giesen, U. The PTB single ion microbeam for irradiation of living cells. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 2004, 217, 505–512. [Google Scholar] [CrossRef]
- Schultz, L.B.; Chehab, N.H.; Malikzay, A.; Halazonetis, T.D. P53 Binding Protein 1 (53bp1) Is an Early Participant in the Cellular Response to DNA Double-Strand Breaks. J. Cell Biol. 2000, 151, 1381–1390. [Google Scholar] [CrossRef]
- Marková, E.; Schultz, N.; Belyaev, I.Y. Kinetics and dose-response of residual 53BP1/γ-H2AX foci: Co-localization, relationship with DSB repair and clonogenic survival. Int. J. Radiat. Biol. 2007, 83, 319–329. [Google Scholar] [CrossRef]
- Plante, I.; Slaba, T.; Shavers, Z.; Hada, M. A Bi-Exponential Repair Algorithm for Radiation-Induced Double-Strand Breaks: Application to Simulation of Chromosome Aberrations. Genes 2019, 10, 936. [Google Scholar] [CrossRef] [PubMed]
- Rabus, H.; Barbieri, S.; Baiocco, G.; Ottolenghi, A.; Giesen, U. Investigation into uncertainty contributions in foci-based assays. Radiat. Prot. Dosim. 2018, 183, 126–130. [Google Scholar] [CrossRef] [PubMed]
- Abu Shqair, A.; Lee, U.-S.; Kim, E.-H. Computational modelling of γ-H2AX foci formation in human cells induced by alpha particle exposure. Sci. Rep. 2022, 12, 14360. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter (2010). Nucl. Instrum. Methods B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Carpenter, A.E.; Jones, T.R.; Lamprecht, M.R.; Clarke, C.; Kang, I.H.; Friman, O.; Guertin, D.A.; Chang, J.H.; Lindquist, R.A.; Moffat, J.; et al. CellProfiler: Image analysis software for identifying and quantifying cell phenotypes. Genome Biol. 2006, 7, R100. [Google Scholar] [CrossRef]
- Markwardt, C.B. Non-linear Least Squares Fitting in IDL with MPFIT. arXiv, 2009; arXiv:0902.2850. [Google Scholar]
- Ugenskienė, R.; Prise, K.; Folkard, M.; Lekki, J.; Stachura, Z.; Zazula, M.; Stachura, J. Dose response and kinetics of foci disappearance following exposure to high- and low-LET ionizing radiation. Int. J. Radiat. Biol. 2009, 85, 872–882. [Google Scholar] [CrossRef]
- Canhoto, J.d.F. LET-and Radiation Quality-Dependence of the Complexity of DNA Damages. Master’s Thesis, University of Lisbon, Lisbon, Portugal, 2018. Available online: https://repositorio.ul.pt/handle/10451/36798 (accessed on 24 October 2022).
- Belchior, A.; Canhoto, J.; Giesen, U.; Rabus, H. The impact of detection thresholds in automatic scoring of radiation-induced and background DNA damage foci. In Proceedings of the International Conference on Dosimetry and its Applications, Lisbon, Portugal, 27–31 May 2019. [Google Scholar]
- Rucinski, A.; Biernacka, A.M.; Schulte, R.W. Applications of nanodosimetry in particle therapy planning and beyond. Phys. Med. Biol. 2021, 66, 24TR01. [Google Scholar] [CrossRef]
- Goodhead, D.T. The Initial Physical Damage Produced by Ionizing Radiations. Int. J. Radiat. Biol. 1989, 56, 623–634. [Google Scholar] [CrossRef] [PubMed]
- Schulte, R.W.; Wroe, A.J.; Bashkirov, V.A.; Garty, G.Y.; Breskin, A.; Chechik, R.; Shchemelinin, S.; Gargioni, E.; Grosswendt, B.; Rosenfeld, A.B. Nanodosimetry-based quality factors for radiation protection in space. Z. Für Med. Phys. 2008, 18, 286–296. [Google Scholar] [CrossRef]
- Carabe-Fernandez, A.; Dale, R.G.; Jones, B. The incorporation of the concept of minimum RBE (RBEmin) into the linear-quadratic model and the potential for improved radiobiological analysis of high-LET treatments. Int. J. Radiat. Biol. 2007, 83, 27–39. [Google Scholar] [CrossRef]
- Wedenberg, M.; Lind, B.K.; Hårdemark, B. A model for the relative biological effectiveness of protons: The tissue specific parameter α/β of photons is a predictor for the sensitivity to LET changes. Acta Oncol. 2012, 52, 580–588. [Google Scholar] [CrossRef] [PubMed]
- Underwood, T.S.; McMahon, S.J. Proton relative biological effectiveness (RBE): A multiscale problem. Br. J. Radiol. 2018, 92, 20180004. [Google Scholar] [CrossRef] [PubMed]

| Particle Type and Beam Energy | Estimated Energy at Cell Nucleus Center (MeV) | Estimated LET at Cell Nucleus Center (keV/µm) |
|---|---|---|
| α-particles | ||
| 20 MeV | 17.8 ± 0.2 | 36 ± 1 |
| 10 MeV | 5.5 ± 0.4 | 85 ± 4 |
| 8 MeV | 1.9 ± 0.6 | 170 ± 40 |
| Protons | ||
| 3 MeV | 1.6 ± 0.2 | 19 ± 2 |
| (1) Radiation Beam | (2) LET (keV/µm) |
(3) Mean Number of Foci Per Track, |
(4) Proportion of Persistent Foci, |
(5) Mean Number of Persistent Foci Per Track, |
(6) Repair Rate, |
(7) Repair Rate, |
|---|---|---|---|---|---|---|
| Protons 3 MeV | 19 ± 2 | 0.37 ± 0.02 0.37 ± 0.02 | 0.17 ± 0.12 0.28 ± 0.12 | 0.06 ± 0.04 0.10 ± 0.04 | 0.27 ± 0.05 0.32 ± 0.07 | 0.01 ± 0.03 0.04 ± 0.02 |
| α—particles 20 MeV | 36 ± 1 | 0.63 ± 0.04 0.63 ± 0.04 | 0.10 ± 0.07 0.16 ± 0.08 | 0.06 ± 0.04 0.11 ± 0.05 | ||
| 10 MeV | 85 ± 4 | 1.08 ± 0.06 1.09 ± 0.07 | 0.11 ± 0.08 0.21 ± 0.10 | 0.12 ± 0.08 0.23 ± 0.11 | ||
| 8 MeV | 170 ± 40 | 1.66 ± 0.18 1.68 ± 0.18 | 0.11 ± 0.08 0.21 ± 0.10 | 0.19 ± 0.14 0.33 ± 0.16 |
| (1) Radiation Beam | (2) LET (keV/µm) |
(3) Mean Number of Foci Per Track, |
(4) Proportion of Persistent Foci, |
(5) Mean Number of Persistent Foci Per Track, |
(6) Repair Rate, |
(7) Repair Rate, |
|---|---|---|---|---|---|---|
| Protons 3 MeV | 19 ± 2 | 0.37 ± 0.02 0.37 ± 0.02 | 0.42 ± 0.06 0.38 ± 0.05 | 0.15 ± 0.02 0.14 ± 0.02 | 0.43 ± 0.01 0.41 ± 0.01 | 0.06 ± 0.01 0.05 ± 0.01 |
| α—particles 20 MeV | 36 ± 1 | 0.69 ± 0.04 0.69 ± 0.04 | 0.25 ± 0.06 0.22 ± 0.05 | 0.17 ± 0.04 0.15 ± 0.03 | ||
| 10 MeV | 85 ± 4 | 1.13 ± 0.06 1.13 ± 0.06 | 0.33 ± 0.06 0.30 ± 0.05 | 0.38 ± 0.08 0.34 ± 0.06 | ||
| 8 MeV | 170 ± 40 | 1.68 ± 0.18 1.68 ± 0.18 | 0.31 ± 0.08 0.27 ± 0.07 | 0.52 ± 0.15 0.47 ± 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belchior, A.; Canhoto, J.F.; Giesen, U.; Langner, F.; Rabus, H.; Schulte, R. Repair Kinetics of DSB-Foci Induced by Proton and α-Particle Microbeams of Different Energies. Life 2022, 12, 2040. https://doi.org/10.3390/life12122040
Belchior A, Canhoto JF, Giesen U, Langner F, Rabus H, Schulte R. Repair Kinetics of DSB-Foci Induced by Proton and α-Particle Microbeams of Different Energies. Life. 2022; 12(12):2040. https://doi.org/10.3390/life12122040
Chicago/Turabian StyleBelchior, Ana, João F. Canhoto, Ulrich Giesen, Frank Langner, Hans Rabus, and Reinhard Schulte. 2022. "Repair Kinetics of DSB-Foci Induced by Proton and α-Particle Microbeams of Different Energies" Life 12, no. 12: 2040. https://doi.org/10.3390/life12122040
APA StyleBelchior, A., Canhoto, J. F., Giesen, U., Langner, F., Rabus, H., & Schulte, R. (2022). Repair Kinetics of DSB-Foci Induced by Proton and α-Particle Microbeams of Different Energies. Life, 12(12), 2040. https://doi.org/10.3390/life12122040







