1. Introduction
The idea that chemical evolution led to the origin of life was proposed independently by Oparin [
1] and Haldane [
2]. It was later shown to be plausible through the experiments of Miller [
3]. Recently, different variants of these experiments were repeated, and analyzed with state-of-the-art molecular analysis technology [
4,
5]. This revealed the presence of thousands of molecular species, including many classes of organic and catalytic ones. However, it still leaves open the question of how such spontaneous chemical evolution can give rise to a coherent, self-reproducing collective of molecules.
One possible answer to this question was proposed in the form of the emergence of autocatalytic sets [
6,
7]. Informally, an autocatalytic set is a chemical reaction network in which the molecules mutually catalyze each other’s formation, and which is self-sustaining given a basic food source. That such autocatalytic sets can indeed form spontaneously was already shown early on through computer simulations [
8,
9,
10]. Later on, they were also successfully constructed with real molecules in the lab [
11,
12,
13,
14], and shown to exist in the metabolic networks of prokaryotes [
15,
16,
17]. The notion of autocatalytic sets was formalized and studied extensively as reflexively autocatalytic and food-generated (RAF) sets (see, for example, [
18,
19] and references therein).
Recently, a simple model of combinatorial innovation, referred to as the
theory of the adjacent possible (TAP), was studied formally [
20]. In general, TAP states that evolving systems create their own future possibilities in an ever-increasing “adjacent possible”. In particular, the number of “things” that can come into existence (or be created) next increases as a combinatorial function of what is currently in existence. As such, this model can also be interpreted in the context of chemical evolution, where the “things” are molecular species. The more molecular species that are currently in existence, the more potential new species that can come into existence next through (spontaneous) chemical reactions between arbitrary combinations of currently existing molecules. An initial investigation of the combination of the TAP and RAF models was presented in the context of technological evolution [
21]. Here, we present results of a further investigation into this model combination, with both theoretical and computer simulation results, and more specifically in the context of chemical evolution and how it could lead to the formation of mutually catalytic and self-reproducing collectives of molecules as a possible step towards the (or an) origin of life.
3. Results
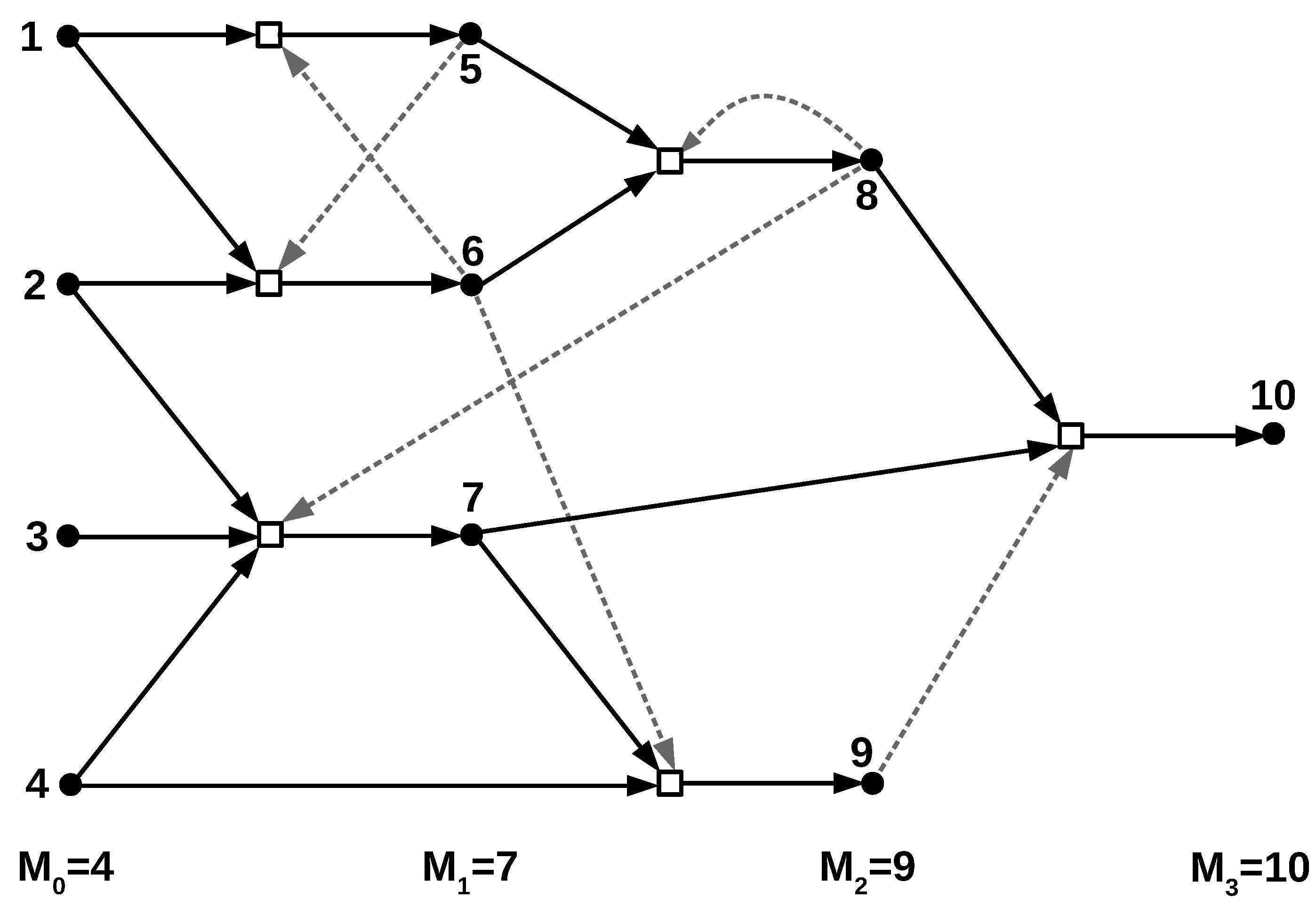
Consider an instance of the TAP model, described by (for ) where is a set of molecular species generated up to time t and is the set of all reactions involved in generating starting from . We let and denote the number of molecular species in and reactions in , respectively. Note that these families of sets (and their sizes) are random variables for each . We assume throughout this section that , and for at least one value of . We also explicitly assume in this section that for each pair where and , x catalyzes r with probability p, and that these catalysis events are stochastically independent.
Throughout this section we do not specifically require that , nor do we place any upper bound (such as ) on unless otherwise stated, or any bound (such as K) on the number of reactants of a reaction.
Since every reaction in the TAP model creates exactly one new product, we have:
Lemma 1. In the TAP model, is nondecreasing, and with probability 1, as t grows.
Proof. is a Markovian random walk on the positive integers, with for all t, and the probability of the event is uniformly bounded away from 0 for all values of t. By a standard probability argument, for any positive integer k, the event that holds for all t has probability 0. Thus, which ensures that with probability 1. □
Remark 1. If an upper bound is imposed on (so that the process terminates when ) then Lemma 1 implies that is certain to eventually hit . Note also that the version of the TAP model studied theoretically in [20] takes place in continuous (rather than discrete) time, in which case Lemma 1 has a sharper statement: Provided that and for at least one other value of i, then with probability 1, tends to infinity in finite
time. Here, we are modeling a system in discrete time, and so this “explosion in finite time” phenomenon does not arise. Nevertheless, in our simulation results, where we explicitly stop the process when molecular species have been produced, a sudden and rapid increase still occurs. Next, consider the probability that the entire collection of reactions involved in generating (i.e., ) is an RAF. As the following lemma shows, this probability depends only on only through the size of this set (i.e., ), and so we denote the probability by .
Proof. is
F-generated, and so it forms an RAF precisely if each reaction in
is catalyzed by at least one molecule type in
. By the independence assumption concerning catalysis assignments, the probability that any given reaction
is catalyzed by at least one molecular species in
is
, and since there are
reactions, the probability that all reactions in
are catalyzed is
which equals
by Equation (
2). □
We can now state our main theorem.
Theorem 1. For the TAP + catalysis model, the following hold.
- (a)
For any value of , , where is a term that tends to zero as .
- (b)
Suppose that at some fixed time . Then the following hold:
- (i)
If for , thenwhere is a term that converges to 0 as . - (ii)
The expected number of reactions that each molecule type (not in ) catalyzes (i.e., ) in order for to equal θ is given by:where as . In particular, for each such value of θ, f grows logarithmically with m.
Proof. Part (a): Let
, and let
. By the inequality
for
, we obtain
, and thus, by Lemma 2, we obtain:
(since
for
). Thus,
as
Part (b-i): Conditional on
, and setting
, Lemma 2 gives:
where ∼ refers to asymptotic identity as
m grows. Exponentiating gives
, as required.
Part (b-ii): Conditional on
, and setting
for a value
(to be determined), gives:
From Part (b), and again conditional on
, the equation
gives
where
tends to 0 as
m grows. Noting also that
, the result now follows from Equation (
4). □
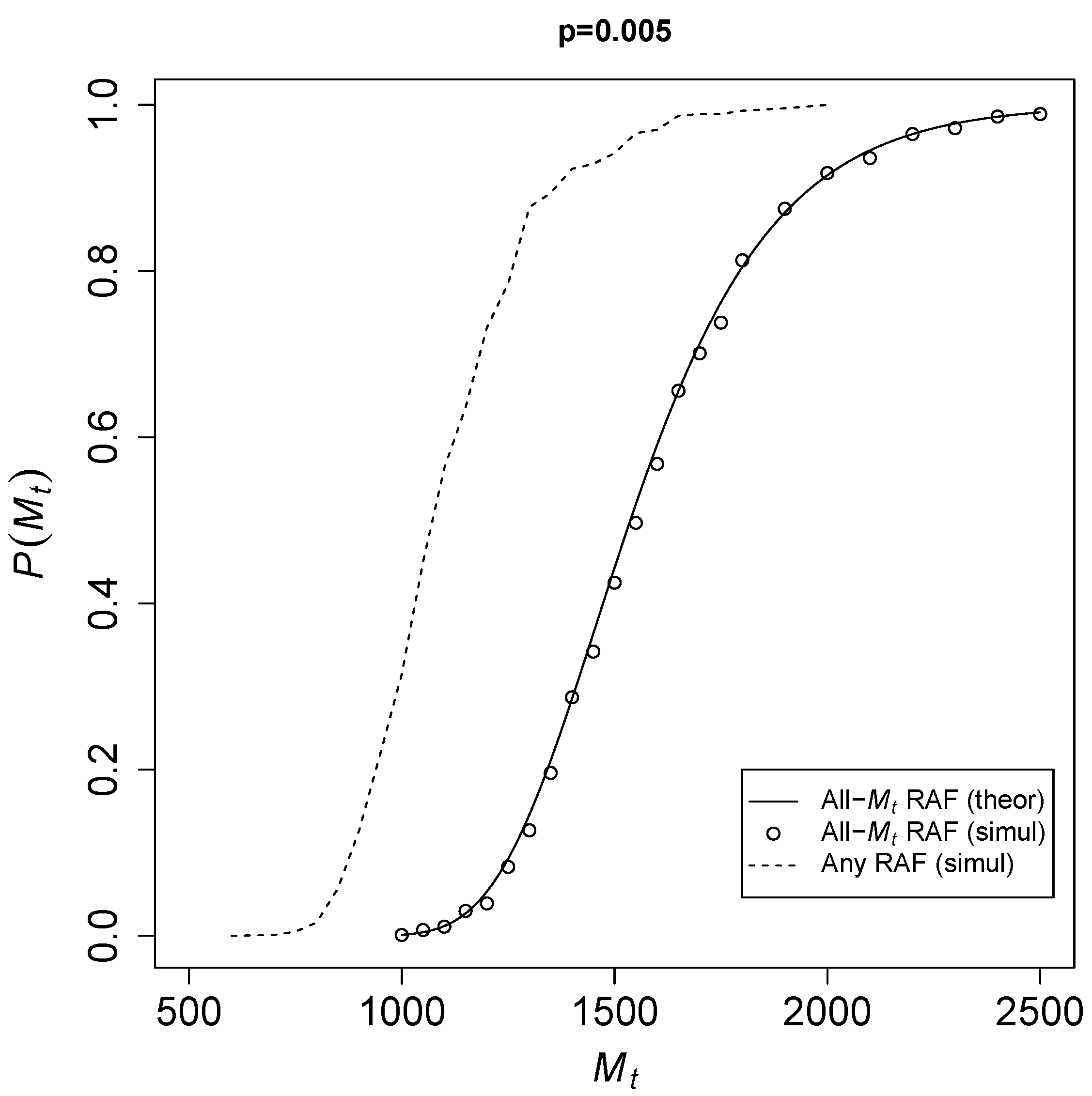
To see how fast
converges to 1,
Figure 2 shows the theoretical probability of Equation (
3) for an all-
RAF (solid line) against
for a catalysis probability
. The open circles represent results from the TAP model simulations. The dashed line shows simulation results for any-sized RAF (i.e., an RAF consisting of any number of reactions).
Given a fixed probability of catalysis p, it is clear that once the total number of molecular species becomes large enough, there is a sharp transition from RAF sets not existing at all to them existing in almost every instance of the model. Of course, RAFs of any size (dotted line) already occur at smaller values of than all- RAFs, but theoretically it is easier to deal with all- RAFs, as they are always automatically food-generated. Thus, the theoretical expression forms an upper bound on the actual probabilities .
Another way to consider these probabilities is to fix the number of molecular species
and then see what the required level of catalysis
is to obtain RAF sets with high probability. This level of catalysis indicates the average number of reactions catalyzed per molecule type. To see how this increases with increasing
,
Figure 3 shows the theoretical probability (solid lines) of an all-
RAF against
for different values of
. The dots are values obtained from computer simulations of the TAP model, to again compare with the theoretical results. As expected, the curves move slowly to the right for larger values of
, but the distance between each next pair of adjacent curves seems to be decreasing.
Taking the “transition point” to a high probability of RAFs to be at
, Theorem 1(b-ii) predicts that
should be close to
.
Figure 4 shows this function for a range of values of
, with the open circles representing results from computer simulations (interpolated from the simulation data shown in
Figure 3). These simulation results closely fit with the theoretically predicted logarithmic curve.
Finally, a comparison is made between the probabilities of any-sized RAFs previously obtained from simulations of the TAP model [
21], and earlier results from a related model known as the binary polymer model [
23]. In this related model, smaller polymers can ligate into larger and larger ones, and larger polymers can cleave into smaller and smaller ones. This model has been investigated extensively in the context of RAF sets in the past [
18,
19].
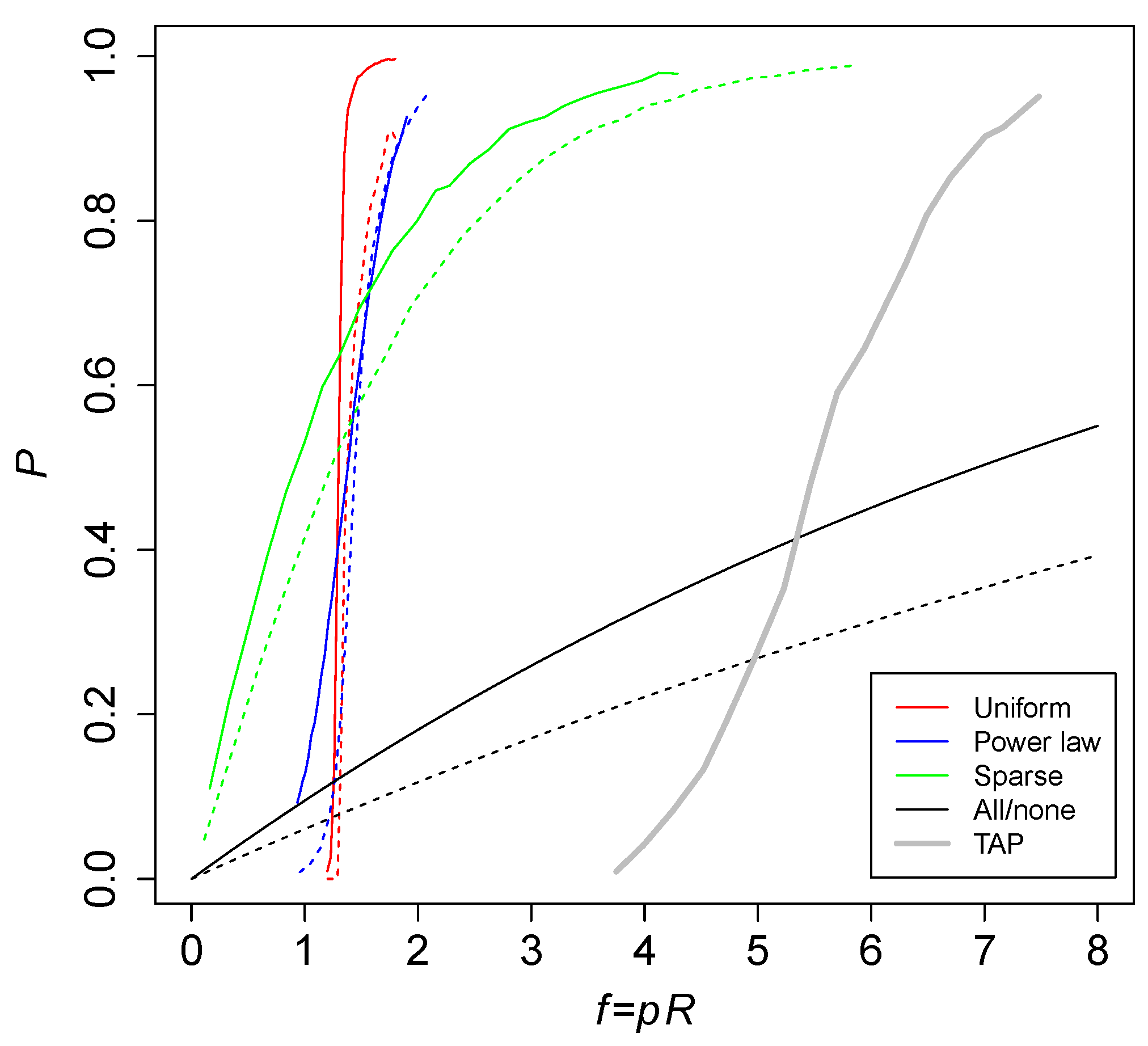
Figure 5 shows the probability
P of an RAF against the level of catalysis
for various versions of the binary polymer model that use different ways of assigning catalysis. The red curves are the standard (uniform) catalysis distribution, the blue curves are a power law catalysis distribution, and the green lines are a sparse catalysis distribution [
23]. These results were obtained from computer simulations. The black curves are the theoretically calculated probabilities for an all-or-nothing catalysis distribution. Solid lines are maximum polymer length
, while dashed lines are
. The thick gray line shows simulation results for the TAP model, with an average number of molecular species of
.
Clearly, the required level of catalysis to cause RAF sets to arise is higher in the TAP model (five to seven reactions catalyzed per molecule type, on average) than in the binary polymer model (one to two). However, this can be explained by the fact that in the TAP model there is always only one reaction that produces a given molecular species, whereas in the binary polymer model there are multiple reactions that can produce a given polymer. In other words, there is a large amount of redundancy in the reaction networks resulting from the binary polymer model, allowing for a lower level of catalysis (given that only one or two of the multiple reactions that produce a given polymer need to be catalyzed).
Note also that we restricted the chemical reactions in the TAP model to only generate one product. In general, reactions can produce more than one product, in which case there could be significantly more molecular species than reactions. It is therefore expected that in such a more general model version the required level of catalysis
f will be lower than the five to seven suggested by
Figure 5.
4. Conclusions
We reinterpreted a simple model of combinatorial innovation known as TAP (theory of the adjacent possible) in the context of chemical evolution and autocatalytic sets. We then derived theoretical expressions for the probabilities of such autocatalytic sets arising in instances of the TAP model. These theoretical predictions were verified with results from computer simulations.
These results show that autocatalytic sets do indeed have a high probability of arising in instances of the TAP model, given a large enough number of molecular species and/or level of catalysis. Of course this is still a very general model, as it is assumed that any molecular species can chemically react with any other, and catalysis is assigned randomly. However, previous work on a related model, known as the binary polymer model, showed that more realistic assumptions can be easily incorporated in such a model, and do not change the overall results very much, at least not qualitatively. Moreover, the quantitative changes can often be predicted from the more general basic model version [
18].
Generally, the level of catalysis (i.e., the average number of reactions catalyzed per molecule type) needs to be somewhat higher in the TAP model than in the binary polymer model. However, this can be explained by the redundancy present in reaction networks resulting from the binary polymer model. One could easily imagine a version of the TAP model where certain molecular species can also be produced by multiple reactions.
In conclusion, the results presented here may suggest a possible step towards the (or an) origin of life, where self-sustaining and reproducing autocatalytic sets arise during a process of chemical evolution. In fact, Wollrab et al. [
4] conclude from their “Miller-type” chemical evolution experiments that “organic catalysts that appear in the broth may well lead to the production of molecular species that would normally not be favored under the conditions in the reactor, further enhancing the molecular richness”. If even just some of those species happen to form a closed loop, mutually catalyzing each other, autocatalytic sets would indeed arise spontaneously.