Mechanically Induced Cavitation in Biological Systems
Abstract
1. Introduction
2. Theoretical Background: Static and Dynamic Approaches
2.1. Static Approach
2.2. Dynamics
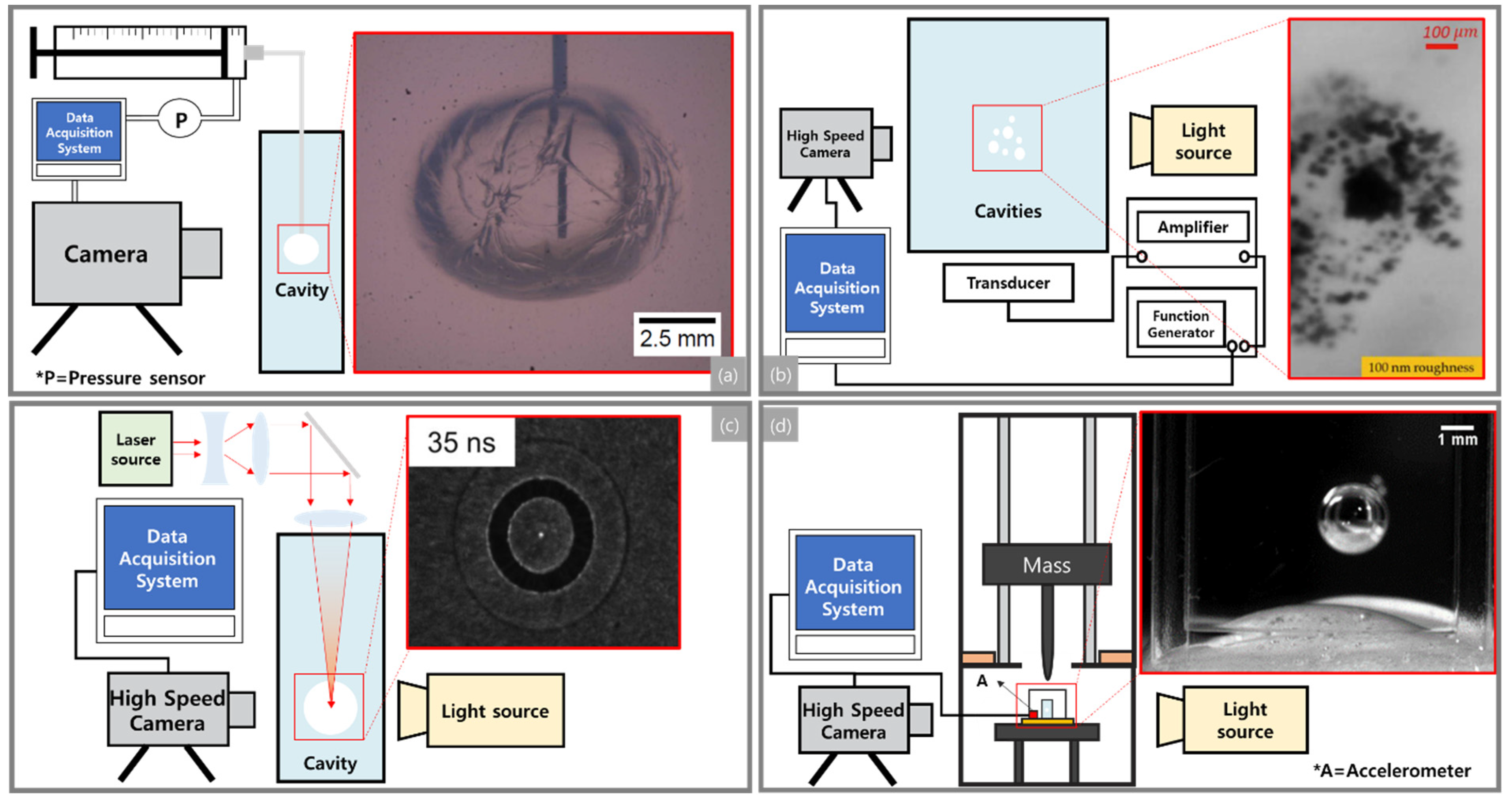
3. Experimental Methods for Cavitation-Induced Damage to the Biological Systems
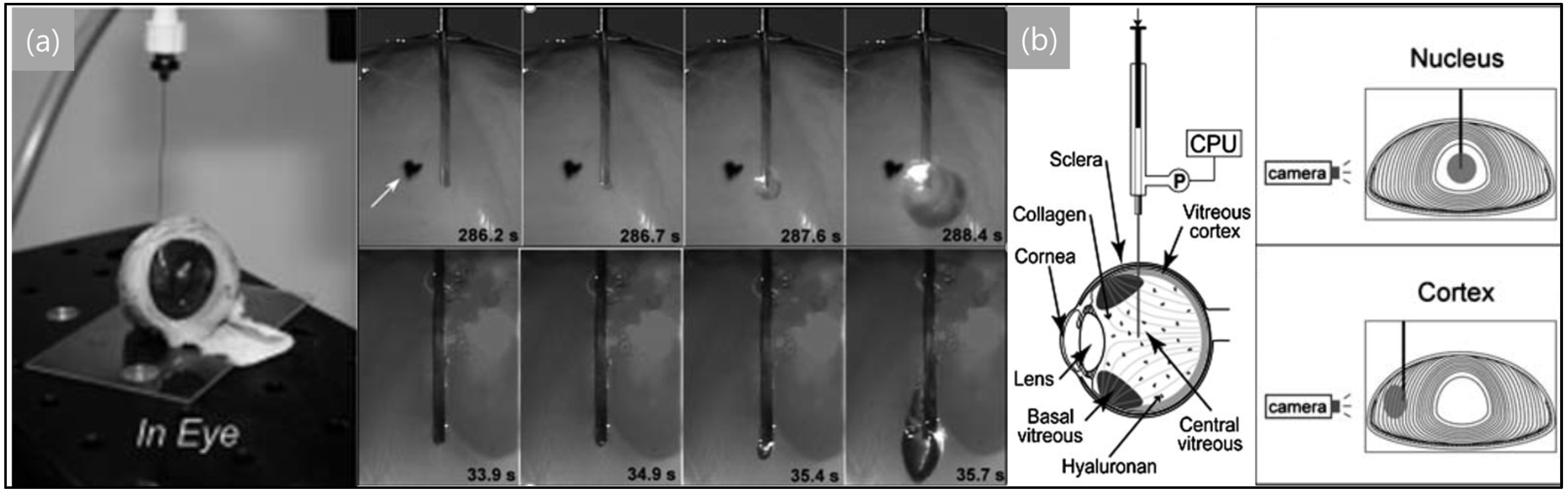
3.1. Needle-Induced Cavitation
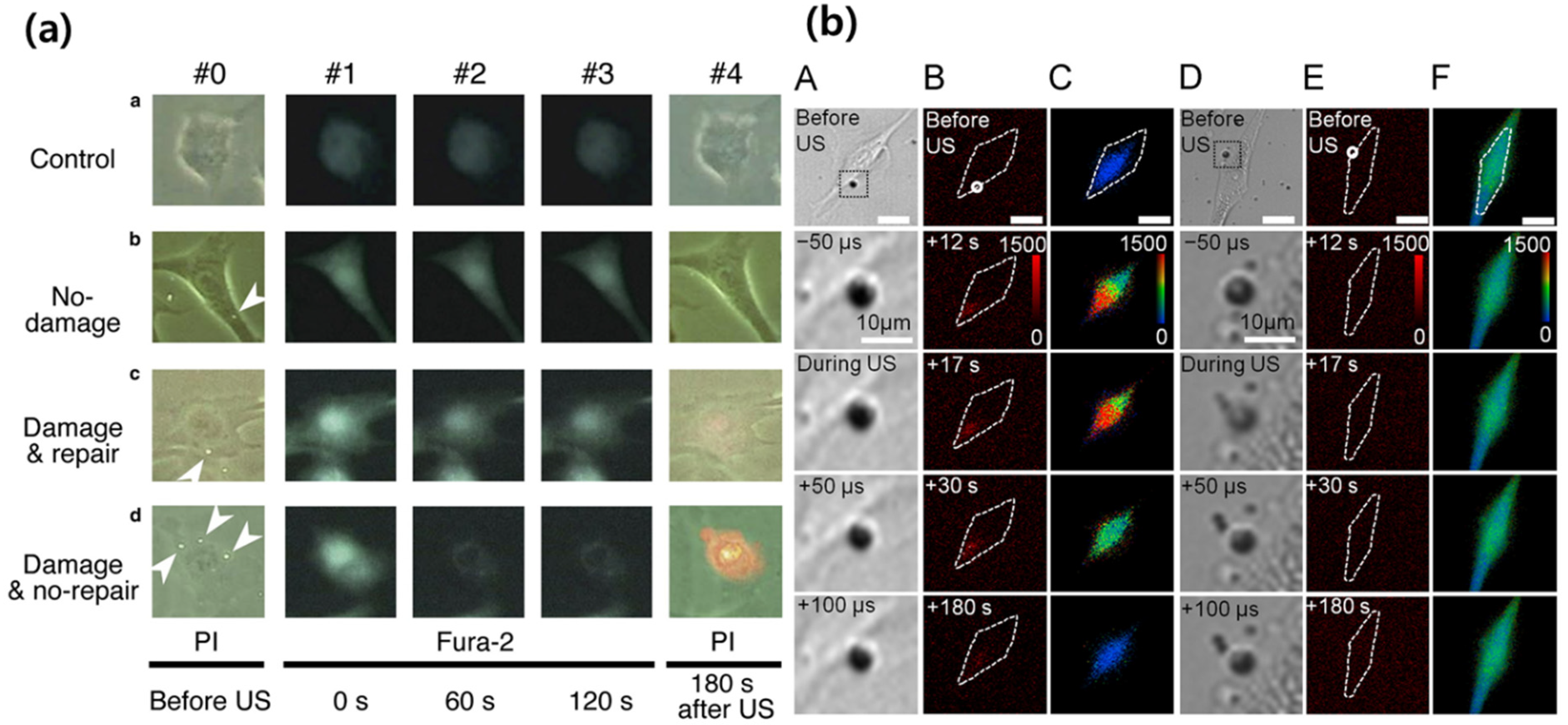
3.2. Acoustically Induced Cavitation
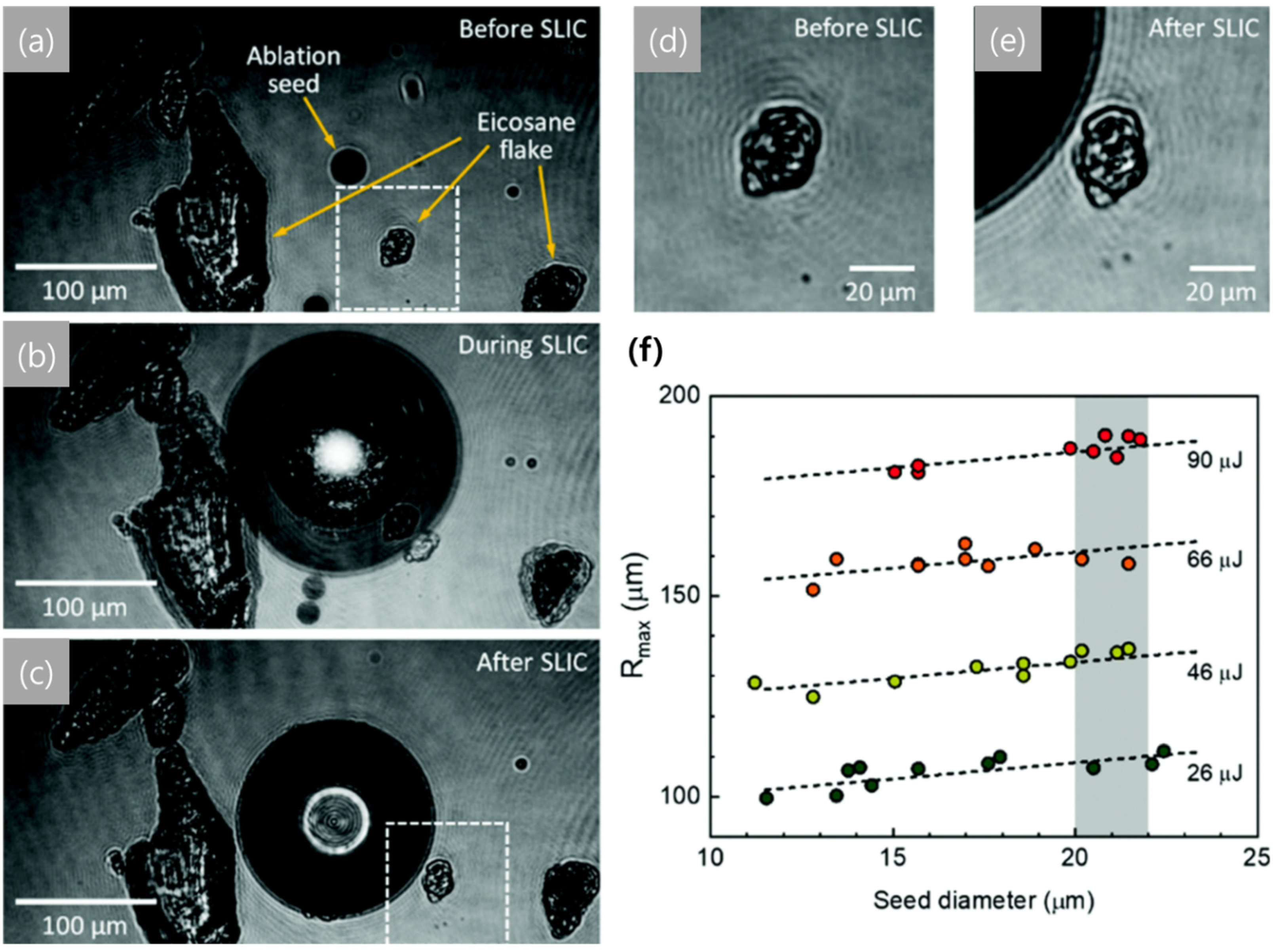
3.3. Laser-Induced Cavitation
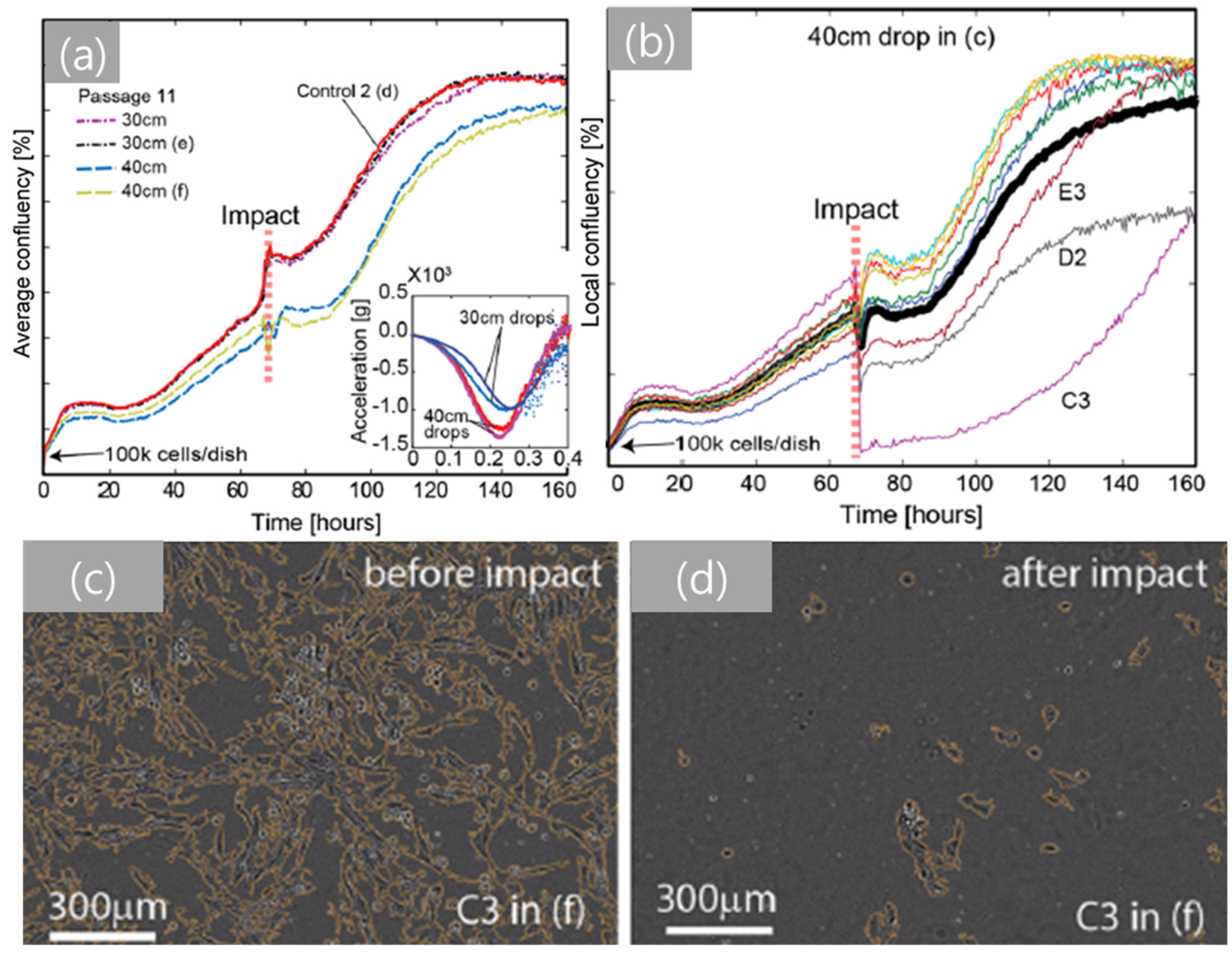
3.4. Integrated Drop Tower System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Sass, W.; Bräunlich, M.; Dreyer, H.P.; Matura, E.; Folberth, W.; Preismeyer, H.G.; Seifert, J. The mechanisms of stone disintegration by shock waves. Ultrasound Med. Biol. 1991, 17, 239–243. [Google Scholar] [CrossRef]
- Sauerbruch, T.; Delius, M.; Paumgartner, G.; Holl, J.; Wess, O.; Weber, W.; Hepp, W.; Brendel, W. Fragmentation of gallstones by extracorporeal shock waves. N. Engl. J. Med. 1986, 314, 818–822. [Google Scholar] [CrossRef] [PubMed]
- Holmer, N.G.; Almquist, L.O.; Hertz, T.G.; Holm, A.; Lindstedt, E.; Persson, H.W.; Hertz, C.H. On the mechanism of kidney stone disintegration by acoustic shock waves. Ultrasound Med. Biol. 1991, 17, 479–489. [Google Scholar] [CrossRef]
- Chaussy, C.H.; Brendel, W.; Schmiedt, E. Extracorporeally Induced Destruction of Kidney Stones by Shock Waves. Lancet 1980, 316, 1265–1268. [Google Scholar] [CrossRef]
- Kaude, J.V.; Williams, C.M.; Millner, M.R.; Scott, K.N.; Finlayson, B. Renal morphology and function immediately after extracorporeal shock-wave lithotripsy. AJR Am. J. Roentgenol. 1985, 145, 305–313. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, D.L.; Bailey, M.R.; Crum, L.A. Use of a dual-pulse lithotripter to generate a localized and intensified cavitation field. J. Acoust. Soc. Am. 2001, 110 Pt 1, 1685–1695. [Google Scholar] [CrossRef]
- Ikeda, T.; Yoshizawa, S.; Tosaki, M.; Allen, J.S.; Takagi, S.; Ohta, N.; Kitamura, T.; Matsumoto, Y. Cloud cavitation control for lithotripsy using high intensity focused ultrasound. Ultrasound Med. Biol. 2006, 32, 1383–1397. [Google Scholar] [CrossRef]
- Pishchalnikov, Y.A.; Sapozhnikov, O.A.; Bailey, M.R.; Williams, J.C., Jr.; Cleveland, R.O.; Colonius, T.; Crum, L.A.; Evan, A.P.; McAteer, J.A. Cavitation bubble cluster activity in the breakage of kidney stones by lithotripter shockwaves. J. Endourol. 2003, 17, 435–446. [Google Scholar] [CrossRef]
- Johnsen, E.; Colonius, T. Shock-induced collapse of a gas bubble in shockwave lithotripsy. J. Acoust. Soc. Am. 2008, 124, 2011–2020. [Google Scholar] [CrossRef]
- Yoshizawa, S.; Ikeda, T.; Ito, A.; Ota, R.; Takagi, S.; Matsumoto, Y. High intensity focused ultrasound lithotripsy with cavitating microbubbles. Med. Biol. Eng. Comput. 2009, 47, 851–860. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, P.K.; Hammer, D.X.; Rockwell, B.A. Laser-induced breakdown in aqueous media. Prog. Quantum Electron. 1997, 21, 155–248. [Google Scholar] [CrossRef]
- Zysset, B.; Fujimoto, J.G.; Deutsch, T.F. Time-resolved measurements of picosecond optical breakdown. Appl. Phys. B 1989, 48, 139–147. [Google Scholar] [CrossRef]
- Husseini, G.A.; Pitt, W.G. Micelles and nanoparticles for ultrasonic drug and gene delivery. Adv. Drug Deliv. Rev. 2008, 60, 1137–1152. [Google Scholar] [CrossRef] [PubMed]
- Graham, S.M.; Carlisle, R.; Choi, J.J.; Stevenson, M.; Shah, A.R.; Myers, R.S.; Fisher, K.; Peregrino, M.B.; Seymour, L.; Coussios, C.C. Inertial cavitation to non-invasively trigger and monitor intratumoral release of drug from intravenously delivered liposomes. J. Control. Release 2014, 178, 101–107. [Google Scholar] [CrossRef]
- Husseini, G.A.; Diaz de la Rosa, M.A.; Richardson, E.S.; Christensen, D.A.; Pitt, W.G. The role of cavitation in acoustically activated drug delivery. J. Control. Release 2005, 107, 253–261. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Yang, C.; Yuan, F.; Liao, D.; Li, T.; Guilak, F.; Zhong, P. Dynamics and mechanisms of intracellular calcium waves elicited by tandem bubble-induced jetting flow. Proc. Natl. Acad. Sci. USA 2018, 115, E353–E362. [Google Scholar] [CrossRef]
- Lo, C.-W.; Chen, S.-F.; Li, C.-P.; Lu, P.-C. Cavitation Phenomena in Mechanical Heart Valves: Studied by Using a Physical Impinging Rod System. Ann. Biomed. Eng. 2010, 38, 3162–3172. [Google Scholar] [CrossRef] [PubMed]
- Chao, T.-C.; Ros, A. Microfluidic single-cell analysis of intracellular compounds. J. R. Soc. Interface 2008, 5 (Suppl. 2), S139–S150. [Google Scholar] [CrossRef]
- Goldsmith, W. The state of head injury biomechanics: Past, present, and future: Part 1. Crit. Rev. Biomed. Eng. 2001, 29, 441–600. [Google Scholar] [CrossRef] [PubMed]
- Lubock, P.; Goldsmith, W. Experimental cavitation studies in a model head-neck system. J. Biomech. 1980, 13, 1041–1052. [Google Scholar] [CrossRef]
- Farjo, L.A.; Miclau, T. Ballistics and mechanisms of tissue wounding. Injury 1997, 28, C12–C17. [Google Scholar] [CrossRef]
- Hu, J.; Lee, J.B.; Yang, K.H.; King, A.I. Injury patterns and sources of non-ejected occupants in trip-over crashes: A survey of NASS-CDS database from 1997 to 2002. Annu. Proc. Assoc. Adv. Automot. Med. 2005, 49, 119–132. [Google Scholar]
- Estrada, J.B.; Scimone, M.T.; Cramer, H.C.; Mancia, L.; Johnsen, E.; Franck, C. Microcavitation as a Neuronal Damage Mechanism in an In Vitro Model of Blast Traumatic Brain Injury. Biophys. J. 2017, 112 (Suppl. 1), 159a. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.-T.; Adnan, A. Effect of Shock-Induced Cavitation Bubble Collapse on the damage in the Simulated Perineuronal Net of the Brain. Sci. Rep. 2017, 7, 5323. [Google Scholar] [CrossRef]
- Kanagaraj, J.; Chen, B.; Xiao, S.; Cho, M. Reparative Effects of Poloxamer P188 in Astrocytes Exposed to Controlled Microcavitation. Ann. Biomed. Eng. 2018, 46, 354–364. [Google Scholar] [CrossRef]
- Estrada, J.B.; Barajas, C.; Henann, D.L.; Johnsen, E.; Franck, C. High strain-rate soft material characterization via inertial cavitation. J. Mech. Phys. Solids 2018, 112, 291–317. [Google Scholar] [CrossRef]
- Kang, W.; Adnan, A.; O’Shaughnessy, T.; Bagchi, A. Cavitation nucleation in gelatin: Experiment and mechanism. Acta Biomater. 2018, 67, 295–306. [Google Scholar] [CrossRef]
- Kang, W.; Raphael, M. Acceleration-induced pressure gradients and cavitation in soft biomaterials. Sci. Rep. 2018, 8, 15840. [Google Scholar] [CrossRef] [PubMed]
- Jansen, L.E.; Birch, N.P.; Schiffman, J.D.; Crosby, A.J.; Peyton, S.R. Mechanics of intact bone marrow. J. Mech. Behav. Biomed. Mater. 2015, 50, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Zimberlin, J.A.; Sanabria-DeLong, N.; Tew, G.N.; Crosby, A.J. Cavitation rheology for soft materials. Soft Matter 2007, 3, 763–767. [Google Scholar] [CrossRef] [PubMed]
- Rayleigh, L., VIII. On the pressure developed in a liquid during the collapse of a spherical cavity. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Beeching, R. Resistance to cavitation erosion. Trans. Instn. Engrs. Shipb. Scot. 1942, 85, 210–276. [Google Scholar]
- Gilmore, F.R.; California Institute of Technology; Hydrodynamics Laboratory. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid; California Institute of Technology: Pasadena, CA, USA, 1952. [Google Scholar]
- Hutchens, S.B.; Crosby, A.J. Soft-solid deformation mechanics at the tip of an embedded needle. Soft Matter 2014, 10, 3679–3684. [Google Scholar] [CrossRef]
- Barney, C.W.; Zheng, Y.; Wu, S.; Cai, S.; Crosby, A.J. Residual strain effects in needle-induced cavitation. Soft Matter 2019, 15, 7390–7397. [Google Scholar] [CrossRef]
- Hutchens, S.B.; Fakhouri, S.; Crosby, A.J. Elastic cavitation and fracture via injection. Soft Matter 2016, 12, 2557–2566. [Google Scholar] [CrossRef] [PubMed]
- Barney, C.W.; Dougan, C.E.; McLeod, K.R.; Kazemi-Moridani, A.; Zheng, Y.; Ye, Z.; Tiwari, S.; Sacligil, I.; Riggleman, R.A.; Cai, S.; et al. Cavitation in soft matter. Proc. Natl. Acad. Sci. USA 2020, 117, 9157–9165. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.; Crosby, A.J. Cavitation and fracture behavior of polyacrylamide hydrogels. Soft Matter 2009, 5, 3963–3968. [Google Scholar] [CrossRef]
- Macosko, C.W. Rheology: Principles, Measurements, and Applications; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Yang, X.; Church, C.C. A model for the dynamics of gas bubbles in soft tissue. J. Acoust. Soc. Am. 2005, 118, 3595–3606. [Google Scholar] [CrossRef] [PubMed]
- Ogden, R.W. Non-Linear Elastic Deformations; Courier Corporation: Chelmsford, MA, USA, 1997; p. 532. [Google Scholar]
- Rivlin, R.S.; Rideal, E.K. Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. The Elasticity of Rubber. Rubber Chem. Technol. 1992, 65, 51–66. [Google Scholar] [CrossRef]
- Mihai, L.A.; Goriely, A. How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170607. [Google Scholar] [CrossRef]
- Gent, A.N. A New Constitutive Relation for Rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Czerner, M.; Fasce, L.A.; Martucci, J.F.; Ruseckaite, R.; Frontini, P.M. Deformation and fracture behavior of physical gelatin gel systems. Food Hydrocoll. 2016, 60, 299–307. [Google Scholar] [CrossRef]
- Ogden, R.W.; Hill, R. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Mihai, L.A.; Budday, S.; Holzapfel, G.A.; Kuhl, E.; Goriely, A. A family of hyperelastic models for human brain tissue. J. Mech. Phys. Solids 2017, 106, 60–79. [Google Scholar] [CrossRef]
- Umale, S.; Deck, C.; Bourdet, N.; Dhumane, P.; Soler, L.; Marescaux, J.; Willinger, R. Experimental mechanical characterization of abdominal organs: Liver, kidney & spleen. J. Mech. Behav. Biomed. Mater. 2013, 17, 22–33. [Google Scholar] [PubMed]
- Fung, Y.C.; Fronek, K.; Patitucci, P. Pseudoelasticity of arteries and the choice of its mathematical expression. Am. J. Physiol. Content 1979, 237, H620–H631. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Barrangou, L.M.; Daubert, C.R.; Allen Foegeding, E. Textural properties of agarose gels. I. Rheological and fracture properties. Food Hydrocoll. 2006, 20, 184–195. [Google Scholar] [CrossRef]
- Zhu, J.; Li, T.; Cai, S.; Suo, Z. Snap-through Expansion of a Gas Bubble in an Elastomer. J. Adhes. 2011, 87, 466–481. [Google Scholar] [CrossRef]
- Raayai-Ardakani, S.; Chen, Z.; Earl, D.R.; Cohen, T. Volume-controlled cavity expansion for probing of local elastic properties in soft materials. Soft Matter 2019, 15, 381–392. [Google Scholar] [CrossRef] [PubMed]
- Marcombe, R.; Cai, S.; Hong, W.; Zhao, X.; Lapusta, Y.; Suo, Z. A theory of constrained swelling of a pH-sensitive hydrogel. Soft Matter 2010, 6, 784–793. [Google Scholar] [CrossRef]
- Cai, S.; Suo, Z. Mechanics and chemical thermodynamics of phase transition in temperature-sensitive hydrogels. J. Mech. Phys. Solids 2011, 59, 2259–2278. [Google Scholar] [CrossRef]
- Storm, C.; Pastore, J.J.; MacKintosh, F.C.; Lubensky, T.C.; Janmey, P.A. Nonlinear elasticity in biological gels. Nature 2005, 435, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Cai, S. Drying-induced cavitation in a constrained hydrogel. Soft Matter 2015, 11, 1058–1061. [Google Scholar] [CrossRef]
- Wang, H.; Cai, S. Cavitation in a swollen elastomer constrained by a non-swellable shell. J. Appl. Phys. 2015, 117, 154901. [Google Scholar] [CrossRef]
- Zhang, T.; Lin, S.; Yuk, H.; Zhao, X. Predicting fracture energies and crack-tip fields of soft tough materials. Extreme Mech. Lett. 2015, 4, 1–8. [Google Scholar] [CrossRef]
- Movahed, P.; Kreider, W.; Maxwell, A.D.; Hutchens, S.B.; Freund, J.B. Cavitation-induced damage of soft materials by focused ultrasound bursts: A fracture-based bubble dynamics model. J. Acoust. Soc. Am. 2016, 140, 1374–1386. [Google Scholar] [CrossRef] [PubMed]
- Mancia, L.; Vlaisavljevich, E.; Yousefi, N.; Rodriguez, M.; Ziemlewicz, T.J.; Lee, F.T.; Henann, D.; Franck, C.; Xu, Z.; Johnsen, E. Modeling tissue-selective cavitation damage. Phys. Med. Biol. 2019, 64, 225001. [Google Scholar] [CrossRef]
- Johnsen, E.; Colonius, T. Numerical simulations of non-spherical bubble collapse. J. Fluid Mech. 2009, 629, 231–262. [Google Scholar] [CrossRef] [PubMed]
- Dollet, B.; Marmottant, P.; Garbin, V. Bubble Dynamics in Soft and Biological Matter. Annu. Rev. Fluid Mech. 2019, 51, 331–355. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; University Press: Cambridge, UK, 1967. [Google Scholar]
- Hamaguchi, F.; Ando, K. Linear oscillation of gas bubbles in a viscoelastic material under ultrasound irradiation. Phys. Fluids 2015, 27, 113103. [Google Scholar] [CrossRef]
- Jamburidze, A.; De Corato, M.; Huerre, A.; Pommella, A.; Garbin, V. High-frequency linear rheology of hydrogels probed by ultrasound-driven microbubble dynamics. Soft Matter 2017, 13, 3946–3953. [Google Scholar] [CrossRef] [PubMed]
- Fogler, H.S.; Goddard, J.D. Collapse of Spherical Cavities in Viscoelastic Fluids. Phys. Fluids 1970, 13, 1135–1141. [Google Scholar] [CrossRef]
- Allen, J.S.; Roy, R.A. Dynamics of gas bubbles in viscoelastic fluids. I. Linear viscoelasticity. J. Acoust. Soc. Am. 2000, 107, 3167–3178. [Google Scholar] [CrossRef]
- Hua, C.; Johnsen, E. Nonlinear oscillations following the Rayleigh collapse of a gas bubble in a linear viscoelastic (tissue-like) medium. Phys. Fluids 2013, 25, 083101. [Google Scholar] [CrossRef]
- Keller, J.B.; Kolodner, I.I. Damping of Underwater Explosion Bubble Oscillations. J. Appl. Phys. 1956, 27, 1152–1161. [Google Scholar] [CrossRef]
- Epstein, D.; Keller, J.B. Expansion and Contraction of Planar, Cylindrical, and Spherical Underwater Gas Bubbles. J. Acoust. Soc. Am. 1972, 52, 975–980. [Google Scholar] [CrossRef]
- Plesset, M.S.; Prosperetti, A. Bubble Dynamics and Cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Allen, J.S.; Roy, R.A. Dynamics of gas bubbles in viscoelastic fluids. II. Nonlinear viscoelasticity. J. Acoust. Soc. Am. 2000, 108, 1640–1650. [Google Scholar] [CrossRef]
- Jiménez-Fernández, J.; Crespo, A. Bubble oscillation and inertial cavitation in viscoelastic fluids. Ultrasonics 2005, 43, 643–651. [Google Scholar] [CrossRef] [PubMed]
- Naude, J.; Méndez, F. Periodic and chaotic acoustic oscillations of a bubble gas immersed in an Upper Convective Maxwell fluid. J. Non-Newton. Fluid Mech. 2008, 155, 30–38. [Google Scholar] [CrossRef]
- Warnez, M.T.; Johnsen, E. Numerical modeling of bubble dynamics in viscoelastic media with relaxation. Phys. Fluids 2015, 27, 063103. [Google Scholar] [CrossRef]
- Veysset, D.; Gutiérrez-Hernández, U.; Dresselhaus-Cooper, L.; De Colle, F.; Kooi, S.; Nelson, K.A.; Quinto-Su, P.A.; Pezeril, T. Single-bubble and multibubble cavitation in water triggered by laser-driven focusing shock waves. Phys. Rev. E 2018, 97, 053112. [Google Scholar] [CrossRef]
- Tiwari, S.; Kazemi-Moridani, A.; Zheng, Y.; Barney, C.W.; McLeod, K.R.; Dougan, C.E.; Crosby, A.J.; Tew, G.N.; Peyton, S.R.; Cai, S.; et al. Seeded laser-induced cavitation for studying high-strain-rate irreversible deformation of soft materials. Soft Matter 2020, 16, 9006–9013. [Google Scholar] [CrossRef]
- Altay, R.; Sadaghiani, A.K.; Sevgen, M.I.; Şişman, A.; Koşar, A. Numerical and Experimental Studies on the Effect of Surface Roughness and Ultrasonic Frequency on Bubble Dynamics in Acoustic Cavitation. Energies 2020, 13, 1126. [Google Scholar] [CrossRef]
- Yamashita, T.; Ando, K. Low-intensity ultrasound induced cavitation and streaming in oxygen-supersaturated water: Role of cavitation bubbles as physical cleaning agents. Ultrason. Sonochem. 2019, 52, 268–279. [Google Scholar] [CrossRef] [PubMed]
- Zimberlin, J.A.; McManus, J.J.; Crosby, A.J. Cavitation rheology of the vitreous: Mechanical properties of biological tissue. Soft Matter 2010, 6, 3632–3635. [Google Scholar] [CrossRef]
- Cui, J.; Lee, C.H.; Delbos, A.; McManus, J.J.; Crosby, A.J. Cavitation rheology of the eye lens. Soft Matter 2011, 7, 7827–7831. [Google Scholar] [CrossRef]
- Izadifar, Z.; Babyn, P.; Chapman, D. Ultrasound Cavitation/Microbubble Detection and Medical Applications. J. Med. Biol. Eng. 2019, 39, 259–276. [Google Scholar] [CrossRef]
- Mancia, L.; Yang, J.; Spratt, J.-S.; Sukovich, J.R.; Xu, Z.; Colonius, T.; Franck, C.; Johnsen, E. Acoustic cavitation rheometry. Soft Matter 2021, 17, 2931–2941. [Google Scholar] [CrossRef] [PubMed]
- Brohult, S. Splitting of the Hæmocyanin Molecule by Ultra-sonic Waves. Nature 1937, 140, 805. [Google Scholar] [CrossRef]
- Pohlman, R. Über die richtende Wirkung des Schallfeldes auf Suspensionen nicht kugelförmiger Teilchen. Z. Phys. 1937, 107, 497–508. [Google Scholar] [CrossRef]
- Carstensen, E.L.; Li, K.; Schwan, H.P. Determination of the Acoustic Properties of Blood and its Components. J. Acoust. Soc. Am. 1953, 25, 286–289. [Google Scholar] [CrossRef]
- Bailey, M.R.; Khokhlova, V.A.; Sapozhnikov, O.A.; Kargl, S.G.; Crum, L.A. Physical mechanisms of the therapeutic effect of ultrasound (a review). Acoust. Phys. 2003, 49, 369–388. [Google Scholar] [CrossRef]
- Coleman, A.J.; Saunders, J.E.; Crum, L.A.; Dyson, M. Acoustic cavitation generated by an extracorporeal shockwave lithotripter. Ultrasound Med. Biol. 1987, 13, 69–76. [Google Scholar] [CrossRef]
- Crum, L.A. Cavitation microjets as a contributory mechanism for renal calculi disintegration in ESWL. J. Urol. 1988, 140, 1587–1590. [Google Scholar] [CrossRef]
- Kennedy, J.E. High-intensity focused ultrasound in the treatment of solid tumours. Nat. Rev. Cancer 2005, 5, 321–327. [Google Scholar] [CrossRef] [PubMed]
- Fechheimer, M.; Boylan, J.F.; Parker, S.; Sisken, J.E.; Patel, G.L.; Zimmer, S.G. Transfection of mammalian cells with plasmid DNA by scrape loading and sonication loading. Proc. Natl. Acad. Sci. USA 1987, 84, 8463–8467. [Google Scholar] [CrossRef]
- Bailey, M.R. Control of acoustic cavitation with application to lithotripsy. J. Acoust. Soc. Am. 1997, 102, 221. [Google Scholar] [CrossRef]
- Carnell, M.T.; Alcock, R.D.; Emmony, D.C. Optical imaging of shock waves produced by a high-energy electromagnetic transducer. Phys. Med. Biol. 1993, 38, 1575–1588. [Google Scholar] [CrossRef] [PubMed]
- Cathignol, E.; Tavakkoli, J.; Birer, A.; Arefiev, A. Comparison between the effects of cavitation induced by two different pressure-time shock waveform pulses. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 788–799. [Google Scholar] [CrossRef] [PubMed]
- Church, C.C. A theoretical study of cavitation generated by an extracorporeal shock wave lithotripter. J. Acoust Soc. Am. 1989, 86, 215–227. [Google Scholar] [CrossRef]
- Philipp, A.; Delius, M.; Scheffczyk, C.; Vogel, A.; Lauterborn, W. Interaction of lithotripter-generated shock waves with air bubbles. J. Acoust. Soc. Am. 1993, 93, 2496–2509. [Google Scholar] [CrossRef]
- Sapozhnikov, O.A.; Khokhlova, V.A.; Bailey, M.R.; Williams, J.C., Jr.; McAteer, J.A.; Cleveland, R.O.; Crum, L.A. Effect of overpressure and pulse repetition frequency on cavitation in shock wave lithotripsy. J. Acoust. Soc. Am. 2002, 112, 1183–1195. [Google Scholar] [CrossRef]
- Ikeda, T.; Yoshizawa, S.; Koizumi, N.; Mitsuishi, M.; Matsumoto, Y. Focused Ultrasound and Lithotripsy. In Advances in Experimental Medicine and Biology; Springer: Berlin/Heidleberg, Germany, 2016; Volume 880, pp. 113–129. [Google Scholar]
- Brujan, E.A.; Ikeda, T.; Matsumoto, Y. Shock wave emission from a cloud of bubbles. Soft Matter 2012, 8, 5777–5783. [Google Scholar] [CrossRef]
- Brujan, E.A.; Ikeda, T.; Yoshinaka, K.; Matsumoto, Y. The final stage of the collapse of a cloud of bubbles close to a rigid boundary. Ultrason. Sonochem. 2011, 18, 59–64. [Google Scholar] [CrossRef]
- Evan, A.P.; Willis, L.R.; Lingeman, J.E.; McAteer, J.A. Renal Trauma and the Risk of Long-Term Complications in Shock Wave Lithotripsy. Nephron 1998, 78, 1–8. [Google Scholar] [CrossRef]
- Evan, A.P.; Willis, L.R.; McAteer, J.A.; Bailey, M.R.; Connors, B.A.; Shao, Y.; Lingeman, J.E.; Williams, J.C., Jr.; Fineberg, N.S.; Crum, L.A. Kidney damage and renal functional changes are minimized by waveform control that suppresses cavitation in shock wave lithotripsy. J. Urol. 2002, 168 Pt 1, 1556–1562. [Google Scholar] [CrossRef]
- Kodama, T.; Tomita, Y. Cavitation bubble behavior and bubble–shock wave interaction near a gelatin surface as a study of in vivo bubble dynamics. Appl. Phys. B 2000, 70, 139–149. [Google Scholar] [CrossRef]
- Zhong, P.; Zhou, Y.; Zhu, S. Dynamics of bubble oscillation in constrained media and mechanisms of vessel rupture in SWL. Ultrasound Med. Biol. 2001, 27, 119–134. [Google Scholar] [CrossRef]
- Chen, H.; Brayman, A.A.; Bailey, M.R.; Matula, T.J. Blood vessel rupture by cavitation. Urol. Res. 2010, 38, 321–326. [Google Scholar] [CrossRef] [PubMed]
- Van Wamel, A.; Kooiman, K.; Harteveld, M.; Emmer, M.; ten Cate, F.J.; Versluis, M.; de Jong, N. Vibrating microbubbles poking individual cells: Drug transfer into cells via sonoporation. J. Control. Release 2006, 112, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Kudo, N.; Okada, K.; Yamamoto, K. Sonoporation by single-shot pulsed ultrasound with microbubbles adjacent to cells. Biophys. J. 2009, 96, 4866–4876. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Fan, Z.; Deng, C.X. Effects of shear stress cultivation on cell membrane disruption and intracellular calcium concentration in sonoporation of endothelial cells. J. Biomech. 2011, 44, 164–169. [Google Scholar] [CrossRef]
- Shohet, R.V.; Chen, S.; Zhou, Y.T.; Wang, Z.; Meidell, R.S.; Unger, R.H.; Grayburn, P.A. Echocardiographic destruction of albumin microbubbles directs gene delivery to the myocardium. Circulation 2000, 101, 2554–2556. [Google Scholar] [CrossRef] [PubMed]
- Carson, A.R.; McTiernan, C.F.; Lavery, L.; Grata, M.; Leng, X.; Wang, J.; Chen, X.; Villanueva, F.S. Ultrasound-targeted microbubble destruction to deliver siRNA cancer therapy. Cancer Res. 2012, 72, 6191–6199. [Google Scholar] [CrossRef]
- Dalecki, D. Mechanical bioeffects of ultrasound. Annu. Rev. Biomed. Eng. 2004, 6, 229–248. [Google Scholar] [CrossRef] [PubMed]
- Kimmel, E. Cavitation bioeffects. Crit. Rev. Biomed. Eng. 2006, 34, 105–161. [Google Scholar] [CrossRef]
- O’Brien, W.D., Jr. Ultrasound-biophysics mechanisms. Prog. Biophys. Mol. Biol. 2007, 93, 212–255. [Google Scholar] [CrossRef]
- Krasovitski, B.; Frenkel, V.; Shoham, S.; Kimmel, E. Intramembrane cavitation as a unifying mechanism for ultrasound-induced bioeffects. Proc. Natl. Acad. Sci. USA 2011, 108, 3258–3263. [Google Scholar] [CrossRef]
- Iida, Y.; Ashokkumar, M.; Tuziuti, T.; Kozuka, T.; Yasui, K.; Towata, A.; Lee, J. Bubble population phenomena in sonochemical reactor: II. Estimation of bubble size distribution and its number density by simple coalescence model calculation. Ultrason. Sonochem. 2010, 17, 480–486. [Google Scholar] [CrossRef] [PubMed]
- Burdin, F.; Tsochatzidis, N.A.; Guiraud, P.; Wilhelm, A.M.; Delmas, H. Characterisation of the acoustic cavitation cloud by two laser techniques. Ultrason. Sonochem. 1999, 6, 43–51. [Google Scholar] [CrossRef]
- Chen, W.S.; Matula, T.J.; Crum, L.A. The disappearance of ultrasound contrast bubbles: Observations of bubble dissolution and cavitation nucleation. Ultrasound Med. Biol. 2002, 28, 793–803. [Google Scholar] [CrossRef]
- Tsochatzidis, N.A.; Guiraud, P.; Wilhelm, A.M.; Delmas, H. Determination of velocity, size and concentration of ultrasonic cavitation bubbles by the phase-Doppler technique. Chem. Eng. Sci. 2001, 56, 1831–1840. [Google Scholar] [CrossRef]
- Lee, J.; Ashokkumar, M.; Kentish, S.; Grieser, F. Determination of the Size Distribution of Sonoluminescence Bubbles in a Pulsed Acoustic Field. J. Am. Chem. Soc. 2005, 127, 16810–16811. [Google Scholar] [CrossRef] [PubMed]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Javan, A.; Bennett, W.R.; Herriott, D.R. Population Inversion and Continuous Optical Maser Oscillation in a Gas Discharge Containing a He-Ne Mixture. Phys. Rev. Lett. 1961, 6, 106–110. [Google Scholar] [CrossRef]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 1975, 72, 391–399. [Google Scholar] [CrossRef]
- Brujan, E.-A.; Nahen, K.; Schmidt, P.; Vogel, A. Dynamics of laser-induced cavitation bubbles near elastic boundaries: Influence of the elastic modulus. J. Fluid Mech. 2001, 433, 283–314. [Google Scholar] [CrossRef]
- Frenz, M.; Pratisto, H.; Konz, F.; Jansen, E.D.; Welch, A.J.; Weber, H.P. Comparison of the effects of absorption coefficient and pulse duration of 2.12-/spl mu/m and 2.79-/spl mu/m radiation on laser ablation of tissue. IEEE J. Quantum Electron. 1996, 32, 2025–2036. [Google Scholar] [CrossRef]
- Asshauer, T.; Rink, K.; Delacrétaz, G. Acoustic transient generation by holmium-laser-induced cavitation bubbles. J. Appl. Phys. 1994, 76, 5007–5013. [Google Scholar] [CrossRef]
- Chen, C.; Li, X.; Zhang, X.; Zhan, Z.; Xie, S. Influence of Static Pressure on Dynamic Characteristics of Laser-Induced Cavitation and Hard-Tissue Ablation under Liquid Environment. In Proceedings of the SPIE, Beijing, China, 9–11 October 2014; Volume 9268, p. 92682C. [Google Scholar]
- Hutson, M.S.; Ma, X. Plasma and cavitation dynamics during pulsed laser microsurgery in vivo. Phys. Rev. Lett. 2007, 99, 158104. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.-w.; Xia, J.; Lombardo, M.; Perez, C.; Arnal, B.; Larson-Smith, K.; Pelivanov, I.; Matula, T.; Pozzo, L.; O’Donnell, M. Laser-induced cavitation in nanoemulsion with gold nanospheres for blood clot disruption: In vitro results. Opt. Lett. 2014, 39, 2599–2602. [Google Scholar] [CrossRef]
- Rau, K.R.; Quinto-Su, P.A.; Hellman, A.N.; Venugopalan, V. Pulsed Laser Microbeam-Induced Cell Lysis: Time-Resolved Imaging and Analysis of Hydrodynamic Effects. Biophys. J. 2006, 91, 317–329. [Google Scholar] [CrossRef] [PubMed]
- Quinto-Su, P.A.; Suzuki, M.; Ohl, C.-D. Fast temperature measurement following single laser-induced cavitation inside a microfluidic gap. Sci. Rep. 2014, 4, 5445. [Google Scholar] [CrossRef] [PubMed]
- Sacchi, C. Laser-induced electric breakdown in water. J. Opt. Soc. Am. B Opt. Phys. 1991, 8, 337–345. [Google Scholar] [CrossRef]
- Doukas, A.G.; McAuliffe, D.J.; Flotte, T.J. Biological effects of laser-induced shock waves: Structural and functional cell damage in vitro. Ultrasound Med. Biol. 1993, 19, 137–146. [Google Scholar] [CrossRef]
- Khalkhal, E.; Razzaghi, M.; Rostami-Nejad, M.; Rezaei-Tavirani, M.; Heidari Beigvand, H.; Rezaei Tavirani, M. Evaluation of Laser Effects on the Human Body After Laser Therapy. J. Lasers Med. Sci. 2020, 11, 91–97. [Google Scholar] [CrossRef]
- Cremers, D.A.; Radziemski, L.J.; Loree, T.R. Spectrochemical Analysis of Liquids Using the Laser Spark. Appl. Spectrosc. 1984, 38, 721–729. [Google Scholar] [CrossRef]
- Nakamura, S.; Ito, Y.; Sone, K.; Hiraga, H.; Kaneko, K.-i. Determination of an Iron Suspension in Water by Laser-Induced Breakdown Spectroscopy with Two Sequential Laser Pulses. Anal. Chem. 1996, 68, 2981–2986. [Google Scholar] [CrossRef] [PubMed]
- Stratis, D.N.; Eland, K.L.; Angel, S.M. Dual-Pulse LIBS Using a Pre-ablation Spark for Enhanced Ablation and Emission. Appl. Spectrosc. 2000, 54, 1270–1274. [Google Scholar] [CrossRef]
- Angel, S.M.; Stratis, D.N.; Eland, K.L.; Lai, T.; Berg, M.A.; Gold, D.M. LIBS using dual- and ultra-short laser pulses. Fresenius’ J. Anal. Chem. 2001, 369, 320–327. [Google Scholar] [CrossRef]
- St-Onge, L.; Sabsabi, M.; Cielo, P. Analysis of solids using laser-induced plasma spectroscopy in double-pulse mode. Spectrochim. Acta Part B At. Spectrosc. 1998, 53, 407–415. [Google Scholar] [CrossRef]
- Pichahchy, A.E.; Cremers, D.A.; Ferris, M.J. Elemental analysis of metals under water using laser-induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 1997, 52, 25–39. [Google Scholar] [CrossRef]
- Kang, W.; Chen, Y.; Bagchi, A.; O’Shaughnessy, T.J. Characterization and detection of acceleration-induced cavitation in soft materials using a drop-tower-based integrated system. Rev. Sci. Instrum. 2017, 88, 125113. [Google Scholar] [CrossRef]
- Fu, Y.; Lu, H.; Nian, G.; Wang, P.; Lin, N.; Hu, X.; Zhou, H.; Yu, H.; Qu, S.; Yang, W. Size-dependent inertial cavitation of soft materials. J. Mech. Phys. Solids 2020, 137, 103859. [Google Scholar] [CrossRef]
- Kang, W.; Robitaille, M.C.; Merrill, M.; Teferra, K.; Kim, C.; Raphael, M.P. Mechanisms of cell damage due to mechanical impact: An in vitro investigation. Sci. Rep. 2020, 10, 12009. [Google Scholar] [CrossRef] [PubMed]
| Name of Model | Strain Energy Density (W) | Reference |
|---|---|---|
| Neo-Hookean Model | [43] | |
| Mooney–Rivlin Model | [44,45] | |
| Gent Model | [47] | |
| Ogden Model | [49] | |
| Fung Model | [52,53] |
| Name of Model | Strain Energy Density (W) | Description | Reference |
|---|---|---|---|
| Newtonian | Viscous stresses linearly dependent on the local strain rate | [67] | |
| Kelvin–Voigt | A spring and a dashpot in parallel; Viscoelastic solid; Creep behavior | [41,68,69] | |
| Maxwell | A spring and a dashpot in series; Viscoelastic liquid; Stress relaxation | [70,71] | |
| Standard Linear solid | Both creep and stress relaxation | [72] |
| NIC | AIC | LIC | Drop Tower Test | |
|---|---|---|---|---|
| Driving force | Pressure energy | Wave energy | Potential energy | |
| Strain rate | 10−4–103 | 103–108 | 101–108 | 100–105 |
| Scale (µm) | 100–105 | 103 | 10−1–102 | 102–105 |
| Pressure (Pa) | ≤105 | ≤107 | ≤108 | ≤106 |
| Cavity type | Single | Multiple | Single and Multiple | Single and Multiple |
| Level of accessibility | Low | High | High | Intermediate |
| Approach type | Contact | Noncontact | Noncontact | Noncontact |
| Thermal effect | Low | Intermediate | High | Low |
| Application | Drug delivery | Lithotripsy Imaging, Drug delivery | Drug delivery, Microsurgery, Medical diagnostic, High strain rate material properties | High strain rate material properties (Isothermal) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Choi, W.J.; Ng, Y.; Kang, W. Mechanically Induced Cavitation in Biological Systems. Life 2021, 11, 546. https://doi.org/10.3390/life11060546
Kim C, Choi WJ, Ng Y, Kang W. Mechanically Induced Cavitation in Biological Systems. Life. 2021; 11(6):546. https://doi.org/10.3390/life11060546
Chicago/Turabian StyleKim, Chunghwan, Won June Choi, Yisha Ng, and Wonmo Kang. 2021. "Mechanically Induced Cavitation in Biological Systems" Life 11, no. 6: 546. https://doi.org/10.3390/life11060546
APA StyleKim, C., Choi, W. J., Ng, Y., & Kang, W. (2021). Mechanically Induced Cavitation in Biological Systems. Life, 11(6), 546. https://doi.org/10.3390/life11060546






