Context-Dependent Stability and Robustness of Genetic Toggle Switches with Leaky Promoters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model to Account for the Scarcity of Resources
2.2. Stability Analysis
2.3. Robustness Analysis
2.4. Population-Level Analysis
2.5. Context Effects
3. Results
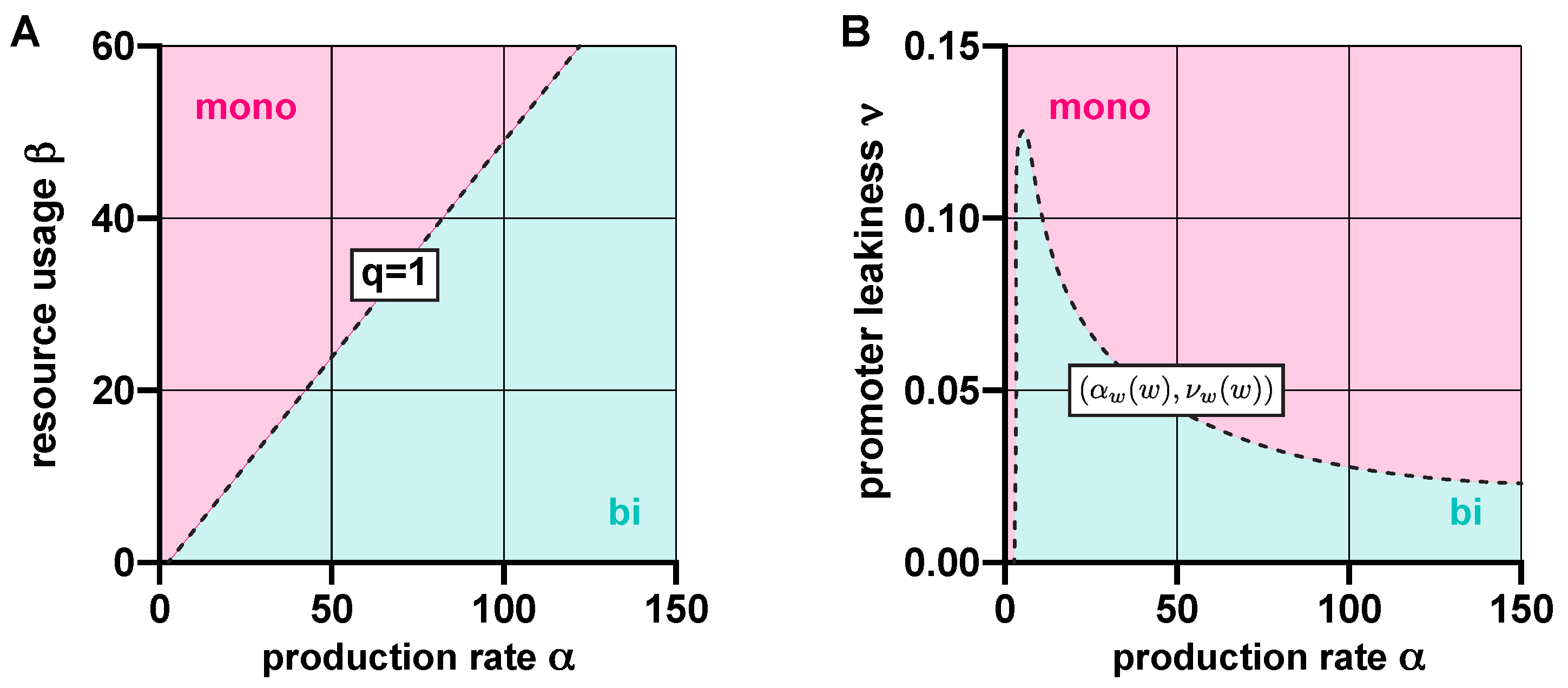
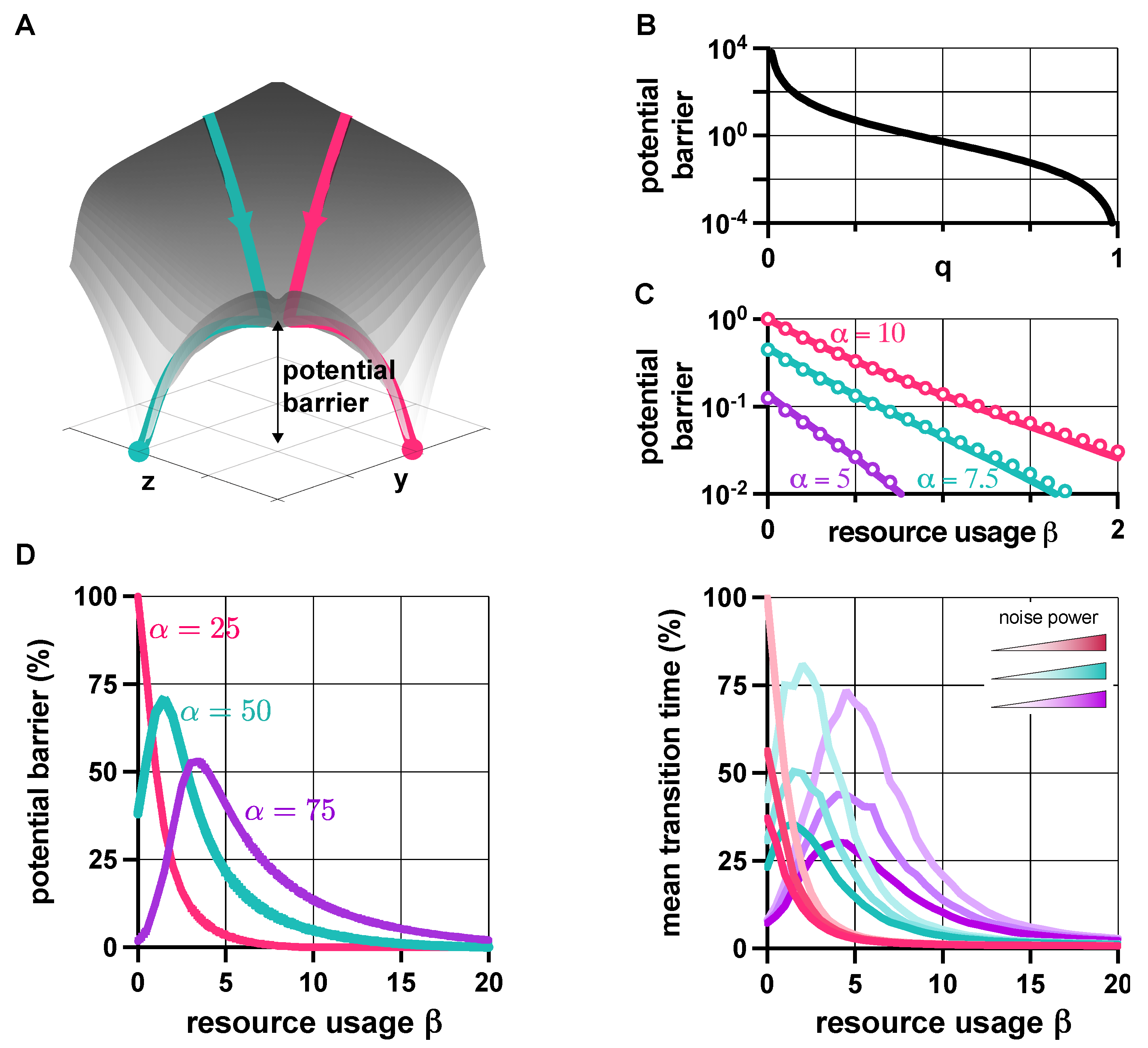
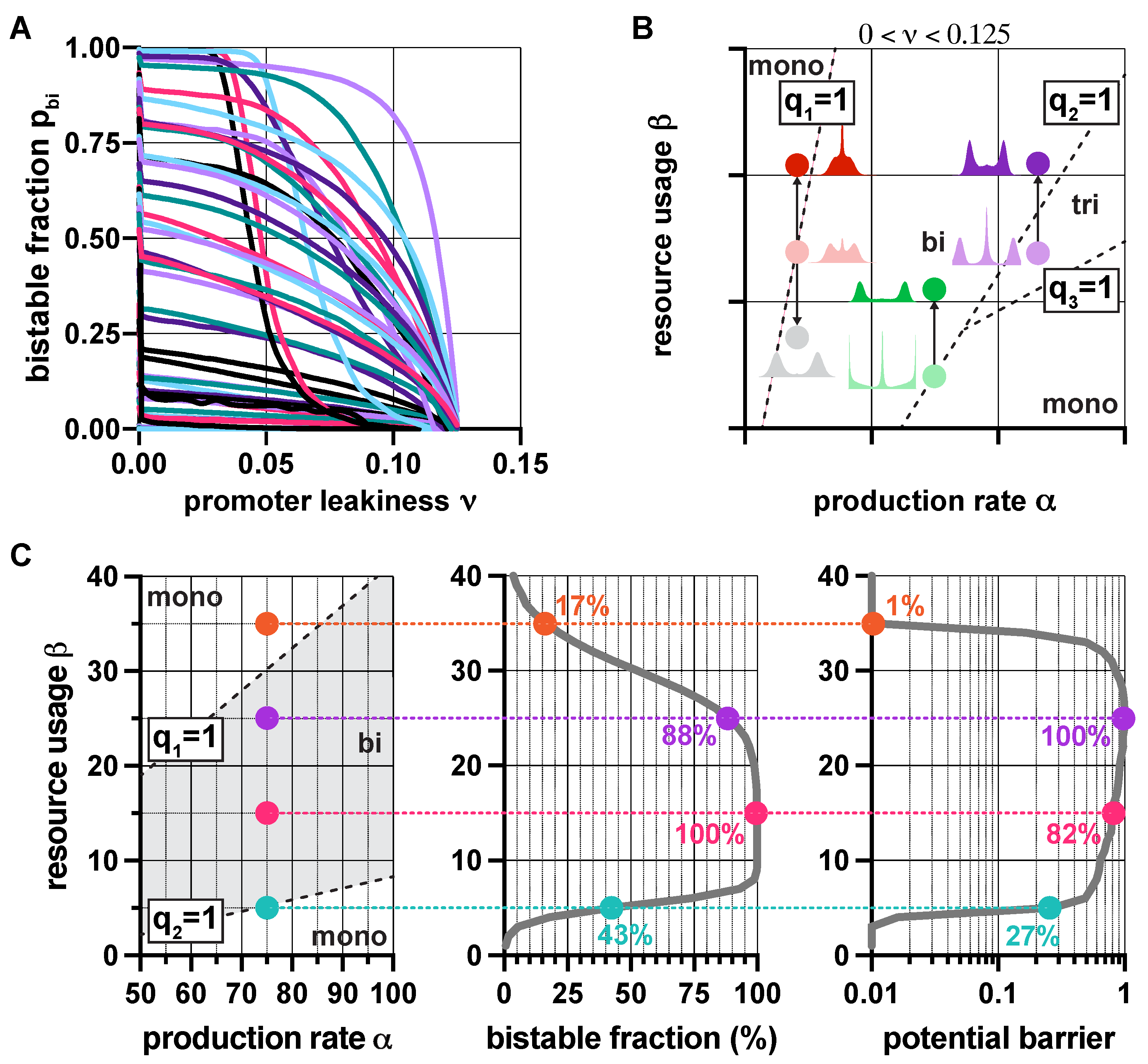
3.1. Stability Analysis
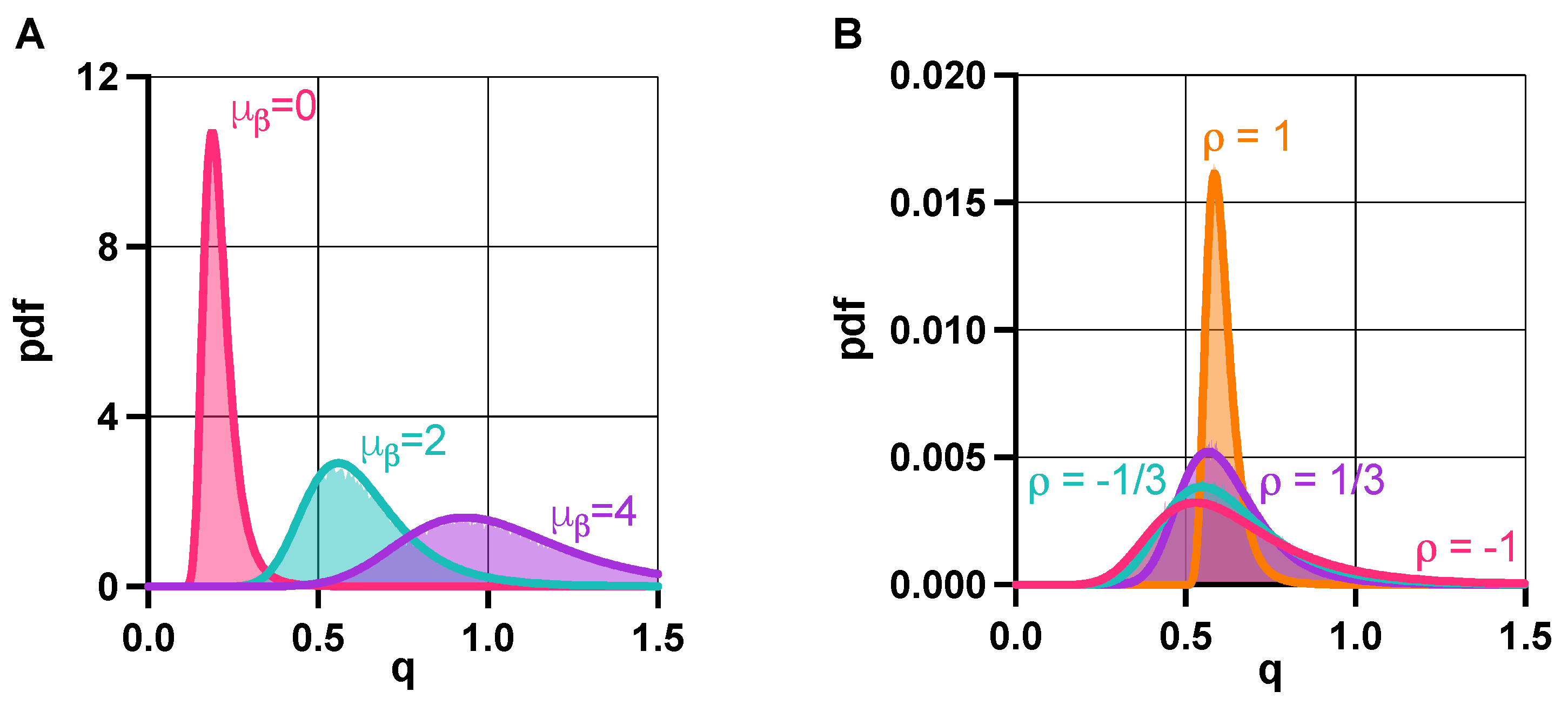
3.2. Robustness Analysis
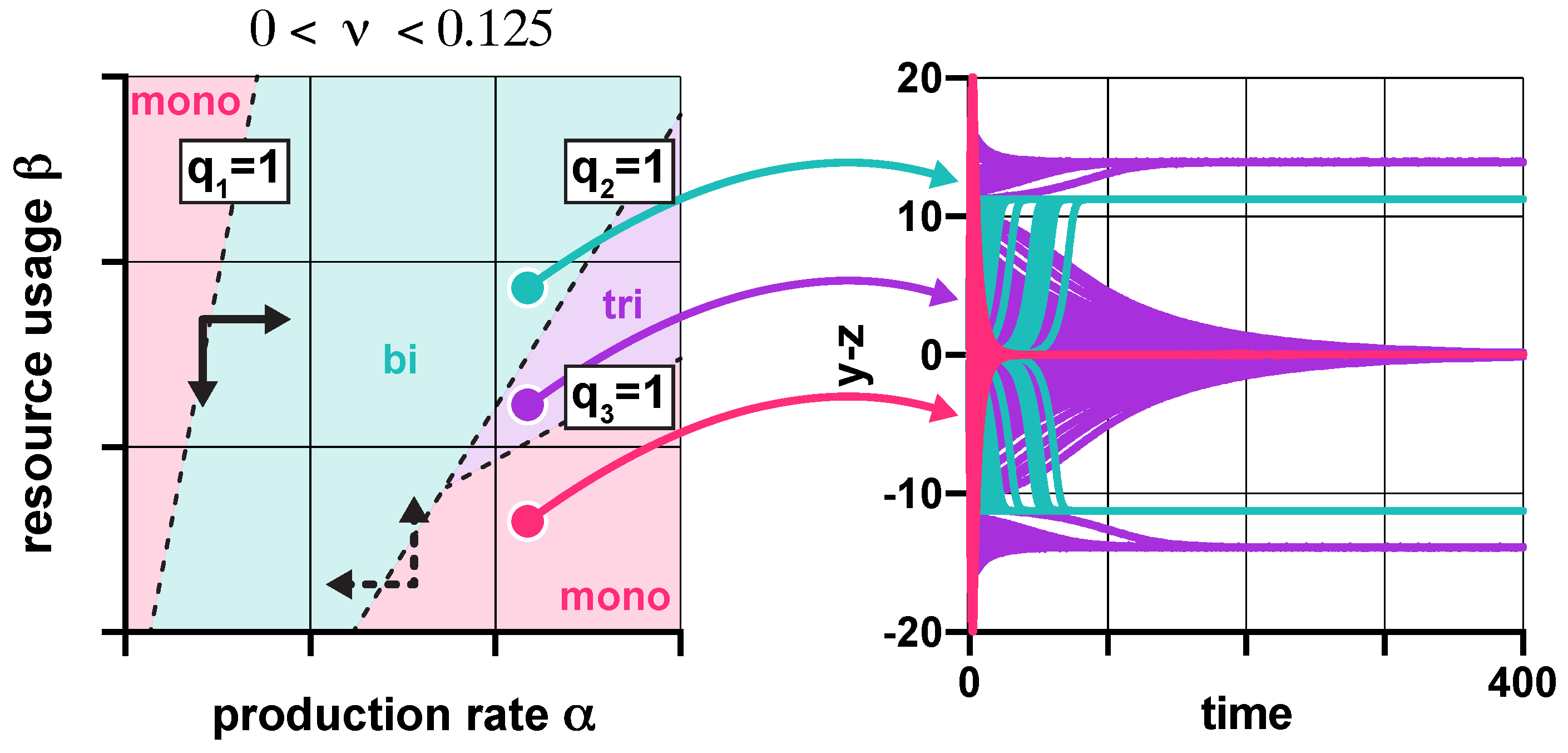
3.3. Population-Level Analysis
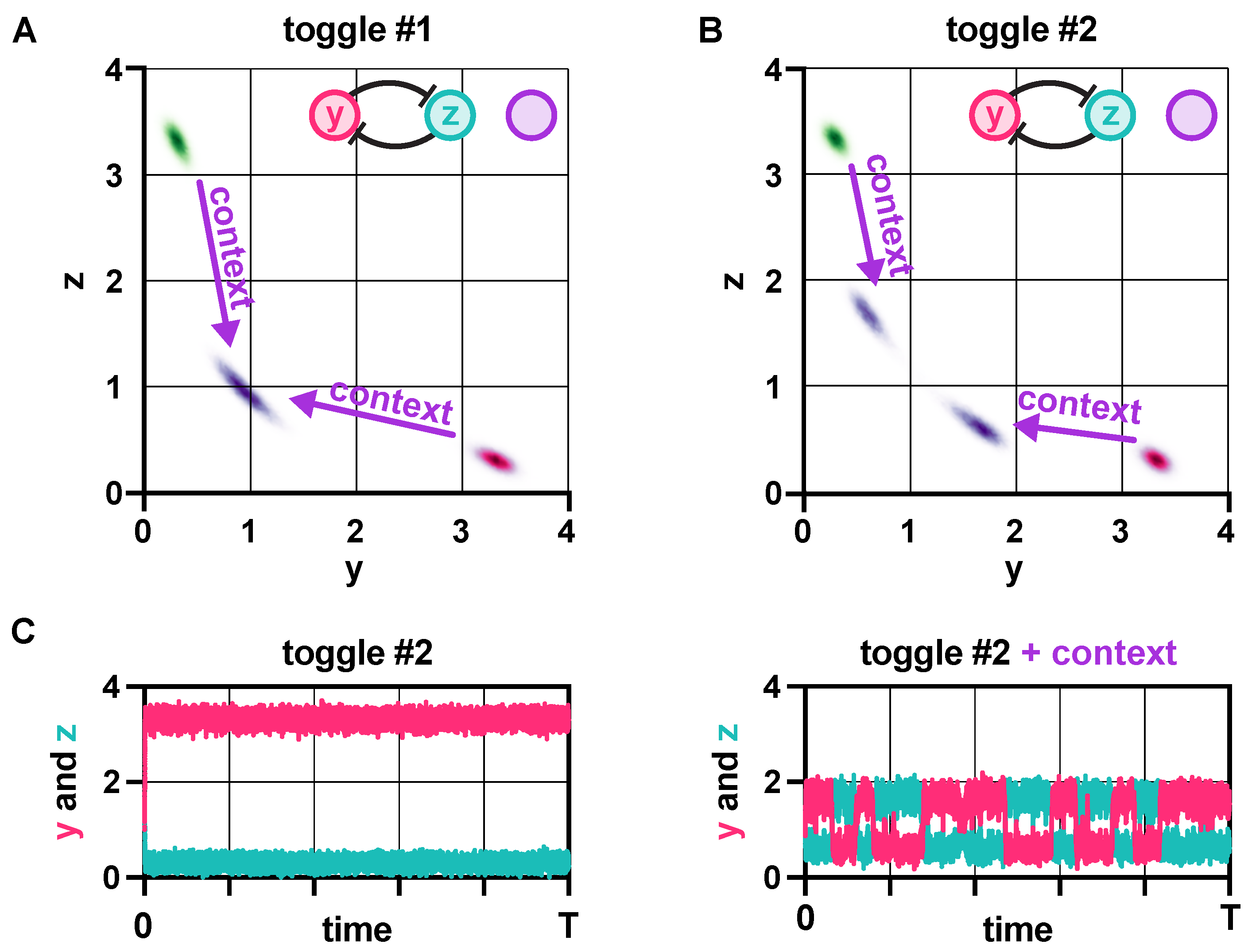
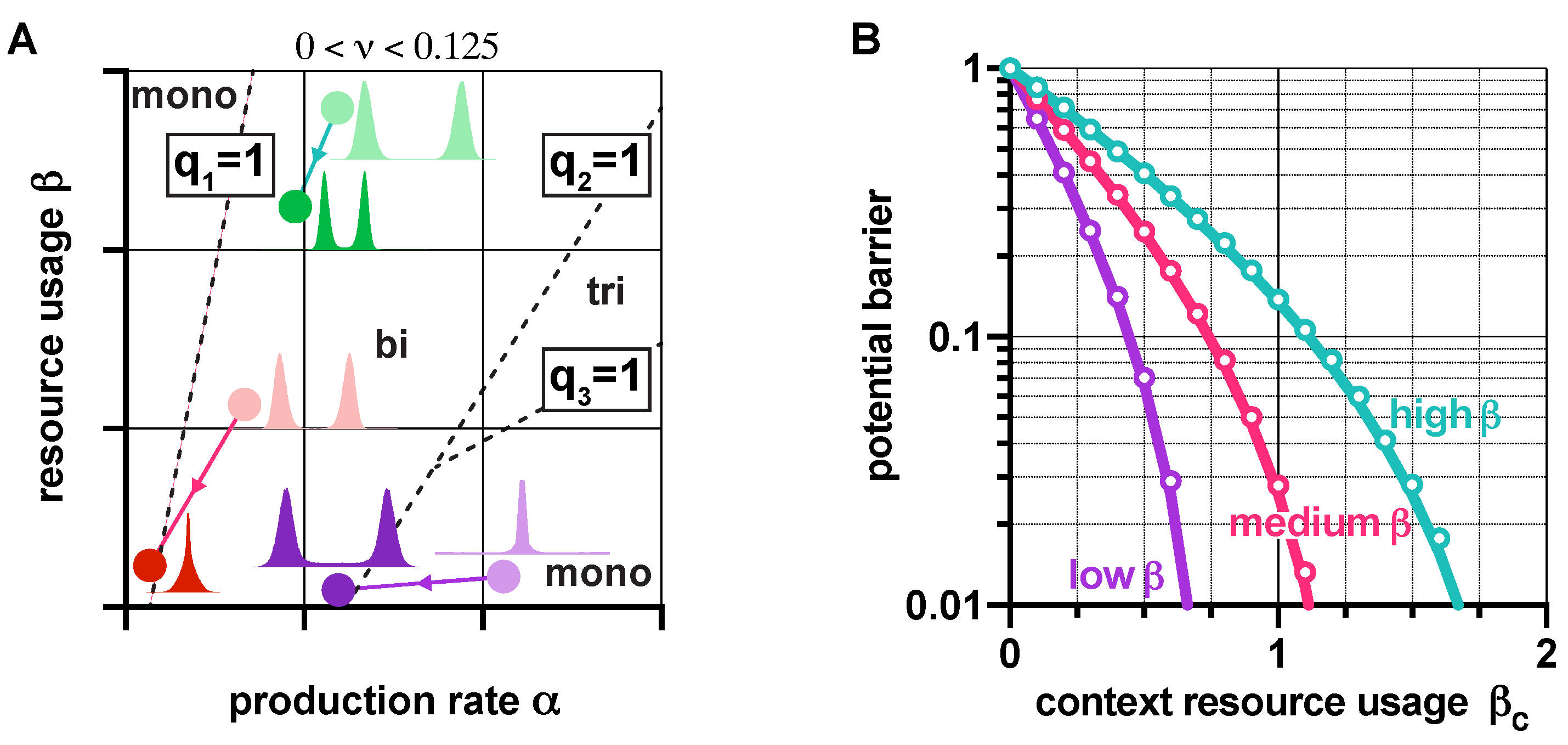
3.4. Context Effects
4. Discussion
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benner, S.A.; Sismour, A.M. Synthetic biology. Nat. Rev. Genet. 2005, 6, 533–543. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; McBride, C.; Del Vecchio, D. Programming Cells to Work for Us. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 411–440. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Rai, N.; Merchel Piovesan Pereira, B.; Eetemadi, A.; Tagkopoulos, I. Accelerated knowledge discovery from omics data by optimal experimental design. Nat. Commun. 2020, 11, 5026. [Google Scholar] [CrossRef]
- Angenent-Mari, N.M.; Garruss, A.S.; Soenksen, L.R.; Church, G.; Collins, J.J. A deep learning approach to programmable RNA switches. Nat. Commun. 2020, 11, 5057. [Google Scholar] [CrossRef]
- Grozinger, L.; Amos, M.; Gorochowski, T.E.; Carbonell, P.; Oyarzún, D.A.; Stoof, R.; Fellermann, H.; Zuliani, P.; Tas, H.; Goñi-Moreno, A. Pathways to cellular supremacy in biocomputing. Nat. Commun. 2019, 10, 5250. [Google Scholar] [CrossRef]
- Charbonneau, M.R.; Isabella, V.M.; Li, N.; Kurtz, C.B. Developing a new class of engineered live bacterial therapeutics to treat human diseases. Nat. Commun. 2020, 11, 1738. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peralta-Yahya, P.P.; Zhang, F.; del Cardayre, S.B.; Keasling, J.D. Microbial engineering for the production of advanced biofuels. Nature 2012, 488, 320–328. [Google Scholar] [CrossRef]
- Arpino, J.A.J.; Hancock, E.J.; Anderson, J.; Barahona, M.; Stan, G.B.V.; Papachristodoulou, A.; Polizzi, K. Tuning the dials of Synthetic Biology. Microbiology 2013, 159, 1236–1253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smanski, M.J.; Bhatia, S.; Zhao, D.; Park, Y.; Woodruff, L.B.A.; Giannoukos, G.; Ciulla, D.; Busby, M.; Calderon, J.; Nicol, R.; et al. Functional optimization of gene clusters by combinatorial design and assembly. Nat. Biotechnol. 2014, 32, 1241–1249. [Google Scholar] [CrossRef] [PubMed]
- Cardinale, S.; Arkin, A.P. Contextualizing context for synthetic biology–identifying causes of failure of synthetic biological systems. Biotechnol. J. 2012, 7, 856–866. [Google Scholar] [CrossRef]
- Gyorgy, A.; Del Vecchio, D. Modular Composition of Gene Transcription Networks. PLoS Comput. Biol. 2014, 10, e1003486. [Google Scholar] [CrossRef]
- Yeung, E.; Dy, A.J.; Martin, K.B.; Ng, A.H.; Del Vecchio, D.; Beck, J.L.; Collins, J.J.; Murray, R.M. Biophysical Constraints Arising from Compositional Context in Synthetic Gene Networks. Cell Syst. 2017, 5, 11–24.e12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, Y.; Huang, H.H.; Jiménez, J.I.; Del Vecchio, D. Resource Competition Shapes the Response of Genetic Circuits. ACS Synth. Biol. 2017, 6, 1263–1272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scott, M.; Gunderson, C.W.; Mateescu, E.M.; Zhang, Z.; Hwa, T. Interdependence of Cell Growth and Gene Expression: Origins and Consequences. Science 2010, 330, 1099–1102. [Google Scholar] [CrossRef] [PubMed]
- Ceroni, F.; Algar, R.; Stan, G.B.; Ellis, T. Quantifying cellular capacity identifies gene expression designs with reduced burden. Nat. Methods 2015, 12, 415–418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gyorgy, A.; Jiménez, J.I.; Yazbek, J.; Huang, H.H.; Chung, H.; Weiss, R.; Del Vecchio, D. Isocost Lines Describe the Cellular Economy of Genetic Circuits. Biophys. J. 2015, 109, 639–646. [Google Scholar] [CrossRef] [Green Version]
- Siegal-Gaskins, D.; Tuza, Z.A.; Kim, J.; Noireaux, V.; Murray, R.M. Gene Circuit Performance Characterization and Resource Usage in a Cell-Free “Breadboard”. ACS Synth. Biol. 2014, 3, 416–425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borkowski, O.; Ceroni, F.; Stan, G.; Ellis, T. Overloaded and stressed: Whole-cell considerations for bacterial synthetic biology. Curr. Opin. Microbiol. 2016, 33, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Weiße, A.Y.; Oyarzún, D.A.; Danos, V.; Swain, P.S. Mechanistic links between cellular trade-offs, gene expression, and growth. Proc. Natl. Acad. Sci. USA 2015, 112, E1038–E1047. [Google Scholar] [CrossRef] [Green Version]
- Raveh, A.; Margaliot, M.; Sontag, E.D.; Tuller, T. A model for competition for ribosomes in the cell. J. R. Soc. Interface 2016, 13, 20151062. [Google Scholar] [CrossRef]
- Gorochowski, T.E.; Avcilar-Kucukgoze, I.; Bovenberg, R.A.L.; Roubos, J.A.; Ignatova, Z. A Minimal Model of Ribosome Allocation Dynamics Captures Trade-offs in Expression between Endogenous and Synthetic Genes. ACS Synth. Biol. 2016, 5, 710–720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frei, T.; Cella, F.; Tedeschi, F.; Gutiérrez, J.; Stan, G.B.; Khammash, M.; Siciliano, V. Characterization and mitigation of gene expression burden in mammalian cells. Nat. Commun. 2020, 11, 4641. [Google Scholar] [CrossRef]
- Tan, C.; Marguet, P.; You, L. Emergent bistability by a growth-modulating positive feedback circuit. Nat. Chem. Biol. 2009, 5, 842–848. [Google Scholar] [CrossRef]
- Marguet, P.; Tanouchi, Y.; Spitz, E.; Smith, C.; You, L. Oscillations by Minimal Bacterial Suicide Circuits Reveal Hidden Facets of Host-Circuit Physiology. PLoS ONE 2010, 5, e11909. [Google Scholar] [CrossRef] [Green Version]
- Vecchio, D.D.; Qian, Y.; Murray, R.M.; Sontag, E.D. Future systems and control research in synthetic biology. Annu. Rev. Control 2018, 45, 5–17. [Google Scholar] [CrossRef]
- Andrianantoandro, E.; Basu, S.; Karig, D.K.; Weiss, R. Synthetic biology: New engineering rules for an emerging discipline. Mol. Syst. Biol. 2006, 2, 5–17. [Google Scholar] [CrossRef] [Green Version]
- Bandiera, L.; Hou, Z.; Kothamachu, V.B.; Balsa-Canto, E.; Swain, P.S.; Menolascina, F. On-Line Optimal Input Design Increases the Efficiency and Accuracy of the Modelling of an Inducible Synthetic Promoter. Processes 2018, 6, 148. [Google Scholar] [CrossRef] [Green Version]
- Sakurai, Y.; Hori, Y. Optimization-based synthesis of stochastic biocircuits with statistical specifications. J. R. Soc. Interface 2018, 15, 20170709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bokes, P.; Hojcka, M.; Singh, A. MicroRNA based feedforward control of intrinsic gene expression noise. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 18, 272–282. [Google Scholar] [CrossRef] [PubMed]
- Gorochowski, T.E.; Grierson, C.S.; di Bernardo, M. Organization of feed-forward loop motifs reveals architectural principles in natural and engineered networks. Sci. Adv. 2018, 4, eaap9751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cuba Samaniego, C.; Giordano, G.; Kim, J.; Blanchini, F.; Franco, E. Molecular Titration Promotes Oscillations and Bistability in Minimal Network Models with Monomeric Regulators. ACS Synth. Biol. 2016, 5, 321–333. [Google Scholar] [CrossRef] [PubMed]
- Siegal-Gaskins, D.; Franco, E.; Zhou, T.; Murray, R.M. An analytical approach to bistable biological circuit discrimination using real algebraic geometry. J. R. Soc. Interface 2015, 12, 20150288. [Google Scholar] [CrossRef] [Green Version]
- Giordano, G.; Cuba Samaniego, C.; Franco, E.; Blanchini, F. Computing the structural influence matrix for biological systems. J. Math. Biol. 2016, 72, 1927–1958. [Google Scholar] [CrossRef] [PubMed]
- Blanchini, F.; Franco, E.; Giordano, G. A Structural Classification of Candidate Oscillatory and Multistationary Biochemical Systems. Bull. Math. Biol. 2014, 76, 2542–2569. [Google Scholar] [CrossRef]
- Franco, E.; Giordano, G.; Forsberg, P.O.; Murray, R.M. Negative Autoregulation Matches Production and Demand in Synthetic Transcriptional Networks. ACS Synth. Biol. 2014, 3, 589–599. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prescott, T.P.; Lang, M.; Papachristodoulou, A. Quantification of Interactions between Dynamic Cellular Network Functionalities by Cascaded Layering. PLoS Comput. Biol. 2015, 11, e1004235. [Google Scholar] [CrossRef]
- Purcell, O.; di Bernardo, M.; Grierson, C.S.; Savery, N.J. A Multi-Functional Synthetic Gene Network: A Frequency Multiplier, Oscillator and Switch. PLoS ONE 2011, 6, e16140. [Google Scholar] [CrossRef]
- Cuba Samaniego, C.; Franco, E. A Robust Molecular Network Motif for Period-Doubling Devices. ACS Synth. Biol. 2018, 7, 75–85. [Google Scholar] [CrossRef]
- Ren, X.; Samaniego, C.C.; Murray, R.M.; Franco, E. Bistable State Switch Enables Ultrasensitive Feedback Control in Heterogeneous Microbial Populations. In Proceedings of the 2021 American Control Conference, New Orleans, LA, USA, 26–28 May 2021; pp. 652–659. [Google Scholar] [CrossRef]
- Egbert, R.G.; Klavins, E. Fine-tuning gene networks using simple sequence repeats. Proc. Natl. Acad. Sci. USA 2012, 109, 16817–16822. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Goetz, H.; Melendez-Alvarez, J.; Li, J.; Ding, T.; Wang, X.; Tian, X.J. Winner-takes-all resource competition redirects cascading cell fate transitions. Nat. Commun. 2021, 12, 853. [Google Scholar] [CrossRef] [PubMed]
- Elowitz, M.B.; Leibler, S. A synthetic oscillatory network of transcriptional regulators. Nature 2000, 403, 335–338. [Google Scholar] [CrossRef]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Ando, T.; Meguro, T.; Yamato, I. Multiple Time Step Brownian Dynamics for Long Time Simulation of Biomolecules. Mol. Simul. 2003, 29, 471–478. [Google Scholar] [CrossRef]
- Copperman, J.; Guenza, M.G. Coarse-Grained Langevin Equation for Protein Dynamics: Global Anisotropy and a Mode Approach to Local Complexity. J. Phys. Chem. B 2015, 119, 9195–9211. [Google Scholar] [CrossRef]
- Gyorgy, A. Sharing Resources Can Lead to Monostability in a Network of Bistable Toggle Switches. IEEE Control Syst. Lett. 2018, 3, 308–313. [Google Scholar] [CrossRef]
- Yong, C.; Gyorgy, A. Stability and Robustness of Unbalanced Genetic Toggle Switches in the Presence of Scarce Resources. Life 2021, 11, 271. [Google Scholar] [CrossRef] [PubMed]
- Leon, M.; Woods, M.L.; Fedorec, A.J.H.; Barnes, C.P. A computational method for the investigation of multistable systems and its application to genetic switches. BMC Syst. Biol. 2016, 10, 130. [Google Scholar] [CrossRef] [Green Version]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic Gene Expression in a Single Cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef] [Green Version]
- Gyorgy, A.; Murray, R.M. Quantifying resource competition and its effects in the TX-TL system. In Proceedings of the 55th IEEE Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 3363–3368. [Google Scholar] [CrossRef] [Green Version]
- Salis, H.M. Chapter two—The Ribosome Binding Site Calculator. In Synthetic Biology, Part B; Voigt, C., Ed.; Methods in Enzymology; Academic Press: Cambridge, MA, USA, 2011; Volume 498, pp. 19–42. [Google Scholar] [CrossRef]
- Lee, J.W.; Gyorgy, A.; Cameron, D.E.; Pyenson, N.; Choi, K.R.; Way, J.C.; Silver, P.A.; Del Vecchio, D.; Collins, J.J. Creating Single-Copy Genetic Circuits. Mol. Cell 2016, 63, 329–336. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Tague, N.; Whelan, S.; Dunlop, M.J. Programmable gene regulation for metabolic engineering using decoy transcription factor binding sites. Nucleic Acid Res. 2020, 49, 1163–1172. [Google Scholar] [CrossRef]
- Gardner, T.S.; Cantor, C.R.; Collins, J.J. Construction of a genetic toggle switch in E. coli. Nature 2000, 403, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Jaruszewicz-Błońska, J.; Lipniacki, T. Genetic toggle switch controlled by bacterial growth rate. BMC Syst. Biol. 2017, 11, 117. [Google Scholar] [CrossRef] [Green Version]
- Pokhilko, A.; Ebenhöh, O.; Stark, W.M.; Colloms, S.D. Mathematical model of a serine integrase-controlled toggle switch with a single input. J. R. Soc. Interface 2018, 15, 20180160. [Google Scholar] [CrossRef]
- Lugagne, J.B.; Carrillo, S.S.; Kirch, M.; Köhler, A.; Batt, G.; Hersen, P. Balancing a genetic toggle switch by real-time feedback control and periodic forcing. Nat. Commun. 2017, 8, 1671. [Google Scholar] [CrossRef] [PubMed]
- Guarino, A.; Fiore, D.; Salzano, D.; di Bernardo, M. Balancing Cell Populations Endowed with a Synthetic Toggle Switch via Adaptive Pulsatile Feedback Control. ACS Synth. Biol. 2020, 9, 793–803. [Google Scholar] [CrossRef]
- Du, P.; Zhao, H.; Zhang, H.; Wang, R.; Huang, J.; Tian, Y.; Luo, X.; Luo, X.; Wang, M.; Xiang, Y.; et al. De novo design of an intercellular signaling toolbox for multi-channel cell–cell communication and biological computation. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef]
- Gyorgy, A. Bistability requires better balanced toggle switches in the presence of competition for shared cellular resources. In Proceedings of the American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 154–156. [Google Scholar]
- Shao, B.; Rammohan, J.; Anderson, D.A.; Alperovich, N.; Ross, D.; Voigt, C.A. Single-cell measurement of plasmid copy number and promoter activity. Nat. Commun. 2021, 12, 1475. [Google Scholar] [CrossRef]
- Darlington, A.P.S.; Kim, J.; Jimenez, J.I.; Bates, D.G. Dynamic allocation of orthogonal ribosomes facilitates uncoupling of co-expressed genes. Nat. Commun. 2018, 9, 695. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Schiavon, M.; Dods, G.; El-Samad, H.; Ng, A.H. Multidimensional Characterization of Parts Enhances Modeling Accuracy in Genetic Circuits. ACS Synth. Biol. 2020, 9, 2917–2926. [Google Scholar] [CrossRef] [PubMed]
- Vecchio, D.D.; Murray, R.M. Biomolecular Feedback Systems; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Bhattacharya, S.; Zhang, Q.; Andersen, M.E. A deterministic map of Waddington’s epigenetic landscape for cell fate specification. BMC Syst. Biol. 2011, 5, 85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verd, B.; Crombach, A.; Jaeger, J. Classification of transient behaviours in a time-dependent toggle switch model. BMC Syst. Biol. 2014, 8, 43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gyorgy, A. Scarcity of Cellular Resources Decreases the Robustness of Toggle Switches to Noise. In Proceedings of the American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- So/rensen, M.R.; Voter, A.F. Temperature-accelerated dynamics for simulation of infrequent events. J. Chem. Phys. 2000, 112, 9599–9606. [Google Scholar] [CrossRef] [Green Version]
- Geary, R.C. The Frequency Distribution of the Quotient of Two Normal Variates. J. R. Stat. Soc. 1930, 93, 442–446. [Google Scholar] [CrossRef]
- Marsaglia, G. Ratios of Normal Variables and Ratios of Sums of Uniform Variables. J. Am. Stat. Assoc. 1965, 60, 193–204. [Google Scholar] [CrossRef]
- Hinkley, D.V. On the Ratio of Two Correlated Normal Random Variables. Biometrika 1969, 56, 635–639. [Google Scholar] [CrossRef]
- Marsaglia, G. Ratios of Normal Variables. J. Stat. Softw. 2006, 16, 1–10. [Google Scholar] [CrossRef]
- Gyorgy, A. How Cell-to-Cell Heterogeneity and Scarce Resources Shape the Population-Level Stability Profile of Toggle Switches. In Proceedings of the 58th IEEE Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019. [Google Scholar]
- Andrews, L.B.; Nielsen, A.A.K.; Voigt, C.A. Cellular checkpoint control using programmable sequential logic. Science 2018, 361, eaap8987. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rotoli, M.; Russo, G.; di Bernardo, M. Stabilizing Quorum-Sensing Networks via Noise. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 647–651. [Google Scholar] [CrossRef]
- Russo, G.; Wirth, F.; Shorten, R. On Synchronization in Continuous-Time Networks of Nonlinear Nodes with State-Dependent and Degenerate Noise Diffusion. IEEE Trans. Autom. Control 2019, 64, 389–395. [Google Scholar] [CrossRef]
- Lynch, M.; Marinov, G.K. The bioenergetic costs of a gene. Proc. Natl. Acad. Sci. USA 2015, 112, 15690–15695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorochowski, T.E.; Chelysheva, I.; Eriksen, M.; Nair, P.; Pedersen, S.; Ignatova, Z. Absolute quantification of translational regulation and burden using combined sequencing approaches. Mol. Syst. Biol. 2019, 15. [Google Scholar] [CrossRef]
- Espah Borujeni, A.; Zhang, J.; Doosthosseini, H.; Nielsen, A.A.K.; Voigt, C.A. Genetic circuit characterization by inferring RNA polymerase movement and ribosome usage. Nat. Commun. 2020, 11, 5001. [Google Scholar] [CrossRef] [PubMed]
- Greco, F.V.; Pandi, A.; Erb, T.J.; Grierson, C.S.; Gorochowski, T.E. Harnessing the central dogma for stringent multi-level control of gene expression. Nat. Commun. 2021, 12, 1738. [Google Scholar] [CrossRef] [PubMed]
- Bandiera, L.; Gomez-Cabeza, D.; Gilman, J.; Balsa-Canto, E.; Menolascina, F. Optimally Designed Model Selection for Synthetic Biology. ACS Synth. Biol. 2020, 9, 3134–3144. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.C.; Jewett, M.C.; Chin, J.W.; Voigt, C.A. Toward an orthogonal central dogma. Nat. Chem. Biol. 2018, 14, 103–106. [Google Scholar] [CrossRef]
- Aleksashin, N.A.; Szal, T.; d’Aquino, A.E.; Jewett, M.C.; Vázquez-Laslop, N.; Mankin, A.S. A fully orthogonal system for protein synthesis in bacterial cells. Nat. Commun. 2020, 11, 1858. [Google Scholar] [CrossRef] [Green Version]
- Ceroni, F.; Boo, A.; Furini, S.; Gorochowski, T.E.; Borkowski, O.; Ladak, Y.N.; Awan, A.R.; Gilbert, C.; Stan, G.B.; Ellis, T. Burden-driven feedback control of gene expression. Nat. Methods 2018, 15, 387–393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, H.H.; Qian, Y.; Del Vecchio, D. A quasi-integral controller for adaptation of genetic modules to variable ribosome demand. Nat. Commun. 2018, 9, 5415. [Google Scholar] [CrossRef] [Green Version]
- Jones, R.D.; Qian, Y.; Siciliano, V.; DiAndreth, B.; Huh, J.; Weiss, R.; Del Vecchio, D. An endoribonuclease-based feedforward controller for decoupling resource-limited genetic modules in mammalian cells. Nat. Commun. 2020, 11, 5690. [Google Scholar] [CrossRef]
- Ali Al-Radhawi, M.; Tran, A.P.; Ernst, E.A.; Chen, T.; Voigt, C.A.; Sontag, E.D. Distributed implementation of Boolean functions by transcriptional synthetic circuits. ACS Synth. Biol. 2020, 9, 2172–2187. [Google Scholar] [CrossRef]
- Cookson, N.A.; Mather, W.H.; Danino, T.; Mondragón-Palomino, O.; Williams, R.J.; Tsimring, L.S.; Hasty, J. Queueing up for enzymatic processing: Correlated signaling through coupled degradation. Mol. Syst. Biol. 2011, 7, 561. [Google Scholar] [CrossRef] [Green Version]
- Butzin, N.C.; Hochendoner, P.; Ogle, C.T.; Mather, W.H. Entrainment of a Bacterial Synthetic Gene Oscillator through Proteolytic Queueing. ACS Synth. Biol. 2017, 6, 455–462. [Google Scholar] [CrossRef]
- Butzin, N.C.; Mather, W.H. Crosstalk between Diverse Synthetic Protein Degradation Tags in Escherichia coli. ACS Synth. Biol. 2018, 7, 54–62. [Google Scholar] [CrossRef]
- Deter, H.S.; Abualrahi, A.H.; Jadhav, P.; Schweer, E.K.; Ogle, C.T.; Butzin, N.C. Proteolytic Queues at ClpXP Increase Antibiotic Tolerance. ACS Synth. Biol. 2020, 9, 95–103. [Google Scholar] [CrossRef]
- Nikolados, E.M.; Weiße, A.Y.; Ceroni, F.; Oyarzún, D.A. Growth Defects and Loss-of-Function in Synthetic Gene Circuits. ACS Synth. Biol. 2019, 8, 1231–1240. [Google Scholar] [CrossRef] [Green Version]
- Dong, H.; Nilsson, L.; Kurland, C.G. Gratuitous overexpression of genes in Escherichia coli leads to growth inhibition and ribosome destruction. J. Bacteriol. 1995, 177, 1497–1504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoebel, D.M.; Dean, A.M.; Dykhuizen, D.E. The Cost of Expression of Escherichia coli lac Operon Proteins Is in the Process, Not in the Products. Genetics 2008, 178, 1653–1660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carrera, J.; Rodrigo, G.; Singh, V.; Kirov, B.; Jaramillo, A. Empirical model and in vivo characterization of the bacterial response to synthetic gene expression show that ribosome allocation limits growth rate. Biotechnol. J. 2011, 6, 773–783. [Google Scholar] [CrossRef]
- Klumpp, S.; Hwa, T. Bacterial growth: Global effects on gene expression, growth feedback and proteome partition. Curr. Opin. Biotechnol. 2014, 28, 96–102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shachrai, I.; Zaslaver, A.; Alon, U.; Dekel, E. Cost of Unneeded Proteins in E. coli Is Reduced after Several Generations in Exponential Growth. Mol. Cell 2010, 38, 758–767. [Google Scholar] [CrossRef]
- Liao, C.; Blanchard, A.E.; Lu, T. An integrative circuit–host modelling framework for predicting synthetic gene network behaviours. Nat. Microbiol. 2017, 2, 1658–1666. [Google Scholar] [CrossRef] [PubMed]
- Sickle, J.J.; Ni, C.; Shen, D.; Wang, Z.; Jin, M.; Lu, T. Integrative Circuit-Host Modeling of a Genetic Switch in Varying Environments. Sci. Rep. 2020, 10, 8383. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.A.K.; Der, B.S.; Shin, J.; Vaidyanathan, P.; Paralanov, V.; Strychalski, E.A.; Ross, D.; Densmore, D.; Voigt, C.A. Genetic circuit design automation. Science 2016, 352, aac7341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gyorgy, A. Context-Dependent Stability and Robustness of Genetic Toggle Switches with Leaky Promoters. Life 2021, 11, 1150. https://doi.org/10.3390/life11111150
Gyorgy A. Context-Dependent Stability and Robustness of Genetic Toggle Switches with Leaky Promoters. Life. 2021; 11(11):1150. https://doi.org/10.3390/life11111150
Chicago/Turabian StyleGyorgy, Andras. 2021. "Context-Dependent Stability and Robustness of Genetic Toggle Switches with Leaky Promoters" Life 11, no. 11: 1150. https://doi.org/10.3390/life11111150
APA StyleGyorgy, A. (2021). Context-Dependent Stability and Robustness of Genetic Toggle Switches with Leaky Promoters. Life, 11(11), 1150. https://doi.org/10.3390/life11111150