Digital Twin-Driven Mating Performance Analysis for Precision Spool Valve
Abstract
:1. Introduction
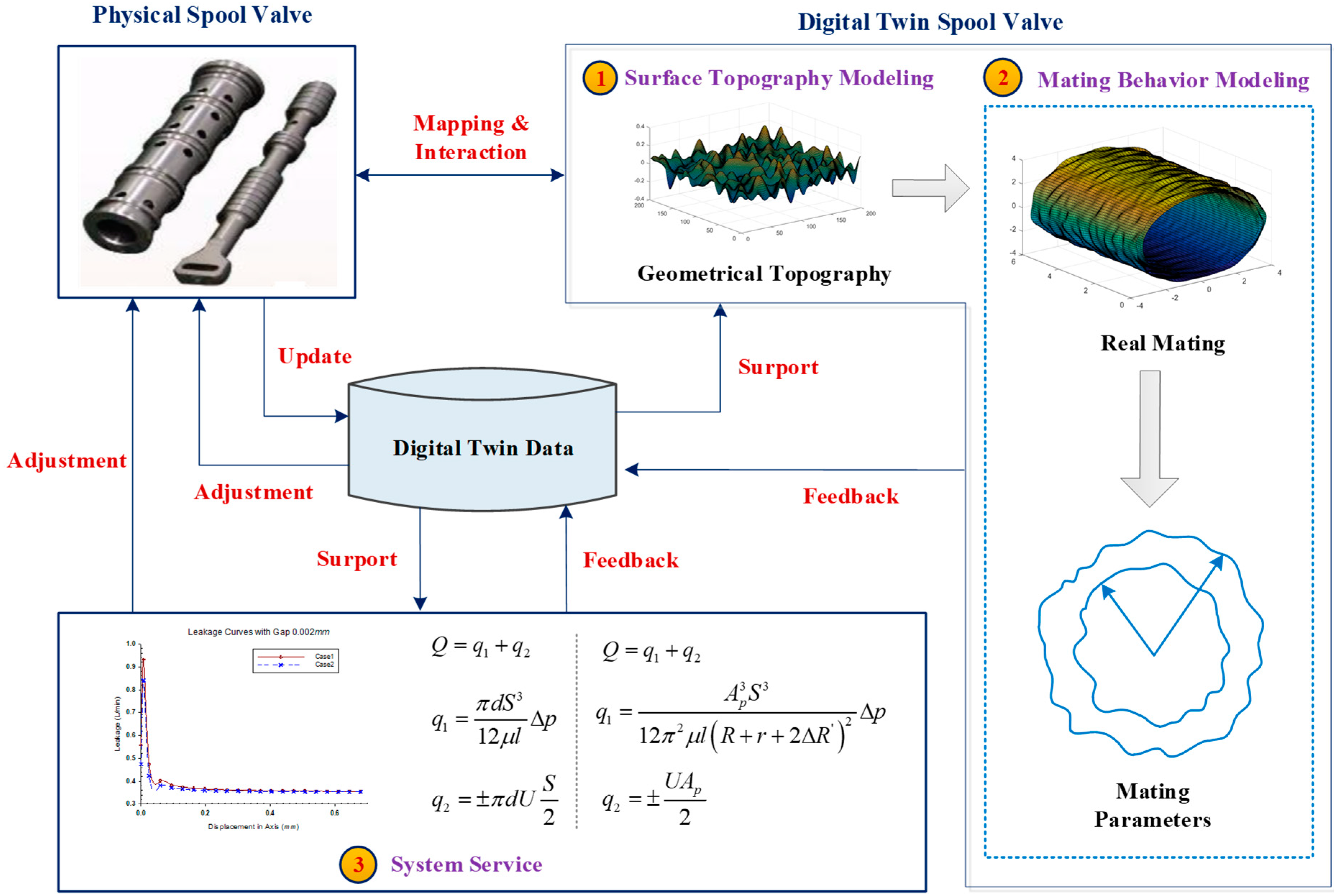
2. Overall Framework of Analyzing Mating Performance of Precision Spool Valves Based on Digital Twin
3. Digital Twin Modeling of Precision Spool Valve
3.1. Overall Outline
3.2. Key Methods
4. Mating Behavior Modeling of Precision Spool Valve Based on Digital Twin
4.1. Overall Outline
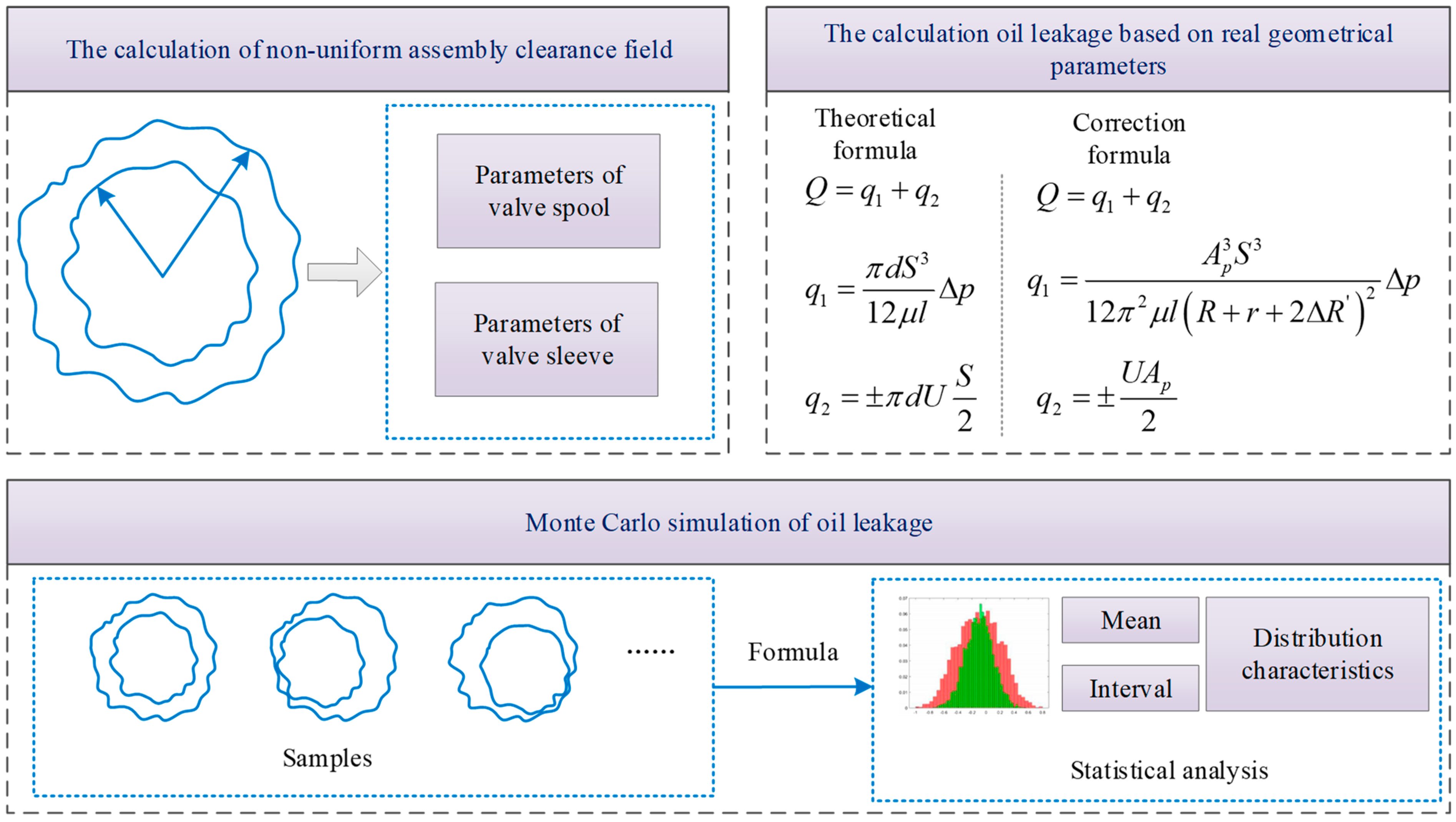
4.2. Key Methods
5. Example Verification and Results
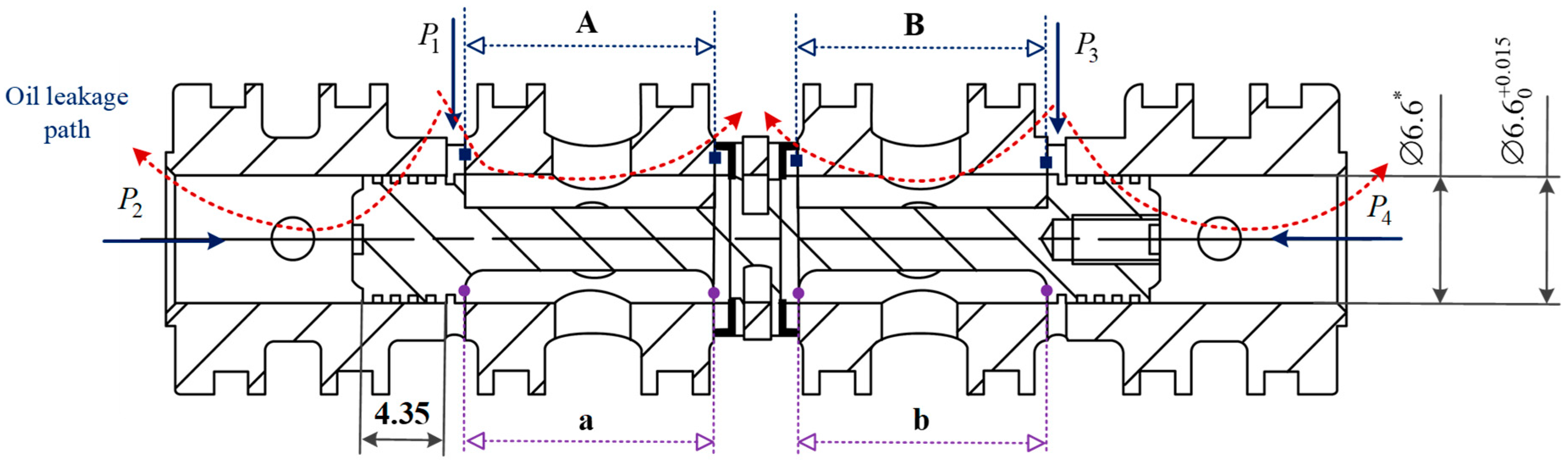
5.1. A Case of Precision Spool Valve
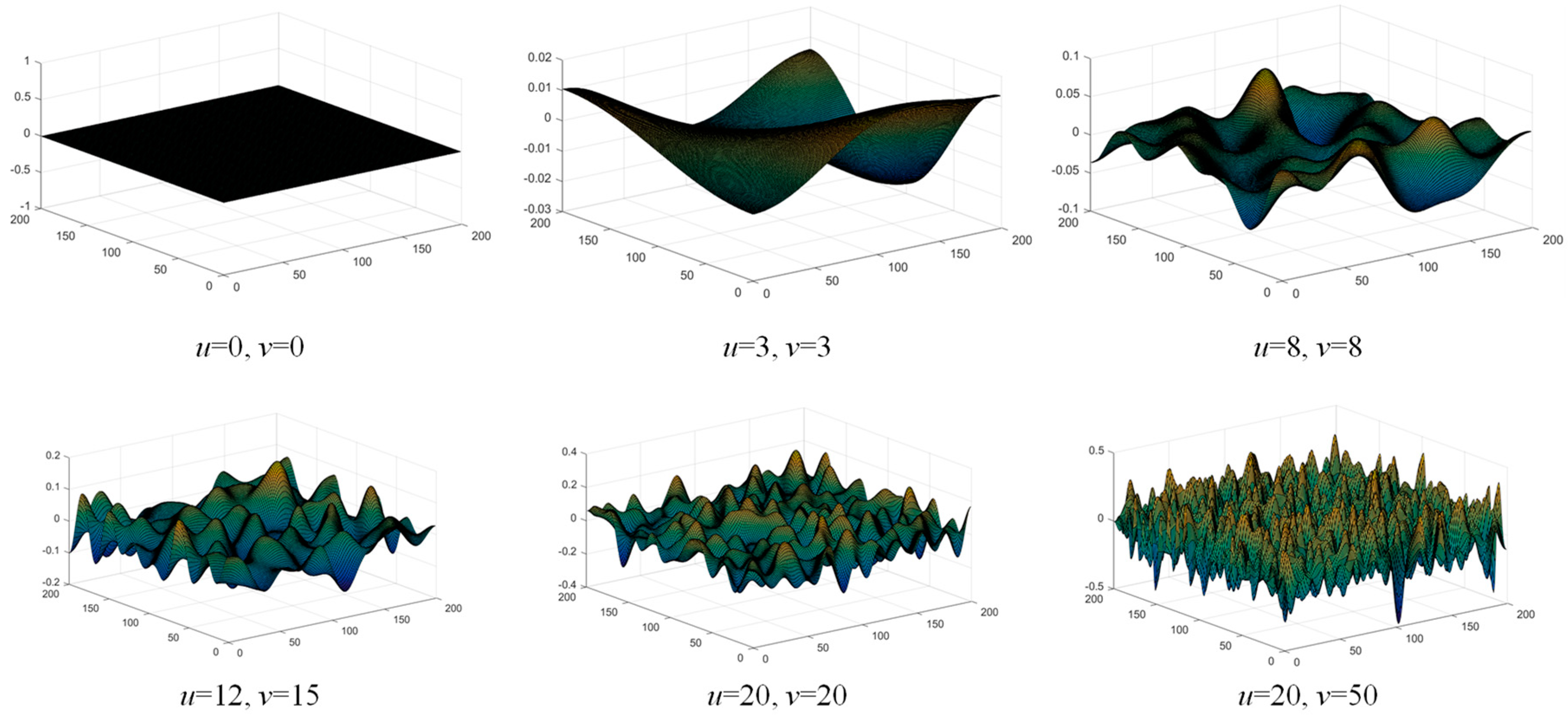
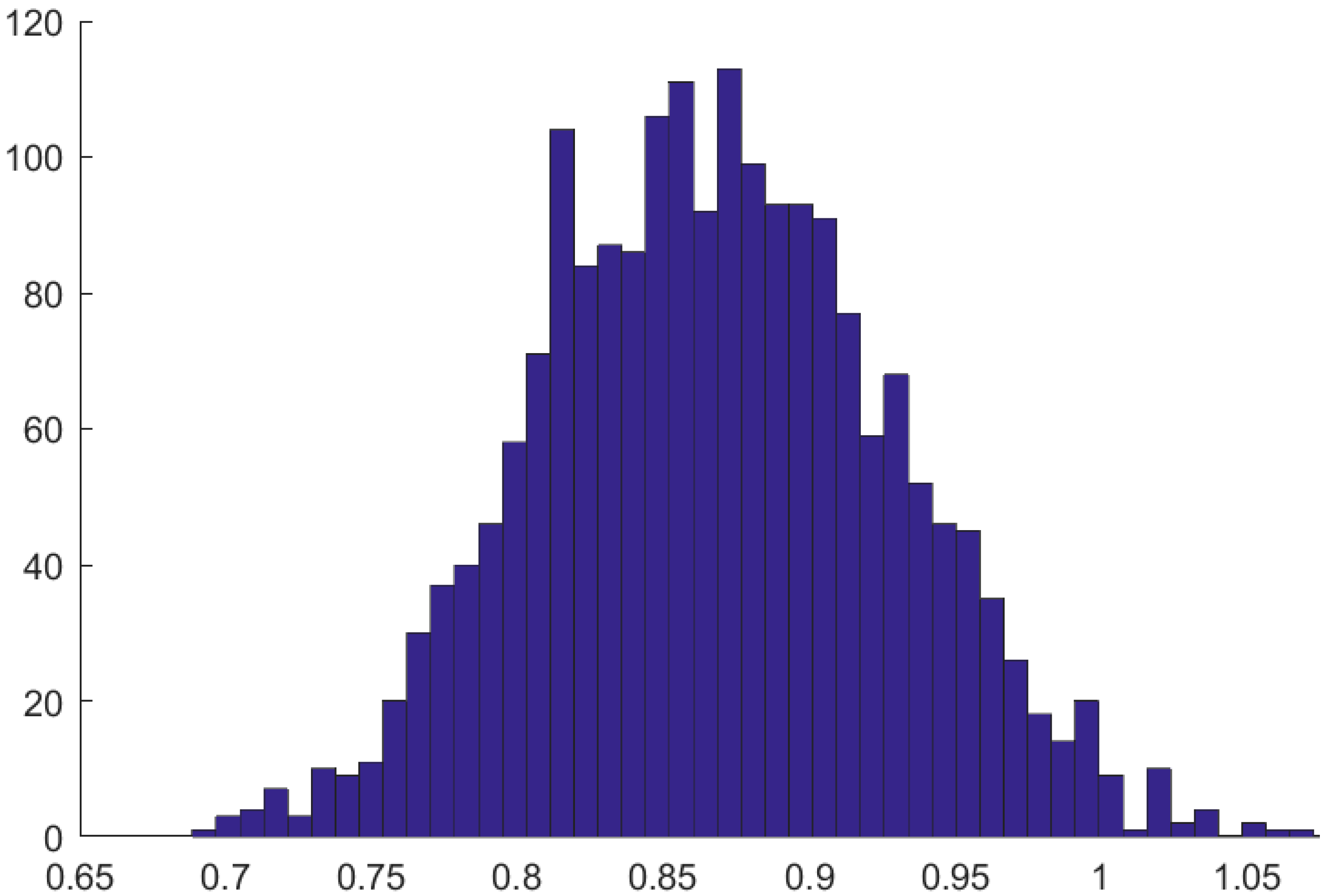
5.2. Modeling of Geometrical Topography of the Assembly Interface
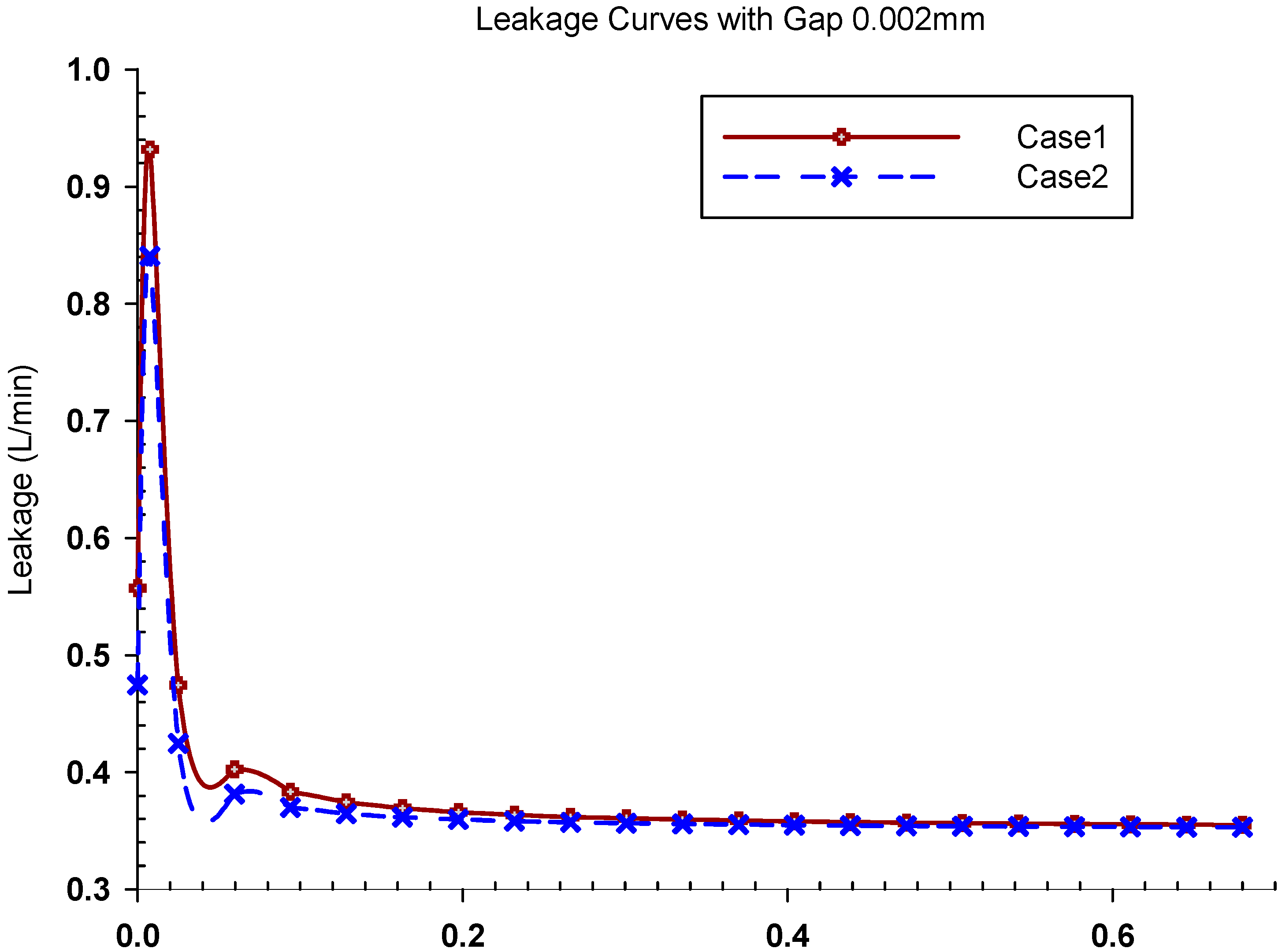
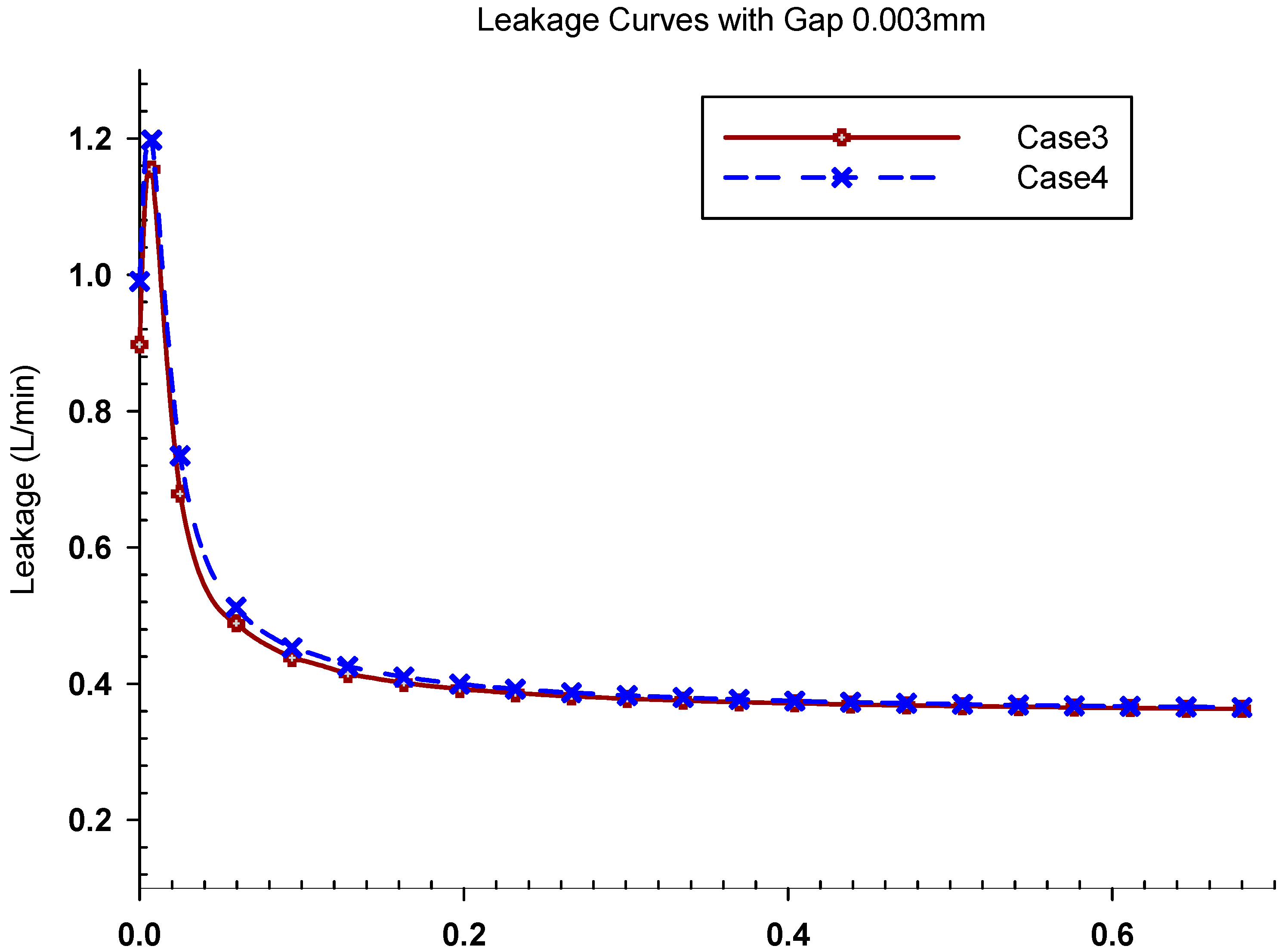
5.3. Analysis of Mating Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.Y.; Lu, C.; Liu, T.; Xu, Z.B. Adaptive Cutting Control for Roadheaders Based on Performance Optimization. Machines 2021, 9, 46. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, Z.Y.; Bu, W.H.; Tan, J.R. Hybrid dimension based modeling of part surface topography and identification of its characteristic parameters. Appl. Surf. Sci. 2012, 258, 7082–7093. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, Z.Y.; Peng, X.; Tan, J.R. A Non-Ideal Geometry Based Prediction Approach of Fitting Performance and Leakage Characteristic of Precision Couplings. IEEE Access 2018, 6, 58204–58212. [Google Scholar]
- Luo, C.; Franciosa, P.; Ceglarek, D.; Ni, Z.; Jia, F. A novel geometric tolerance modeling inspired by parametric space envelope. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1386–1398. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Zhang, Z.J.; Jin, X.; Zhang, Q.S. A novel modelling method of geometric errors for precision assembly. Int. J. Adv. Manuf. Technol. 2018, 94, 1139–1160. [Google Scholar] [CrossRef]
- Anwer, N.; Ballu, A.; Mathieu, L. The skin model, a comprehensive geometric model for engineering design. CIRP Ann. 2013, 62, 143–146. [Google Scholar] [CrossRef]
- Schleich, B.; Wartzack, S. Evaluation of geometric tolerances and generation of variational part representatives for tolerance analysis. Int. J. Adv. Manuf. Technol. 2015, 79, 959–983. [Google Scholar] [CrossRef]
- Yan, X.; Ballu, A. Generation of consistent skin model shape based on FEA method. Int. J. Adv. Manuf. Technol. 2017, 92, 789–802. [Google Scholar] [CrossRef]
- Sun, Q.C.; Zhao, B.B.; Liu, X.; Mu, X.K.; Zhang, Y.L. Assembling deviation estimation based on the real mating status of assembly. Comput. Aided Des. 2019, 115, 244–255. [Google Scholar] [CrossRef]
- Sun, X.M.; Bao, J.S.; Li, J.; Zhang, Y.M.; Liu, S.M.; Zhou, B. A digital twin-driven approach for the assembly-commissioning of high precision products. Robot. Comput. Integr. Manuf. 2020, 61, 101839. [Google Scholar] [CrossRef]
- Schleich, B.; Wartzack, S. Novel approaches for the assembly simulation of rigid Skin Model Shapes in tolerance analysis. Comput. Aided Des. 2018, 101, 1–11. [Google Scholar] [CrossRef]
- Grandjean, J.; Ledoux, Y.; Samper, S. On the role of form defects in assemblies subject to local deformations and mechanical loads. Int. J. Adv. Manuf. Technol. 2013, 65, 1769–1778. [Google Scholar] [CrossRef]
- Mondal, M.K.; Manna, N.K.; Saha, R. Study of leakage flow through a spool valve under blocked-actuator port condition-Simulation and experiment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1405–1417. [Google Scholar] [CrossRef]
- Afatsun, A.C.; Balkan, R.T. A Mathematical Model for Simulation of Flow Rate and Chamber Pressures in Spool Valves. J. Dyn. Syst. Meas. Control. 2019, 141, 021004. [Google Scholar] [CrossRef]
- Wang, K.; Liu, D.X.; Liu, Z.Y.; Tan, J.R. An assembly precision analysis method based on a general part digital twin model. Robot. Comput. Integr. Manuf. 2021, 68, 102089. [Google Scholar] [CrossRef]
- Liu, M.N.; Fang, S.L.; Dong, H.Y.; Xu, C.Z. Review of digital twin about concepts, technologies, and industrial applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Semeraro, C.; Lezoche, M.; Panetto, H. Digital twin paradigm: A systematic literature review. Comput. Ind. 2021, 130, 103469. [Google Scholar] [CrossRef]
- Tao, F.; Anwer, N.; Liu, A.; Wang, L.; Nee, A.Y.; Li, L.; Zhang, M. Digital twin towards smart manufacturing and industry 4.0. J. Manuf. Syst. 2021, 58, 1–2. [Google Scholar] [CrossRef]
- Cai, H.; Zhu, J.; Zhang, W. Quality Deviation Control for Aircraft Using Digital Twin. J. Comput. Inf. Sci. Eng. 2021, 21, 031008. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, Q.; Sun, W.; Mu, X.; Wang, Y. A construction method of digital twin model for contact characteristics of assembly interface. Int. J. Adv. Manuf. Technol. 2021, 113, 2685–2699. [Google Scholar] [CrossRef]
- Tao, F.; Sui, F.Y.; Liu, A.; Qi, Q.L.; Zhang, M.; Song, B.Y.; Guo, Z.R.; Lu, S.C.Y.; Nee, A.Y.C. Digital twin-driven product design framework. Int. J. Prod. Res. 2019, 57, 3935–3953. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.M.; Lu, Y.Q.; Li, J.; Song, D.Q.; Sun, X.M.; Bao, J.S. Multi-scale evolution mechanism and knowledge construction of a digital twin mimic model. Robot. Comput. Integr. Manuf. 2021, 71, 102123. [Google Scholar] [CrossRef]
- Villalonga, A.; Negri, E.; Biscardo, G.; Castano, F.; Haber, R.E.; Fumagalli, L.; Macchi, M. A decision-making framework for dynamic scheduling of cyber-physical production systems based on digital twins. Annu. Rev. Control. 2021, 51, 357–373. [Google Scholar] [CrossRef]
- Fang, Y.L.; Peng, C.; Lou, P.; Zhou, Z.D.; Hu, J.M.; Yan, J.W. Digital-Twin-Based Job Shop Scheduling Toward Smart Manufacturing. IEEE Trans. Ind. Inform. 2019, 15, 6425–6435. [Google Scholar] [CrossRef]
- Castaño, F.; Haber, R.E.; Mohammed, W.M.; Nejman, M.; Villalonga, A.; Martinez Lastra, J.L. Quality monitoring of complex manufacturing systems on the basis of model driven approach. Smart Struct. Syst. 2020, 26, 495–506. [Google Scholar]
- Moretti, M.; Rossi, A.; Senin, N. In-process monitoring of part geometry in fused filament fabrication using computer vision and digital twins. Addit. Manuf. 2021, 37, 101609. [Google Scholar]
- Söderberg, R.; Warmefjord, K.; Carlson, J.S.; Lindkvist, L. Toward a Digital Twin for real-time geometry assurance in individualized production. CIRP Ann. 2017, 66, 137–140. [Google Scholar] [CrossRef]
- Schleich, B.; Anwer, N.; Mathieu, L.; Wartack, S. Shaping the digital twin for design and production engineering. CIRP Ann. 2017, 66, 141–144. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.H.; Zhang, Z.Q.; Ding, X.Y.; Shao, N. Integrating form errors and local surface deformations into tolerance analysis based on skin model shapes and a boundary element method. Comput. Aided Des. 2018, 104, 45–59. [Google Scholar] [CrossRef]
- Tang, W.B.; Xu, G.S.; Zhangm, S.J. Dimensional variation analysis for rigid part assembly with an improvement of Monte Carlo simulation. IEEE Access 2020, 8, 5862–5872. [Google Scholar] [CrossRef]
- Liu, J.; Sun, S.L.; Liu, Q.D.; Huang, S.Y.; Li, Z.H.; Xin, J.H. Effect of Alignability of Three-position Reversal Spool Valve. Trans. Chin. Soc. Agric. Mach. 2001, 32, 72–74. (In Chinese) [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, W.; Xu, G.; Zhang, S.; Jin, S.; Wang, R. Digital Twin-Driven Mating Performance Analysis for Precision Spool Valve. Machines 2021, 9, 157. https://doi.org/10.3390/machines9080157
Tang W, Xu G, Zhang S, Jin S, Wang R. Digital Twin-Driven Mating Performance Analysis for Precision Spool Valve. Machines. 2021; 9(8):157. https://doi.org/10.3390/machines9080157
Chicago/Turabian StyleTang, Wenbin, Guangshen Xu, Shoujing Zhang, Shoufeng Jin, and Runxiao Wang. 2021. "Digital Twin-Driven Mating Performance Analysis for Precision Spool Valve" Machines 9, no. 8: 157. https://doi.org/10.3390/machines9080157
APA StyleTang, W., Xu, G., Zhang, S., Jin, S., & Wang, R. (2021). Digital Twin-Driven Mating Performance Analysis for Precision Spool Valve. Machines, 9(8), 157. https://doi.org/10.3390/machines9080157





