A Variable Parameter Ambient Vibration Control Method Based on Quasi-Zero Stiffness in Robotic Drilling Systems
Abstract
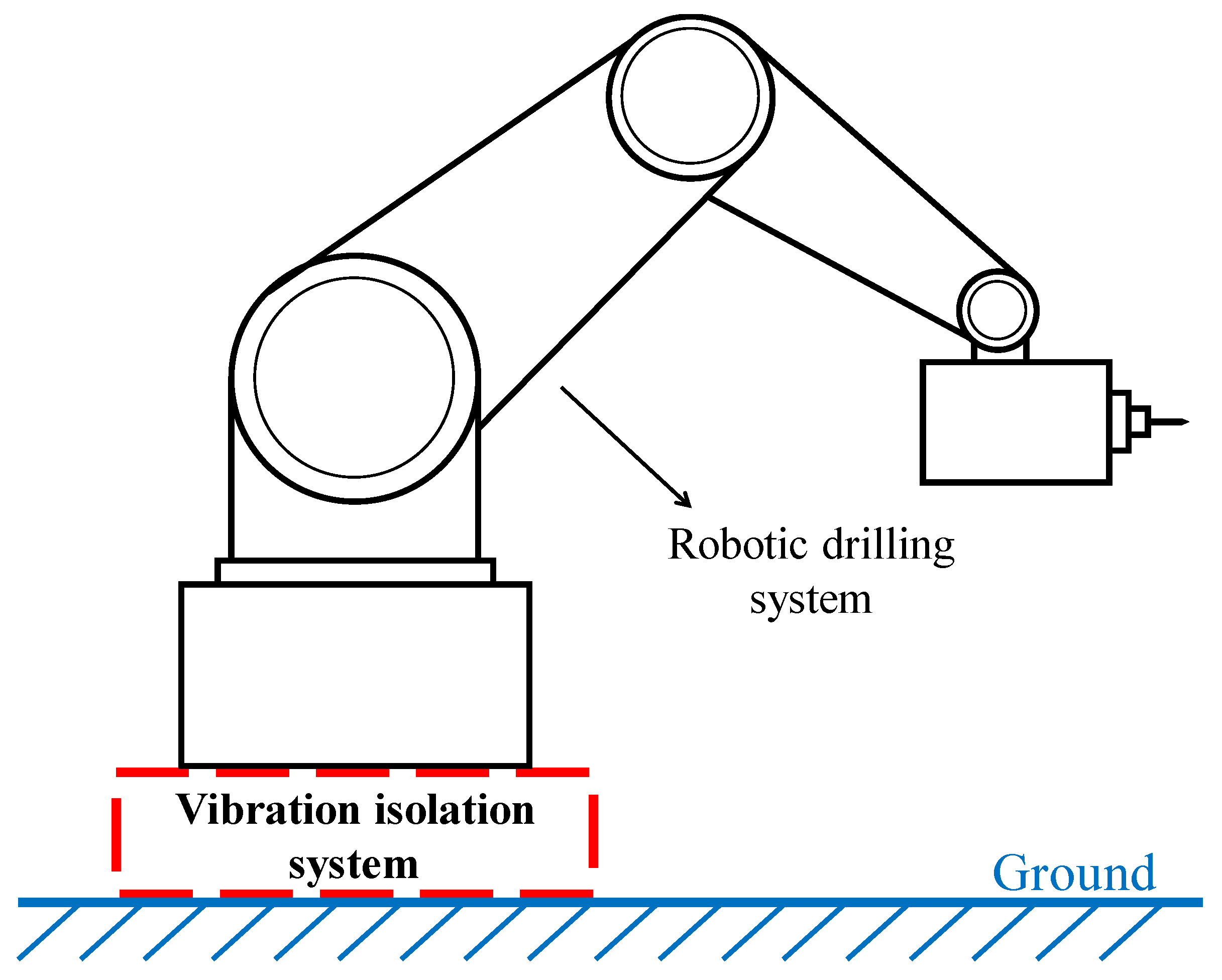
1. Introduction
2. Design of the Vibration Control Mechanism Based on Quasi-Zero Stiffness
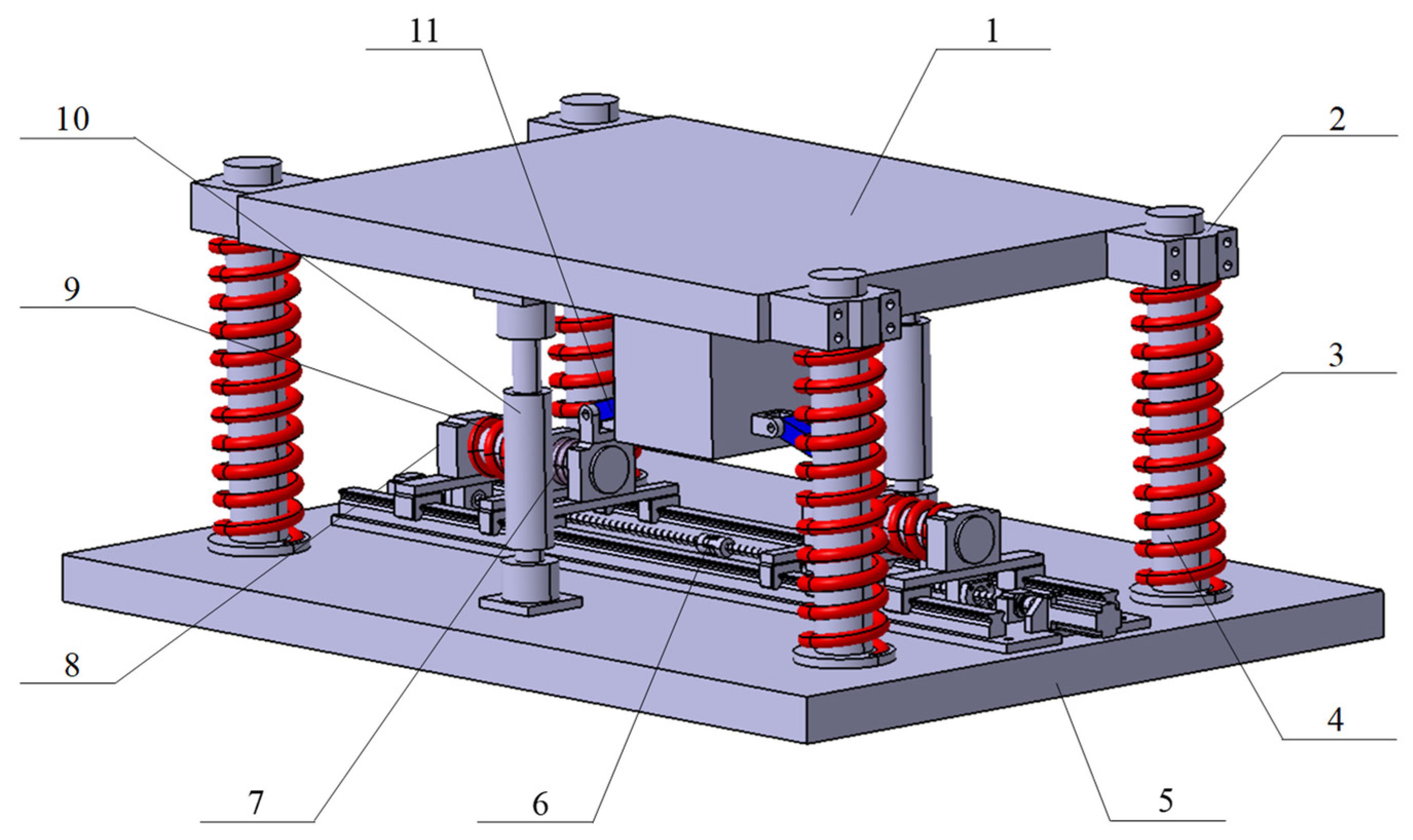
2.1. Structural Design
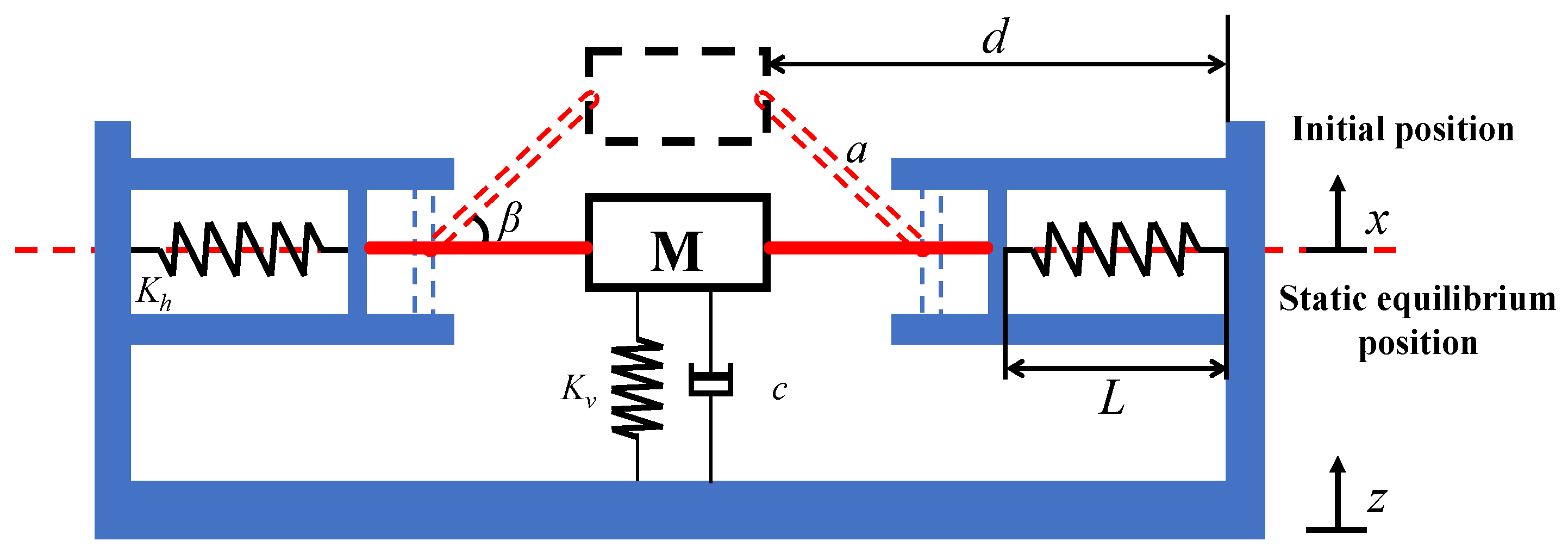
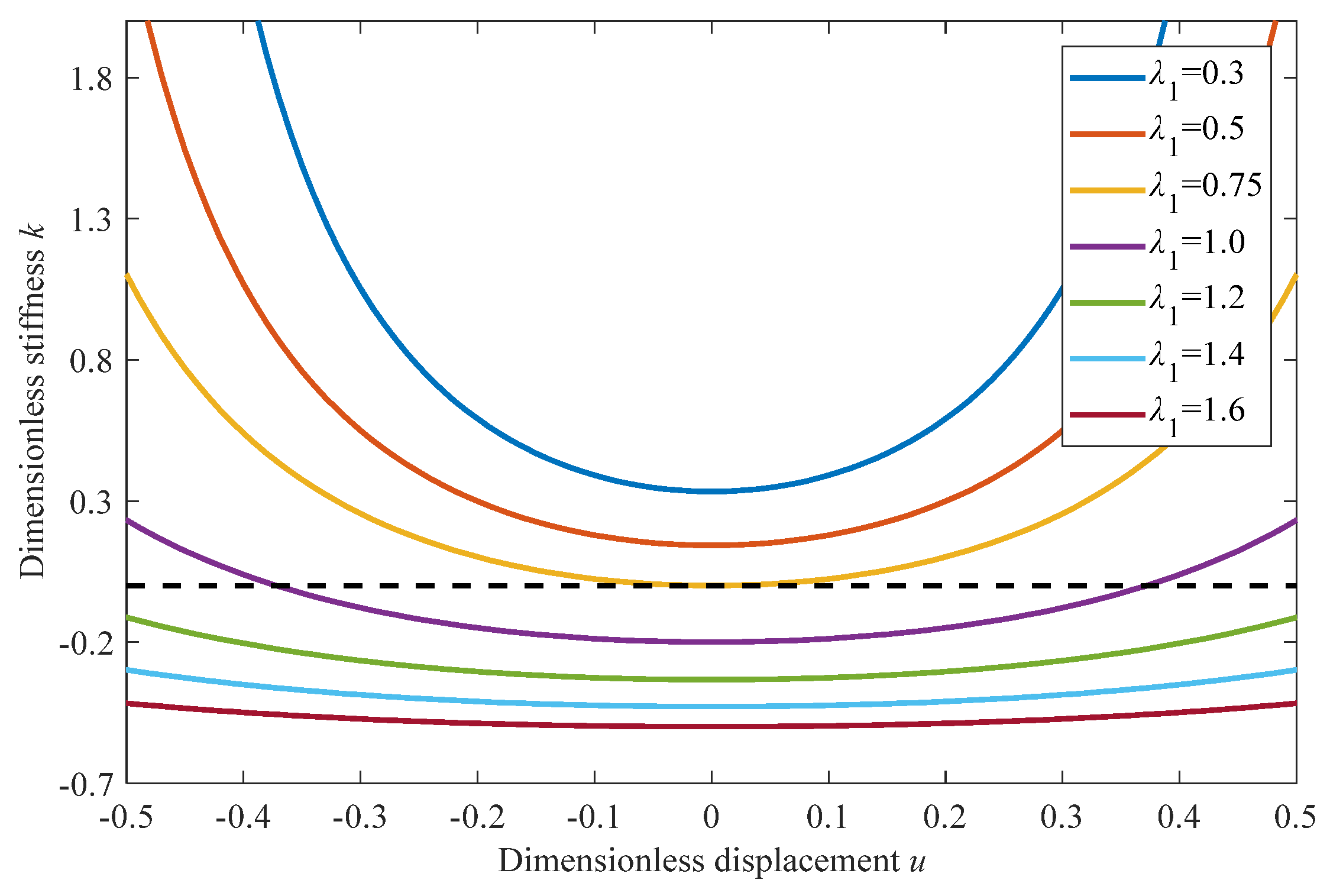
2.2. Passive Structural Parameters Analysis
3. Dynamics Analysis and Modeling
3.1. Dynamic Modeling and Solution of Quasi-Zero Stiffness Vibration Control Mechanism
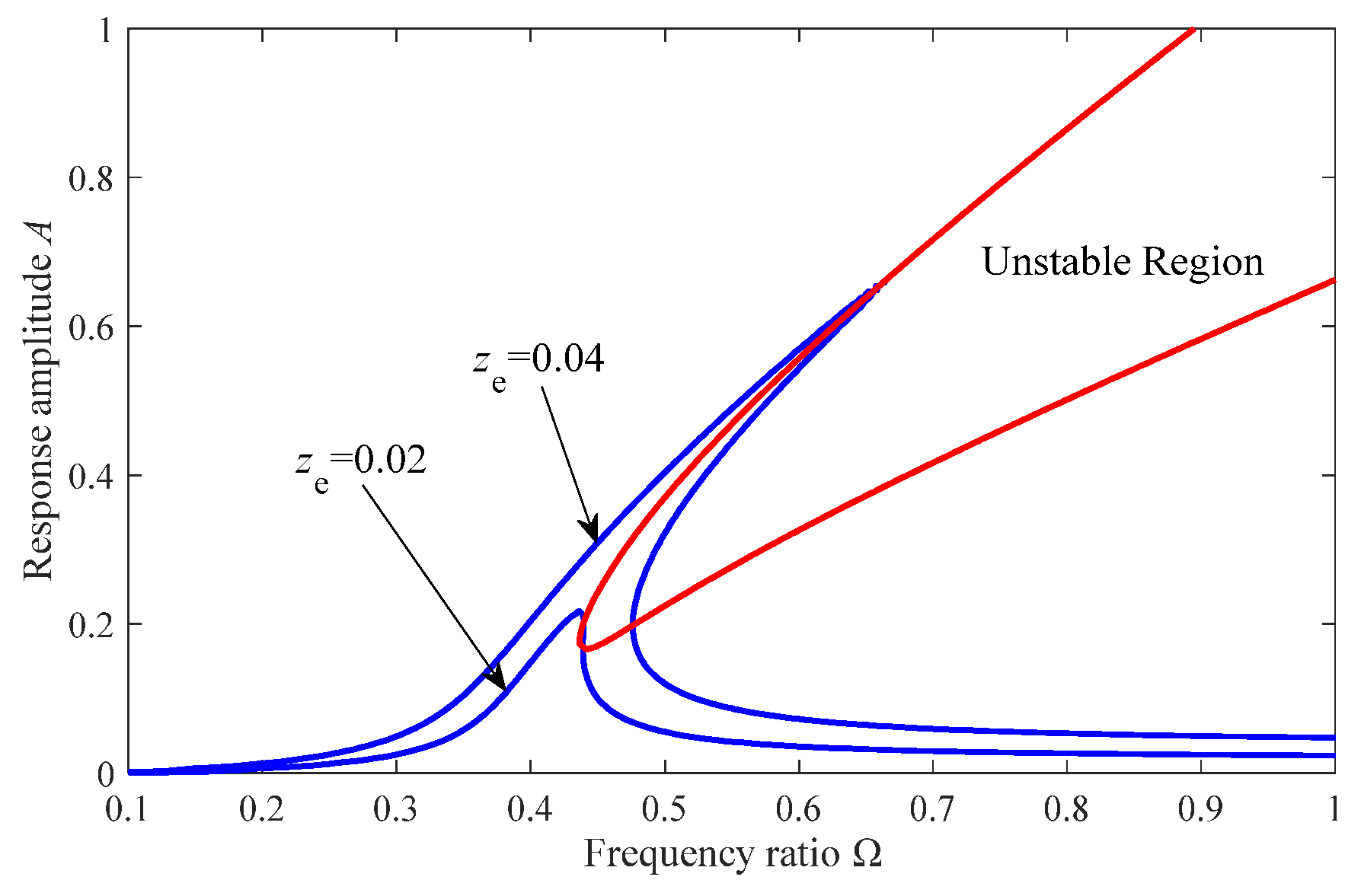
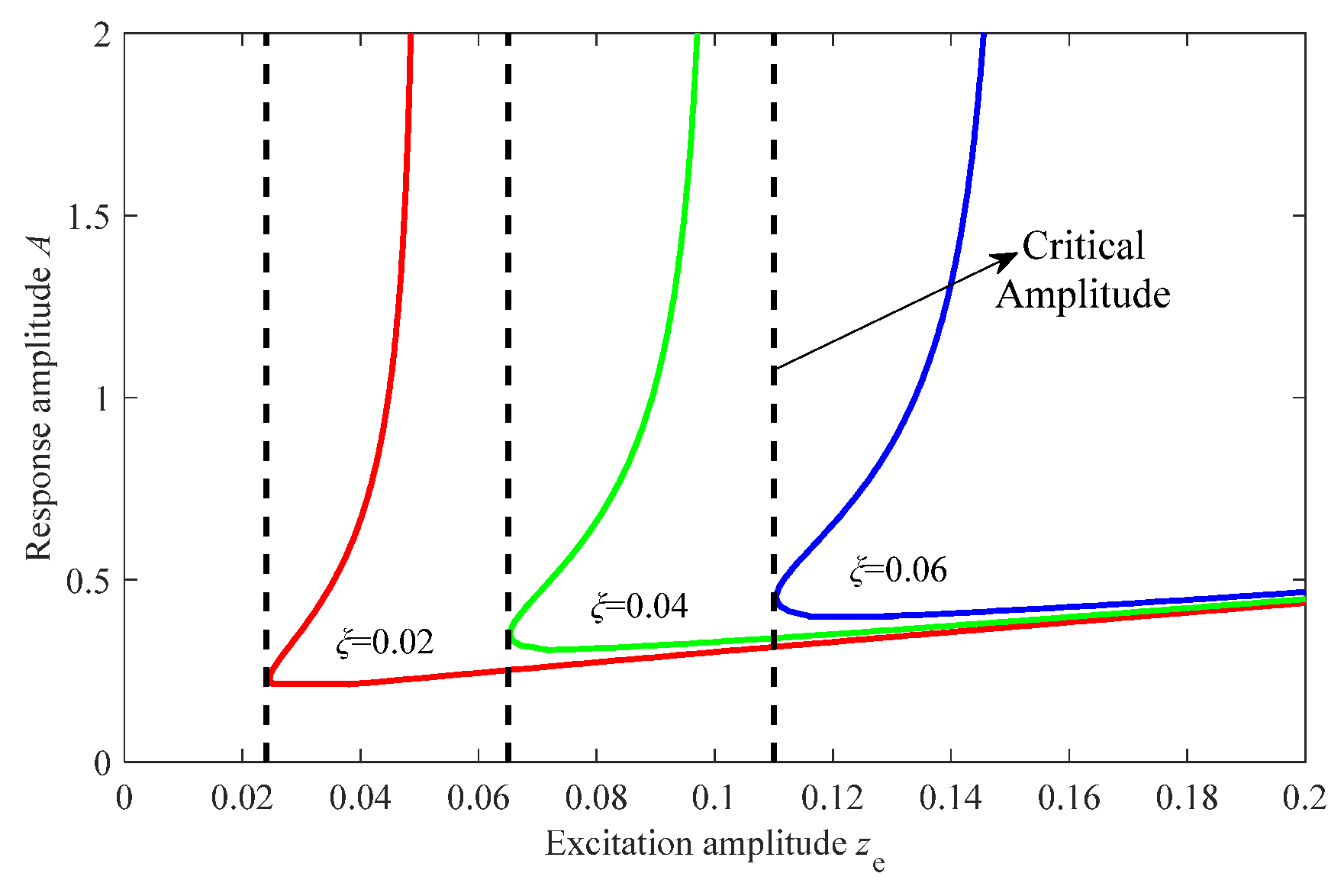
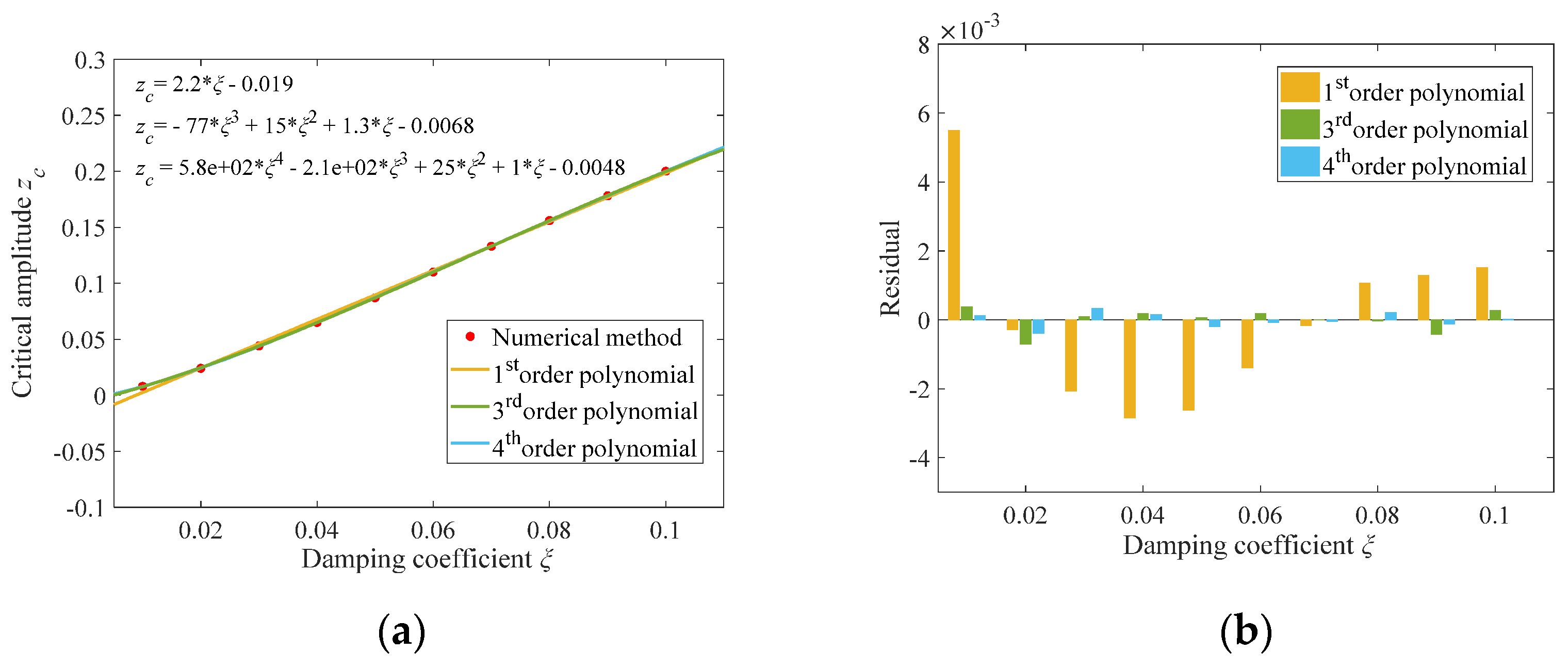
3.2. Stability Analysis
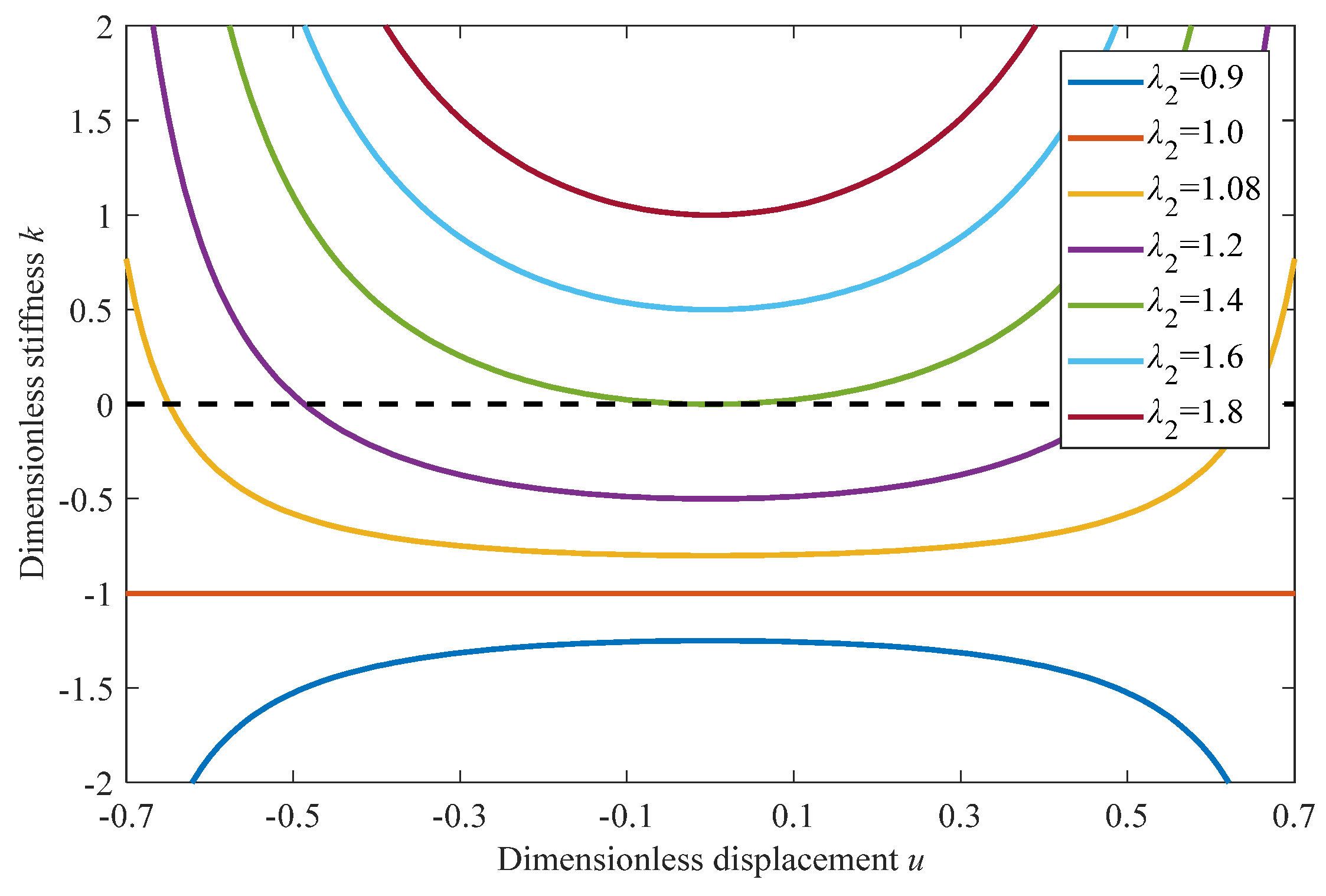
3.3. The Effects of the Parameters on Vibration Control Performance
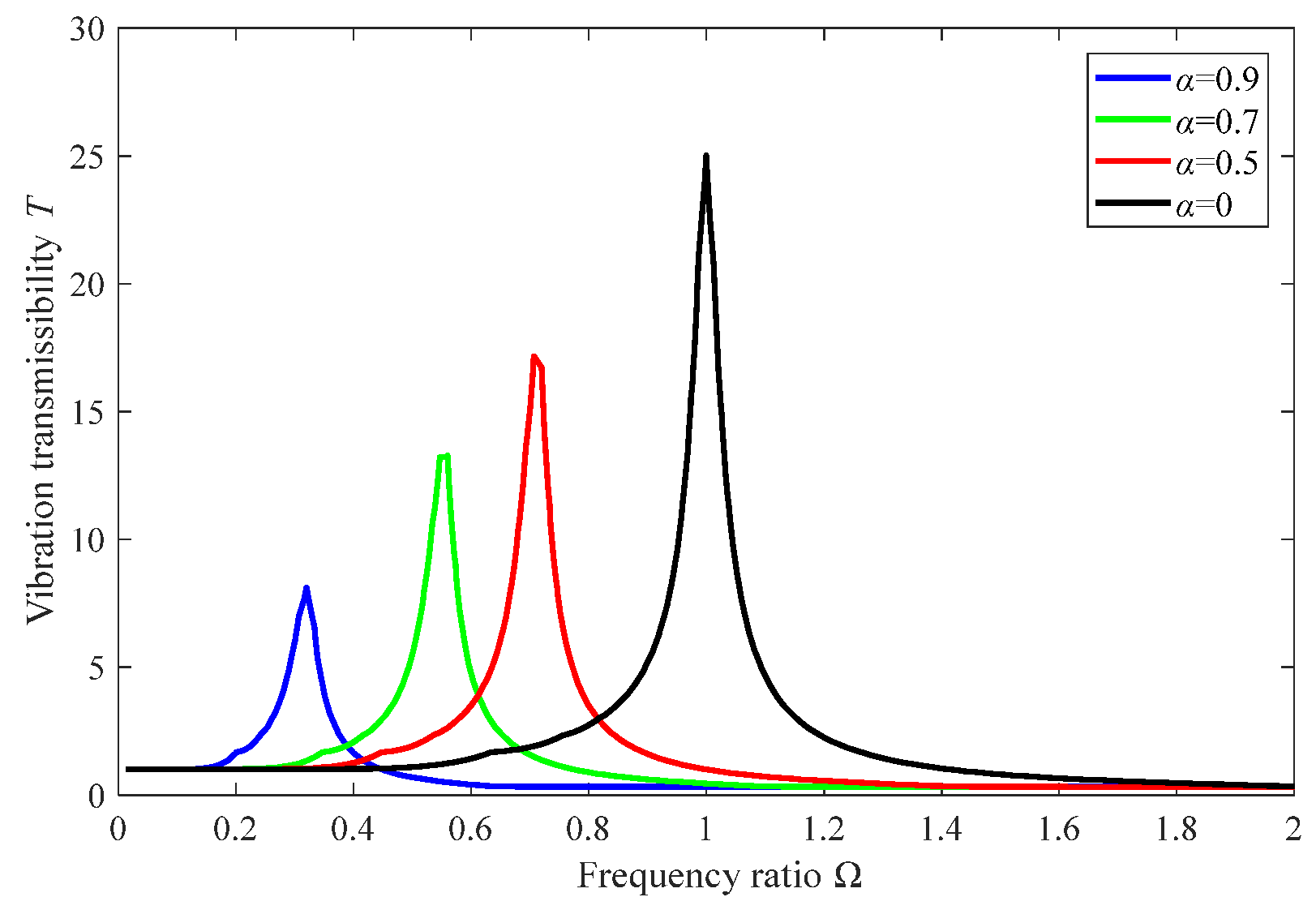
3.3.1. Effects of Stiffness Ratio on Vibration Control Performance
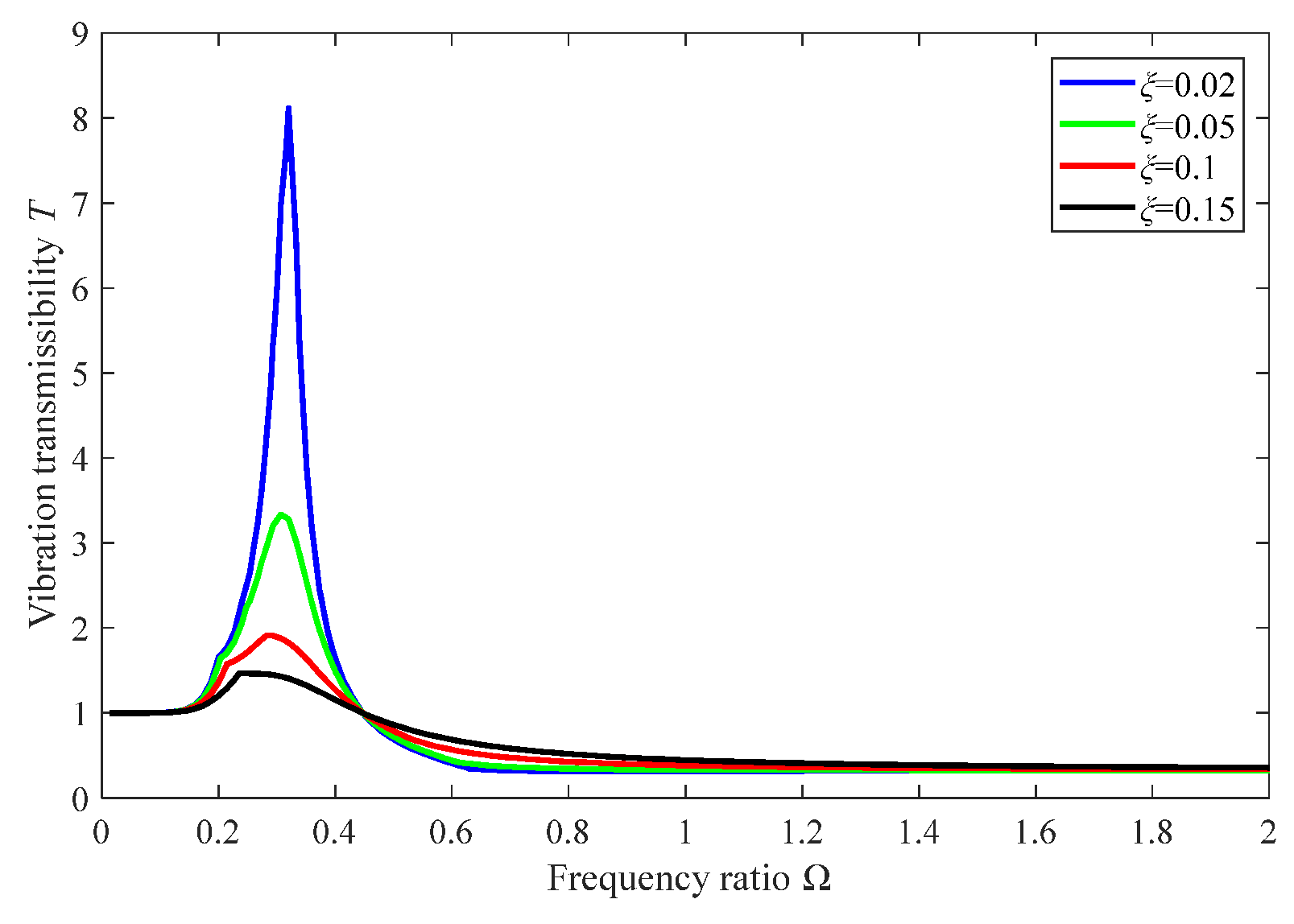
3.3.2. Effects of Damping Coefficient on Vibration Control Performance
4. Parameter Adjustment
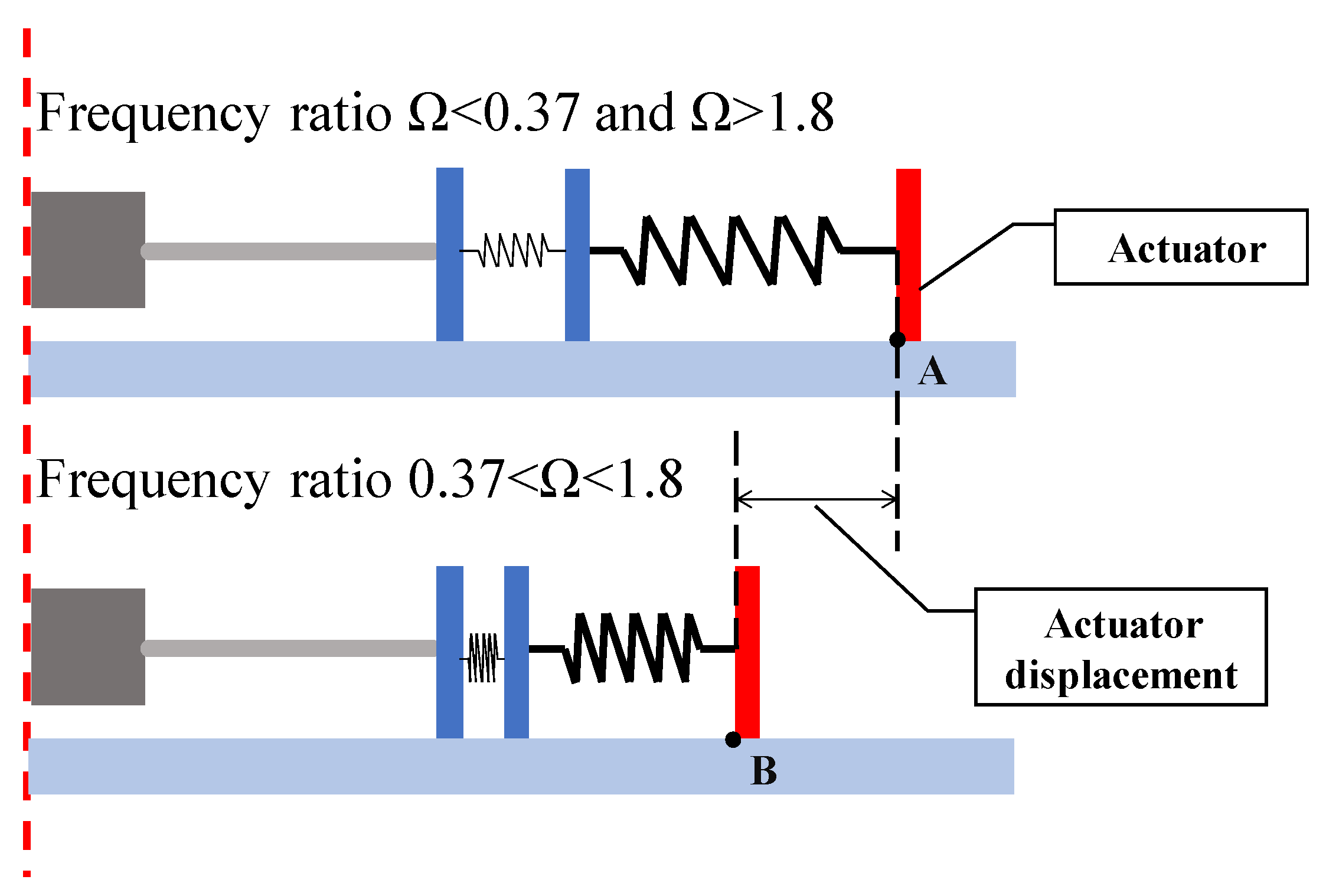
4.1. Variable Stiffness Control
4.2. Variable Damping Control
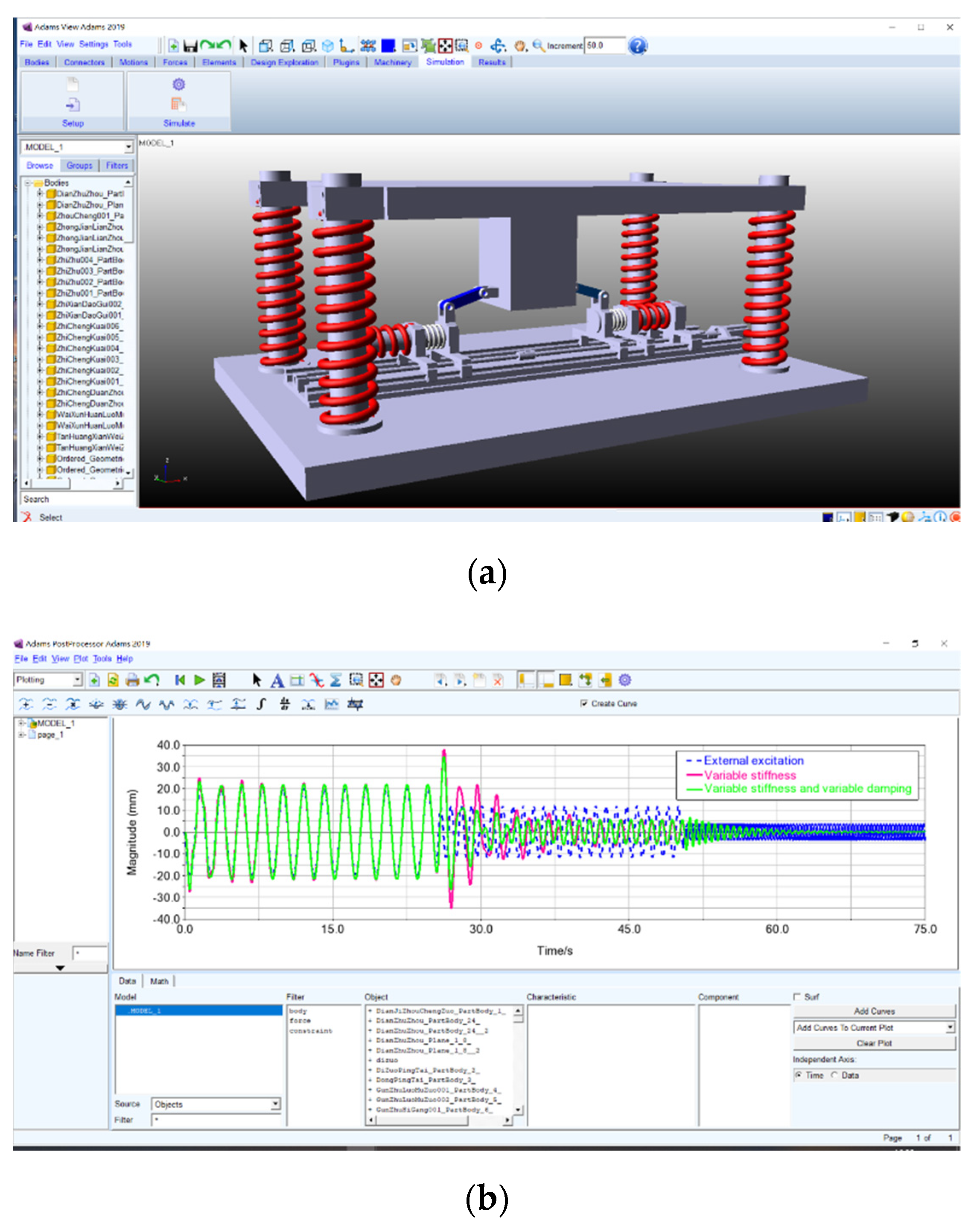
5. Simulation
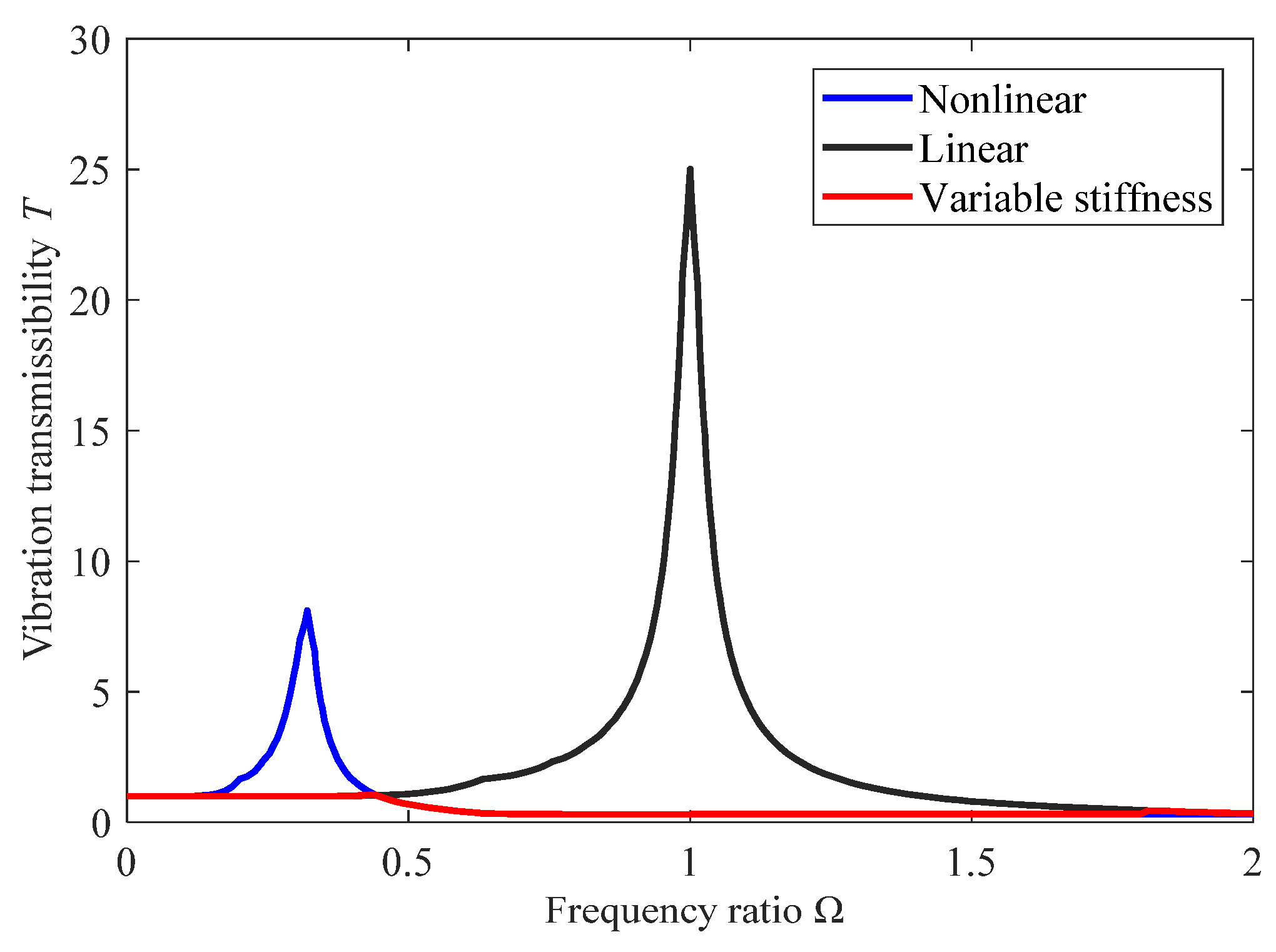
5.1. Simulation of the Vibration Control System with Variable Stiffness
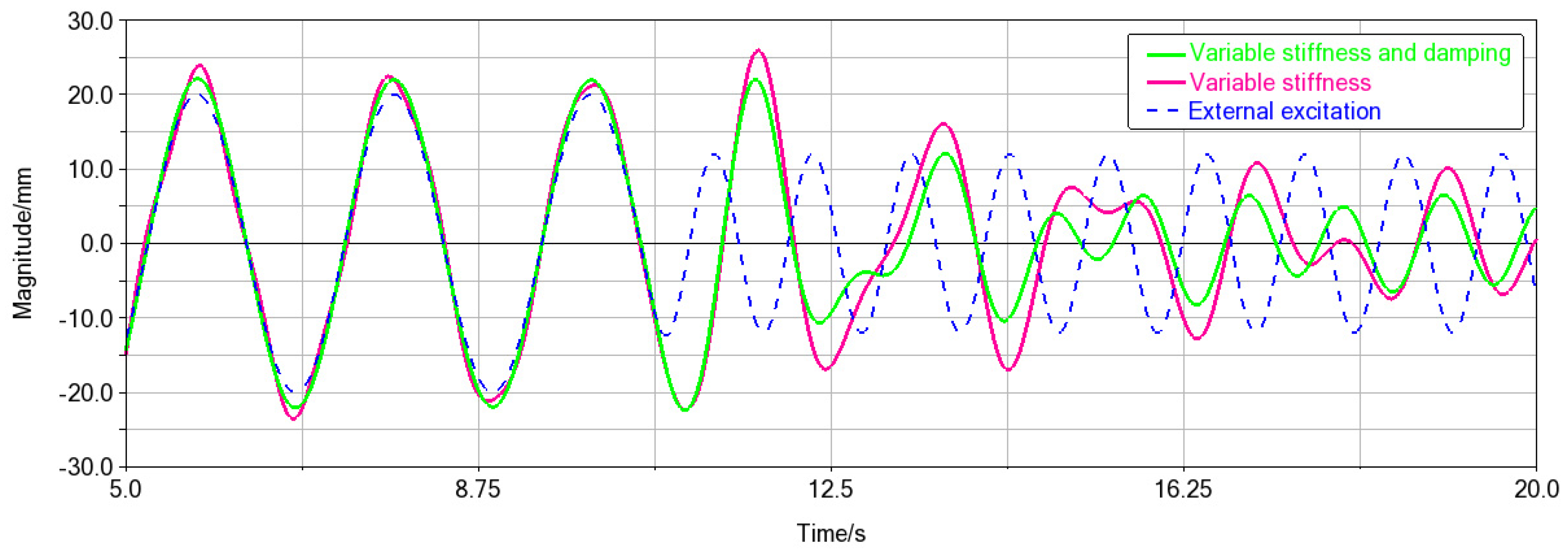
5.2. Simulation of the Vibration Control System with Variable Stiffness and Damping
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Calawa, R.; Smith, S.; Moore, I.; Jackson, T. HAWDE five axis wing surface drilling machine. In Proceedings of the Aerospace Manufacturing and Automated Fastening Conference and Exhibition, St. Louis, MO, USA, 20–23 September 2004. [Google Scholar]
- Zhang, L.X.; Dhupia, J.S.; Wu, M.L.; Huang, H. A Robotic Drilling End-Effector and Its Sliding Mode Control for the Normal Adjustment. Appl. Sci. 2018, 8, 1892. [Google Scholar] [CrossRef]
- Zhang, L.X.; Dhupia, J.S.; Wu, M.L. Analysis and comparison of control strategies for normal adjustment of a robotic drilling end-effector. J. Vibroeng. 2018, 20, 2651–2667. [Google Scholar]
- Schneider, U.; Drust, M.; Ansaloni, M.; Lehmann, C.; Pellicciari, M.; Leali, F.; Gunnink, J.W.; Verl, A. Improving robotic machining accuracy through experimental error investigation and modular compensation. Int. J. Adv. Manuf. Technol. 2016, 85, 3–15. [Google Scholar] [CrossRef]
- Cano, R.; de Garayo, O.I.; Castillo, M.A.; Marin, R.; Ascorbe, H.; de los Santos, J.R. Flexible and Low-Cost Robotic System for Drilling Material Stacks. SAE Tech. Pap. 2016. [Google Scholar] [CrossRef]
- Mejri, S.; Gagnol, V.; Le, T.P.; Sabourin, L.; Ray, P.; Paultre, P. Dynamic characterization of machining robot and stability analysis. Int. J. Adv. Manuf. Technol. 2016, 82, 351–359. [Google Scholar] [CrossRef]
- Sun, L.F.; Liang, F.Y.; Fang, L.J. Design and performance analysis of an industrial robot arm for robotic drilling process. Ind. Robot 2019, 46, 7–16. [Google Scholar] [CrossRef]
- Tao, J.F.; Qin, C.J.; Xiao, D.Y.; Shi, H.T.; Liu, C.L. A pre-generated matrix-based method for real-time robotic drilling chatter monitoring. Chin. J. Aeronaut. 2019, 32, 2755–2764. [Google Scholar] [CrossRef]
- Andreas, F.; Jens, K.; Ira, E. Multi-sensor measurement system for robotic drilling. Robot Comput-Integr. Manuf. 2017, 47, 4–10. [Google Scholar]
- Rodríguez, A.; Calleja, A.; de Lacalle, L.N.L.; Pereira, O.; Rubio-Mateos, A.; Rodríguez, G. Drilling of CFRP-Ti6Al4V stacks using CO2-cryogenic cooling. J. Manuf. Process. 2021, 64, 58–66. [Google Scholar] [CrossRef]
- Al, K.T.; Bendemra, H.; Anwar, M.; Swart, D.; Dias, J. Introducing data analytics to the robotic drilling process. Ind. Robot 2018, 45, 371–378. [Google Scholar]
- Kumar, T.; Kumar, R.; Jain, S.C. Numerical Investigation of Semi-active Torsional Vibration Control of Heavy Turbo-generator Rotor using Magnetorheological Fluid Dampers. J. Vib. Eng. Technol. 2021. [Google Scholar] [CrossRef]
- Christopher, L.; Antoine, A.; Maxime, M. A magneto-rheological damper for on-site machining vibration control: From design to experimental characterization of its performance. Vibroeng. Procedia 2020, 34, 34–38. [Google Scholar]
- Arka, M.; Saptarshi, S.; Arunasis, C.; Sourav, D. Sway vibration control of floating horizontal axis wind turbine by modified spar-torus combination. Ocean Eng. 2021, 219, 108232. [Google Scholar]
- He, W.; Wang, T.T.; He, X.Y.; Yang, L.J.; Kaynak, O. Dynamical Modeling and Boundary Vibration Control of a Rigid-Flexible Wing System. IEEE ASME Trans. Mechatron. 2020, 25, 2711–2721. [Google Scholar] [CrossRef]
- Al, F.M.S.H.; Moghadam, S.A.; Dehini, R.; Shan, L.J.; Habibi, M.; Safarpour, H. Vibration control of a smart shell reinforced by graphene nanoplatelets under external load: Semi-numerical and finite element modeling. Thin-Walled Struct. 2021, 159, 107242. [Google Scholar]
- Alabuzhev, P.; Gritchin, A.; Kim, L.; Migirenko, G.; Chon, V.; Stepanov, P. Vibration Protecting and Measuring Systems with Quasi-Zero Stiffness; Rivin, E., Ed.; Hemisphere Pub. Corp.: New York, NY, USA, 1989; pp. 10–54. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V., Jr. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Cheng, C.; Li, S.M.; Wang, Y.; Jiang, X.X. Dynamic Analysis of Quasi-Zero Stiffness Vibration Isolator Considering Load Variation. J. Vib. Meas. Diag. 2017, 37, 743–749. [Google Scholar]
- Shi, P.C.; Yang, J.F.; Li, J.; Xiao, P. Design and simulation of shear-tension spring-type quasi-zero stiffness isolator. Vibroeng. Procedia 2020, 33, 159–163. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C.; Brown, J. Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vib. 2020, 471, 115198. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.C.; Ye, K.; Luo, Q.T. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int. J. Mech. Sci. 2021, 192, 106093. [Google Scholar] [CrossRef]
- Zhu, G.N.; Liu, J.Y.; Cao, Q.J.; Cheng, Y.F.; Lu, Z.C.; Zhu, Z.B. A two degree of freedom stable quasi-zero stiffness prototype and its applications in aseismic engineering. Sci. China Techol. Sci. 2020, 63, 496–505. [Google Scholar] [CrossRef]
- Sun, Y.; Gong, D.; Zhou, J.S.; Sun, W.J.; Xia, Z.H. Low frequency vibration control of railway vehicles based on a high static low dynamic stiffness dynamic vibration absorber. Sci. China Techol. Sci. 2019, 62, 60–69. [Google Scholar] [CrossRef]
- Ding, H.; Ji, J.C.; Chen, L.Q. Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mech. Syst. Signal Process. 2019, 121, 675–688. [Google Scholar] [CrossRef]
- Ding, H.; Chen, L.Q. Designs, analysis, and applications of nonlinear energy sinks. Nonlinear Dyn. 2020, 100, 3061–3107. [Google Scholar] [CrossRef]



| Name | Value |
|---|---|
| Mass M | 300 kg |
| Stiffness of horizontal spring Kh | 27 N/mm |
| Stiffness of vertical spring Kv | 30 N/mm |
| Vertical damping coefficient c | 0.12 N·s/mm |
| Connecting rod length a | 160 mm |
| Original length of horizontal spring L0 | 200 mm |
| Configurative parameter d | 280 mm |
| Excitation amplitude Z | 1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhao, C.; Qian, F.; Dhupia, J.S.; Wu, M. A Variable Parameter Ambient Vibration Control Method Based on Quasi-Zero Stiffness in Robotic Drilling Systems. Machines 2021, 9, 67. https://doi.org/10.3390/machines9030067
Zhang L, Zhao C, Qian F, Dhupia JS, Wu M. A Variable Parameter Ambient Vibration Control Method Based on Quasi-Zero Stiffness in Robotic Drilling Systems. Machines. 2021; 9(3):67. https://doi.org/10.3390/machines9030067
Chicago/Turabian StyleZhang, Laixi, Chenming Zhao, Feng Qian, Jaspreet Singh Dhupia, and Mingliang Wu. 2021. "A Variable Parameter Ambient Vibration Control Method Based on Quasi-Zero Stiffness in Robotic Drilling Systems" Machines 9, no. 3: 67. https://doi.org/10.3390/machines9030067
APA StyleZhang, L., Zhao, C., Qian, F., Dhupia, J. S., & Wu, M. (2021). A Variable Parameter Ambient Vibration Control Method Based on Quasi-Zero Stiffness in Robotic Drilling Systems. Machines, 9(3), 67. https://doi.org/10.3390/machines9030067








