Simulation Modeling of First Rise Section of Water Supply System with Installed Complex of Automatic Pump Performance Control †
Abstract
1. Introduction
- Mathematical description and computer implementation of the interconnections of the “Electric network—Electric drive—Pump—Pipeline—Reservoir—Control system” complex. The key ones are the dependences of the level in the reservoir and the temperature of the water at the end of the pipeline on the flow rate and the supply electric frequency;
- Possibility of assessing the economic parameters of the facility functioning, such as the amount of power consumption and overflow of water from the reservoir;
- Flexible design of a pipeline from the same-type of elements to achieve a more realistic modeling process;
- Implementation of a non-standard way to control the pump performance by the water level in the reservoir and the temperature of water at the pipeline end.
- Selection of the main parameters of the system, taken into account in the simulation;
- Determination of mathematical dependences existing between the selected parameters (building a mathematical model);
- Development of the model general structure. In the model, it is necessary to implement the following basic blocks: frequency-controlled asynchronous electric motor; centrifugal pump; overhead laying pipeline; storage reservoir, control system;
- Defining the optimal way of object management, calculating the coefficients of the governing laws;
- Trial calculation of the model using specially selected parameters. Collecting and analyzing data obtained during the trial model implementation. Defining the output parameters of the control system.
- (1)
- A list of input, output and internal parameters of the model has been determined, which provide a systematic approach to a comprehensive analysis of the first rise section of the water supply system.
- (2)
- Mathematical dependencies were selected and adapted for calculating the controlled parameters of the model, such as supply in the pipeline, water level in the reservoir, water temperature at the end of the pipeline.
- (3)
- A block diagram of the simulation model has been developed, which is implemented in the MATLAB Simulink computer modeling environment. The structure of the model completely repeats the section of the first rise to achieve a sufficient level of accuracy.
- (4)
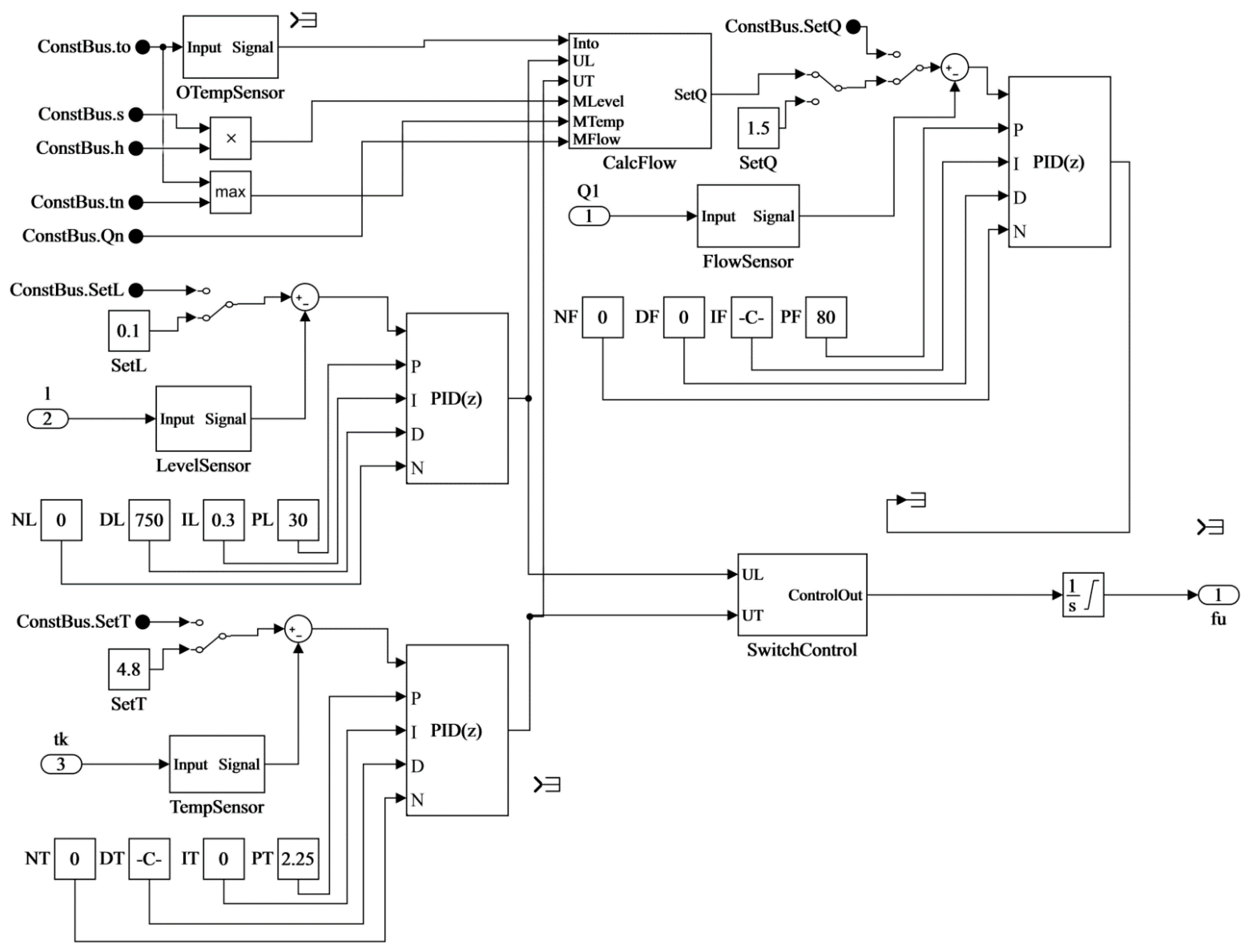
- A model of the control system for the first rise section has been developed, which ensures the minimization excessive operation of pump, while protecting the pipeline from freezing. The model is based on a two-channel PID controller with optimal control elements, which allows calculating and maintaining the flow rate in terms of the level in the reservoir and the temperature in the pipeline.
- (5)
- The results of calculating the model of the first rise section in transient modes are obtained, and the proposed control system is also investigated. The calculation results showed the effectiveness of the developed solutions, and also made it possible to determine the optimal parameters of the control algorithm.
2. Materials and Methods
2.1. Model Parameters
2.2. Model Equations and Block Diagram
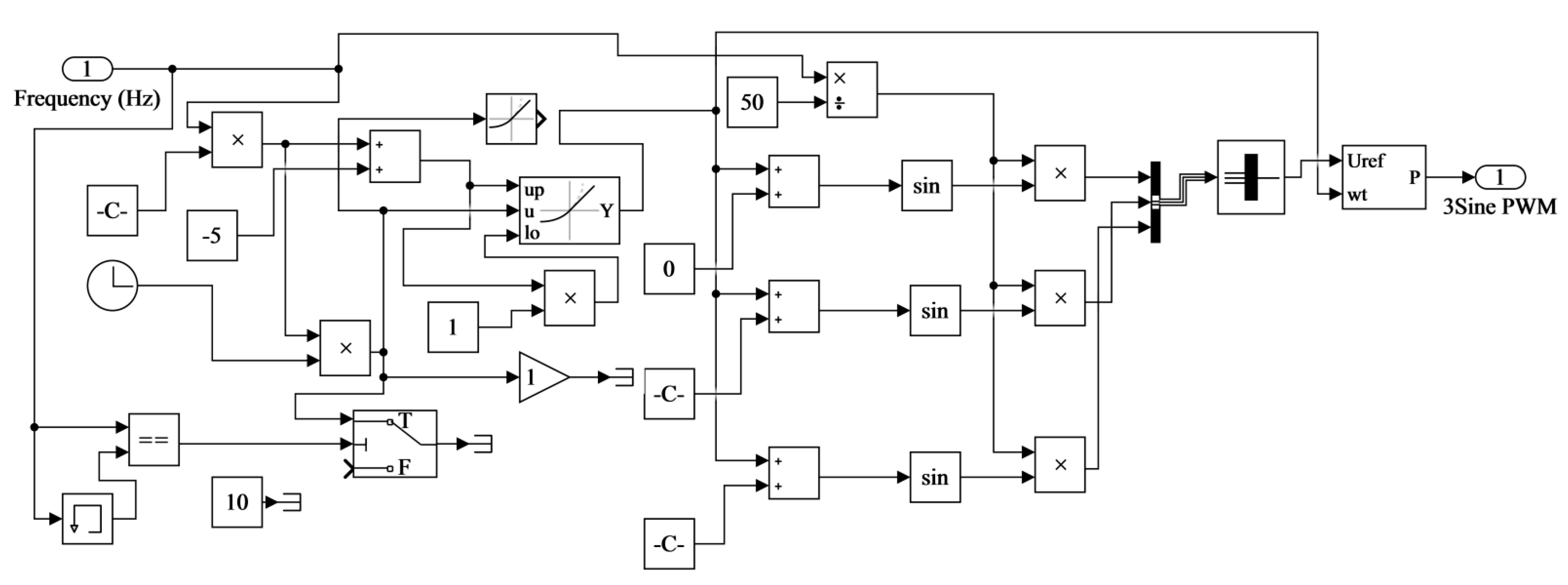
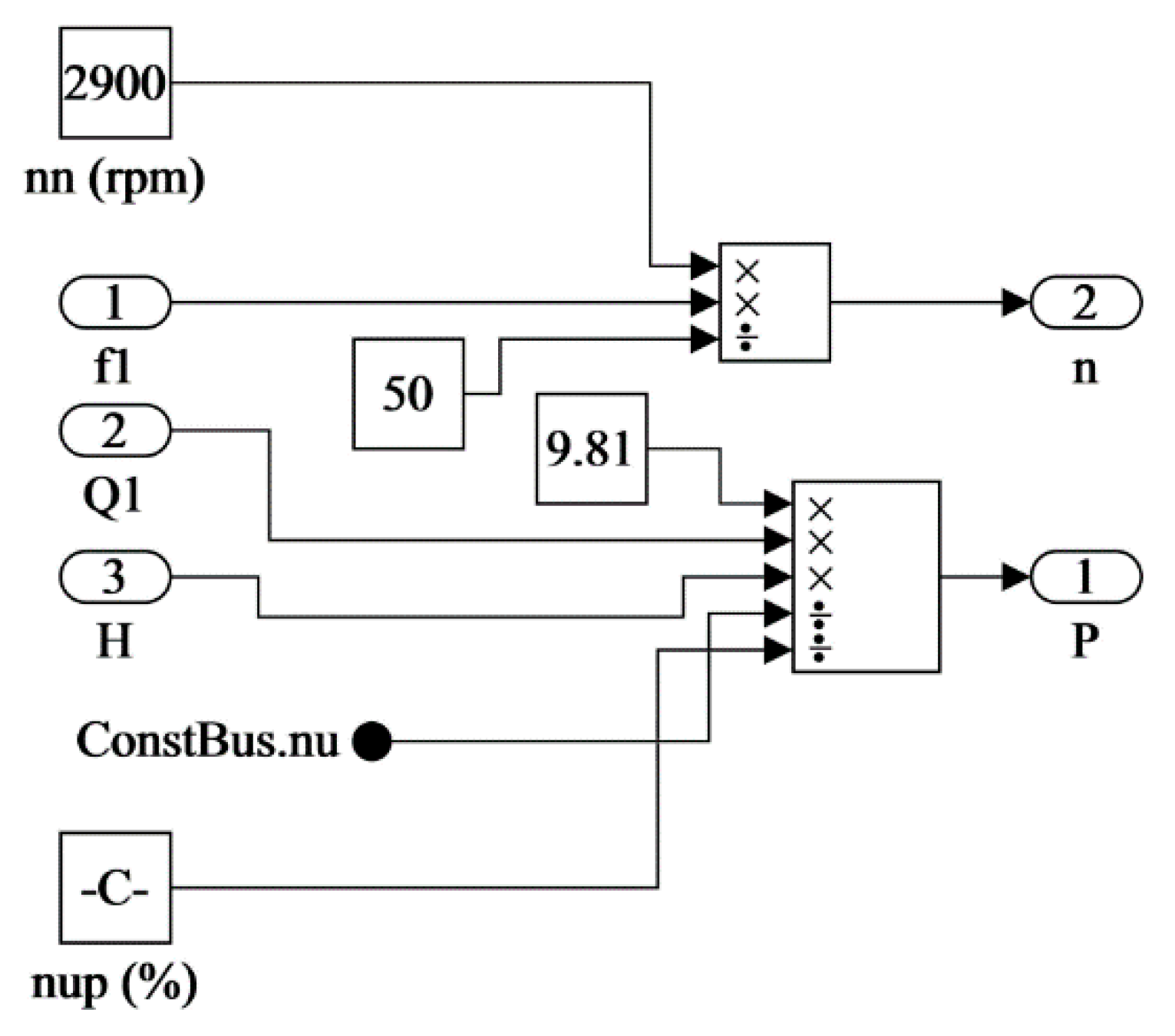
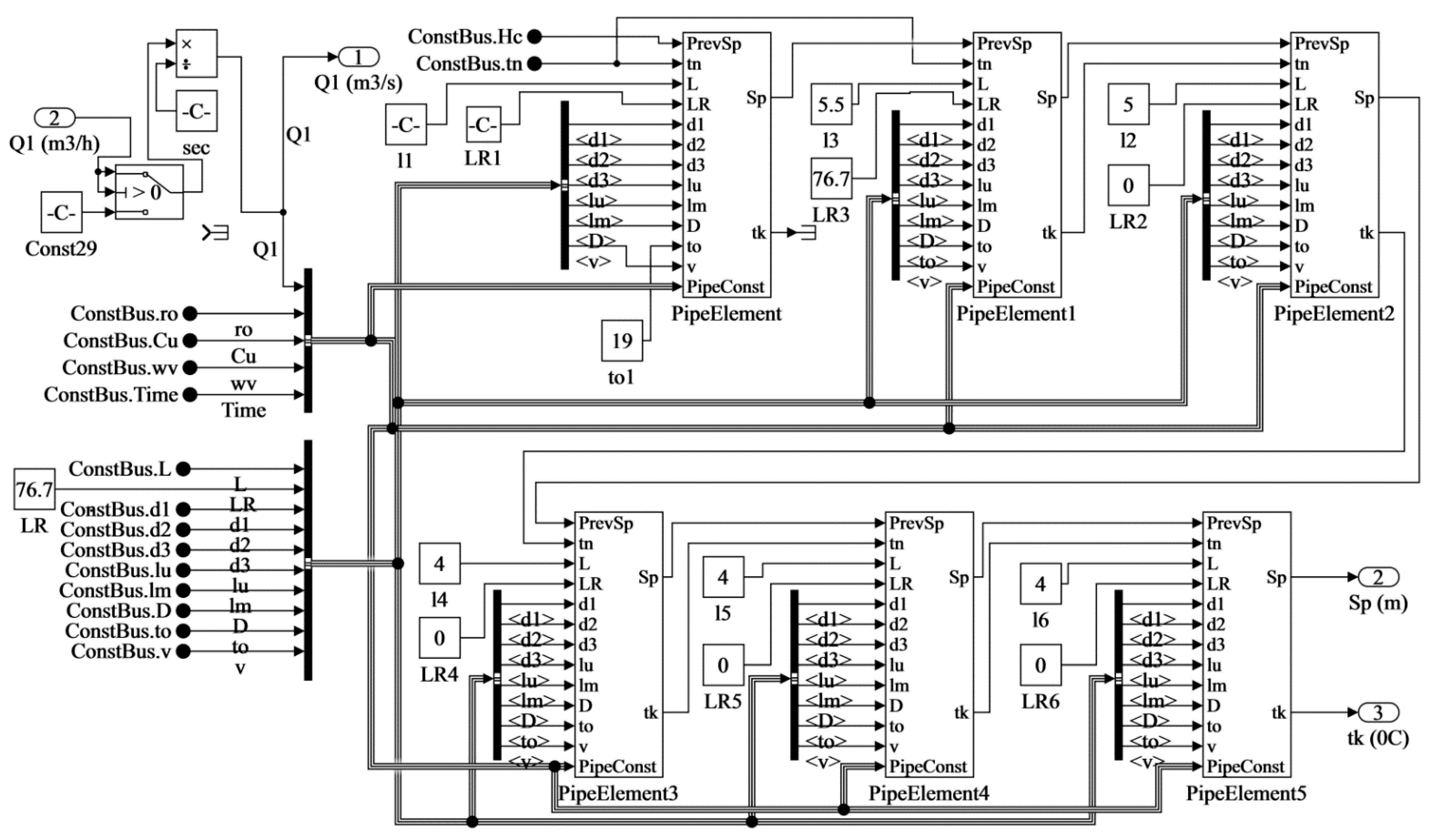
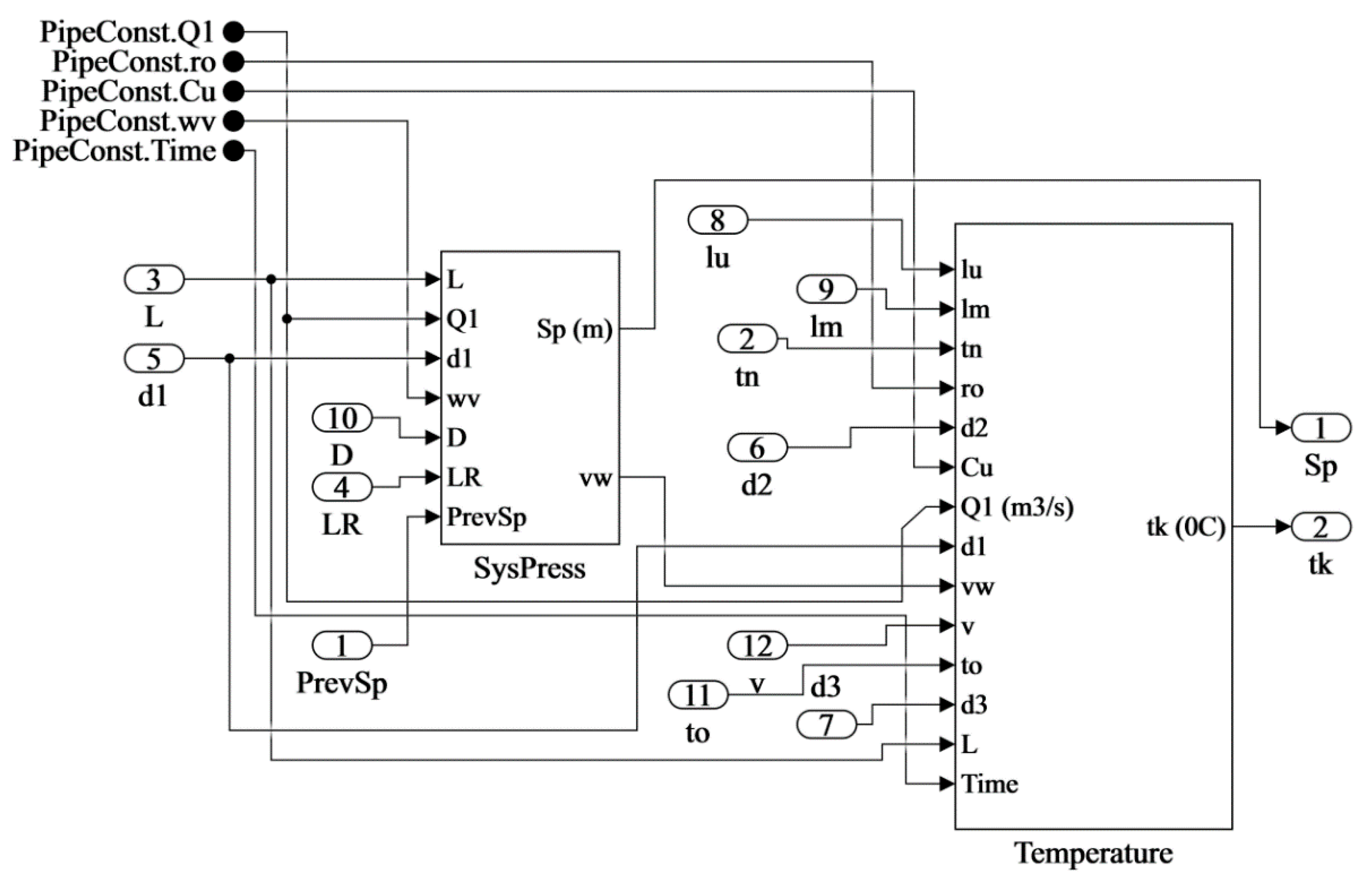
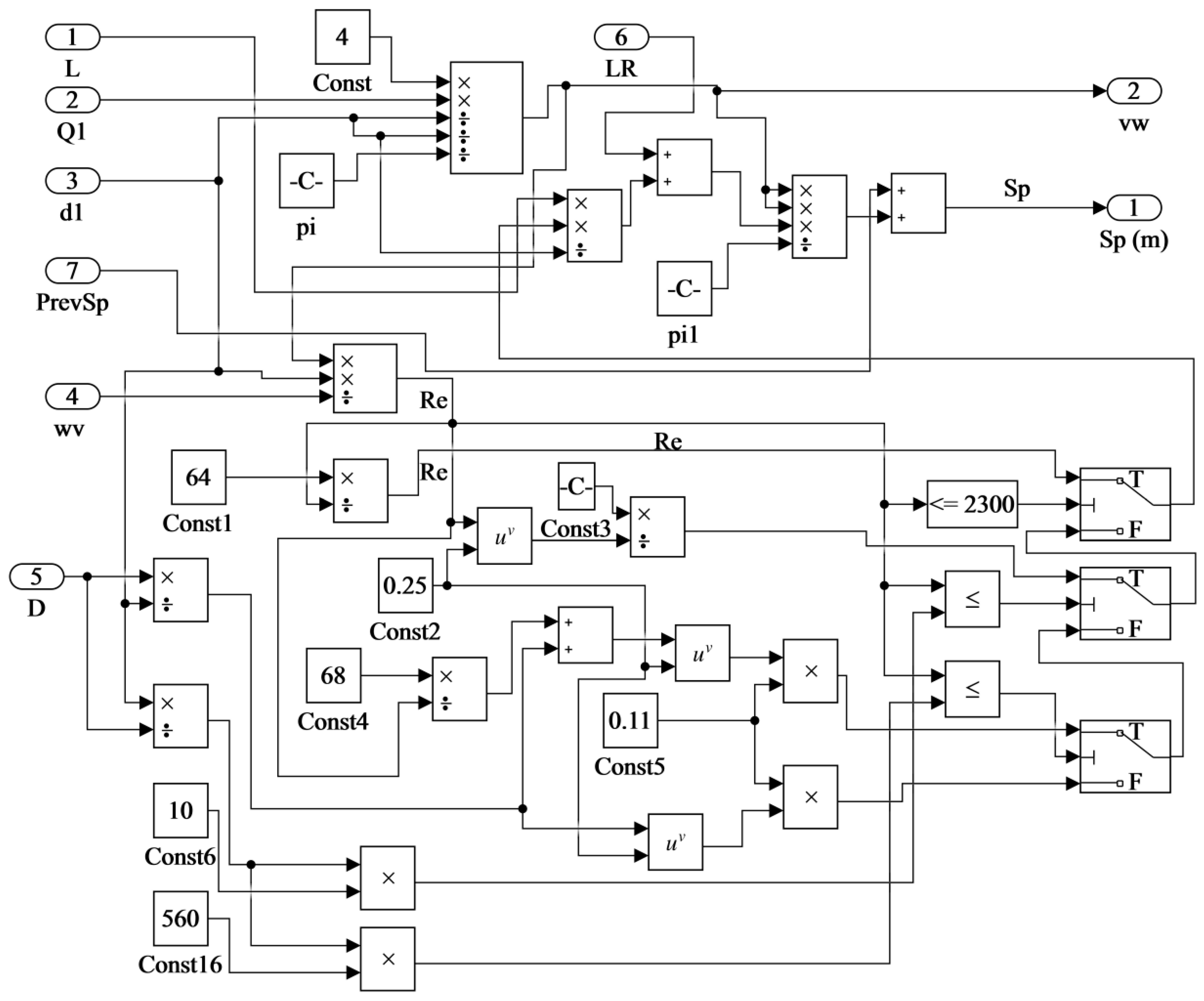
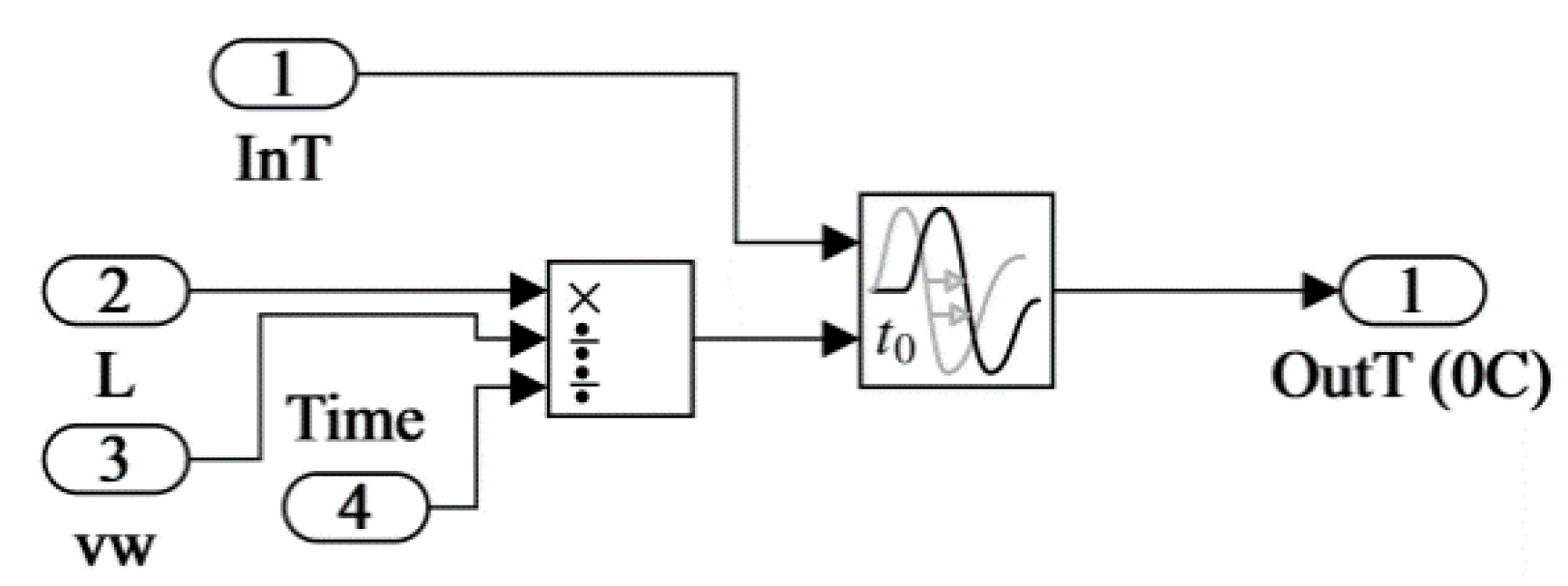
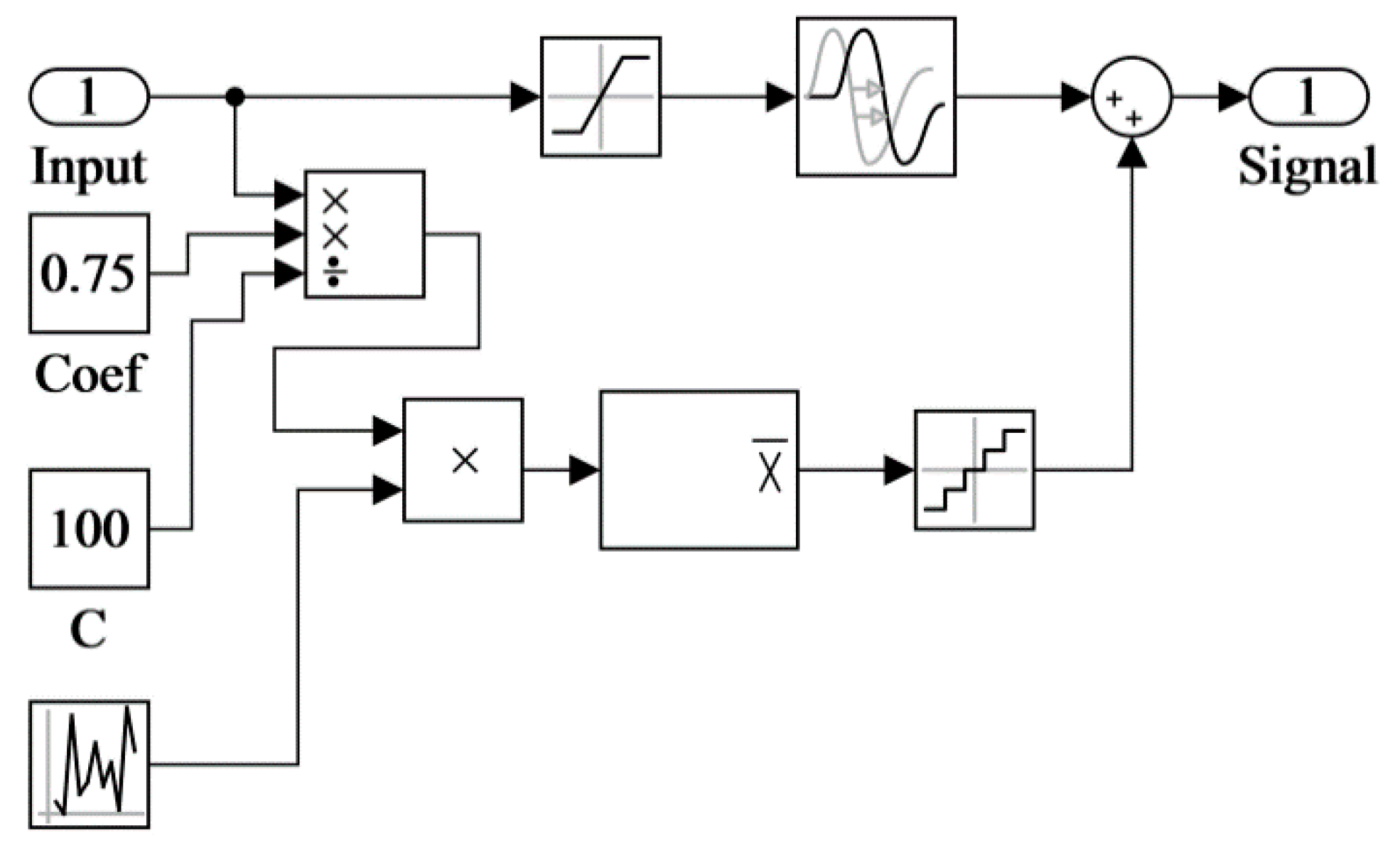
2.3. Simulink Imitation Model
2.3.1. Model of Controlled Object
2.3.2. Model of the Control System
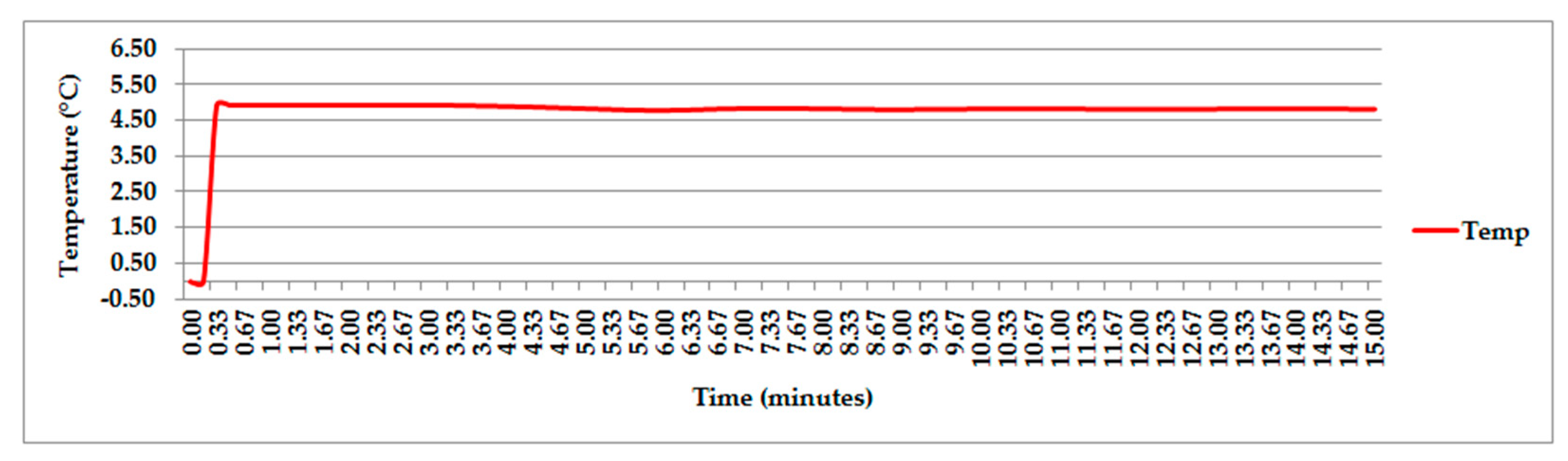
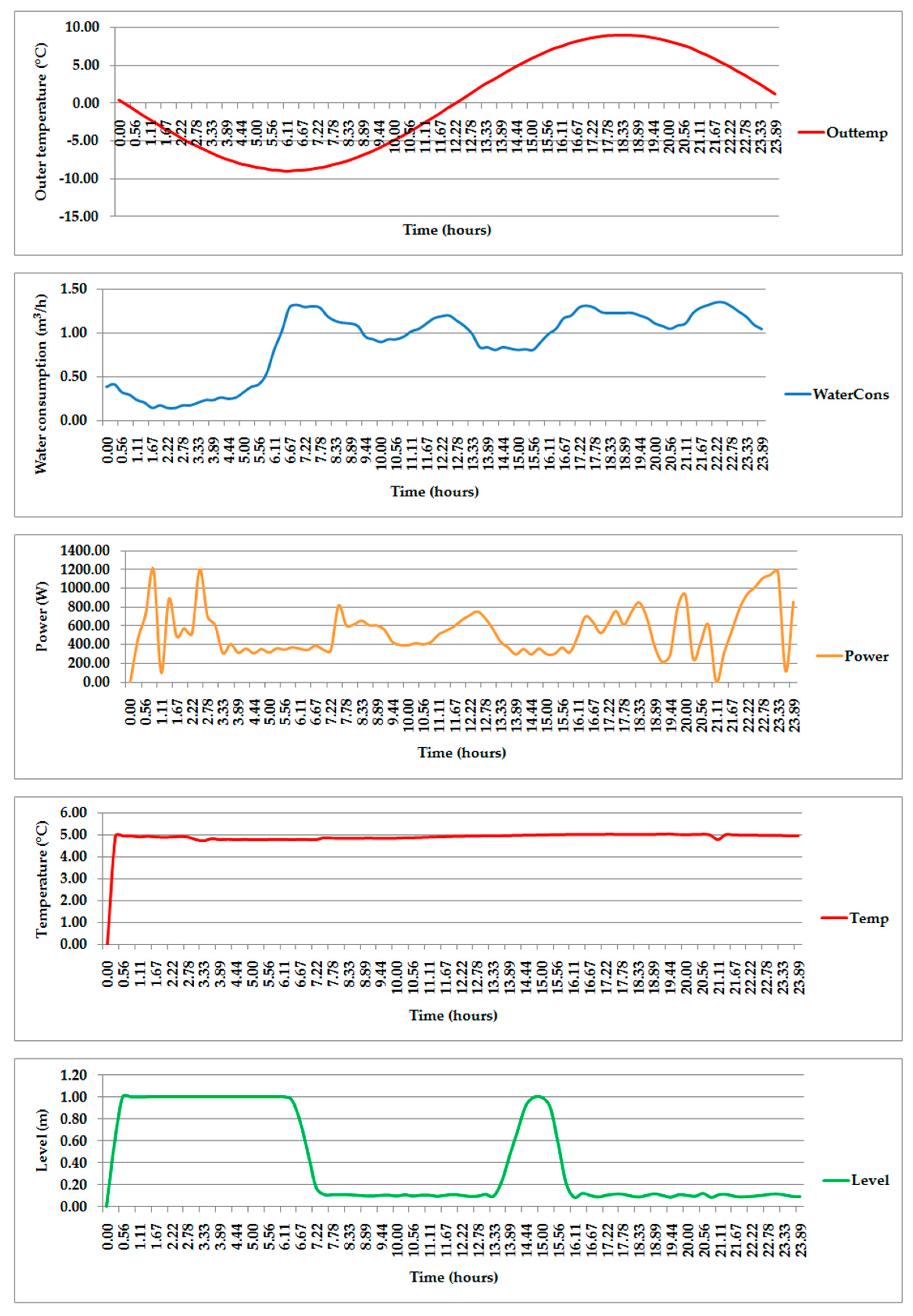
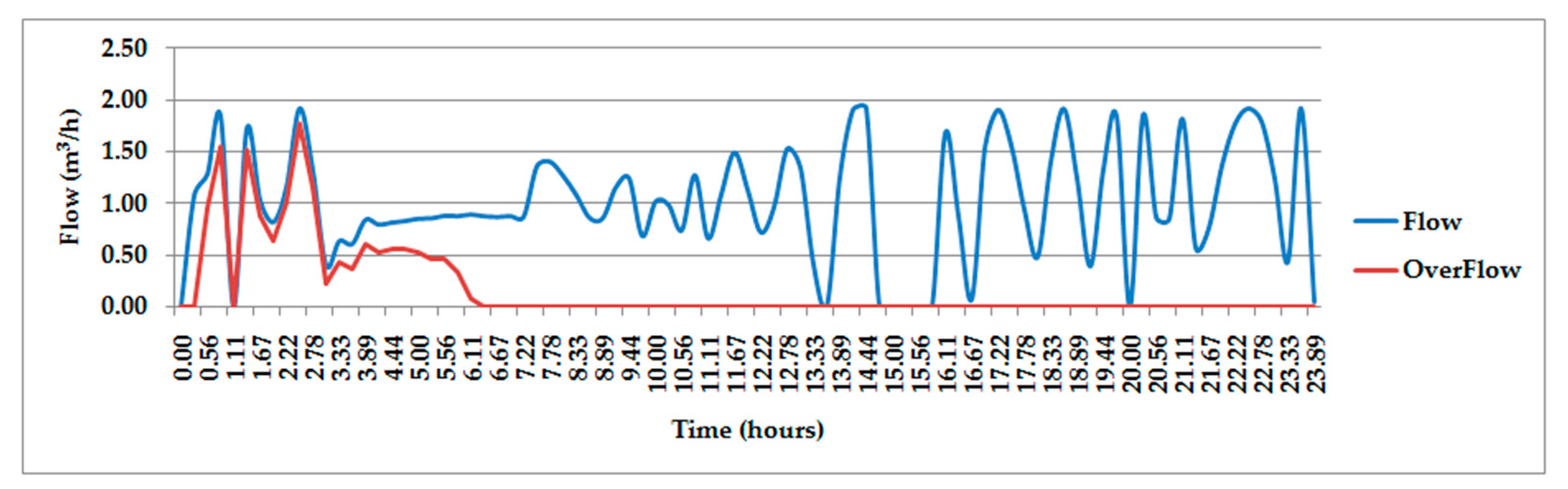
3. Results
3.1. Experiment Plan
| Parameter | Value | Unit |
|---|---|---|
| Pipeline and Environment | ||
| d1 | 0.022 | m |
| d2 = d3 | 0.032 | m |
| polypropylene λm | 0.190 | W/m °C |
| Total pipe length | 45 | m |
| L | 22.5 | m |
| v | 0.1 | m/s |
| fu | 15–50 | Hz |
| Hc | 3 | m |
| Δ [46] | 0.000005 | m |
| tn | 5 | °C |
| to | −9 | °C |
| s | 0.4 | m2 |
| h | 1 | m |
| Total LR | 76.7 | - |
| Pump K50-32-125 | ||
| Hf | 21.41 | m |
| Sf | 0.009 | s2/m5 |
| nn | 2950 | rpm |
| η | 55 | % |
| Electric motor 80MA2 [47] | ||
| Pn | 1500 | W |
| Rs | 5.34 | Ω |
| Ls | 0.01 | H |
| Rr’ | 3.11 | Ω |
| Lr’ | 0.02 | H |
| Lm | 0.5 | H |
| p | 1 | - |
| i | 0.0017 | kg·m2 |
| F | 0.006 | N·m·s |
| Sn | 5 | % |
- Determination of the nominal pump flow.
- Calculations and analysis of transient processes with a smooth exit to the nominal feed.
- Analysis of control algorithms, selection of coefficients of control laws.
- Calculation of the model with the optimal control option for a time interval of 24 h.
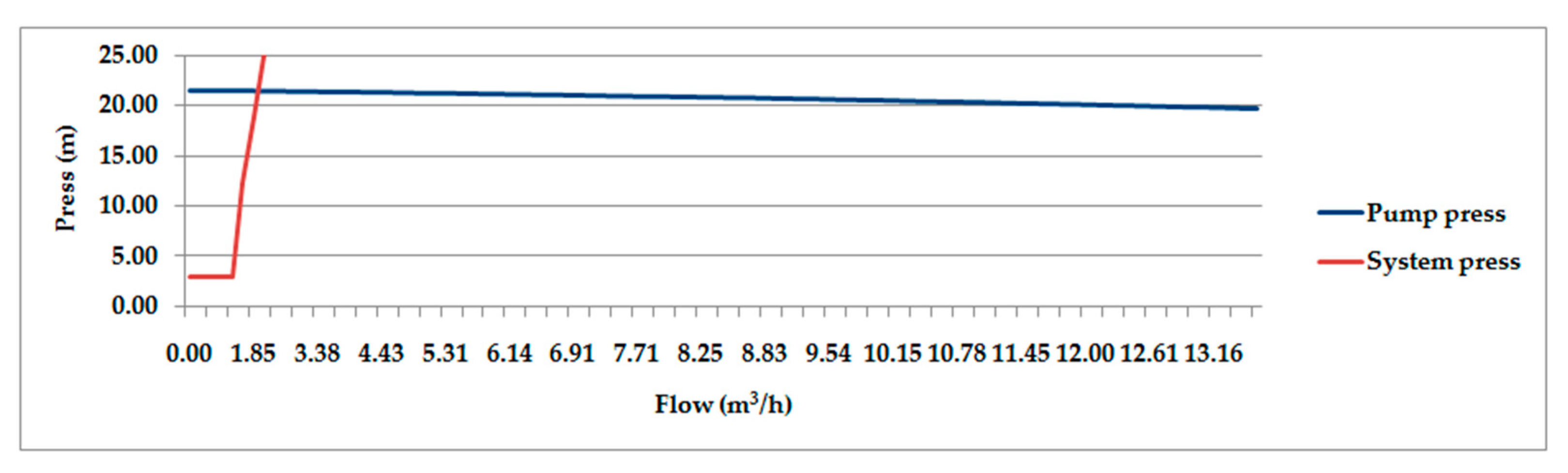
3.2. Determination of the Nominal Pump Flow
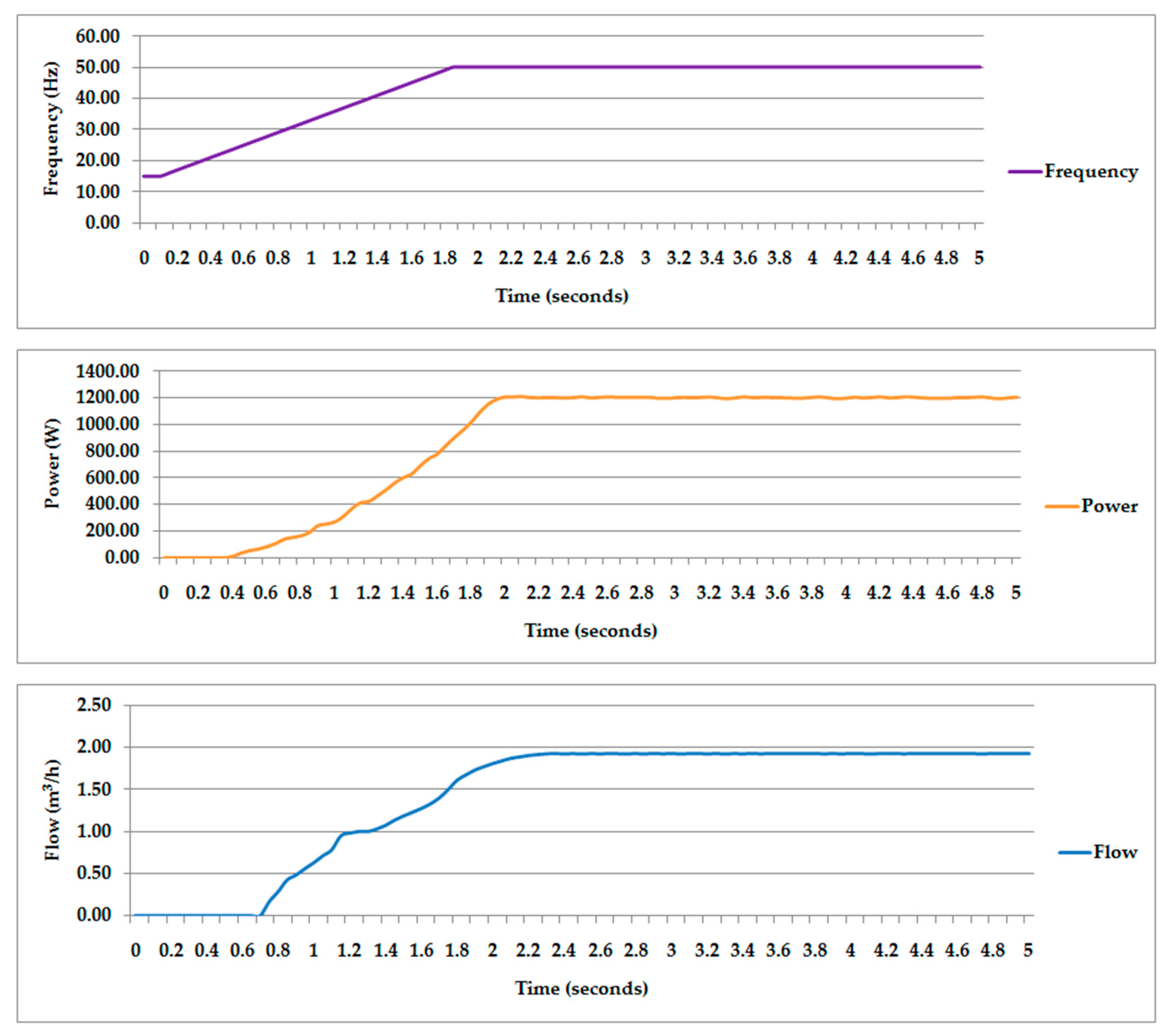
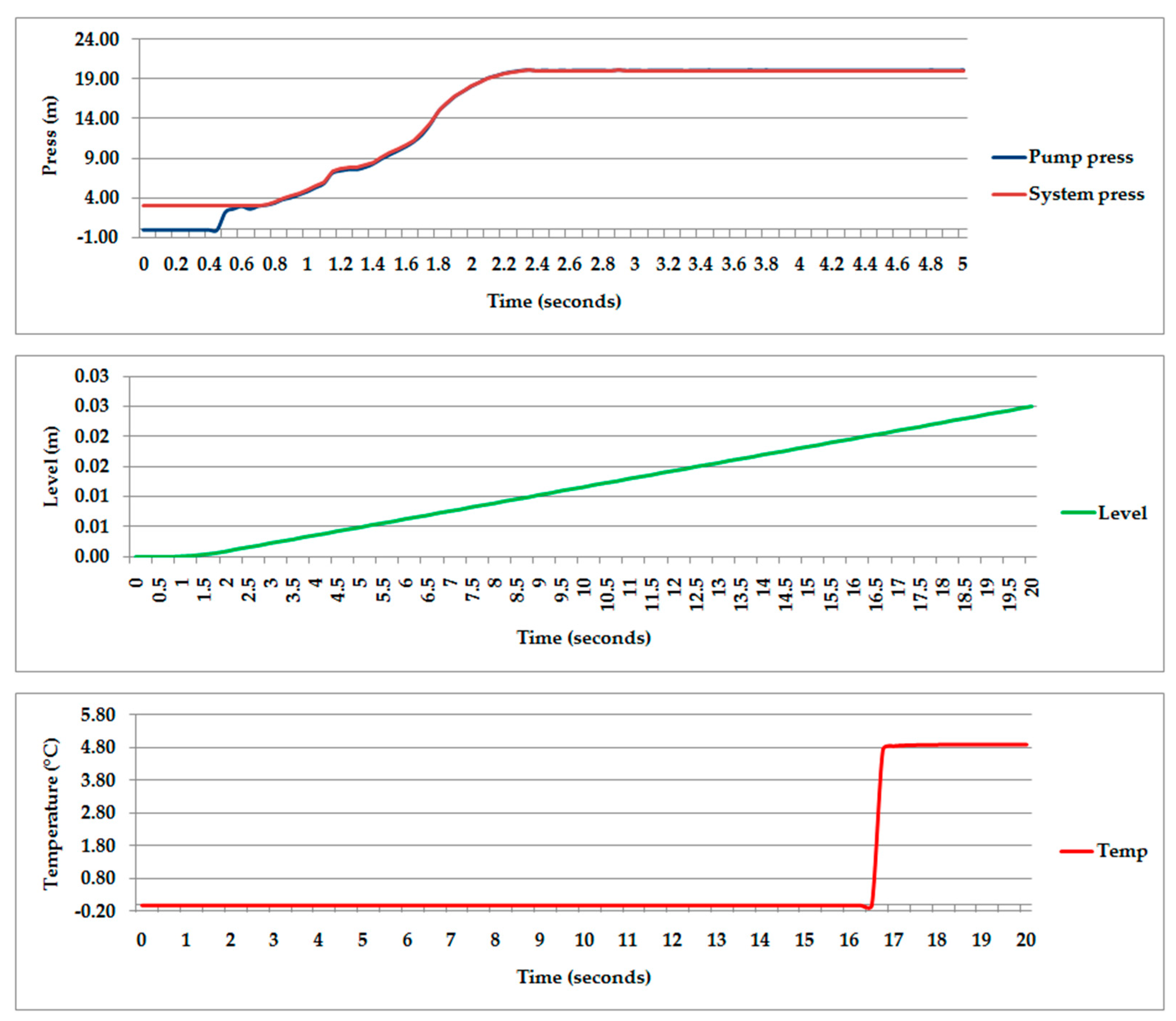
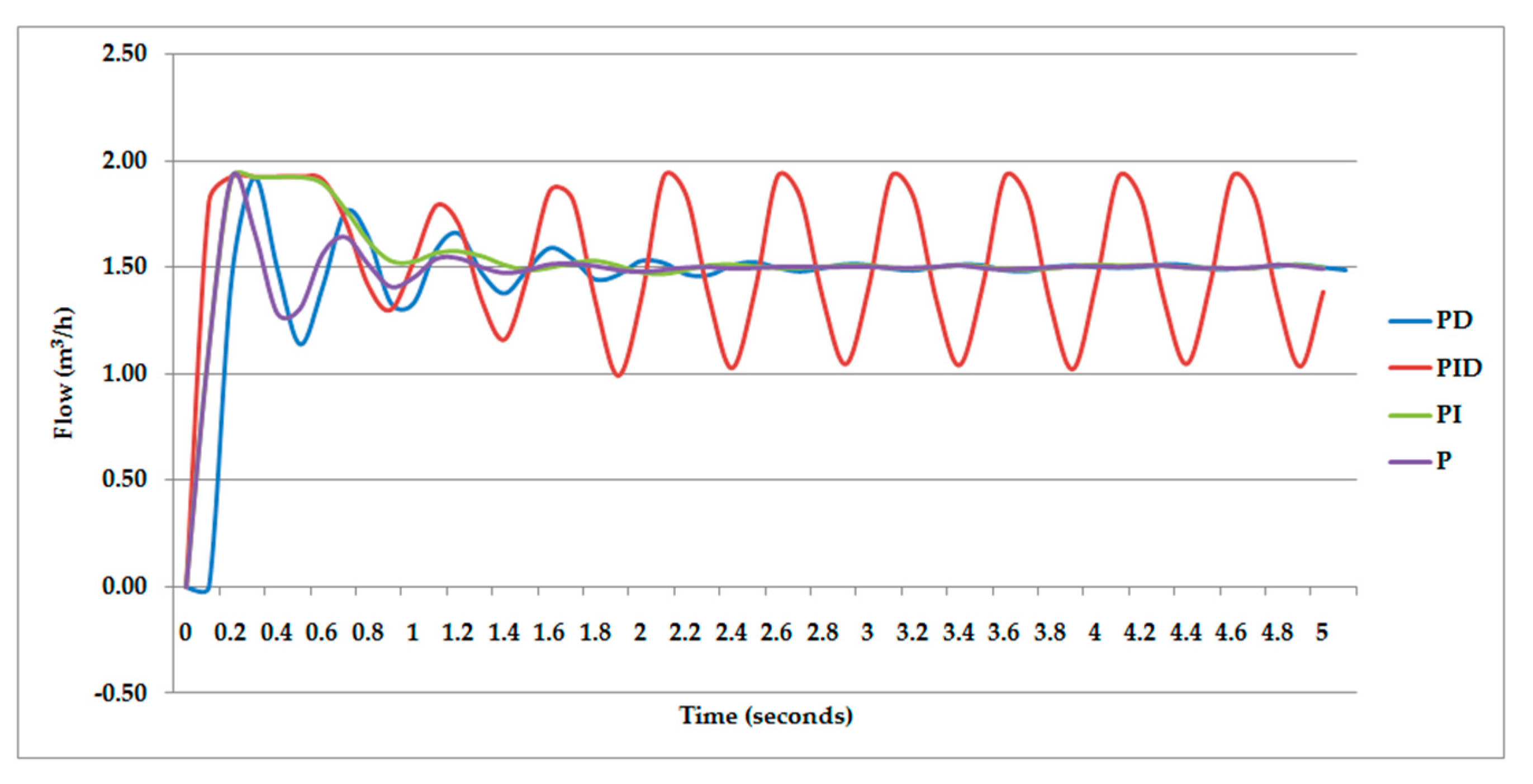
3.3. Calculation of Transients
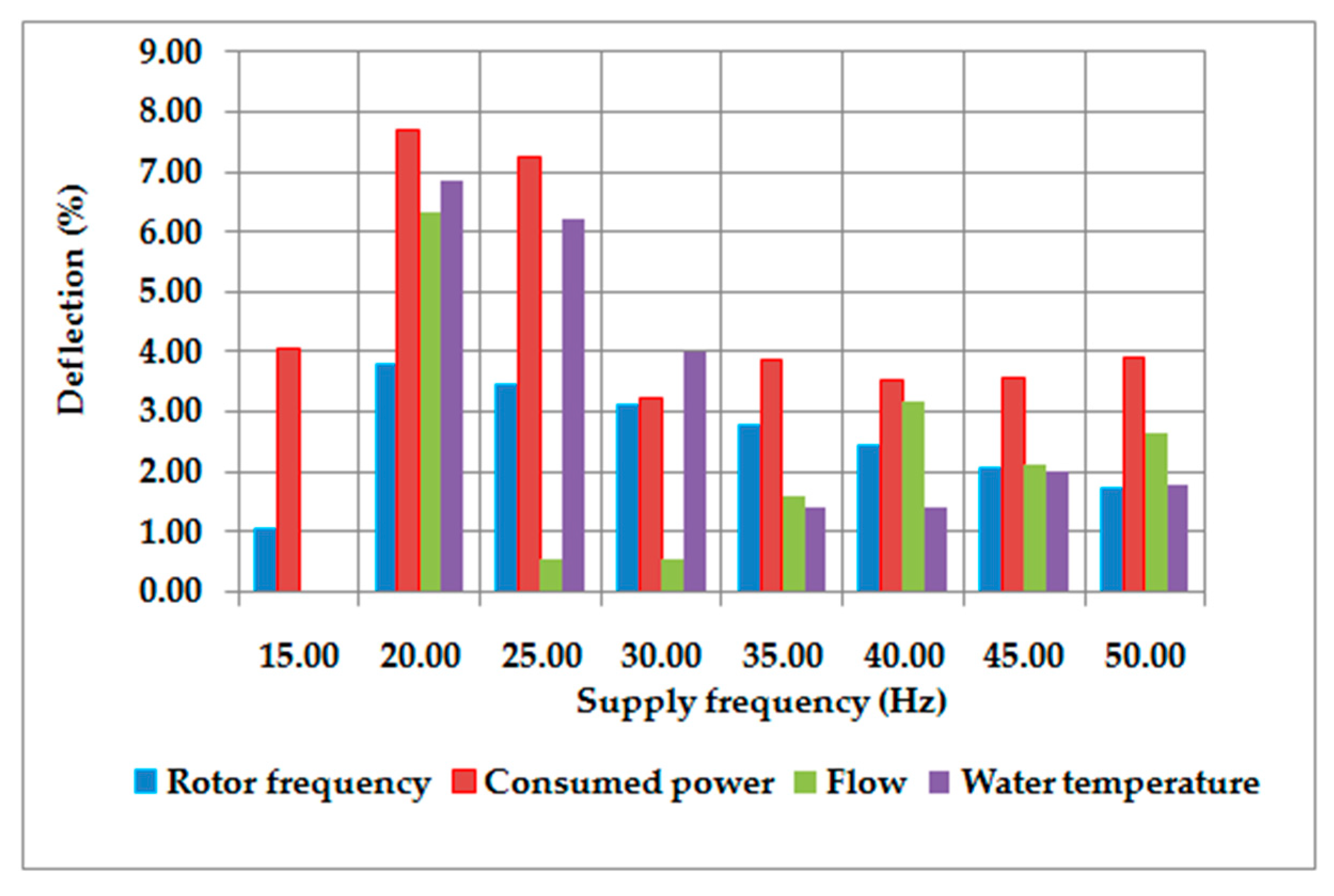
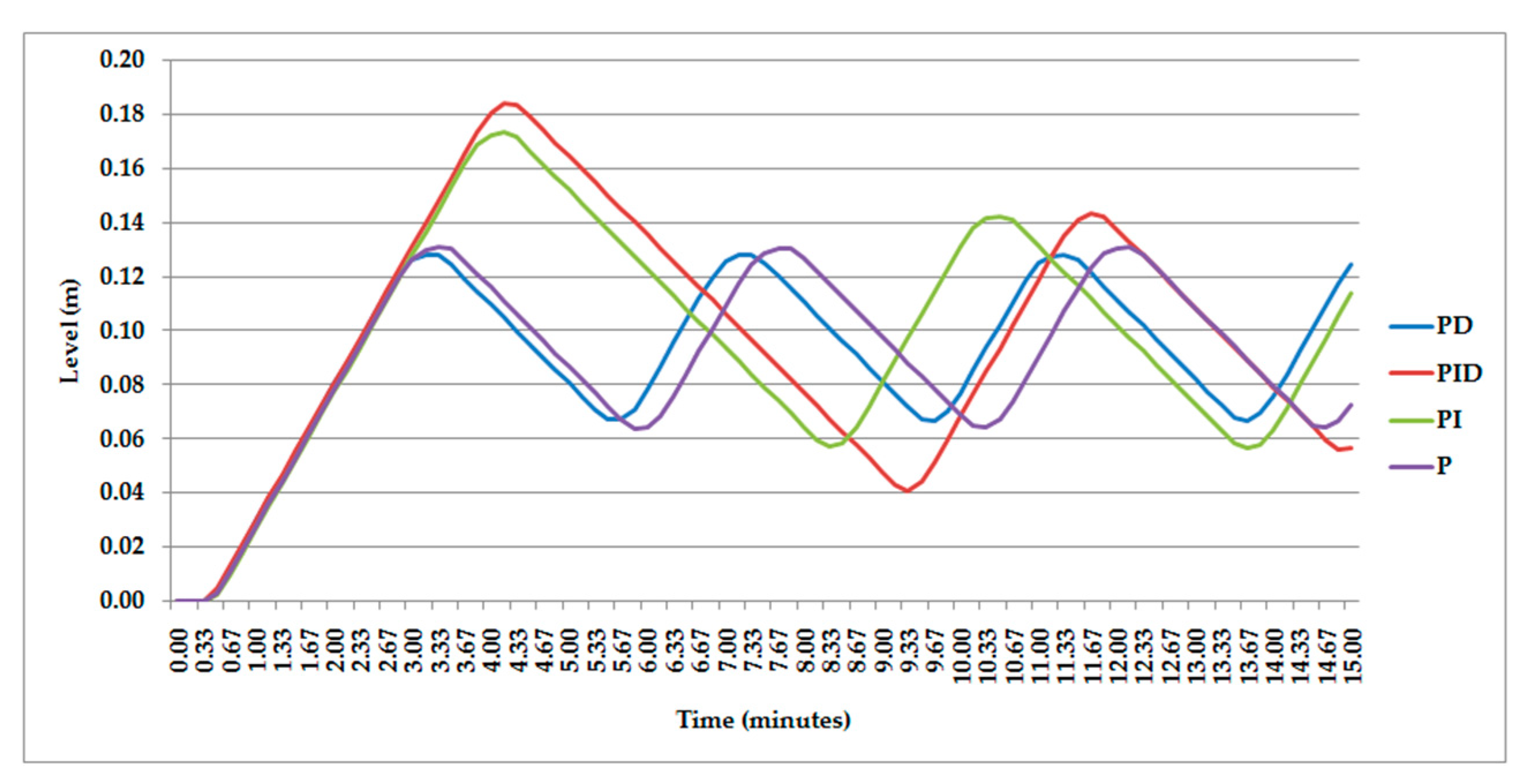
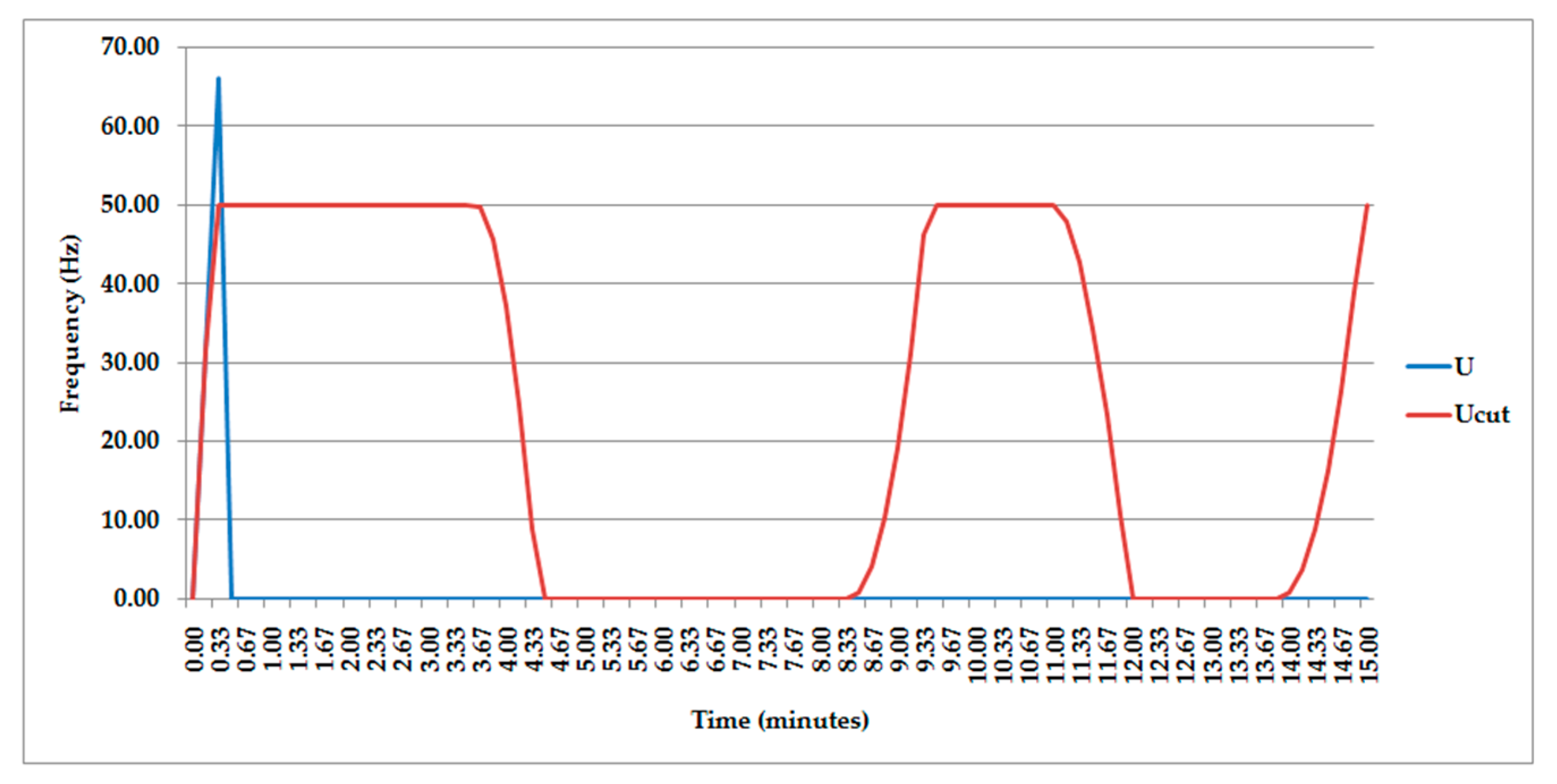
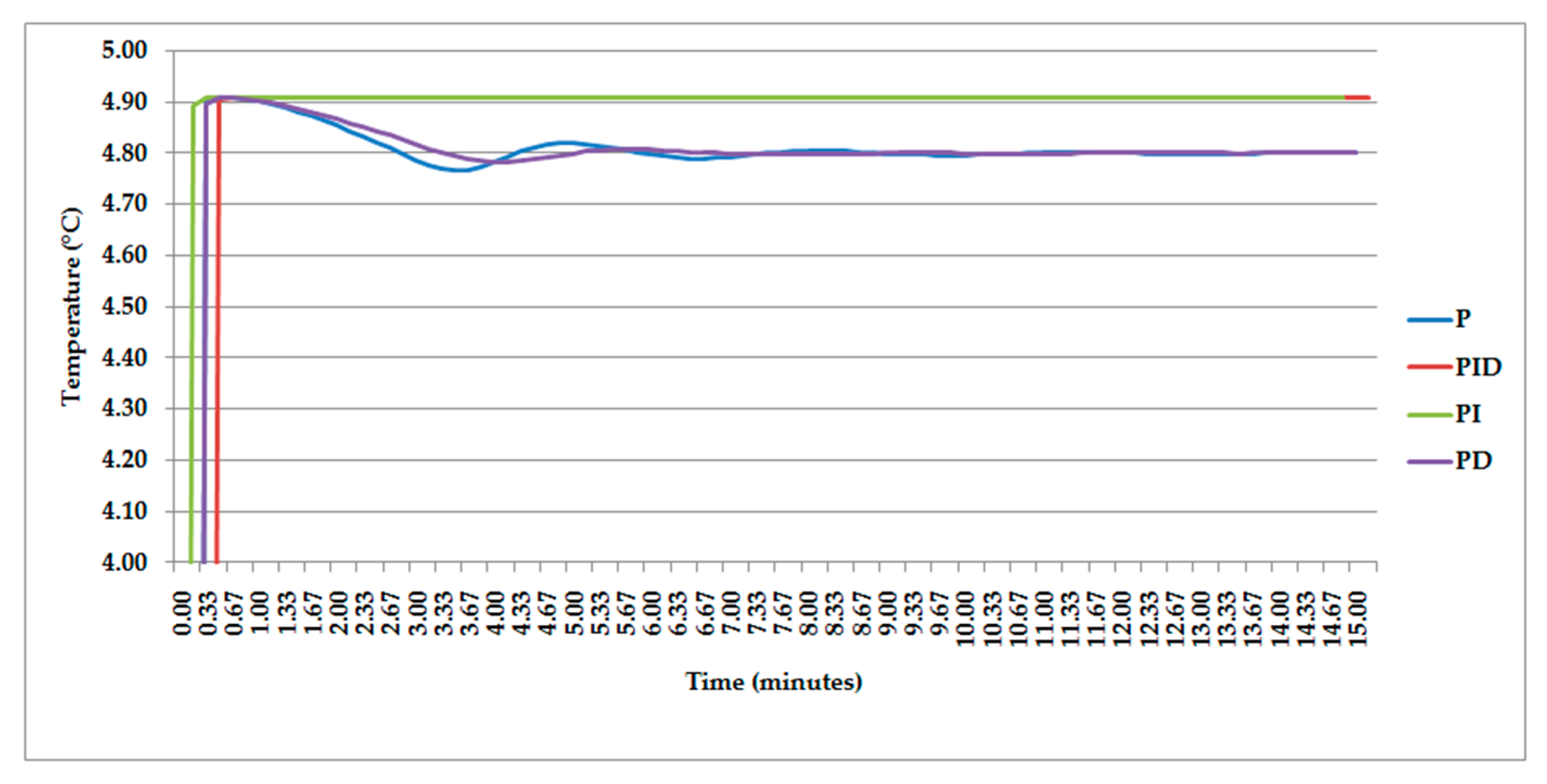
3.4. Analysis of Control Algorithms
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ginzburg, A.V. Improving the Efficiency of Water Supply and Sanitation Systems in Difficult Natural Conditions: Dis. Cand. Tech. Sciences; Moscow, Russia, 2005; p. 211. [Google Scholar]
- Kitaev, D.N.; Kotlyarov, O.I.; Monahov, A.I. Experimental investigations of liquid cooling in pipelines in the absence of motion. Young Sci. 2017, 21, 131–133. [Google Scholar]
- Zhao, J.Q.; Rajani, B.B.; Daigle, L. Thermal performance of trench backfills used for frost protection of water service lines. Can. Geotech. J. 2001, 38, 161–174. [Google Scholar] [CrossRef]
- Sepehr, K.; Goodrich, L.E. Frost protection of buried PVC water mains in western Canada. Can. Geotech. J. 1994, 31, 491–501. [Google Scholar] [CrossRef]
- Terekhov, L.; Akimov, D.O.; Akimova, V.; Yu, M. Water Supply and Sanitation in Northern Climatic Conditions; FESURT: Khabarovsk, Russia, 2008; p. 124. [Google Scholar]
- Samarin, O.D. Speed estimation to prevent freezing of water when moving in heat pipes. Energy Sav. Water Treat. 2015, 4, 31–34. [Google Scholar]
- Reeve, H.E. A Study of the Thermal Field Surrounding Buried District Heating Pipes. Master’s Thesis, University Ottawa, ON, Canada, 1997. [Google Scholar]
- Majny, S.B.; Terekhov, L.D.; Zaborshchikova, N.P. Technique of determination the minimum laying depth of the initial site of sewer pipelines in severe climatic conditions. Bull. Civ. Eng. 2016, 3, 116–122. [Google Scholar]
- Palkin, G.; Suvorov, I. Development of a simulation model of the first rise area of a water supply system with a storage reservoir. In Proceedings of the 2020 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 5–11 September 2020; pp. 804–809. [Google Scholar] [CrossRef]
- Tamminen, J.; Ahonen, T.; Kosonen, A.; Ahola, J.; Tolvanen, J. Variable speed drive-based pressure optimization of a pumping system comprising individual branch flow control elements. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–11. [Google Scholar] [CrossRef]
- Ahmed, A.; Moharam, B.; Rashad, E. Power Saving of Multi Pump-Motor Systems Using Variable Speed Drives. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 839–844. [Google Scholar] [CrossRef]
- Zheng, G.; Huang, Q. Energy optimization study of rural deep well two-stage water supply pumping station. IEEE Trans. Control Syst. Technol. 2016, 24, 1308–1316. [Google Scholar] [CrossRef]
- Fulai, Y.; Hexu, S. Optimal control in variable-speed pumping stations. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 2397–2401. [Google Scholar] [CrossRef]
- Zhuan, X.; Xia, X. Development of efficient model predictive control strategy for cost-optimal operation of a water pumping station. IEEE Trans. Control Syst. Technol. 2013, 21, 1449–1454. [Google Scholar] [CrossRef]
- Gorunov, A.N.; Onishenko, G.B. Regulated electrodrive for pump set of the first rise water supply station. ISPEU Bull. 2012, 6, 131–134. [Google Scholar]
- Likhodedov, A.D. Improve Energy Efficiency and Operational Reliability of the Electric Drive in Supply System: Dis. Cand. Tech. Sciences; Petropavlovsk-Kamchatsky, Russia, 2015; p. 211. [Google Scholar]
- Palkin, G.; Suvorov, I.; Gorbunov, R. Evaluation of ways to improve the energy efficiency of sites of first rise supply water systems with storage tank by laboratory modeling. In Proceedings of the 2018 International Ural Conference on Green Energy (UralCon), Chelyabinsk, Russia, 4–6 October 2018; pp. 227–234. [Google Scholar] [CrossRef]
- Palkin, G.A.; Suvorov, I.F. Improving the fault tolerance of the water supply system by controlling the pumping units. In Collection of Scientific Articles of the I All-Russian Scientific Conference: Information Technologies in Modeling and Management: Approaches, Methods, Solutions; Kachalin, A.V., Ed.; Tolyatti Publisher: Tolyatti, Samara Oblast, Russia, 2017; p. 656. [Google Scholar]
- Ovchinnikova, A.P. The automatic pump control system for maintaining water level in the tank. Youth Mod. Inf. Technol. 2016, 1, 255–257. [Google Scholar]
- Palkin, G.A.; Suvorov, I.F. Control of the first lifting pumping units on water supply system with storage reservoir. Mod. H. Technol. 2017, 7, 55–60. [Google Scholar]
- Khasanov, A.R.; Starodubtseva, V.A. Analysis of Technological Solutions for the Use of Frequency Converters. All-Russian Scientific and Technical Conference of Graduate Students, Undergraduates and Young Scientists with International Participation Young Scientists – Accelerating Scientific and Technical Progress in the Xxi Century; INNOVA: Moscow, Russia, 2016; pp. 956–963. [Google Scholar]
- Kukishev, D.; Meshcheryakov, V.; Boikov, A.; Evseev, A. Energy saving in the scalar control system of an asynchronous electric drive. In Proceedings of the 2018 X International Conference on Electrical Power Drive Systems (ICEPDS), Novocherkassk, Russia, 3–6 October 2018; pp. 30–31. [Google Scholar] [CrossRef]
- Ibraev, K.A.; Sarsembieva, E.K. Energy saving in electric drives and control of these processes in the sphere of housing and communal services. In Proceedings of the 2017 International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Kazakbaev, V.; Prakht, V.; Dmitrievskii, V.; Sarapulov, S.; Askerov, D. Comparison of power consumption of synchronous reluctance and induction motor drives in a 0.75 kW pump unit. In Proceedings of the 2017 International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Muravleva O., O.; Tyuteva P., V. Operation features of the improved induction motors in the variable speed drive of pump units. In Proceedings of the IEEE EUROCON 2009, St. Petersburg, Russia, 18–23 May 2009; pp. 703–708. [Google Scholar] [CrossRef]
- Gumerova, R.K.H.; Chernyakhovsky, V.A. Modeling of electric power consumption by pump drives under throttling and frequency regulation of productivity. News H. Educ. Inst. Energy Probl. 2017, 19, 96–106. [Google Scholar]
- Jahmeerbacus, M.I. Flow rate regulation of a variable speed driven pumping system using fuzzy logic. In Proceedings of the 2015 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 24–26 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Sirový, M.; Peroutka, Z.; Molnár, J.; Michalík, J.; Byrtus, M. Sophisticated software for design and optimization of variable speed drives for high-power pumps: Hydrodynamic coupling versus frequency converter. In Proceedings of the IECON 2011–37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 955–960. [Google Scholar] [CrossRef]
- Ferreira, F.J.; Fong, J.A.; Almeida, A.T. Ecoanalysis of variable-speed drives for flow regulation in pumping systems. IEEE Trans. Ind. Electron. 2011, 58, 2117–2125. [Google Scholar] [CrossRef]
- Pöyhönen, S.; Simola, A.; Ahola, J. Variable-speed-drive-based sensorless estimation of pump system reservoir fluid level. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 1–7 September 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Arribas, J.R.; Gonzalez, C.V. Optimal vector control of pumping and ventilation induction motor drives. IEEE Trans. Ind. Electron. 2002, 49, 889–895. [Google Scholar] [CrossRef]
- Vladimir, P.; Dmitry, S. To issue of designing scalar closed-loop controllers for frequency controlled induction motor drives. In Proceedings of the 2018 17th International Ural Conference on AC Electric Drives (ACED), Ekaterinburg, Russia, 26–30 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Kolesnikov, E.B.; Shprekher, D.M.; Malkov, S.B. Automated system ensuring uninterrupted water supply for small settlements. In Proceedings of the 2019 International Ural Conference on Electrical Power Engineering (UralCon), Chelyabinsk, Russia, 1–3 October 2019; pp. 13–17. [Google Scholar] [CrossRef]
- Yacamini, R.; Lihua, H.U.; Stewart, I.D. CAD representation of variable speed drives for downhole pump applications. In Proceedings of the 1989 Fourth International Conference on Electrical Machines and Drives, London, UK, 13–15 September 1989; pp. 16–20. [Google Scholar]
- Gevorkov, L.; Rassõlkin, A.; Kallaste, A.; Vaimann, T. Simulation study of a centrifugal pumping plant’s power consumption at throttling and speed control. In Proceedings of the 2017 IEEE 58th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Lysenko, A.; Simakov, A.V. The Pump Hydraulic Load Effect Determination on the Parameters of an Frequency-Controlled Asynchronous Electric Drive, 2019 Dynamics of Systems, Mechanisms and Machines; Dynamics: Omsk, Russia, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Gevorkov, L.; Rassõlkin AKallaste, A.; Vaimann, T. Simulink based model for flow control of a centrifugal pumping system. In Proceedings of the 2018 25th International Workshop on Electric Drives: Optimization in Control of Electric Drives (IWED), Moscow, Russia, 31 January–2 February 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Kepa, U. Use of the hydraulic model for the operational analysis of the water supply network: A case study. Water 2021, 13, 326. [Google Scholar] [CrossRef]
- Sperlich, A.; Pfeiffer, D.; Burgschweiger, J.; Campbell, E.; Beck, M.; Gnirss, R.; Ernst, M. Energy efficient operation of variable speed submersible pumps: Simulation of a ground water well field. Water 2018, 10, 1255. [Google Scholar] [CrossRef]
- Leznov, B.S. Frequency-Controlled Electric Drive of Pumping Installations; Mashinostroenie: Moscow, Russia, 2013; p. 176. [Google Scholar]
- Cost-Effective Ways to Regulate the Operating Modes of Pumping Units. Available online: https://mybiblioteka.su/tom2/3-53819.html (accessed on 30 May 2020).
- Palkin, G.A. Modeling of Sections of the First Rise of Water Supply Systems, Kulaginsky Readings: Techniques and Technologies of Production Processes: XIV International Scientific-Practical Conference: Sat. Art; Chita, Russia, 2019; p. 232. [Google Scholar]
- Implementation of the Power Source of the Inverter in the Form of a Rectifier. Available online: https://studme.org/165352/informatika/realizatsiya_istochnika_pitaniya_invertora_vide_vypryamitelya (accessed on 30 May 2020).
- Pantel, O.V. Methodic or calculating parameters of an asynchronous motor for modeling its operating modes in the environment Matlab/Simulink. Academy 2015, 2, 7–11. [Google Scholar]
- Kravchik A., E.; Shlaf M., M.; Afonin V., I.; Sobolenskaya E., A. Asynchronous Motors of the 4a Series, Reference Book; Energoizdat: Moscow, Russia, 1982; p. 504. [Google Scholar]
- Roughness of Polyethylene Pipes. Calculation of Hydraulic Pressure Losses in a Plastic Pipeline. Available online: https://polyplastic.ua/news/news-111.html/ (accessed on 30 May 2020).
- Electric Motor AIR80A2, 5A80MA2 and A80A2 (1.5 kW). Available online: http://tech-privod.com/index.pl?act=PRODUCT&id=1275/ (accessed on 30 May 2020).
- Lan, H.; Lepeng, S. The pump house constant pressure fuzzy self-tuning PID control system simulation. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 25–27 March 2011; pp. 5525–5527. [Google Scholar] [CrossRef]


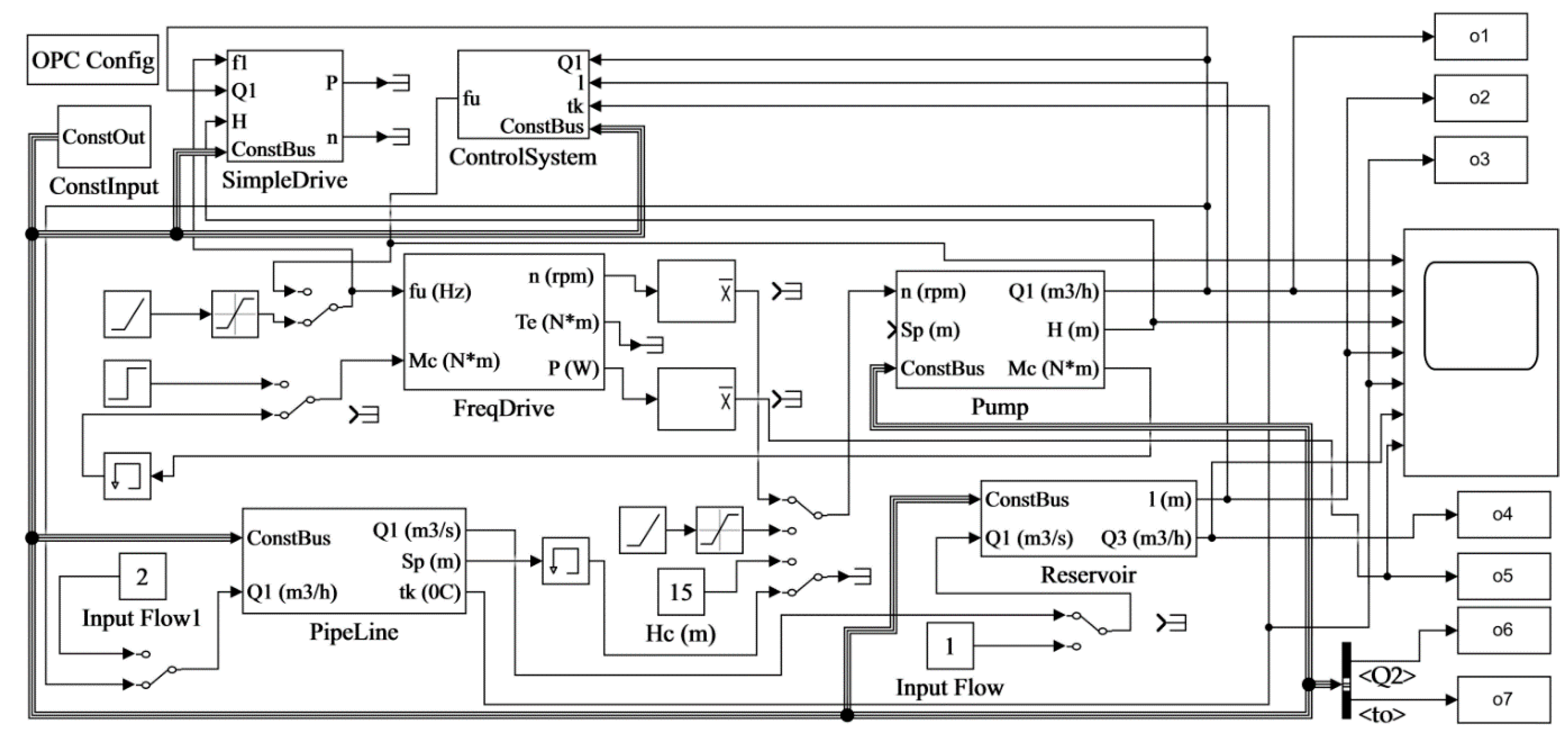
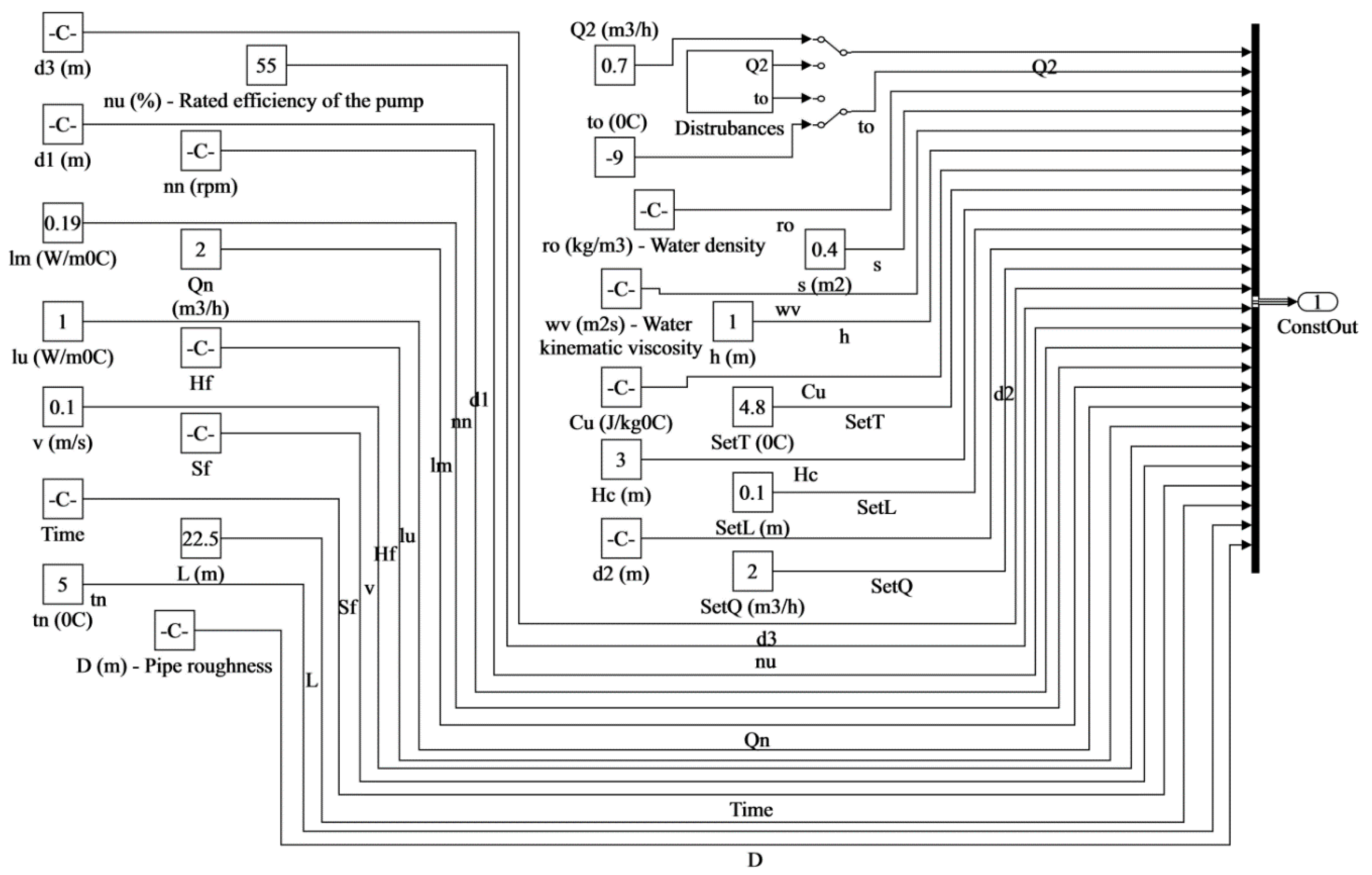
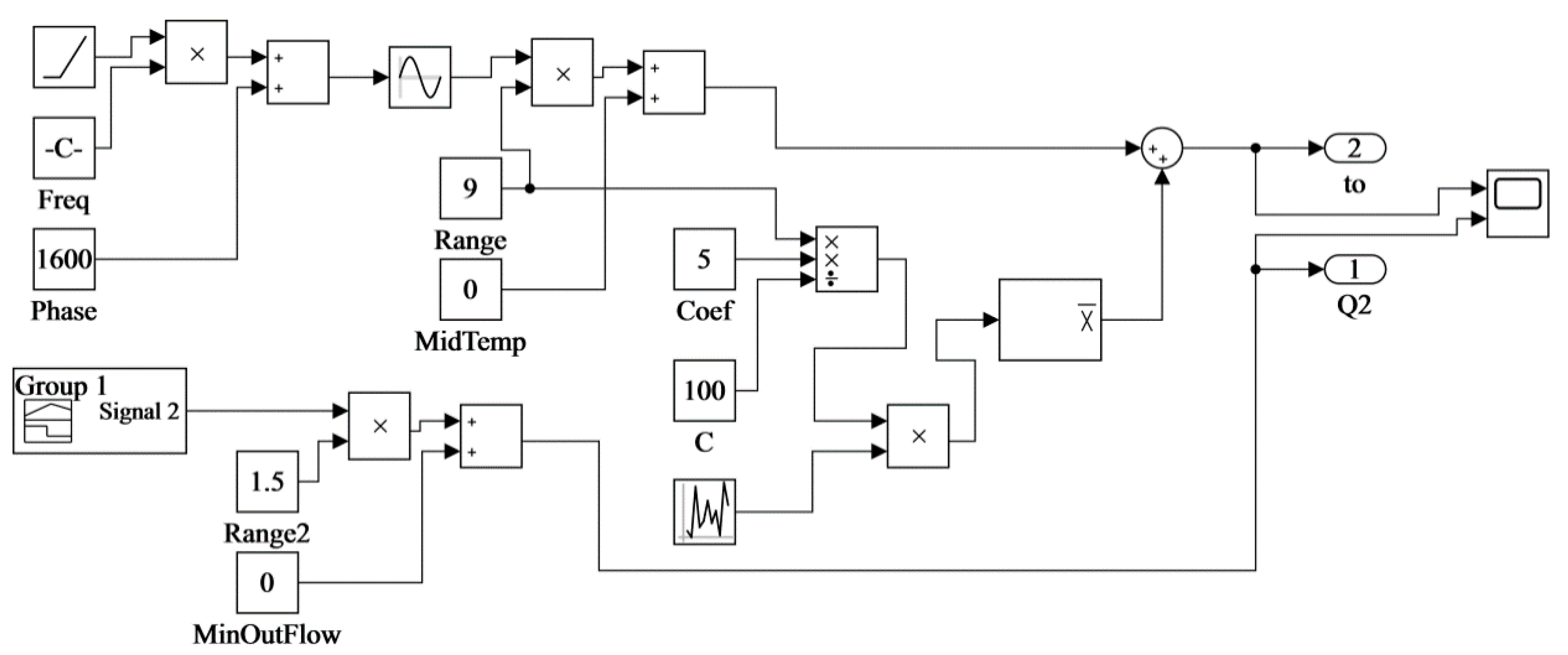
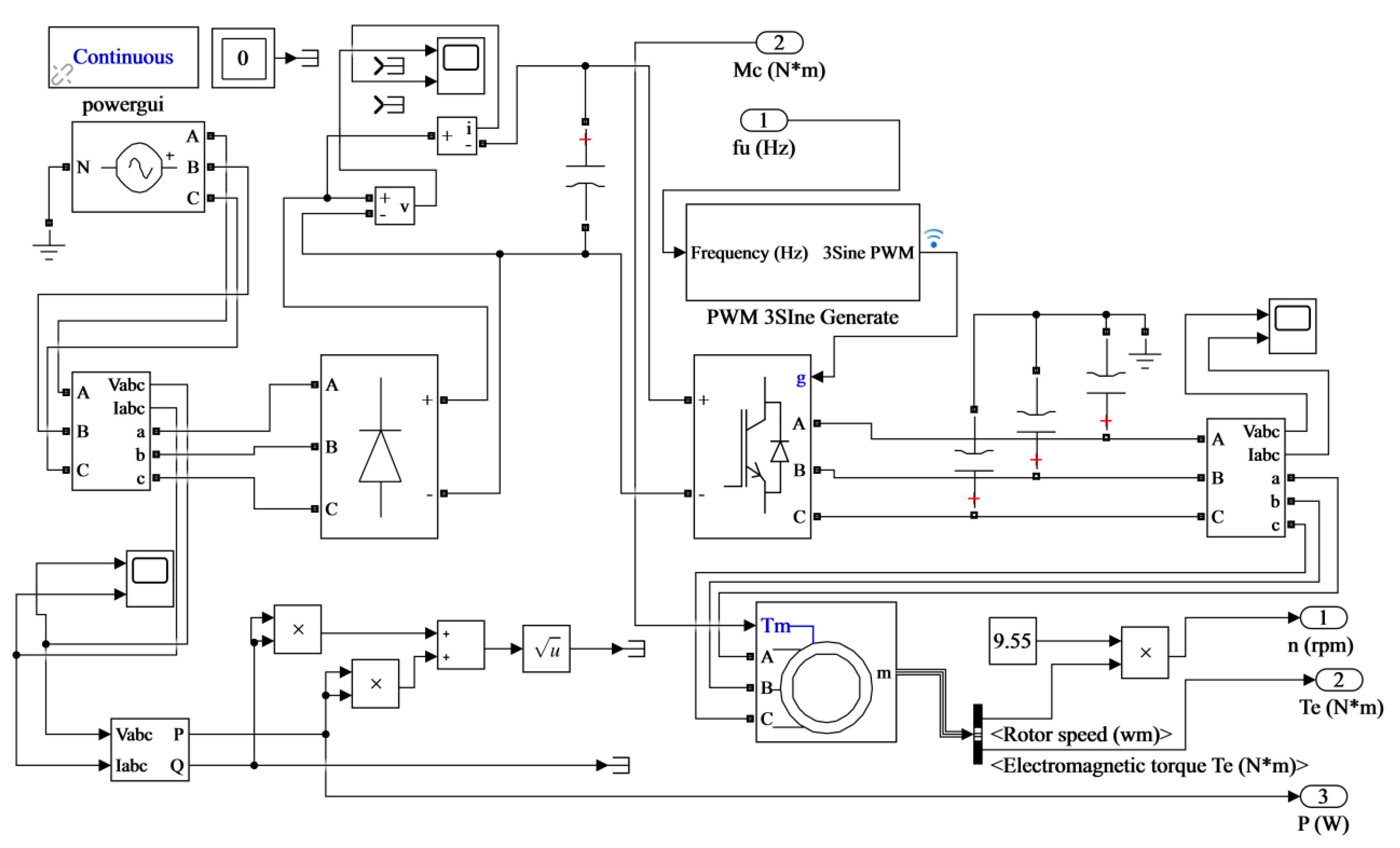






| Name | Symbol | Unit |
|---|---|---|
| Outer input Parameters | ||
| Supply voltage | V | V |
| Supply current | A | A |
| Supply frequency | f | Hz |
| Volumetric flow rate at the outlet from the reservoir (consumer needs) | Q2 | m3/s |
| Ambient temperature | to | °C |
| Internal Communications | ||
| Frequency converter output voltage | V1 | V |
| Frequency converter output current | A1 | A |
| Frequency at the output of the frequency converter | f1 | Hz |
| Control action on the frequency converter | fu | Hz |
| The moment of resistance of the pump on the shaft of the electric motor | Mc | N·m |
| Mechanical frequency of rotation of the electric motor shaft | n | rpm |
| Volume flow (supply) in the pipeline | Q1 | m3/s |
| Pump head | H | m |
| Head of the pipeline system | Sp | m |
| Output Parameters | ||
| Power consumed by the pump electric drive | P | W |
| Overflow of water from the reservoir | Q3 | m3/s |
| Water temperature at the end of the pipeline | tk | °C |
| Water level in the reservoir | l | m |
| Name | Symbol (in Simulink) | Unit |
|---|---|---|
| Motor Parameters | ||
| Rated speed of the motor shaft | nn | rpm |
| Rated power | Pn | W |
| Stator windings resistance | Rs | Ω |
| Stator windings inductance | Ls | H |
| Rotor windings resistance | Rr’ | Ω |
| Rotor windings inductance | Lr’ | H |
| Mutual inductance | Lm | H |
| Motor number of pairs of poles | p | - |
| Motor moment of inertia | i | kg·m2 |
| Motor friction factor | F | N·m·s |
| Motor coefficient of slip | Sn | % |
| Pump electric drive efficiency | ηp (nup) | % |
| Electromagnetic torque | Te | N·m |
| Pump Parameters | ||
| Nominal pump flow at the current hydraulic resistance of the system | Qn | m3/s |
| Fictitious pump head | Hf | m |
| Hydraulic fictitious resistance of the pump | Sf | s2/m5 |
| Rated efficiency of the pump | η (nu) | % |
| Pipeline Parameters (or environmental parameters affecting the calculation of the pipe) | ||
| Static head of the system | Hc | m |
| Water density | ρ (ro) | kg/m3 |
| Acceleration of gravity | g | m/s2 |
| Resistance of the pipeline [40] | S | - |
| Water temperature at the beginning of the pipeline | tn | °C |
| Dissipative heat of friction | qt | W/m |
| Heat transfer coefficient from water to the pipe wall | k1 | W/m·°C |
| Reduced heat transfer coefficient | kpr | W/m·°C |
| Length of the pipeline | L | m |
| Volumetric heat capacity of water | Cv | J/m3·°C |
| Water specific heat capacity | Cu | J/kg·°C |
| Water kinematic viscosity | υ (wv) | m2·s |
| Pipe wall coefficient of thermal conductivity | lm | W/m·°C |
| Passive insulation layer coefficient of thermal conductivity | lu | W/m·°C |
| Pipeline inner diameter | d1 | m |
| Pipeline outer diameter | d2 | m |
| Pipeline full diameter with thermal insulation | d3 | m |
| Mean wind speed | v | m/s |
| Pipeline roughness | Δ (D) | m |
| Total or local resistance of non-linear sections of the pipeline | LR | - |
| Water speed | vw | m/s |
| Simulation time correcting coefficient | Time | - |
| Reservoir Parameters | ||
| Area of the bottom of the reservoir | s | m2 |
| Reservoir height | h | m |
| Control System Parameters | ||
| Control action by level | uL | - |
| Control action by temperature | uT | - |
| Equation | Condition |
|---|---|
| Transient regime | |
| Regulator Type | Regulator Coefficients | Maximum Overshoot (%) | Oscillation Period (s) |
|---|---|---|---|
| P | PL = 25 | 3 | 260 |
| PI | PL = 22.5 | 7.1 | 298 |
| IL = 0.135 | |||
| PD | PL = 30 | 2.8 | 240 |
| DL = 750 | |||
| PID | PL = 30 | 8.5 | 360 |
| IL = 0.3 | |||
| DL = 750 |
| Regulator Type | Regulator Coefficients | Maximum Overshoot (%) | Decay Period of Basic Oscillations (s) |
|---|---|---|---|
| P | PT = 1.85 | 12 | 840 |
| PI | PT = 1.68 | 12 | - |
| IT = 0.011 | |||
| PD | PT = 2.25 | 12 | 540 |
| DT = 52.03 | |||
| PID | PT = 2.25 | 12 | - |
| IT = 0.024 | |||
| DT = 52.03 |
| Regulator Type | Regulator Coefficients | Maximum Overshoot (%) | Decay Period of Basic Oscillations (s) |
|---|---|---|---|
| P | PF = 221.233 | 20 | 3 |
| PI | PF = 199.11 | 20 | 2.6 |
| IF = 508.366 | |||
| PD | PF = 265.48 | 18 | 4 |
| DF = 15.597 | |||
| PID | PF = 265.48 | 18 | - |
| IF = 1129.7 | |||
| DF = 15.597 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palkin, G.; Suvorov, I. Simulation Modeling of First Rise Section of Water Supply System with Installed Complex of Automatic Pump Performance Control. Machines 2021, 9, 63. https://doi.org/10.3390/machines9030063
Palkin G, Suvorov I. Simulation Modeling of First Rise Section of Water Supply System with Installed Complex of Automatic Pump Performance Control. Machines. 2021; 9(3):63. https://doi.org/10.3390/machines9030063
Chicago/Turabian StylePalkin, George, and Ivan Suvorov. 2021. "Simulation Modeling of First Rise Section of Water Supply System with Installed Complex of Automatic Pump Performance Control" Machines 9, no. 3: 63. https://doi.org/10.3390/machines9030063
APA StylePalkin, G., & Suvorov, I. (2021). Simulation Modeling of First Rise Section of Water Supply System with Installed Complex of Automatic Pump Performance Control. Machines, 9(3), 63. https://doi.org/10.3390/machines9030063







