Abstract
The optimisation of complex engineering design problems is highly challenging due to the consideration of various design variables. To obtain acceptable near-optimal solutions within reasonable computation time, metaheuristics can be employed for such problems. However, a plethora of novel metaheuristic algorithms are developed and constantly improved and hence it is important to evaluate the applicability of the novel optimisation strategies and compare their performance using real-world engineering design problems. Therefore, in this paper, eight recent population-based metaheuristic optimisation algorithms—African Vultures Optimisation Algorithm (AVOA), Crystal Structure Algorithm (CryStAl), Human-Behaviour Based Optimisation (HBBO), Gradient-Based Optimiser (GBO), Gorilla Troops Optimiser (GTO), Runge–Kutta optimiser (RUN), Social Network Search (SNS) and Sparrow Search Algorithm (SSA)—are applied to five different mechanical component design problems and their performance on such problems are compared. The results show that the SNS algorithm is consistent, robust and provides better quality solutions at a relatively fast computation time for the considered design problems. GTO and GBO also show comparable performance across the considered problems and AVOA is the most efficient in terms of computation time.
1. Introduction
An engineering design problem comprises of designing products that meet the functional requirements by considering a multitude of values for decision variables [1]. With the increase in the complexity of the design and its application, the number of decision variables increases along with the candidate solutions [2]. Therefore, it is highly challenging to use exhaustive search methods to solve the optimisation problems [3]. To overcome this issue, it is possible to use the class of optimisation algorithms that fall under the category of metaheuristics such that the design space is explored with a guiding heuristic technique [4].
Metaheuristic algorithms can be classified into the following branches: evolutionary, physics-based, plant-based, swarm intelligence, and human-based algorithms [5]. The evolutionary algorithms mimic the principle of evolution and include genetic algorithm [6], differential evolution [7,8], genetic programming [9], biogeography-based optimisation [10], evolution strategies [11], etc. The physics-based algorithms are derived from real-world physical processes and comprise of simulated annealing [12], Henry’s gas solubility optimisation [13], atom search optimisation [14], black hole algorithm [15], colliding bodies optimisation [16] and many others. The plant-based metaheuristics mimic the behaviour of the plants and include flower pollination algorithm [17], and invasive weed optimisation [18]. The swarm optimisation algorithms are inspired from collective bodies or entities in nature and include particle swarm optimisation [19], ant colony optimisation [20], tunicate swarm algorithm [21], manta ray foraging optimization algorithm [22], sailfish optimizer [23], barnacles mating optimizer algorithm [24], firefly algorithm [25], artificial bee colony algorithm [26], dolphin echolocation [27], salp swarm optimisation algorithm [28] and cuckoo search [29]. The human-based algorithms include but are not limited to queuing search algorithm [30] and kidney-inspired algorithm [31].
Population-based metaheuristics start with a population of candidate solutions that are either selected at random or introduced using a custom script. The algorithms then perform global exploration and local exploitation and are able to provide acceptable good solutions for complex problems within reasonable computation time. They are easy to implement and have the capability to bypass the local optima [32]. In recent years, a number of novel algorithms have been proposed in the literature, such as African Vultures Optimisation Algorithm (AVOA) [33], Crystal Structure Algorithm (CryStAl) [34], Human-Behaviour Based Optimisation (HBBO) [35], Gradient-Based Optimiser (GBO) [36], Gorilla Troops Optimiser (GTO) [37], Runge–Kutta optimiser (RUN) [38], Social Network Search (SNS) [39], and Sparrow Search Algorithm (SSA) [40]. However, a comparison of these new-generation metaheuristic optimisation algorithms on their applicability and performance on various engineering design problems has not been evaluated. Therefore, in this paper, the above-mentioned eight new-generation population-based metaheuristic optimisation algorithms are compared and evaluated on five different classical mechanical machinery component design problems such as the tension/compression spring design, crane hook design, reduction gear design, pressure vessel design and hydrostatic thrust bearing design. To the best of the authors’ knowledge, this is the first benchmark research study that quantitatively and qualitatively evaluates the selected eight new-generation metaheuristic optimisation algorithms by applying them in various mechanical machinery component design problems. This article contributes to knowledge by providing a comprehensive comparison and discussion of the applicability of the selected algorithms.
The rest of the paper is organised as follows. Section 2 briefly explains the meta-heuristics optimisation algorithms used in this study. Section 3 describes the selected mechanical component design problems, and the results of the computer experiments. Section 4 discusses the findings of the paper, and provides an outlook for the future work. Finally, Section 5 concludes the paper.
2. Optimisation Algorithms
In this section, the selected optimisation algorithms are briefly explained. All technical details associated with these algorithms can be found in the foundation references.
2.1. African Vultures Optimisation Algorithm (AVOA)
The AVOA, proposed by [33], simulates the foraging and navigation behaviours of the African vultures. The algorithm comprises of an initial population of vultures and the first and second best solutions are considered. The algorithm comprises of four phases: (i) determining the best vulture in a group, (ii) rate of starvation of vultures, (iii) exploration and (iv) exploitation. The rate of starvation of vultures helps determine whether they are in exploration phase or exploitation phase. Two different strategies for exploration are used and the strategy is chosen with a parameter ‘’. For the exploitation phase, two different strategies of rotating flight and siege-fight strategies are employed depending on the parameter ‘’. The AVOA is found to perform faster than other algorithms due to lower computational complexity. From our understanding, we believe that this algorithm has not been applied elsewhere with the exception of the foundation paper.
2.2. Crystal Structure Algorithm (CryStAl)
The CryStAl proposed by [34] was inspired by the principles of the formation of crystals in nature. It is a parameter-free novel metaheuristic algorithm in which the balance between the exploration and exploitation phases is not controlled by parameters. During initialisation of the algorithm, the solution candidates are considered to be crystals and those which occupy the corners are called the main crystals. The new positions are determined by four kinds of position updates: (i) simple cubicle, (ii) cubicle with mean crystals, (iii) cubical with best crystals, and (iv) cubicle with best and mean crystals. The exclusion of the parameter to tune the exploration and exploitation phases can help overcome the problems associated with local optima entrapment and convergence. The authors believe that this algorithm has not been applied in any research problem apart from the foundation paper.
2.3. Human Behavior-Based Optimisation Algorithm (HBBO)
The HBBO algorithm was developed based on the behaviour of human beings and has five main steps: (i) initialisation, (ii) education, (iii) consultation, (iv) field changing probability, and (v) finalisation [35]. In the initialisation step, the individual human beings who form the population are spread across different fields. Each field has an expert individual who has the best function value and the members of the field educate and improve themselves to move around the best individual. The individuals of the various fields who are not the expert individuals meet with a random advisor from the society to change the solution variables. On finding a better solution, the existing solution is replaced with the better one. The individuals are capable of changing the field based on a probability value. The finalisation step involves calculating the fitness function and checking the stopping criteria. The algorithm is tested against benchmark problems to understand its reliability, result accuracy and convergence speed. The HBBO has recently been used in variety of research domain including manufacturing cell design [41] and cryptography [42], etc.
2.4. Gradient-Based Optimiser (GBO)
The GBO, initially developed by [36], is a population-based meta-heuristic algorithm. It uses two operators, the Gradient Search Rule (GSR) and Local Escaping Operator (LEO) to explore the search space. The gradient search rule, which is based on Newton’s method, promotes the exploration capability of the GBO. It comprises of a direction of movement term to enable movement towards promising solutions. The gradient-based optimisation benefits from two search methods that enable the exploration and exploitation, respectively. The local escaping operator allows the algorithm to escape from local optimum using six different values of the solution candidates. It comprises of adaptive parameters that allows the smooth transition from exploration to exploitation. The GBO has been used in a variety of applications, such as economic load dispatch problem [43], parameter extraction in photovoltaic models [44] and feature selection [45], etc.
2.5. Gorilla Troops Optimiser (GTO)
The gorilla troops optimiser is a novel meta-heuristic that was inspired by the social behaviour of gorillas and was proposed by [37]. The exploration phase of the algorithm comprises of three different mechanisms: (i) migration to unknown place, (ii) movement to other gorillas which balances the exploration and exploitation, and (iii) migration to a known location. The silverback gorilla represents the best solution and the candidate solutions move towards this best solution. Follow the silverback gorilla and competition for female gorillas are two mechanisms employed for the exploitation phase. The search history, convergence behavior, the average fitness of the population, and the trajectory of the first gorilla are considered for evaluation of the algorithm. From our understanding, we believe that this algorithm has not been applied elsewhere with the exception of the foundation paper.
2.6. Runge–Kutta Optimisation (RUN)
The Runge–Kutta optimizer, proposed by [38], was derived from the ideas of the Runge–Kutta method which is used in the field of mathematics to solve ordinary differential equations. It is a population-based optimisation algorithm which employs the Enhanced Solution Quality (ESQ) to avoid getting trapped in local optima and improve the solution quality. The exploration and exploitation phases are improved with the help of the scale factor. The convergence rate of the algorithm is improved by providing the choice of choosing the new solution based on its quality and thereby increasing the efficiency of global search while ensuring good quality local search. The balance between the exploration and the exploitation phases is provided with the help of two random variables. The performance of the RUN algorithm was qualitatively assessed by three metrics: (i) search history, (ii) trajectory graph, and (iii) convergence curve and the algorithm was compared with benchmark problems to assess its ability to explore and exploit the design space efficiently. From a review of literature, it is understood that this algorithm is yet to be applied on other design problems apart from those mentioned in the original work.
2.7. Social Network Search (SNS)
The SNS is a novel meta-heuristic algorithm that was inspired by the behaviour of users across the social network platforms [39]. Four different moods are considered in the algorithm: (i) imitation, (ii) conversation, (iii) disputation, and (v) innovation. The search agents are the social media users and one of the four moods will be chosen randomly for each user. Depending on the considered mood, the opinions of the user will change. The decision to share a view will depend on whether it is better than the current one. The algorithm comprises of three levels: initialisation, increasing popularity and termination. It is also important to note that the SNS algorithm uses non-parametric statistical methods. The algorithm is novel and it is believed that it has not been applied to any problems apart from the work done in the foundation paper.
2.8. Sparrow Search Algorithm (SSA)
The group wisdom, foraging and anti-predation behaviour of sparrows are considered for the novel swarm intelligence algorithm known as sparrow search algorithm [40]. The population is divided into producers and scroungers. The producers have two modes of search depending on whether a predator is nearby or not. The scroungers monitor the producers and compete with them for food. If a sparrow is at the edge of the group, it constantly tries to get a better position to avoid the predators. On the other hand, if a sparrow is at the centre of the group, it moves closer towards its neighbours. SSA is seen to have good performance in diverse search spaces. The SSA has been recently employed in various applications, including but not limited to: optimal model parameters identification of the Proton Exchange Membrane Fuel Cell (PEMFC) [46], optimal brain tumor diagnosis [47], pulmonary nodule detection [48], carbon price forecasting [49] and 3D route planning for UAVs [50].
3. Computer Experiments
In this section, the performance of the above-mentioned metaheuristic optimisation algorithms is analysed by performing the five design problems, namely: tension/compression spring design, crane hook design, reduction gear design, pressure vessel design and hydrostatic thrust bearing design. The mathematical formulation of each design study can be found in the Appendix A. All computer operations were performed in MATLAB environment, where the computer was configured with Intel(R) Core (TM) i7-11850H CPU @2.60 GHz and 32 GB RAM.
3.1. Parameter Settings
In the computer experiments, an exterior penalty function is deployed to deal with design constraints. The parameter settings of each optimisation algorithms were selected based on the values provided by the foundation papers that were referenced in the Section 2; they are provided in Table 1. The maximum iteration number and the population size for each case study are selected based on the complexity of the problem and are given in Table 2 along with the number of function evaluations (FEs). In order to analyse the robustness of the selected optimisation algorithms, each case is repeated 100 times and the best, mean, worst, standard deviation, convergence history, and the mean computation times are recorded. The best results obtained in each case are presented in bold in Tables 4, 6, 8, 10 and 12.

Table 1.
Specific parameter settings of used algorithms.

Table 2.
The number of function evaluations , maximum iteration number and the population size () for each design optimisation problem.
3.2. Tension/Compression Spring Design
The tension/compression spring design problem depicted in Figure 1 is a continuous constrained problem. The objective of this design problem is to minimise the weight of the coil spring subjected to the constraints of shear stress, surge frequency, and minimum deflection. The problem contains three design variables namely: the number of active coils (), the diameter of the winding (), and diameter of the wire ().
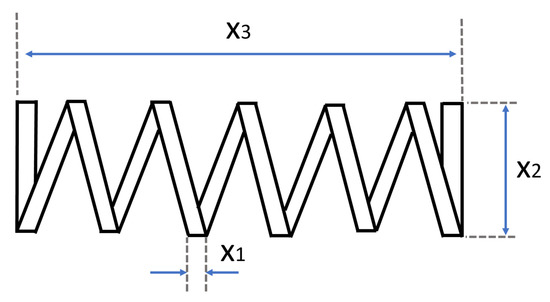
Figure 1.
Schematic view of the tension/compression spring problem.
The best solutions for each algorithm are presented in Table 3 and the results of the simulation are provided in Table 4 for the tension/compression spring design problem. From Figure 2, it can be seen that for the best replication run, all the algorithms are able to converge to the global optimum approximately around 70 iterations. From Table 4, SNS performs well for across all the criteria, however, AVOA performs better in terms of the computation time. SNS is the most robust with a value of 5.3324 × , followed by GBO, CryStAl, GTO, HBBO, AVOA, RUN and SSA. The performance of the GBO is similar to that of the SNS; this could be due to the use of a Local Escaping Operator (LEO) which significantly changes the position of a solution. Although the HBBO has the best result across the replication runs, the standard deviation indicates that it is not able to consistently arrive at the global optimum for this particular design problem.

Table 3.
Best optimum solution of each algorithm for the tension/compression spring design optimisation problem.

Table 4.
Statistical findings of the bench-marked algorithms for the tension/compression spring design problem.
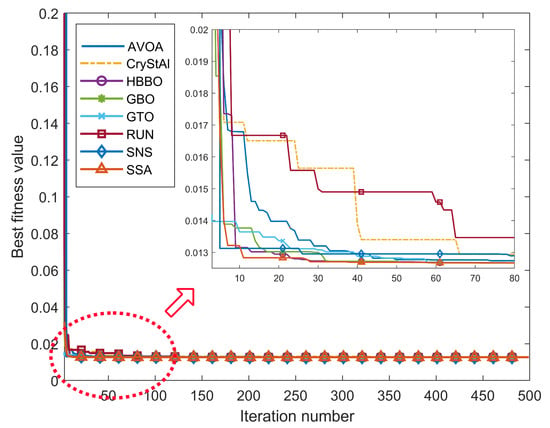
Figure 2.
Best run convergence curves of each meta-heuristic algorithms (out of 100 repetitions) in the tension/compression spring design optimisation problem.
3.3. Crane Hook Design
The crane hook is a rectangular wire ring that is clipped and bent to give the final hook shape. The aim of the crane hook design optimisation is to minimise the volume of the hook subjected to the constraints of yield stress and geometric feasibility. There are three design parameters, namely: the outer radius of the hook (), the inner radius of the hook (), and width of the hook (). Schematic view of the crane hook is given in Figure 3.
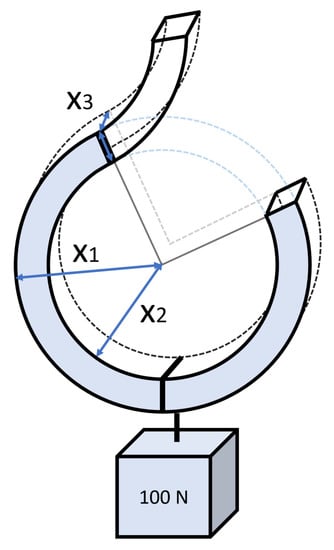
Figure 3.
Schematic view of the crane hook design problem.
Table 5 and Table 6 present the best solution and the statistical simulation results obtained by the algorithms for the crane hook design problem. Figure 4 indicates that for the best replication run, all the algorithms are able to converge to the global optimum approximately around 500 iterations. From Table 6, the SNS is the most robust and is followed by GBO, SSA, GTO, RUN, AVOA, CryStAl and HBBO. GBO has the best mean across the 100 replication runs. The mean value for the SNS algorithm is very close to the GBO with only a difference of 2.9792 × . It can also be seen that AVOA has the best performance in terms of the computation time followed by SNS and SSA.

Table 5.
Best optimum solution of each algorithm for the crane hook design optimisation problem.

Table 6.
Statistical findings of the bench-marked algorithms for the crane hook design problem.

Figure 4.
Best run convergence curves of each meta-heuristic algorithms (out of 100 repetitions) in the crane hook design optimisation problem.
3.4. Reduction Gear Design
The reduction gear design problem is one of the widely used engineering design optimisation benchmark problems and is initially conceptualised by [51]. Figure 5 depicts the schematic view of the reduction gear problem. The objective of this design problem is to find an acceptable near-optimal set of variables, i.e., that can provide a minimum total weight under eleven geometric constraints. The problem has seven design variables, namely: () the face width, () the module of the teeth, () the number of teeth on the pinion, () the length of the first shaft between bearings, () the length of the second shaft between bearings, () the diameter of the first shaft and () the diameter of the second shaft. The constraints are (i) the limits of the bending stress on the gear teeth, (ii) surface stress, (iii) transverse deflections of both shafts and (iv) stress in both shafts. Please note that the third variable in this design problem is an integer while the remaining are continuous variables.
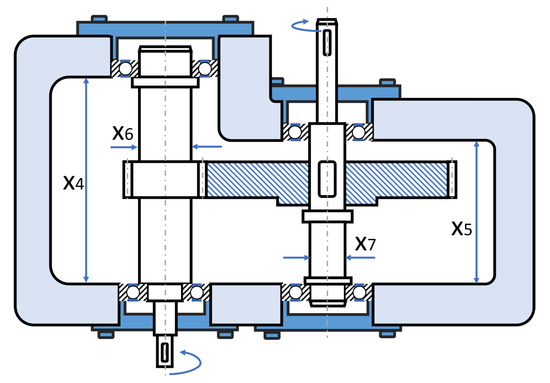
Figure 5.
Schematic view of the reduction gear design problem.
For the reduction gear design, the algorithms slightly different ‘best’ solutions and they are presented in Table 7; Table 8 presents the best solution and simulation results obtained by the eight algorithms. From Figure 6, for the best replication run, all algorithms are capable of converging to the global optimum around 600 iterations. From Table 8, GBO, GTO, SNS and SSA have good performance across all evaluation criteria. GBO is the most robust with a value of 3.635 × followed by SNS, SSA, RUN, AVOA, GTO, HBBO and CryStAl. AVOA has the best performance in terms of the computation time and it is closely followed by SSA and SNS. GTO does find the global optimum with a relatively fast computation time, however, the standard deviation indicates that it is not as robust as a few other algorithms with the considered parameter values for the reduction gear design problem.

Table 7.
Best optimum solution of each algorithm for the reduction gear design optimisation problem.

Table 8.
Statistical findings of the bench-marked algorithms for the reduction gear design problem.
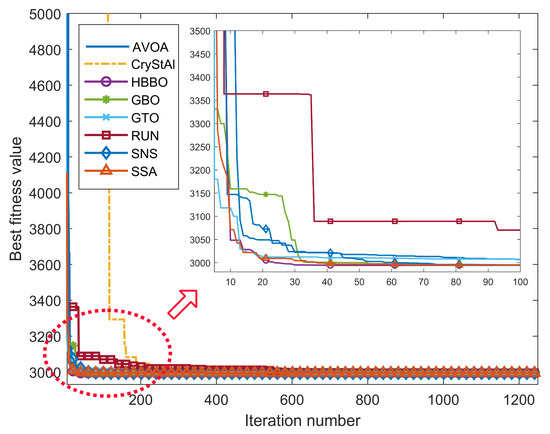
Figure 6.
Best run convergence curves of each meta-heuristic algorithms (out of 100 repetitions) in the reduction gear design optimisation problem.
3.5. Cylindrical Pressure Vessel Design
The pressure vessel design problem is initially conceptualised by [52] which is one of the most used design optimisation benchmarks. The objective of this problem is to minimise the total manufacturing cost of the cylindrical pressure vessel which is a combination of material, forming and welding costs. The pressure vessel has covered at the split ends while the head part has a hemispherical shape. Figure 7 shows the schematic representation of the problem. This problem has four variables, namely: thickness of the shell (), thickness of the head (), inner radius () and the length of the vessel (). The problem has four inequalities.
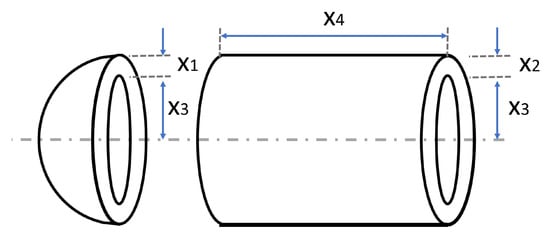
Figure 7.
Schematic view of the cylindrical pressure vessel design problem.
Table 9 and Table 10 present the best solution for each algorithm and the statistical simulation results obtained by the algorithms for the pressure vessel design problem, respectively. From Figure 8, for the best replication run, it can be seen that all the algorithms are able to converge to the global optimum approximately around 200 iterations. In particular, as seen from Table 10, the GBO algorithm is the most robust with a standard deviation value of 68.523 for the pressure vessel design problem and has good scores across all the evaluation criteria. It is followed by the SNS, CryStAl, HBBO, GTO, SSA, AVOA and RUN. The GBO algorithm has a local escaping operator that prevents entrapment at the local optima; this could the reason for the robustness of the algorithm. In terms of the time to converge, SSA, HBBO and AVOA converge earlier, approximately around 80 iterations. In terms of the mean computation time across the replications, similar to the previous design problems (see Table 6 and Table 8), AVOA has the best performance. It can be seen that SNS also has a similar performance in terms of the computation time in addition to having a low standard deviation. In SNS, clear a distinction between the exploration and exploitation phases is not provided; the balance between the two phases is not controlled using parameters. Instead, the candidate solutions of the population are randomly subjected to one of the four strategies. Therefore, the exploration and exploitation phases happen at random depending on the chosen strategy which avoids the entrapment at local optima; this could be the reason why the SNS has a slightly higher computation time despite its robust performance.

Table 9.
Best optimum solution of each algorithm for the cylindrical pressure vessel design optimisation problem.

Table 10.
Statistical findings of the bench-marked algorithms for the cylindrical pressure vessel design problem.
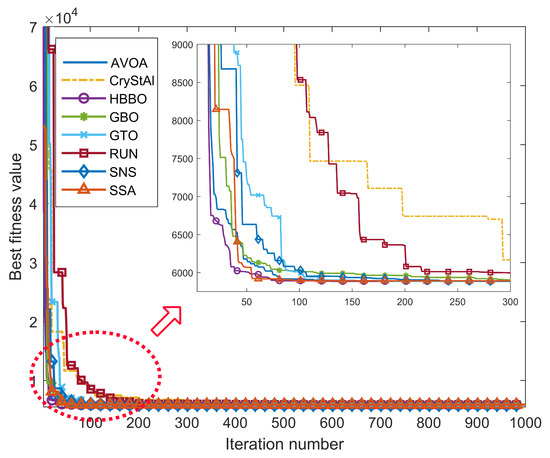
Figure 8.
Best run convergence curves of each meta-heuristic algorithms (out of 100 repetitions) in the pressure vessel design optimisation problem.
3.6. Hydrostatic Thrust Bearing Design
In this design optimisation problem defined by [53], four design variables are considered as follows: bearing step radius (), recess radius (), viscosity () and flow rate (). The objective of the optimisation is to minimise the power loss during the operation of the hydrostatic plain bearing. Figure 9 shows the schematic representation of the problem. The seven nonlinear constraints of weight capacity , inlet oil pressure , oil temperature rise , oil film thickness , step radius , exit loss significance and contact pressure are also considered (please see Appendix A).
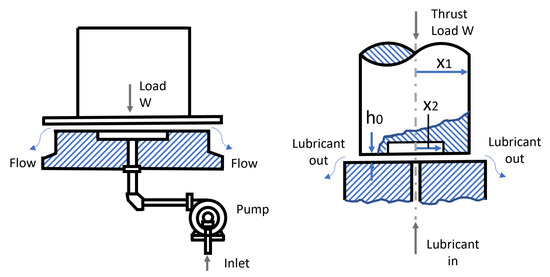
Figure 9.
Schematic view of the hydrostatic thrust bearing design problem.
Table 11 and Table 12 present the best solution for each algorithm and the statistical simulation results obtained by the algorithms for the hydrostatic thrust bearing design problem, respectively. From Figure 10, for the best replication run, it can be seen that all the algorithms are able to converge to the global optimum approximately around 600 iterations. In particular, as seen from Table 12, the SNS algorithm is the most robust with a standard deviation value of 16.597 for the hydrostatic thrust bearing design problem and has good scores across all the evaluation criteria. It is followed by the CryStAl, GBO, GTO, RUN, AVOA, HBBO, and SSA. In terms of the time to converge, AVOA converges earlier, approximately around 500 iterations. It can be seen that SNS also has a similar performance in terms of the computation time in addition to having a low standard deviation. Although SNS is the most robust, the best value of the objective function is relatively higher than the values found by the GBO, GTO, and RUN algorithms.

Table 11.
Best optimum solution of each algorithm for the Hydrostatic thrust bearing design optimisation problem.

Table 12.
Statistical findings of the bench-marked algorithms for the Hydrostatic thrust bearing design problem.
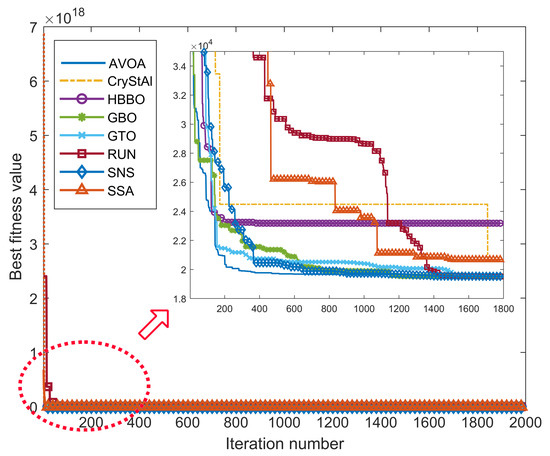
Figure 10.
Best run convergence curves of each meta-heuristic algorithms (out of 100 repetitions) in the hydrostatic thrust bearing design optimisation problem.
4. Discussion
4.1. Observations from the Benchmark Study
This research study applies eight different metaheuristic algorithms on five mechanical component design problems to provide an insight into the efficiency and robustness of the algorithms for design optimisation. Following a detailed analysis of the various algorithms, it was understood that the performance of the algorithms vary across the different applications.
Across the selected mechanical design problems, it can be seen that SNS and GBO have very good results across the evaluation criteria. SNS performs very well in the tension/compression spring design, crane hook design, reduction gear design and hydrostatic thrust bearing design problems. For the pressure vessel design problem, however, GBO performs better than SNS. In the SNS algorithm, the candidate solutions represent the users and their moods are selected at random. The choice of mood greatly impacts the exploration and exploitation behaviour of the algorithm. Although it means that the algorithm might not have a strong sense of direction towards the global optimum, the computation time is still fast. The prevention of local optima entrapment facilitated by the structure of the algorithm might ensure that the algorithm is consistently able to find the global optimum across the 100 replications.
The GBO algorithm includes an escaping mechanism that introduces randomness to prevent entrapment in local optima. This suggests that the algorithm is able to provide a reasonably good performance and is comparable to SNS across all the design problems. SSA shows good performance overall and has good computation time and comparable robustness; in particular, it performs very well for the reduction gear design problem. However, in the hydrostatic thrust bearing design problem, SSA performed significantly poorly. This might be owing to the incompatibility of the selected algorithm parameters for this design case, which is the most complicated of the five case studies. It can also be seen that the HBBO, GTO, RUN and SSA algorithms also perform well and are able to find the near-optimal solutions in a majority of the problems. GTO also has good computation time across the design problems and this can be attributed to the movement to a known location and other gorillas during the exploration phase and the directional focus and best position update provided by the following of the silverback gorilla and competition for females, respectively, during the exploitation phase. The CryStal algorithm, on the other hand, performed consistently across all specified mechanical component design problems. However, it was observed that it performed badly in terms of convergence to the global optimum when compared to other algorithms. Because it is intended to be a simple and easy-to-use algorithm with no internal or external parameters to tune, a modified version of CryStal with improved exploration/exploration balance could be a feasible optimisation technique, particularly in mechanical component design optimisation problems.
The AVOA has consistently good performance across all five design optimisation problems in terms of computation time. As explained previously, the reason behind the fast computational speed of AVOA can be attributed to the two different exploration strategies which are chosen based on the satiation of the vulture, the best vulture’s position and the boundaries of the problem. Additionally, the exploitation phase employs four different strategies for local searches. AVOA is able to reach the near-optimal solutions fairly quickly; the performance across the replications, however, suggests that the AVOA is less robust than SNS and GBO. Therefore, for design problems which are time-sensitive and the variables need not be selected to a very high level degree of precision, AVOA is a good choice due to its fast computation time.
4.2. A Comparison with Traditional Optimisation Techniques
A further benchmark of the algorithms with two widely used meta-heuristics, GA and PSO was done and provided in Figure 11, such that the readers can appreciate and compare the performance of the novel algorithms with the classical widely used optimisation algorithms. The parameters of the GA are selected as follows: distribution index for crossover , distribution index for mutation , crossover probability , mutation probability . On the other hand, PSO parameters are selected as follows: inertia weight , inertia weight damping ratio , personal learning coefficient and global learning coefficient . The population size and maximum number of iterations are same as highlighted in Table 2.
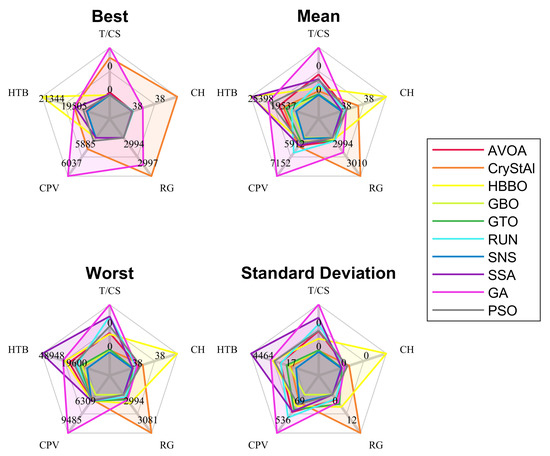
Figure 11.
A spider plot comparison of eight recent and two widely used (i.e., GA and PSO) population-based metaheuristic optimisation techniques was undertaken on the five component design problems. Please remember that smaller values indicate better performance. The annotations are as follows: T/CS, tension/compression spring; CH, crane hook; RG, reduction gear; CPV, cylindrical pressure vessel; HTB, hydrostatic thrust bearing.
From Figure 11, there are four spider plots; the best scores for each algorithm acquired over 100 replications show if the algorithm is capable of discovering solutions that are near to the global optimum. A lower mean value of the observations across replications indicates the consistency of the algorithms under consideration. The radar chart displaying standard deviation can be used to evaluate the algorithm’s repeatability. The obtained results for GA and PSO for each design problem are given in Table 13. Figure 11 shows that, with the exception of the crane hook design problem, which is the simplest case, most recent optimisation algorithms outperform GA. PSO, on the other hand, performs well across all of the specified design optimisation problems. However, the majority of the selected recent optimisation methods outperformed PSO in terms of both accuracy and repeatability. Comparing with recent metaheuristics, as seen in Figure 11’s mean and standard deviation plots, PSO produced slightly poor results, excluding the reduction gear design optimisation problem. In terms of finding the global optimum, nearly all recent metaheuristic algorithms outperformed PSO and GA in various design challenges, with the exceptions of HBBO and CryStal. Nearly all of the selected recent metaheuristics outperform GA and PSO in terms of overall performance over 100 repetitions. This explicitly showcases that the superiority of new-generation population-based meta-heuristics over the vanilla versions of traditional GA and PSO optimisation algorithms.

Table 13.
Statistical findings of the GA and PSO for the selected design problems.
4.3. Limitations and Future Work
The presented work considers the eight recent population-based meta-heuristic algorithms with the optimisation parameters selected from the foundation parameters. Performing a detailed sensitivity analysis to identify the best parameters for each algorithm was not done. A more detailed analysis will be done as part of the future work. Additionally, an extensive comparison of the performance of the algorithms on other design problems and engineering applications will also be done. From the presented comparison, it can be concluded that each algorithm has its strengths and weaknesses, and there is no distinct meta-heuristic that outperforms all others. Therefore, there is the possibility of combining the best of different algorithms to provide hybrid-approaches that will help overcome any issues with the these meta-heuristic approaches. Although the various tables and figures presented in this paper may be useful to practitioners when selecting an algorithm, it may be more beneficial to select a suitable one using a formal multi-criteria decision-making (MCDM) approach that allows quantitative comparison of the various optimisation algorithms based on their applicability on a specific type of engineering design problem. As a consequence, future study will evaluate various algorithms using MCDM techniques in order to provide a fair analysis that might be used to improve algorithm selection.
5. Conclusions
The complex mechanical design problems involve multiple objectives with a combination of variables along with the consideration of a multitude of constraints and boundary conditions. Therefore, the problem of identifying optimum design for a specific application involves rigorous exploration of the design space which might not be feasible within a practical time-frame. For this purpose, metaheuristics can be applied to such problems to search the design space with a guiding heuristic that ensures a near-optimal acceptable solution within a reasonable time-frame. In this research study, eight novel metaheuristic algorithms, namely AVOA, RUN, HBBO, CryStAl, GBO, GTO, SNS, and SSA, are applied on five different mechanical component design problems and their ability to choose acceptable solutions across multiple runs of optimisation, the robustness of the algorithms and computation time are calculated. From the performance comparison, it was understood that the SNS, GBO and GTO algorithms perform well across all mechanical component design problems, and AVOA algorithm has good performance in terms of computation time. In machinery component design optimisation problems, the SNS method is shown to be the best suited choice in terms of solution quality, robustness, and convergence speed with given parameter settings.
Author Contributions
Conceptualization, B.A. and M.K.C.; methodology, B.A. and M.K.C.; software, B.A. and M.K.C.; validation, B.A. and M.K.C.; formal analysis, B.A. and M.K.C.; investigation, B.A. and M.K.C.; writing—original draft preparation, B.A. and M.K.C.; writing—review and editing, B.A. and M.K.C.; visualization, B.A. and M.K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The corresponding author states that the results presented in this paper can be reproduced by the implementation details provided in the foundation papers. Researchers or interested parties are welcome to contact the corresponding author for further explanation, who may also provide the MATLAB codes upon request.
Conflicts of Interest
The authors reported no potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AVOA | African Vultures Optimisation Algorithm |
| CryStAl | Cyrstal Structure Algorithm |
| FE | Function Evolution |
| HBBO | Human-Behaviour Based Optimisation |
| GA | Genetic Algorithm |
| GBO | Gradient Based Optimiser |
| GP | Genetic Programming |
| GTO | Gorilla Troops Optimiser |
| NP | The population size |
| PSO | Particle Swarm Optimisation |
| RUN | RUNge Kutta Optimiser |
| SNS | Social Network Search |
| SSA | Sparrow Search Algorithm |
Appendix A
Appendix A.1. Tension/Compression Spring Design Problem
The objective function of the tension/compression spring design problem can be written as follows:
Subject to: , , and .
Variable ranges: , , and .
Appendix A.2. Crane Hook Design Problem
The objective function of the crane hook design problem can be written as follows:
Subject to: , and .
where , , , , , , , , , , and .
Variable ranges: , and .
Appendix A.3. Reduction Gear Design Problem
The objective function of the reduction gear design problem can be written as follows:
Subject to: , , , , , , , , , and .
Variable ranges: , , , , , and .
Appendix A.4. Pressure Vessel Design Problem
The objective function of the pressure vessel design problem can be written as follows:
Subject to: , , and .
Variable ranges: , , and .
Appendix A.5. Hydrostatic Thrust Bearing Design Problem
The objective function of the Hydrostatic thrust bearing problem (for SAE 20 type grade oil) can be written as follows:
Subject to: , , , , , and
where , , , and .
Variable ranges: , , and .
References
- Ahmad, M.; Ahmad, B.; Harrison, R.; Alkan, B.; Vera, D.; Meredith, J.; Bindel, A. A framework for automatically realizing assembly sequence changes in a virtual manufacturing environment. Procedia CIRP 2016, 50, 129–134. [Google Scholar] [CrossRef][Green Version]
- Alkan, B.; Vera, D.; Ahmad, B.; Harrison, R. A method to assess assembly complexity of industrial products in early design phase. IEEE Access 2017, 6, 989–999. [Google Scholar] [CrossRef]
- Wang, L.; Ng, A.H.; Deb, K. Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Gandomi, A.H.; Yang, X.S.; Talatahari, S.; Alavi, A.H. Metaheuristic algorithms in modeling and optimization. In Metaheuristic Applications in Structures and Infrastructures; Elsevier: London, UK, 2013. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996; pp. 519–523. [Google Scholar]
- Koza, J.R.; Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolutionsstrategien. In Simulationsmethoden in der Medizin und Biologie; Springer: Berlin/Heidelberg, Germany, 1978; pp. 83–114. [Google Scholar]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1987; pp. 7–15. [Google Scholar]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V.R. Colliding bodies optimization: A novel meta-heuristic method. Comput. Struct. 2014, 139, 18–27. [Google Scholar] [CrossRef]
- Yang, X.S. Flower pollination algorithm for global optimization. In Proceedings of the International Conference on Unconventional Computing and Natural Computation, Orléans, France, 3–7 September 2012; pp. 240–249. [Google Scholar]
- Mehrabian, A.R.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95. Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 11–13 December 1991; Volume 142, pp. 134–142. [Google Scholar]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Shadravan, S.; Naji, H.; Bardsiri, V.K. The Sailfish Optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 80, 20–34. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H. Barnacles mating optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103330. [Google Scholar] [CrossRef]
- Yang, X.S. Engineering Optimization: An Introduction with Metaheuristic Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Kaveh, A.; Farhoudi, N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013, 59, 53–70. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Zhang, J.; Xiao, M.; Gao, L.; Pan, Q. Queuing search algorithm: A novel metaheuristic algorithm for solving engineering optimization problems. Appl. Math. Model. 2018, 63, 464–490. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Alvankarian, J.; Abdullah, S. Kidney-inspired algorithm for optimization problems. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 358–369. [Google Scholar] [CrossRef]
- Kaveh, A. Advances in Metaheuristic Algorithms for Optimal Design of Structures; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Talatahari, S.; Azizi, M.; Tolouei, M.; Talatahari, B.; Sareh, P. Crystal Structure Algorithm (CryStAl): A Metaheuristic Optimization Method. IEEE Access 2021, 9, 71244–71261. [Google Scholar] [CrossRef]
- Ahmadi, S.A. Human behavior-based optimization: A novel metaheuristic approach to solve complex optimization problems. Neural Comput. Appl. 2017, 28, 233–244. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Talatahari, S.; Bayzidi, H.; Saraee, M. Social Network Search for Global Optimization. IEEE Access 2021, 9, 92815–92863. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Soto, R.; Crawford, B.; González, F.; Vega, E.; Castro, C.; Paredes, F. Solving the manufacturing cell design problem using human behavior-based algorithm supported by autonomous search. IEEE Access 2019, 7, 132228–132239. [Google Scholar] [CrossRef]
- Soto, R.; Crawford, B.; González, F.; Olivares, R. Human behaviour based optimization supported with self-organizing maps for solving the S-box design Problem. IEEE Access 2021, 9, 84605–84618. [Google Scholar] [CrossRef]
- Deb, S.; Abdelminaam, D.S.; Said, M.; Houssein, E.H. Recent methodology-based gradient-based optimizer for economic load dispatch problem. IEEE Access 2021, 9, 44322–44338. [Google Scholar] [CrossRef]
- Ismaeel, A.A.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Jiang, Y.; Luo, Q.; Wei, Y.; Abualigah, L.; Zhou, Y. An efficient binary Gradient-based optimizer for feature selection. Math. Biosci. Eng. MBE 2021, 18, 3813–3854. [Google Scholar] [CrossRef]
- Zhu, Y.; Yousefi, N. Optimal parameter identification of PEMFC stacks using Adaptive Sparrow Search Algorithm. Int. J. Hydrog. Energy 2021, 46, 9541–9552. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Z.; Wu, L.; Badami, B. An optimal brain tumor detection by convolutional neural network and Enhanced Sparrow Search Algorithm. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2021, 235, 459–469. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, K.; He, Z.; Yin, Z.; Wang, S. Semi-Supervised Ensemble Classifier with Improved Sparrow Search Algorithm and Its Application in Pulmonary Nodule Detection. Math. Probl. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, D. Carbon Price Forecasting Based on Improved CEEMDAN and Extreme Learning Machine Optimized by Sparrow Search Algorithm. Sustainability 2021, 13, 4896. [Google Scholar] [CrossRef]
- Liu, G.; Shu, C.; Liang, Z.; Peng, B.; Cheng, L. A modified sparrow search algorithm with application in 3d route planning for UAV. Sensors 2021, 21, 1224. [Google Scholar] [CrossRef]
- Golinski, J. Optimal synthesis problems solved by means of nonlinear programming and random methods. J. Mech. 1970, 5, 287–309. [Google Scholar] [CrossRef]
- Kannan, B.; Kramer, S.N. An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J. Mech. Des. 1994, 116, 405–411. [Google Scholar] [CrossRef]
- Siddall, J.N. Optimal Engineering Design: Principles and Applications; CRC Press: Boca Raton, FL, USA, 1982. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).