Approximation of Non-Linear Rotor Dynamic Resonance Behavior of Vertically Aligned Hydro-Units Guided by Tilting-Pad Bearings
Abstract
:1. Introduction
2. Materials and Methods
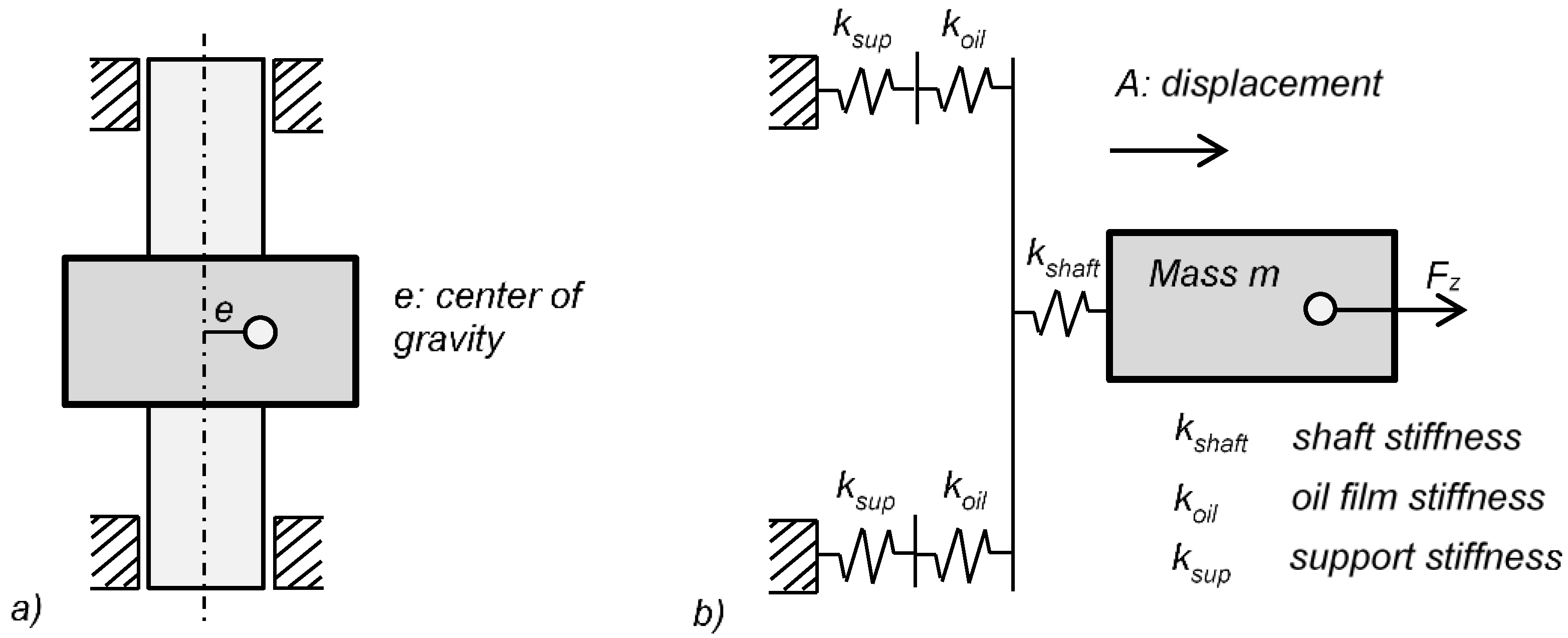
2.1. Rotor Modelling
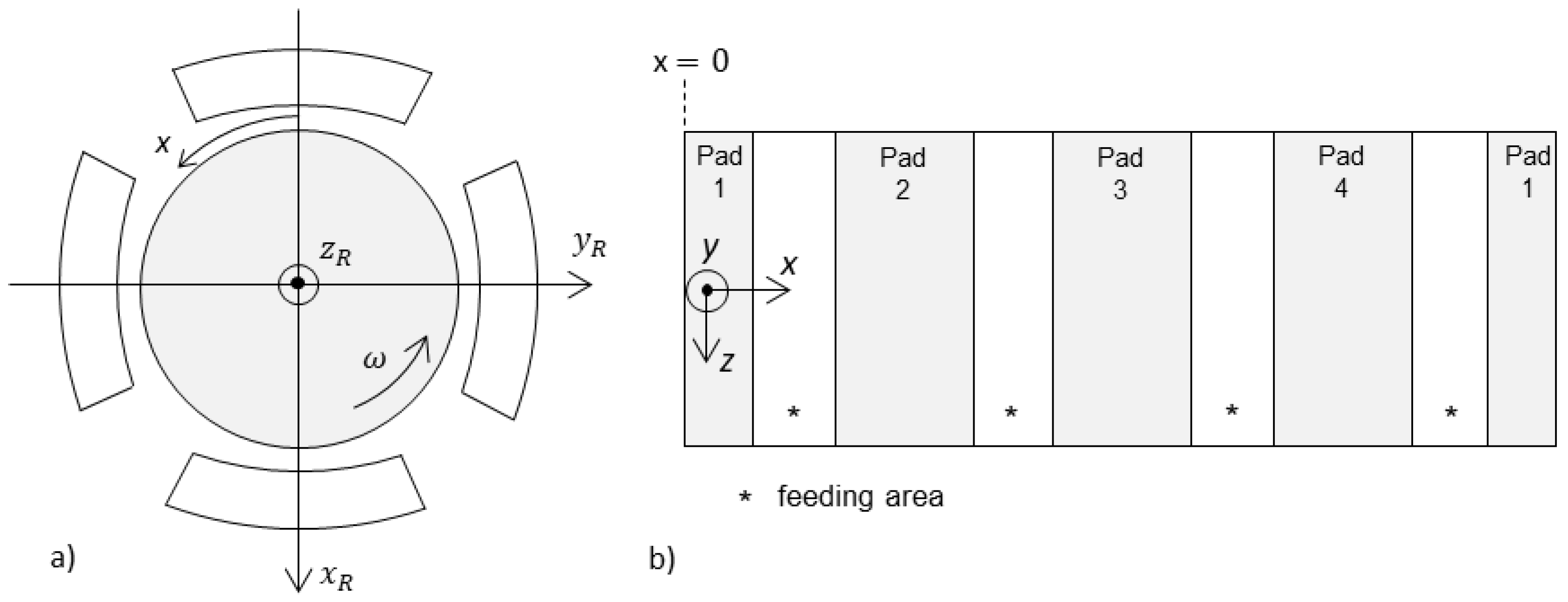
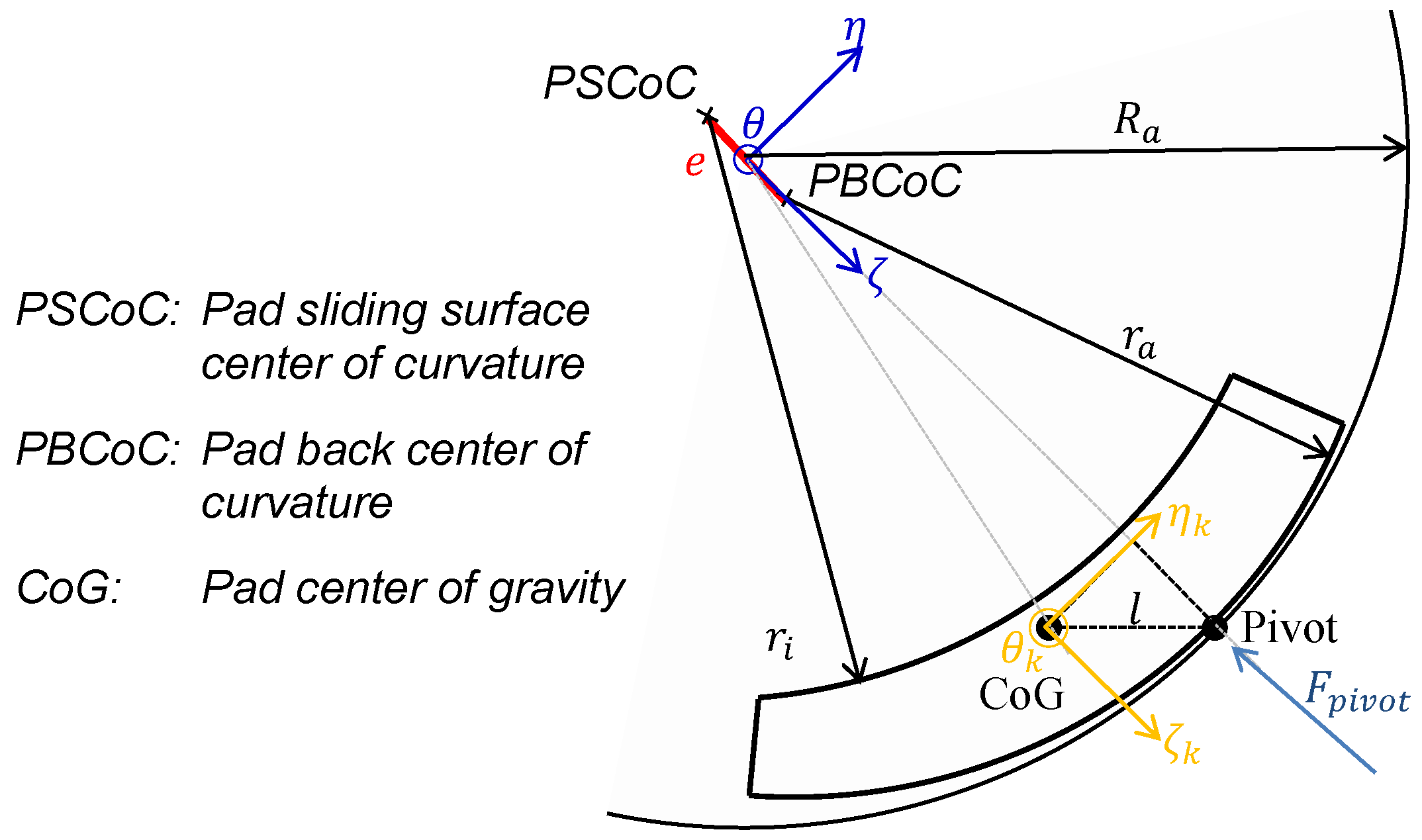
2.2. Non-Linear Bearing Modelling (NLIN)
2.3. Linear Bearing Modelling (LIN)
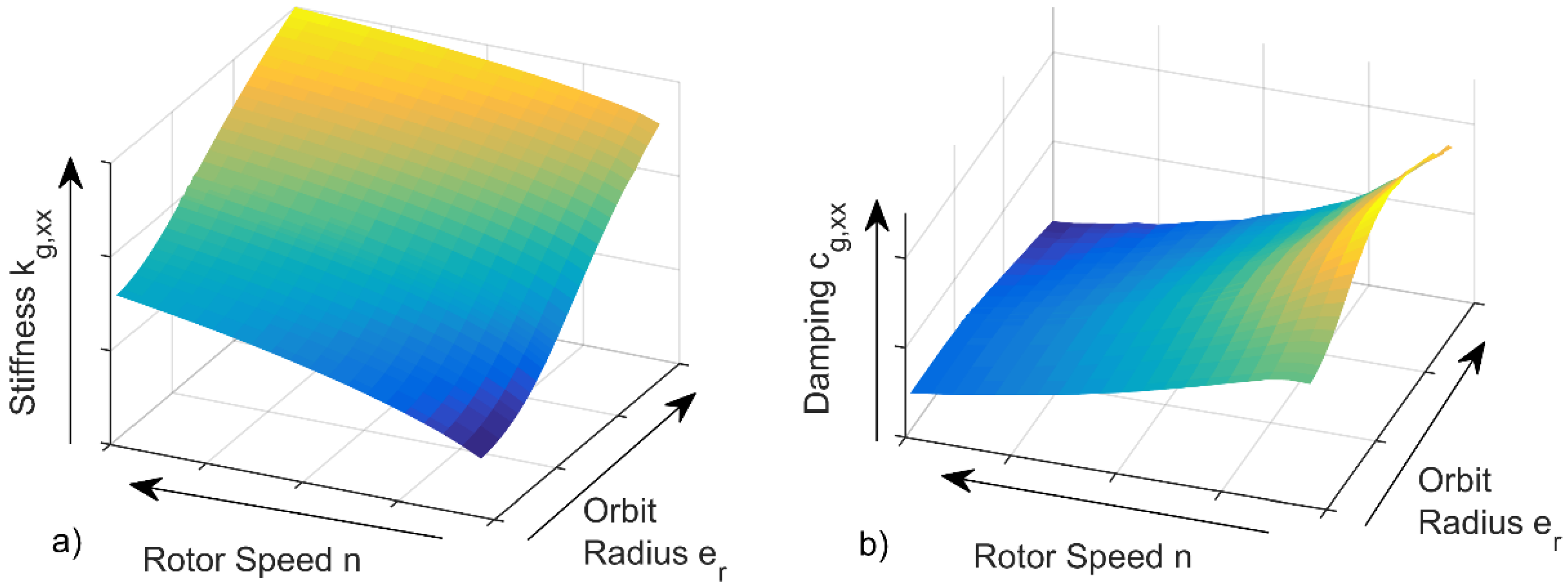
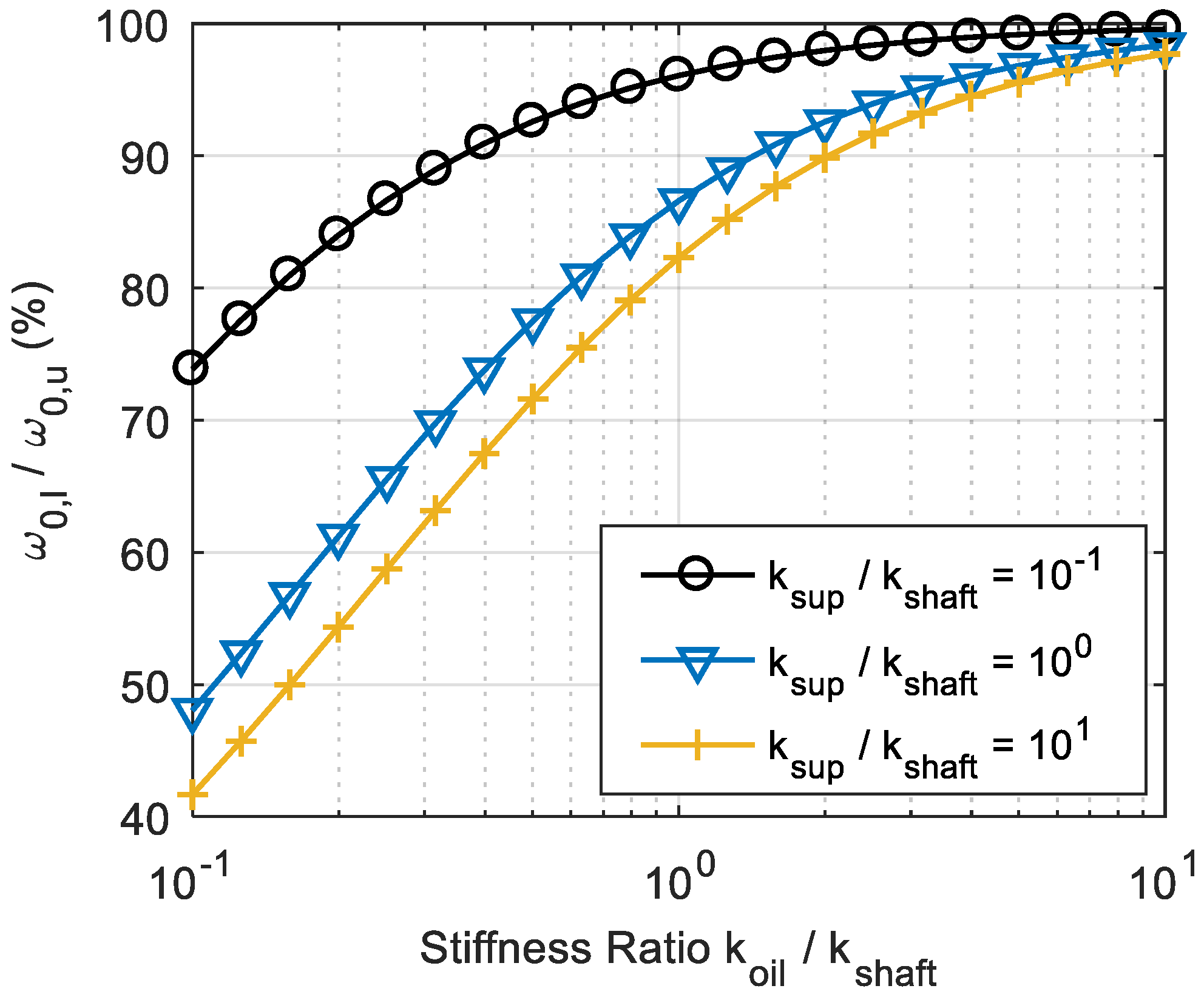
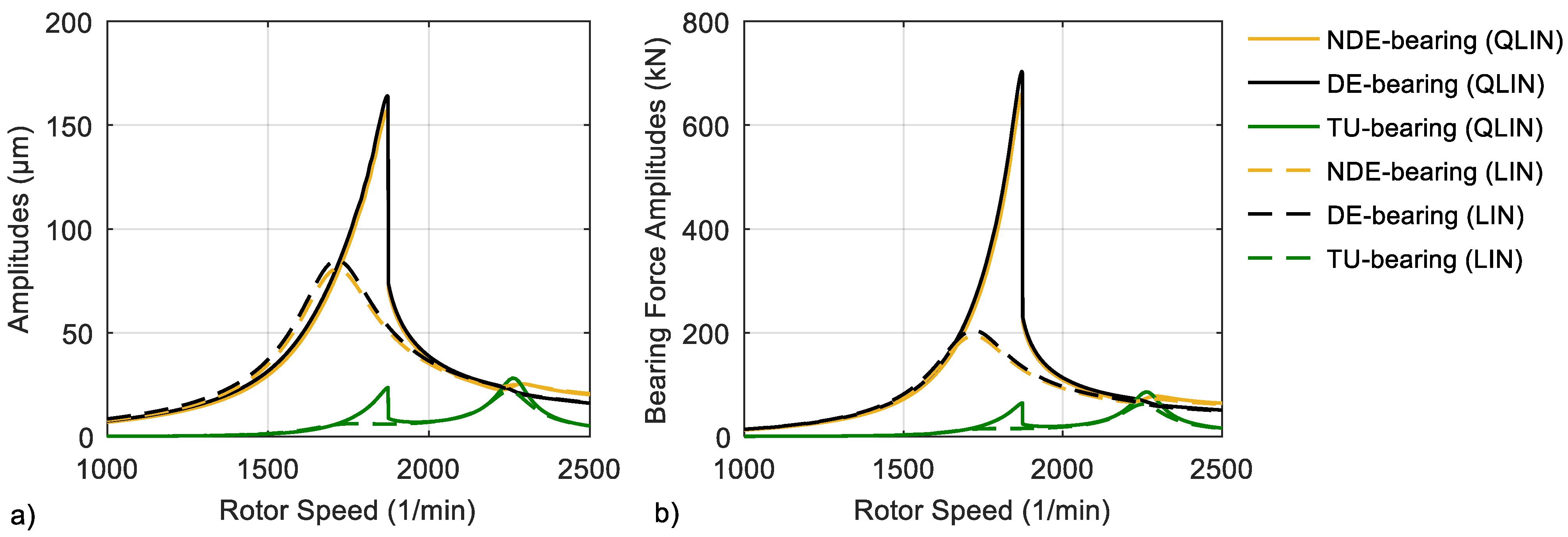
2.4. Approximation of Non-Linear Bearing Characteristics (QLIN)
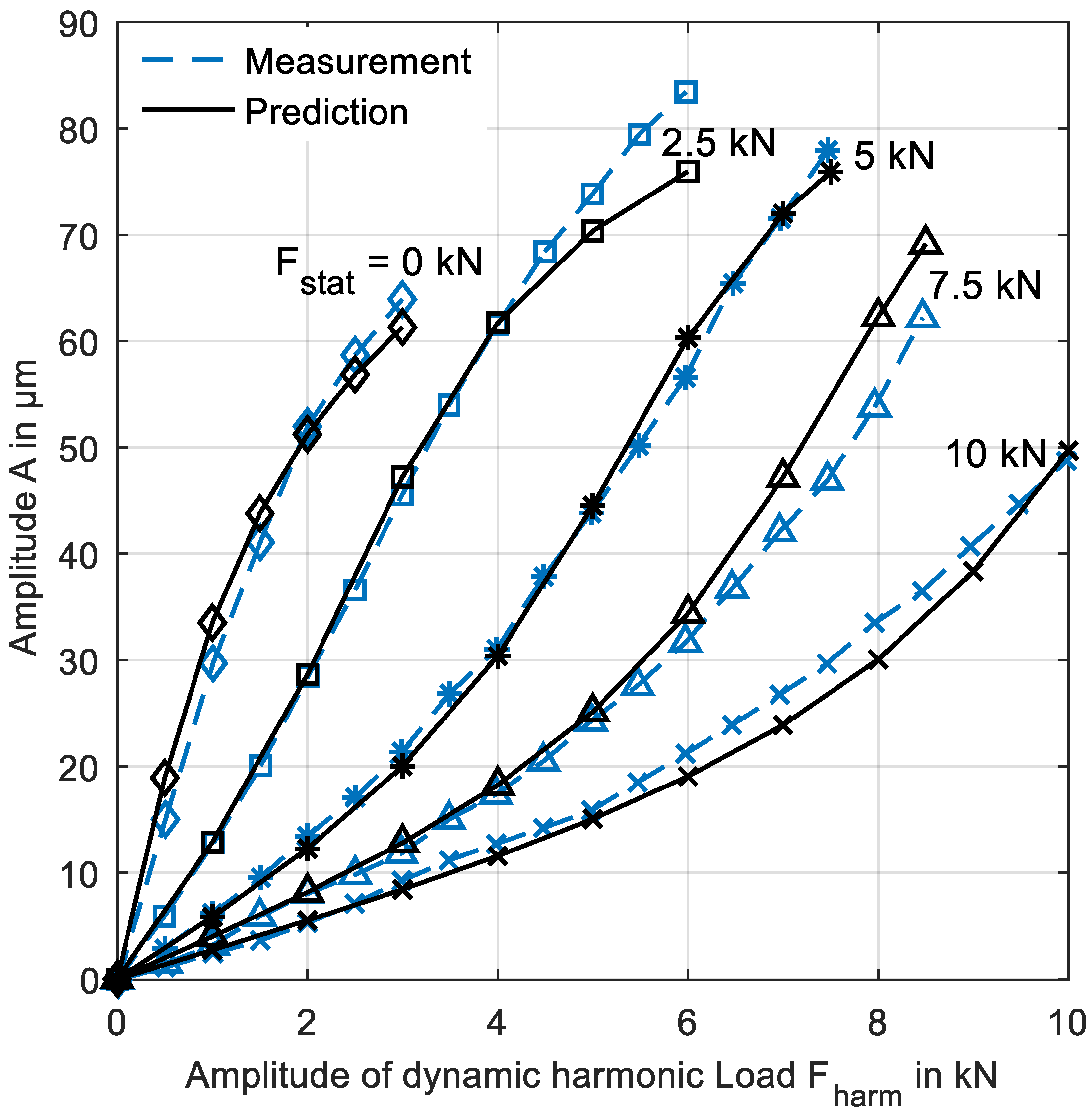
2.5. Validation of the Non-Linear Bearing Model (NLIN)
3. Results
3.1. Preliminary Considerations
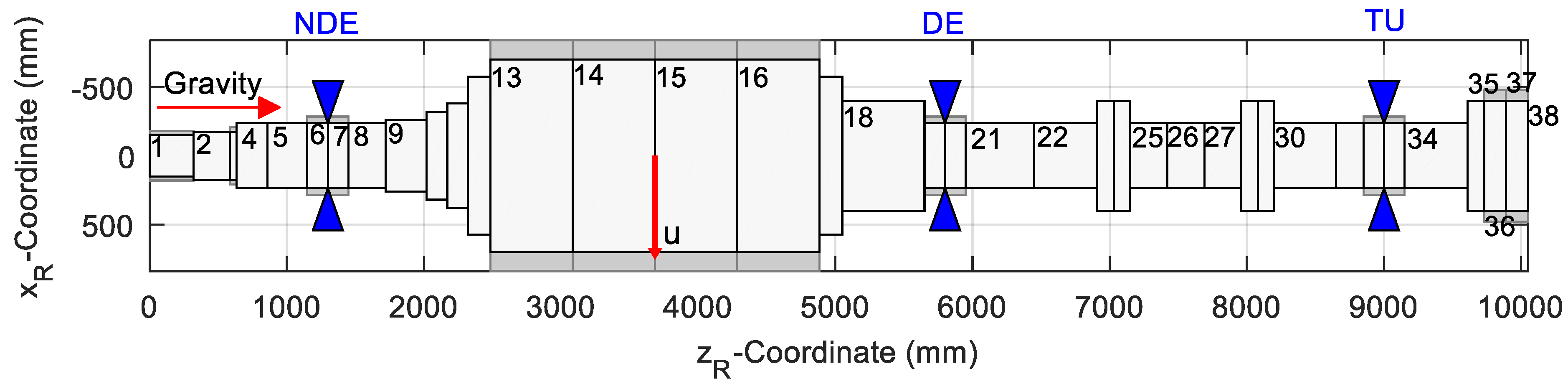
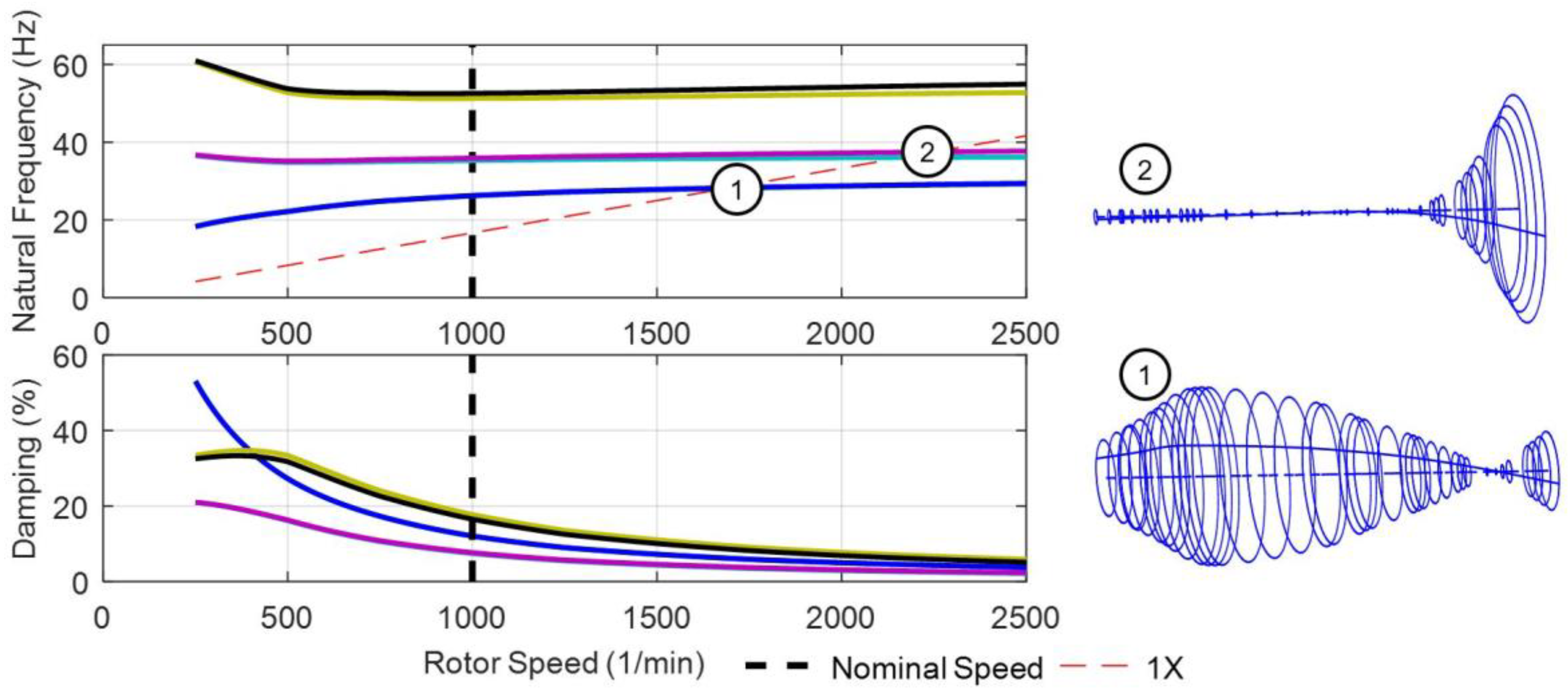
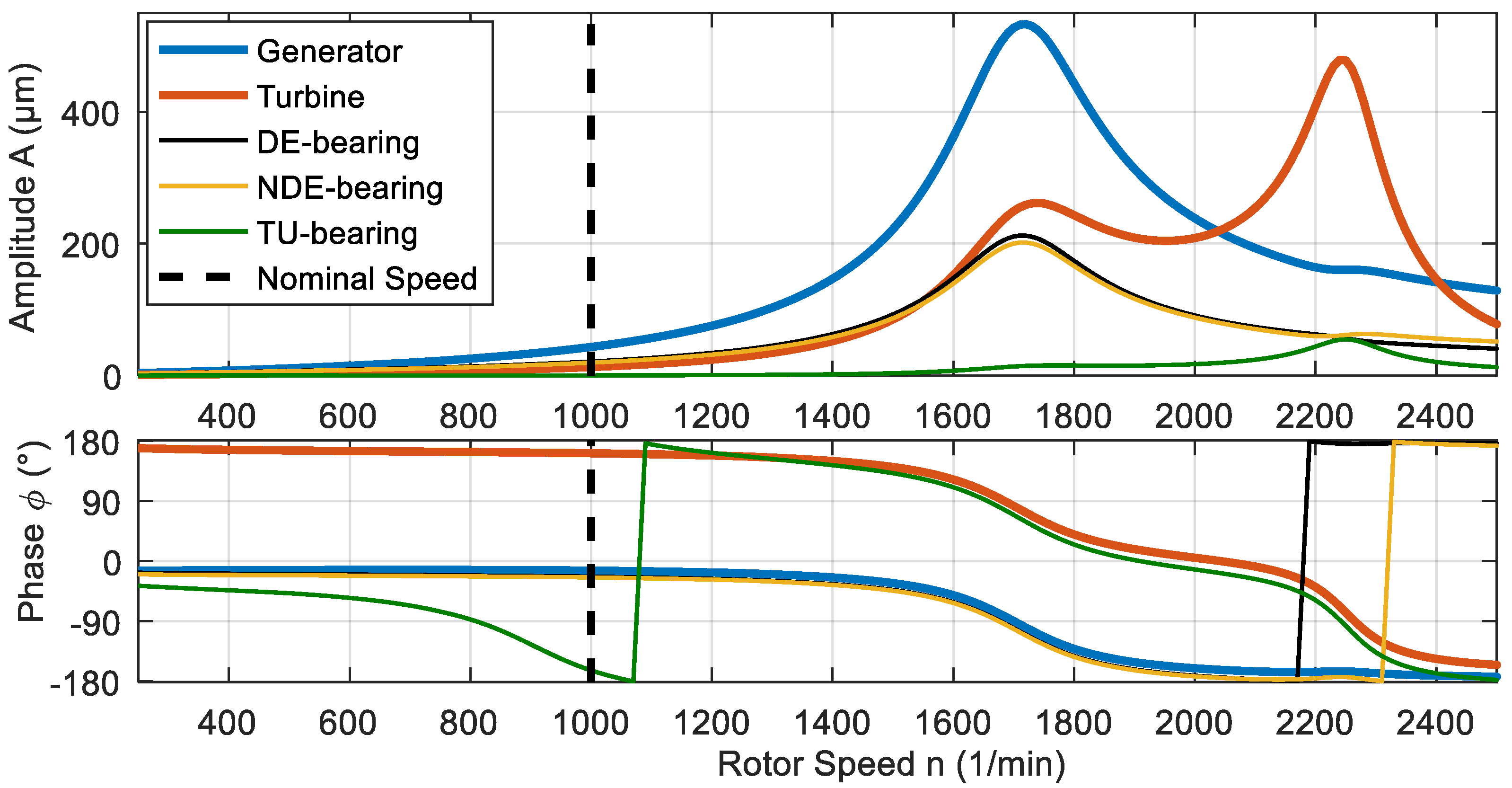
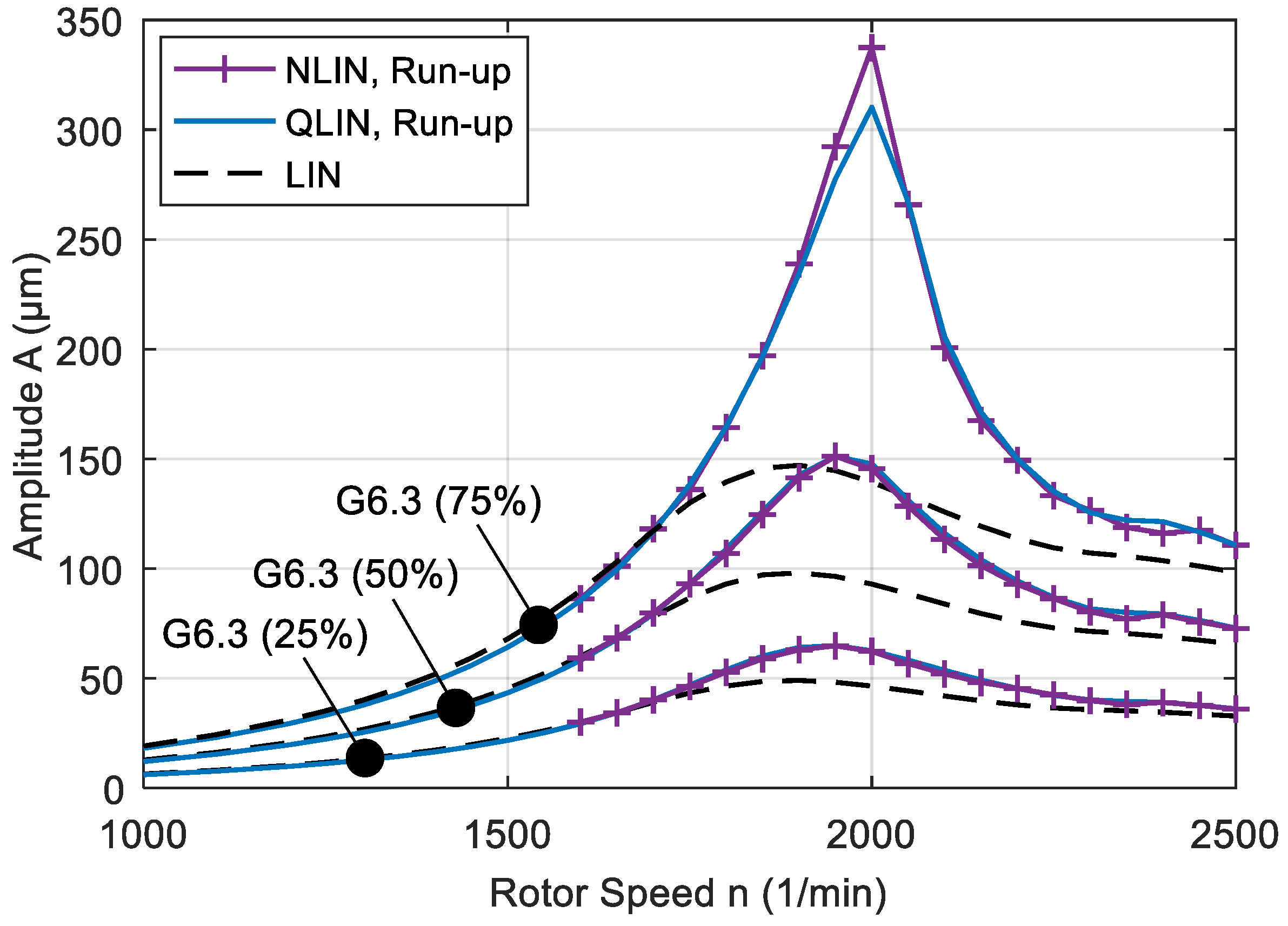
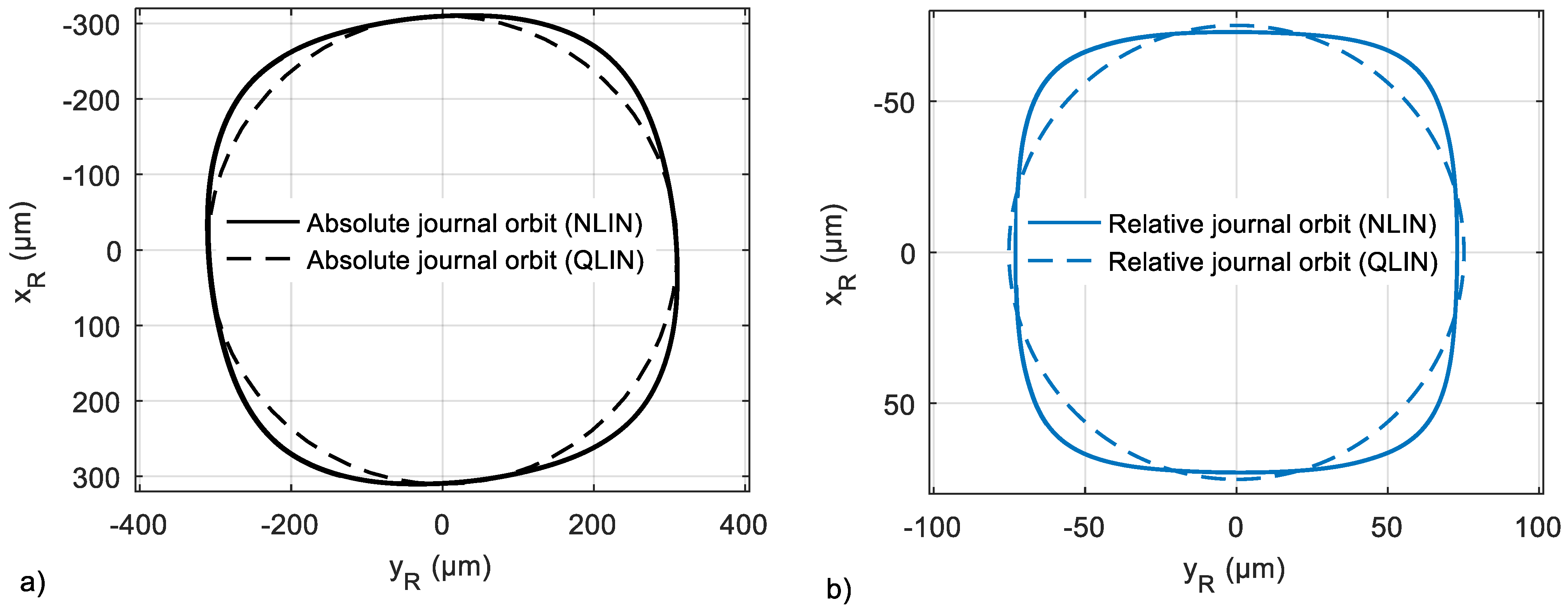
3.2. Investigation of a Hydro Plant Rotor
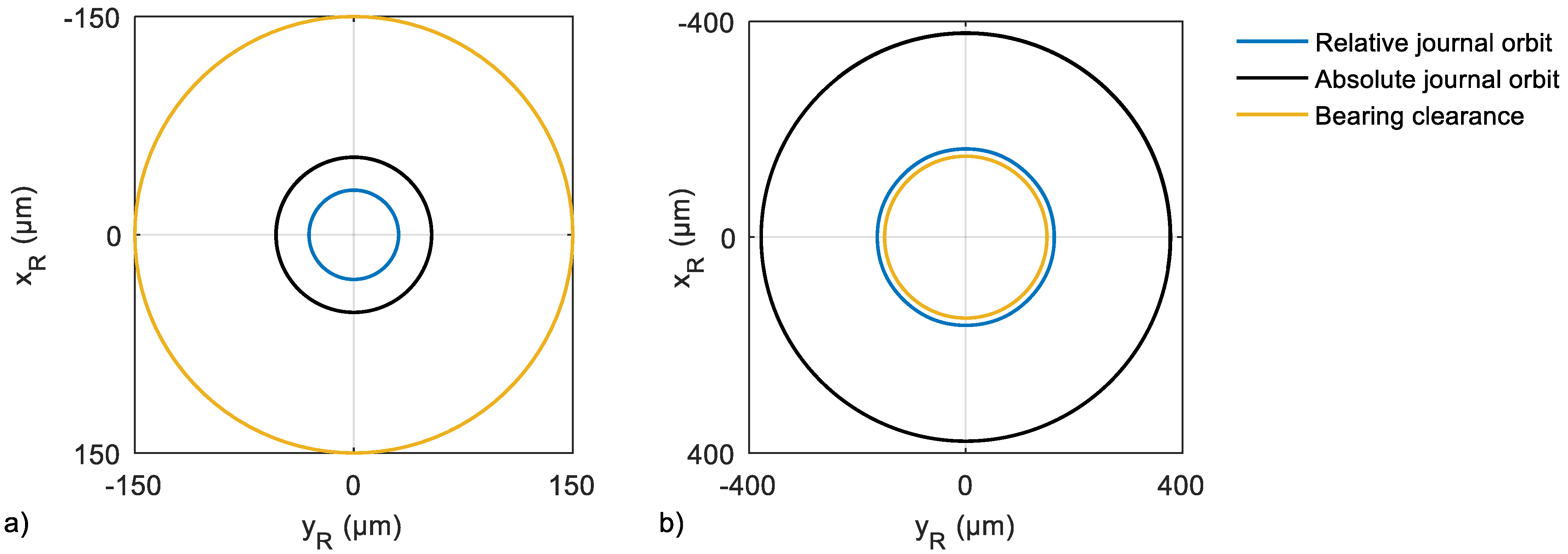
3.3. Application to Non-Cricular Orbits
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | orbit radius |
| A | system matrix of the state space model |
| B | input matrix of the state space model |
| c | damping coefficient |
| C | damping matrix |
| journal orbit radius and tangential orbit velocity | |
| film forces in radial and tangential direction | |
| F0, F1, F2 | viscosity factors |
| film forces/pivot forces in and direction | |
| F | force vector |
| F* | modified force vector for non-linear analysis |
| G | gyroscopic matrix |
| h | local gap height |
| mass moment of inertia of a single pad | |
| stiffness coefficient | |
| oil film stiffness | |
| bearing stiffness | |
| pivot stiffness | |
| resulting stiffness | |
| shaft stiffness | |
| support stiffness | |
| , | factors for turbulent flow approximation |
| K | stiffness matrix |
| distance from pivot to center of gravity of the pad in and direction | |
| m | mass |
| film moment with regard to the center of gravity of the pad | |
| M | mass matrix |
| n | rotor speed |
| number of pads | |
| p | film pressure |
| q | state vector of the state space model |
| t | time |
| T | rotation matrix |
| unbalance | |
| U | sliding velocity of the shaft |
| x | displacement vector |
| x, y, z | coordinates of the lubricant gap solution domain |
| xR, yR, zR | coordinates of the rotor system |
| coordinates for the transversal motion of the pads | |
| coordinates for the tilting motion of the pads | |
| dynamic viscosity of the lubricant | |
| local fill factor | |
| angular rotor speed | |
| angular eigenfrequency | |
| angular pivot position of the i-th pad |
Abbreviations
| DE | drive end |
| NDE | non-drive end |
| TU | turbine end |
| LIN | linear analysis |
| NLIN | non-linear analysis |
| QLIN | quasi-linear analysis |
| G6.3 | balance quality G6.3 grade |
References
- Merker, H.-J. Über den Nichtlinearen Einfluß von Gleitlagern auf die Schwingungen von Rotoren. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, 1981. [Google Scholar]
- Ma, L.-F.; Zhang, X.-Z. Numerical Simulation of Nonlinear Oil-Film Forces of Tilting-Pad Guide Bearing in Large Hydro-unit. Int. J. Rotating Mach. 2000, 6, 345–353. [Google Scholar] [CrossRef]
- Gadangi, R.K.; Palazzolo, A.B.; Kim, J. Transient Analysis of Plain and Tilt Pad Journal Bearings Including Fluid Film Temperature Effects. J. Tribol. 1996, 118, 423–430. [Google Scholar] [CrossRef]
- Abu-Mahfouz, I.; Adams, M.L. Numerical Study of Some Nonlinear Dynamics of a Rotor Supported on a Three-Pad Tilting Pad Journal Bearing (TPJB). J. Vib. Acoust. 2005, 127, 262–272. [Google Scholar] [CrossRef]
- Shi, Z.; Jin, Y.; Yuan, X. Influence of pivot design on nonlinear dynamic analysis of vertical and horizontal rotors in tilting pad journal bearings. Tribol. Int. 2019, 140, 105859. [Google Scholar] [CrossRef]
- Springer, H. Nichtlineare Schwingungen Schwerer Rotoren mit Vertikaler Welle und Kippsegmentradiallagern. Forsch. Im Ing. A 1979, 45, 119–132. [Google Scholar] [CrossRef]
- Nässelqvist, M.; Gustavsson, R.; Aidanpää, J.-O. Experimental and Numerical Simulation of Unbalance Response in Vertical Test Rig with Tilting-Pad Bearings. Int. J. Rotating Mach. 2014, 10, 309767. [Google Scholar] [CrossRef]
- Cha, M.; Glavatskih, S. Nonlinear dynamic behaviour of vertical and horizontal rotors in compliant liner tilting pad journal bearings: Some design considerations. Tribol. Int. 2015, 82, 142–152. [Google Scholar] [CrossRef]
- Synnegård, E.; Gustavsson, R.; Aidanpää, J.-O. Forced response of a vertical rotor with tilting pad bearings. In Proceedings of the International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 10–15 April 2016. [Google Scholar]
- White, M.F.; Torbergsen, E.; Lumpkin, V.A. Rotordynamic analysis of a vertical pump with tilting-pad journal bearings. Wear 1997, 207, 128–136. [Google Scholar] [CrossRef]
- Shi, M.; Wang, D.; Zhang, J. Nonlinear dynamic analysis of a vertical rotor-bearing system. J. Mech. Sci. Technol. 2013, 27, 9–19. [Google Scholar] [CrossRef]
- Nelson, H.D. A Finite Rotating Shaft Element Using Timoshenko Beam Theory. J. Mech. Des. 1980, 102, 793–803. [Google Scholar] [CrossRef]
- Cowper, G.R. The Shear Coefficient in Timoshenko’s Beam Theory. J. Appl. Mech. 1966, 33, 335–340. [Google Scholar] [CrossRef]
- Hosea, M.E.; Shampine, L.F. Analysis and implementation of TR-BDF2. Appl. Numer. Math. 1996, 20, 21–37. [Google Scholar] [CrossRef]
- Vetter, D.; Hagemann, T.; Schwarze, H. Potentials and limitations of an extended approximation method for nonlinear dynamic journal and thrust bearing forces. In Proceedings of the ASME Turbo Expo, Oslo, Norway, 11–15 June 2018. [Google Scholar] [CrossRef]
- Dowson, D. A Generalized Reynolds Equation for Fluid Film Lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai sur la théorie des eaux courantes, Mémoires présentés par divers savants à I’Académie des Sciences de I’Institut de France. Sci. Math. Phys. Tome 1877, 23, 46–47. [Google Scholar]
- Constantinescu, V.N.; Pan, C.H.T.; Smalley, A.J.; Vohr, J.H. Lubrication Phenomena in a Film of Low Kinematic Viscosity. Rev. Roum. Sci. Techn.-Mèc. Appl. 1970, 15, 479–502. [Google Scholar]
- Elrod, H.G. A cavitation algorithm. J. Lubr. Technol. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- Mermertas, Ü. Nichtlinearer Einfluss von Radialgleitlagern auf die Dynamik Schnelllaufender Rotoren. Ph.D. Thesis, Clausthal University of Technology, Clausthal, Germany, 2007. [Google Scholar]
- Hagemann, T.; Kukla, S.; Schwarze, H. Measurement and prediction of the static operating conditions of a large turbine tilting-pad bearing under high circumferential speeds and heavy loads. In Proceedings of the ASME Turbo Expo, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar] [CrossRef]
- Hagemann, T.; Schwarze, H. A model for oil flow and fluid temperature inlet mixing in hydrodynamic journal bearings. J. Tribol. 2019, 141, 021701. [Google Scholar] [CrossRef]
- Lund, J.W. Spring and Damping Coefficients for the Tilting-Pad Journal Bearing. Asle Trans. 1964, 7, 342–352. [Google Scholar] [CrossRef]
- Lund, J.W.; Pedersen, L.B. The Influence of Pad Flexibility on the Dynamic Coefficients of a Tilting-Pad Journal Bearing. J. Tribol. 1987, 109, 65–70. [Google Scholar] [CrossRef]
- Rondon, D.; Benti, G.B.; Aidanpää, J.-O.; Gustavsson, R. Rotordynamic Characterization of Tilting-Pad Bearings with Eight Pads in Vertical Rotors. J. Energy Resour. Technol. 2022, 144, 012111. [Google Scholar] [CrossRef]
- Glienicke, J.; Eilers, M.; Gerdes, R. Nichtlineare Rotordynamik. In FVV-Report 437; FVV e.V.: Frankfurt am Main, Germany, 1993. [Google Scholar]




| Parameter | Value |
|---|---|
| Rotor speed, 1/min | 3600 |
| Number of pads | 5 |
| Inner diameter, mm | 120 |
| Length, mm | 52.8 |
| Pad thickness, mm | 17.8 |
| Pad preload | 0.643 |
| Pad arc length, ° | 50 |
| Pivot offset | 0.5 |
| Lubricant ISO VG | 32 |
| Supply temperature, °C | 50 |
| Parameter | Value |
|---|---|
| Total mass, t | 70.4 |
| Generator mass, t | 59.7 |
| Turbine mass, t | 5.5 |
| First critical speed, rigid bearings, 1/min | 3120 |
| Second critical speed, rigid bearings, 1/min | 3493 |
| Distance between bearings, m (NDE-DE/DE-TU) | 4.5/3.2 |
| Parameter | All Variants | Variant 1 | Variant 2 | Variant 3 | Variant 4 |
|---|---|---|---|---|---|
| Number of pads | 8 | ||||
| Radial clearance, µm | 150 | 200 | 250 | 150 | |
| Preload | 0.9167 | 0.8889 | 0.8611 | 0.9167 | |
| Diameter, mm | 800 | ||||
| Length, mm | 210 | ||||
| Angular span of pads, ° | 27 | ||||
| Bearing support stiffness, kN/µm, NDE | 2 | 2 | 2 | 4 | |
| Bearing support stiffness, kN/µm, DE | 3.33 | 3.33 | 3.33 | 6.66 | |
| Bearing support stiffness, kN/µm, TU | 1.25 | 1.25 | 1.25 | 2.5 | |
| Pivot support stiffness of each pad, kN/µm | 5 | ||||
| Pivot offset | 0.5 | ||||
| Lubricant | ISO VG 46 | ||||
| Supply temperature, °C | 45 |
| Parameter | Value |
|---|---|
| Number of pads | 4 |
| Radial clearance, µm | 150 |
| Preload | 0.9167 |
| Angular span of pads, ° | 55 |
| Pivot support stiffness of each pad, kN/µm | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vetter, D.; Hagemann, T.; Schubert, A.; Schwarze, H. Approximation of Non-Linear Rotor Dynamic Resonance Behavior of Vertically Aligned Hydro-Units Guided by Tilting-Pad Bearings. Machines 2021, 9, 334. https://doi.org/10.3390/machines9120334
Vetter D, Hagemann T, Schubert A, Schwarze H. Approximation of Non-Linear Rotor Dynamic Resonance Behavior of Vertically Aligned Hydro-Units Guided by Tilting-Pad Bearings. Machines. 2021; 9(12):334. https://doi.org/10.3390/machines9120334
Chicago/Turabian StyleVetter, Daniel, Thomas Hagemann, Andreas Schubert, and Hubert Schwarze. 2021. "Approximation of Non-Linear Rotor Dynamic Resonance Behavior of Vertically Aligned Hydro-Units Guided by Tilting-Pad Bearings" Machines 9, no. 12: 334. https://doi.org/10.3390/machines9120334
APA StyleVetter, D., Hagemann, T., Schubert, A., & Schwarze, H. (2021). Approximation of Non-Linear Rotor Dynamic Resonance Behavior of Vertically Aligned Hydro-Units Guided by Tilting-Pad Bearings. Machines, 9(12), 334. https://doi.org/10.3390/machines9120334








