Tilting Pad Journal Bearing Ball and Socket Pivots: Experimental Determination of Stiffness
Abstract
:1. Introduction
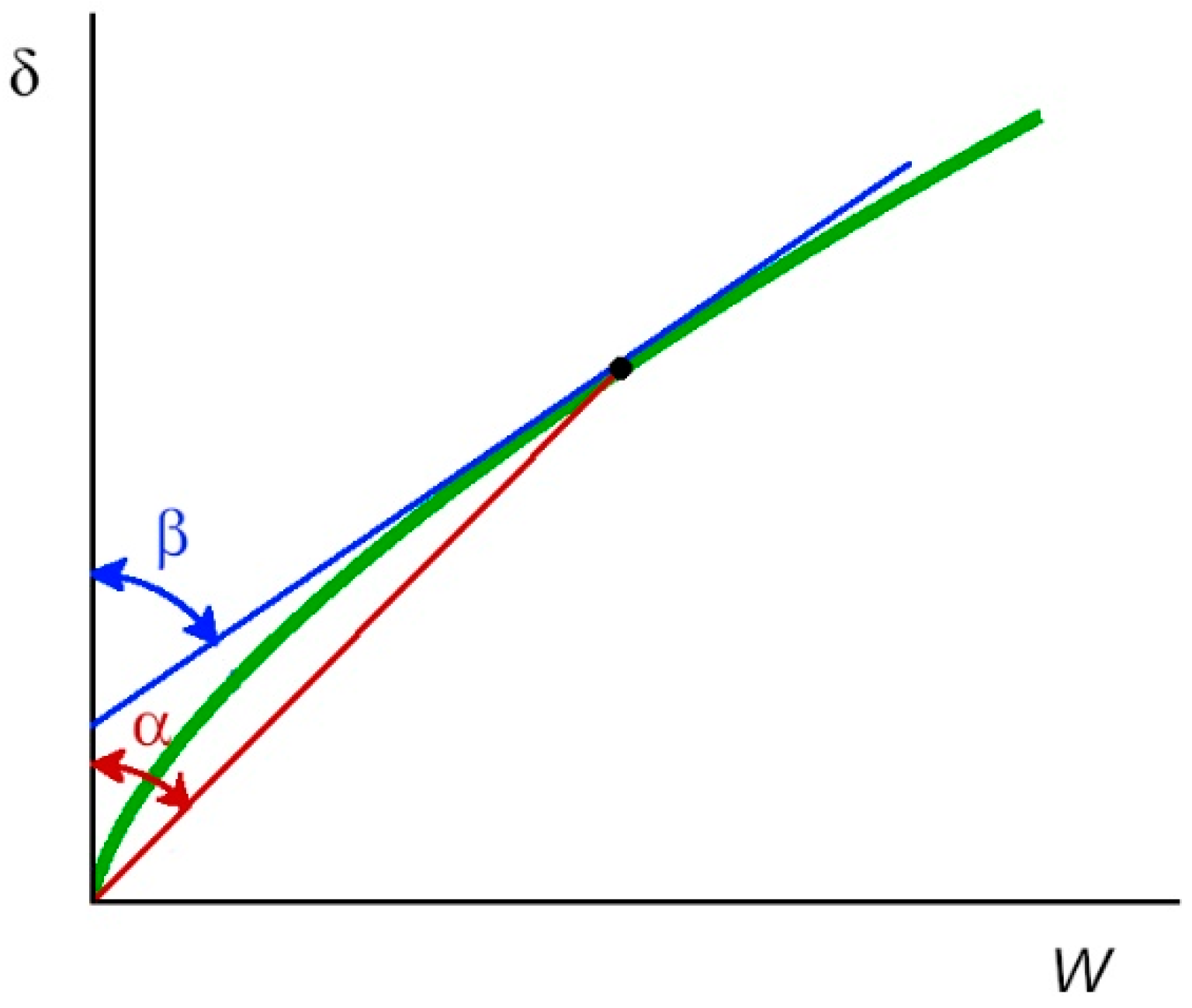
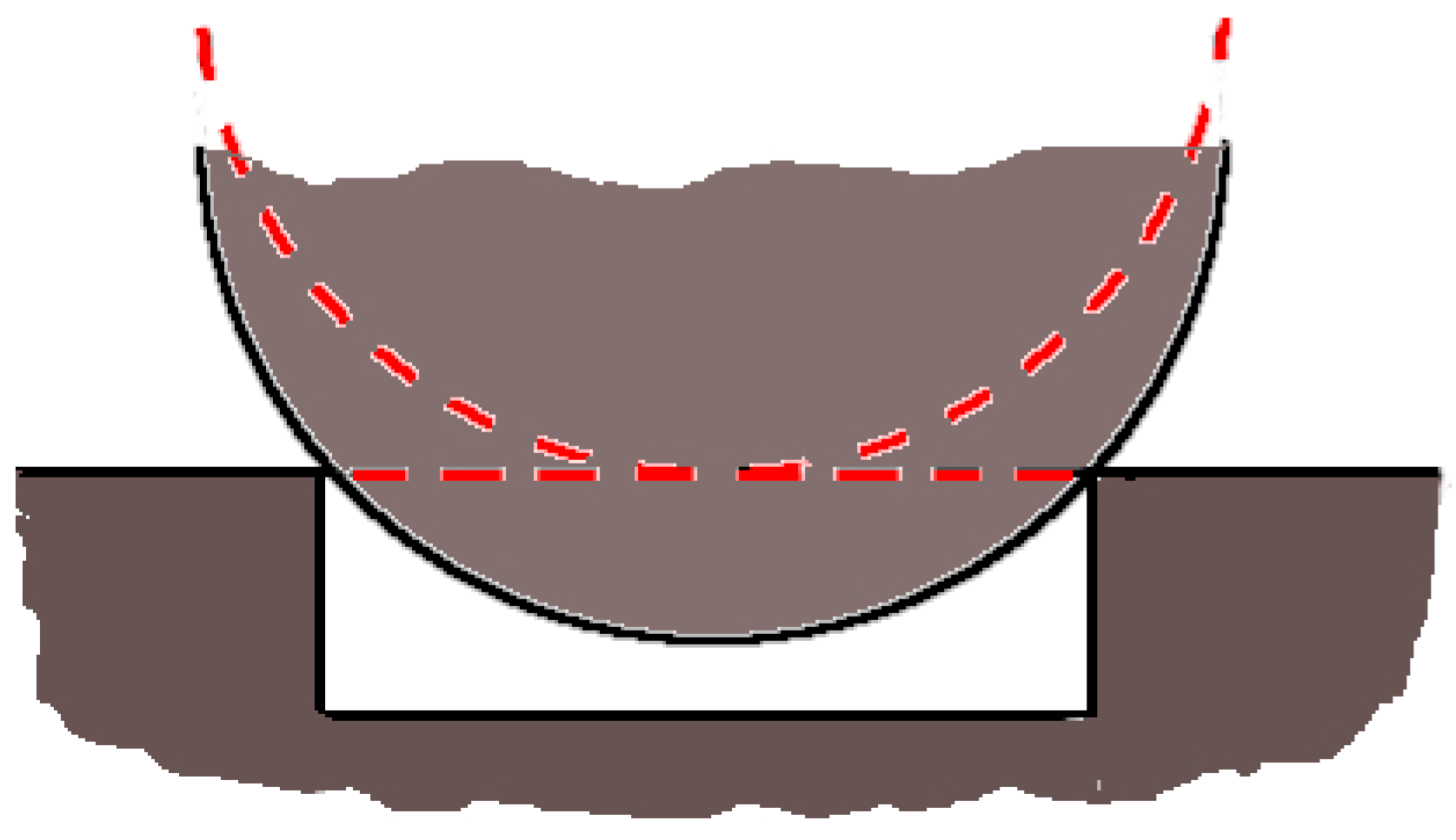
Relevant Hertzian Formulas for Deformation and Stiffness in Point Contacts
2. Materials and Methods
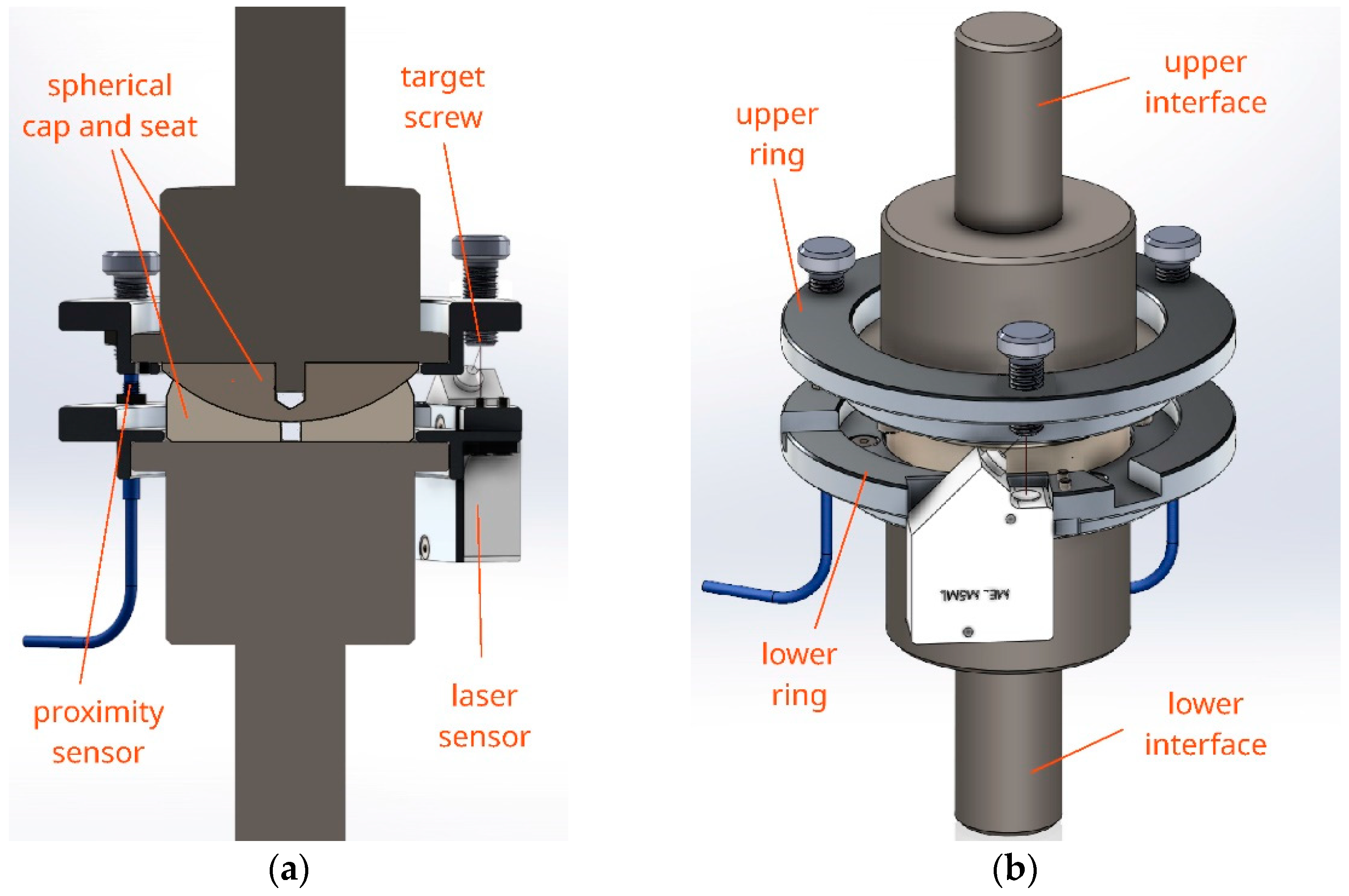
2.1. The Experimental Apparatus
2.2. The Test Articles
2.3. The Test Procedure
2.4. Stiffness Evaluation
3. Results
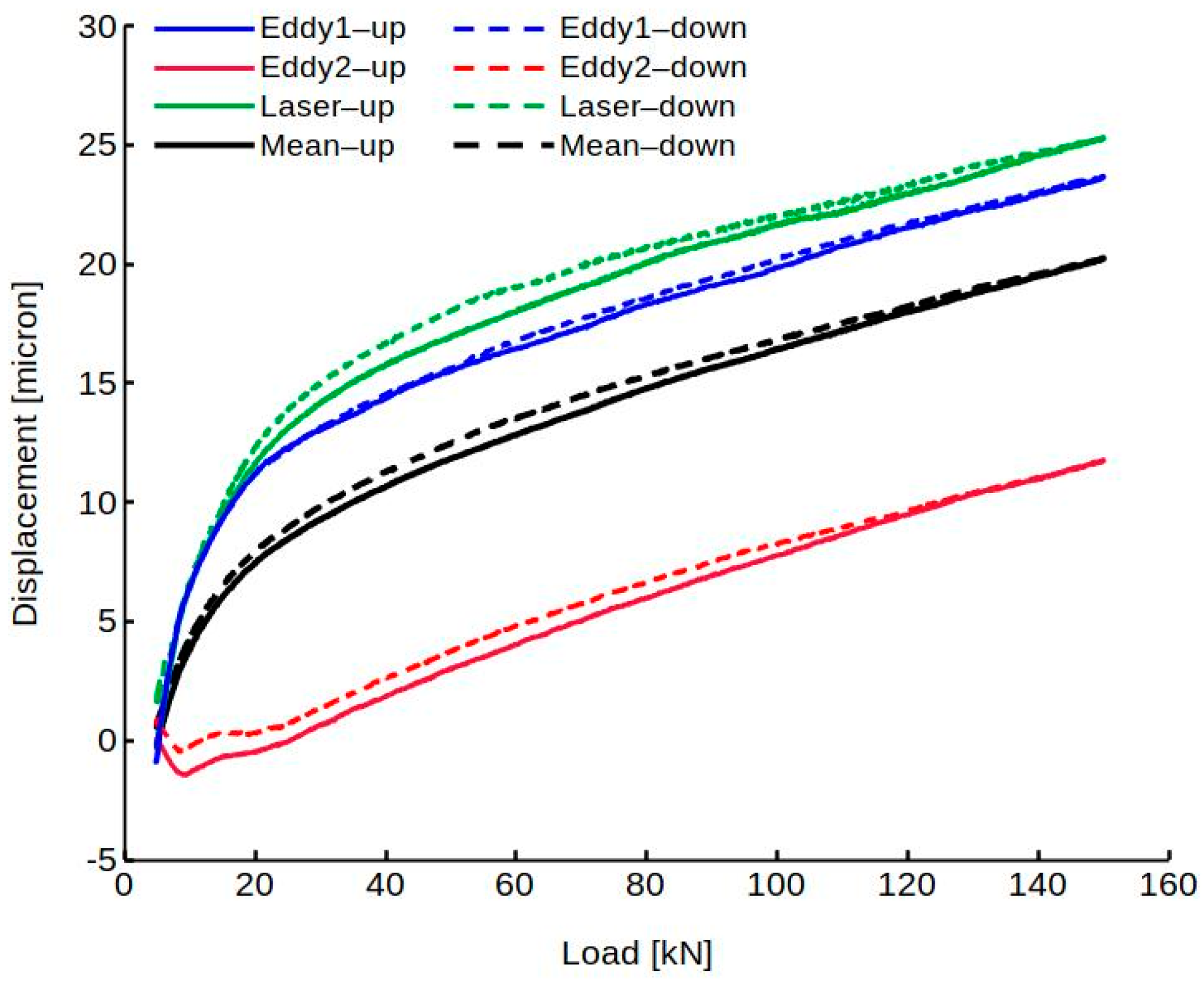
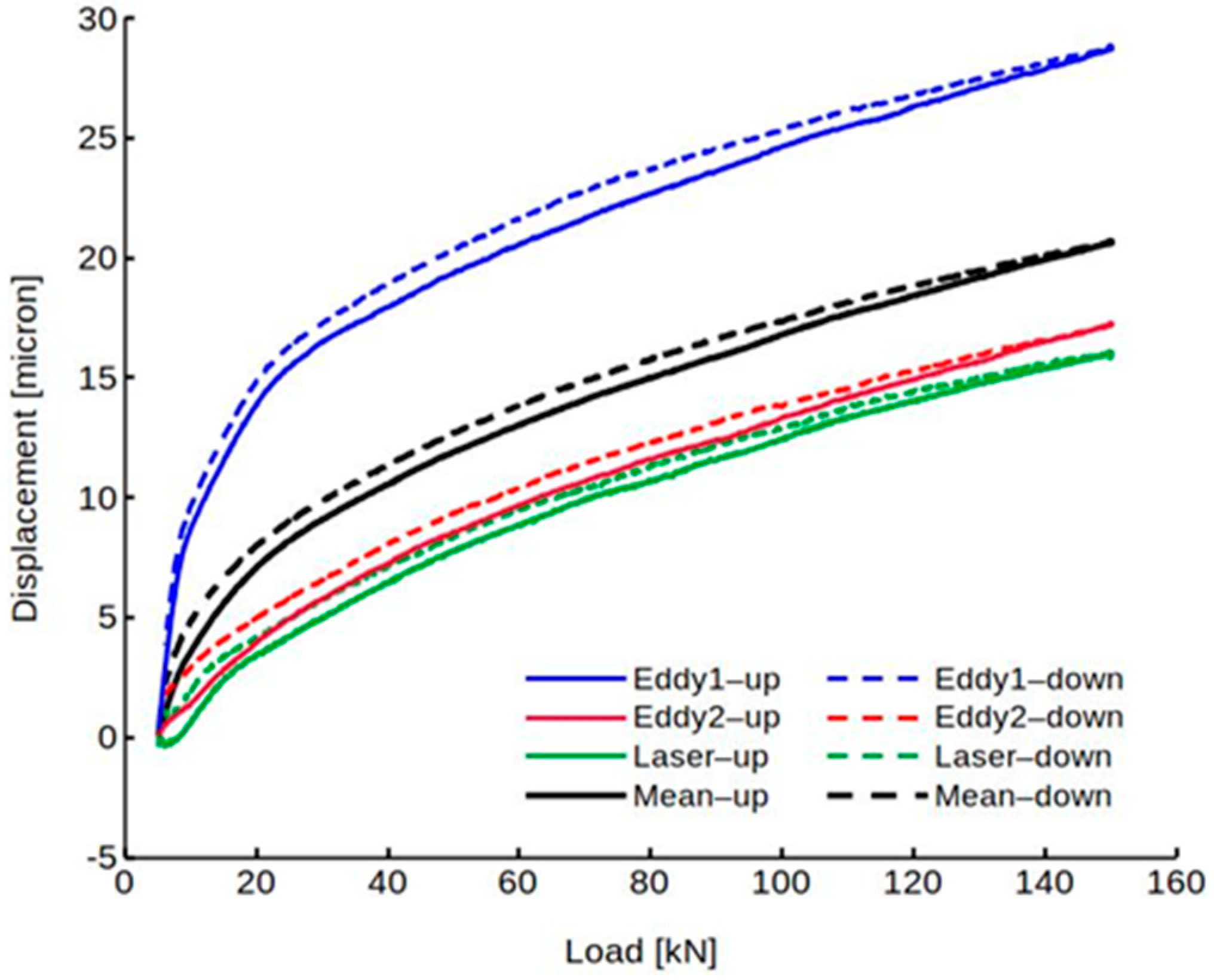
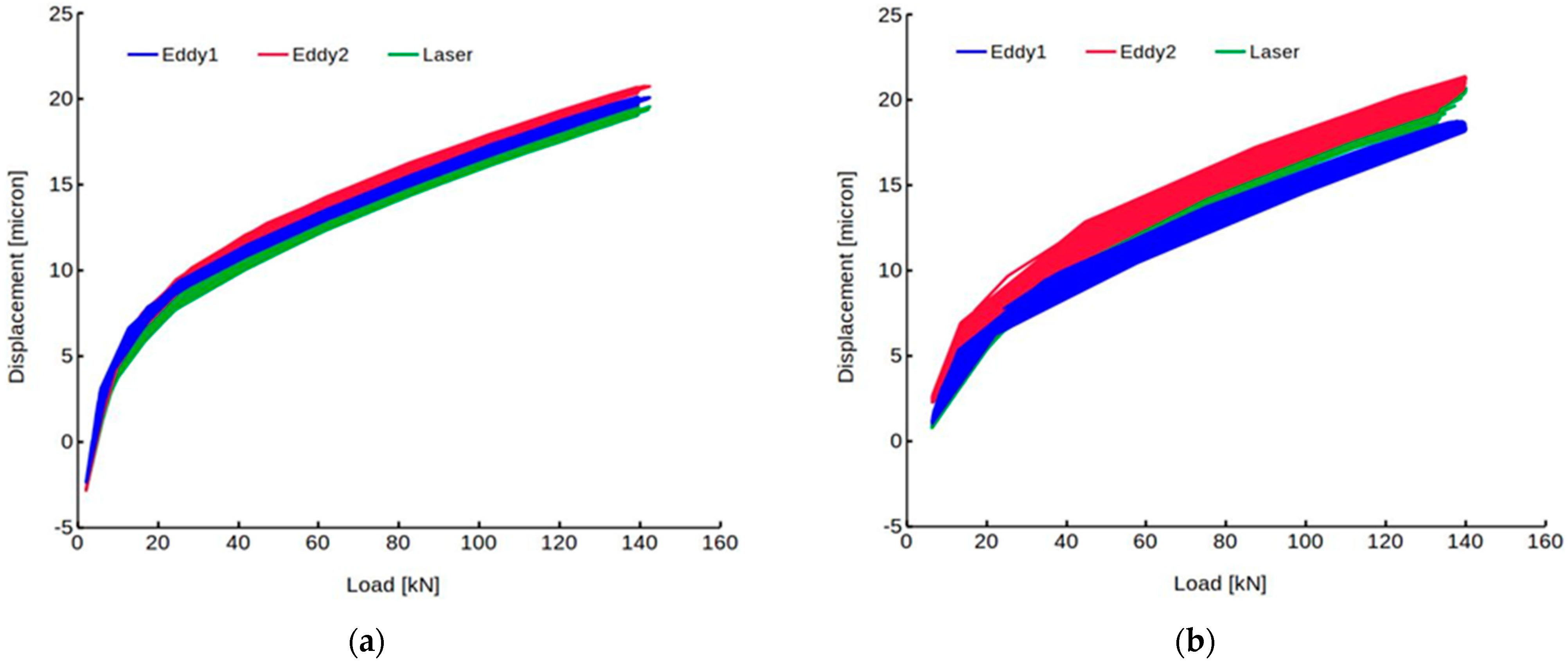
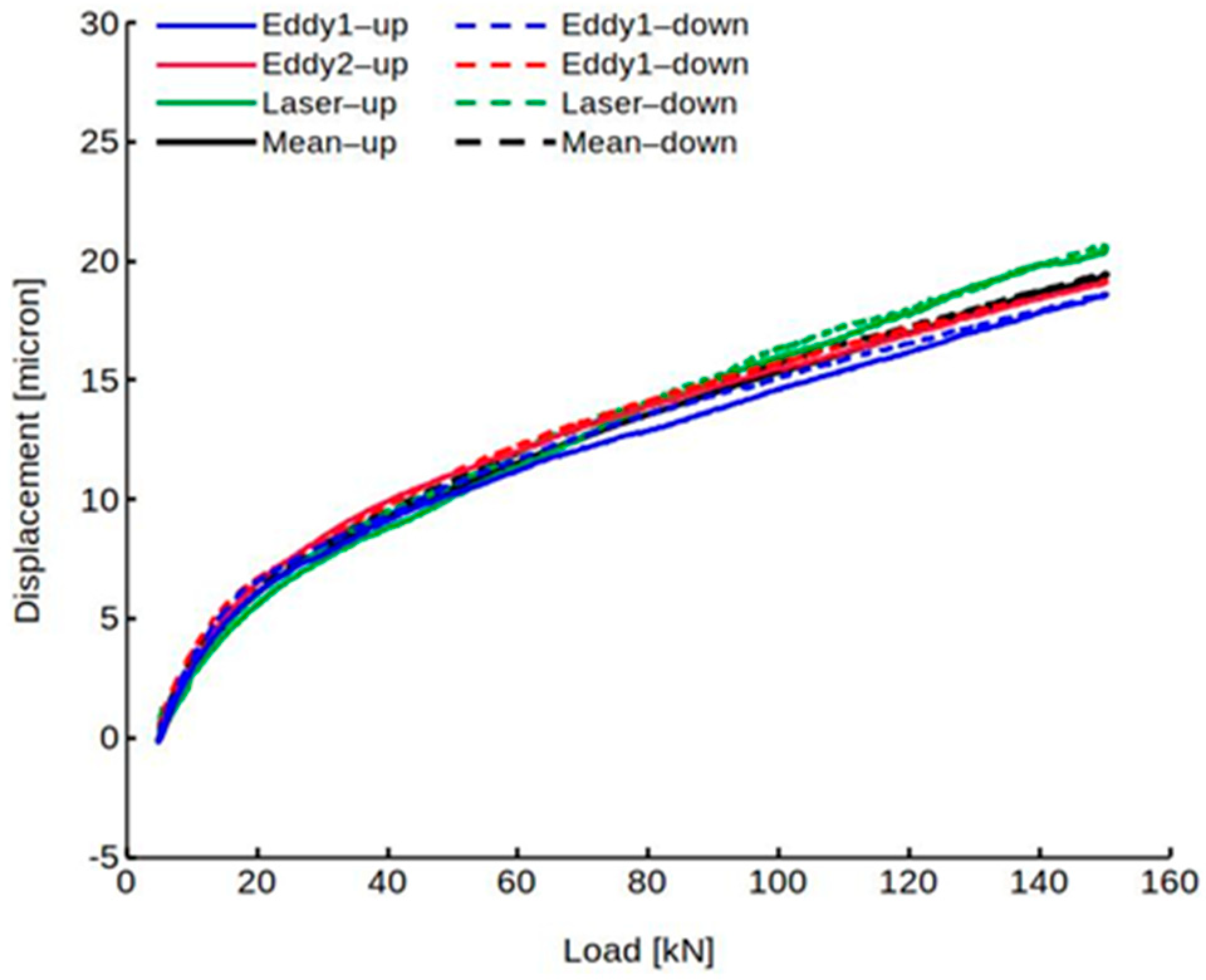
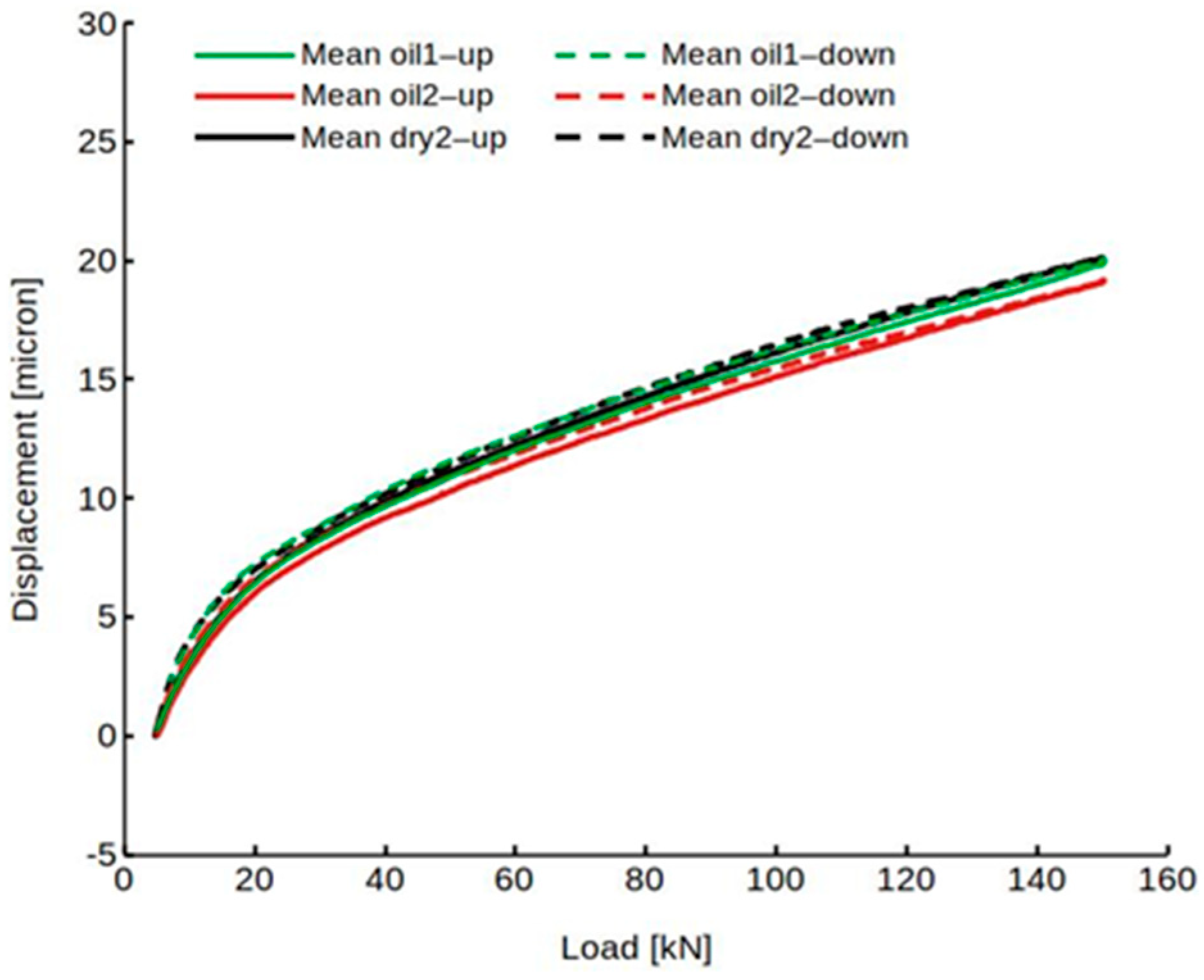
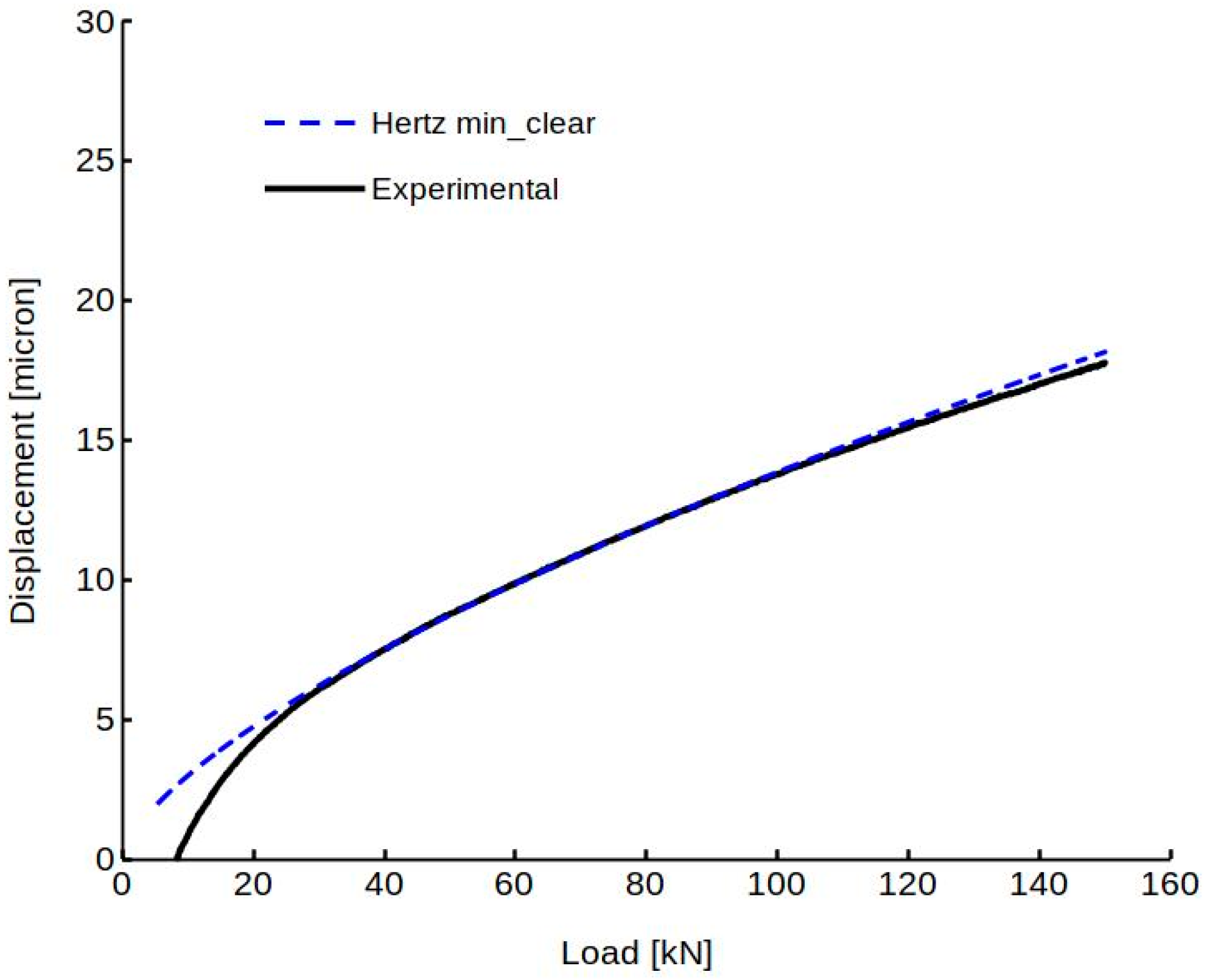
3.1. Displacement Measurements
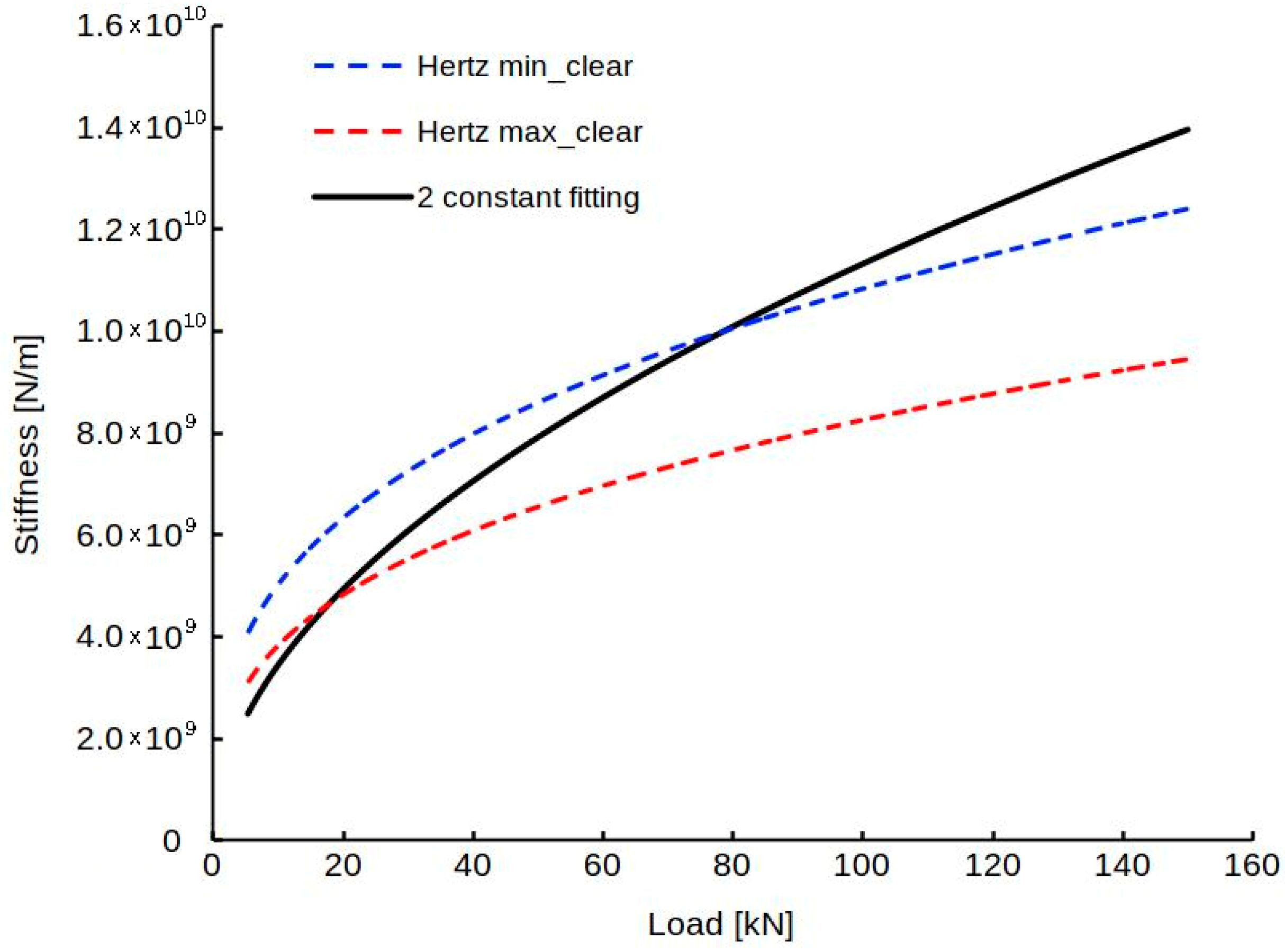
3.2. Evaluated Stiffness
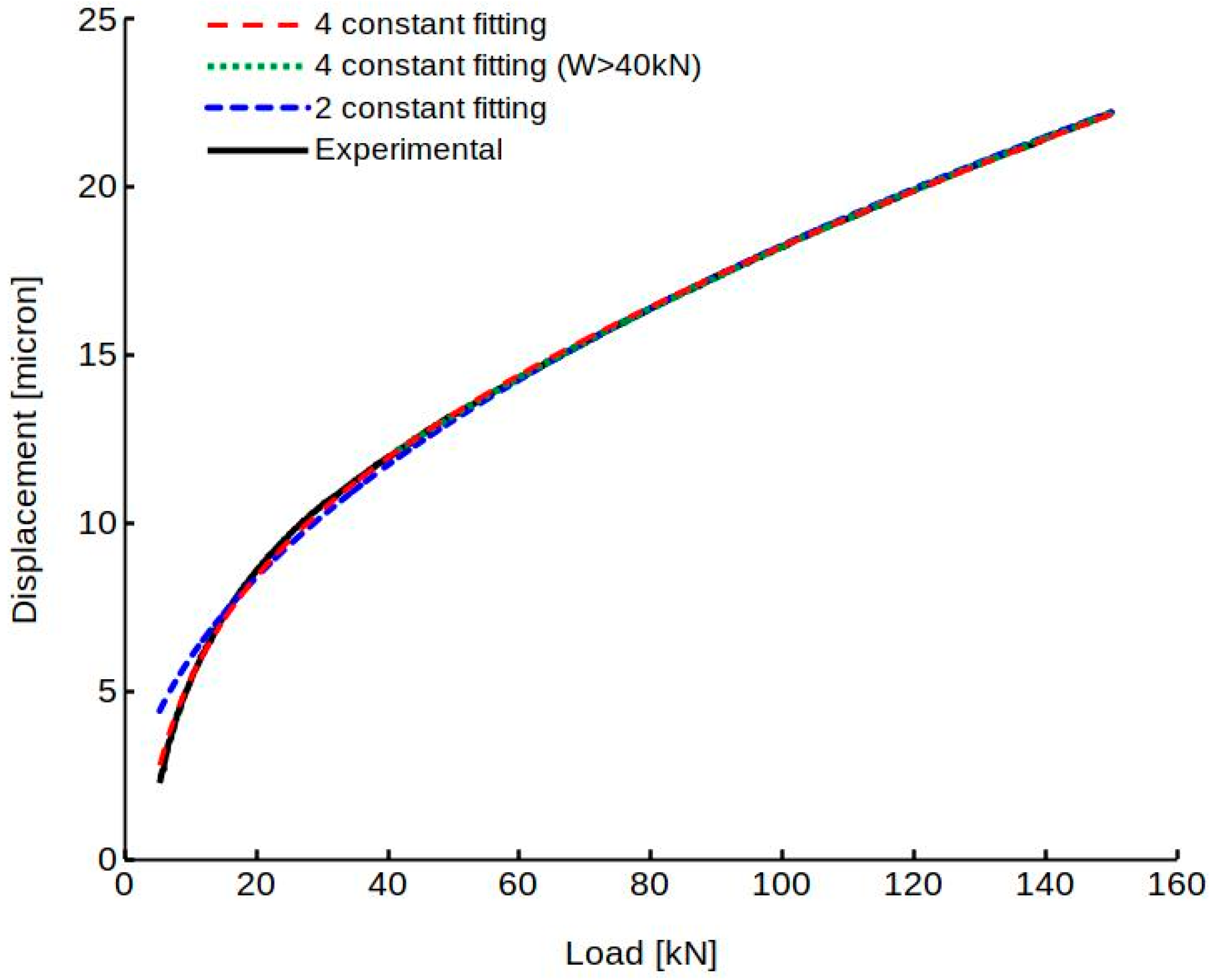
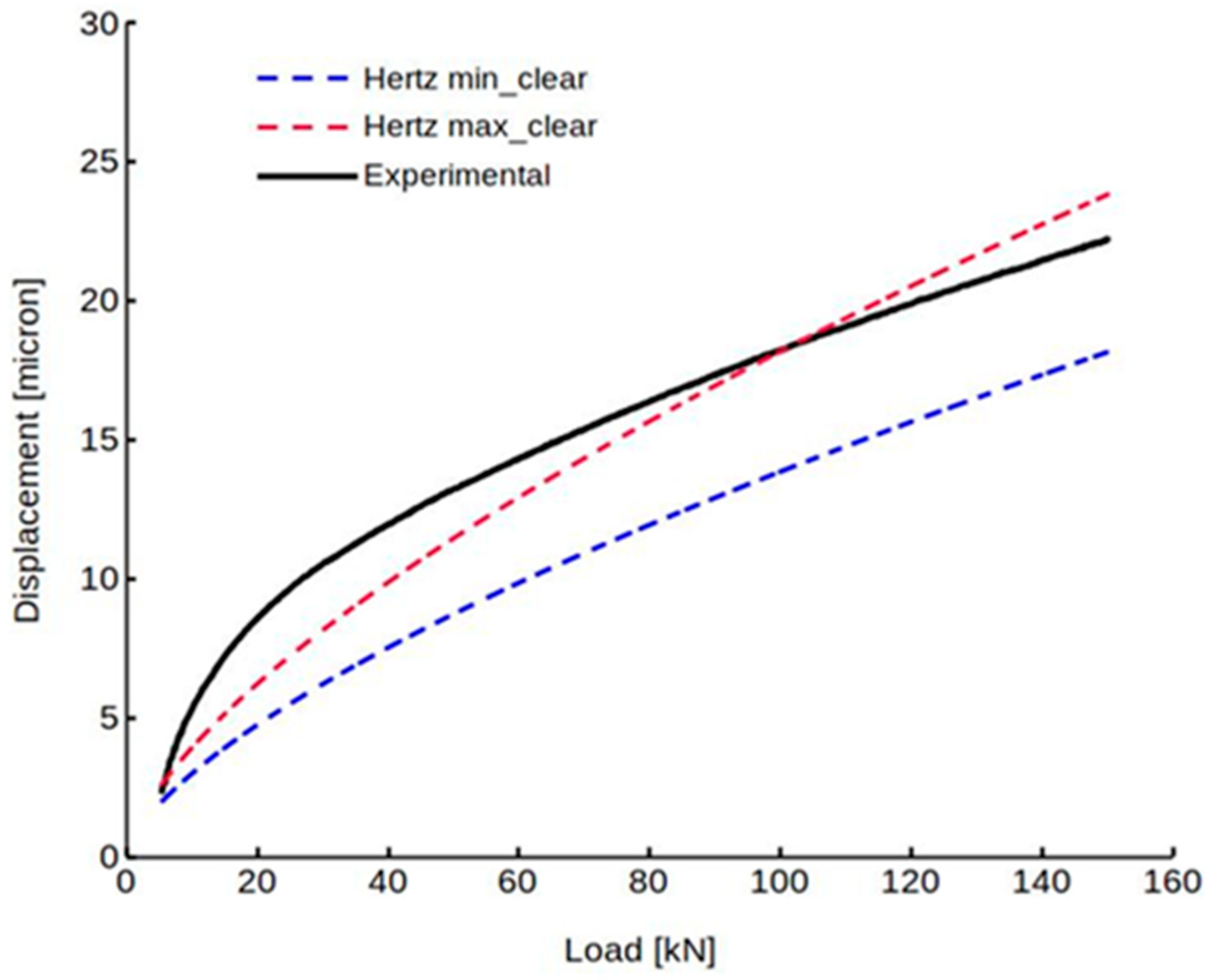
3.3. Comparison with Results of Hertzian Formulas
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Dmochowski, W. Dynamic properties of tilting-pad journal bearings: Experimental and theoretical investigation of frequency effects due to pivot flexibility. J. Eng. Gas Turbines Power 2006, 129, 865–869. [Google Scholar] [CrossRef]
- San Andres, L.; Tao, Y. The role of pivot stiffness on the dynamic force coefficients of tilting pad journal bearings. J. Eng. Gas Turbines Power 2013, 135, 112505. [Google Scholar] [CrossRef]
- Mehdi, S.M.; Jang, K.E.; Kim, T.H. Effects of pivot design on performance of tilting pad journal bearings. Tribol. Int. 2018, 119, 175–189. [Google Scholar] [CrossRef]
- Kirk, R.G.; Reedy, S.W. Evaluation of Pivot Stiffness for Typical Tilting-Pad Journal Bearing Designs. J. Vib. Acoust. Stress 1988, 110, 165–171. [Google Scholar] [CrossRef]
- Nicholas, J.C.; Wygant, K.D. Tilting pad journal bearing pivot design for high load applications. In Proceedings of the 24th Turbomachinery Symposium; Texas A&M: College Station, TX, USA, 1995; pp. 33–48. [Google Scholar] [CrossRef]
- Sun, Z.; Hao, C. Conformal Contact Problems of Ball-socket and Ball. Phys. Procedia 2012, 25, 209–214. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Zhang, C.; Chen, X.; Wang, Y.; Tan, Y. A new universal approximate model for conformal contact and non-conformal contact of spherical surfaces. Acta Mech. 2014, 226, 1657–1672. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, C.; Chen, X.; Wang, Y.; Tan, Y. Newly developed theoretical solution and numerical model for conformal contact pressure distribution and free-edge effect in spherical plain bearings. Tribol. Int. 2015, 84, 48–60. [Google Scholar] [CrossRef]
- He, W.; Chen, Y.; He, J.; Xiong, W.; Tang, T.; OuYang, H. Spherical contact mechanical analysis of roller cone drill bits journal bearing. Petroleum 2016, 2, 208–214. [Google Scholar] [CrossRef] [Green Version]
- Yuan, L.; Bao, H.; Yao, X.; Lu, J.; Liu, J. Distribution of conformal contact pressure in spherical plain bearings considering friction and free-edge effects. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 1851–1867. [Google Scholar] [CrossRef]
- Johns-Rahnejat, P.M.; Dolatabadi, N.; Rahnejat, H. Analytical elastostatic contact mechanics of highly-loaded contacts of varying conformity. Lubricants 2020, 8, 89. [Google Scholar] [CrossRef]
- Askari, E. Mathematical models for characterizing non-Hertzian contacts. Appl. Math. Model. 2021, 90, 432–447. [Google Scholar] [CrossRef]
- Blanco-Lorenzo, J.; Santamaria, J.; Vadillo, E.G.; Correa, N. On the influence of conformity on wheel–rail rolling contact mechanics. Tribol. Int. 2016, 103, 647–667. [Google Scholar] [CrossRef] [Green Version]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Wu, C.-E.; Lin, K.-H.; Juang, J.-Y. Hertzian load-displacement relation holds for spherical indentation on soft elastic solids undergoing large deformations. Tribol. Int. 2016, 97, 71–76. [Google Scholar] [CrossRef]
- Solhjoo, S.; Müser, M.H.; Vakis, A.I. Nanocontacts and Gaussian Filters: Insights into the Idea of Filtering Contact Stress Fields for Removing the Effects of Surface Roughness at the Atomic Scale. Tribol. Lett. 2019, 67, 94. [Google Scholar] [CrossRef] [Green Version]
- Germaneau, A.; Peyruseigt, F.; Mistou, S.; Doumalin, P.; Dupré, J.-C. A 3D mechanical analysis of aeronautical plain bearings: Validation of a finite element model from measurement of displacement fields by digital volume correlation and optical scanning tomography. Opt. Lasers Eng. 2010, 48, 676–683. [Google Scholar] [CrossRef] [Green Version]
- Nouira, D.; Tonazzi, D.; Meziane, A.; Baillet, L.; Massi, F. Numerical and Experimental Analysis of Nonlinear Vibrational Response due to Pressure-Dependent Interface Stiffness. Lubricants 2020, 8, 73. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, J.; Zhang, Z.; Hong, J. Normal contact stiffness model considering 3D surface topography and actual contact status. Mech. Sci. 2021, 12, 41–50. [Google Scholar] [CrossRef]
- Childs, D.W.; Harris, J.M. Static performance characteristics and rotordynamic coefficients for a four-pad ball-in-socket tilting pad journal bearing. J. Eng. Gas Turbines Power 2009, 131, 062502. [Google Scholar] [CrossRef]
- Dang, P.V.; Chatterton, S.; Pennacchi, P. The Effect of Pivot Stiffness on the Performances of Five-Pad Tilting Pad Bearings. Lubricants 2019, 7, 61. [Google Scholar] [CrossRef] [Green Version]
- Hertz, H. On the contact of rigid elastic solids and on hardness. In Miscellaneous Papers; Jones, D.E.; Schott, G.A., Translators; Macmillan: London, UK, 1896; Chapter VI; pp. 163–183. [Google Scholar]
- Hamrock, B.J. Fundamental of Fluid Film Lubrication; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Bhushan, B. Principles and Applications of Tribology; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Khonsari, M.M.; Booser, E.R. Applied Tribology, 2nd ed.; John Wiley & Sons: Chicester, UK, 2008. [Google Scholar]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain, 7th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciulli, E.; Forte, P.; Antonelli, F.; Minelli, R.; Panara, D. Tilting Pad Journal Bearing Ball and Socket Pivots: Experimental Determination of Stiffness. Machines 2022, 10, 81. https://doi.org/10.3390/machines10020081
Ciulli E, Forte P, Antonelli F, Minelli R, Panara D. Tilting Pad Journal Bearing Ball and Socket Pivots: Experimental Determination of Stiffness. Machines. 2022; 10(2):81. https://doi.org/10.3390/machines10020081
Chicago/Turabian StyleCiulli, Enrico, Paola Forte, Flavio Antonelli, Roberto Minelli, and Daniele Panara. 2022. "Tilting Pad Journal Bearing Ball and Socket Pivots: Experimental Determination of Stiffness" Machines 10, no. 2: 81. https://doi.org/10.3390/machines10020081
APA StyleCiulli, E., Forte, P., Antonelli, F., Minelli, R., & Panara, D. (2022). Tilting Pad Journal Bearing Ball and Socket Pivots: Experimental Determination of Stiffness. Machines, 10(2), 81. https://doi.org/10.3390/machines10020081






