Formation Control of Dual Auto Guided Vehicles Based on Compensation Method in 5G Networks
Abstract
:1. Introduction
- (1)
- Out-of-order and packet dropout. Due to the data multichannel transmission mechanism, data packets from the same node sometimes reach the receiving end out of order. The setting sequence number in packet and data buffer in receiving end could set data in order but may mean that there is no new data for control system. The transmission process could cause data dropout because of the signal attenuation and resource conflict. The network system usually uses retransmission to ensure the correctness of data packet. However, retransmission will increase the transmission delay. For the control system, if data packet cannot arrive in one control cycle, the data will be dropped out. The packet loss will cause the system to have no new data available.
- (2)
- Delay. The network system is responsible for the data transmission and exchange of all nodes. Due to the limited bandwidth, many nodes can only share network bandwidth resources. Network congestion will inevitably bring communication delays, especially when multiple nodes send signals at the same time. There will be a delay which cannot be ignored compared to the control cycle. The real-time performance of the control signal and feedback signal will be reduced, and the control system is prone to problems such as losing accuracy and stability. How to deal with the problem of delay is the key issue in applying 5G networks to real-time control.
- (3)
- Control cycle. To meet the needs of different tasks in real-time control, there are often multiple control cycles on the controller. How to set the control cycle considering 5G R15 capability to access the requirements needs to be discussed. Due to the data sharing, each cycle will be coupled with others. The influence of other control cycles cannot be ignored when analyzing NCS control.
2. 5G Networks Characteristics
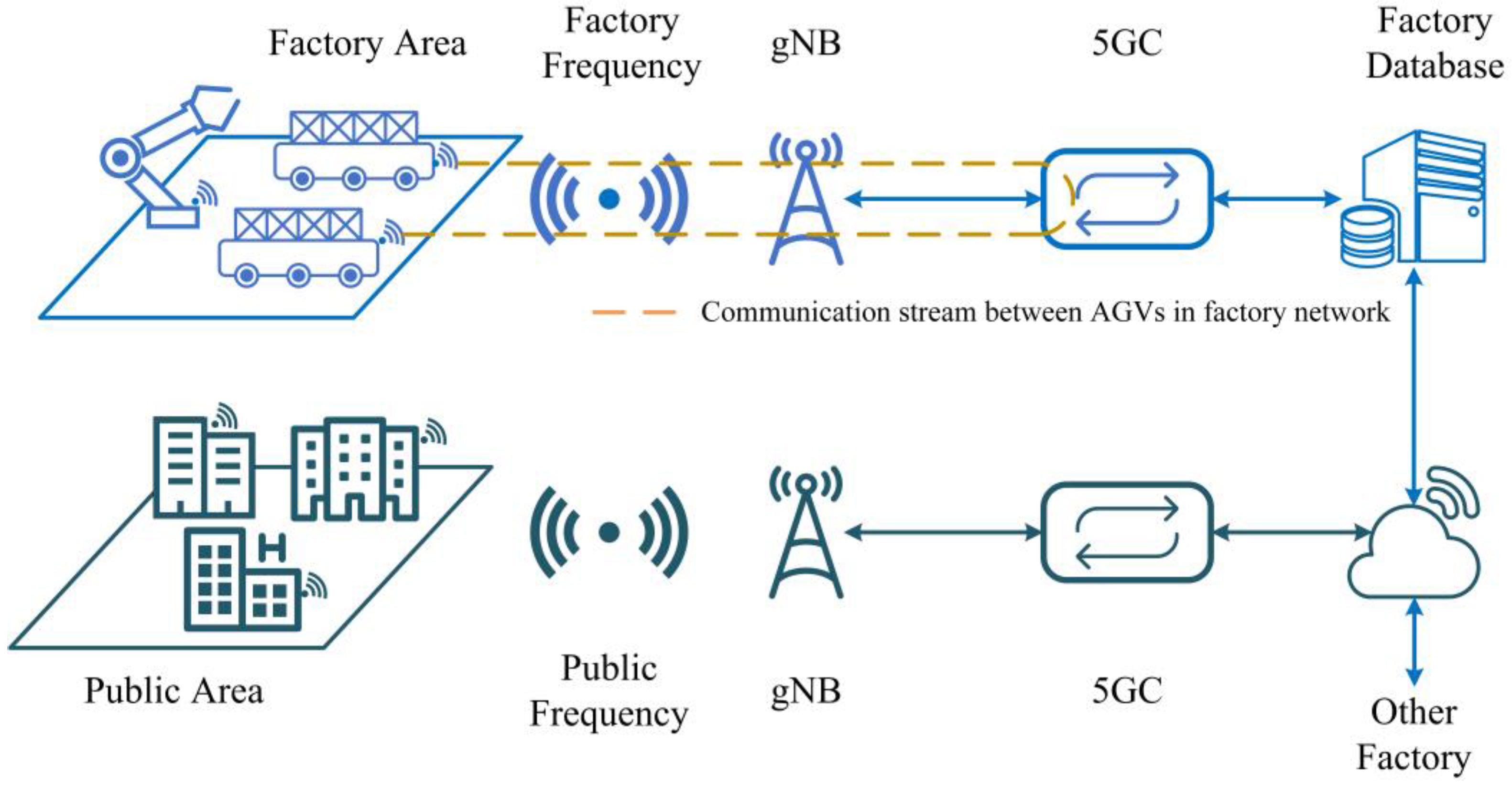
2.1. 5G Private Network Structure
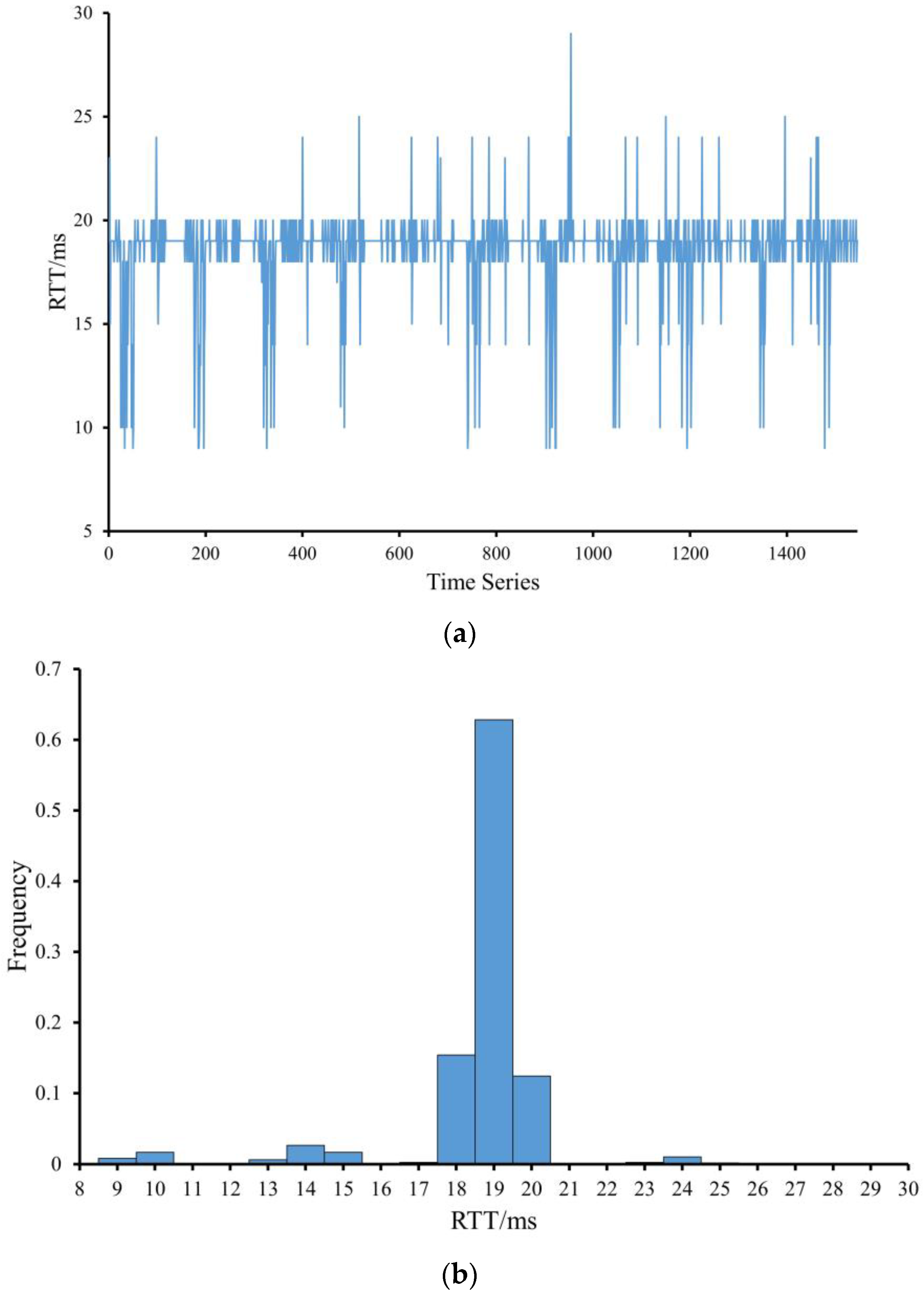
2.2. 5G Networks Delay Measurement and Analysis
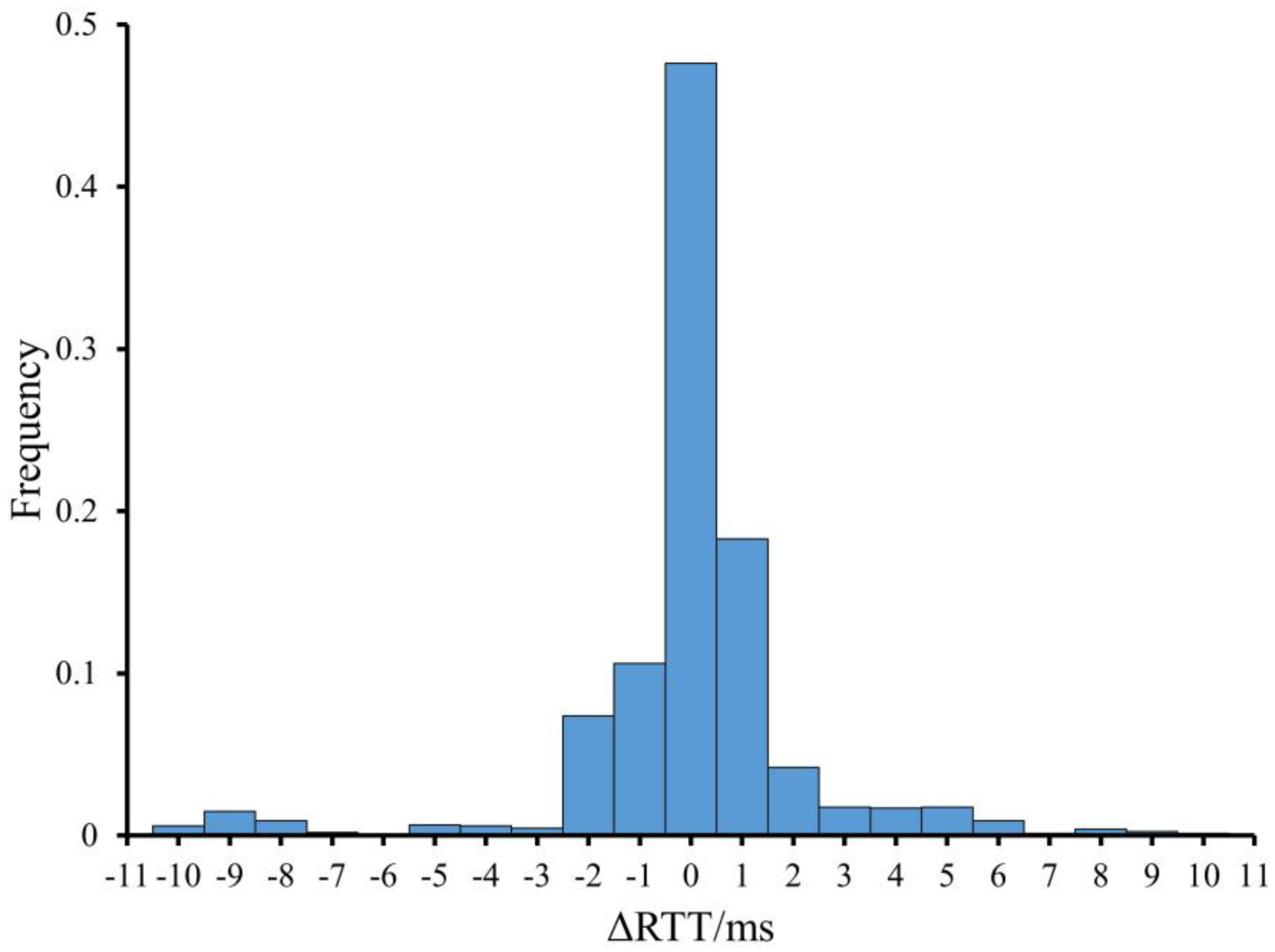
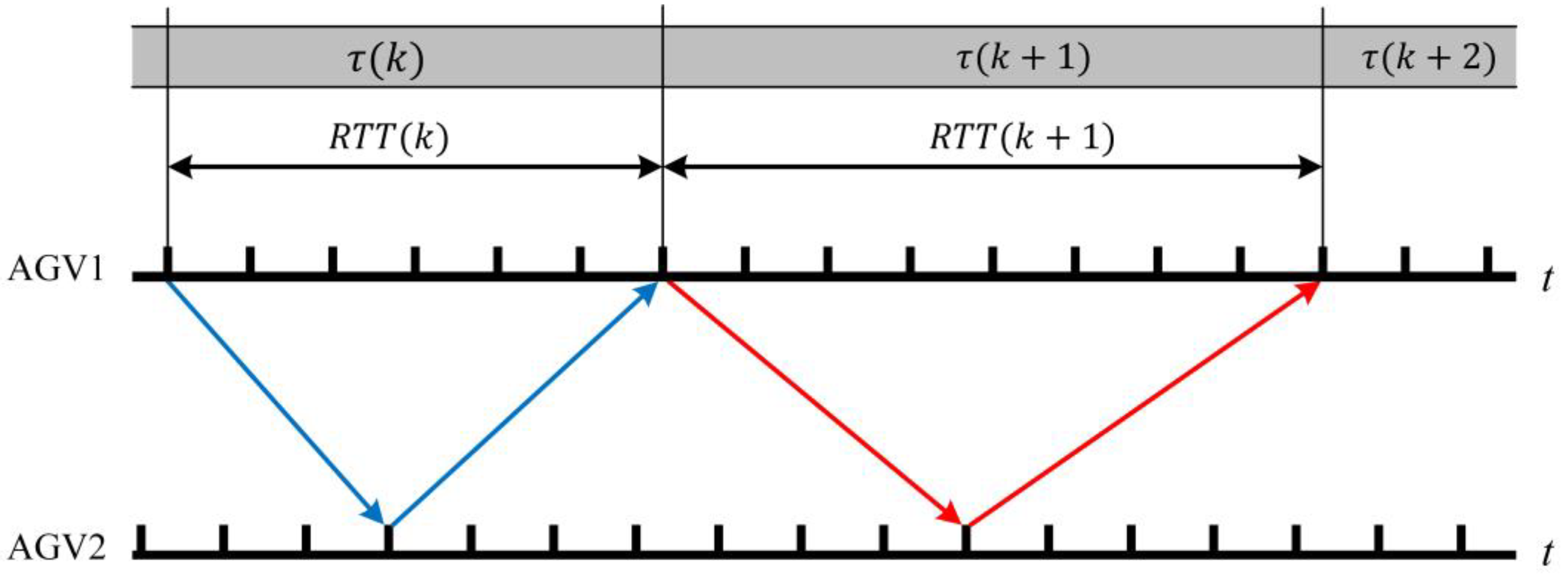
2.3. 5G Delay Estimation
- (1)
- In a round-trip transmission, the two E2E delay are equal.
- (2)
- The communication network is relatively stable between two RTT measurements.
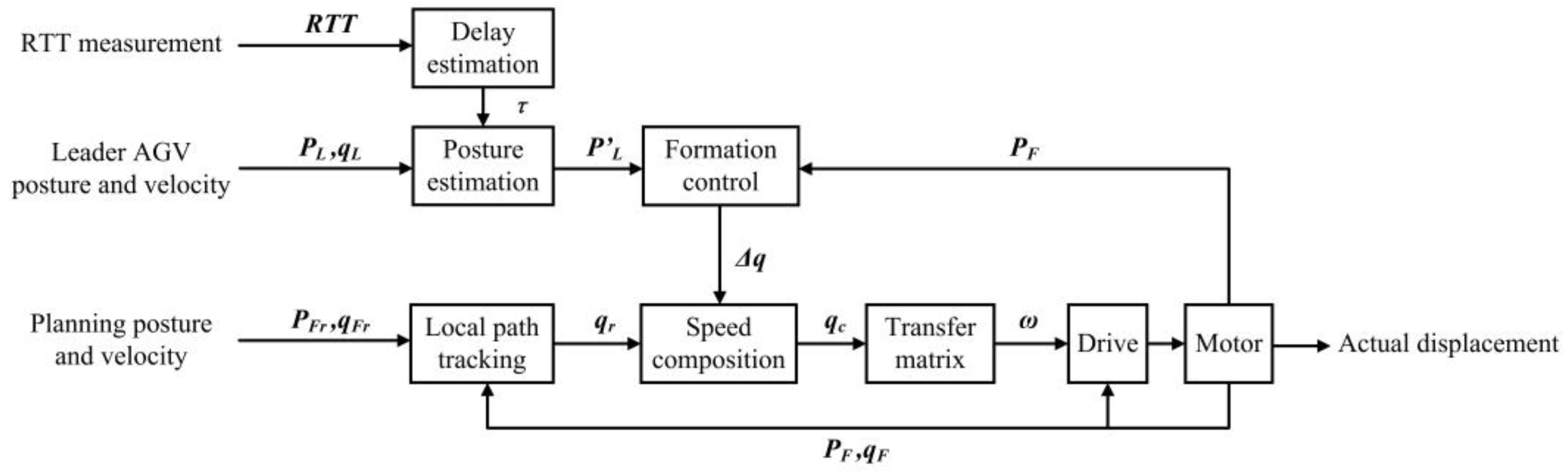
3. Formation Control System Design
3.1. Delay Analysis in Control System
- (1)
- Network transmission delay τcom: This delay describes the time that takes for data packet to AGV2 application layer from AGV1 application layer, which is the E2E delay mentioned above.
- (2)
- Execution waiting delay τcontrol: This delay describes the time that takes for data packet from being received to being processed.
3.2. Discussion on Control Method Considering 5G Delay
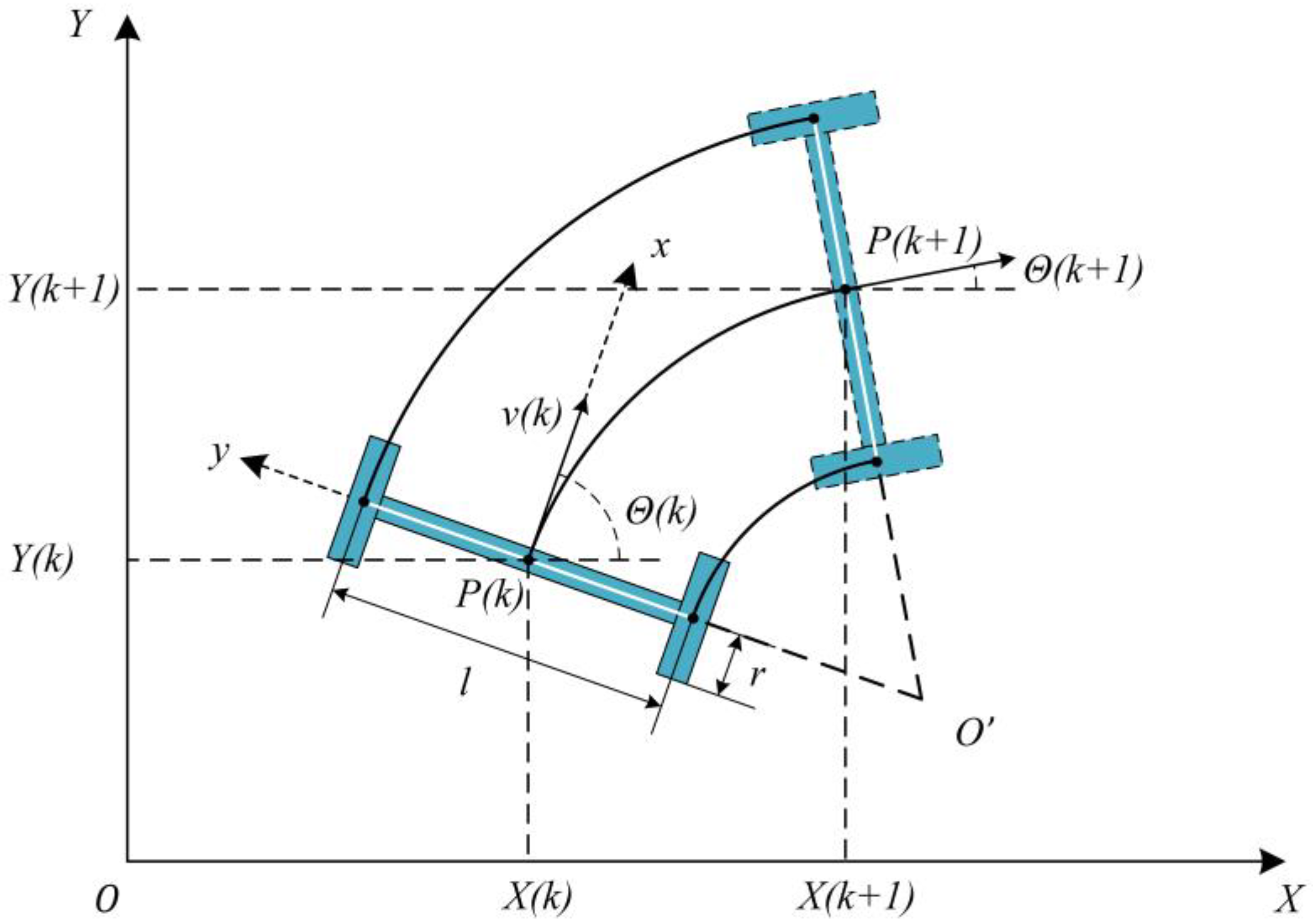
3.3. AGV Kinematic Model and Posture Estimation
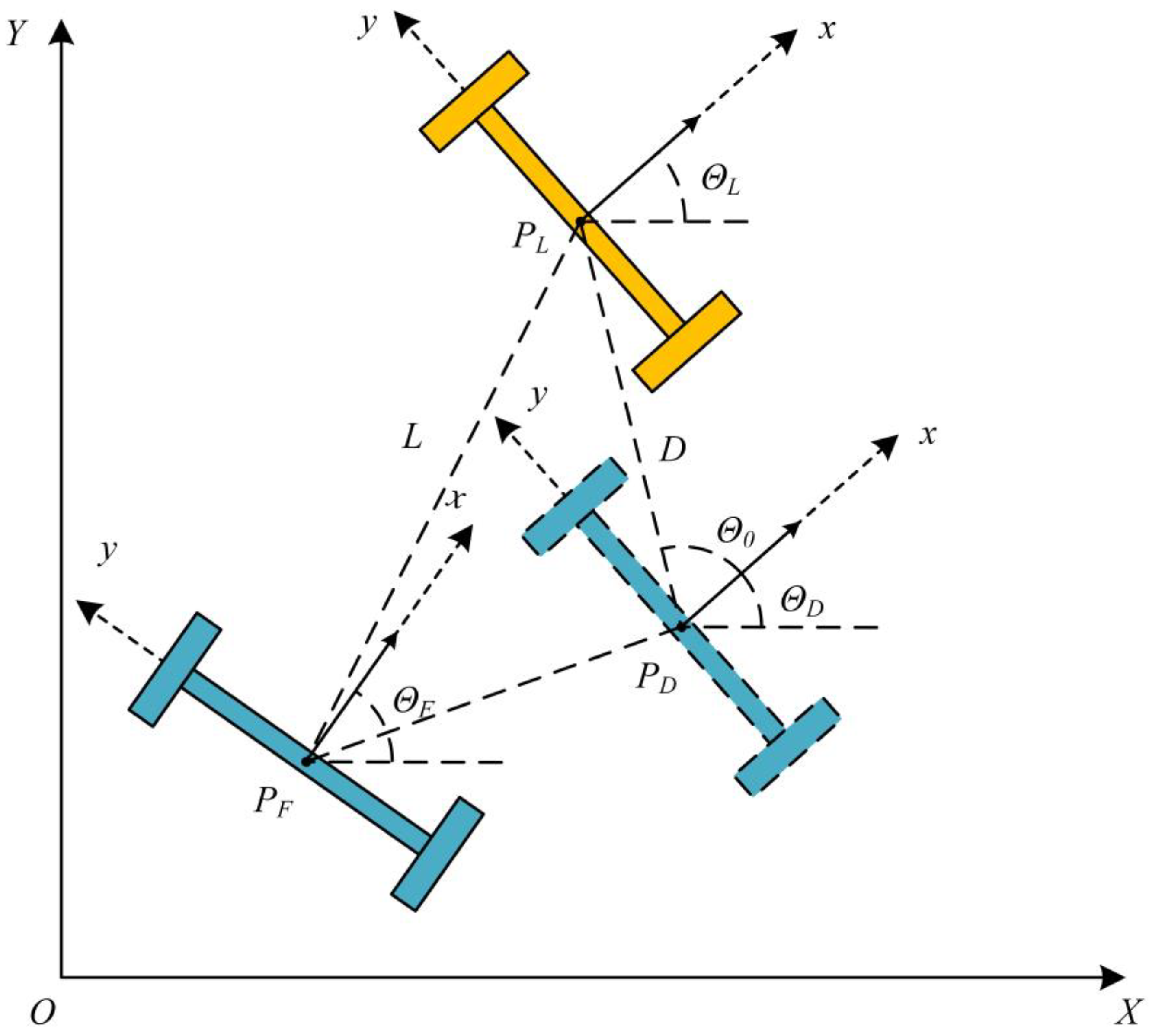
3.4. Formation Control and Speed Composition
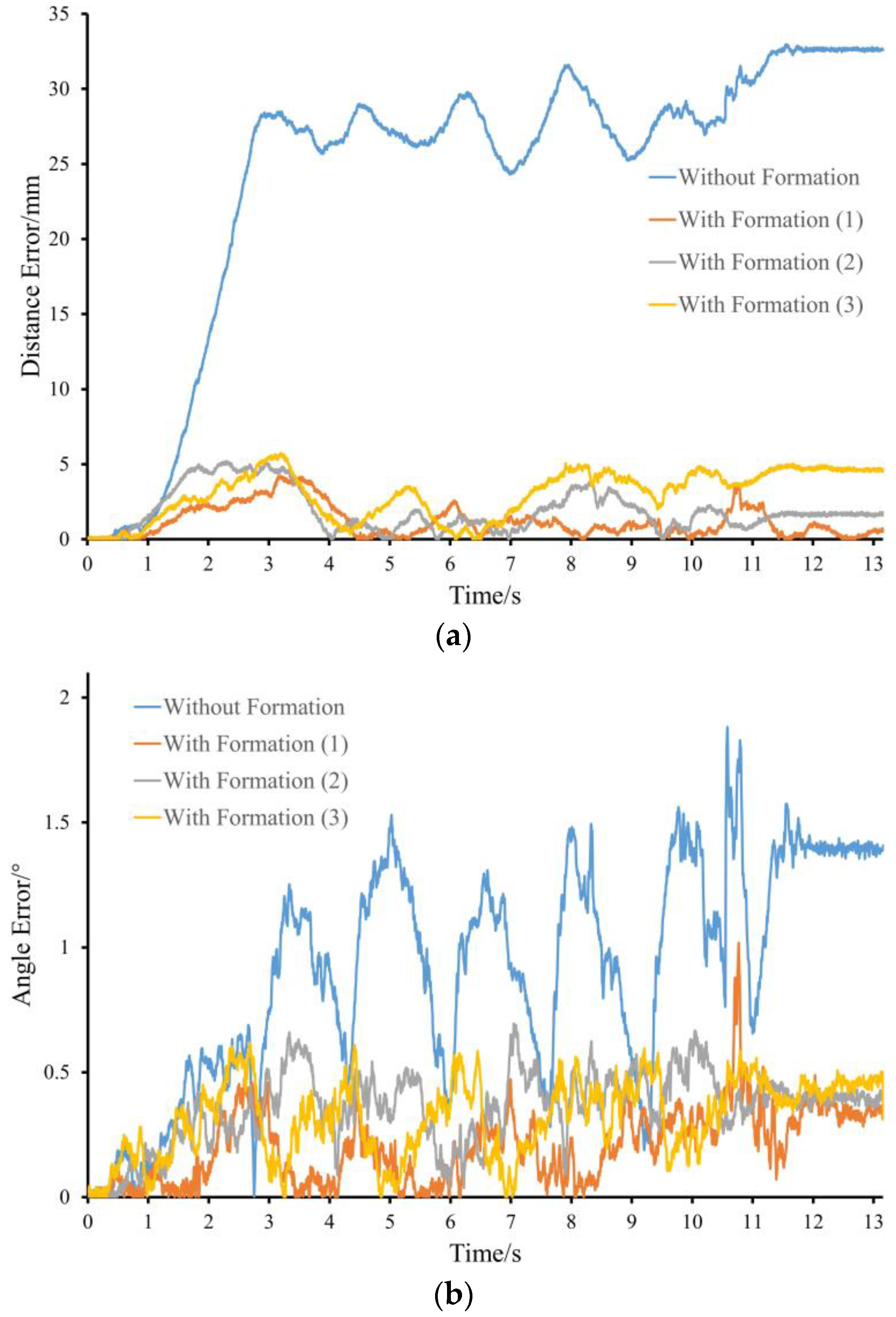
4. Experiment and Result
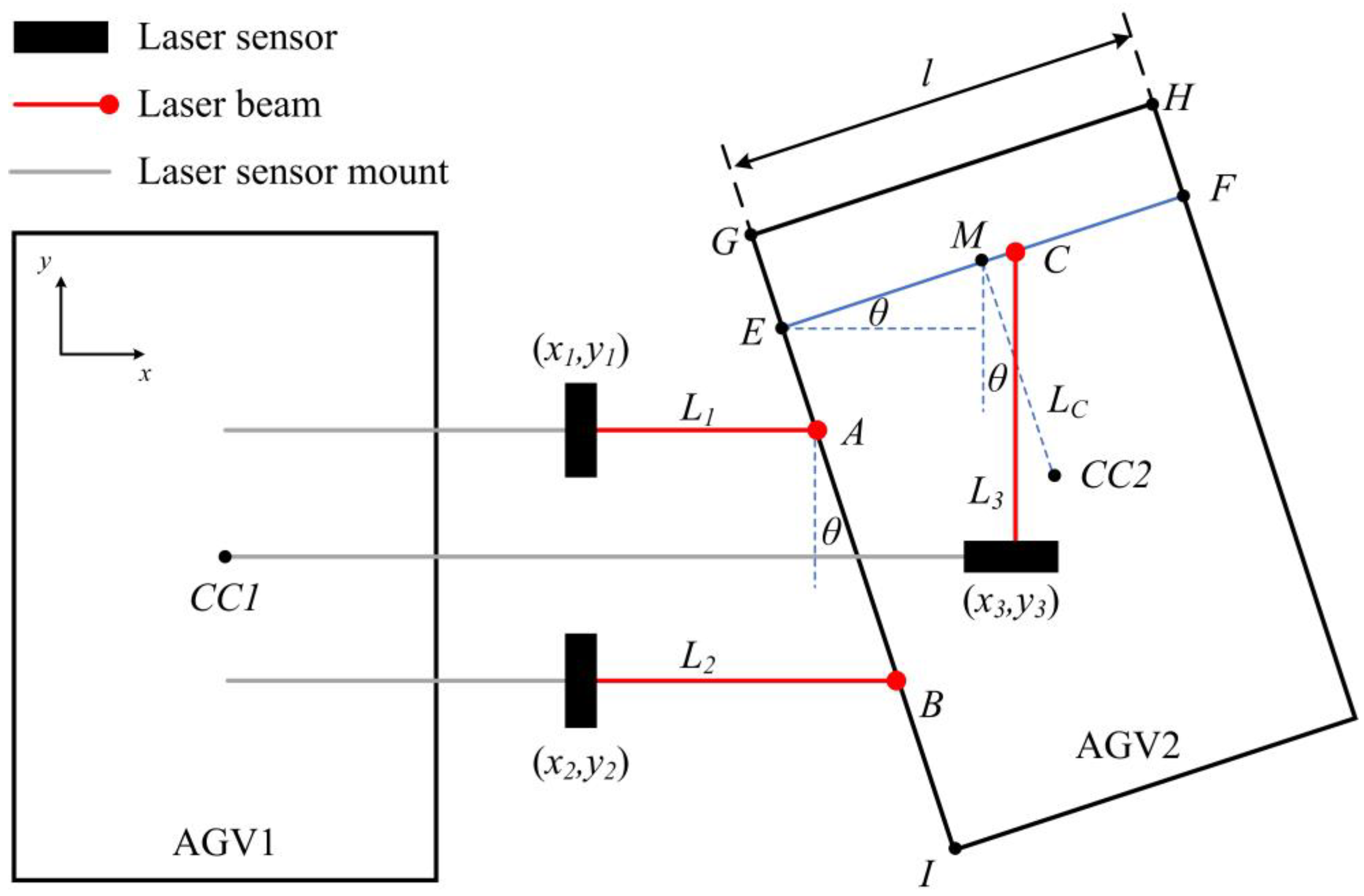
- (1)
- The measurement equipment is installed accurately to ensure ⫽ , ⫽ , EF ⫽ GH. Therefore, |EF| = l and |DCC2| = LC.
- (2)
- There is no deformation on both AGV’s body and measurement equipment during measurement operation.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rodriguez, I.; Mogensen, R.S.; Schjorring, A.; Razzaghpour, M.; Maldonado, R.; Berardinelli, G.; Adeogun, R.; Christensen, P.H.; Mogensen, P.; Madsen, O.; et al. 5G Swarm Production: Advanced Industrial Manufacturing Concepts Enabled by Wireless Automation. IEEE Commun. Mag. 2021, 59, 48–54. [Google Scholar] [CrossRef]
- 5G Use Cases for Verticals China 2020. Available online: https://www.gsma.com/greater-china/resources/5g-use-cases-for-verticals-china-2020-3/ (accessed on 1 September 2021).
- Report on Implementation of Options for Monitoring of Workpiece and Machines. Available online: https://5gsmart.eu/wp-content/uploads/5G-SMART-D3.3-v1.0.pdf (accessed on 15 September 2021).
- Release 16 Description; Summary of Rel-16 Work Items. Available online: https://www.3gpp.org/ (accessed on 10 September 2021).
- Ghosh, A.; Maeder, A.; Baker, M.; Chandramouli, D. 5G Evolution: A View on 5G Cellular Technology beyond 3GPP Release 15. IEEE Access 2019, 7, 127639–127651. [Google Scholar] [CrossRef]
- Rodriguez, I.; Mogensen, R.S.; Fink, A.; Raunholt, T.; Markussen, S.; Christensen, P.H.; Berardinelli, G.; Mogensen, P.; Schou, C.; Madsen, O. An Experimental Framework for 5G Wireless System Integration into Industry 4.0 Applications. Energies 2021, 14, 4444. [Google Scholar] [CrossRef]
- Rost, P.; Mannweiler, C.; Michalopoulos, D.S.; Sartori, C.; Sciancalepore, V.; Sastry, N.; Holland, O.; Tayade, S.; Han, B.; Bega, D.; et al. Network Slicing to Enable Scalability and Flexibility in 5G Mobile Networks. IEEE Commun. Mag. 2017, 55, 72–79. [Google Scholar] [CrossRef] [Green Version]
- 5G Smart Project. Available online: https://5gsmart.eu/ (accessed on 15 September 2021).
- Holfeld, B.; Wieruch, D.; Wirth, T.; Thiele, L.; Ashraf, S.A.; Huschke, J.; Aktas, I.; Ansari, J. Wireless Communication for Factory Automation: An opportunity for LTE and 5G systems. IEEE Commun. Mag. 2016, 54, 36–43. [Google Scholar] [CrossRef]
- Industrial 5G for the Industry of Tomorrow. Available online: https://new.siemens.com/global/en/products/automation/industrial-communication/industrial-5g.html (accessed on 10 September 2021).
- Koumaras, H.; Makropoulos, G.; Batistatos, M.; Kolometsos, S.; Gogos, A.; Xilouris, G.; Sarlas, A.; Kourtis, M.-A. 5G-Enabled UAVs with Command and Control Software Component at the Edge for Supporting Energy Efficient Opportunistic Networks. Energies 2021, 14, 1480. [Google Scholar] [CrossRef]
- Montonen, J.; Koskinen, J.; Makela, J.; Ruponen, S.; Heikkila, T.; Hentula, M. Applying 5G and Edge Processing in Smart Manufacturing. In Proceedings of the 2021 IFIP Networking Conference (IFIP Networking), Espoo, Finland, 21–24 June 2021; pp. 1–2. [Google Scholar]
- Ding, H.; Zhang, Y.; Xia, L.; Wang, Q. Use Cases and Practical System Design for URLLC from Operation Perspective. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 11 July 2019; pp. 1–6. [Google Scholar]
- Oyekanlu, E.A.; Smith, A.C.; Thomas, W.P.; Mulroy, G.; Hitesh, D.; Ramsey, M.; Kuhn, D.J.; McGhinnis, J.D.; Buonavita, S.C.; Looper, N.A.; et al. A Review of Recent Advances in Automated Guided Vehicle Technologies: Integration Challenges and Research Areas for 5G-Based Smart Manufacturing Applications. IEEE Access 2020, 8, 202312–202353. [Google Scholar] [CrossRef]
- Yoshioka, C.; Namerikawa, T. Formation Control of Nonholonomic Multi-Vehicle Systems based on Virtual Structure. IFAC Proc. Vol. 2008, 41, 5149–5154. [Google Scholar] [CrossRef] [Green Version]
- Tlale, N.S. Fuzzy logic controller with slip detection behaviour for Mecanum-wheeled AGV. Robotica 2005, 23, 455–456. [Google Scholar] [CrossRef]
- Consolini, L.; Morbidi, F.; Prattichizzo, D.; Tosques, M. Leader–follower formation control of nonholonomic mobile robots with input constraints. Automatica 2008, 44, 1343–1349. [Google Scholar] [CrossRef]
- Wang, R.; Jing, H.; Hu, C.; Yan, F.; Chen, N. Robust H-infinity Path Following Control for Autonomous Ground Vehicles With Delay and Data Dropout. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2042–2050. [Google Scholar] [CrossRef]
- Lozoya, C.; Martí, P.; Velasco, M.; Fuertes, J.M.; Martín, E.X. Simulation study of a remote wireless path tracking control with delay estimation for an autonomous guided vehicle. Int. J. Adv. Manuf. Technol. 2010, 52, 751–761. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, J.; Zong, X. Leader-follower synchronization controller design for a network of boundary-controlled wave PDEs with structured time-varying perturbations and general disturbances. J. Frankl. Inst. 2021, 358, 834–855. [Google Scholar] [CrossRef]
- Wang, J.Q.; Gao, J.F.; Zhang, X.J.; He, J.J. Formation Control of Time-varying Multi-agent System Based on BP Neural Network. In Proceedings of the 16th IEEE International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020; pp. 707–712. [Google Scholar]
- Yang, Y.Q.; Jiang, H.J. Formation Control Based on Leader—Following Method for Multi—Robot to Reduce Path deviation. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 6607–6613. [Google Scholar]
- Aijaz, A. Private 5G: The Future of Industrial Wireless. IEEE Ind. Electron. Mag. 2020, 14, 136–145. [Google Scholar] [CrossRef]
- 5G Industry Application White Book. Available online: http://www.itei.cn/ewebeditor/uploadfile/20200914093949947.pdf (accessed on 10 September 2021).
- Rischke, J.; Sossalla, P.; Itting, S.; Fitzek, F.H.P.; Reisslein, M. 5G Campus Networks: A First Measurement Study. IEEE Access 2021, 9, 121786–121803. [Google Scholar] [CrossRef]
- Uitto, M.; Hoppari, M.; Heikkila, T.; Isto, P.; Anttonen, A.; Mammela, A. Remote Control Demonstrator Development in 5G Test Network. In Proceedings of the 2019 European Conference on Networks and Communications (EuCNC), Valencia, Spain, 15 August 2019; pp. 101–105. [Google Scholar]
- Zhihao, G.; Malakooti, B. Delay Prediction for Intelligent Routing in Wireless Networks Using Neural Networks. In Proceedings of the 2006 IEEE International Conference on Networking, Sensing and Control, Ft. Lauderdale, FL, USA, 14 August 2006; pp. 625–630. [Google Scholar]
- Guo, S.; Zhang, Y.; Zhu, S. Prediction of network signal transmission delay based on time aeries analysis. Railw. Comput. Appl. 2013, 22, 11–13. [Google Scholar] [CrossRef]
- Zheng, L.; Vanijjirattikhan, R.; Chow, M.; Viniotis, Y. Comparison of real-time network traffic estimator models in gain scheduler middleware by unmanned ground vehicle network-based controller. In Proceedings of the Conference of IEEE Industrial Electronics Society, Raleigh, NC, USA, 16 January 2005. [Google Scholar]
- Kanayama, Y.; Kimura, Y.; Miyazaki, F.; Noguchi, T. A stable tracking control method for an autonomous mobile robot. In Proceedings of the Proceedings., IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 384–389. [Google Scholar]




| Parameters | Value |
|---|---|
| Frequency | 2.6 GHz |
| Bandwidth | 100 MB |
| Signal to Noise Ratio | 20 dB |
| Reference Signal Receiving Power | −85 dBm |
| Method | Se/ms |
|---|---|
| Kalman Filter | 1.8916 |
| Mean | 2.0482 |
| Median | 2.0329 |
| Max value | 2.0914 |
| Parameter | Value | Unit |
|---|---|---|
| Size | 1000 × 805 × 300 | mm |
| Weight | 210 | kg |
| Maximum load | 500 | kg |
| Radius of driving wheel | 105 | mm |
| Distance between driving wheel | 718 | mm |
| Maximum accelerates | 0.6 | m/s2 |
| Guided method | QR | - |
| Drive method | Different drive | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, Q.; Zang, C.; Zhu, S.; Gan, C.; Liu, Y. Formation Control of Dual Auto Guided Vehicles Based on Compensation Method in 5G Networks. Machines 2021, 9, 318. https://doi.org/10.3390/machines9120318
Wang L, Liu Q, Zang C, Zhu S, Gan C, Liu Y. Formation Control of Dual Auto Guided Vehicles Based on Compensation Method in 5G Networks. Machines. 2021; 9(12):318. https://doi.org/10.3390/machines9120318
Chicago/Turabian StyleWang, Liuquan, Qiang Liu, Chenxin Zang, Sanying Zhu, Chaoyang Gan, and Yanqiang Liu. 2021. "Formation Control of Dual Auto Guided Vehicles Based on Compensation Method in 5G Networks" Machines 9, no. 12: 318. https://doi.org/10.3390/machines9120318
APA StyleWang, L., Liu, Q., Zang, C., Zhu, S., Gan, C., & Liu, Y. (2021). Formation Control of Dual Auto Guided Vehicles Based on Compensation Method in 5G Networks. Machines, 9(12), 318. https://doi.org/10.3390/machines9120318




