Assessment of Dynamic Bayesian Models for Gas Turbine Diagnostics, Part 2: Discrimination of Gradual Degradation and Rapid Faults
Abstract
:1. Introduction
2. Methods
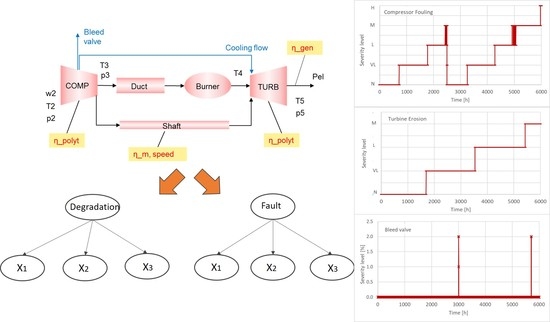
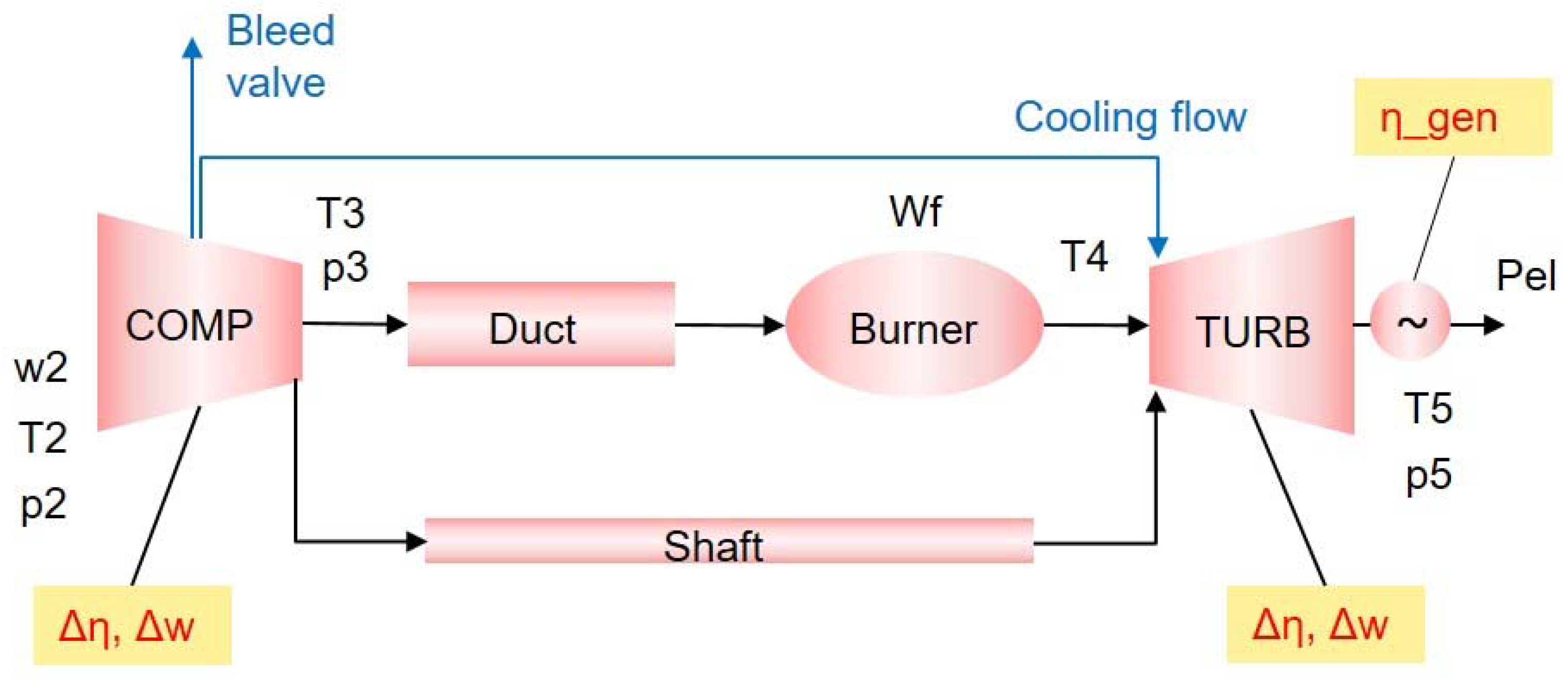
2.1. Gas Turbine Model
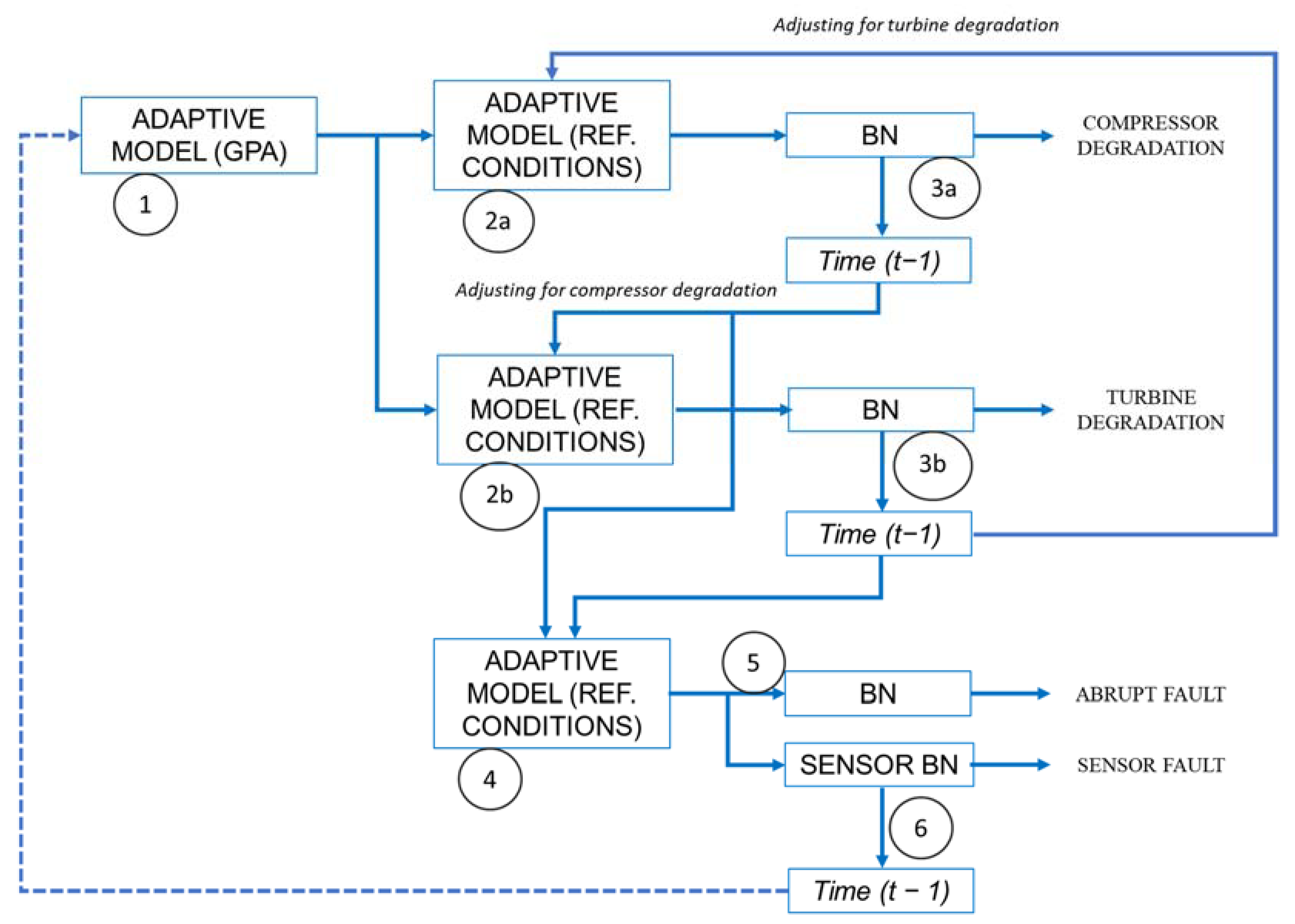
2.2. Muti-Layer Diagnostic System
- 1
- Estimate performance deviation factors in the rotating components via means of gas path analysis (GPA) with the performance model;
- 2a
- Adjust for turbine degradation: take the difference between turbine performance factors at time t and t − 1 to use in the next step, then simulate the GT system at reference (REF) conditions using the compressor performance factors from step 1 and the adjusted turbine performance factors;
- 2b
- Adjust for compressor degradation: take the difference between compressor performance factors at time t and t − 1 to use in the next step, then simulate the GT system at reference conditions using the turbine performance factors from step 1 and the adjusted compressor performance factors;
- 3a
- Feed the results of step 2a to a dynamic Bayesian network to identify compressor degradation, which gives the compressor performance for time t + 1;
- 3b
- Feed the results of step 2b to a dynamic Bayesian network to identify turbine degradation, which gives the compressor performance for time t + 1;
- 4
- Adjust for compressor and turbine degradation: performance factors for both compressor and turbine are taken as the difference between t and t − 1 and the model is run at reference conditions to isolate the effect of rapid or abrupt faults;
- 5
- Feed the residuals from step 4 to a BN to identify an abrupt fault (e.g., BV leakage);
- 6
- Feed the residuals from step 4 to the final BN to identify a sensor fault, and send the information to adjust the matching scheme at the next time step t + 1.
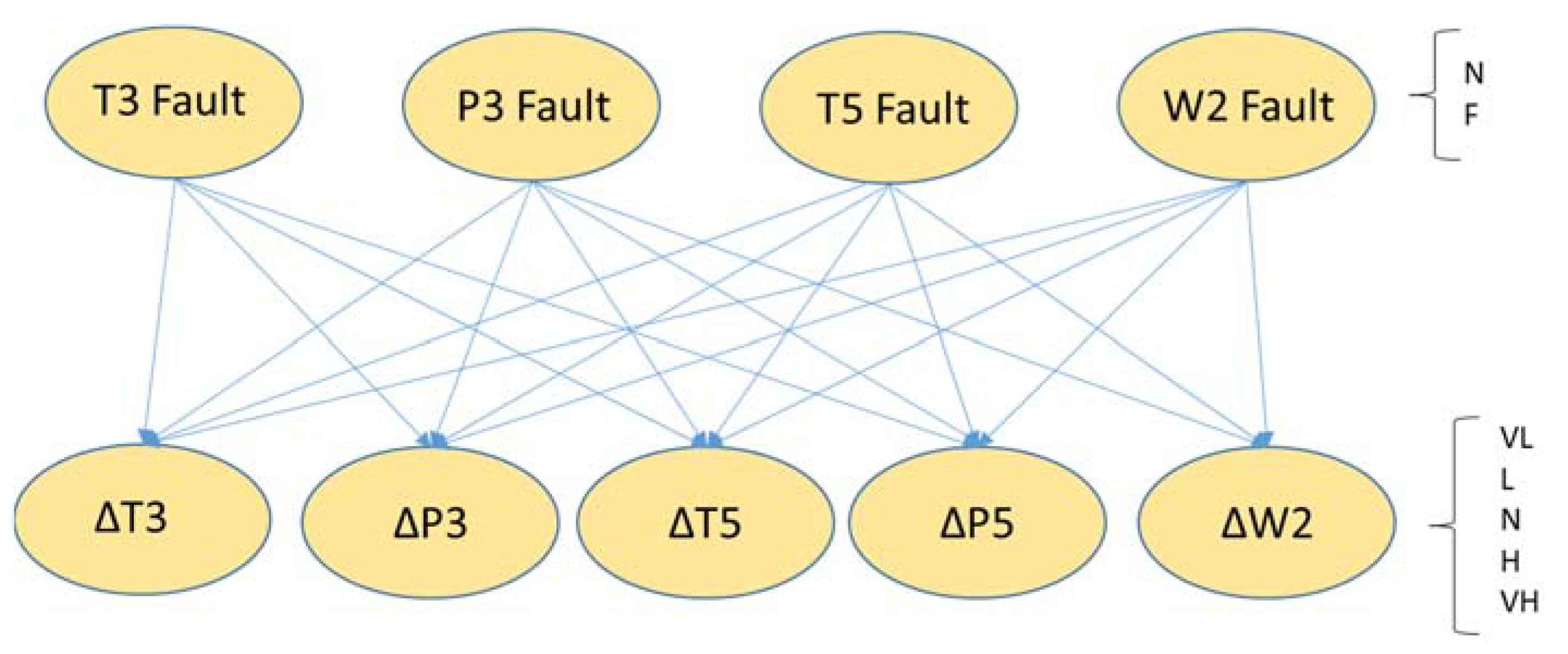
2.3. Bayesian Networks
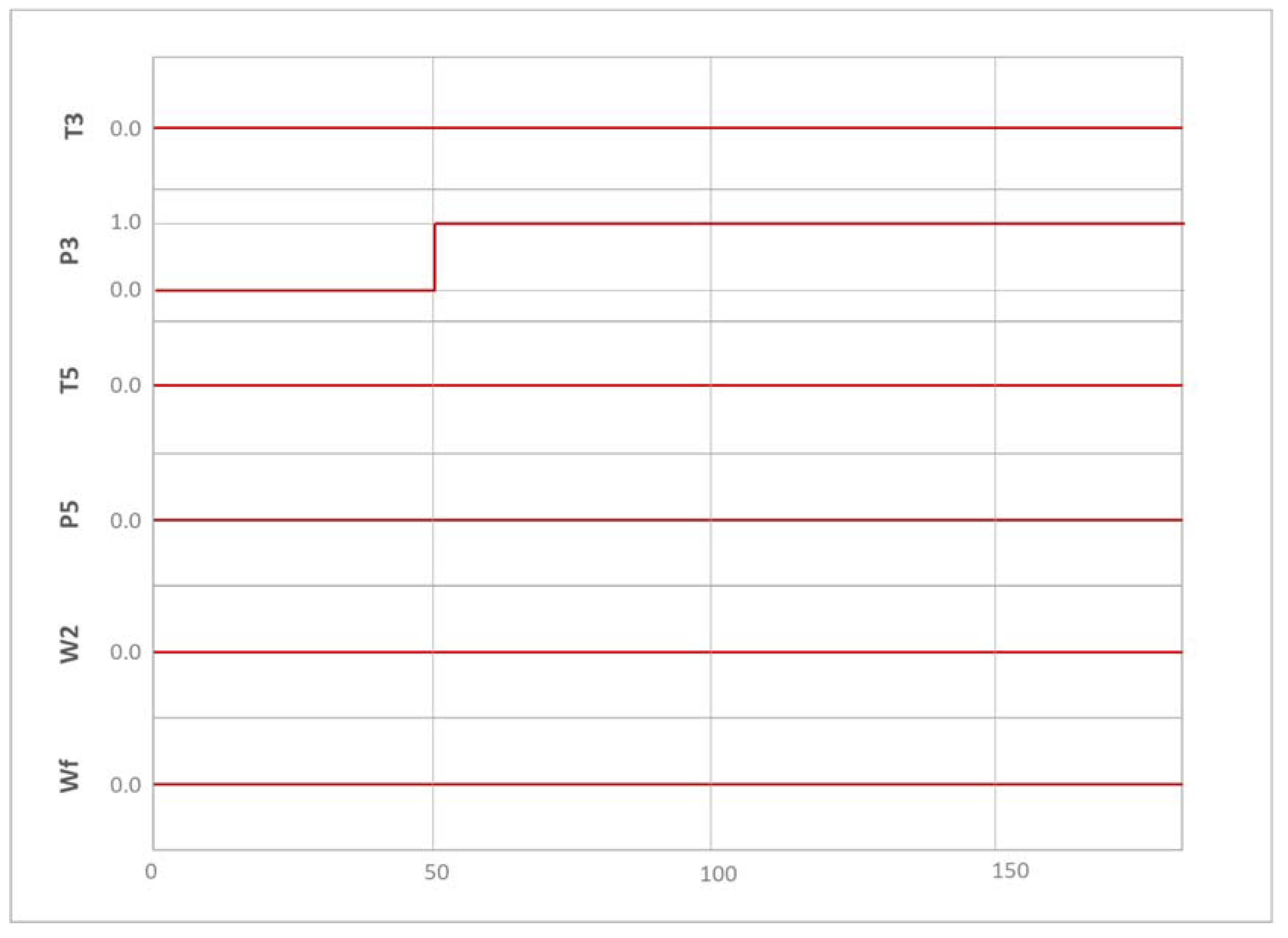
2.4. Tested Scenarios
3. Results and Discussion
3.1. Scenario 1
3.2. Scenario 2
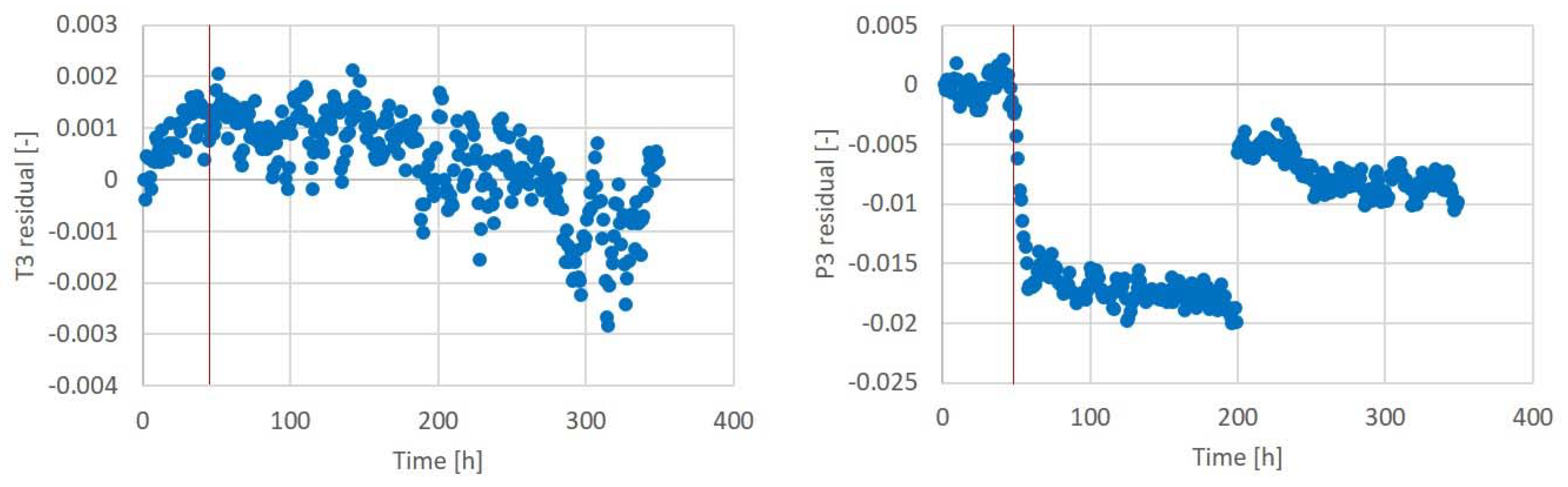
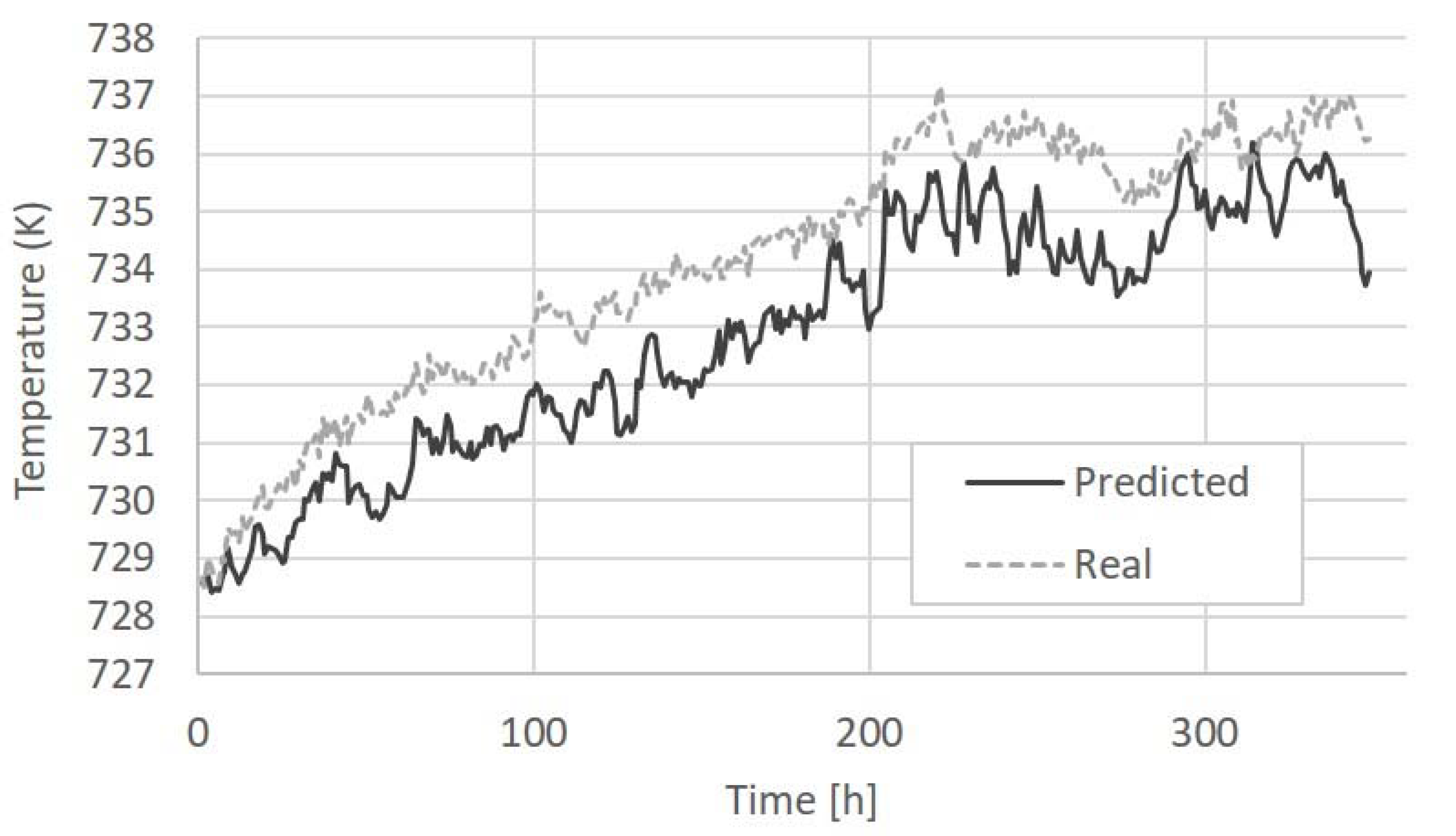
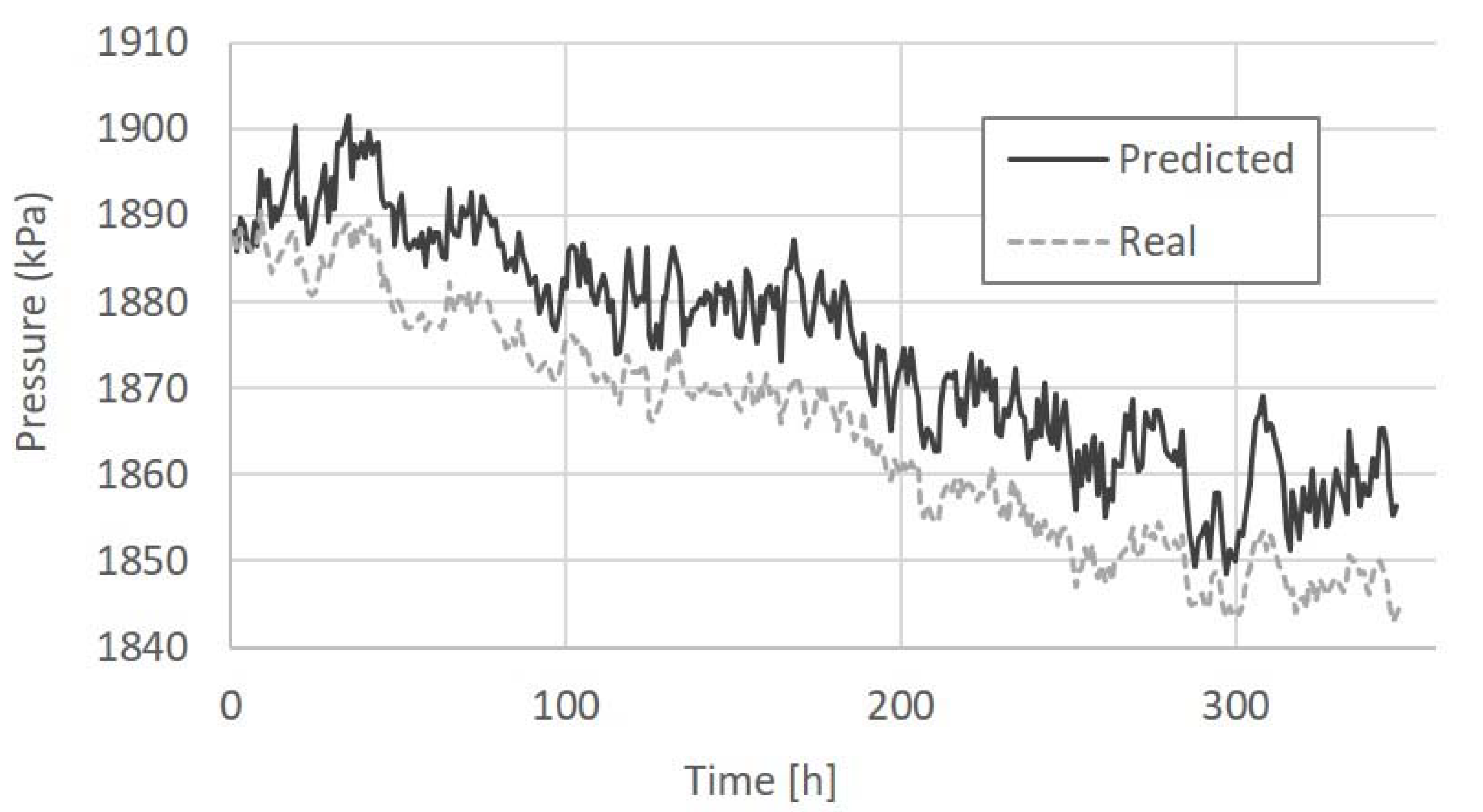
3.3. Scenario 3
3.4. Adaptability to Different Machines
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | |
| ANN | Artificial neural network |
| BN | Bayesian network |
| BV | Bleed valve |
| CF | Compressor fouling |
| CPT | Conditional probability table |
| DBN | Dynamic Bayesian network |
| GPA | Gas path analysis |
| GT | Gas turbine |
| H | High |
| IGV | Inlet guide vane |
| L | Low |
| M | Medium |
| N | Normal |
| TE | Turbine erosion |
| VH | Very high |
| VL | Very low |
| Symbols and Greek Letter | |
| r | Residual |
| S | Fault severity |
| Flow capacity | |
| z | Measurement |
| η | Efficiency |
| Subscripts | |
| ref | Reference conditions |
| t | Time |
References
- Lin, Y.; Li, X.; Hu, Y. Deep Diagnostics and Prognostics: An Integrated Hierarchical Learning Framework in PHM Applications. Appl. Soft Comput. 2018, 72, 555–564. [Google Scholar] [CrossRef]
- Marinai, L.; Singh, R.; Curnock, B.; Probert, D. Detection and prediction of the performance deterioration of a turbofan engine. In Proceedings of the ASME Turbo Expo, Atlanta, GA, USA, 16–19 June 2003. [Google Scholar]
- Simon, D.L. An Integrated Architecture for On-Board Aircraft Engine Performance Trend Monitoring and Gas Path Fault Diagnostics; Technical Memorandum; NASA Glenn Research Center: Cleveland, OH, USA, 2010.
- Kobayashi, T.; Simon, D.L. Integration of On-Line and Off-Line Diagnostic Algorithms for Aircraft Engine Health Management. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Volponi, A.J. Gas Turbine Engine Health Management: Past, Present, and Future Trends. J. Eng. Gas Turbines Power 2014, 136, 051201. [Google Scholar] [CrossRef]
- Kestner, B.K.; Lee, Y.K.; Voleti, G.; Mavris, D.N.; Kumar, V.; Lin, T. Diagnostics of highly degraded industrial gas turbines using Bayesian networks. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Fentaye, A.D.; Zaccaria, V.; Kyprianidis, K. Discrimination of rapid and gradual deteriorations for an enhanced gas turbine life-cycle monitoring and diagnostics. Int. J. Progn. Health Manag. 2021, 12. [Google Scholar] [CrossRef]
- Simon, D.L. Propulsion Diagnostic Method Evaluation Strategy (ProDiMES) User’s Guide. NASA/TM—2010-215840. June 2010. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20100005639.pdf (accessed on 30 March 2021).
- Liu, Y.; Su, M. Nonlinear Model Based Diagnostic of Gas Turbine Faults: A Case Study. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Lu, F.; Gao, T.; Huang, J.; Qiu, X. A novel distributed extended Kalman filter for aircraft engine gas-path health estimation with sensor fusion uncertainty. Aerosp. Sci. Technol. 2019, 84, 90–100. [Google Scholar] [CrossRef]
- Cruz-Manzo, S.; Panov, V.; Zhang, Y. Gas Path Fault and Degradation Modelling in Twin-Shaft Gas Turbines. Machines 2018, 6, 43. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Quan, H.L.; Tang, H. An Approach for Optimal Measurements Selection on Gas Turbine Engine Fault Diagnosis. J. Eng. Gas Turbines Power 2015, 137, 071203. [Google Scholar] [CrossRef]
- Zhong, S.-S.; Fu, S.; Lin, L. A novel gas turbine fault diagnosis method based on transfer learning with CNN. Measurement 2019, 137, 435–453. [Google Scholar] [CrossRef]
- Mathioudakis, K.; Romessis, C. Probabilistic neural networks for validation of on-board jet engine data. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 218, 59–72. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, H.; Weng, S. A New Gas Path Fault Diagnostic Method of Gas Turbine Based on Support Vector Machine. J. Eng. Gas Turbines Power 2015, 137, 102605. [Google Scholar] [CrossRef]
- Loboda, I.; Pérez-Ruiz, J.L.; Yepifanov, S. A benchmarking analysis of a data-driven gas turbine diagnostic approach. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Wu, Z.; Lin, W.; Ji, Y. An Integrated Ensemble Learning Model for Imbalanced Fault Diagnostics and Prognostics. IEEE Access 2018, 6, 8394–8402. [Google Scholar] [CrossRef]
- Roumeliotis, I.; Aretakis, N.; Alexiou, A. Industrial gas turbine health and performance assessment with field data. J. Eng. Gas Turbines Power 2017, 139, 051202. [Google Scholar] [CrossRef]
- Kyriazis, A.; Mathioudakis, K. Gas turbines diagnostics using weighted parallel decision fusion framework. In Proceedings of the 8th European Turbomachinery Conference, Graz, Austria, 23–27 March 2009. [Google Scholar]
- Palmé, T.; Liard, F.; Cameron, D. Hybrid Modeling of Heavy Duty Gas Turbines for On-Line Performance Monitoring. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Kyriazis, A.; Mathioudakis, K. Enhanced fault localization using probabilistic fusion with gas path analysis algorithms. J. Eng. Gas Turbines Power 2009, 131, 051601. [Google Scholar] [CrossRef]
- Zaccaria, V.; Fentaye, A.D.; Stenfelt, M.; Kyprianidis, K. Probabilistic Model for Aero-Engine Fleet Condition Monitoring. Aerospace 2020, 7, 66. [Google Scholar] [CrossRef]
- Rohmer, J. Uncertainties in conditional probability tables of discrete Bayesian Belief Networks: A comprehensive review. Eng. Appl. Artif. Intell. 2020, 88, 103384. [Google Scholar] [CrossRef] [Green Version]
- Losi, E.; Venturini, M.; Manservigi, L. Gas Turbine Health State Prognostics by Means of Bayesian Hierarchical Models. In Proceedings of the ASME TURBO EXPO 2019: Power for Land, Sea and Air, Phoenix, AZ, USA, 11–15 June 2019. [Google Scholar]
- Lee, Y.K.; Mavris, D.N.; Volovoi, V.V.; Yuan, M.; Fisher, T. A fault diagnosis method for industrial gas turbines using Bayesian data analysis. J. Eng. Gas Turbines Power 2010, 132, 041602. [Google Scholar] [CrossRef]
- Li, J.; Ying, Y. A method to improve the robustness of gas turbine gas-path fault diagnosis against sensor faults. IEEE Trans. Reliab. 2018, 67, 3–12. [Google Scholar] [CrossRef]
- Jombo, G.; Zhang, Y.; Griffiths, J.D.; Latimer, T. Automated Gas Turbine Sensor Fault Diagnostics. In Proceedings of the ASME Turbo Expo 2018, Oslo, Norway, 11–15 June 2018. [Google Scholar] [CrossRef]
- Hu, Y.; Zhu, J.; Sun, Z.; Gao, L. Sensor fault diagnosis of gas turbine engines using an integrated scheme based on improved least squares support vector regression. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 607–623. [Google Scholar] [CrossRef]
- Zhang, Y.; Bingham, C.; Garlick, M.; Gallimore, M. Applied fault detection and diagnosis for industrial gas turbine systems. Int. J. Autom. Comput. 2017, 14, 463–473. [Google Scholar] [CrossRef] [Green Version]
- Zaccaria, V.; Fentaye, A.D.; Kyprianidis, K. Assessment of dynamic Bayesian models for gas turbine diagnostics, Part 1: Prior probability analysis. Machines 2021, 9, 298. [Google Scholar] [CrossRef]
- Kurz, R.; Brun, K. Degradation in gas turbine systems. ASME J. Eng. Gas Turbine Power 2001, 123, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Yuan, H.; Wu, N.; Chen, X.; Wang, Y. Fault Diagnosis of Rolling Bearing Based on Shift Invariant Sparse Feature and Optimized Support Vector Machine. Machines 2021, 9, 98. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Kim, K.; Uluyol, O.; Parthasarathy, G.; Mylaraswamy, D. Fault Diagnosis of Gas Turbine Engine LRUs Using the Startup Characteristics. In Proceedings of the Conference of Prognostics and Health Management Society, Minneapolis, MN, USA, 23–27 September 2012. [Google Scholar]
- Zaccaria, V.; Stenfelt, M.; Sjunnesson, A.; Hansson, A.; Kyprianidis, K. A model-based solution for gas turbine diagnostics: Simulations and experimental verification. In Proceedings of the ASME TURBO EXPO 2019: Power for Land, Sea and Air, Phoenix, AZ, USA, 11–15 June 2019. [Google Scholar]
- Najafi Saatlou, E.; Kyprianidis, K.G.; Sethi, V.; Abu, A.O.; Pilidis, P. On the trade-off between minimum fuel burn and maximum time between overhaul for an intercooled aeroengine. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 2424. [Google Scholar] [CrossRef]
- Stenfelt, M.; Zaccaria, V.; Kyprianidis, K. Automatic gas turbine matching scheme adaptation for robust GPA diagnostics. In Proceedings of the ASME Turbo Expo 2019: Power for Land, Sea and Air, Phoenix, AZ, USA, 11–15 June 2019. [Google Scholar]
- Pgmpy Documentation. Available online: pgmpy.org (accessed on 6 July 2021).
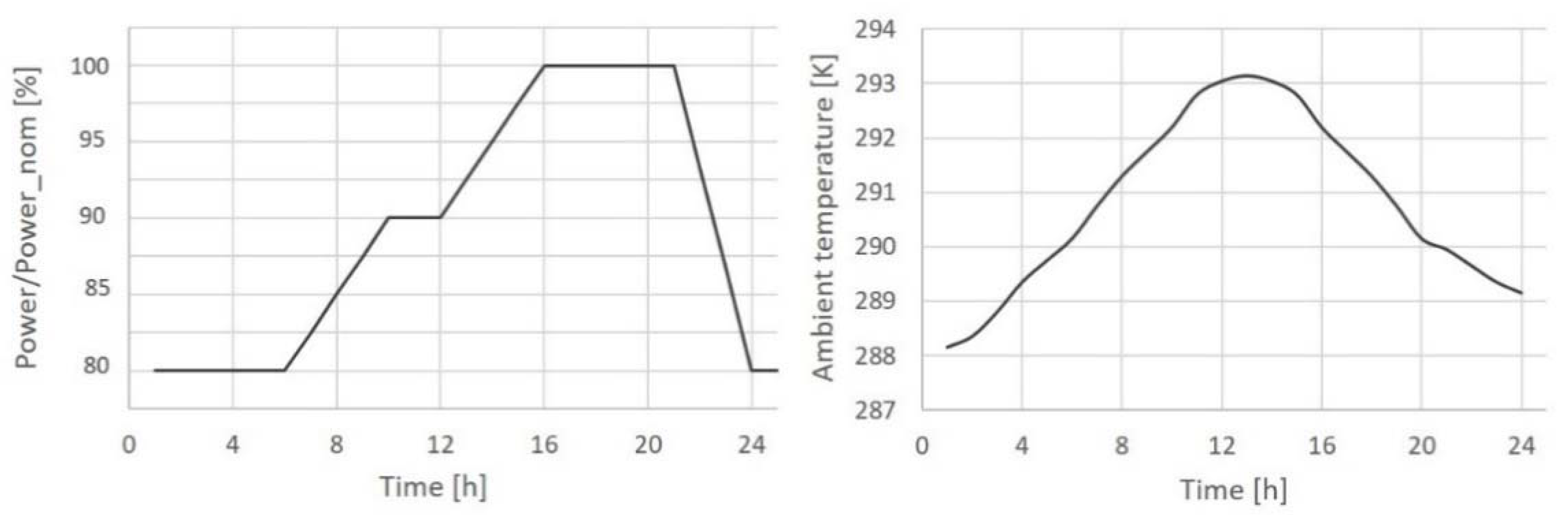
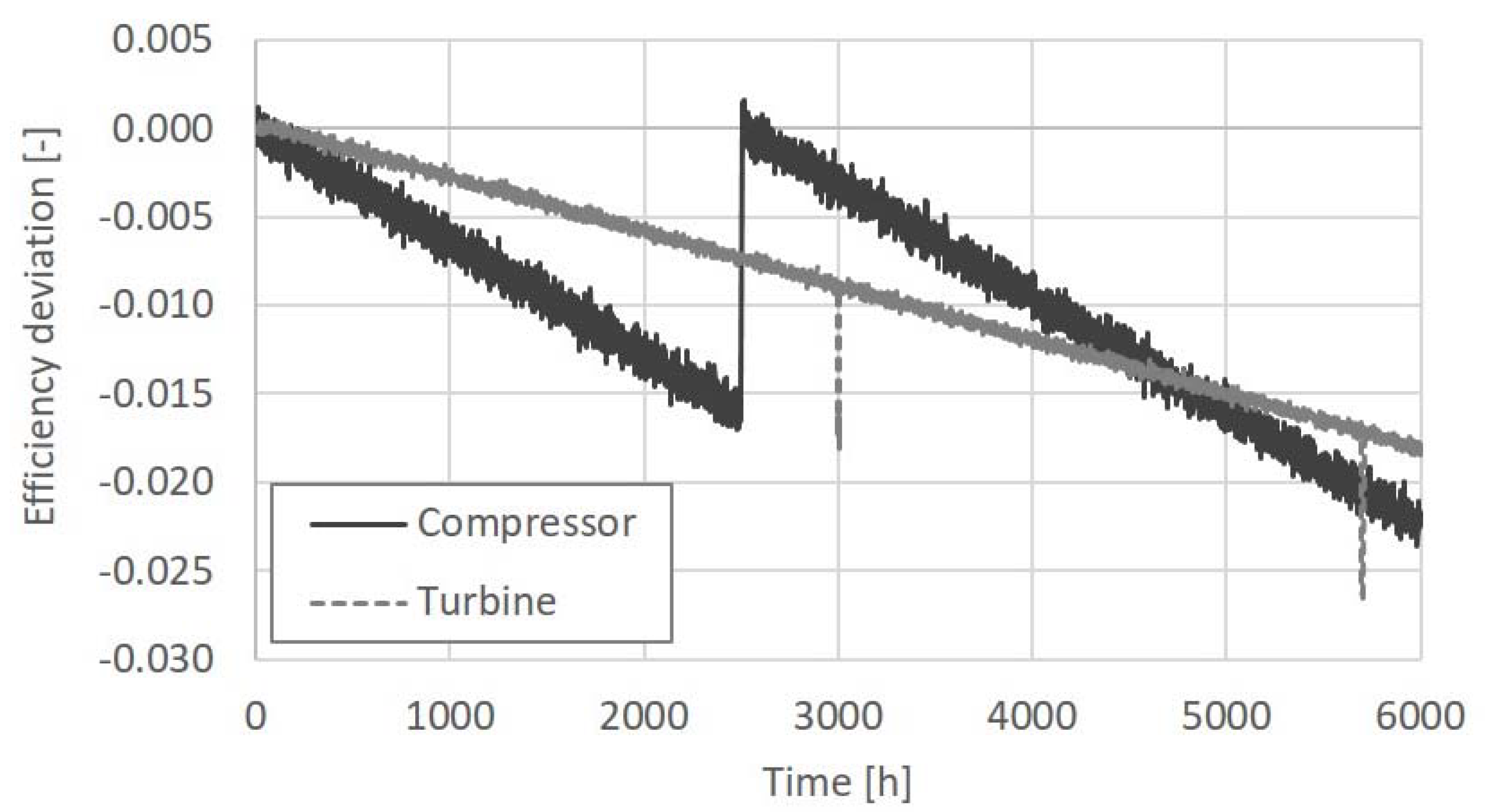


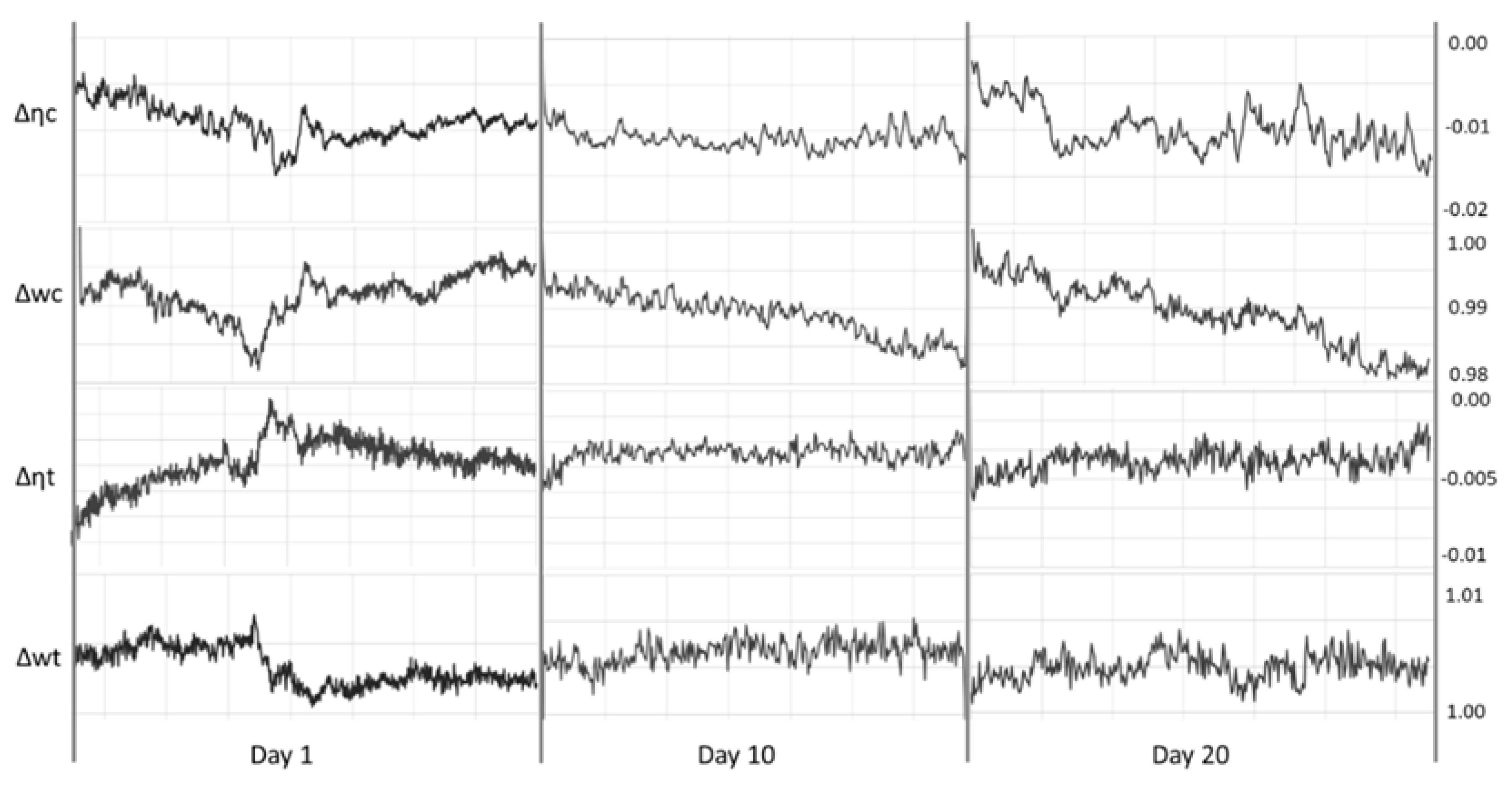



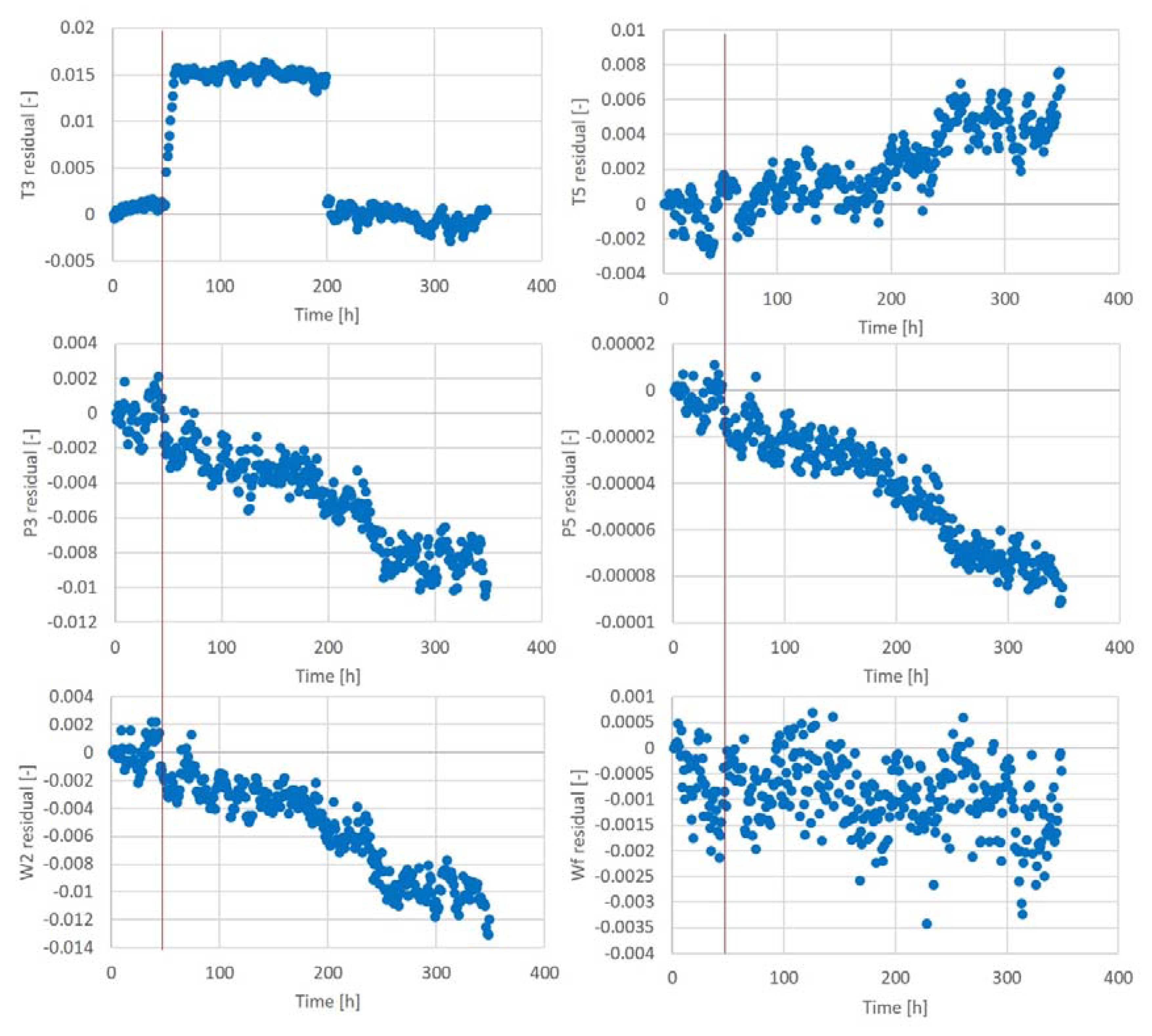

| Ambient temperature (Tamb) | 298.15 K |
| Ambient pressure (pamb) | 101.325 kPa |
| Relative humidity (RH) | 60% |
| GT power | 50 MW |
| N | VL | L | M | H |
|---|---|---|---|---|
| 99% | 0.25% | 0.25% | 0.25% | 0.25% |
| Scenario | Gradual Compressor Degradation | Gradual Turbine Degradation | Abrupt Fault |
|---|---|---|---|
| 1: Simulated | From 0% to 4% Maintenance at 2500 h | From 0% to 3% | BV 2% |
| 2: Field data | Unknown | Unknown | BV unknown% |
| 3: Field data + simulated | Unknown | Unknown | T3 and P3 faults 12.5% |
| Fault Type | True Positive Rate | False Positive Rate | True Negative Rate | False Negative Rate |
|---|---|---|---|---|
| CF | 99% | 4% | 96% | 1% |
| TE | 99% | 3.5% | 96.5% | 1% |
| BV | 99% | 0% | 100% | 1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaccaria, V.; Fentaye, A.D.; Kyprianidis, K. Assessment of Dynamic Bayesian Models for Gas Turbine Diagnostics, Part 2: Discrimination of Gradual Degradation and Rapid Faults. Machines 2021, 9, 308. https://doi.org/10.3390/machines9120308
Zaccaria V, Fentaye AD, Kyprianidis K. Assessment of Dynamic Bayesian Models for Gas Turbine Diagnostics, Part 2: Discrimination of Gradual Degradation and Rapid Faults. Machines. 2021; 9(12):308. https://doi.org/10.3390/machines9120308
Chicago/Turabian StyleZaccaria, Valentina, Amare Desalegn Fentaye, and Konstantinos Kyprianidis. 2021. "Assessment of Dynamic Bayesian Models for Gas Turbine Diagnostics, Part 2: Discrimination of Gradual Degradation and Rapid Faults" Machines 9, no. 12: 308. https://doi.org/10.3390/machines9120308
APA StyleZaccaria, V., Fentaye, A. D., & Kyprianidis, K. (2021). Assessment of Dynamic Bayesian Models for Gas Turbine Diagnostics, Part 2: Discrimination of Gradual Degradation and Rapid Faults. Machines, 9(12), 308. https://doi.org/10.3390/machines9120308