Stiffness Modelling and Performance Evaluation of a Soft Cardiac Fixator Flexible Arm with Granular Jamming
Abstract
1. Introduction
2. Methods
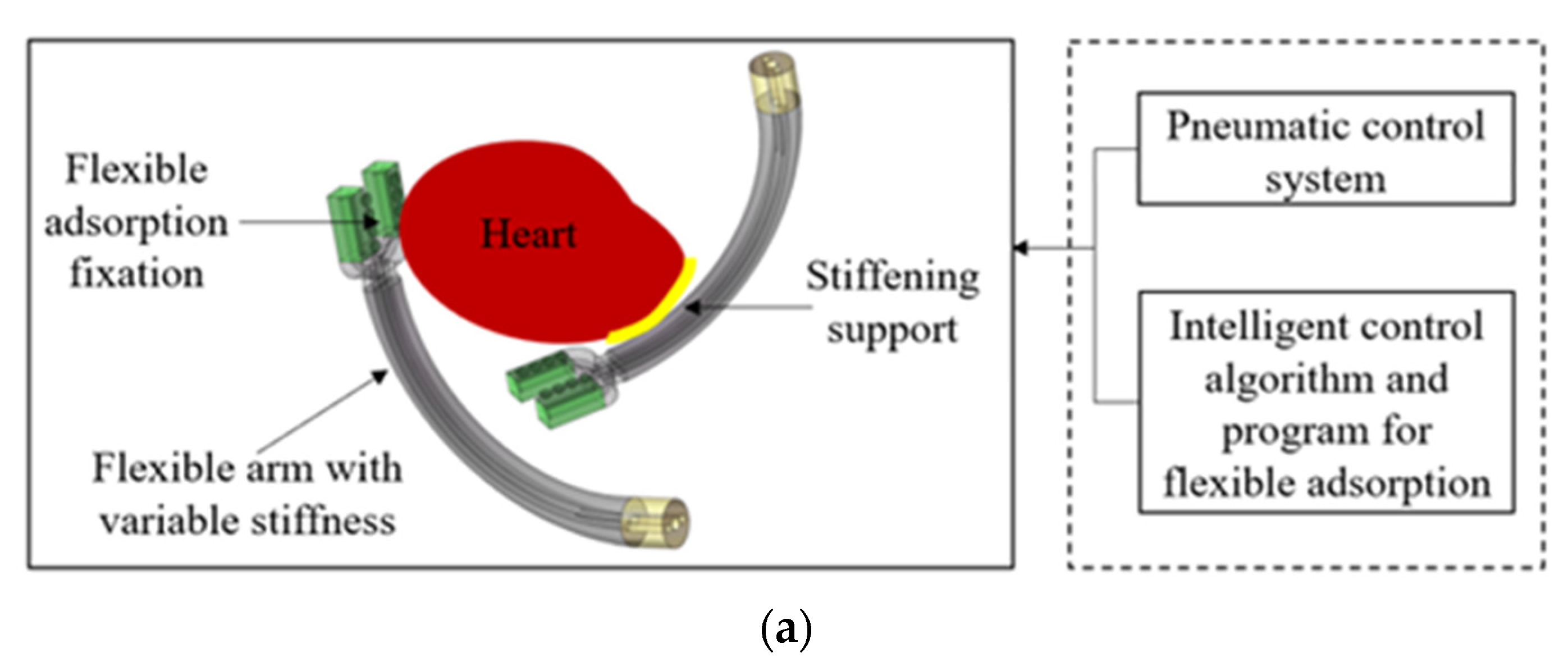
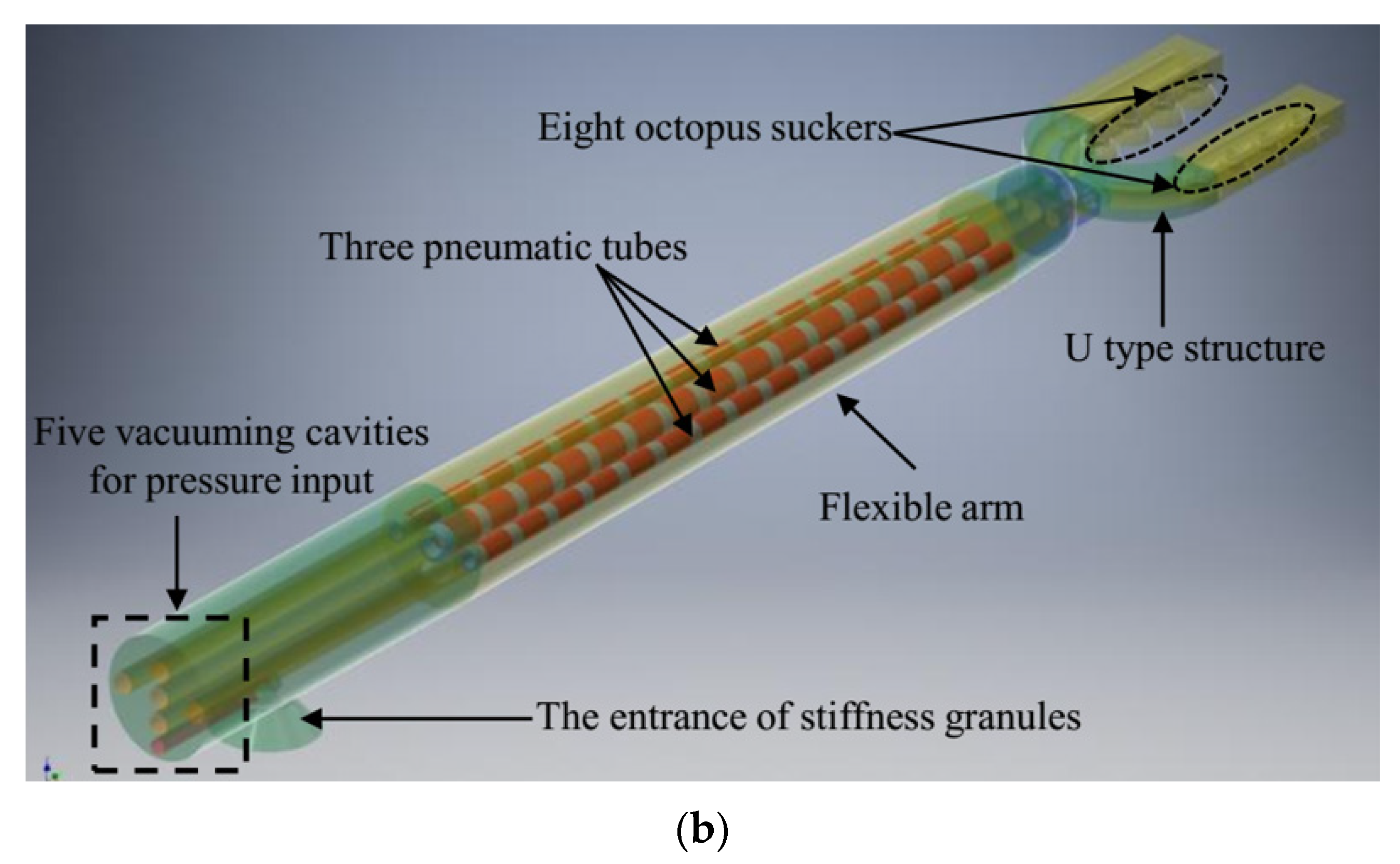
2.1. Design of the Soft Cardiac Fixator with Variable Stiffness
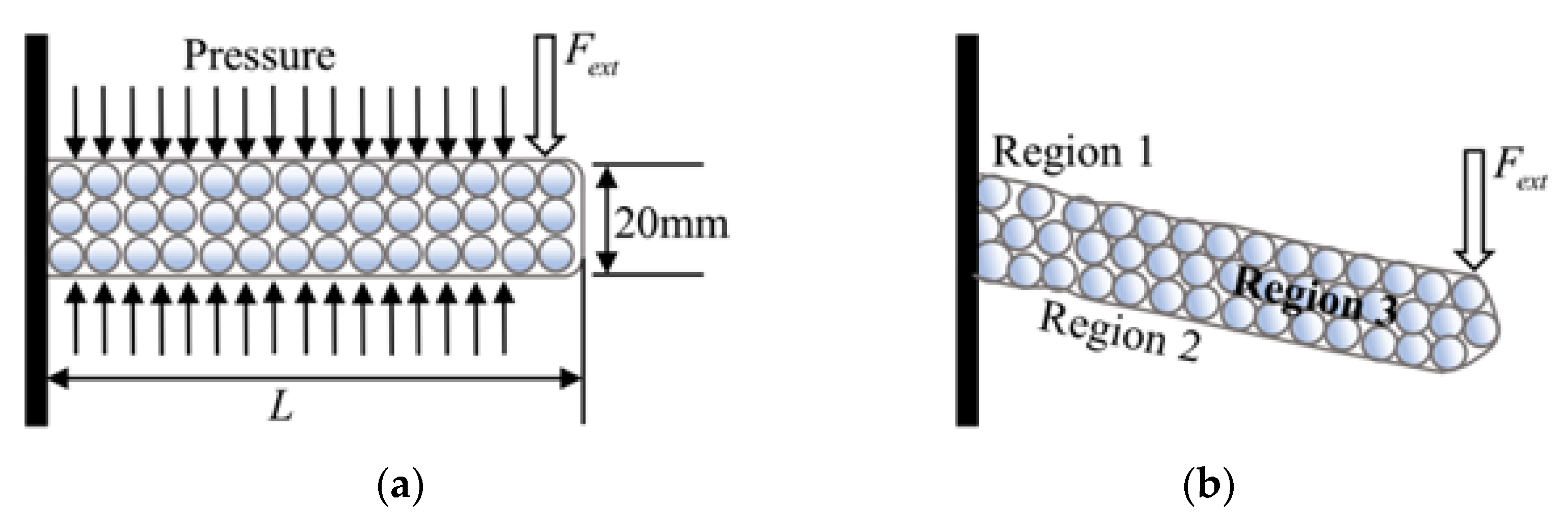
2.2. Modelling the Variable Stiffness of the Flexible Arm
2.3. Experiments on the Soft Manipulator
3. Results and Discussion
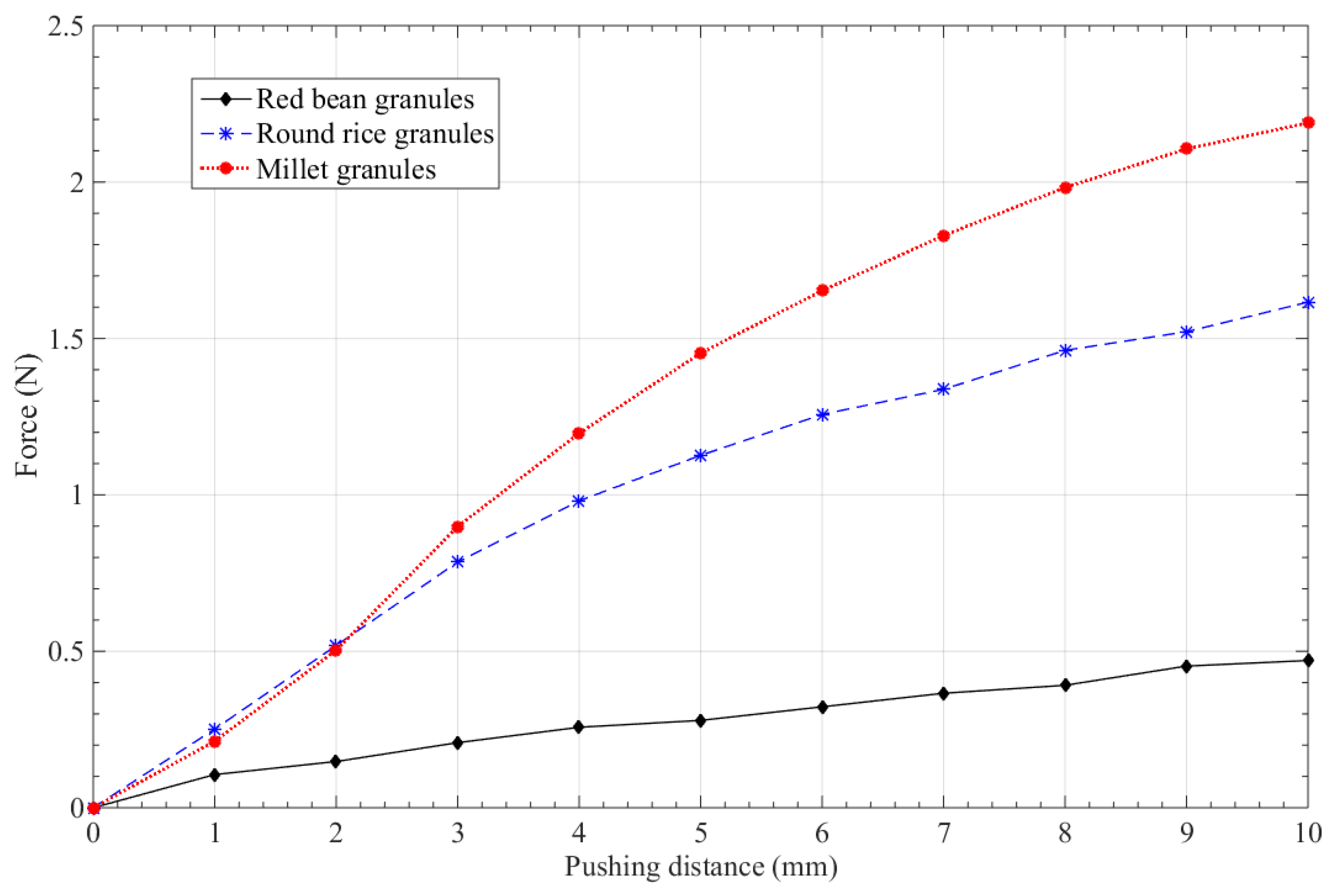
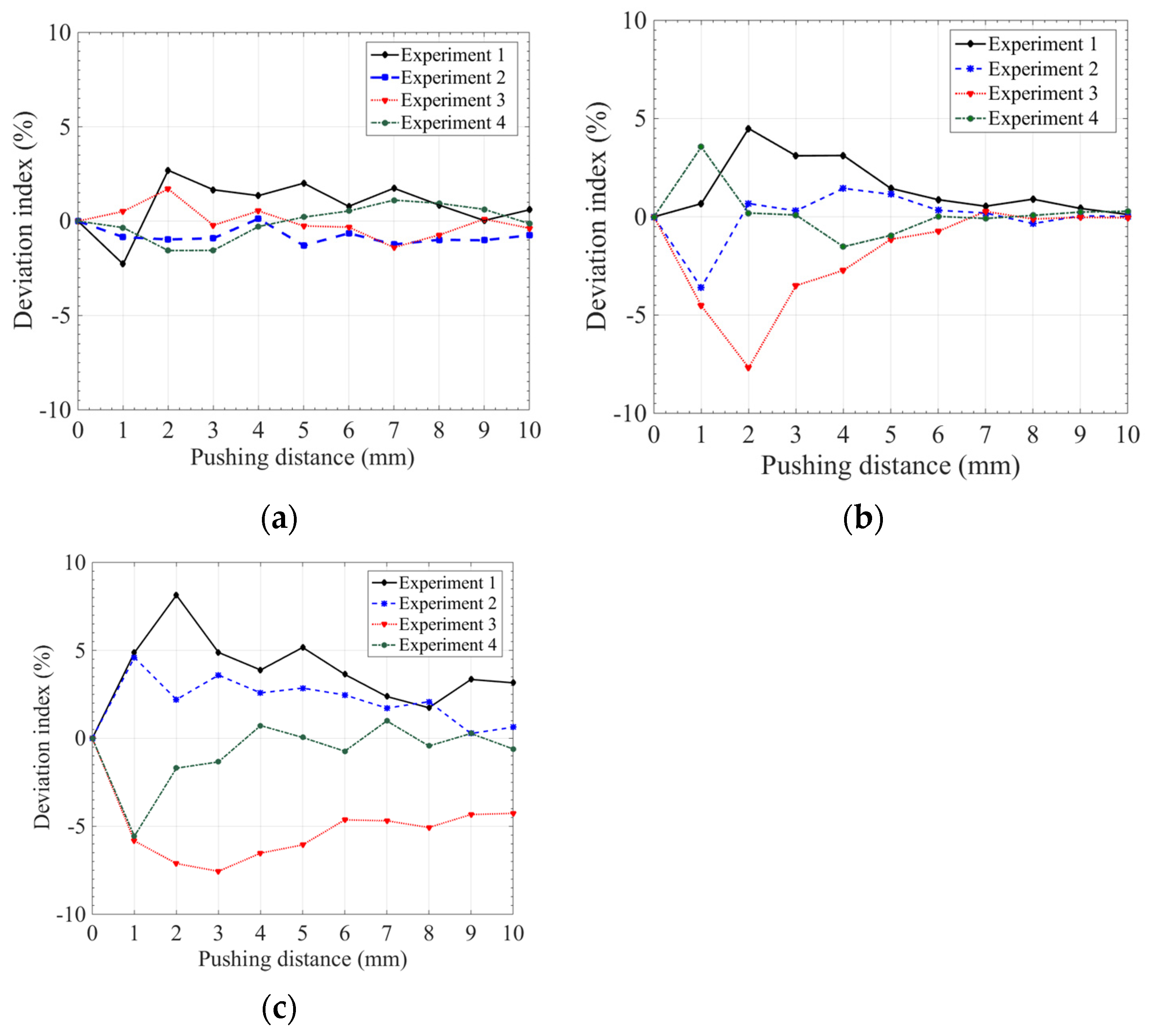
3.1. Effect of Granular Size
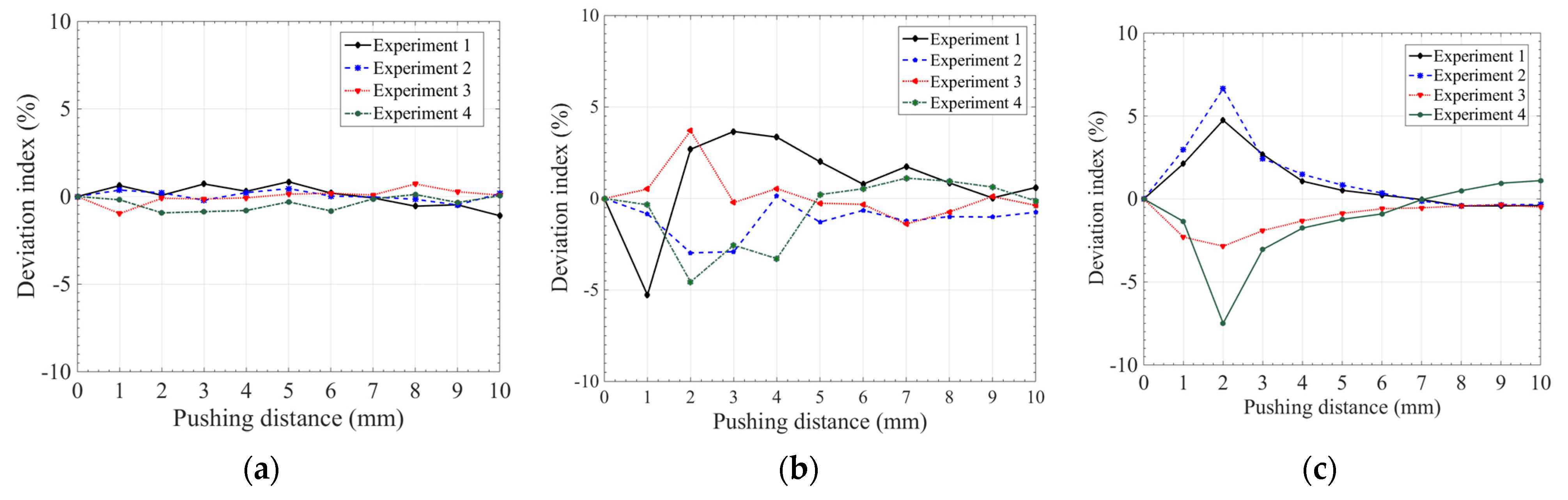
3.2. Effect of Manipulator Length
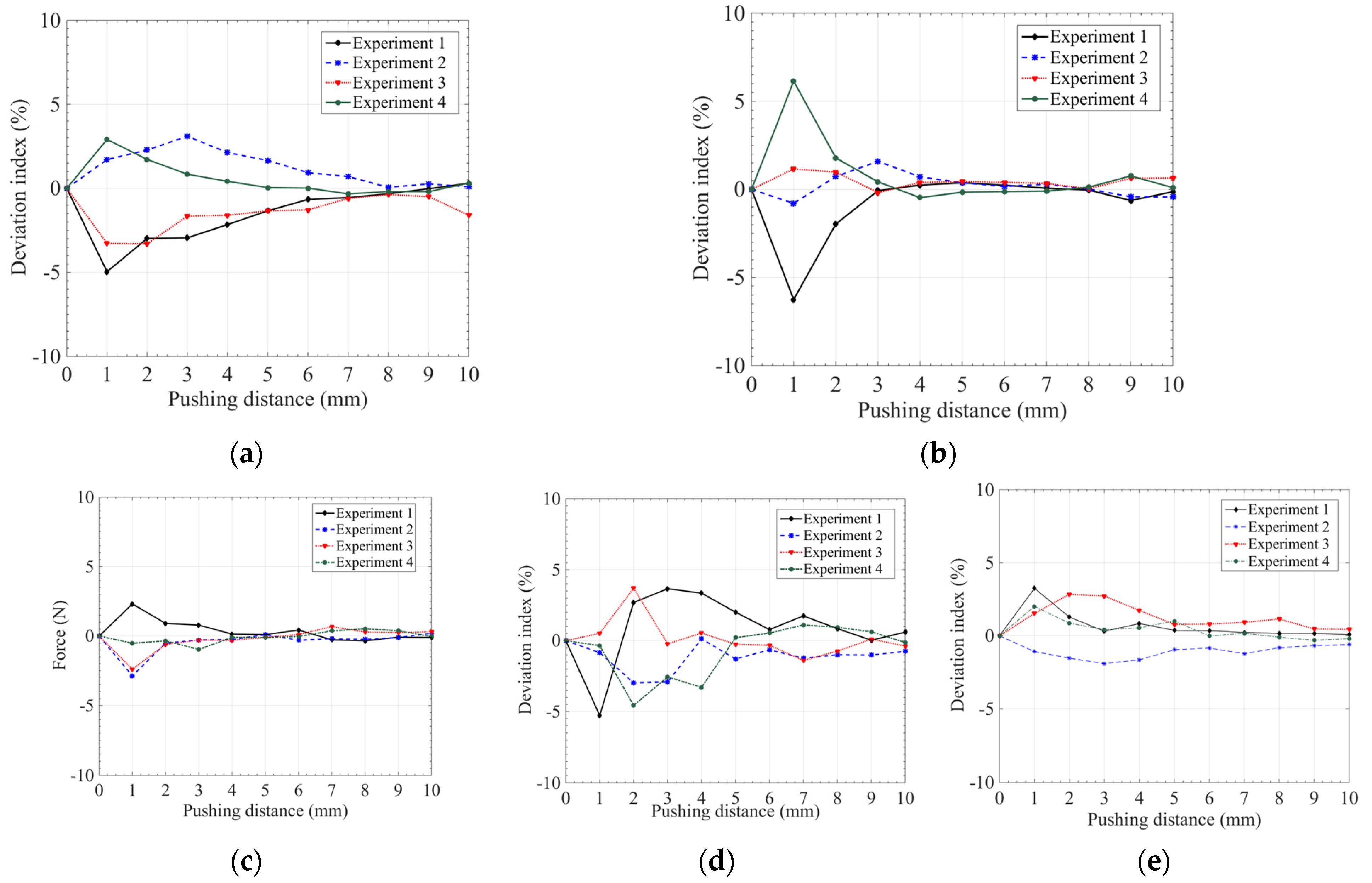
3.3. Effect of Input Pressure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soltoski, P.; Bergsland, J.; Salerno, T.A.; Karamanoukian, H.L.; D’Anconet, G.; Ricci, M.; Panosal, A.L. Techniques of Exposure and Stabilization in Off-Pump Coronary Artery Bypass Graft. Echocardiography 1999, 2, 392–400. [Google Scholar] [CrossRef]
- Cianchetti, M.; Ranzani, T.; Gerboni, G.; De Falco, I.; Laschi, C.; Menciassi, A. STIFF-FLOP surgical manipulator: Mechanical design and experimental characterization of the single module. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3576–3581. [Google Scholar]
- Nabil, E.; Belhassen-Chedli, B.; Grigore, G. Soft material modeling for robotic task formulation and controlling the muscle separation process. Robot. Comput. Integr. Manuf. 2015, 32, 37–52. [Google Scholar] [CrossRef]
- Tang, G.; Webb, P.; Thrower, J. The development and evaluation of Robot Light Skin: A novel robot signalling system to improve communication in industrial human–robot collaboration. Robot. Comput. Integr. Manuf. 2019, 56, 85–94. [Google Scholar] [CrossRef]
- Ranzani, T.; Gerboni, G.; Cianchetti, M.; Menciassi, A. A bioinspired soft manipulator for minimally invasive surgery. Bioinspir. Biomim. 2015, 10, 035008. [Google Scholar] [CrossRef]
- Zhao, H.; Jalving, J.; Huang, R.; Knepper, R.; Ruina, A.; Shepherd, R. A Helping Hand: Soft Orthosis with Integrated Optical Strain Sensors and EMG Control. IEEE Robot. Autom. Mag. 2016, 23, 55–64. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Galloway, K.C. Soft manipulatoric glove for combined assistance and at-home rehabilitation. Manip. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef]
- Sareh, S.; Althoefer, K.; Li, M.; Noh, Y.; Tramacere, F.; Sareh, P.; Mazzolai, B.; Kovac, M. Anchoring like octopus: Biologically inspired soft artificial sucker. J. R. Soc. Interface 2017, 14, 20170395. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Kouzani, A.Z.; Khoo, S.Y.; Moghadam, A.A.A.; Gibson, I.; Kaynak, A. Evolution of 3D printed soft actuators. Sens. Actuators A Phys. 2016, 250, 258–272. [Google Scholar] [CrossRef]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef]
- Luo, M.; Skorina, E.H.; Tao, W.; Chen, F.; Ozel, S.; Sun, Y.; Onal, C.D. Toward Modular Soft Robotics: Proprioceptive Curvature Sensing and Sliding-Mode Control of Soft Bidirectional Bending Modules. Soft Robot. 2017, 4, 117–125. [Google Scholar] [CrossRef]
- Robertson, M.A.; Paik, J. New soft robots really suck: Vacuum-powered systems empower diverse capabilities. Sci. Robot. 2017, 2, eaan6357. [Google Scholar] [CrossRef]
- Sandesh, R.S.; Venkatesan, N. Novel approach to control of robotic hand using flex sensors. Int. J. Robot. Autom. 2014, 3, 3234–3244. [Google Scholar]
- Ranzani, T.; Cianchetti, M.; Gerboni, G.; De Falco, I.; Menciassi, A. A Soft Modular Manipulator for Minimally Invasive Surgery: Design and Characterization of a Single Module. IEEE Trans. Robot. 2016, 32, 187–200. [Google Scholar] [CrossRef]
- Zouari, L.; Abid, H.; Abid, M. Backstepping Controller for Electrically Driven Flexible Joint Manipulator Under Uncertainties. IAES Int. J. Robot. Autom. 2014, 4, 156–163. [Google Scholar] [CrossRef]
- Payne, C.J.; Wamala, I.; Bautista-Salinas, D.; Saeed, M.; Van Story, D.; Thalhofer, T.; Horvath, M.A.; Abah, C.; del Nido, P.J.; Walsh, C.J.; et al. Soft robotic ventricular assist device with septal bracing for therapy of heart failure. Sci. Robot. 2017, 2, eaan6736. [Google Scholar] [CrossRef]
- Cheng, N.G.; Lobovsky, M.B.; Keating, S.J.; Setapen, A.M.; Gero, K.I.; Hosoi, A.E.; Iagnemma, K.D. Design and Analysis of a Robust, Low-cost, Highly Articulated manipulator enabled by jamming of granular media. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–19 May 2012; pp. 4328–4333. [Google Scholar]
- Kim, Y.-J.; Cheng, S.; Kim, S.; Iagnemma, K. A Novel Layer Jamming Mechanism with Tunable Stiffness Capability for Minimally Invasive Surgery. IEEE Trans. Robot. 2013, 29, 1031–1042. [Google Scholar] [CrossRef]
- Kim, Y.J.; Cheng, S.; Kim, S.; Iagnemma, K. A stiffness-adjustable hyper redundant manipulator using a variable neutral-line mechanism for minimally invasive surgery. IEEE Trans. Robot. 2014, 30, 382–395. [Google Scholar] [CrossRef]
- Camarillo, D.B.; Milne, C.F.; Carlson, C.R.; Zinn, M.R.; Salisbury, J.K. Mechanics Modeling of Tendon-Driven Continuum Manipulators. IEEE Trans. Robot. 2008, 24, 1262–1273. [Google Scholar] [CrossRef]
- Khodambashi, R.; Alsaid, Y.; Rico, R.; Marvi, H.; Peet, M.M.; Fisher, R.E.; Berman, S.; He, X.; Aukes, D.M. Heterogeneous Hydrogel Structures with Spatiotemporal Reconfigurability using Addressable and Tunable Voxels. Adv. Mater. 2021, 33, 2005906. [Google Scholar] [CrossRef]
- Park, J.E.; Jeon, J.; Park, S.J.; Won, S.; Ku, Z.; Wie, J.J. Enhancement of Magneto-Mechanical Actuation of Micropillar Arrays by Anisotropic Stress Distribution. Small 2020, 16, 2003179. [Google Scholar] [CrossRef] [PubMed]
- Degani, A.; Choset, H.; Zubiate, B.; Ota, T.; Zenati, M. Highly articulated robotic probe for minimally invasive surgery. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 17 June 2008; pp. 3273–3276. [Google Scholar] [CrossRef]
- Simaan, N. Snake-Like Units Using Flexible Backbones and Actuation Redundancy for Enhanced Miniaturization. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3012–3017. [Google Scholar]
- Jiang, S.; Chen, B.; Qi, F.; Cao, Y.; Ju, F.; Bai, D.; Wang, Y. A variable-stiffness continuum manipulators by an SMA-based sheath in minimally invasive surgery. Int. J. Med Robot. Comput. Assist. Surg. 2020, 16, e2081. [Google Scholar] [CrossRef]
- Dupont, P.E.; Lock, J.; Itkowitz, B.; Butler, E.J. Design and Control of Concentric-Tube Robots. IEEE Trans. Robot. 2010, 26, 209–225. [Google Scholar] [CrossRef]
- Suresh, A.; Udupa, G.; Gaba, D. Design and development of soft robotic hand for vertical farming in spacecraft. IAES Int. J. Robot. Autom. 2020, 9, 6–16. [Google Scholar] [CrossRef][Green Version]
- Cha, H.-J.; Koh, K.C.; Yi, B.-J. Stiffness modeling of a soft finger. Int. J. Control. Autom. Syst. 2014, 12, 111–117. [Google Scholar] [CrossRef]
- Stilli, A.; Wurdemann, H.A.; Althoefer, K. A Novel Concept for Safe, Stiffness-Controllable Robot Links. Soft Robot. 2017, 4, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Morrison, T.; Su, H.-J. Stiffness modeling of a variable stiffness compliant link. Mech. Mach. Theory 2020, 153, 104021. [Google Scholar] [CrossRef]
- Yufei, H.; Tianmiao, W.; Xi, F.; Kang, Y.; Ling, M.; Juan, G.; Li, W. A variable stiffness soft robotic gripper with low-melting-point alloy. In Proceedings of the 2017 36th Chinese Control Conference, Dalian, China, 26–28 July 2017; pp. 6781–6786. [Google Scholar]
- Wang, H.; Chen, Z.; Zuo, S. Flexible Manipulator with Low-Melting-Point Alloy Actuation and Variable Stiffness. Soft Robot. 2021. [CrossRef]
- Teall, O.; Pilegis, M.; Sweeney, J.; Gough, T.; Thompson, G.; Jefferson, A.; Lark, R.; Gardner, D. Development of high shrinkage polyethylene terephthalate (PET) shape memory polymer tendons for concrete crack closure. Smart Mater. Struct. 2017, 26, 045006. [Google Scholar] [CrossRef]
- Mitsuda, T.; Kuge, S.; Wakabayashi, M.; Kawamura, S. Wearable haptic display by the use of a Particle Mechanical Constraint. In Proceedings of the Proceedings 10th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Orlando, FL, USA, 24–25 March 2002; pp. 153–158. [Google Scholar]
- Amend, J.R.; Brown, E.; Rodenberg, N.; Jaeger, H.M.; Lipson, H. A Positive Pressure Universal Gripper Based on the Jamming of Granular Material. IEEE Trans. Robot. 2012, 28, 341–350. [Google Scholar] [CrossRef]
- Jiang, A.; Xynogalas, G.; Dasgupta, P.; Althoefer, K.; Nanayakkara, T. Design of a variable stiffness flexible manipulator with composite granular jamming and membrane coupling. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2922–2927. [Google Scholar]
- Tomokazu, T.; Kikuchi, S.; Suzuki, M.; Aoyagi, S. Vacuum gripper imitated octopus sucker-effect of liquid membrane for absorption. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–3 October 2015; pp. 2929–2936. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; He, Y.; Zhu, H.; Sun, G.; Zhu, L. Stiffness Modelling and Performance Evaluation of a Soft Cardiac Fixator Flexible Arm with Granular Jamming. Machines 2021, 9, 303. https://doi.org/10.3390/machines9120303
Gao L, He Y, Zhu H, Sun G, Zhu L. Stiffness Modelling and Performance Evaluation of a Soft Cardiac Fixator Flexible Arm with Granular Jamming. Machines. 2021; 9(12):303. https://doi.org/10.3390/machines9120303
Chicago/Turabian StyleGao, Likun, Yanlin He, Hangwei Zhu, Guangkai Sun, and Lianqing Zhu. 2021. "Stiffness Modelling and Performance Evaluation of a Soft Cardiac Fixator Flexible Arm with Granular Jamming" Machines 9, no. 12: 303. https://doi.org/10.3390/machines9120303
APA StyleGao, L., He, Y., Zhu, H., Sun, G., & Zhu, L. (2021). Stiffness Modelling and Performance Evaluation of a Soft Cardiac Fixator Flexible Arm with Granular Jamming. Machines, 9(12), 303. https://doi.org/10.3390/machines9120303




