Experimental Research and Numerical Analysis of Pressure Fluctuation Characteristics of Rim Driven Propulsion Pump Outlet
Abstract
:1. Introduction
2. The Research Model and Test
2.1. Research Model
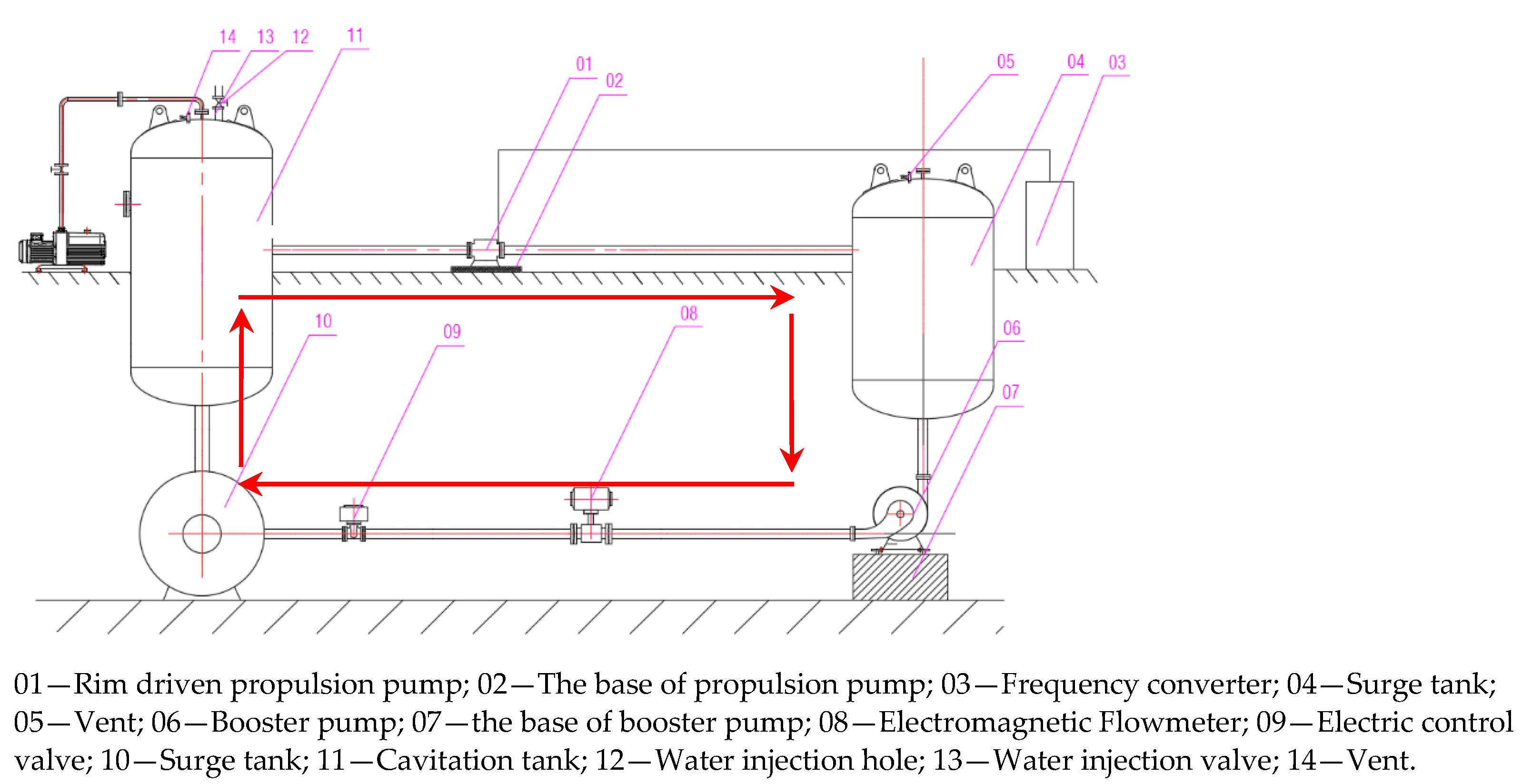
2.2. The Introduction of Test Rig
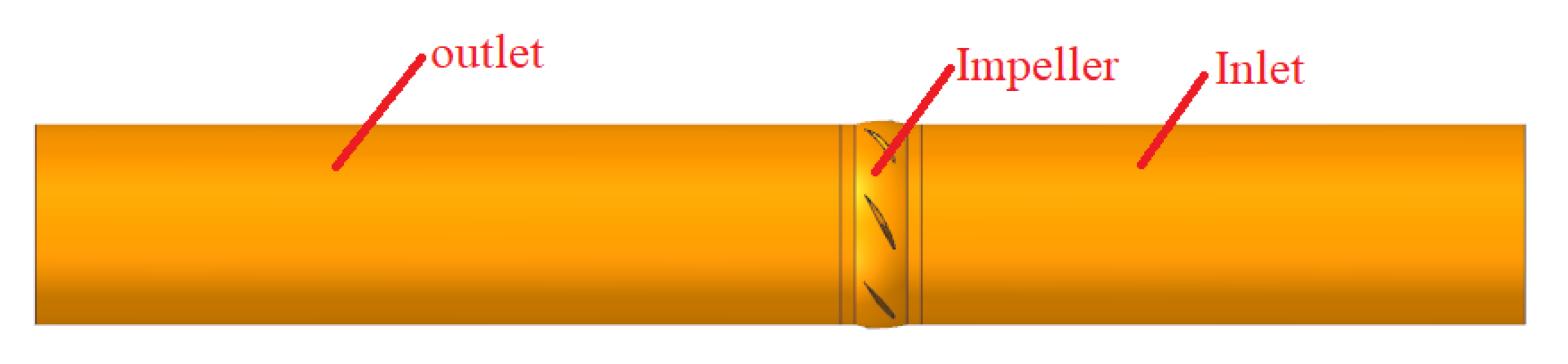
2.3. The Distribution of Pressure Measuring Points
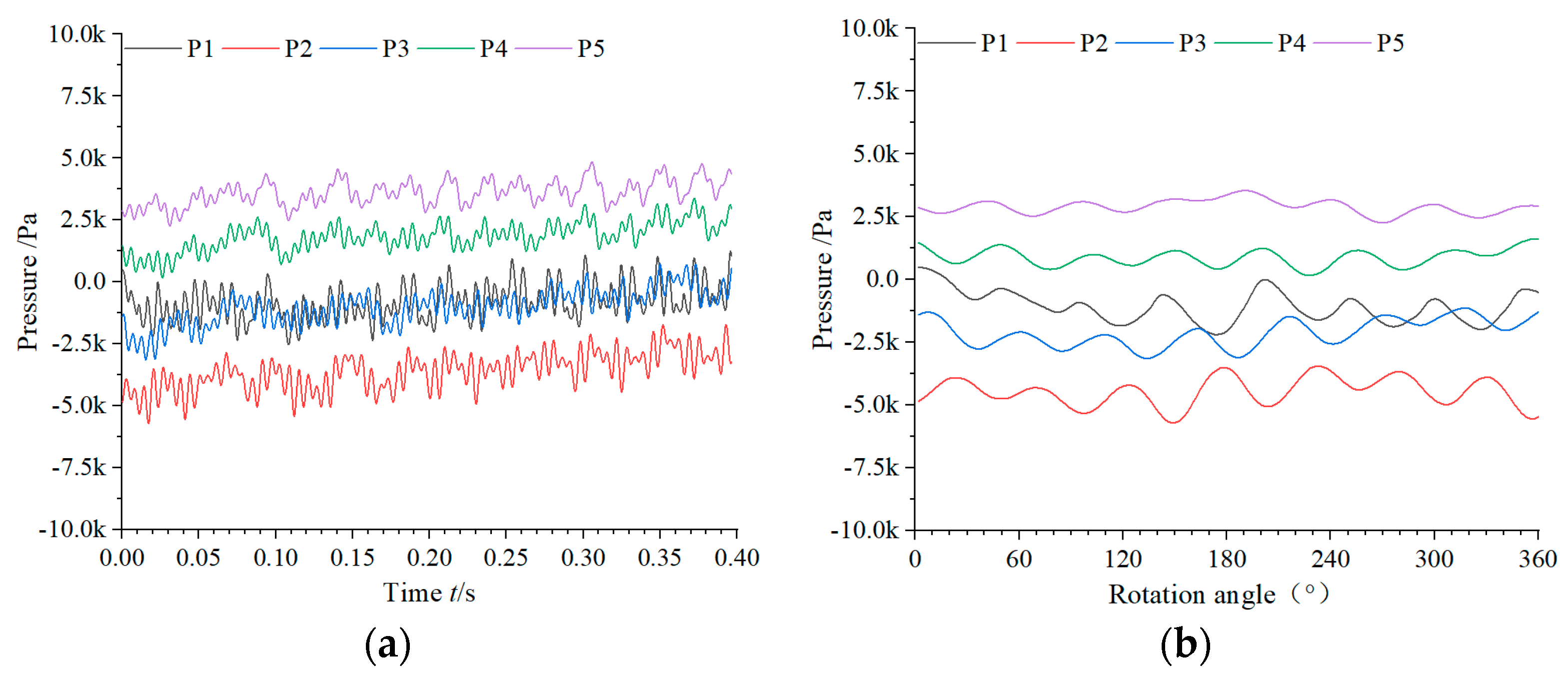
2.4. The Experimental Results of Pressure Fluctuation
3. The Unsteady Numerical Simulation for Rim Driven Propulsion Pump
3.1. Research Model and Numerical Simulation
3.1.1. Research Model
3.1.2. Mesh Division and Calculation Settings
3.1.3. The Distribution of Pressure Monitors
3.1.4. Grid Independence Test
3.2. Analysis of Numerical Simulation
3.2.1. Analysis of External Characteristics
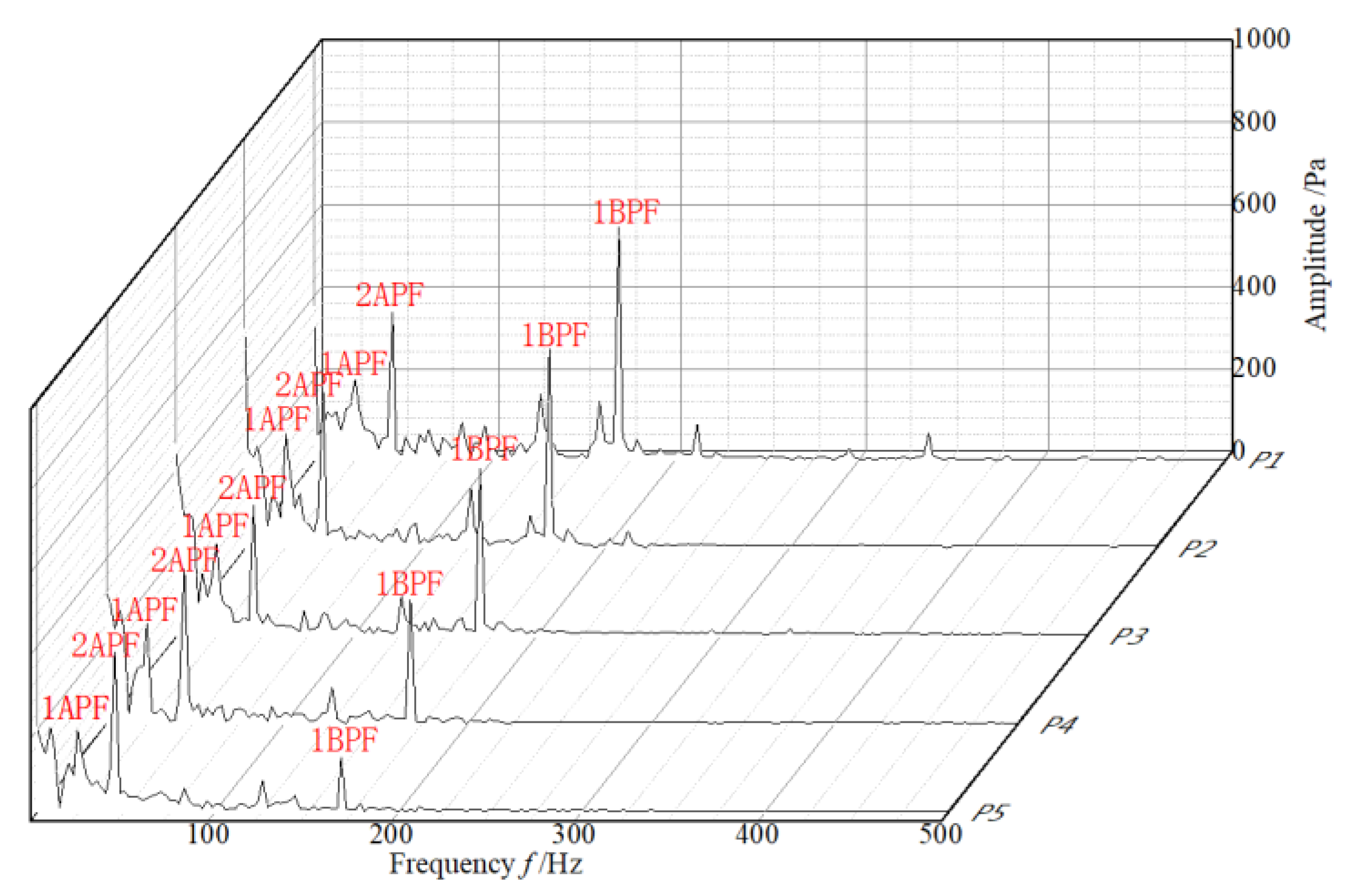
3.2.2. Analysis of Simulation for Pressure Fluctuation
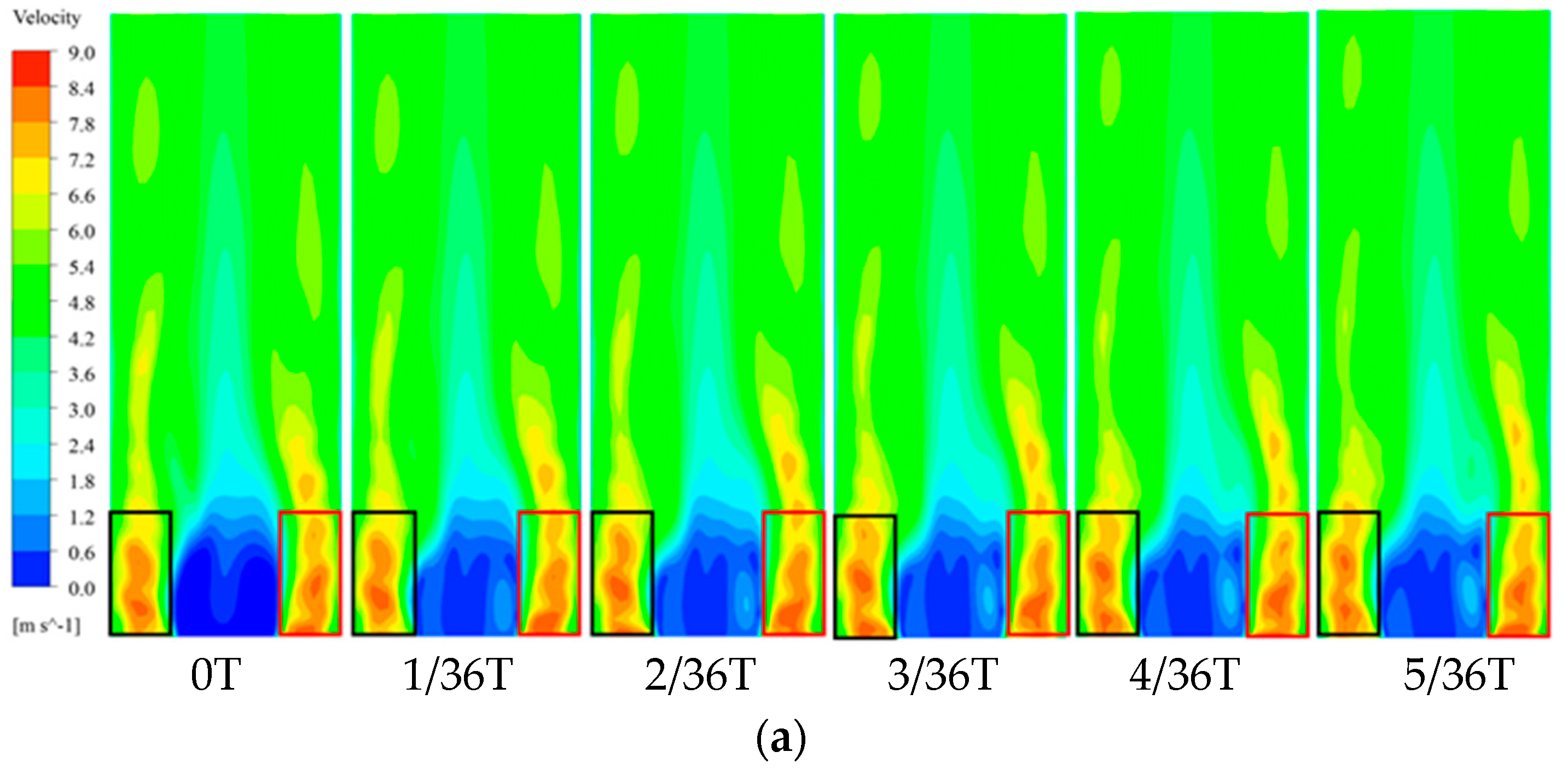
3.2.3. Analysis of Internal Flow
4. Conclusions
- (1)
- The periodicity of pressure fluctuation gradually weakens as the distance from the impeller outlet increases. The main frequency of the pressure fluctuation closing to the impeller is 1BPF, and when the distance from the impeller exceeds 1D, the main frequency becomes 2APF.
- (2)
- The amplitude of 1BPF becomes smaller as the axial distance between the monitoring point and impeller increases. When the distance exceeds 1D, the BPF characteristics nearly disappeared. In the low frequency band, the results of the numerical simulation are in good agreement with the experimental results.
- (3)
- The 1BPF frequency of pressure fluctuation is caused by the periodic movement of the tandem high-pressure and high-speed zone near the wall. The main reason for 2APF is the movement of the large-scale double vortex structure on both sides of the low-pressure zone in the middle section. The wall vortex cluster may be the main factor that induces 1APF.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tan, W.Z.; Yan, X.P.; Liu, Z.L. Technology Development and Prospect of Shaftless Rim-driven Propulsion System. J. Wuhan Univ. Technol. (Tran. Sci. Eng.) 2015, 39, 601–605. [Google Scholar]
- Kort, L. Elektrisch Angertriebene Schiffsschraube. German Patent 688,114, 13 February 1940. [Google Scholar]
- Li, Z.S. The Design of Rim-Driven Propeller and Flow Characteristics. Master’s Thesis, National Cheng Kung University, Tainan, Taiwan, 2005. [Google Scholar]
- Shi, Y.H. The Geometry Design and Performance Analysis of a Remotely Operated Vehicle’s Rim-Driven Propulsor. Master’s Thesis, National Cheng Kung University, Tainan, Taiwan, 2003. [Google Scholar]
- Chen, Y.H. The Design and Flow Field Analysis of a Ring-Driven Propeller a Remotely Operated Vehicle’s Rim-Driven Propulsor. Master’s Thesis, National Cheng Kung University, Tainan, Taiwan, 2003. [Google Scholar]
- Ye, Y.H. Integrated Design and Realization of a Hubless Rim-Driven Thruster. Master’s Thesis, National Cheng Kung University, Tainan, Taiwan, 2008. [Google Scholar]
- Andersen, T.P. Design of Rim Driven Waterjet Pump for Small Rescue Vessel. Master’s Thesis, Chalmers University of Technology, Goteborg, Sweden, 2014. [Google Scholar]
- John, A. Marine waterjet propulsion. Soc. Nav. Archit. Mar. Eng. Trans. 1993, 101, 275–335. [Google Scholar]
- Spence, R.; Amaral-Teixeira, J. A CFD parametric study of geometrical variations on the pressure pulsations and performance characteristics of a centrifugal pump. Comput. Fluids 2009, 38, 1243–1257. [Google Scholar]
- González, J.; Santolaria, C. Unsteady flow structure and global variables in a centrifugal pump. J. Fluids Eng. 2006, 128, 937–946. [Google Scholar]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the impeller blade with a slot structure on the centrifugal pump performance. Energies 2020, 13, 1628. [Google Scholar]
- Miyabe, M.; Maeda, H.; Umeki, I.; Jittani, Y. Unstable head-flow characteristic generation mechanism of a low specific speed mixed flow pump. Int. J. Therm. Sci. 2006, 15, 115–120. [Google Scholar]
- Miyabe, M.; Furukawa, A.; Maeda, H.; Umeki, I.; Jittani, Y. A behavior of the diffuser rotating stall in a low specific speed mixed-flow pump. Int. J. Fluid Mach. Syst. 2009, 2, 31–39. [Google Scholar]
- Wang, Y.; Lv, Y.; Wu, X.F.; Liu, H.L. Measurement and analysis of pressure pulsation in mixed flow pump. Water Resour. Power 2017, 10, 5. [Google Scholar]
- Zhang, L.; Wang, C.; Zhang, Y.; Xiang, W.; He, Z.; Shi, W. Numerical study of coupled flow in blocking pulsed jet impinging on a rotating wall. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 508. [Google Scholar]
- Wang, H.; Qian, Z.; Zhang, D.; Wang, T.; Wang, C. Numerical study of the normal impinging water jet at different impinging height, based on Wray–Agarwal turbulence model. Energies 2020, 13, 1744. [Google Scholar]
- Shi, L.; Zhu, J.; Tang, F.; Wang, C. Multi-Disciplinary optimization design of axial-flow pump impellers based on the approximation model. Energies 2020, 13, 779. [Google Scholar]
- Yakovlev, A.Y.; Sokolov, M.A.; Marinich, N.V. Numerical design and experimental verification of a rim-driven thruster. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Song, B.W.; Wang, Y.; Tian, W. Open water performance comparison between hub-type and hubless rim driven thrusters based on CFD method. Ocean Eng. 2015, 103, 55–63. [Google Scholar]
- Su, B. Research on Flow Characteristics and Structure Optimization of Small-Scale Shaftless Hydraulic Propeller. Master’s Thesis, North University of China, Taiyuan, China, 2018. [Google Scholar]
- Zhou, J.; Zhao, M.; Wang, C.; Gao, Z. Optimal design of diversion piers of lateral intake pumping station based on orthogonal test. Shock Vib. 2021, 2021, 6616456. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Q.; Yang, Y.; Wang, C. Performance differences of electrical submersible pump under variable speed schemes. Int. J. Simul. Modell. 2021, 20, 76–86. [Google Scholar]
- Dubas, A.J.; Bressloff, N.W.; Sharkh, S.M. Numerical modelling of rotor–stator interaction in rim driven thrusters. Ocean Eng. 2015, 106, 281–288. [Google Scholar]
- Shi, J.Q. Research on the Influence of Fluid Parameters on the Vibration Characteristics of Pipeline Fluid-Solid Coupling. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2016. [Google Scholar]
- Zhou, H.; Liu, Y.T.; Yue, Z.F. Calculation Analyze of Pressure Pulsation in Fluid Flowing Pipeline. Mech. Sci. Technol. 2011, 9, 1435–1438. [Google Scholar]








| Scheme | Inlet | Impeller | Outlet | Total | Head/m |
|---|---|---|---|---|---|
| 1 | 405,673 | 1,480,526 | 564,032 | 2,450,231 | 6.31 |
| 2 | 695,264 | 1,953,263 | 925,664 | 3,574,191 | 6.12 |
| 3 | 897,632 | 2,496,352 | 1,296,326 | 4,690,310 | 5.96 |
| 4 | 1,156,943 | 3,037,964 | 1,596,453 | 5,791,361 | 5.91 |
| 5 | 1,469,369 | 1,465,231 | 1,809,759 | 4,744,359 | 5.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Liu, H. Experimental Research and Numerical Analysis of Pressure Fluctuation Characteristics of Rim Driven Propulsion Pump Outlet. Machines 2021, 9, 293. https://doi.org/10.3390/machines9110293
Zhu Z, Liu H. Experimental Research and Numerical Analysis of Pressure Fluctuation Characteristics of Rim Driven Propulsion Pump Outlet. Machines. 2021; 9(11):293. https://doi.org/10.3390/machines9110293
Chicago/Turabian StyleZhu, Zhipeng, and Houlin Liu. 2021. "Experimental Research and Numerical Analysis of Pressure Fluctuation Characteristics of Rim Driven Propulsion Pump Outlet" Machines 9, no. 11: 293. https://doi.org/10.3390/machines9110293
APA StyleZhu, Z., & Liu, H. (2021). Experimental Research and Numerical Analysis of Pressure Fluctuation Characteristics of Rim Driven Propulsion Pump Outlet. Machines, 9(11), 293. https://doi.org/10.3390/machines9110293





