On the Asymptotic Behavior and Parameter Estimation of a Double-Sided LCC-Compensated Wireless Power Transfer System

Abstract

This study investigates the statistic behavior and parameter estimation problems of a double-sided, LCC-compensated, wireless power transfer system. Based on the commonly used wireless charging circuit model, this study proposes a five-step parameter estimation method, which is applicable to automotive static wireless charging systems. The eight parameters in the circuit model of this study are the most important key components of the wireless charging system. The study also found that, under certain conditions, the statistic mode of wireless charging systems has a specific distribution. However, the current status of these eight components for wireless charging of electric vehicles will have complex parameter drift problems. These drift problems will deteriorate the performance of the vehicle power systems. This study probes these factors and proposes some related mathematical theories. The noted factors can be applied to the analysis of the wireless charging system and provide alternative solutions to explain the deteriorations from coil misalignments. Both simulations and experiments are given to show the evaluated issues of the proposed study.

1. Introduction

A wireless power transfer (WPT) system is a resonant circuit consisting of transmitting and receiving coils and a compensation circuit. The compensation circuit determines the system performance, so its topology and parameter design have become the most important part of WPT systems. Regarding the wireless power transfer, many approaches are referenced and studied, such as magnetic flux induction, two-coil loosely coupled transformer, microwaves, and lasers [1,2]. Herein, the two-coil loosely coupled transformer, which can transfer power wirelessly with high efficiency across large air gaps, is of note. Four basic topologies are often referenced. Depending on how the compensation capacitors are added to the transmitting and receiving coils, they are simply named as series–series (SS), series–parallel (SP), parallel–series (PS), and parallel–parallel (PP) topologies [3,4]. Compared with the conventional topologies, the double-sided LCC compensation network is shown in Figure 1. It works as a current source to both the input and output [5,6,7,8,9], which is suitable for light and heavy load conditions. Even when no load is placed in the load side, this topology can maintain suitable power distributions. This feature is very suitable for dynamic WPT because misalignment will commonly appear during the dynamic charging. The compensation capacitor is determined by the self-inductance, so coil misalignment does not significantly affect the resonance. Moreover, the circuit can realize unity power factor at the input, so there is no reactive power in the system. Furthermore, the circuit can be designed to provide zero-voltage-switching (ZVS) for the input inverter and eliminate the reverse recovery loss in the rectifier, so the system efficiency can reach 96%. Also, two of the inductors can be designed as planar inductors, integrated with the main coils to save space [10,11]. As illustrated in Figure 1a, this topology consists of one inductor and two capacitors at both the primary and secondary sides. Note that in Figure 1a, the double-sided LCC compensation topology was applied in the WPT unit of this paper. Its applications are highly suitable for both dynamic and static WPT of electric vehicles [12,13]. Additionally, due to the coils, the system can be placed under the chassis. Such structure of WPT is also easy to integrate into autonomous vehicles [14,15]. Eight parameters in the LCC circuit model are applied in the wireless charging system. These factors affect the system performance such as power, efficiency, and safety [16]. Basically, temperature, DC bias, and stochastic process may affect the parameter drift significantly. In practice, these drift affections will deteriorate the output performance of the vehicle systems. Clearly, parameter drift problems in static WPT and misalignment issues in dynamic WPT reveal similar effects to unsteady output, which are both important issues that could be investigated.

Figure 1. Double-sided LCC compensation topology. (a) Double-sided LCC resonant circuit. (b) Equivalent circuit.

From Figure 1a, the equivalent circuit can be obtained, as Figure 1b. The circuit in Figure 1b can be described by the following equations:

$$\left[\begin{array}{c}{V}_1\\ 0\\ 0\\ 0\end{array}\right]=\left[\begin{array}{cccc}a& \frac{-1}{j\omega C_{f1}}& 0& 0\\ \frac{-1}{j\omega C_{f1}}& b& j\omega L_M& 0\\ 0& j\omega L_M& c& \frac{-1}{j\omega C_{f2}}\\ 0& 0& \frac{-1}{j\omega C_{f2}}& d\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_{L1}\\ I_{L2}\\ I_2\end{array}\right]$$

(1)

where

$$\begin{array}{l}a=j\omega L_{f1}+\frac{1}{j\omega C_{f1}}\\ b=\frac{1}{j\omega C_1}+\frac{1}{j\omega C_{f1}}+j\omega L_1\\ c=\frac{1}{j\omega C_2}+\frac{1}{j\omega C_{f2}}+j\omega L_2\\ d=j\omega L_{f2}+\frac{1}{j\omega C_{f2}}+R_L.\end{array}$$

(2)

Note that $L_M=k\sqrt{L_1{L}_2}$ stands for the mutual inductance and k is the coupling coefficient. The resonance can be obtained in many ways. The useful conditions are obtained when all the diagonal elements are real and no imaginary part is present. Thus, the following resonant conditions can be derived:

$$\begin{array}{l}{\omega }^2{L}_{f1}{C}_{f1}={\omega }^2{L}_{f2}{C}_{f2}=1\\ {\omega }^2\left(L_1-L_{f1}\right)C_1={\omega }^2\left(L_2-L_{f2}\right)C_2=1\end{array}$$

(3)

Clearly, the resonant frequency $\omega$ should be controlled under the condition of

$$\begin{array}{ll}\omega & =\frac{1}{\sqrt{L_{f1}{C}_{f1}}}=\frac{1}{\sqrt{L_{f2}{C}_{f2}}}\\ & =\frac{1}{\sqrt{\left(L_1-L_{f1}\right)C_1}}=\frac{1}{\sqrt{\left(L_2-L_{f2}\right)C_2}}.\end{array}$$

(4)

Accordingly, in order to obtain all the diagonal elements being real, with no imaginary parts, the following assumption is imposed in the sequel:

Hypothesis 1.

Assume that$L_{f1}{C}_{f1}=L_{f2}{C}_{f2}=\left(L_1-L_{f1}\right)C_1=\left(L_2-L_{f2}\right)C_2<0$.

2. Problem Formulations

In this study, we consider a stochastic model $\left(V_1(t),I_{L_1}(t),I_{L_2}(t),I_2(t)\right)$ of the wireless power transfer as follows:

$$d{I}_1(t)=\sigma dB(t)-\rho I_1(t)dt,$$

(5)

$$\left[\begin{array}{c}{V}_1(t)\\ 0\\ 0\\ 0\end{array}\right]=\left[\begin{array}{cccc}a& e& 0& 0\\ e& b& f& 0\\ 0& f& c& g\\ 0& 0& g& d\end{array}\right]\left[\begin{array}{c}{I}_1(t)\\ I_{L_1}(t)\\ I_{L_2}(t)\\ I_2(t)\end{array}\right],$$

(6)

where ${\left\{B(t)\right\}}_{t\ge 0}$ is a one dimensional Brownian motion, and $\sigma >0$, $\rho >0$, $e=\frac{-1}{j\omega C_{f1}}$, $f=j\omega L_M$, $g=\frac{-1}{j\omega C_{f2}}$. $\sigma$, $\rho$, $L_M$, and $R_L$ are given parameters; and

$$\omega =\frac{j}{\sqrt{-L_{f1}{C}_{f1}}}=\frac{j}{\sqrt{-\left(L_1-L_{f1}\right)C_1}},$$

$L_1$, $L_2$, $L_{f1}$, $L_{f2}$, $C_1$, $C_2$, $C_{f1}$, and $C_{f2}$ are parameters that need to be estimated. For simplicity, we denote that $\theta =\left({\theta }_1,{\theta }_2,\cdots ,{\theta }_8\right)=\left(L_1,L_2,L_{f1},L_{f2},C_1,C_2,C_{f1},C_{f2}\right)$ hereafter.

From Formula (6), we have

$$\begin{array}{l}{V}_1=a{I}_1+e{I}_{L_1},\\ 0=e{I}_1+b{I}_{L_1}+f{I}_{L_2},\\ 0=f{I}_{L_1}+c{I}_{L_2}+g{I}_2,\\ 0=g{I}_{L_2}+d{I}_2.\end{array}$$

This gives

$$I_2=\frac{efg}{b{g}^2-bcd+d{f}^2}{I}_1,I_{L_2}=-\frac{d}{g}{I}_2=-\frac{defg}{b{g}^3-bcdg+d{f}^{2}g}{I}_1,$$

$$I_{L_1}=\left(\frac{cd}{fg}-\frac{g}{f}\right)I_2=\frac{cdefg-ef{g}^3}{bf{g}^3-bcdfg+d{f}^{3}g}{I}_1,$$

$$\begin{array}{ll}{V}_1& =a{I}_1+e{I}_{L_1}=\left(a+\frac{cd{e}^{2}fg-e^{2}f{g}^3}{bf{g}^3-bcdfg+d{f}^{3}g}\right)I_1\\ & =\frac{abf{g}^3-abcdfg+ad{f}^{3}g+cd{e}^{2}fg-e^{2}f{g}^3}{bf{g}^3-bcdfg+d{f}^{3}g}{I}_1.\end{array}$$

For simplicity, denote

$${\alpha }_1=\frac{abf{g}^3-abcdfg+ad{f}^{3}g+cd{e}^{2}fg-e^{2}f{g}^3}{bf{g}^3-bcdfg+d{f}^{3}g}$$

$${\alpha }_2=\frac{cdefg-ef{g}^3}{bf{g}^3-bcdfg+d{f}^{3}g},{\alpha }_3=-\frac{defg}{b{g}^3-bcdg+d{f}^{2}g},{\alpha }_4=\frac{efg}{b{g}^2-bcd+d{f}^2}.$$

We obtain $V_1(t)={\alpha }_1{I}_1(t),I_{L_1}(t)={\alpha }_2{I}_1(t),I_{L_2}(t)={\alpha }_3{I}_1(t),I_2(t)={\alpha }_4{I}_1(t)$.

3. Steady Behavior of Primary Current I₁(t)

In order to clarify the asymptotic behavior of ${\left\{I_1(t)\right\}}_{t\ge 0}$, we propose the following definition at first:

Definition 1.

${\left\{I_1(t)\right\}}_{t\ge 0}$is said to have the invariant measure$\mu (\cdot )$if, and only if, there exists the probability measure$\mu (\cdot )$, such that

$${\displaystyle {\int }_{-\infty }^{\infty }P\left(I_1(t)\in A|I_1(0)=x\right)}\mu \left(x\right)dx=\mu \left(A\right)$$

(7)

for any Borel set$A$and each fixed$t>0$. From Formula (5), we obtain

$$I_1\left(t\right)=e^{-\rho t}{I}_1\left(0\right)+\sigma {\displaystyle {\int }_0^t{e}^{-\rho (t-s)}dB(s)}.$$

As a matter of fact, it is well known that ${\left\{I_1(t)\right\}}_{t\ge 0}$ is the Ornstein–Uhlenbeck process. Thus, we point out that Bhattacharya and Waymire’s study [17] is a readable literature devoted to the proof.

Result 3.1.

${\left\{I_1(t)\right\}}_{t\ge 0}$has the following probability density function:

$$P\left(I_1(t)=y|I_1(0)=x\right)=\frac{1}{\sqrt{2\pi }}{\left\{\frac{{\sigma }^2}{2\rho }\left(1-e^{-2\rho t}\right)\right\}}^{-0.5}\exp \left\{-\frac{\rho {\left(y-x{e}^{-\rho t}\right)}^2}{{\sigma }^2\left(1-e^{-2\rho t}\right)}\right\}.$$

Result 3.2.

${\left\{I_1(t)\right\}}_{t\ge 0}$has the following invariant measure:

$$\mu \left(x\right)dx=\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho x^2}{{\sigma }^2}\right\}dx$$

Proof. 

By Result 3.1, if we take $\underset{t\to \infty }{\lim }$ on both sides of Formula (7), we obtain the following:

$${\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_A\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho y^2}{{\sigma }^2}\right\}dy}}\mu \left(x\right)dx={\displaystyle {\int }_A\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho y^2}{{\sigma }^2}\right\}dy}.$$

This yields that

$$\mu \left(x\right)dx=\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho x^2}{{\sigma }^2}\right\}dx$$

is the invariant measure of ${\left\{I_1(t)\right\}}_{t\ge 0}$. This completes the proof. □

Accordingly, the random variable $I_1(\infty )$ has the probability density function $\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho y^2}{{\sigma }^2}\right\}$.

4. Synthesis Process

4.1. Probability Density Function

Let

$$\begin{array}{l}{P}_{\theta }\left(x_1\right)=P_{\theta }\left(V_1(\infty )=x_1\right),P_{\theta }\left(x_2\right)=P_{\theta }\left(I_{L_1}(\infty )=x_2\right),\\ P_{\theta }\left(x_3\right)=P_{\theta }\left(I_{L_2}(\infty )=x_3\right),P_{\theta }\left(x_4\right)=P_{\theta }\left(I_2(\infty )=x_4\right).\end{array}$$

Clearly, for any $x_1,x_2,x_3,x_4\in R$, we have

$$\begin{array}{l}{P}_{\theta }\left(x_1\right)=P_{\theta }\left({\alpha }_1{I}_1(\infty )=x_1\right)=P\left(I_1(\infty )=\frac{x_1}{{\alpha }_1}\right),\\ P_{\theta }\left(x_2\right)=P_{\theta }\left({\alpha }_2{I}_1(\infty )=x_2\right)=P\left(I_1(\infty )=\frac{x_2}{{\alpha }_2}\right),\\ P_{\theta }\left(x_3\right)=P_{\theta }\left({\alpha }_3{I}_1(\infty )=x_3\right)=P\left(I_1(\infty )=\frac{x_3}{{\alpha }_3}\right),\\ P_{\theta }\left(x_4\right)=P_{\theta }\left({\alpha }_4{I}_1(\infty )=x_4\right)=P\left(I_1(\infty )=\frac{x_4}{{\alpha }_4}\right).\end{array}$$

Since ${\alpha }_1$ and ${\alpha }_i$, $i=2,3,4$ are dependent on $\left({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5,{\theta }_6,{\theta }_7,{\theta }_8\right)$ and $\left({\theta }_1,{\theta }_2,{\theta }_4,{\theta }_5,{\theta }_6,{\theta }_7,{\theta }_8\right)$, respectively, the values $P\left(I_1(\infty )=\frac{x_1}{{\alpha }_1}\right)$ and $P\left(I_1(\infty )=\frac{x_i}{{\alpha }_i}\right)$, $i=2,3,4$ are also dependent on $\left({\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5,{\theta }_6,{\theta }_7,{\theta }_8\right)$ and $\left({\theta }_1,{\theta }_2,{\theta }_4,{\theta }_5,{\theta }_6,{\theta }_7,{\theta }_8\right)$, respectively.

Result 4.1.

Under Hypothesis 1, for any$x_1,x_2,x_3,x_4\in R$, we obtain the following:

$$\begin{array}{l}{P}_{\theta }\left(x_1\right)=P\left(I_1(\infty )=\frac{x_1}{{\alpha }_1}\right),P_{\theta }\left(x_2\right)=P\left(I_1(\infty )=\frac{x_2}{{\alpha }_2}\right),\\ P_{\theta }\left(x_3\right)=P\left(I_1(\infty )=\frac{x_3}{{\alpha }_3}\right),P_{\theta }\left(x_4\right)=P\left(I_1(\infty )=\frac{x_4}{{\alpha }_4}\right).\end{array}$$

Proof. 

It is trivial from the statement of this section above. This completes the proof. □

4.2. Homogeneous Markov Chain

In this section, we assume $\rho =0.5$, $\sigma =1$, and $R_L=0$. Therefore, by Result 3.1, we have the following:

$$P\left(I_1(\infty )=x\right)=\frac{1}{\sqrt{2\pi }}\exp \left\{-\frac{x^2}{2}\right\}.$$

Let ${\theta }_i\in \left(c_i,d_i\right)$ for $i=1,2,\cdots ,8$, and

$$h\left(\theta |x_1\right)=\frac{P\left(I_1(\infty )=\frac{x_1}{{\alpha }_1}\right)}{{\displaystyle {\int }_{V}P\left(I_1(\infty )=\frac{x_1}{{\alpha }_1}\right)d{\theta }_{1}d{\theta }_2\cdots d{\theta }_8}}=\frac{\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)}{{\displaystyle {\int }_V\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)d{\theta }_{1}d{\theta }_2\cdots d{\theta }_8}},$$

where $V=\left(c_1,d_1\right)\times \left(c_2,d_2\right)\times \cdots \times \left(c_8,d_8\right).$

Take a proposal density function $q:V\times V\to R^{+}$ by

$$q\left({\theta }^{\prime },\theta \right)=\frac{1}{{\displaystyle \prod _{i=1}^8\left(d_i-c_i\right)}},$$

for each ${\theta }^{\prime },\theta \in V$ and define

$$p\left({\theta }^{\prime },\theta \right)=\min \left\{1,\frac{h\left(\theta |x\right)q\left({\theta }^{\prime },\theta \right)}{h\left({\theta }^{\prime }|x\right)q\left(\theta ,{\theta }^{\prime }\right)}\right\}.$$

In terms of Result 3.2, we have

$$p\left({\theta }^{\prime },\theta \right)=\min \left\{1,\exp \left(-\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1}\right)}^2+\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1^{\prime }}\right)}^2\right)\right\},$$

where ${\alpha }_1^{\prime }$ is determined by ${\theta }^{\prime }$. Now, define the time homogeneous Markov chains ${\left\{{\Theta }_n\right\}}_{n=0}^{\infty }$ on $V$ by the following transition probability: for any Borel, set $A$, $A\subset V$,

$$P\left({\Theta }_1\in A|{\Theta }_0={\theta }^{\prime }\right)={\displaystyle {\int }_{A}p\left({\theta }^{\prime },\theta \right)q\left({\theta }^{\prime },\theta \right)d\theta }+{\delta }_{{\theta }^{\prime }}\left(A\right)\left(1-{\displaystyle {\int }_{V}p\left({\theta }^{\prime },\theta \right)q\left({\theta }^{\prime },\theta \right)d\theta }\right),$$

where the dirac measure ${\delta }_{{\theta }^{\prime }}$ is defined by

$${\delta }_{{\theta }^{\prime }}=\{\begin{array}{l}1,\mathrm{if}{\theta }^{\prime }\in A,\\ 0,\mathrm{if}{\theta }^{\prime }\notin A.\end{array}$$

Result 4.2.

Under Hypothesis 1 and$\rho =0.5$, $\sigma =1$, $R_L=0$, ${\left\{{\Theta }_n\right\}}_{n=0}^{\infty }$has the invariant measure$\mu (\cdot )$with density function

$$\mu \left(\theta \right)=\frac{\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)}{{\displaystyle {\int }_V\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)d{\theta }_{1}d{\theta }_2\cdots d{\theta }_8}}.$$

Proof. 

By the definition of $p\left({\theta }^{\prime },\theta \right)$, for ${\theta }^{\prime },\theta \in V$ satisfying

$$\exp \left(-\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1}\right)}^2+\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1^{\prime }}\right)}^2\right)\le 1,$$

we see

$$p\left({\theta }^{\prime },\theta \right)=\exp \left(-\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1}\right)}^2+\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1^{\prime }}\right)}^2\right),p\left(\theta ,{\theta }^{\prime }\right)=1,$$

which implies

$$\begin{array}{ll}\mu \left({\theta }^{\prime }\right)p\left({\theta }^{\prime },\theta \right)q\left({\theta }^{\prime },\theta \right)& =\frac{\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)}{{\displaystyle \prod _{i=1}^8\left(d_i-c_i\right)}{\displaystyle {\int }_V\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)d{\theta }_{1}d{\theta }_2\cdots d{\theta }_8}}\\ & =\mu \left(\theta \right)p\left(\theta ,{\theta }^{\prime }\right)q\left(\theta ,{\theta }^{\prime }\right)\end{array}$$

On the other hand, for ${\theta }^{\prime },\theta \in V$, satisfying

$$\exp \left(-\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1}\right)}^2+\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1^{\prime }}\right)}^2\right)>1,$$

we see

$$p\left({\theta }^{\prime },\theta \right)=1, p\left(\theta ,{\theta }^{\prime }\right)=\exp \left(-\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1}\right)}^2+\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1^{\prime }}\right)}^2\right),$$

which also implies

$$\begin{array}{ll}\mu \left({\theta }^{\prime }\right)p\left({\theta }^{\prime },\theta \right)q\left({\theta }^{\prime },\theta \right)& =\frac{\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)}{{\left(d-c\right)}^8{\displaystyle {\int }_V\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)d{\theta }_{1}d{\theta }_2\cdots d{\theta }_8}}\\ & =\mu \left(\theta \right)p\left(\theta ,{\theta }^{\prime }\right)q\left(\theta ,{\theta }^{\prime }\right)\end{array}$$

Combining the above arguments, we obtain

$$\mu \left({\theta }^{\prime }\right)p\left({\theta }^{\prime },\theta \right)q\left({\theta }^{\prime },\theta \right)=\mu \left(\theta \right)p\left(\theta ,{\theta }^{\prime }\right)q\left(\theta ,{\theta }^{\prime }\right),$$

(8)

for any ${\theta }^{\prime },\theta \in V$. Now, from definition 1 and (8), for any Borel, set $A$, $A\subset V$, we integrate the following with respect to ${\theta }^{\prime }\in V$,

This establishes

$${\displaystyle {\int }_{V}P\left({\Theta }_1\in A|{\Theta }_0=x\right)\mu \left(x\right)dx}=\mu \left(A\right)$$

Moreover, since

$$P\left({\Theta }_2\in A|{\Theta }_0=x\right)={\displaystyle {\int }_{V}P\left({\Theta }_1\in A|{\Theta }_0=y\right)P\left({\Theta }_1\in dy|{\Theta }_0=x\right)},$$

we have

$${\displaystyle {\int }_{V}P\left({\Theta }_2\in A|{\Theta }_0=x\right)\mu \left(x\right)dx}=\mu \left(A\right).$$

By induction, we obtain

$${\displaystyle {\int }_{V}P\left({\Theta }_n\in A|{\Theta }_0=x\right)\mu \left(x\right)dx}=\mu \left(A\right),$$

for any Borel set $A$, $A\subset V$ and each fixed positive number $n$. Hence, $\mu (\cdot )$ is the invariant measure of ${\left\{{\Theta }_n\right\}}_{n=0}^{\infty }$. This completes the proof. □

4.3. Estimation Algorithm

For sake of estimating $\left({\theta }_1,{\theta }_2,\cdots ,{\theta }_8\right)\in V$, we refer to the assumptions of Result 3.1 and [18] via Metropolis–Hastings algorithm as follows. Result 4.2 ensures the convergence of the following estimation algorithm.

Step 1: Given any initial state $\left({\theta }_1^{(1)},{\theta }_2^{(1)},\cdots ,{\theta }_8^{(1)}\right)$ on $V$.

Step 2: Generate a candidate state $\left({\theta }_1^{(2)},{\theta }_2^{(2)},\cdots ,{\theta }_8^{(2)}\right)$ from a uniform distribution on $V$ and a acceptance value $\lambda$ from a uniform distribution on $[0,1]$.

Step 3: Calculate

$$p\left(\left({\theta }_1^{(1)},{\theta }_2^{(1)},\cdots ,{\theta }_8^{(1)}\right),\left({\theta }_1^{(2)},{\theta }_2^{(2)},\cdots ,{\theta }_8^{(2)}\right)\right)=\min \left\{1,\exp \left(-\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1}\right)}^2+\frac{1}{2}{\left(\frac{x_1}{{\alpha }_1^{\prime }}\right)}^2\right)\right\},$$

where ${\alpha }_1$ is determined by $\left({\theta }_1^{(2)},{\theta }_2^{(2)},\cdots ,{\theta }_8^{(2)}\right)$ and ${\alpha }_1^{\prime }$ is determined by $\left({\theta }_1^{(1)},{\theta }_2^{(1)},\cdots ,{\theta }_8^{(1)}\right)$.

Step 4: If $\lambda \le p\left({\theta }^{\prime },\theta \right)$, then we accept $\left({\theta }_1^{(2)},{\theta }_2^{(2)},\cdots ,{\theta }_8^{(2)}\right)$, otherwise, take

$$\left({\theta }_1^{(2)},{\theta }_2^{(2)},\cdots ,{\theta }_8^{(2)}\right)=\left({\theta }_1^{(1)},{\theta }_2^{(1)},\cdots ,{\theta }_8^{(1)}\right),$$

and go back to Step 2.

Step 5: Repeat the previous steps until we obtain a convergent chain.

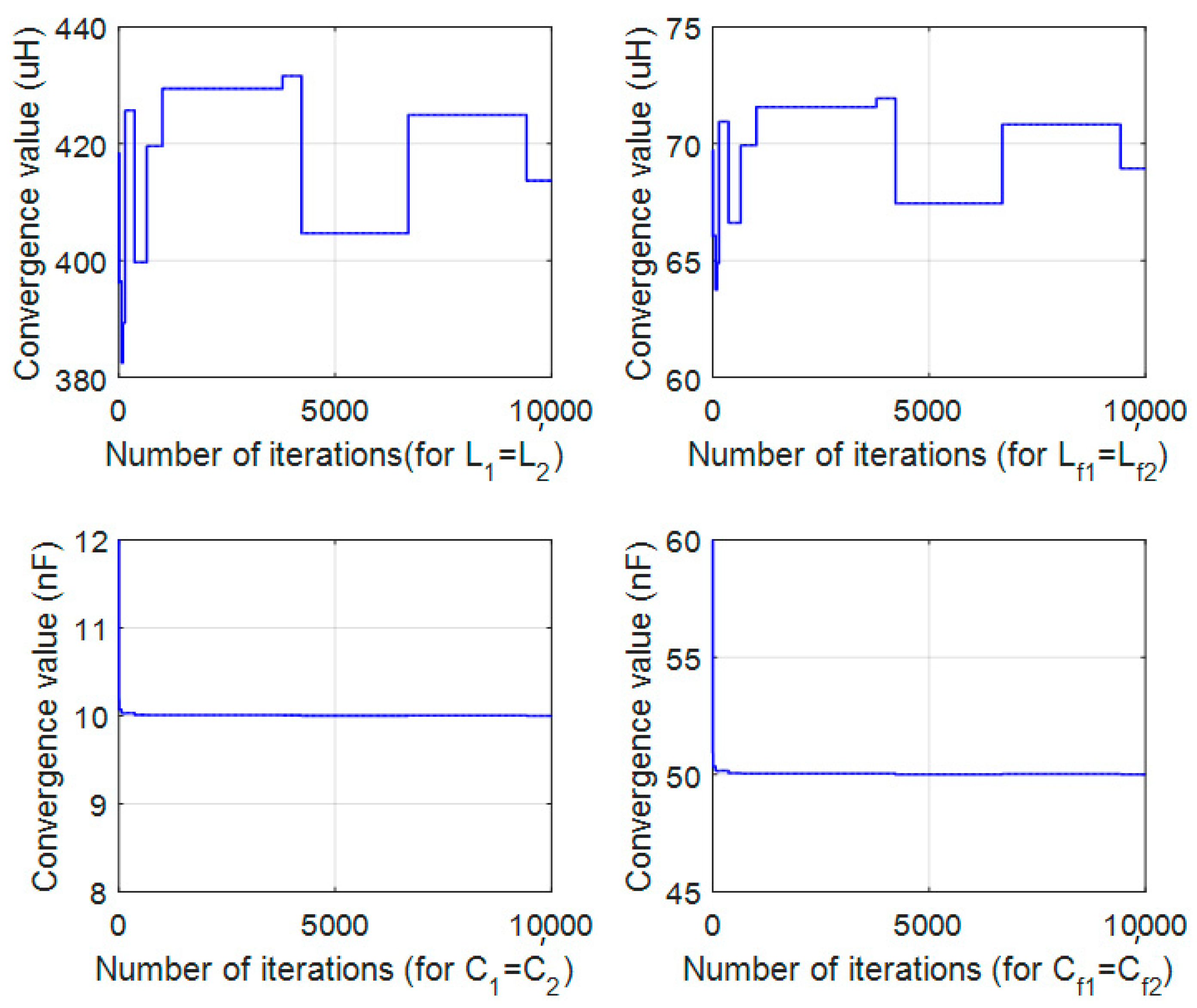
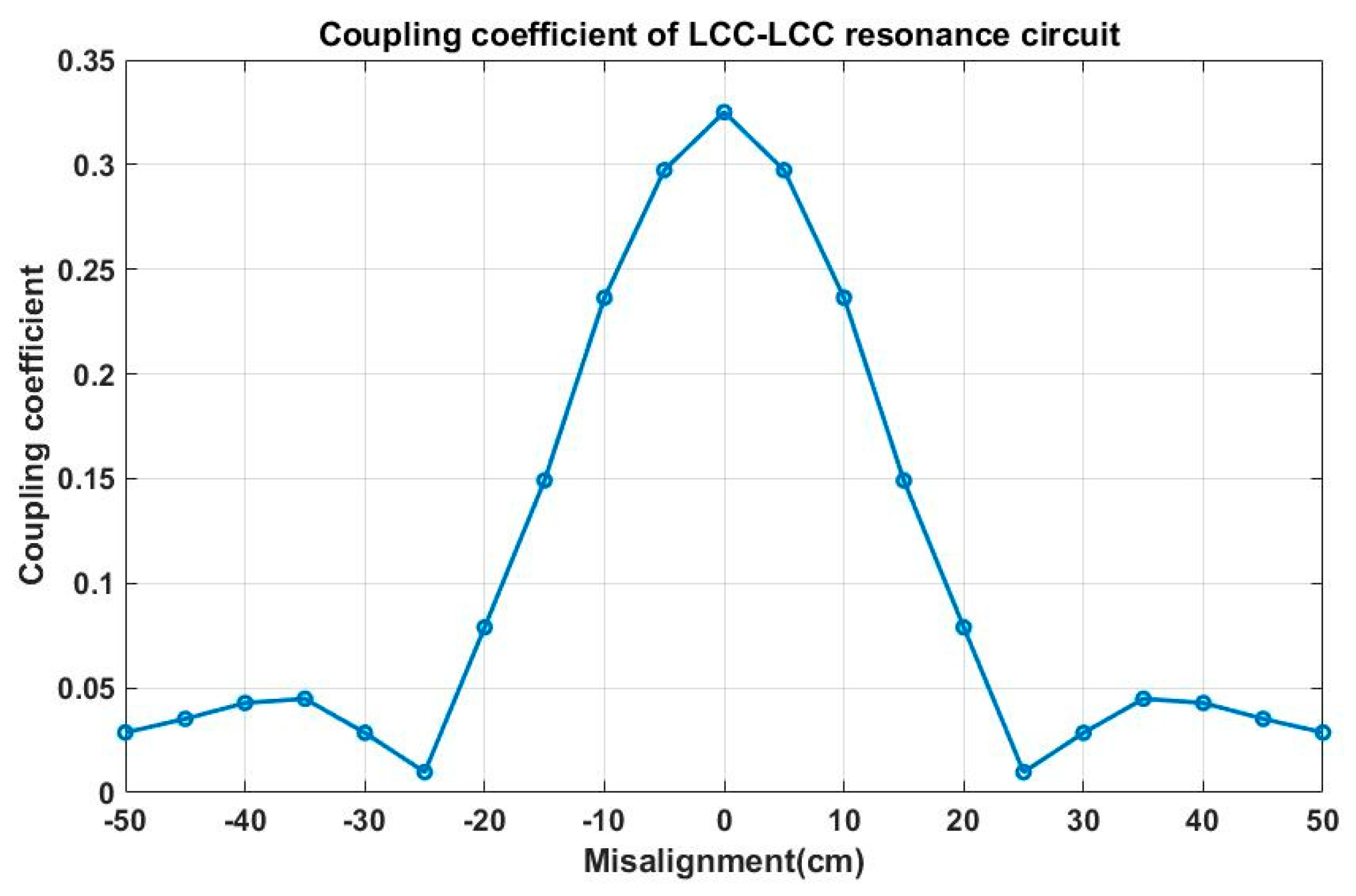
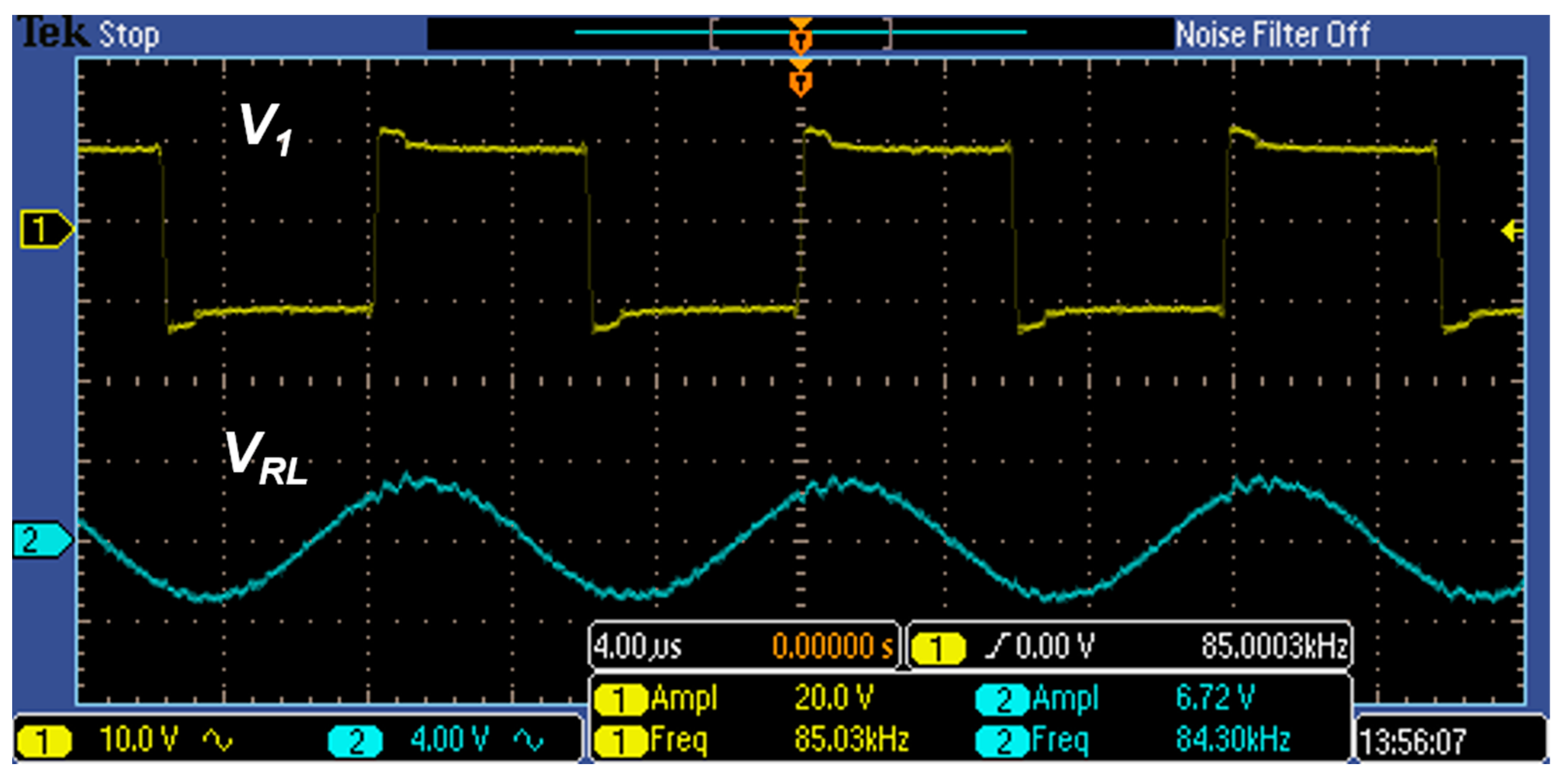
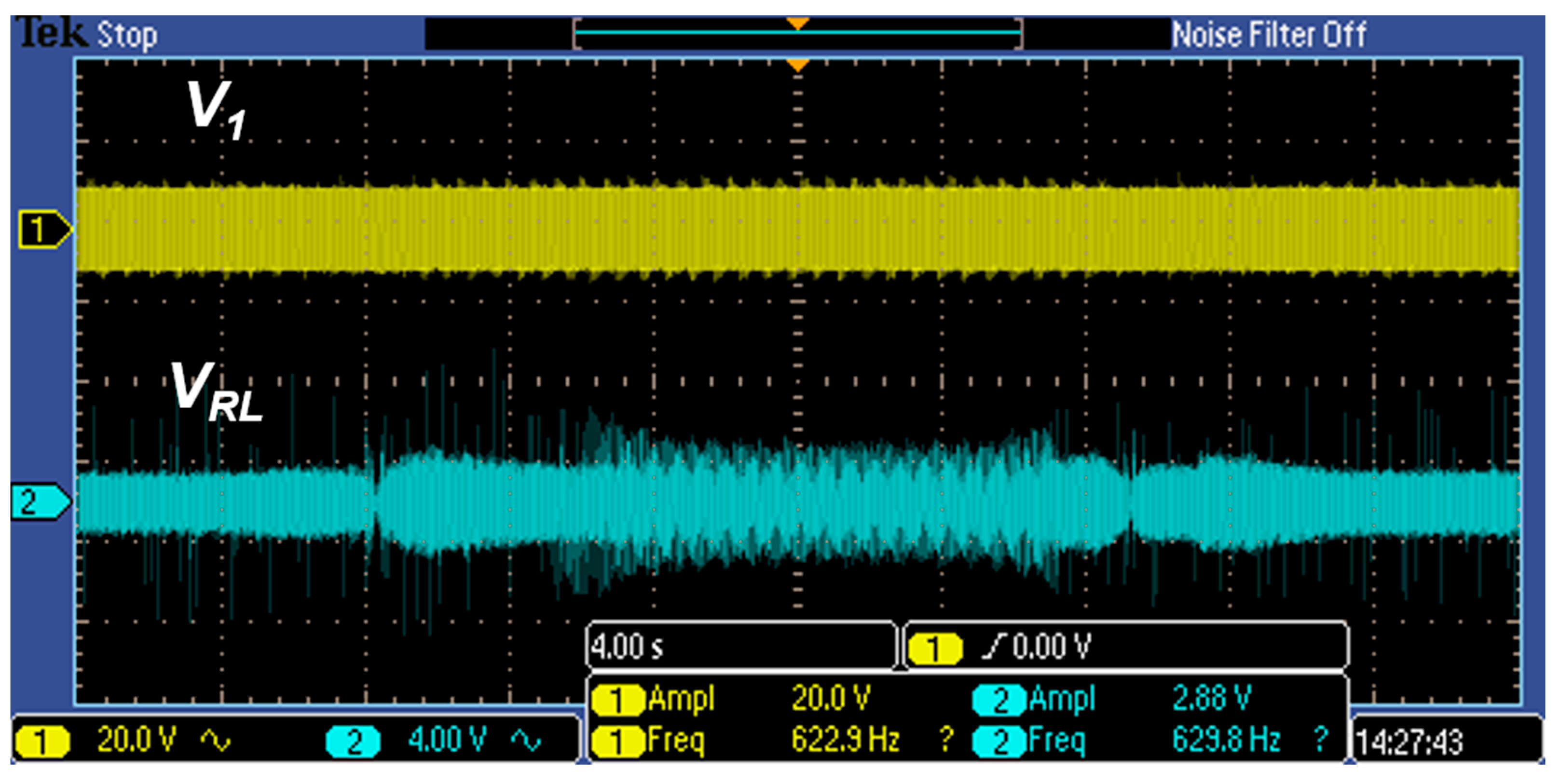
5. Simulations and Experiments

Under Hypothesis 1 and $\rho =0.5$, $\sigma =1$, $R_L=0$, for the sake of simplifying a simulation, we set $x_1=1$, $L_M=0.3\sqrt{L_1{L}_2}$, and ${\theta }_1^{(i)}={\theta }_2^{(i)}$, ${\theta }_3^{(i)}={\theta }_4^{(i)}$, ${\theta }_5^{(i)}={\theta }_6^{(i)}$, ${\theta }_7^{(i)}={\theta }_8^{(i)}$, ${\theta }_1^{(i)}=6{\theta }_3^{(i)}$, and $5{\theta }_5^{(i)}={\theta }_7^{(i)}$ for each $i$ to guarantee that Hypothesis 1 holds. Additionally, we take $c_1=c_2=354,$ $d_1=d_2=432,$ $c_3=c_4=59,$ $d_3=d_4=72,$ $c_5=c_6=10,$ $d_5=d_6=12,$ $c_7=c_8=60,$ $d_7=d_8=72,$ and an initial state $\left({\theta }_1^{(1)},{\theta }_2^{(1)},\cdots ,{\theta }_8^{(1)}\right)=\left(396,396,66,66,12,12,60,60\right)$. Then, proceed the estimation algorithm as mentioned in Section 4.3. For $i$ from 1 to 10,000, the synthesized values were revealed in Figure 2. In Figure 2, all tests are done by 10,000 iterations. As can be seen in this figure, the sample path is reasonably well converged, which satisfies the conditions that an asymptotic stable circuit should have. Under the condition of Hypothesis 1, the convergent value of capacitance reaches its steady state quickly. However, the inductance has a slower convergent rate. The convergent speed of steady value is different between inductor and capacitor because of the dynamical behavior of LCC topology. Note that only static WPT fits this conclusion.

Figure 2. Sample paths for $\left(L_1,L_2,L_{f1},L_{f2},C_1,C_2,C_{f1},C_{f2}\right)$.

Misalignment in static WPT can be applied to simulate the approaching or leaving statuses (or both) of dynamic WPT. In dynamic WPT, parameter drift affects the transmission power and efficiency, respectively. Basically, the whole process of “approaching–central–leaving” of the dynamic WPT can be treated as a series of parameter varying, which can be modeled by stochastic process. Hence, using the stochastic model to probe the system performance is an appropriate solution. Via simulation, engineers can use the stochastic model to preview the system performance before the activation of dynamic WPT process. For further demonstrating the LCC-compensated performance in dynamic charging, a small scale of experiment was employed to show its feasibility. The verification experiments are carried out on the test bench, as shown in Figure 3. Table 1 illustrates the relevant specifications of test bench. Its rated DC voltage is 10V, which is a small scale of WPT for demonstration. Figure 4 is the measurement data for coupling coefficient. Figure 5 shows the resonant conditions. Clearly, the resonant frequency exactly falls on 85 kHz, which satisfies the requirement from WPT. To test the affections of misalignment, as shown in Figure 6, a scenario of dynamic movement of receiving coils are scheduled. The experimental result is revealed in Figure 7. Clearly, the received energy is sensitive to the misalignment, which is relevant to the coupling coefficient, as shown in Figure 4.

Figure 3. Test bench of the experiment.

Table 1. Specifications of the test bench.

Specification	Value
DC Source	10 V/1 A
$\mathrm{Frequency} \left(f\right)$	85 kHz
$\mathrm{Compensation}\mathrm{Inductance} \left(L_{f1}\right)$	24.24 uH
$\mathrm{Compensation}\mathrm{Capacitance} \left(C_{f1}\right)$	144.5 nF
$\mathrm{Detection}\mathrm{Inductance} \left(L_1\right)$	231.5 uH
$\mathrm{Detection}\mathrm{Capacitance} \left(C_1\right)$	15.36 nF
$\mathrm{Receive}\mathrm{Compensation}\mathrm{Inductance} \left(L_{f2}\right)$	50.12 uH
$\mathrm{Receive}\mathrm{Compensation}\mathrm{Capacitance} \left(C_{f2}\right)$	67.27 nF
$\mathrm{Receive}\mathrm{Inductance} \left(L_2\right)$	229.6 uH
$\mathrm{Receive}\mathrm{Capacitance}\left(C_2\right)$	19.64 nF
$\mathrm{Load}\mathrm{Impedance} \left(R_L\right)$	5 Ω
Air Gap	15 cm

Figure 4. Measurement of coupling coefficient.

Figure 5. Experimental result for WPT evaluation.

Figure 6. Scenario of a dynamic movement.

Figure 7. Misalignment result of the scheduled dynamic WPT.

6. Conclusions

Considering the misalignment in the WPT process, this study investigated the statistic model for double-sided, LCC-compensated, wireless power transfer system. The main contributions are considered as:

For the initial value $I_1(0)=x$, ${\left\{I_1(t)\right\}}_{t\ge 0}$ has the following probability density function:

$$P\left(I_1(t)=y\right)=\frac{1}{\sqrt{2\pi }}{\left\{\frac{{\sigma }^2}{2\rho }\left(1-e^{-2\rho t}\right)\right\}}^{-0.5}\exp \left\{-\frac{\rho {\left(y-x{e}^{-\rho t}\right)}^2}{{\sigma }^2\left(1-e^{-2\rho t}\right)}\right\}.$$

In addition, ${\left\{I_1(t)\right\}}_{t\ge 0}$ has the following invariant measure:

$$\mu \left((-\infty ,x]\right)={\displaystyle {\int }_{-\infty }^x\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho y^2}{{\sigma }^2}\right\}du}.$$

Under Hypothesis 1, for any $x_1,x_2,x_3,x_4\in R$, we obtain

$$\begin{array}{l}{P}_{\theta }\left(x_1\right)=P_{\theta }\left(V_1(\infty )=x_1\right)=P\left(I_1(\infty )=\frac{x_1}{{\alpha }_1}\right)=\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho x_1^2}{{\sigma }^2{\alpha }_1^2}\right\},\\ P_{\theta }\left(x_2\right)=P_{\theta }\left(I_{L_1}(\infty )=x_2\right)=P\left(I_1(\infty )=\frac{x_2}{{\alpha }_2}\right)=\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho x_1^2}{{\sigma }^2{\alpha }_2^2}\right\},\\ P_{\theta }\left(x_3\right)=P_{\theta }\left(I_{L_2}(\infty )=x_3\right)=P\left(I_1(\infty )=\frac{x_3}{{\alpha }_3}\right)=\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho x_3^2}{{\sigma }^2{\alpha }_3^2}\right\},\\ P_{\theta }\left(x_4\right)=P_{\theta }\left(I_2(\infty )=x_4\right)=P\left(I_1(\infty )=\frac{x_4}{{\alpha }_4}\right)=\frac{\sqrt{2\rho }}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{\rho x_4^2}{{\sigma }^2{\alpha }_4^2}\right\}.\end{array}$$

Additionally, if $\rho =0.5$, $\sigma =1$, and $R_L=0$, then the Markov chains ${\left\{{\Theta }_n\right\}}_{n=0}^{\infty }$ with the state space $V=\left(c_1,d_1\right)\times \left(c_2,d_2\right)\times \cdots \times \left(c_8,d_8\right)$ have the following invariant measure:

$$\mu \left(A\right)=\frac{{\displaystyle {\int }_A\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)d{\theta }_{1}d{\theta }_2\cdots d{\theta }_8}}{{\displaystyle {\int }_V\exp \left(-\frac{x_1^2}{2{\alpha }_1^2}\right)d{\theta }_{1}d{\theta }_2\cdots d{\theta }_8}},$$

for any Borel set $A$.

The statistic mode of the wireless charging system constructed in this paper is suitable for dynamic wireless power transfer, based on the LCC topology. The stochastic model can be applied to simulate the deteriorations from misalignment of the static WPT. Therefore, it can be employed to evaluate the system’s features, such as efficiency in advance. After the simulation, engineers can apply the stochastic model to preview the power or the efficiency (or both) before the activation of the dynamic WPT process. This study analyzed eight key components on the circuit. When it is used for dynamic wireless charging scenarios, there will be complex parameter drift problems, which lead to the deterioration of the power systems. In consequence, from the perspective of statistic model, this paper discussed the performance deteriorations and put them into practice in WPT applications of electric vehicles. Additionally, for further evaluations, simulations and experiments were given to show the noted factors of the proposed study.