Fast Attitude Estimation System for Unmanned Ground Vehicle Based on Vision/Inertial Fusion
Abstract
:1. Introduction
- A fast attitude estimate system is proposed. Based on the optimization method, the MEMS pre-integration results and the continuous visual attitude calculation results are fused. In order to eliminate the accumulated error, the pre-measured offline attitude library is introduced to provide a high-precision value.
- The experimental comparison results demonstrate the computational efficiency of the proposed method, and the attitude error will not accumulate with the endurance.
2. Materials and Methods
2.1. System Model
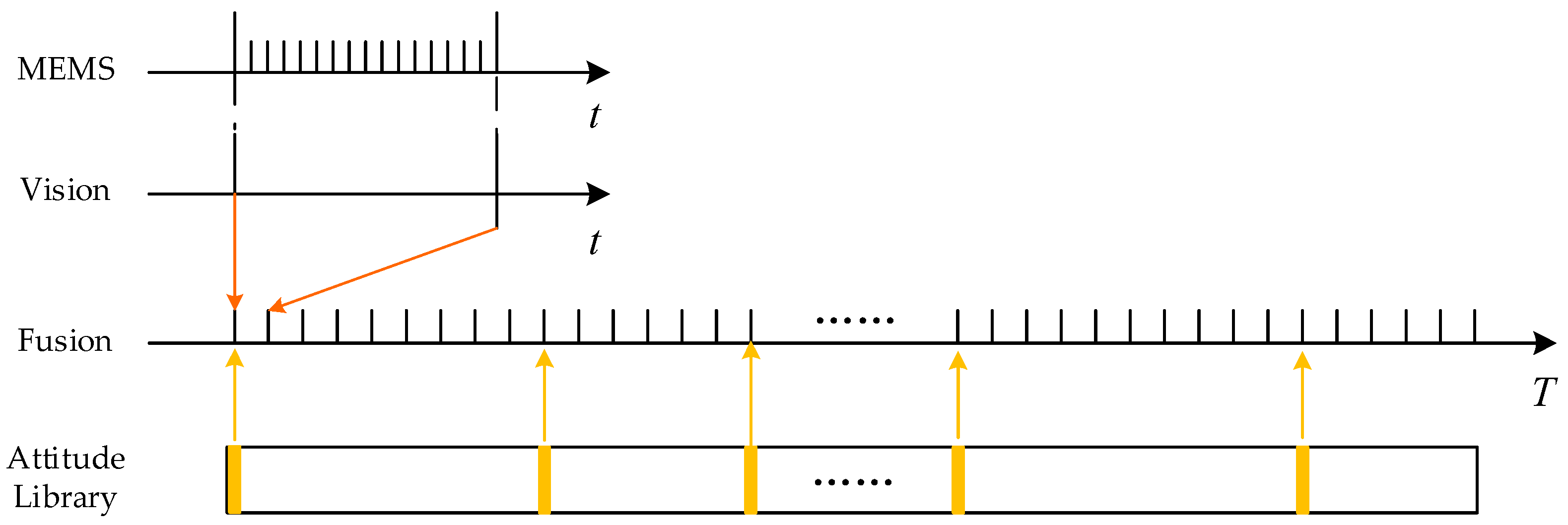
2.2. Attitude Estimate Based on the Vision/Inertial Fusion
2.3. Off-Line Attitude Library Construction Method
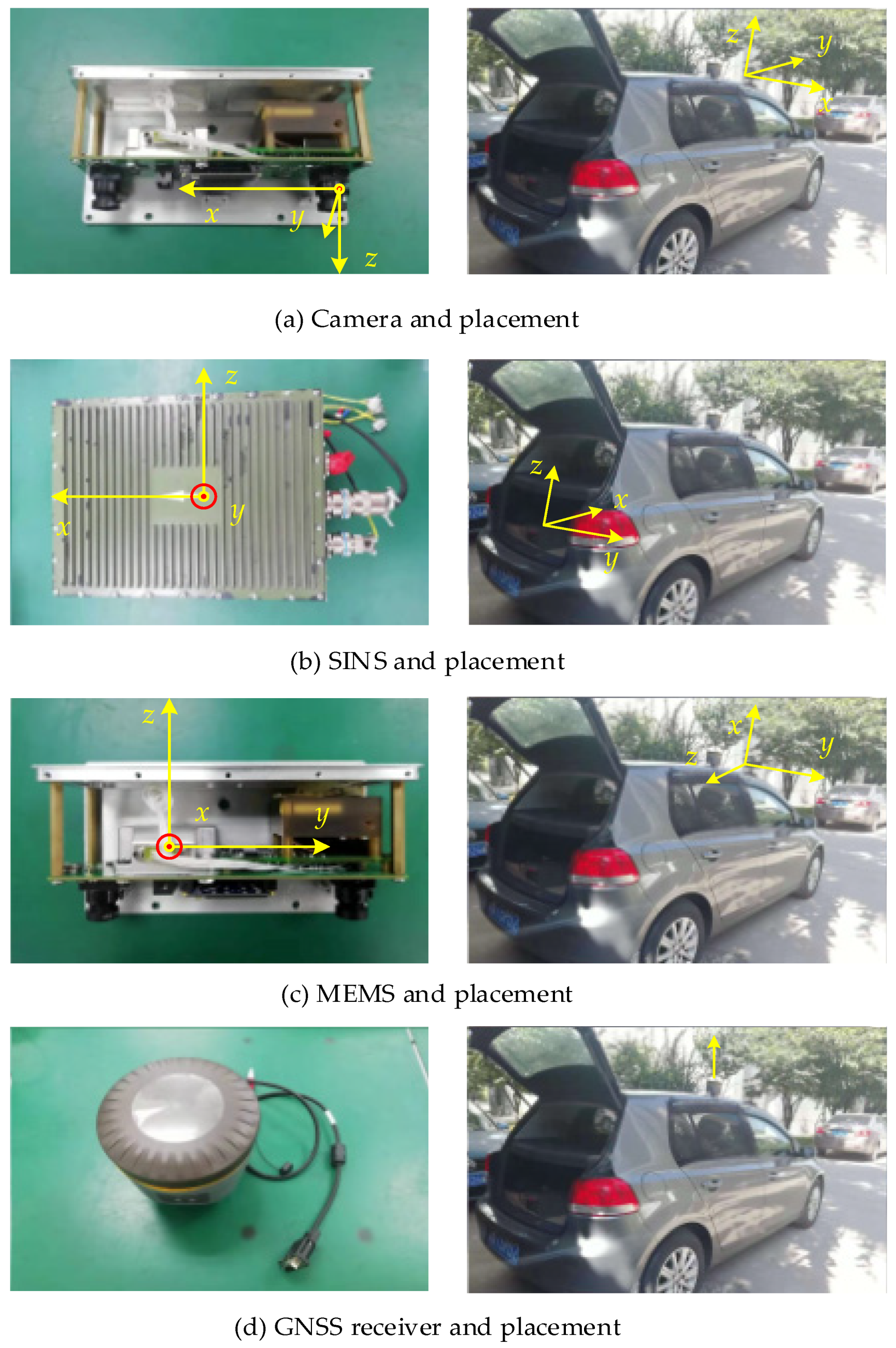
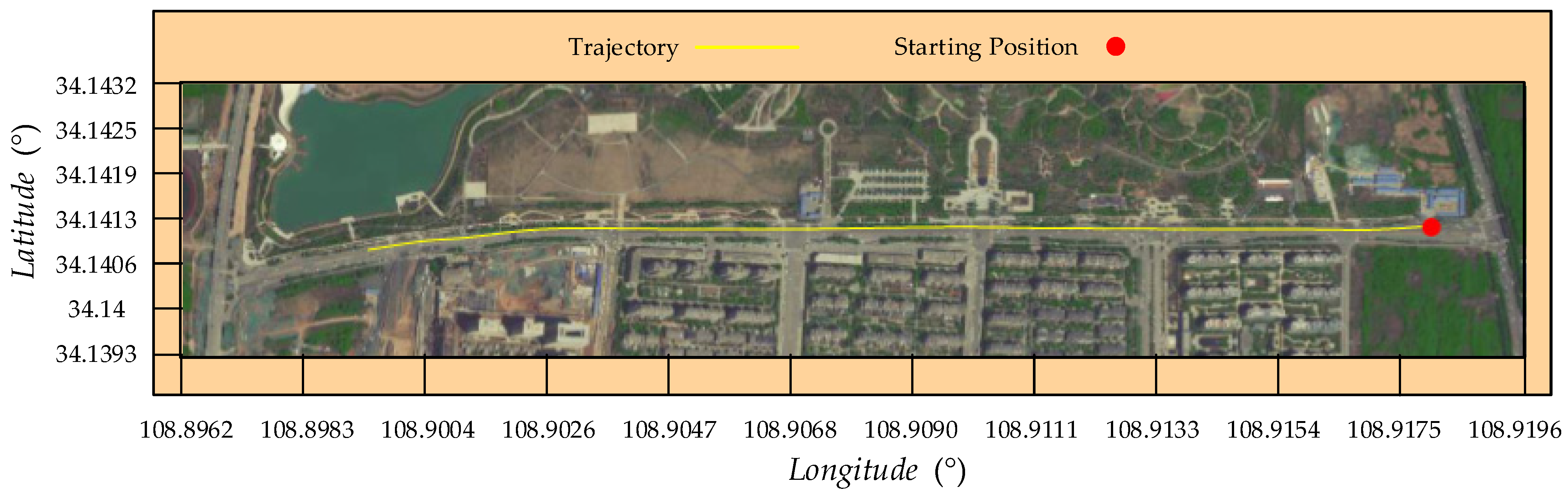
2.4. Platform of Road Test Experiments
3. Results
3.1. Parameters of Sensors
- Parameters of MEMS.
- Parameters of vision.
- Parameters of SINS/GNSS.
3.2. Experiments with KITTI Dataset
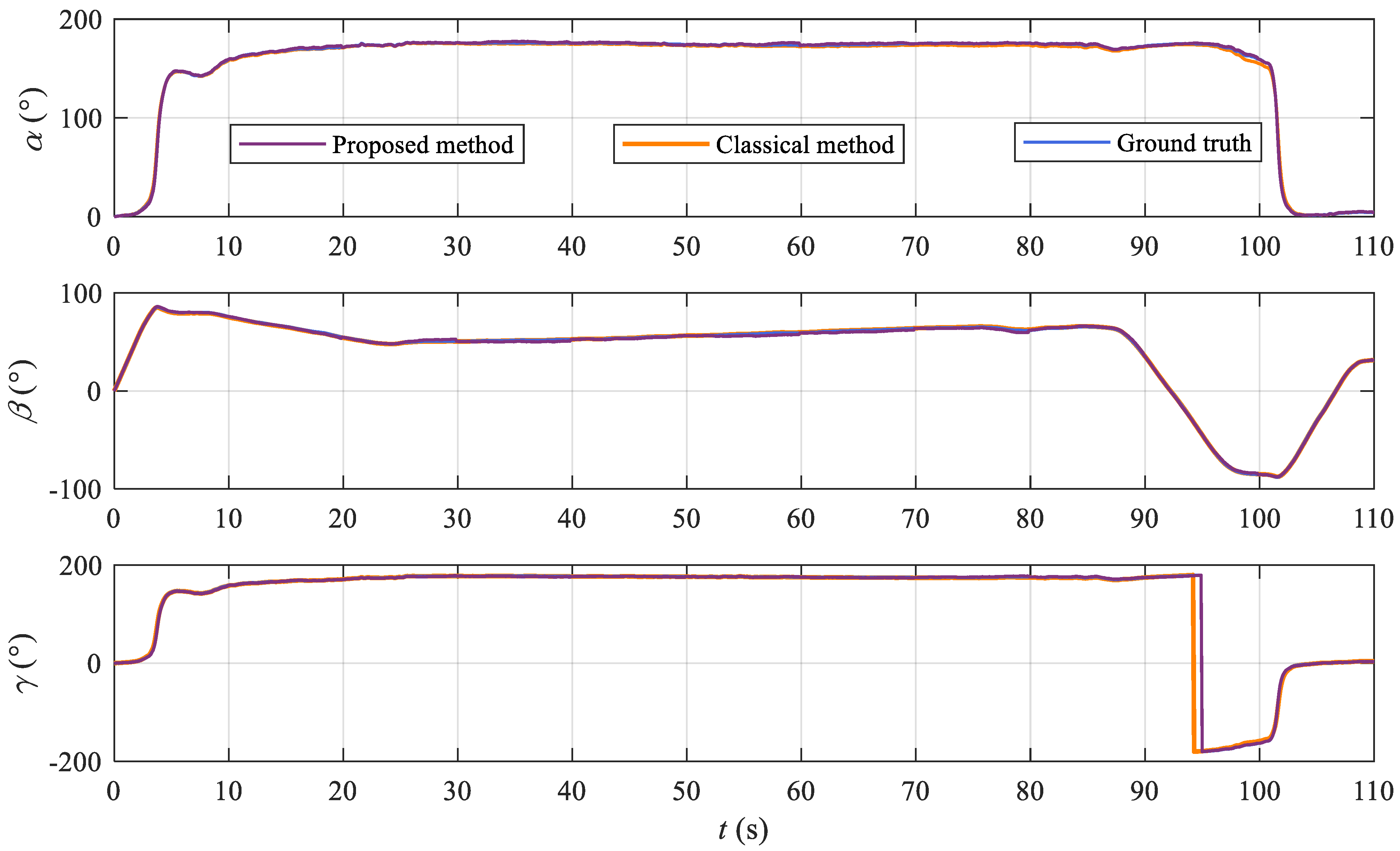
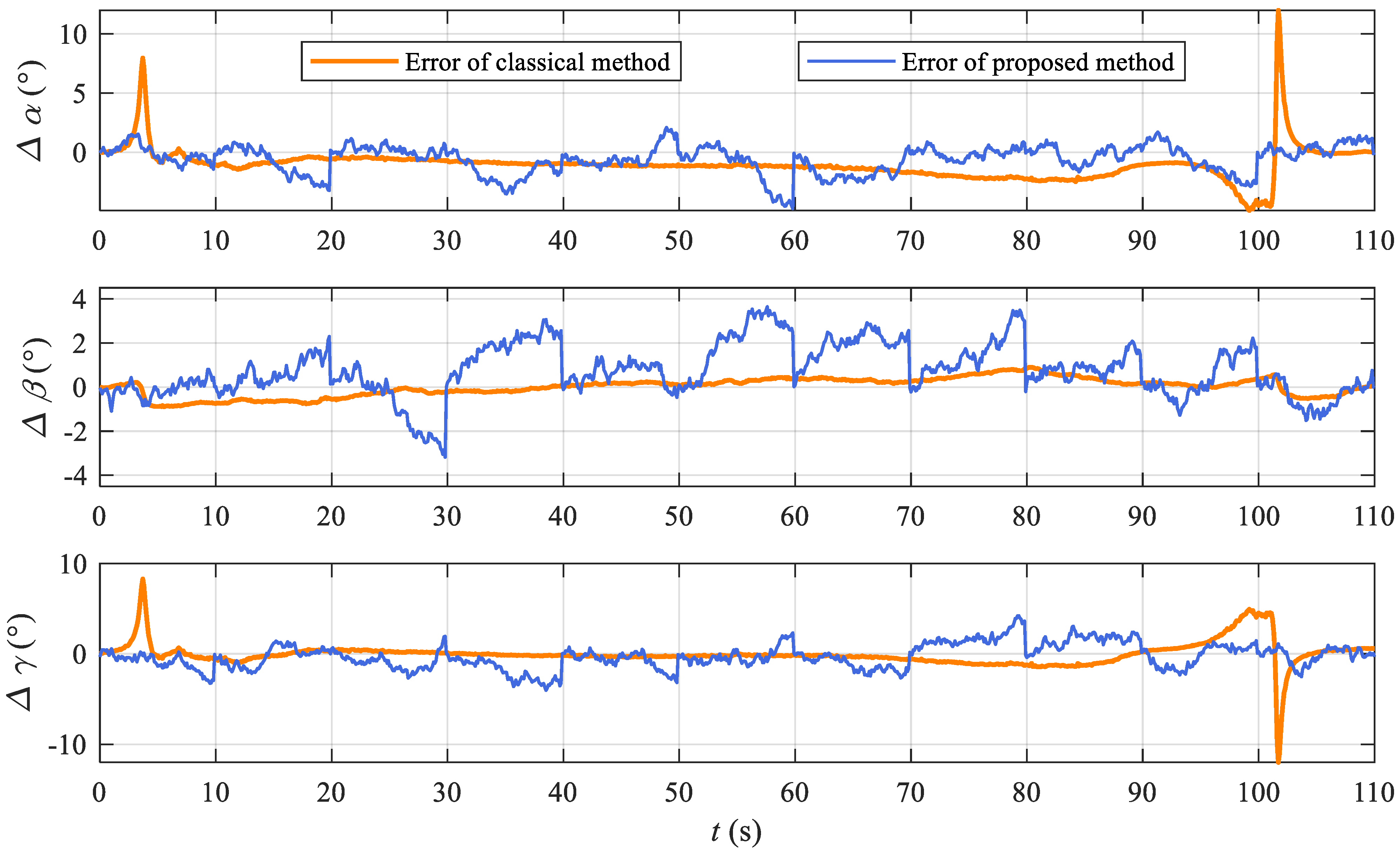
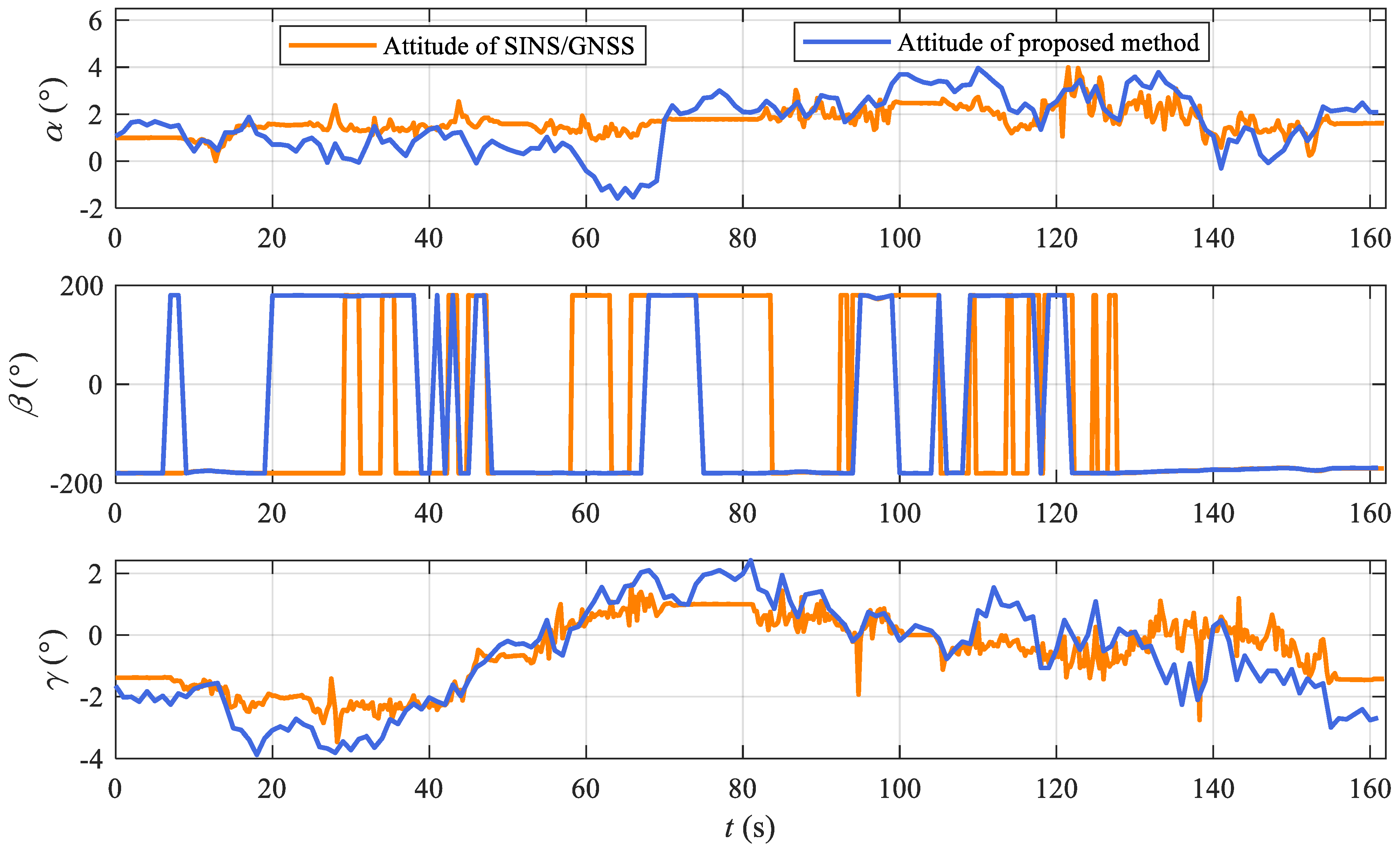
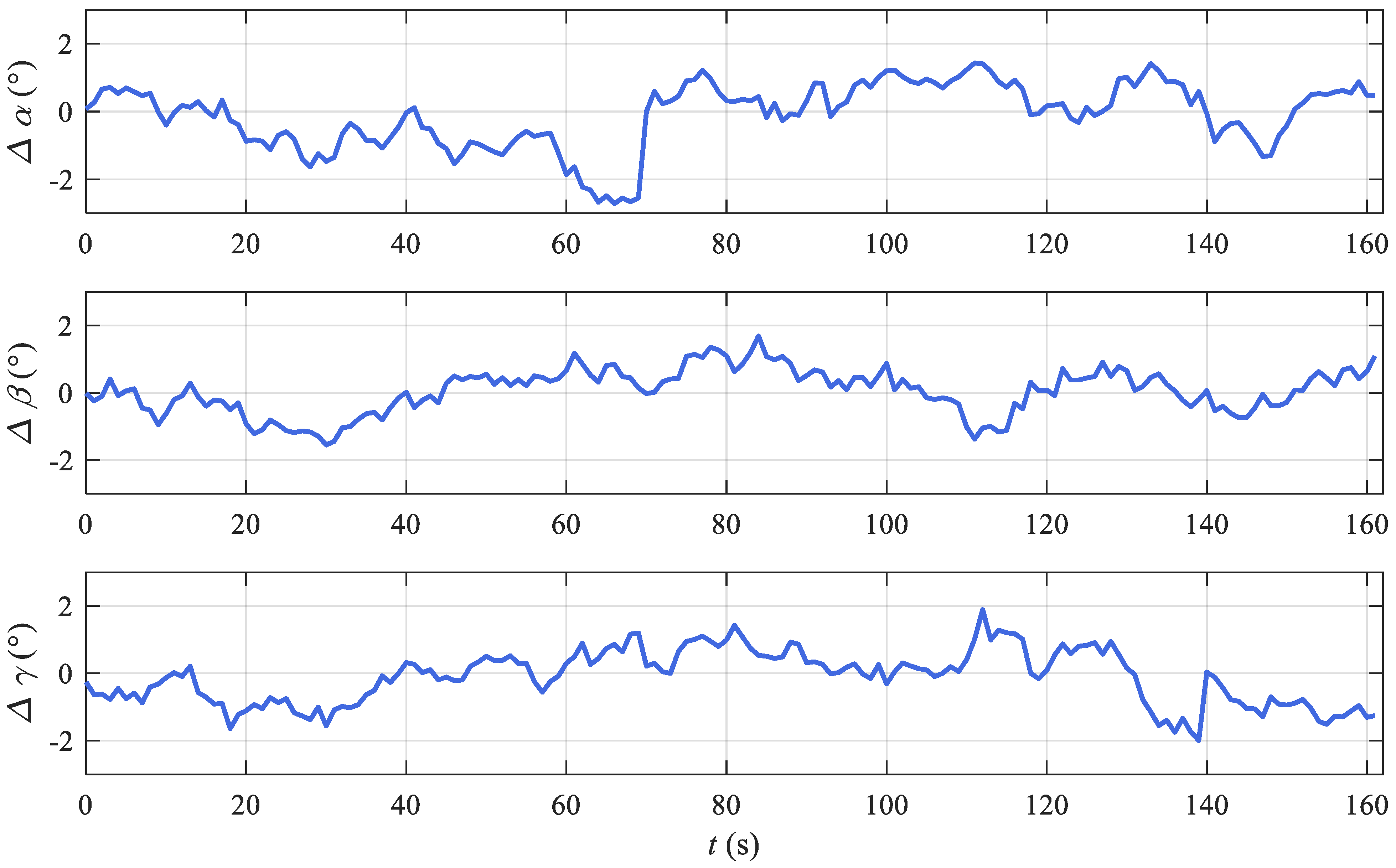
3.3. Experiments with Urban Road Test Data
4. Discussion
4.1. Discussion of the Experiment Results
4.2. Discussion of the Proposed System
4.3. Discussion of Futher Work
5. Conclusions
- This paper proposed a vision/inertial integration navigation system based on optimization to tackle the high computational cost of the classical method. Considering the cumulative error of the continuous vision and inertial pre-integration, the prior attitude information is introduced for correction, which is measured and labeled by an off-line fusion of multi-sensors.
- Experimental results show that in contrast with the classic method, the processing time per frame of the proposed method is reduced from 119 ms to 25 ms, which demonstrates the computational efficiency. Thus, the proposed method can tackle the high computational cost of the current vision/inertial integration method and makes it possible deploy on industrial processors.
- According to the KITTI and road test results, the proposed method is slightly inferior in accuracy. Considering that the attitude error of the proposed method will not accumulate with the endurance of UGVs, the proposed method is more suitable for UGVs in long endurance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.; Liu, D.; Cai, B.; Rizos, C.; Wang, J.; Shangguan, W. A Fault-Tolerant Tightly Coupled GNSS/INS/OVS Integration Vehicle Navigation System Based on an FDP Algorithm. IEEE Trans. Veh. Technol. 2019, 68, 6365–6378. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, inertial, and multisensor integrated navigation systems. Ind. Robot 2013, 67, 191–192. [Google Scholar]
- Song, R.; Fang, Y. Vehicle state estimation for INS/GPS aided by sensors fusion and SCKF-based algorithm. Mech. Syst. Signal Process. 2021, 150, 107315. [Google Scholar] [CrossRef]
- Mostafa, M.; Moussa, A.; El-Sheimy, N.; Sesay, A.B. A smart hybrid vision aided inertial navigation system approach for UAVs in a GNSS denied environment. Navig. J. Inst. Navig. 2018, 65, 533–547. [Google Scholar] [CrossRef]
- Srinara, S.; Lee, C.-M.; Tsai, S.; Tsai, G.-J.; Chiang, K.-W. Performance Analysis of 3D NDT Scan Matching for Autonomous Vehicles Using INS/GNSS/3D LiDAR-SLAM Integration Scheme. 2021 IEEE Int. Symp. Inert. Sens. Syst. 2021. [Google Scholar] [CrossRef]
- Jiang, W.; Yu, Y.; Zong, K.; Cai, B.; Rizos, C.; Wang, J.; Liu, D.; Shangguan, W. A Seamless Train Positioning System Using a Lidar-Aided Hybrid Integration Methodology. IEEE Trans. Veh. Technol. 2021, 70, 6371–6384. [Google Scholar] [CrossRef]
- Zhou, P.; Guo, X.; Pei, X.; Chen, C. T-LOAM: Truncated Least Squares LiDAR-Only Odometry and Mapping in Real Time. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Fan, C.; Hu, X.; Lian, J.; Zhang, L.; He, X. Design and Calibration of a Novel Camera-Based Bio-Inspired Polarization Navigation Sensor. IEEE Sens. J. 2016, 16, 3640–3648. [Google Scholar] [CrossRef]
- He, X.; Cai, Y.; Fan, C.; He, J.; Zhang, L. Bionic Polarized Light Orientation Algorithm for Unmanned Ground Vehicle. Navig. Position. Timing 2020, 6, 231–236. [Google Scholar]
- Fan, C.; He, X.; Fan, Y.; Hu, X.; Zhang, L.; Yu, H. Integrated orientation method based on the micro-inertial and polarized vision. J. Chin. Inert. Technol. 2019, 28, 231–236. [Google Scholar]
- Servières, M.; Renaudin, V.; Dupuis, A. Visual and Visual-Inertial SLAM: State of the Art, Classification, and Experimental Benchmarking. J. Sens. 2021, 1, 1–26. [Google Scholar] [CrossRef]
- Zhai, C.; Wang, M.; Yang, Y.; Shen, K. Robust Vision-Aided Inertial Navigation System for Protection Against Ego-Motion Uncertainty of Unmanned Ground Vehicle. IEEE Trans. Ind. Electron. 2021, 68, 12462–12471. [Google Scholar] [CrossRef]
- Yu, Y.K.; Wong, K.H.; Chang, M.M.Y.; Or, S.H. Recursive Camera-Motion Estimation with the Trifocal Tensor. IEEE Trans. Syst. Man Cybern. Part B 2006, 36, 1081–1090. [Google Scholar] [CrossRef] [PubMed]
- Indelman, V.; Gurfil, P.; Rivlin, E.; Rotstein, H. Real-Time Vision-Aided Localization and Navigation Based on Three-View Geometry. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2239–2259. [Google Scholar] [CrossRef]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual—Inertial Odometry. IEEE Trans. Robot. 2017, 33, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- Campos, C.; Elvira, R.; Rodriguez, J.J.G.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021. [Google Scholar] [CrossRef]
- Wang, J. LearnVIORB. Github. 2017. Available online: https://github.com/jingpang/LearnVIORB (accessed on 10 April 2021).
- Venator, M.; Bruns, E.; Maier, A. Robust Camera Pose Estimation for Unordered Road Scene Images in Varying Viewing Conditions. IEEE Trans. Intell. Veh. 2020, 5, 165–174. [Google Scholar] [CrossRef]
- Guerrero, J.; Murillo, A.; Sagues, C. Localization and Matching Using the Planar Trifocal Tensor with Bearing-Only Data. IEEE Trans. Robot. 2008, 24, 494–501. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.Y. Inertial Navigation; Science Press: Beijing, China, 2006. [Google Scholar]
- Mur-Artal, R.; Tardos, J.D. Visual-Inertial Monocular SLAM with Map Reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef] [Green Version]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]


| Parameters | Unit | Value |
|---|---|---|
| Accelerometer bias | 10−3 g | |
| Accelerometer scale factor | Ppm | |
| Accelerometer installation | Arcsec | |
| Accelerometer white noise | 10−3 g/sqrt(Hz) | |
| Gyroscope bias | °/h | |
| Gyroscope scale factor | Ppm | |
| Gyroscope installation | Arcsec | |
| Gyroscope white noise | °/h/sqrt(Hz) | |
| pdate cycle | Ms | 0.005 |
| Area | Average Velocity (km/h) | Algorithm | Average Attitude Error (°) | Processing Time per Frame (ms) |
|---|---|---|---|---|
| Highway | 75.9 | Classical | 0.79 | 119 |
| Proposed | 1.11 | 25 |
| Area | Average Velocity (km/h) | Average Error (°) | Processing Time per Frame (ms) |
|---|---|---|---|
| Urban | 30–40 | 1.97 | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Yang, P.; Mei, C.; Zhu, Q.; Luo, X. Fast Attitude Estimation System for Unmanned Ground Vehicle Based on Vision/Inertial Fusion. Machines 2021, 9, 241. https://doi.org/10.3390/machines9100241
Fan Z, Yang P, Mei C, Zhu Q, Luo X. Fast Attitude Estimation System for Unmanned Ground Vehicle Based on Vision/Inertial Fusion. Machines. 2021; 9(10):241. https://doi.org/10.3390/machines9100241
Chicago/Turabian StyleFan, Zhenhui, Pengxiang Yang, Chunbo Mei, Qiju Zhu, and Xiao Luo. 2021. "Fast Attitude Estimation System for Unmanned Ground Vehicle Based on Vision/Inertial Fusion" Machines 9, no. 10: 241. https://doi.org/10.3390/machines9100241
APA StyleFan, Z., Yang, P., Mei, C., Zhu, Q., & Luo, X. (2021). Fast Attitude Estimation System for Unmanned Ground Vehicle Based on Vision/Inertial Fusion. Machines, 9(10), 241. https://doi.org/10.3390/machines9100241






