Optimal Vibration Suppression Modification Method for High-Speed Helical Gear Transmission of Battery Electric Vehicles under Full Working Conditions
Abstract
:1. Introduction
- (1)
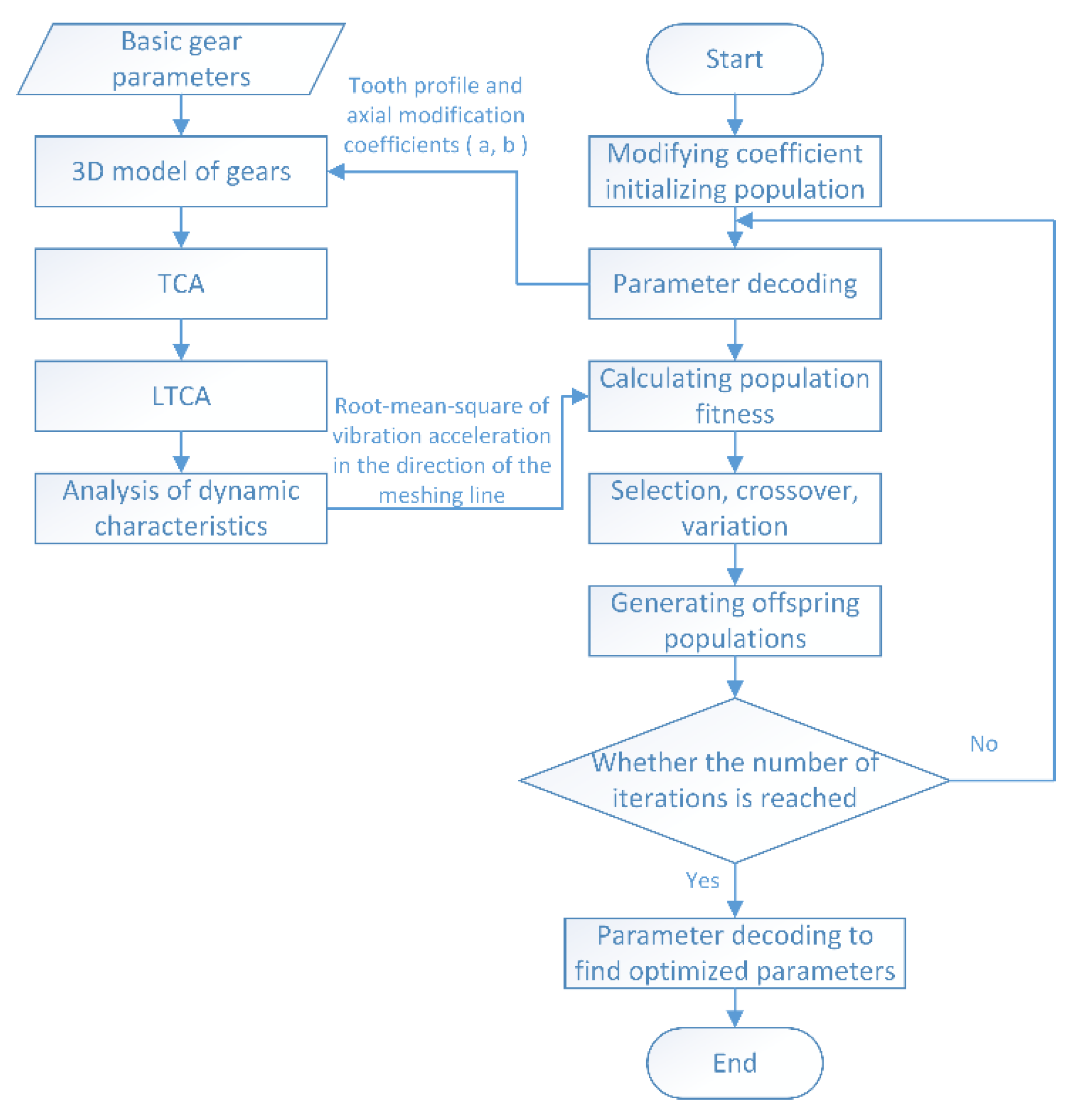
- obtain the optimal tooth profile under full working conditions by combining TCA, LTCA, and genetic optimization algorithms;
- (2)
- study the effect of different modification methods under full working conditions;
- (3)
- obtain the optimal vibration suppression modification strategy for BEV high-speed gear transmission under full working conditions, and further extend the application to other gear transmissions.
2. Mathematical Model
2.1. Dynamic Model of the Gear Transmission
2.2. Excitation
2.3. Tooth Surface Modification
2.4. The Global Optimization Model
3. Experimental Verification and Analysis
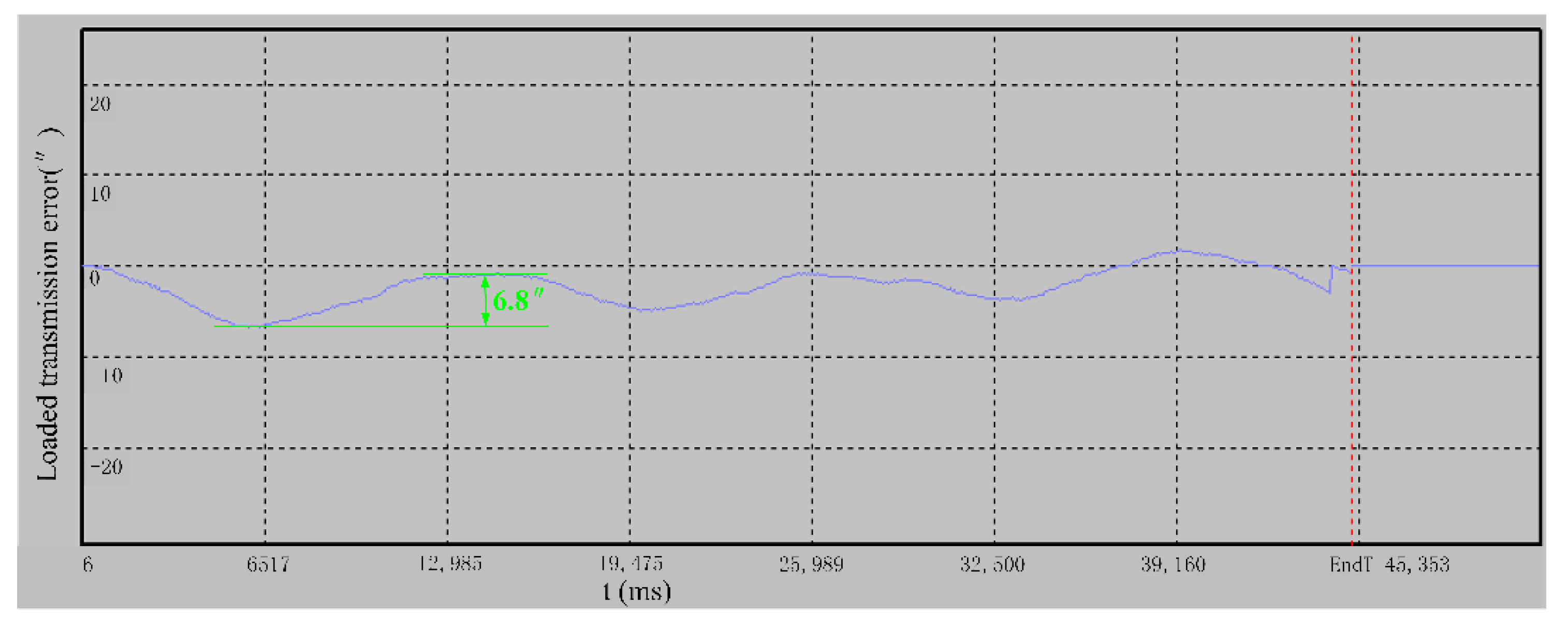
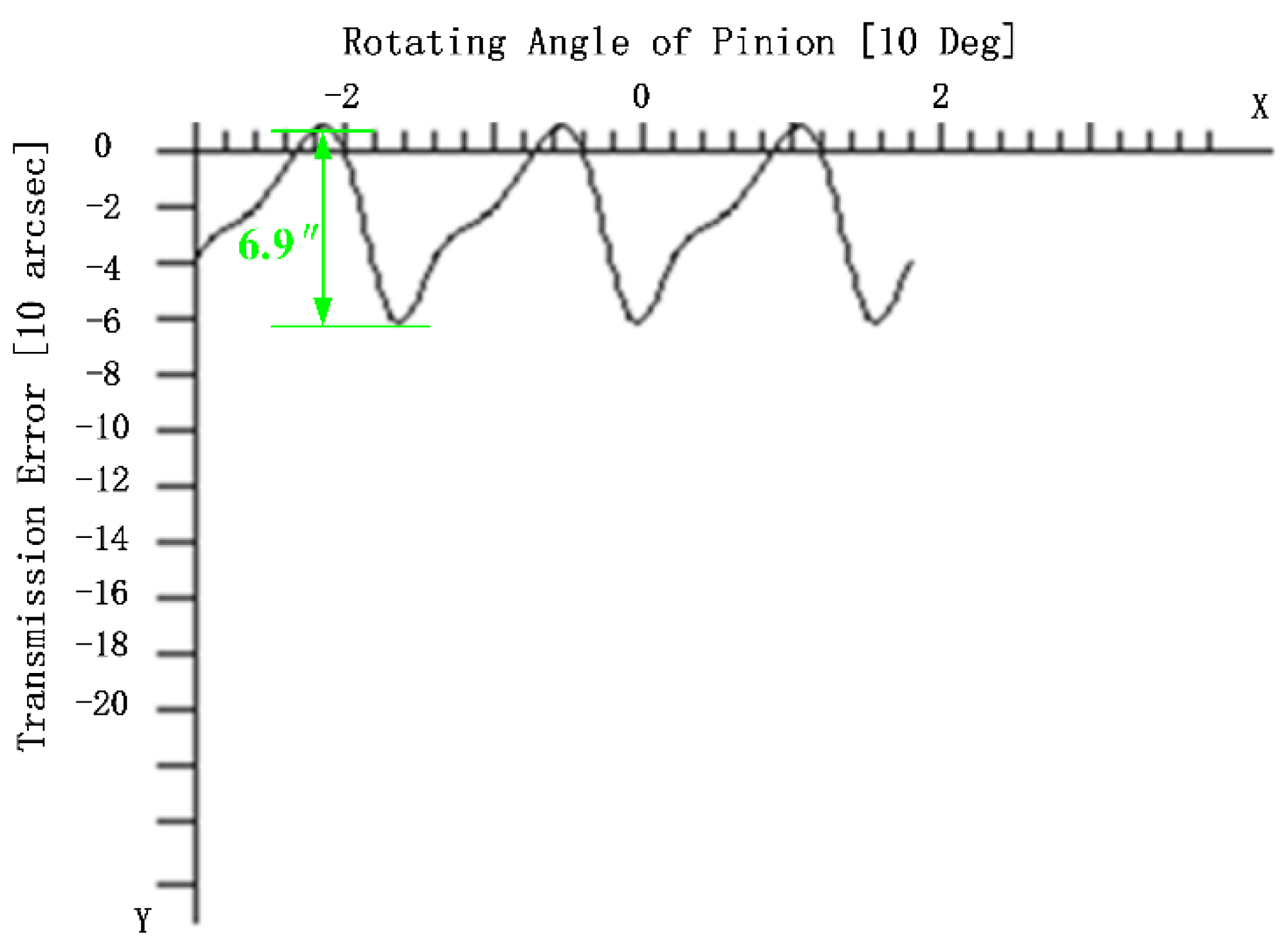
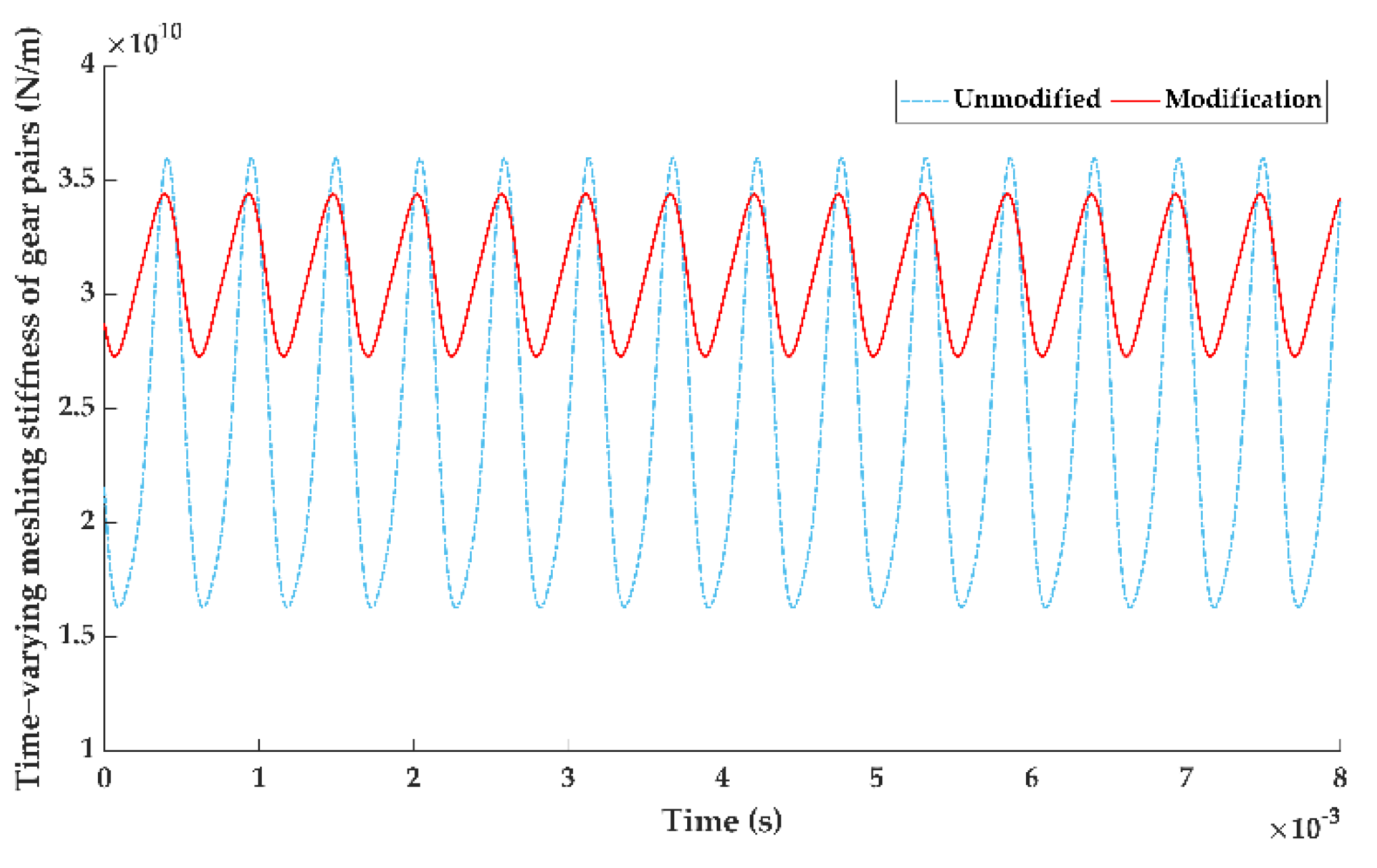
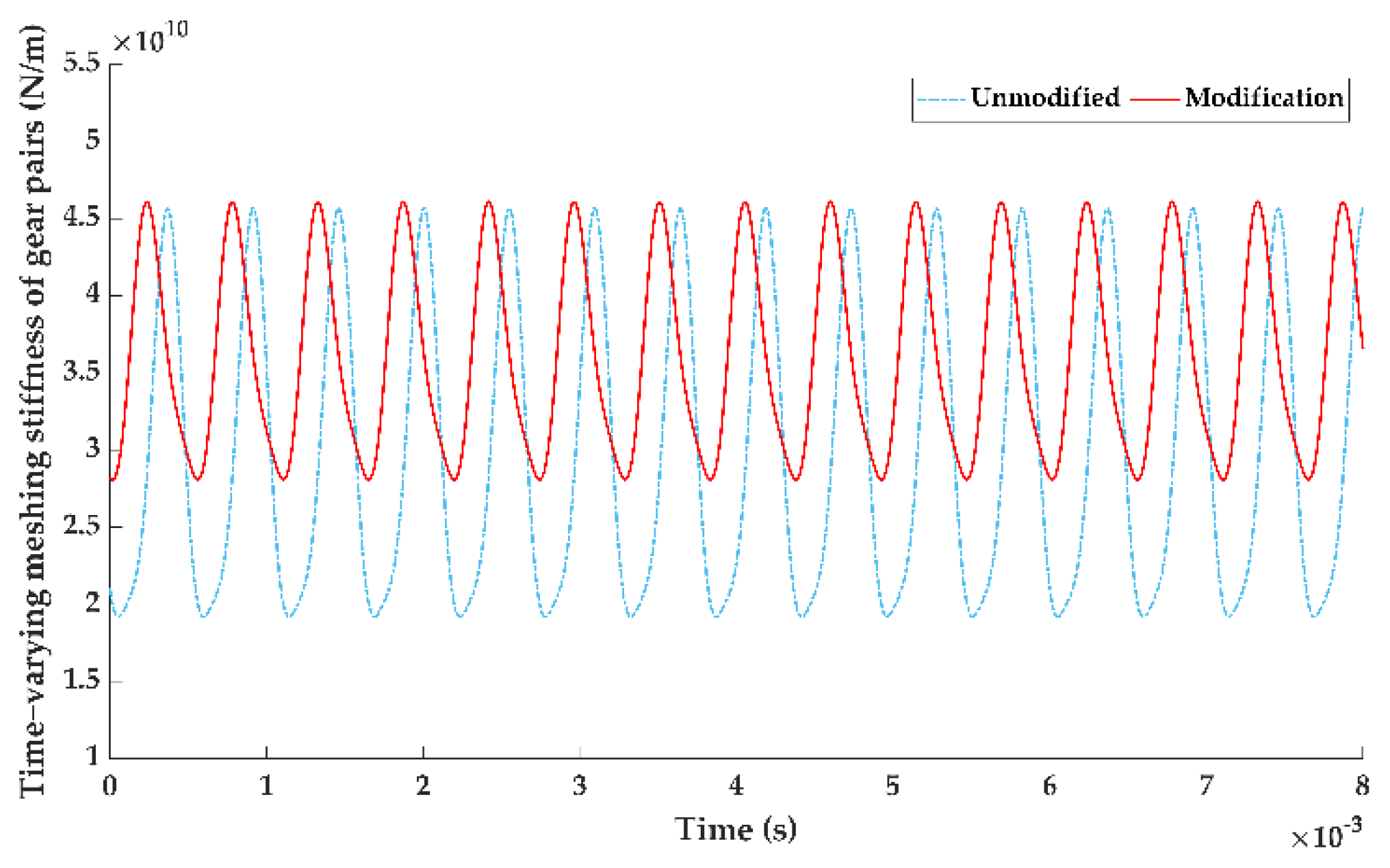
3.1. Experimental Verification of LTE Calculation Accuracy after Tooth Surface Modification
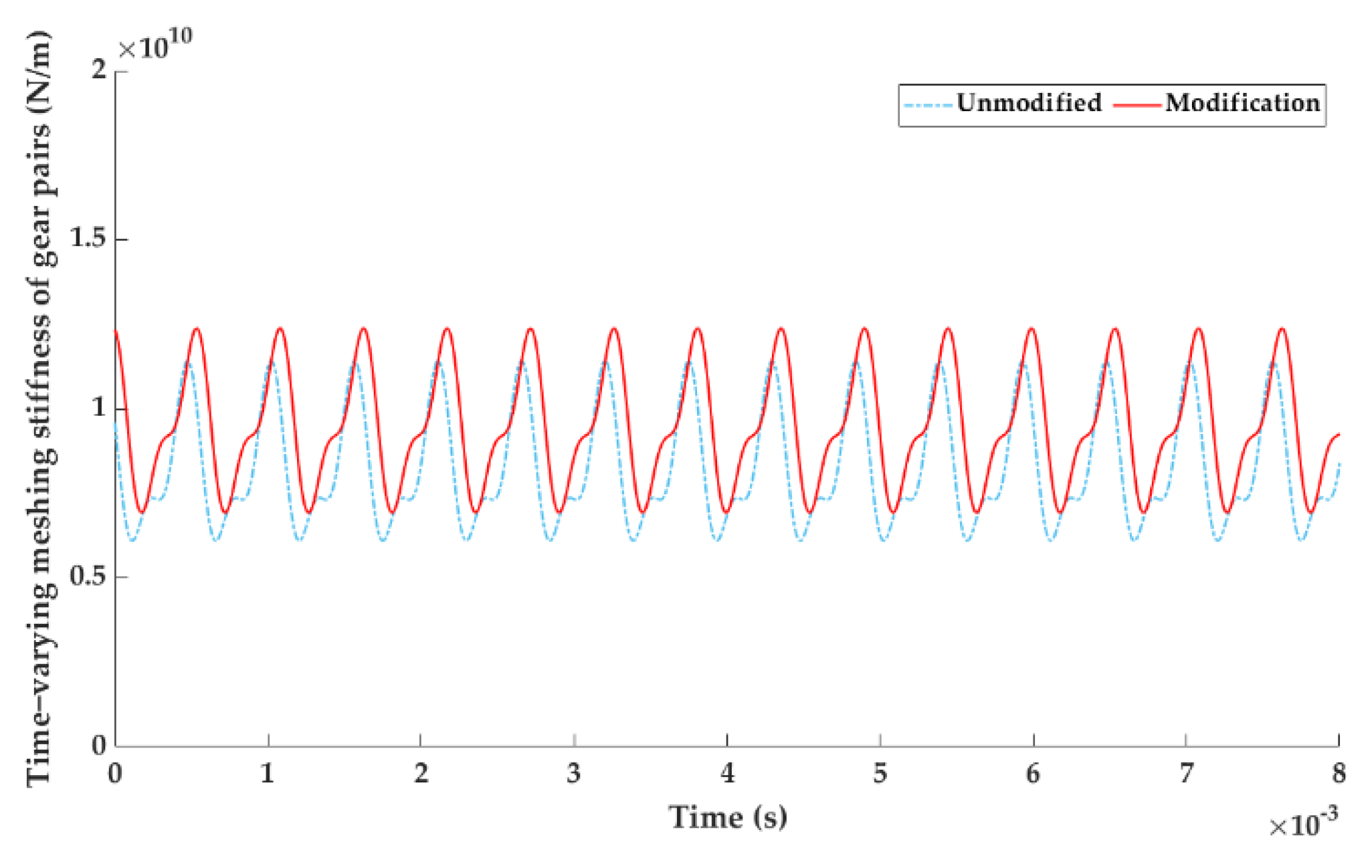
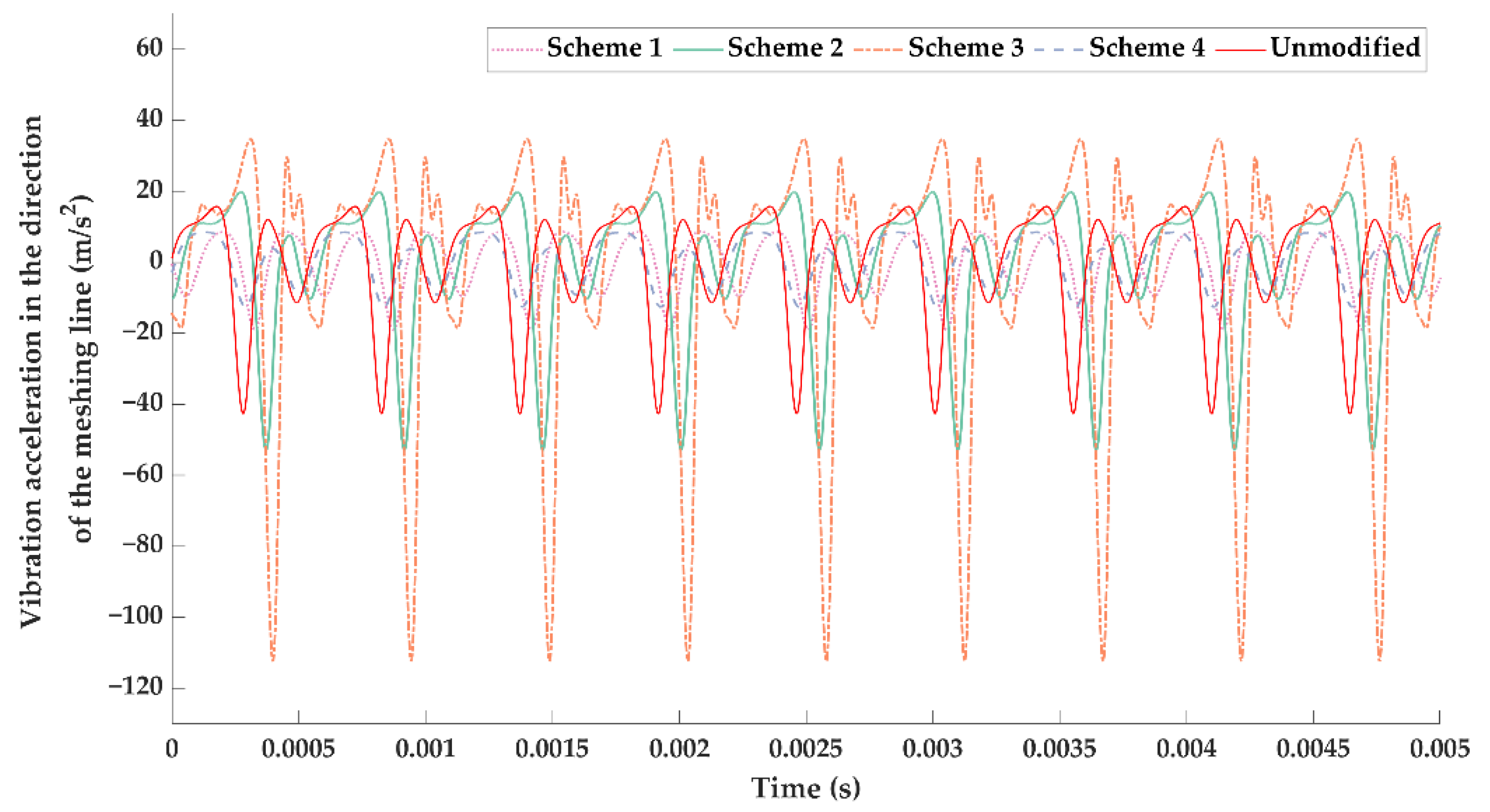
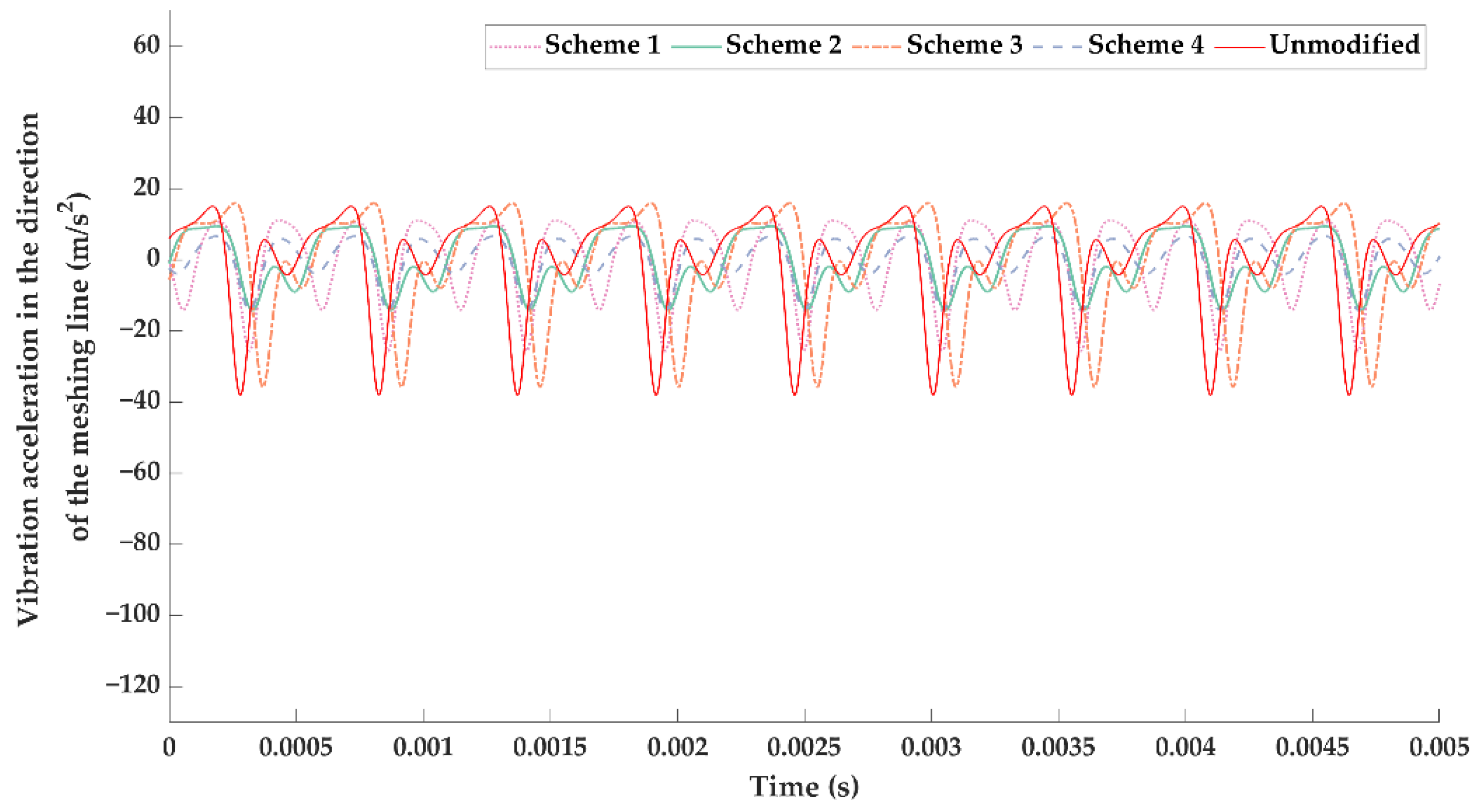
3.2. Optimal Tooth Surface Modification Scheme
4. Conclusions
- (1)
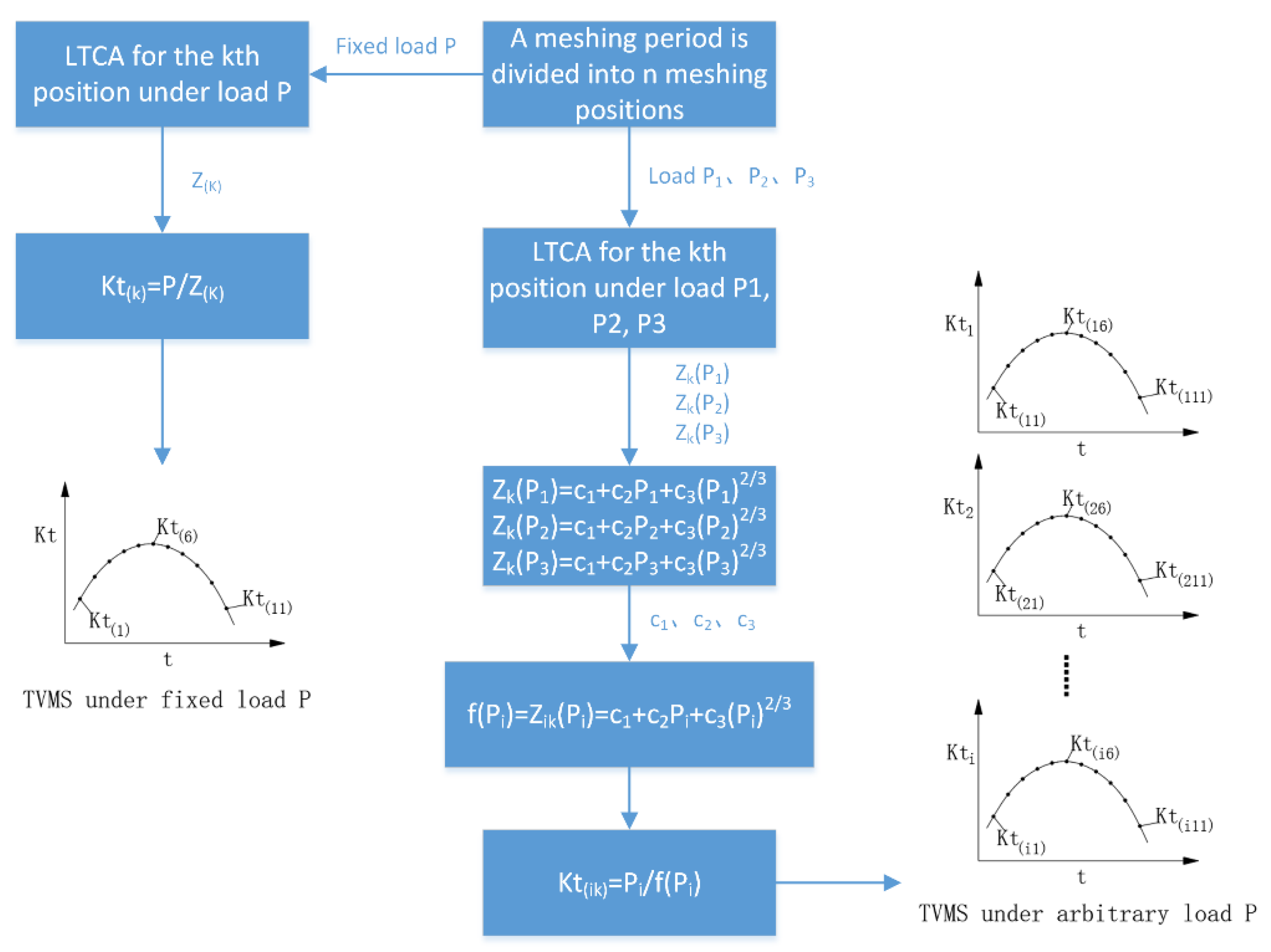
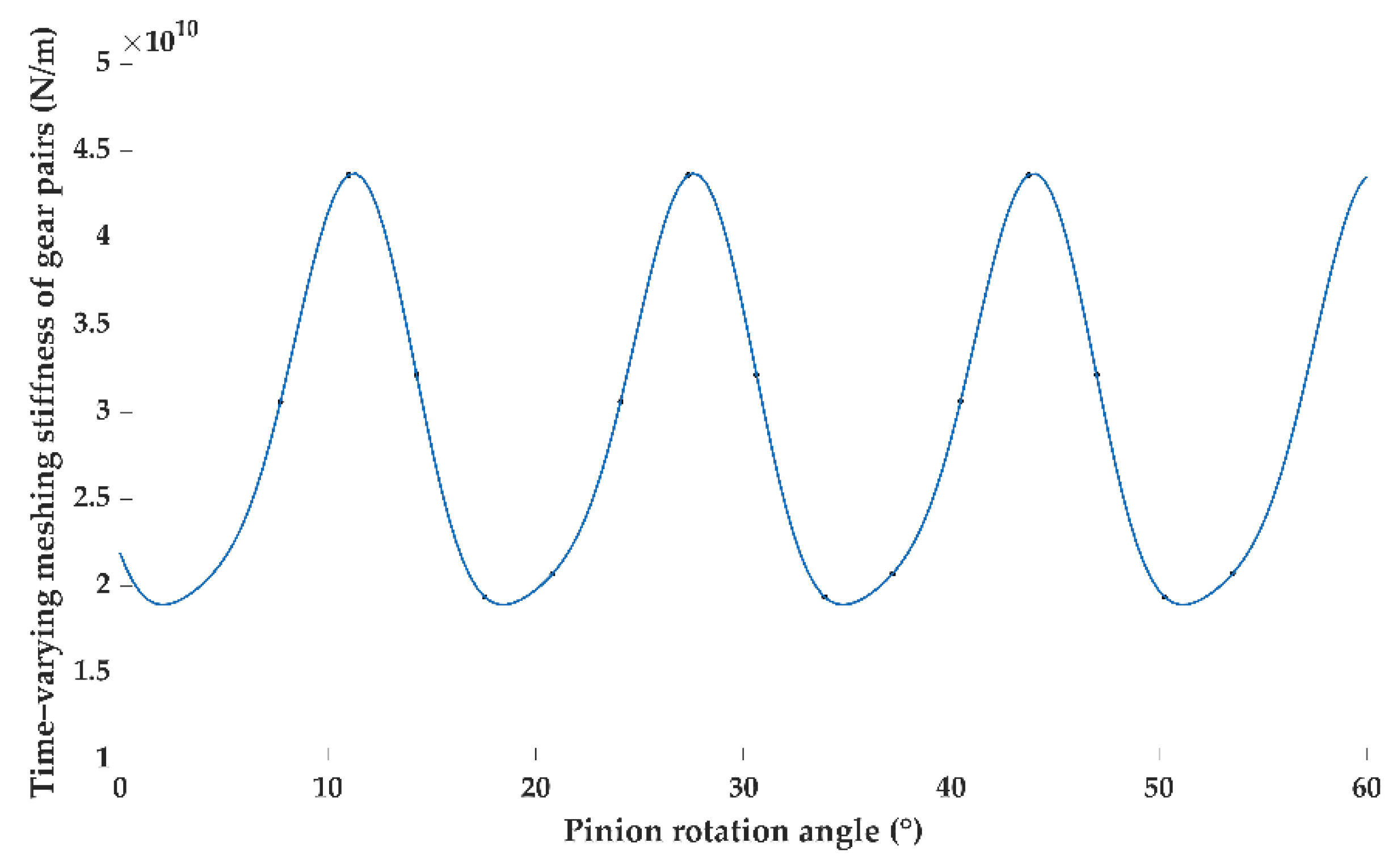
- The bending-torsion-axis-swing coupling dynamics model of the helical gear system considering the stiffness excitation was established, the TVMS of the gear pair was calculated based on LTCA, and the calculation accuracy was verified by experiment.
- (2)
- Tooth profile and axial modifications were realized in TCA. The optimal tooth profile and axial modification parameters for the full working condition were obtained by using a genetic algorithm with the minimum root mean square of vibration acceleration as the optimization objective.
- (3)
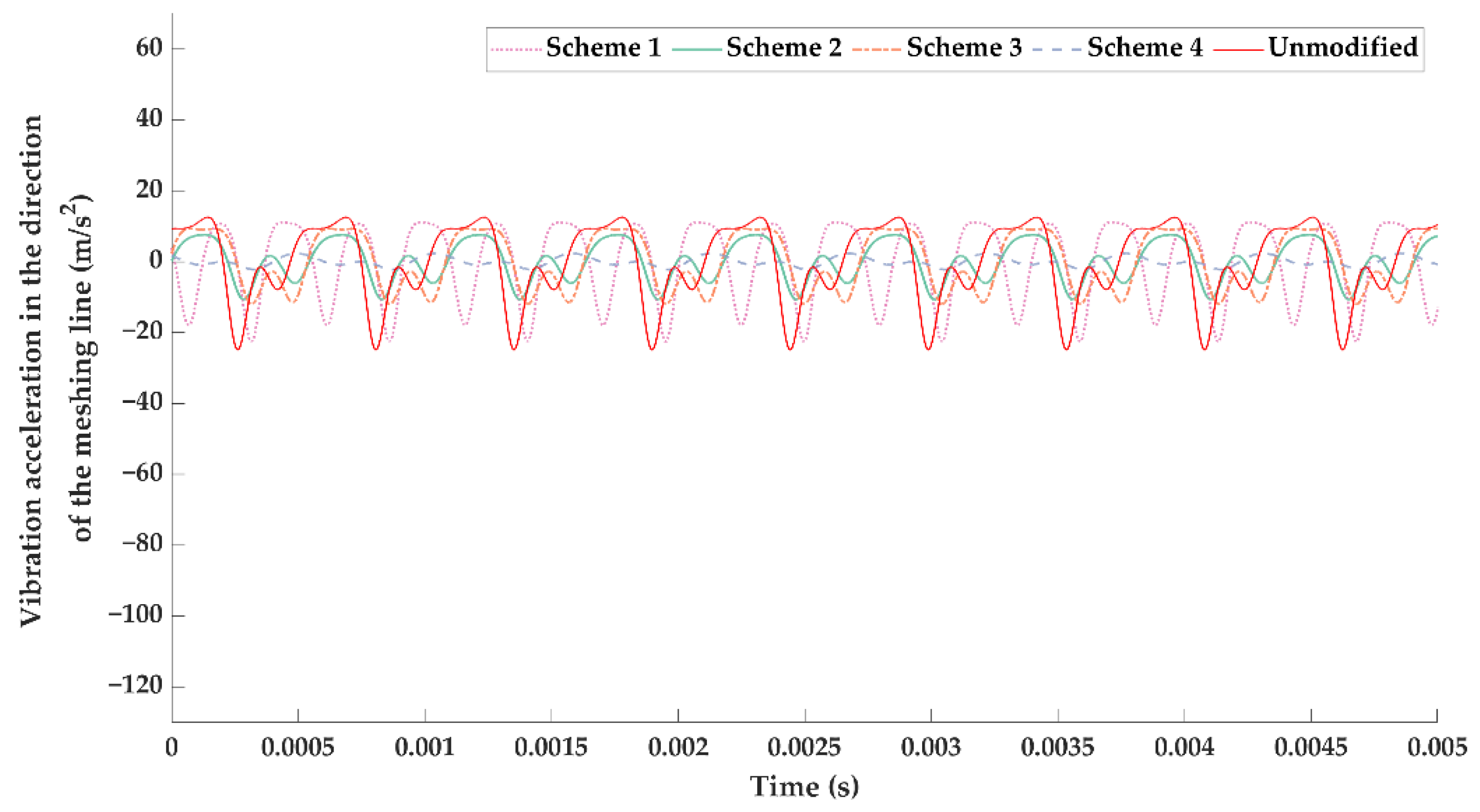
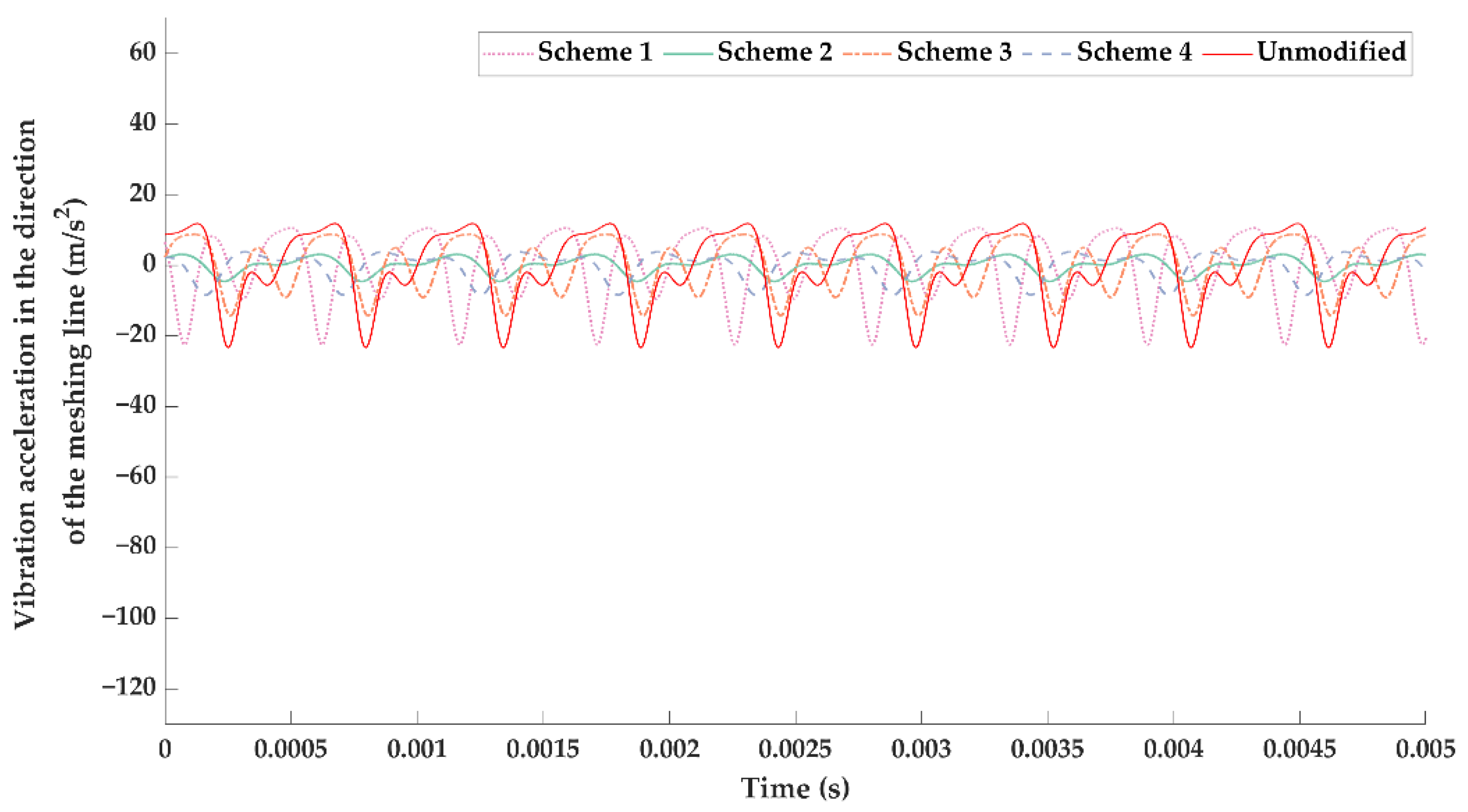
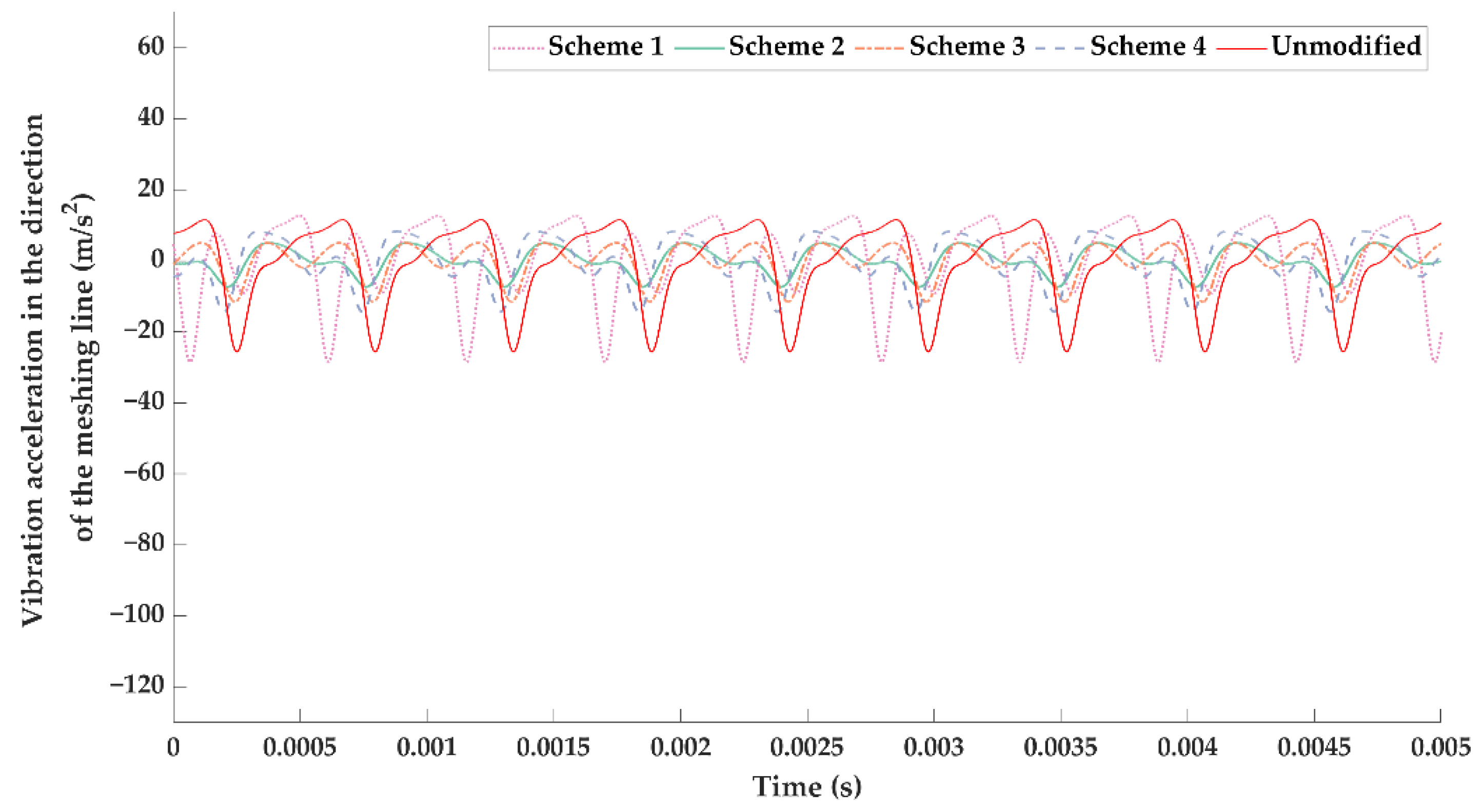
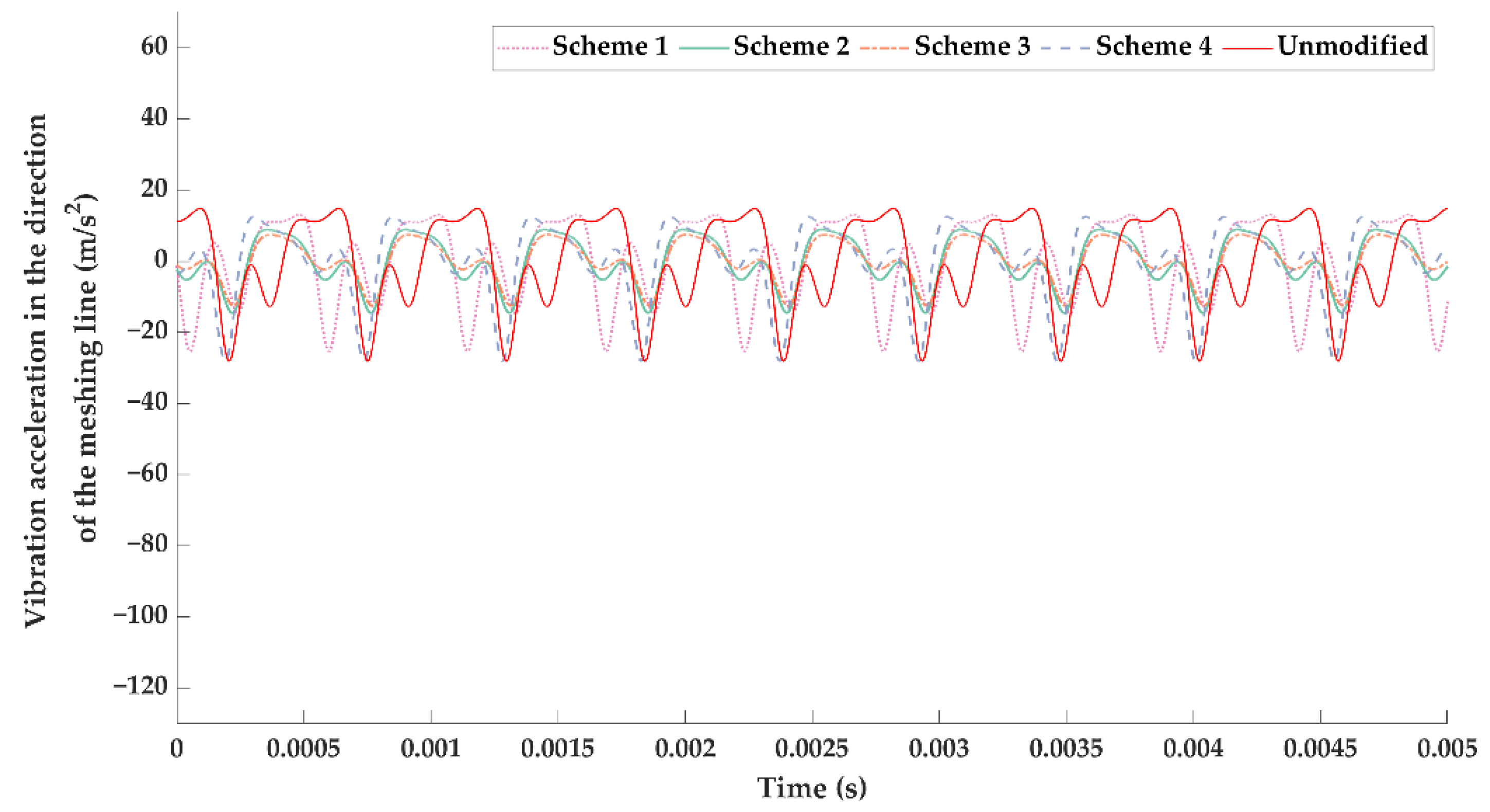
- The vibration reduction effects of the optimal modification under a specific load and the full working condition were significantly different; the optimal modified tooth surface under full working condition had a better vibration suppression effect in the whole working load range. Therefore, more attention should be paid to the tooth surface modification under the full working conditions in BEV high-speed gear transmissions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Fang, Z.; Zhao, N.; Guo, H.; Shen, Y. Design and Analysis of Compensation Modification for Multi-Pair Contact of High-Contact-Ratio Helical Gears. J. Xi’an Jiao Tong Univ. 2020, 54, 56–64. [Google Scholar]
- Jiang, J.; Liu, Z.; Peng, X. Optimization Design of Vibration Reduction for Hypoid Gears with Ease-Off Flank Modification. J. South China Univ. Technol. (Nat. Sci. Ed.) 2020, 48, 134–141. [Google Scholar]
- Yang, S.; He, D.; Tang, J.; Wan, G. Research of the Design of Double Helical Gear Modification based on KISSsoft Software. J. Mech. Transm. 2018, 42, 1–6. [Google Scholar]
- Giorgio, B.; Marco, B.; Francesco, P. Optimum profile modifications of spur gears by means of genetic algorithms. J. Sound Vib. 2007, 313. [Google Scholar] [CrossRef]
- Samani, F.S.; Molaie, M.; Pellicano, F. Nonlinear vibration of the spiral bevel gear with a novel tooth surface modification method. Meccanica 2019, 54, 1071–1081. [Google Scholar] [CrossRef]
- Vilmos, S. Optimal Tooth Surface Modifications in Face-Hobbed Hypoid Gears. Key Eng. Mater. 2014, 572, 351–354. [Google Scholar] [CrossRef]
- Motahar, H.; Samani, F.S.; Molaie, M. Nonlinear vibration of the bevel gear with teeth profile modification. Nonlinear Dyn. 2016, 83, 1875–1884. [Google Scholar] [CrossRef]
- Bahk, C.J.; Parker, R.G. Analytical investigation of tooth profile modification effects on planetary gear dynamics. Mech. Mach. Theory 2013, 70, 298–319. [Google Scholar] [CrossRef]
- Wang, C. Study on 3-D modification for reducing vibration of helical gear based on TCA technology, LTCA technology and system dynamics. Mech. Syst. Signal Process. 2021, 146, 106991. [Google Scholar] [CrossRef]
- Wang, C. Multi-objective optimal design of modification for helical gear. Mech. Syst. Signal Process. 2021, 157, 107762. [Google Scholar] [CrossRef]
- Ghosh, S.S.; Chakraborty, G. On optimal tooth profile modification for reduction of vibration and noise in spur gear pairs. Mech. Mach. Theory 2016, 105, 145–163. [Google Scholar] [CrossRef]
- Cirelli, M.; Valentini, P.P.; Pennestrì, E. A study of the non-linear dynamic response of spur gear using a multibody contact based model with flexible teeth. J. Sound Vib. 2019, 445, 148–167. [Google Scholar] [CrossRef]
- Bruzzone, F.; Maggi, T.; Marcellini, C.; Rosso, C.; Delprete, C. Proposal of a novel approach for 3D tooth contact analysis and calculation of the static transmission error in loaded gears. Procedia Struct. Integr. 2019, 24, 178–189. [Google Scholar] [CrossRef]
- Liu, G.; Parker, R.G. Dynamic Modeling and Analysis of Tooth Profile Modification for Multimesh Gear Vibration. J. Mech. Des. 2008, 130. [Google Scholar] [CrossRef]
- Hu, Y.; Shao, Y.; Chen, Z.; Zuo, M.J. Transient meshing performance of gears with different modification coefficients and helical angles using explicit dynamic FEA. Mech. Syst. Signal Process. 2010, 25, 1786–1802. [Google Scholar] [CrossRef]
- Martini, A.; Bonelli, G.P.; Rivola, A. Virtual Testing of Counterbalance Forklift Trucks: Implementation and Experimental Validation of a Numerical Multibody Model. Machines 2020, 8, 26. [Google Scholar] [CrossRef]
- Schliermann, J.; Krüger, M. Bevel Gearbox with Vertical Drive Attachment for Industrial Trucks. ATZoffhighway Worldw. 2018, 11, 44–47. [Google Scholar] [CrossRef]
- Shen, J.; Cheng, H. Investigation on the Stationary Response of Gear Time-varying System Under Stochastic Excitation. J. Mech. Transm. 2021, 45, 37–40. [Google Scholar]
- Raghuwanshi, N.K.; Parey, A. Experimental measurement of gear mesh stiffness of cracked spur gear by strain gauge technique. Measurement 2016, 86, 266–275. [Google Scholar] [CrossRef]
- Pedersen, N.L.; Jørgensen, M.F. On gear tooth stiffness evaluation. Comput. Struct. 2014, 135, 109–117. [Google Scholar] [CrossRef]
- Jia, C.; Yao, L.; Zhang, J.; Fang, Z. Calculation of Mesh-in Impact of Modified Involute Helical Gears. J. Xi’an Jiao Tong Univ. 2020, 54, 58–65. [Google Scholar]
- Inalpolat, M.; Handschuh, M.; Kahraman, A. Influence of indexing errors on dynamic response of spur gear pairs. Mech. Syst. Signal Process. 2015, 60–61, 391–405. [Google Scholar] [CrossRef]
- Li, S. Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors, assembly errors and tooth modifications. Mech. Mach. Theory 2007, 42, 88–114. [Google Scholar] [CrossRef]
- He, S.; Gunda, R.; Singh, R. Effect of sliding friction on the dynamics of spur gear pair with realistic time-varying stiffness. J. Sound Vib. 2006, 301, 927–949. [Google Scholar] [CrossRef]
- Velex, P.; Sainsot, P. An analytical study of tooth friction excitations in errorless spur and helical gears. Mech. Mach. Theory 2002, 37, 641–658. [Google Scholar] [CrossRef]
- Zhao, N.; Guo, Z.Q.; Fu, C.X.; Lin, Y.H. The Effect of Meshing Stiffness and Meshing Damping on Dynamics Characteristic of Herringbone Gears. Sci. Technol. Eng. 2013, 13, 1757–1763. [Google Scholar]





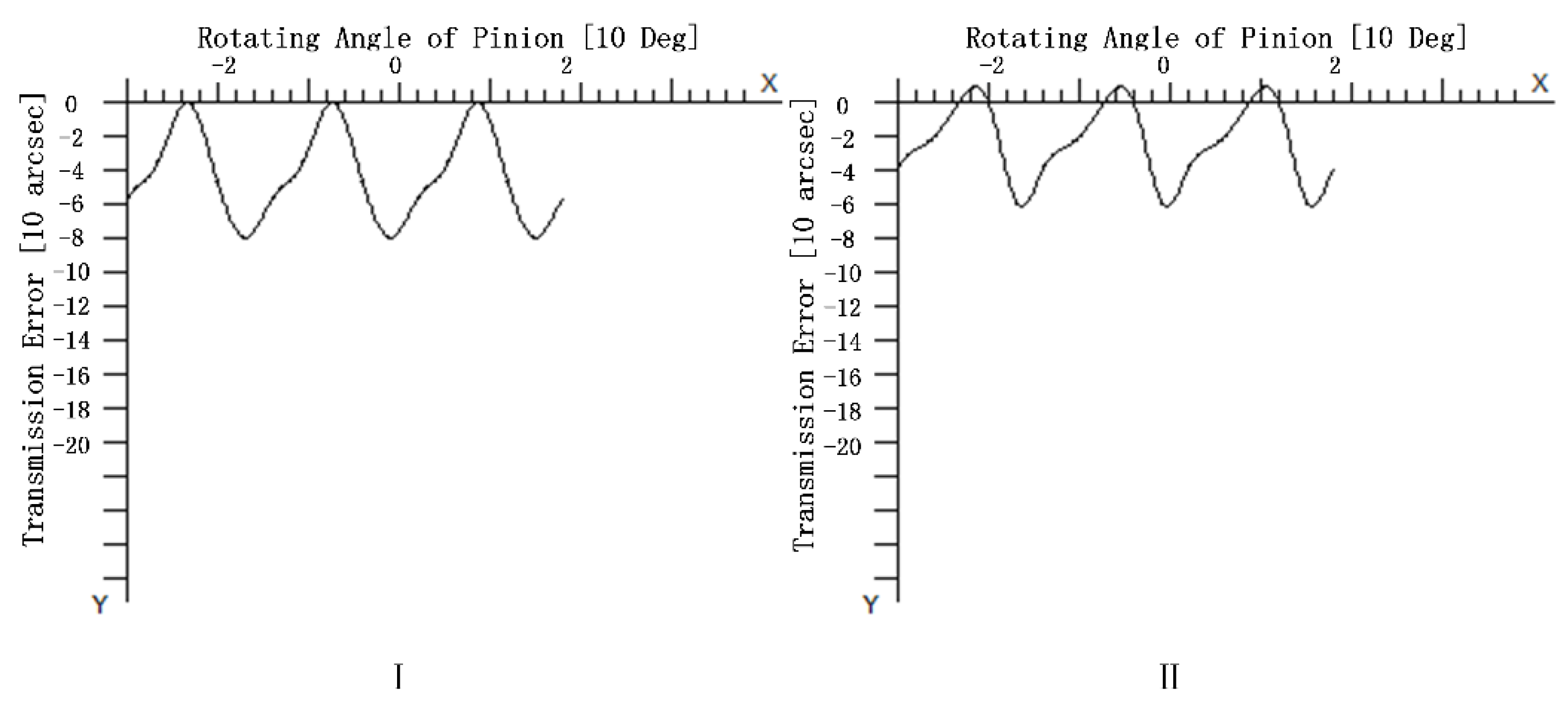
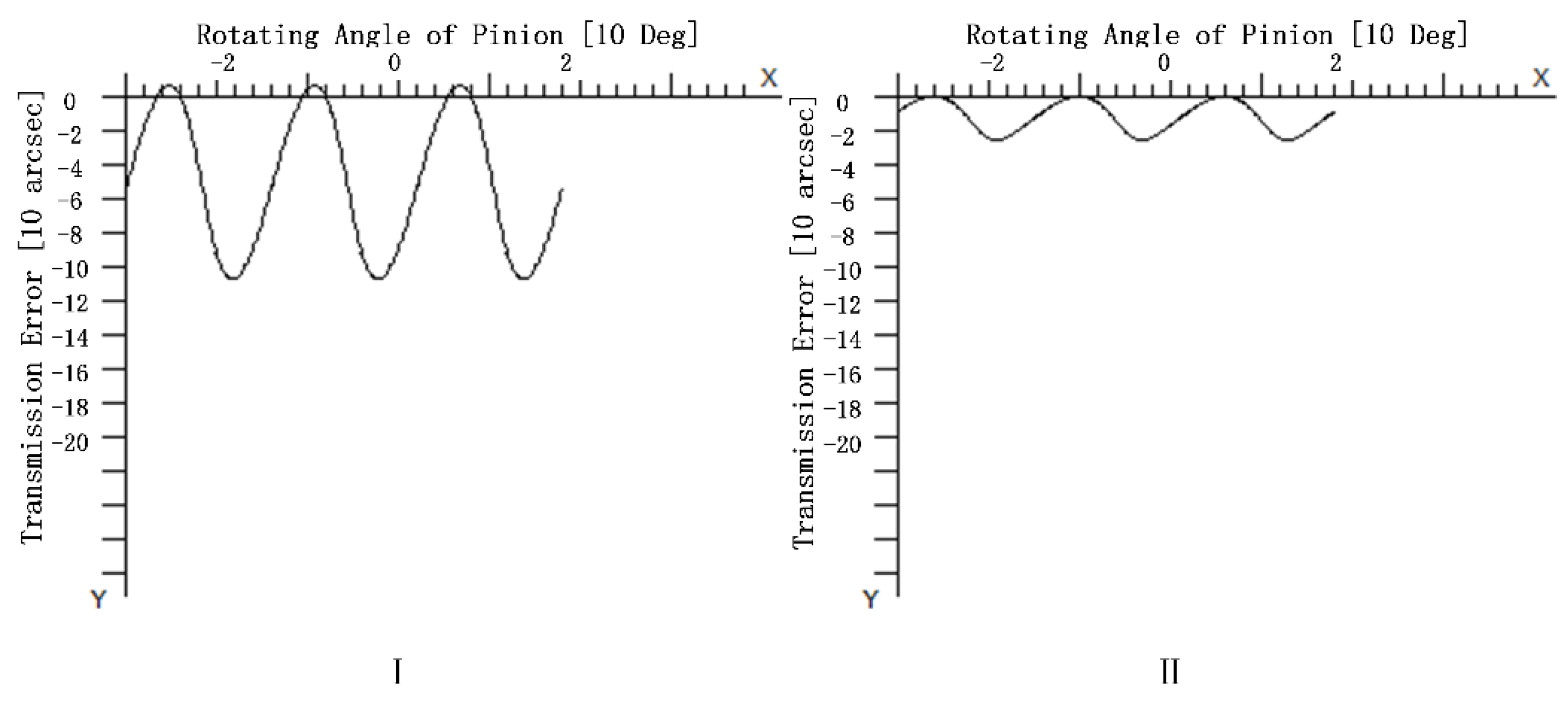
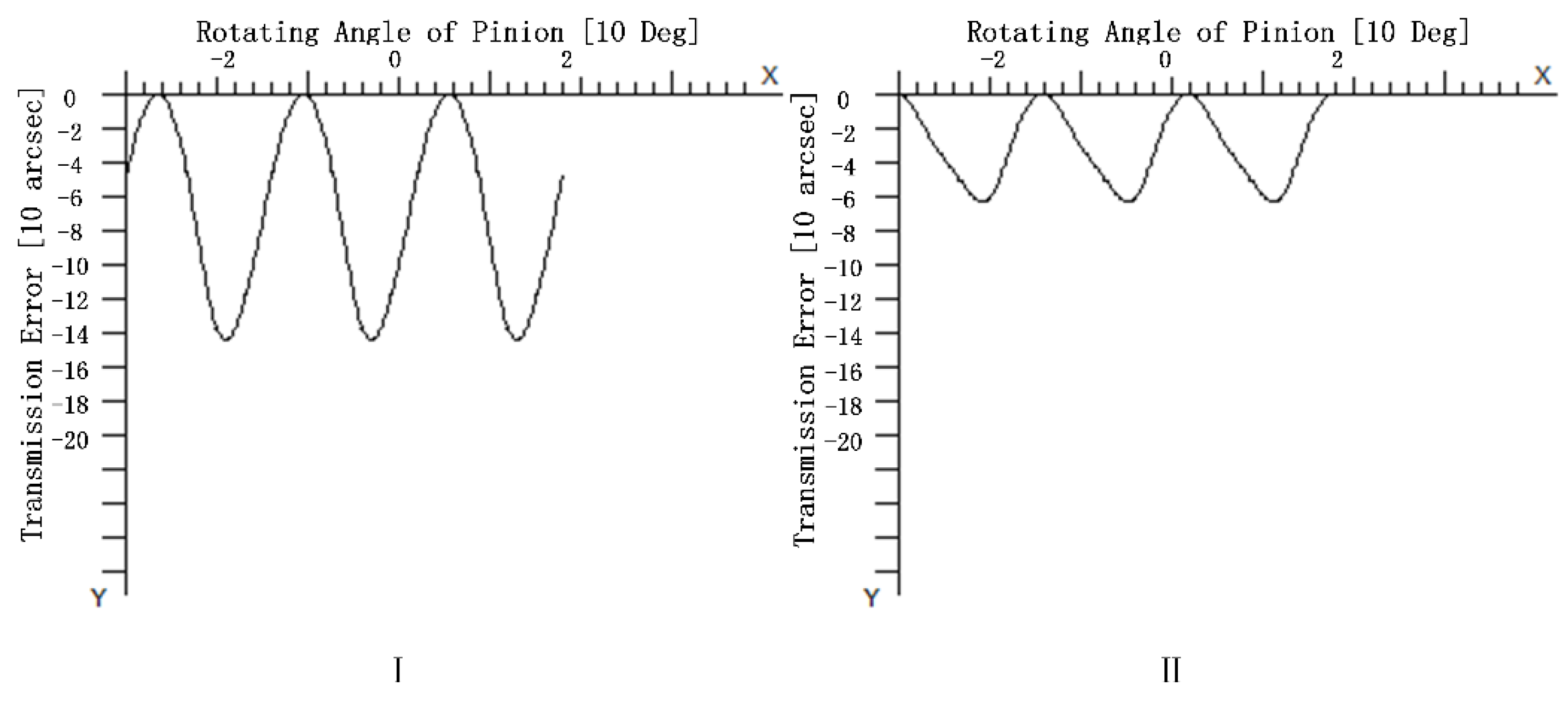

| Symbol | Description |
|---|---|
| a | Parabolic coefficient of profile modification |
| b | Parabolic coefficient of axial modification |
| cix, ciy, ciz | Equivalent support damping of driving and driven gears in Xx, y, and z directions (i = 1,2) |
| cm | Meshing damping |
| cijx, cijy | Damping of the driving and driven gears corresponding to the torsional swing degrees of freedom (j = 1,2) |
| Constants | |
| d0 | One-half of the normal tooth width |
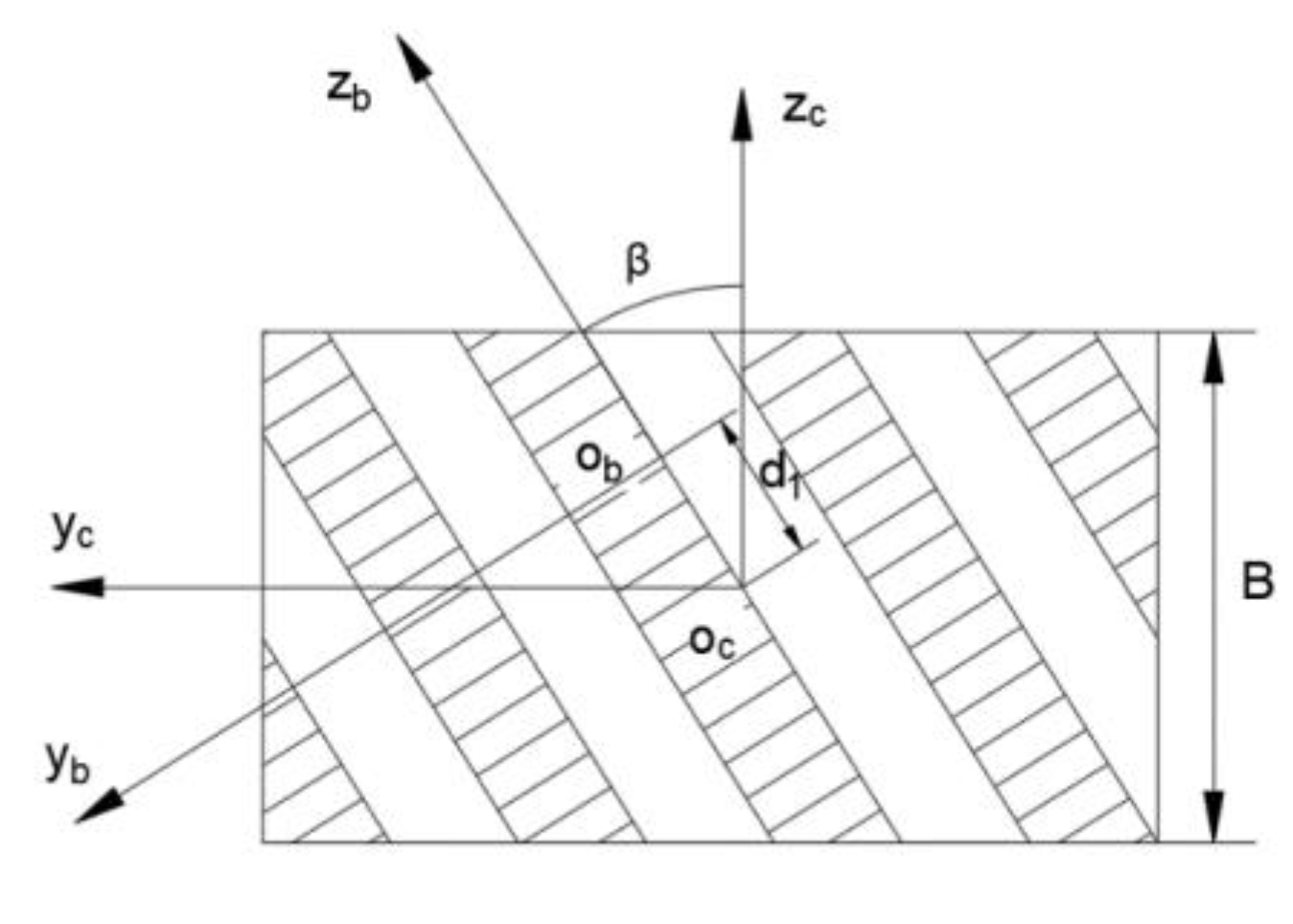
| d1 | Distance between the coordinate system Sb and the coordinate system Sc along the direction of axis |
| F | Dynamic meshing force in the direction of the meshing line |
| i12 | Transmission ratio of the gear pair |
| Ii | Rotational inertia of the driving and driven gears (i = 1,2) |
| kix, kiy, kiz | Equivalent support stiffness of driving and driven gears in x, y, and z directions (i = 1,2) |
| km | Time-varying meshing stiffness |
| kijx, kijy | Stiffness of the driving and driven gears corresponding to the torsional swing degrees of freedom (j = 1,2) |
| Kt | Meshing stiffness |
| me | Equivalent torsional mass of the gear pair |
| Mde, Mec, Mcb, Mba | Coordinate transformation matrices |
| M | Number of meshing points in one meshing period |
| N | Number of the root mean square of the vibration acceleration in the working load range |
| O1, O2 | Geometric centers of driving and driven gears |
| P | Force or moment |
| q | Relative angular displacement |
| Ri | Radius of the base circle of the driving and driven gears (i = 1,2) |
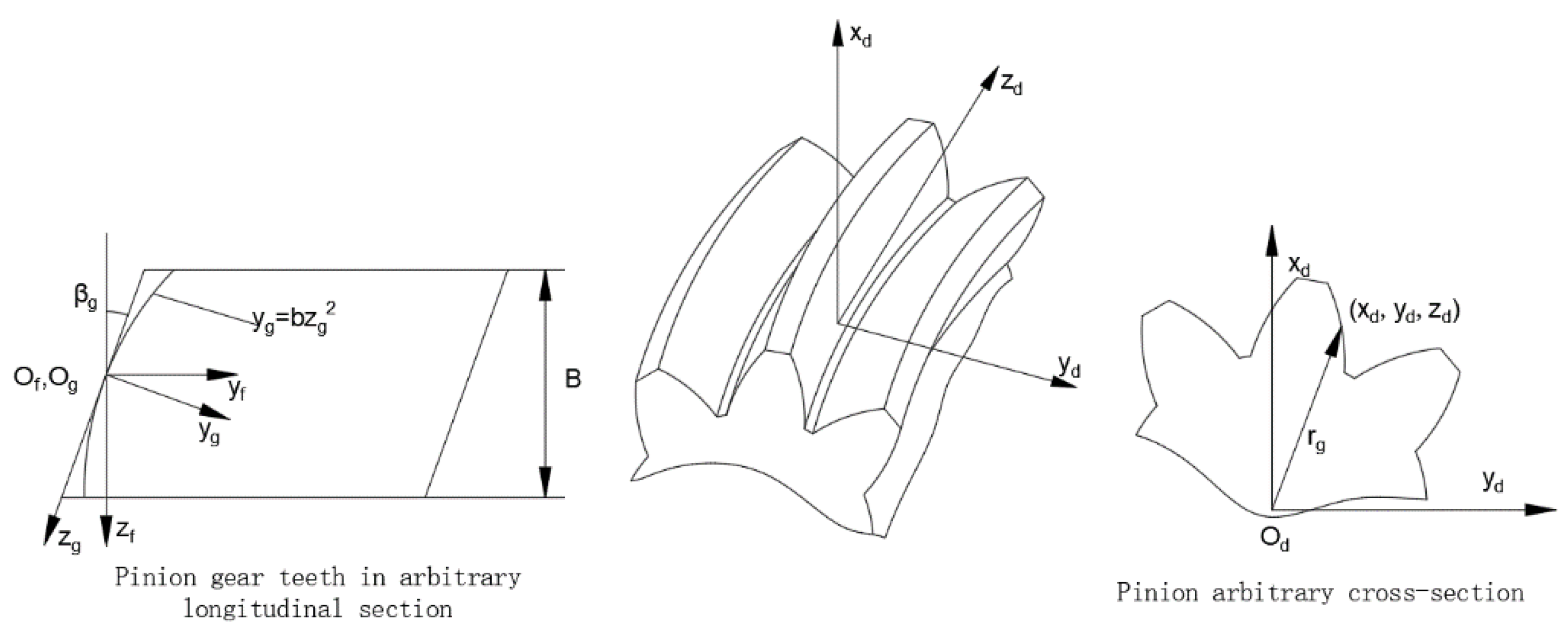
| Sa | Coordinate system established on the normal tooth profile of the tool, moving together with the tool |
| Sb | Coordinate system established on the normal tooth surface of the tool, moving together with the tool |
| Sc | Coordinate system established at the midpoint of the tooth width and pitch line of the transverse tooth surface of the rack tool |
| Sd | Follower coordinate system established on the pinion |
| Se | Fixed coordinate system built on the pinion |
| Sf | Auxiliary coordinate system established on the pinion tooth profile |
| Sg | Coordinate system established on the pinion tooth profile along any helix angle direction |
| T1, T2 | Driving and driven gear torque |
| u | Distance from the point on the tool’s normal tooth profile to the parabolic vertex |
| xi, yi | Bending vibration displacement of driving and driven gears (i = 1,2) |
| X | Root mean square of the vibration acceleration at a certain working load under full working conditions |
| Y | Vibration displacement in the direction of the meshing line |
| zi | Axial vibration displacement of the driving and driven gears (i = 1,2) |
| Z | Line displacement or angular displacement deformation |
| β | Helical gear helix angle |
| Geometric transmission error | |
| Tooth bending deformation | |
| Contact deformation | |
| Δ, Δ | Actual angle of the pinion and gear measured by the circular grating |
| θx, θy | Swings around the x- and y-axes |
| θz | Torsional deformation around the z-axis |
| ξ | Damping ratio |
| Angle between the meshing plane and the positive direction of the y-axis | |
| Rotation angle of the pinion during gear machining |
| Parameters | Pinion | Gear |
|---|---|---|
| Number of teeth | 22 | 59 |
| Spiral direction | RH | LH |
| Normal module (mm) | 2 | |
| Normal pressure angle (°) | 18.5 | |
| Helix angle (°) | 32 | |
| Face width (mm) | 33 | 31.5 |
| Profile shift coefficient (mm) | 0.4578 | −0.31 |
| Elastic modulus (GPa) | 210 | |
| Modification Scheme | Tooth Profile Modification Coefficient: a | Axial Modification Coefficient: b |
|---|---|---|
| Scheme 1 (Optimum modification at a load of 100 N·m) | 1.048 × 10−2 | 1.840 × 10−3 |
| Scheme 2 (Optimum modification at a load of 300 N·m) | 8.600 × 10−3 | 3.950 × 10−3 |
| Scheme 3 (Optimum modification at a load of 400 N·m) | 8.540 × 10−3 | 4.890 × 10−3 |
| Scheme 4 (Optimum modification under full working conditions) | 7.450 × 10−3 | 2.540 × 10−3 |
| Working Load | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 | Unmodified |
|---|---|---|---|---|---|
| 100 N·m | 10.1806 | 40.0622 | 40.3820 | 12.6791 | 12.8866 |
| 150 N·m | 8.2216 | 18.0759 | 34.7084 | 6.6689 | 15.2156 |
| 200 N·m | 10.9045 | 7.8333 | 14.0231 | 5.9006 | 13.6982 |
| 250 N·m | 10.9960 | 5.6143 | 7.9189 | 1.3355 | 10.7765 |
| 300 N·m | 9.4872 | 2.2351 | 7.1550 | 3.6751 | 10.1485 |
| 350 N·m | 11.3276 | 3.6645 | 4.7836 | 6.5724 | 10.7539 |
| 400 N·m | 11.5764 | 6.9905 | 5.6930 | 10.7864 | 12.6968 |
| Average | 10.3849 | 12.0680 | 16.3806 | 6.8026 | 12.3109 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Hu, L.; Mao, J.; Zhang, Y. Optimal Vibration Suppression Modification Method for High-Speed Helical Gear Transmission of Battery Electric Vehicles under Full Working Conditions. Machines 2021, 9, 226. https://doi.org/10.3390/machines9100226
Du J, Hu L, Mao J, Zhang Y. Optimal Vibration Suppression Modification Method for High-Speed Helical Gear Transmission of Battery Electric Vehicles under Full Working Conditions. Machines. 2021; 9(10):226. https://doi.org/10.3390/machines9100226
Chicago/Turabian StyleDu, Jinfu, Liang Hu, Jin Mao, and Yanchao Zhang. 2021. "Optimal Vibration Suppression Modification Method for High-Speed Helical Gear Transmission of Battery Electric Vehicles under Full Working Conditions" Machines 9, no. 10: 226. https://doi.org/10.3390/machines9100226
APA StyleDu, J., Hu, L., Mao, J., & Zhang, Y. (2021). Optimal Vibration Suppression Modification Method for High-Speed Helical Gear Transmission of Battery Electric Vehicles under Full Working Conditions. Machines, 9(10), 226. https://doi.org/10.3390/machines9100226






