Next Article in Journal
Finite-Time Output Feedback Control for Electro-Hydraulic Servo Systems with Parameter Adaptation
Previous Article in Journal
Accurate Parameter Estimation for Master–Slave Operation of a Surgical Robot
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Machines
Volume 9
Issue 10
10.3390/machines9100212
machines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Classification of Design Methodologies to Minimize Vibrations in Gears and Bearings in the 21st Century: A Review

by
Rafael Tuirán Villalba
1,*,
Heriberto Maury Ramírez
2 and
Héctor Águila Estrada
3
1
Faculty of Mechanical Engineering, Universidad Pontificia Bolivariana Seccional Montería, Cra 6 #97A-99, Montería 230002, Colombia
2
Department of Mechanical Engineering, Universidad del Norte, Km. 5 vía Puerto Colombia, Barranquilla 081007, Colombia
3
Department of Mechanical Engineering, Universidad de Magallanes, Avenida Bulnes 01855, Punta Arenas 6200000, Chile
*
Author to whom correspondence should be addressed.
Machines 2021, 9(10), 212; https://doi.org/10.3390/machines9100212
Submission received: 12 August 2021 / Revised: 11 September 2021 / Accepted: 18 September 2021 / Published: 25 September 2021
(This article belongs to the Section Machine Design and Theory)
Browse Figures
Versions Notes

Abstract

:
Associated vibrations in mechanical power transmission elements such as gears and bearings significantly contribute to the dynamic behavior of the system to which they belong. Most research in this field describes measurements and signal processing methods to determine the effect of some design modifications. However, the number of investigations that try to solve the problem from the design stage is much smaller. The following study presents a review of the trends in the analysis of vibrations of power transmission elements and their relationship to the use of systematic design methodologies in the principal power transmission elements. A revision is shown in design considerations to prevent mechanical vibrations or reduce them to acceptable levels. The effects in terms of improvement in reducing vibrations of the most important works that have taken into account the vibrations in design stages are shown. The results show the importance of considering the mechanical vibrations in the design of power transmission elements. Moreover, the analysis of the state of the art shows the areas to be investigated that contemplate the development or application of formal design methodologies that take into account mechanical vibrations.

1. Introduction

Vibrations in power transmission elements are of extreme importance since their appearance outside specific ranges could cause failures in the operations of the element or the system to which it belongs. They can even cause mechanical failure. In this way, vibration measurements in specific points of a power transmission system allow the monitoring and diagnosis of faults [1].
The principal elements in a power transmission system are gears, shafts, bearings, and gearbox housing. Gears and bearings are the central elements related to gearbox damages; the National Renewable Energy Laboratory recorded 257 gearboxes damaged, of which 70% of failures were by bearings, 26% by gears, and 4% by other elements [2]. These elements are mostly associated with mechanical vibrations, and therefore they are the most investigated. The inadequate interaction of these elements can generate vibrations and noise, reflected in an inefficient transmission of power. Historically, vibrations have been studied mainly as a fault detection technique. Vibration analysis has been used to support machinery maintenance decisions [3]. Therefore, many of the investigations focus on maintenance, but a smaller number of works consider vibrations from the design stage.
Significant advances have been made in the study of the dynamic behavior of gear transmissions, and most contributions to the design of gears and bearings come from these studies. One of the first studies in the last two decades about this topic is the work of R.G. Parker et al. [3]. They studied the dynamic response of a spur gear pair under different operating speeds and torques through a finite element/contact mechanics formulation. They probed their formulation with the results of experimentation from previous works with a significant agreement. The free vibration in gears has been studied in the last years, especially in planetary and epicyclic gears. Considerable apports to this field in the last two decades have been the works of R.G Parker et al. [4] and A Kahraman [5]; they predicted the free vibration for unequaled spaced planets [4] in planetary gears and developed dynamic torsional models for different kinematic conditions [5]. M. Inalpolat et al. [6] developed a simplified analytical model to describe the amplitude modulation of planetary gear sets, equally or unequally spaced. They made experimental tests to prove that the model can capture the bulk of the sideband behavior. Another important topic in the dynamic behavior of gear transmission is the transmission error, defined as the departure from uniform angular velocity of the gear pair [7]. Transmission errors have been studied as an input for predicting gear excitations [8] or for minimizing their values [9,10,11,12,13]. Although the dynamic behavior of gear transmission is an important input for a correct design, most of the papers do not focus on developing systematic methodologies with their results.
In recent years, the design methodologies tend to maintain an integrating view that considers the largest number of variables associated with the different stages in the product’s development. Principles and tools as robust design (RD), quality function deployment (QFD), design for manufacturing and assembly (DFMA), computer-aided technologies (CAx), design for service (DFS), design for reliability (DFR), and design for six sigma (DFSS) have been developed since the middle of the last century to develop robust, high-value products at all stages of their life cycle [14]. This paper presents a review of the different studies carried out in the last 20 years in which vibrations were taken into account as a tool for design. Investigations in which design is made to minimize vibrations in gears and bearings are also shown. This research aims to show the benefits of considering the vibrations from the design stage for those interested in developing formal design methodologies that consider the mechanical vibrations in a system.

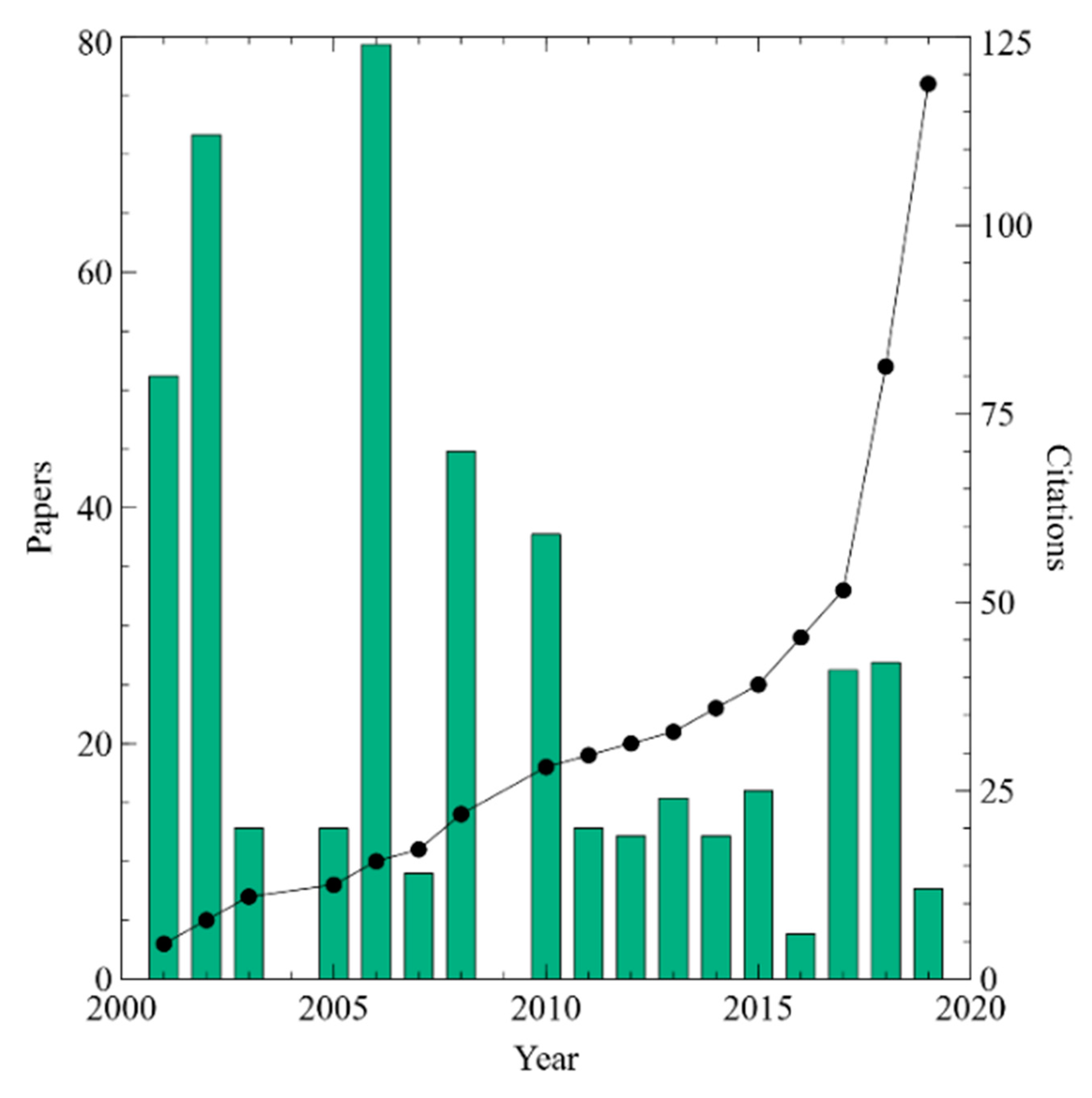
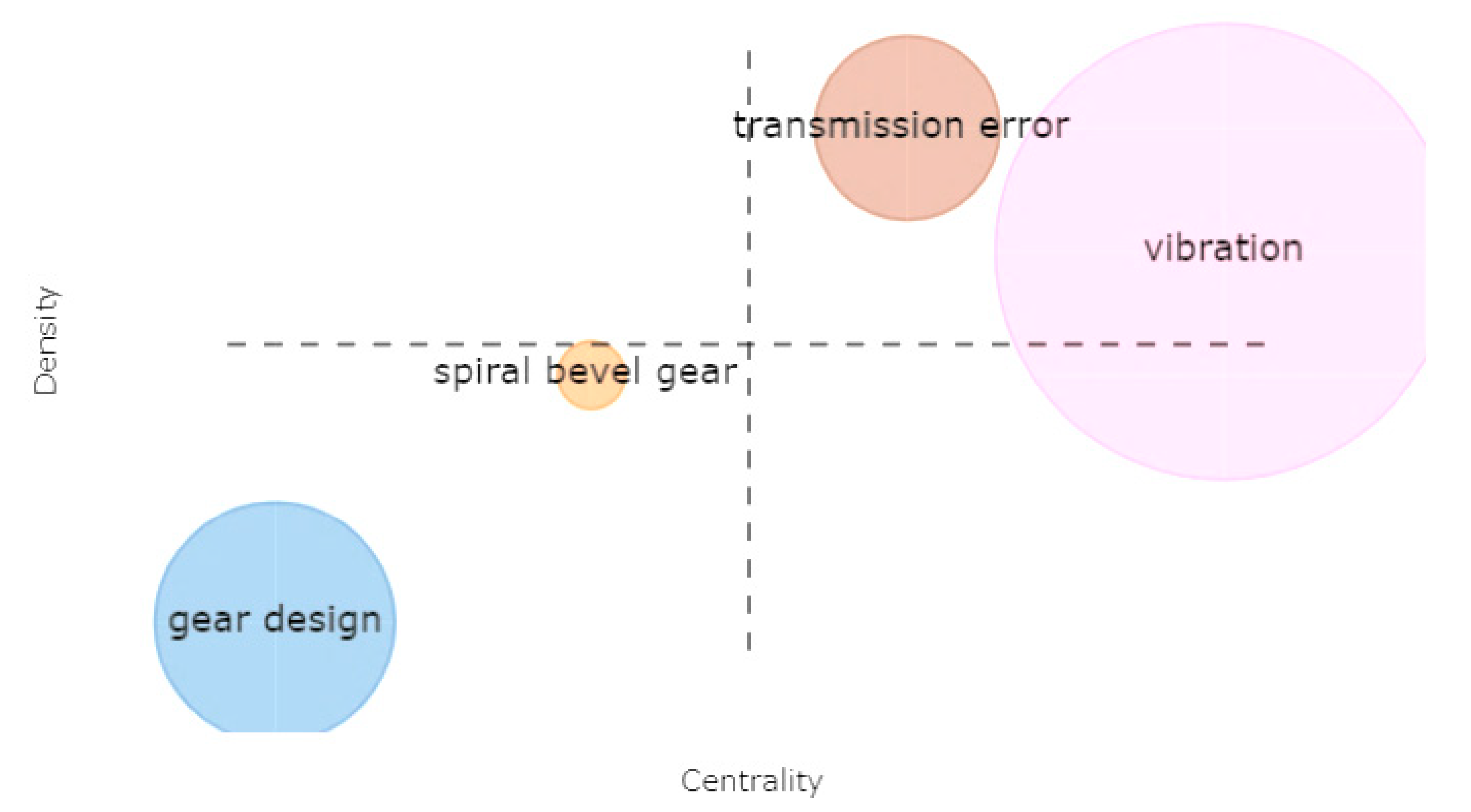
2. Science Mapping Method

We followed the standard five-step method for science mapping [15]. The first step in the research design is to propose the research question. In this review, the principal question is “which are the studies that take into account the vibrations for the design of the principal elements of mechanical transmission as gears and bearings in the last 20 years?”. The second step is the compilation. The databases used were Web of Science and ScienceDirect; the search formula was different for each transmission’s element and explained in the following sections. The analysis, which is the third step, was made through a recent open-source tool called Bibliometrix, which is developed in the statistical computing and graphic R language. In the next sections, visualization and interpretation, which are the fourth and fifth step, were developed.

3. Analysis of Reviews

Since we are interested in knowing the design methods used that take into account vibrations in mechanical transmission elements, the search problem was divided into three main topics: vibrations, mechanical transmission elements, and design methodologies. These are the main topics of the search. This review considers these topics with subdivisions according to the particular interest of each subtopic. The simple topic search, including the above mentioned as search words, yields results that may exclude relevant papers or that may include those that are not closely related to the topic of interest. For this reason, the search must be refined without losing focus that one or more topics classified as significant are implied.
The first step was to determine the elements or systems involved in the mechanical transmissions that had more relevance in the vibrations, and these were bearings, gears, shafts, and gearboxes. The study begins with the search of reviews in which these elements are related to vibrations. A first review search was performed in Web of Science through the search formula: TOPIC (gear or shaft or bearing or transmission or drive train) and TOPIC (vibration). The results were filtered by “review”, and the works related to biology, medicine, civil structures, among others, were excluded. Five main topics were distinguished in the works found: fault diagnosis, dynamic characterization, math tools or signal processing methods, vibration control or noise control, and design. Table 1 shows the 84 reviews found, each article’s main topic, and the corresponding application. A total of 56% of the works are related to the use of vibrations for faults diagnosis in different elements of gear transmission systems. A total of 31% studied the dynamic characterization of bearings, gears, and other more complex systems as gearboxes, carbodies, mechanical structures, among others. A total of 27% of the reviews are about signal processing methods in vibration measurement and mathematical tools for vibration measurement or vibration analysis. The main topics in this area are enhanced fast Fourier transform [16], free and forced vibration analysis of structures with cyclic symmetry [17], wavelet for fault diagnosis [18], finite element analyses [19], and statistical energy analysis in high-intermediate frequency acoustics vibration problems [20]. A total of 13% of works are about vibration control or noise control, and 10% of reviews consider the design as one of their topics.
Most of the design’s reviews focus on gears. F. Li et al. [21] presented essential conclusions for planetary gear design to solve vibration noise by considering mesh phase, tooth profile errors, bearing clearance, bearing contact, tooth profile modification, and gear contact ratio. K. Mohan et al. [22] studied the works related to the gearbox dynamics and the methodologies of analysis for various types of gearboxes. They provided some design guidelines for machine tool structures, gearboxes, and associated rotors, taking into account dynamics characteristics as chatter, vibration, and noise radiation. L. Prášil et al. [19] made a list of published papers on the design, analysis, and simulation of gears and gear drives. The design of bearings was studied too: Q. Gao et al. [23] reviewed the design and optimization of aerostatics bearings; they studied the design from the dynamic performance perspective and considered micro-vibration and suppression of pneumatic hammer vibration. They found two strategies through structural optimization and considering external damping. In a previous review, F. Al-Bender [24] also studied aerostatic bearing films; in his work, he considered the dynamic behavior to complement the determination of static characteristics, which is considered the first step in the bearing design process. S Hong et al. [25] studied the rolling-element bearing modeling due to the high variant loads and high vibration levels that bearings experience in many applications. H. Mahdisoozani et al. [26] focused on vibration reduction and engine modifications for the performance enhancement of internal combustion engines through vibration control, which was classified in Table 1 as design. However, in strict terms, it is redesign. S. Sharma et al. [27] include vibration as an essential variable in the dynamic behavior for the design of aircrafts. Although some works include vibration in the design process, there are no reviews of the state of the art that analyze vibrations and design of elements of power transmission systematically and formally.
An appropriate use of mathematical tools is required for the acquisition and analysis of vibrations, as well as the dynamic characterization of the element to design and the fault diagnosis through vibrations; these are inputs for a fair design process. The applications shown in Table 1 are of interest. Although there are typical applications such as bearings, gears, shafts, and plates, specific ones such as helicopter transmissions and wind turbines are also found. The study of vibrations on wind turbines is justified because the wind power industry experiences a high failure rate and operation and maintenance cost. The transmission failures contribute considerably to that rate [28].
The following section analyzes the papers found in which gears and bearings are designed, taking into account some aspects related to the associated vibrations of these elements.
Table
Table 1. Analysis of reviews in the last 20 years of principal elements of power transmission related to vibrations.
Table 1. Analysis of reviews in the last 20 years of principal elements of power transmission related to vibrations.
Principal TopicApplicationsWorks
Fault DiagnosisBearings, motor bearings, wind turbine planetary gearboxes, solar photovoltaic, rolling element bearings, gears, rotors, rotating machinery, active magnetic bearings, high-speed railway bridges, internal combustion engines, rotating shafts, squirrel-cage induction motors, low-speed bearings, heavy-load slewing bearings, fixed axis gearboxes, power equipment, gerotor pumps, micro-vibration detection, rolling/sliding bearings, hybrid electric vehicles, engines, turbines and motors, gear transmission systems, wind turbine bearings, wind turbines, offshore wind turbines, machinery, planetary gearboxes, induction machines and drive trains in offshore applications, rotating electrical machinery and helicopter transmissions.[1,18,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]
Dynamic characterizationMechanical structures, landing gear shock absorbers, gearbox, carbody vibrations, rolling element bearings, rolling bearing rotor systems, rotating machinery, gearboxes, rotating laminated shafts, spur gear pairs, transmission lines, beams, shafts, plates, aircrafts, gears, journal bearings, drive train systems in wind turbines, journal bearings, flexible rotor-bearing systems, planetary gears, epicyclic gears, mounting elements of rotating machinery, tilting-pad journal bearings, aerostatic bearing films, magnetic bearings, and out-of-round wheels.[21,22,24,25,27,42,59,65,67,70,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88]
Math tools or signal processing methodsBearings, vehicles, ships, aviation, and other transportation engineering fields, complex elastic multibodies, low-speed slew bearings, magnetic bearing systems, joined structures, wind turbine drive trains, marine power transmission systems, rotating machines, mechanical structures with cyclic symmetry, rotary machines, structures coupled with elastic media, gears, and gear drives.[16,17,18,19,20,30,34,36,38,43,44,45,46,49,50,58,66,67,80,89,90,91,92]
Vibration control or noise controlLong shafts, flexible rotors, hybrid magnetic bearings, sliding bearings, dampers, wind turbines, rotors, ergonomic, magnetic bearings, plate-like structures, air bearing systems and shafts of highspeed tooling spindles, automotive components, machine tool transmission housings, nonlinear vibration isolations, aerospace vehicles, and ultralight structures.[22,51,52,62,76,93,94,95,96,97,98]
DesignAerostatic bearings, internal combustion engines, vehicles, and dynamic vibration neutralizers.[21,22,23,24,25,26,27,99]

4. Design and Vibration

The two principal search formulas were: TITTLE (gear*) AND TITTLE (optimization* OR modification* OR dynamic* OR kinematic* OR mesh* OR transmission error OR analysis* OR design* OR vibration*) AND TOPIC (design*) AND TOPIC (vibration*) for gears and TITTLE (bearing*) AND TOPIC (design*) AND (VIBRATION*) for bearings. After checking the results, we found papers with no significant contribution, and therefore they were excluded. Seventy-seven papers were processed in Bibliometrix, and we found an increasing interest in the topic in the last 20 years, as shown in Figure 1. The growth was approximately linear in the first years, with an inflection point in 2017, increasing considerably in 2018 and 2019. That behavior evidences a recent interest in the theme. Although the production articles have increased in the last two years, the most cited papers were produced at the beginning of the century, as shown in Figure 1.
A thematic map shows the state of the topic found in the papers analyzed in terms of their grade of importance and development. A thematic map is divided into two axes: the x-axis shows the centrality, a measure of the theme’s importance in the entire research field. The y-axis shows the density, a measure of the topic’s development.
Figure 2 shows the thematic map of the search made. The analysis was made with the keywords; the word shown in the bubble is the word with the highest occurrence in that cluster, and bubble size is proportional to the cluster word occurrence. The first quadrant contains the highly developed and most important topic according to the citations. The vibration cluster is the most developed and the cluster with the highest importance, followed by the transmission error cluster. The transmission error (TE) has been identified as one of the principal causes of vibration in geared systems; because of their location, these two topics are the motor themes; great numbers of studies consider reducing the TE in order to reduce the vibrations in geared systems.
In the third quadrant of Figure 2, we observe that gear design is an emerging topic, which is corroborated with the increasing slope in the last two years of Figure 1. Gear design is not a recent theme; however, in the context of the search for this review, considering the vibrations, it could be considered an emerging theme. In the gear design cluster, mesh stiffness is the second word in occurrence order that suggests the importance of considering the mesh stiffness in gear design.
The Spiral bevel gear appears as an emerging theme too. That is because of the complexity in the geometry of that type of gear. The most significant research efforts have been in spur and helical gears, as shown in the following sections.
According to the results found, the information has been divided into four main topics: spur gears, helical gears, spiral bevel gears, and bearings. The main findings of design methodologies that consider vibrations for each of the elements mentioned are shown in the following sections.

4.1. Gears

To find the appropriate research papers related to gears, the optimized search formula in Web of Science was: TITTLE (gear* NOT gearbox*) AND TITTLE (optimization* OR modification* OR dynamic* OR kinematic* OR mesh* OR transmission error OR analysis* OR design* OR vibration*) AND TOPIC (design*) AND TOPIC (vibration*). Although there are considerable studies in which the phenomenon of vibration is researched on gears, the ones that show a clear and explicit methodology for the design of gears, taking into account vibrations to reduce it, is much smaller. The main studies are related to spur gears, helical gears, and spiral bevel gears.

4.1.1. Spur Gears

Spur gears have been one of the most studied gears. Vibrations on gears have been of interest since last century, and many papers consider vibrations as a variable to reduce. However, there are few that show an explicit design methodology for reducing vibrations. Abuid Ba and Ameen YM [100] developed a methodology for the optimum design of a two-stage spur gear system. Although the authors did not measure, directly, vibrations on the system, the proposed procedure reduced dynamic factors. The volume of gears and the center distance of the system were also reduced. The dynamic factors were studied in the input shaft, first-teeth meshing, intermediate shaft, second meshing, and the output shaft. The principal goal was to design a compact gear system with quiet running compared to the classical design. The design variables were the numbers of teeth of pinions, stiffness of shafts and teeth, and gears’ inertia. A refined min–max technique as the optimization technique was used, and a direct min–max search method was used in a second stage for refinement. The methodology was compared with classical design, and the dynamic factor was reduced by 22% and 53% in the first and second teeth meshing zones, respectively. Two years later, Fonseca D et al. [101] developed a genetic algorithm for reducing the TE of automotive spur gear sets. The model minimizes the magnitudes of gear mesh frequency components’ weight sum through a formal methodology proposed by Tavakoli, M.S [9], consisting of involute profile generation, profile modification curve-fit, mesh compliance analysis, TE, and load-sharing computations. Jiang, J, and Fanx|g, Z [102] also worked on TE; their method works on the design of tooth surface modifications; the authors used particle swarm optimization for the design of loaded TE. Wang, Y [103] proposed a method to identify a gear system’s dynamic model to make a profile modification for reducing gear noise and vibration. A significant contribution is the relationship between the rotational movement and the acoustical noise from the identified model. Yildirim N et al. [104] proposed a helicopter transmission design by changing the standard low-contact ratio spur gears to a high-contact ratio (HCR) spur gear and applying a profile modification type of “double relief”. The redesign achieved two to four times casing vibration reduction at tooth meshing frequency. Karpat, F [105] developed a computer program for the dynamic analysis of spur gears with symmetric and asymmetric teeth in order to minimize dynamic loads. The authors obtained important conclusions for the design of spur gears with asymmetric teeth; design rules were achieved considering gear contact ratio, pressure angle, and addendum.
The tribo-dynamic performance of spur gear has also been analyzed for guiding gear design. Ouyang T et al. [106] developed a gear dynamic model taking into account the lubricant properties. Gear parameters and lubricant properties are the inputs of the computation program created. The next step is the load distribution model and the gear elastohydrodynamic lubrication model by using a multigrid method. The final step is the gear dynamic model obtained by applying a Runge-Kutta method. In a recent work [107], a method for predicting dynamic characteristics and lubricating property in spur gear of ink vibrator was developed. This was achieved by applying a Runge-Kutta and a multigrid method for solving the governing equations, as the previous work reported [106].
Recently, techniques such as topological optimization have been used for gear design. Ramadani, R et al. [108] designed a gear body as a cellular lattice structure to benefit from weight reduction and vibration behavior. Topology optimization was employed to remove stress concentration and stress levels as much as possible. They found that a lattice structure gear body might notably reduce vibrations and even offer the opportunity to be filled with an adequate polymer, which may further reduce the vibrations.
Xu L. et al. worked on reducing a power turret gear train’s vibrations by modifying design parameters [109]. The gear transmission system of a power turret consisted of a three-stage gear train with four spur gears. Since gear vibration and noise can be reduced by a HCR [110], and this can be changed by modifying such parameters as the outer diameter of gear, the pressure angle, or the number of gear teeth [10], the authors chose the smallest module and pressure angle to enlarge the contact ratio. They found that the improvement of the gear modulus and pressure angle yields better dynamic behavior with a lower vibration than before by comparison in the time domain, and the modification of turret generally decreases the vibration amplitude and nonlinear behavior effectively by comparison in frequency domain.
Figure 3 shows different gear design processes in which the vibration minimization methodology is varied. Studies shown in Figure 3 are those with the most precise design methodology according to its approach. The first one describes a flow chart for the process of the design of a two-stage spur gear system. In the second one [111], design parameters such as the module, pressure angle, face width, and helix angle (for helical gears) are modified. The third one [108] shows a design process for minimum vibration through topological optimization. All of the found methodologies begin with input gear specifications, which are processed according to the approach proposed in each work, and finally, the gear parameters are obtained.

4.1.2. Helical Gears

Helical gears have been the second most researched type, and the main studies focus on tooth modifications for reducing vibrations. One of the first papers, dated 2000, was written by Chong TH et al. [112]. The authors faced the problem of minimizing gear sizes and reducing vibrations in them; they proved that there is a conflicting tendency between the vibrational excitation force by the tooth meshing and the gear size or the geometrical volume of a gear pair. Gear pairs with light weight may have noise or vibration problems. Therefore, a single objective function is not suitable for the purpose since minimizing one design variable can adversely affect another. The authors used the goal programming method as a multi-objective optimization technique (Figure 4) since the vibrations in gears are reduced with the decrease in vibrational excitation forces, which were established as an objective function as well as the size of the gear. The design variables used were normal module, number of teeth in pinion, face width, pressure angle, helix angle, and addendum modifications coefficients. The technique was applied to the redesign of a helical gear pair used in an elevator reduction drive. The volume (mm3) was reduced by 38%, and the vibrational excitation force (N/mm) by 60%.
Komori M et al. [113] worked on optimizing the tooth flank form to perform low vibration and high load-carrying capacity; the author proposed a design algorithm under different misaligned conditions. Hedlund J and Lehtovaara [11] faced the problem of evaluating the mesh stiffness between all meshing teeth, which is one of the principal sources of vibration. The proposed model shows the best combination of gear parameters to minimize parametric excitation in a specific application. Fuentes A et al. [114] studied helical gears finished by plunge shaving. They proposed a computerized method for modifying the geometry of helical gear drives. The optimal design is a partial crowning of the pinion tooth surface, yielding the lower contact stresses and TEs when errors of alignment occur. Wu J et al. [12] also worked on tooth profile modification (TPM) in helical gears for vibration reduction. The authors proposed a dynamic simulation method to evaluate the effect of TPM on vibration reduction in the designing stage; simulations were validated by experimental works. Wang C [115] developed a method for reducing vibration in the double-helical gear by tooth modification through tooth contact analysis (TCA) and loaded tooth contact analysis (LCTA); the algorithm obtains the tooth design parameter when the amplitude of TE is minimum (Figure 4).
Machines 09 00212 g004 550
Figure 4. Design processes of helical gears that consider the minimization of vibration as a design goal. (a) The design process of cylindrical gear pairs for the reduction of gear size and meshing vibration [112]. (b) Modified optimization of double helical gears (Reprinted with permission from ref. [115]. 2021 SAGE Publications). (c) Algorithm for generating CMSG (constant mesh stiffness gears) (Reprinted with permission from ref. [13]. 2021 Elsevier).
Figure 4. Design processes of helical gears that consider the minimization of vibration as a design goal. (a) The design process of cylindrical gear pairs for the reduction of gear size and meshing vibration [112]. (b) Modified optimization of double helical gears (Reprinted with permission from ref. [115]. 2021 SAGE Publications). (c) Algorithm for generating CMSG (constant mesh stiffness gears) (Reprinted with permission from ref. [13]. 2021 Elsevier).
Machines 09 00212 g004
Theerarangsarit K and Ratanasumawong C et al. [111] developed a series of steps to design a parallel-axis gear to minimize power loss and its effect on vibration characteristics. The authors establish that load, operating speed, center distance, gear ratio, and gear material are defined. The steps are as follows: (1) decrease the module, (2) increase the pressure angle, (3) increase the face width, and (4) adjust the helix angle. Once these steps are complete, gear tooth strength is calculated by the AGMA method, and if it is not met in the first iteration, the process is repeated until it meets the minimum strength. Authors verified the design methodology experimentally with a reference gear pair and two gear pairs designed; they proved that the sliding losses of both designed gear pairs are significantly lower than the reference gear pair. Lower vibration amplitude is achieved from this design methodology.
Marafona J et al. [13] developed an algorithm methodology for generating constant mesh stiffness gears (CMSGears) considering the gears’ safety factors and mesh efficiency. The methodology (Figure 4) needs a starting point of gear geometry to initiate the iterations and continues until no further minimization is possible. The CMSGears developed were compared with C14, H501, and H951 gears, and it was concluded that CMS Gears promote a more stable and smooth dynamic performance than conventional gears.
Tanaka. E et al. developed a design of a low-noise gearbox [116]. The design process starts from a phase of determination of the vibrational behavior to add ribs near the gearbox vibration mode antinodes. The first stage consists of three steps: gear-vibration analysis, gearbox vibration analysis, and sound-radiation analysis. The authors validated their method experimentally in an apparatus consisting of second-stage helical reduction gears; they measured the displacement of a gear shaft, the acceleration of points on the gearbox’s surface, and the sound-pressure levels around the gearbox, and the values of the measurements coincided with the calculations made.
Other authors who have worked on decreasing vibrations by improving gear meshing quality are Wang F et al. [117]. They proposed a methodology to determine a tooth surface modification with a sixth-order TE that minimizes vibration noise, which considers the vibration model of a herringbone gear coupling. The methodology consists of the next steps: (1) inputting gear pair basic parameters, (2) initial design parameters, (3) solving the curve coefficients of a higher order polynomial function of TE (H-TE), (4) TCA and LTCA, (5) solving the herringbone gear dynamics model, (6) genetic algorithms optimizing solving, (7) and return to the second step if the optimal solution was not found. They concluded that vibration reduction under meshing vibration acceleration optimization is much better than optimizing the loaded TE amplitude. They also found that in the range of design conditions, the herringbone gear with 6H-TE has the best vibration stability.

4.1.3. Spiral Bevel Gears

The complex geometry of gear tooth surfaces in spiral bevel gears makes the design problem more complicated, and most of the papers focus on reducing TE. Litvin F et al. [118] developed a method for design spiral bevel gear to reduce TE, which reduces noise and vibration through the application of local synthesis algorithm, TCA, and stress analysis through the application of finite element method. Su J et al. [119] proposed an approach to design and implement a seventh-order polynomial function of TE to reduce the running vibration and noise of gear drive and improve the tooth’s loaded distribution through a reverse TCA process. Astoul J et al. [120] also worked to reduce the TE, specifically the quasi-static TE; the developed approach is based on an optimization process including loaded meshing simulations. The optimization strategy consists of minimizing the maximal contact pressure and reducing the quasi-static TE. Mu Y and Fang Z [121] developed a method to design a seventh-order TE for HCR spiral bevel gears for reducing gear vibration and noise.
Mu Y et al. [122] developed a method for designing HCR spiral bevel gears. The authors proposed a tooth surface correction method for modifying HCR spiral bevel gears.
Argyris J et al. [123] proposed an integrated approach for the design and stress analysis of spiral bevel gears. Their method allows the determination of machine-tool settings for the generation of low-noise stable bearing contact spiral bevel gear drives. This method analyses the manufacturing process, and through finite element analysis, it allows the formation of bearing contact during the meshing cycle; the method reduces vibration and noise. Fuentes-Aznar et al. [124] proposed an integrated computerized approach of design, generation, and stress analysis of low-noise, high-endurance face milled spiral bevel gear drives machined using a five-cut process.

4.2. Bearings

The relationship between the design of bearings and vibrations is less systematic than the relationship between the design of gears and vibrations. Yang B et al. worked on the optimum vibration design for the low-pressure steam-turbine rotor of a 1007-MW nuclear power plant [125]. In order to linearize the nonlinear characteristics of the bearings, the authors assumed that vibrations in bearings were small. A hybrid genetic algorithm (HGA) was used for the optimization. The HGA consists of two main processes: global search and local search. Bearing length, bearing clearance, and shaft diameter were optimized through the HGA. These variables were chosen because it is considered that bearing length and diameter have a significant influence on the vibration characteristics; they showed that Q-factor and unbalance response can be improved by the optimization of selected variables.
Ohta H et al. [126] designed crowning to reduce the ball passage vibrations of a linear guideway; this is because of the increase in noise and vibration of machines that use linear bearings due to the increase in the speed of these machines. The design conditions were the length of carriage body, oversize of the balls, distance between adjacent balls, contact angle, and crowning length. The crowning procedure design was developed in six steps; the calculated ball passage vibration amplitude for the designed power function crowning is lower than those of the commercial linear bearing. The designed linear bearing was manufactured, and the vibrations were measured. The ball passage vibrations’ measured amplitude for the designed power function crowning was lower than that of the commercial linear bearing.
Kirk R et al. [127] studied the dynamic characteristics of three custom, fixed bore, bearing designs in a turbocharger of a 3,9 L 130 HP diesel engine. They obtained the two-mode frequency for the different bearings, and they compared it with the initial stock floating bush bearing. A significant contribution is the work of Chasalevris A et al. [128]; they designed and manufactured a variable geometry journal bearing (VGJB) and showed a decrease in the vibration amplitude at resonance by up to 70% compared to a conventional journal bearing.
Cao J et al. [129] considered several bearing designs for a large turbocharger for an industrial reciprocating engine. They showed that a fixed pad bearing design resulted in a highly unstable rotor, and tilting pad journal bearings have greatly reduced cross-coupled forces compared to fixed-geometry bearings. Table 2 shows the principal results of the design methods found related to vibration reduction and the element or system that was applied. Another classification, not by the application but by the methodological approach used, is shown in Figure 5. Since the design of geared systems, taking into account vibrations, is a dynamic problem, all approaches will have a dynamic component in their methodology; therefore, the dynamic models approach covers all of them. Transmission error is one of the principal variables considered since its reduction is reflected in a better vibratory behavior of the system, and this approach has been applied mostly in spiral bevel gears. Other researchers are focused on developing or implementing an optimization algorithm to improve the transmission’s vibratory behavior. The rest of the papers modify design parameters as module, pressure angle, and tooth geometry to obtain a better vibratory response.

5. Conclusions

The main design studies carried out in the last 20 years considering vibrations of power transmission elements such as gears and bearings were shown. It was found that there are clear design methodologies for gears and gearboxes that take into account vibrations. The methods found begin with the initial specifications, and they were optimized taking into account the vibrations and other restrictions to finally obtain the design parameters. Although in some of these papers, it was found that the final design values are functional and generate lower vibrations than the initial ones, there are no studies that apply more robust methodologies that can be applied to more general cases. Some of the studies found apply a method of optimization and prove their efficiency in reducing vibrations.
In the case of bearings, the process is less systematic, and there are fewer papers related to the design, taking into account vibrations. They mainly focus on making modifications in the bearings and then validating the reduction in vibrations generated. Gear design, according to the analysis shown, is an emergent topic. Mesh stiffness and TE are some of the principal variables for gears design considering vibrations. Because the vibration cluster is a motor topic, future research could be directed toward developing design methodologies of gears that emphasize the analysis of mesh stiffness and reducing TE. Although helical gears are of particular interest recently, the development of robust design methodologies should not be left aside for spur gears.

Author Contributions

The idea of the article was proposed and directed by H.M.R., the literature search and data analysis was carried out by R.T.V., and the exhaustive review of the work was carried out by H.Á.E. All authors have read and agreed to the published version of the manuscript.

Funding

The research was supported by MINCIENCIAS through the Ph.D. National Scholarship Program No 785.

Data Availability Statement

The information shown here was taken from the Web of Science and Science direct databases, and the search formulas are shown in the document.

Acknowledgments

The authors would like to thank the Universidad Pontificia Bolivariana, Universidad del Norte, and Universidad de Magallanes for their academic support in this research.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Henriquez, P.; Alonso-Hernández, J.B.; Ferrer, M.A.; Travieso-González, C.M. Review of Automatic Fault Diagnosis Systems Using Audio and Vibration Signals. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 642–652. [Google Scholar] [CrossRef]
  2. Sheng, S.; NREL (National Renewable Energy Laboratory). Gearbox Typical Failure Modes, Detection, and Mitigation Methods (Presentation). In Proceedings of the AWEA Operations & Maintenance and Safety Seminar, San Diego, CA, USA, 15–16 January 2014. [Google Scholar]
  3. Parker, R.G.; Vijayakar, S.M.; Imajo, T. Non-Linear Dynamic Response of a Spur Gear Pair: Modelling and Experimental Comparisons. J. Sound Vib. 2000, 237, 435–455. [Google Scholar] [CrossRef] [Green Version]
  4. Lin, J.; Parker, R. Structured Vibration Characteristics of Planetary Gears With Unequally Spaced Planets. J. Sound Vib. 2000, 233, 921–928. [Google Scholar] [CrossRef]
  5. Kahraman, A. Free torsional vibration characteristics of compound planetary gear sets. Mech. Mach. Theory 2001, 36, 953–971. [Google Scholar] [CrossRef]
  6. Inalpolat, M.; Kahraman, A. A theoretical and experimental investigation of modulation sidebands of planetary gear sets. J. Sound Vib. 2009, 323, 677–696. [Google Scholar] [CrossRef] [Green Version]
  7. Richard, G.; Budynas, J.; Keith, N. Mechanical Engineering Design, 10th ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
  8. Velex, P.; Ajmi, M. On the modelling of excitations in geared systems by transmission errors. J. Sound Vib. 2006, 290, 882–909. [Google Scholar] [CrossRef]
  9. Tavakoli, M.S. Optimization of Spur Gear Transmission Error Using Profile Modifications. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 1983. [Google Scholar]
  10. Andersson, A. An Analytical Study of the Effect of the Contact Ratio on the Spur Gear Dynamic Response. J. Mech. Des. 1999, 122, 508–514. [Google Scholar] [CrossRef]
  11. Hedlund, J.; Lehtovaara, A. A parameterized numerical model for the evaluation of gear mesh stiffness variation of a helical gear pair. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 1321–1327. [Google Scholar] [CrossRef]
  12. Wu, Y.-J.; Wang, J.-J.; Han, Q.-K. Static/dynamic contact FEA and experimental study for tooth profile modification of helical gears. J. Mech. Sci. Technol. 2012, 26, 1409–1417. [Google Scholar] [CrossRef]
  13. Marafona, J.D.; Marques, P.; Martins, R.; Seabra, J.H. Towards constant mesh stiffness helical gears: The influence of integer overlap ratios. Mech. Mach. Theory 2019, 136, 141–161. [Google Scholar] [CrossRef]
  14. Ingeniería Concurrente: Una Metodología Integradora; Riba, C., Molina, A., Eds.; Catalunya, Spain, 2006. Available online: https://upcommons.upc.edu/bitstream/handle/2117/7851/Riba-Molina-2006-Ingenier%C3%ADa%20concurrente...secci%C3%B3n%20V-v5.pdf (accessed on 15 September 2021).
  15. Zupic, I.; Čater, T. Bibliometric methods in management and organization. Organ. Res. Methods 2014, 18, 429–472. [Google Scholar] [CrossRef]
  16. Lin, H.-C.; Ye, Y.-C. Reviews of bearing vibration measurement using fast Fourier transform and enhanced fast Fourier transform algorithms. Adv. Mech. Eng. 2019, 11, 1–12. [Google Scholar] [CrossRef]
  17. Olson, B.J.; Shaw, S.W.; Shi, C.; Pierre, C.; Parker, R.G. Circulant Matrices and Their Application to Vibration Analysis. Appl. Mech. Rev. 2014, 66, 040803. [Google Scholar] [CrossRef] [Green Version]
  18. Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
  19. Prášil, L.; Mackerle, J. Finite element analyses and simulations of gears and gear drives. Eng. Comput. 2008, 25, 196–219. [Google Scholar] [CrossRef]
  20. Su, J.; Zheng, L.; Deng, Z.; Jiang, Y. Research Progress on High-Intermediate Frequency Extension Methods of SEA. Shock. Vib. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
  21. Li, F.; Qin, Y.; Ge, L.; Pang, Z.; Liu, S.; Lin, D. Influences of planetary gear parameters on the dynamic characteristics—A review. J. Vibroeng. 2015, 17, 574–586. [Google Scholar]
  22. Mohan, K.M.; Srinivasan, K.; Ramamurti, V. Dynamics of machine tool drive housings. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 1619–1630. [Google Scholar] [CrossRef]
  23. Gao, Q.; Chen, W.; Lu, L.; Huo, D.; Cheng, K. Aerostatic bearings design and analysis with the application to precision engineering: State-of-the-art and future perspectives. Tribol. Int. 2019, 135, 1–17. [Google Scholar] [CrossRef]
  24. Al-Bender, F. On the modelling of the dynamic characteristics of aerostatic bearing films: From stability analysis to active compensation. Precis. Eng. 2009, 33, 117–126. [Google Scholar] [CrossRef]
  25. Hong, S.-W.; Tong, V.-C. Rolling-element bearing modeling: A review. Int. J. Precis. Eng. Manuf. 2016, 17, 1729–1749. [Google Scholar] [CrossRef]
  26. Mahdisoozani, H.; Mohsenizadeh, M.; Bahiraei, M.; Kasaeian, A.; Daneshvar, A.; Goodarzi, M.; Safaei, M.R. Performance Enhancement of Internal Combustion Engines through Vibration Control: State of the Art and Challenges. Appl. Sci. 2019, 9, 406. [Google Scholar] [CrossRef] [Green Version]
  27. Sharma, S.; Coetzee, E.; Lowenberg, M.; Neild, S.; Krauskopf, B. Numerical continuation and bifurcation analysis in aircraft design: An industrial perspective. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140406. [Google Scholar] [CrossRef] [Green Version]
  28. Wang, T.; Han, Q.; Chu, F.; Feng, Z. Vibration based condition monitoring and fault diagnosis of wind turbine planetary gearbox: A review. Mech. Syst. Signal Process. 2019, 126, 662–685. [Google Scholar] [CrossRef]
  29. Tse, C.K.; Tan, S.-C.; Lai, Y.M. Sliding mode voltage controller for basic DC-DC converter in discontinuous conduction mode. IET Electr.Power Appl. 2001, 67, 263–270. [Google Scholar] [CrossRef]
  30. Lei, Y.; Lin, J.; Zuo, M.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
  31. Smith, W.; Randall, R. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
  32. Liu, W.; Tang, B.; Han, J.; Lu, X.; Hu, N.; He, Z. The structure healthy condition monitoring and fault diagnosis methods in wind turbines: A review. Renew. Sustain. Energy Rev. 2015, 44, 466–472. [Google Scholar] [CrossRef]
  33. Antoniadou, I.; Dervilis, N.; Papatheou, E.; Maguire, E.; Worden, K. Aspects of structural health and condition monitoring of offshore wind turbines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140075. [Google Scholar] [CrossRef] [Green Version]
  34. El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60-61, 252–272. [Google Scholar] [CrossRef]
  35. Babu, T.N.; Raj, T.M.; Lakshmanan, T. A Review on Application of Dynamic Parameters of Journal Bearing for Vibration and Condition Monitoring. J. Mech. 2015, 31, 391–416. [Google Scholar] [CrossRef]
  36. Gómez, M.J.; Castejón, C.; García-Prada, J.C. Review of Recent Advances in the Application of the Wavelet Transform to Diagnose Cracked Rotors. Algorithms 2016, 9, 19. [Google Scholar] [CrossRef]
  37. Goyal, D.; Pabla, B.S. The Vibration Monitoring Methods and Signal Processing Techniques for Structural Health Monitoring: A Review. Arch. Comput. Methods Eng. 2016, 23, 585–594. [Google Scholar] [CrossRef]
  38. Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66–67, 679–698. [Google Scholar] [CrossRef]
  39. Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
  40. Samuel, P.D.; Pines, D.J. A review of vibration-based techniques for helicopter transmission diagnostics. J. Sound Vib. 2005, 282, 475–508. [Google Scholar] [CrossRef]
  41. Li, Z.; Jiang, Y.; Hu, C.; Peng, Z. Recent progress on decoupling diagnosis of hybrid failures in gear transmission systems using vibration sensor signal: A review. Measurement 2016, 90, 4–19. [Google Scholar] [CrossRef]
  42. de Azevedo, H.D.M.; Araújo, A.M.; Bouchonneau, N. A review of wind turbine bearing condition monitoring: State of the art and challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
  43. Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
  44. Javorskyj, I.; Kravets, I.; Matsko, I.; Yuzefovych, R. Periodically correlated random processes: Application in early diagnostics of mechanical systems. Mech. Syst. Signal Process. 2017, 83, 406–438. [Google Scholar] [CrossRef]
  45. Liu, C.; Wang, F.; Su, W.; Xue, Z.; Li, H.; Han, Q. Condition monitoring and fault diagnosis methods for low-speed and heavy-load slewing bearings: A literature review. J. Vibroeng. 2017, 19, 3429–3444. [Google Scholar] [CrossRef]
  46. Tong, X.; Palazzolo, A.; Suh, J. A Review of the Rotordynamic Thermally Induced Synchronous Instability (Morton) Effect. Appl. Mech. Rev. 2017, 69, 060801. [Google Scholar] [CrossRef]
  47. Sabato, A.; Niezrecki, C.; Fortino, G. Wireless MEMS-Based Accelerometer Sensor Boards for Structural Vibration Monitoring: A Review. IEEE Sens. J. 2017, 17, 226–235. [Google Scholar] [CrossRef]
  48. Liu, Y.; Bazzi, A.M. A review and comparison of fault detection and diagnosis methods for squirrel-cage induction motors: State of the art. ISA Trans. 2017, 70, 400–409. [Google Scholar] [CrossRef]
  49. Xu, X.; Wang, H.; Zhang, N.; Liu, Z.; Wang, X. Review of the Fault Mechanism and Diagnostic Techniques for the Range Extender Hybrid Electric Vehicle. IEEE Access 2017, 5, 14234–14244. [Google Scholar] [CrossRef]
  50. Goyal, D.; Vanraj; Pabla, B.S.; Dhami, S.S. Condition Monitoring Parameters for Fault Diagnosis of Fixed Axis Gearbox: A Review. Arch. Comput. Methods Eng. 2016, 24, 543–556. [Google Scholar] [CrossRef]
  51. Sekhar, A.S. Multiple cracks effects and identification. Mech. Syst. Signal Process. 2008, 22, 845–878. [Google Scholar] [CrossRef]
  52. Li, S.; Li, J. Condition monitoring and diagnosis of power equipment: Review and prospective. High Volt. 2017, 2, 82–91. [Google Scholar] [CrossRef]
  53. Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
  54. Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
  55. Xu, S.; Xing, F.; Wang, R.; Li, W.; Wang, Y.; Wang, X. Vibration sensor for the health monitoring of the large rotating machinery: Review and outlook. Sens. Rev. 2018, 38, 44–64. [Google Scholar] [CrossRef]
  56. Delvecchio, S.; Bonfiglio, P.; Pompoli, F. Vibro-acoustic condition monitoring of Internal Combustion Engines: A critical review of existing techniques. Mech. Syst. Signal Process. 2018, 99, 661–683. [Google Scholar] [CrossRef]
  57. Srinivas, R.S.; Tiwari, R.; Kannababu, C. Application of active magnetic bearings in flexible rotordynamic systems—A state-of-the-art review. Mech. Syst. Signal Process. 2018, 106, 537–572. [Google Scholar] [CrossRef]
  58. Touret, T.; Changenet, C.; Ville, F.; Lalmi, M.; Becquerelle, S. On the use of temperature for online condition monitoring of geared systems—A review. Mech. Syst. Signal Process. 2018, 101, 197–210. [Google Scholar] [CrossRef]
  59. Ding, Y.; Ren, P.; Zhao, H.; Miao, C. Structural health monitoring of a high-speed railway bridge: Five years review and lessons learned. Smart Struct. Syst. 2018, 21, 695–703. [Google Scholar] [CrossRef]
  60. Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The Entropy Algorithm and Its Variants in the Fault Diagnosis of Rotating Machinery: A Review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
  61. Qiao, Z.; Lei, Y.; Li, N. Applications of stochastic resonance to machinery fault detection: A review and tutorial. Mech. Syst. Signal Process. 2019, 122, 502–536. [Google Scholar] [CrossRef]
  62. Patil, M.S.; Mathew, J.; Rajendrakumar, P.K. Bearing Signature Analysis as a Medium for Fault Detection: A Review. J. Tribol. 2007, 130, 014001. [Google Scholar] [CrossRef]
  63. Zai, B.A.; Khan, M.; Khan, K.A.; Mansoor, A.; Shah, A.; Shahzad, M. The role of dynamic response parameters in damage prediction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4620–4636. [Google Scholar] [CrossRef] [Green Version]
  64. Malla, C.; Panigrahi, I. Review of Condition Monitoring of Rolling Element Bearing Using Vibration Analysis and Other Techniques. J. Vib. Eng. Technol. 2019, 7, 407–414. [Google Scholar] [CrossRef]
  65. Lu, S.; Yan, R.; Liu, Y.; Wang, Q. Tacholess Speed Estimation in Order Tracking: A Review With Application to Rotating Machine Fault Diagnosis. IEEE Trans. Instrum. Meas. 2019, 68, 2315–2332. [Google Scholar] [CrossRef]
  66. Kumar, A.; Kumar, R. Role of Signal Processing, Modeling and Decision Making in the Diagnosis of Rolling Element Bearing Defect: A Review. J. Nondestruct. Eval. 2019, 38, 5. [Google Scholar] [CrossRef]
  67. Poompavai, T.; Kowsalya, M. Control and energy management strategies applied for solar photovoltaic and wind energy fed water pumping system: A review. Renew. Sustain. Energy Rev. 2019, 107, 108–122. [Google Scholar] [CrossRef]
  68. Wang, D.; Tsui, K.-L.; Miao, Q. Prognostics and Health Management: A Review of Vibration Based Bearing and Gear Health Indicators. IEEE Access 2017, 6, 665–676. [Google Scholar] [CrossRef]
  69. Vieira, A.; De Moura, E.P.; Gonçalves, L.L. Fluctuation Analyses for Pattern Classification in Nondestructive Materials Inspection. EURASIP J. Adv. Signal Process. 2010, 2010, 262869. [Google Scholar] [CrossRef] [Green Version]
  70. Randall, R.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
  71. Cibulka, J.; Ebbesen, M.K.; Hovland, G.; Robbersmyr, K.G.; Hansen, M.R. A Review on Approaches for Condition Based Maintenance in Applications with Induction Machines located Offshore. Model. Identif. Control. A Nor. Res. Bull. 2012, 33, 69–86. [Google Scholar] [CrossRef] [Green Version]
  72. Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
  73. Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
  74. Liu, J.; Shao, Y. Overview of dynamic modelling and analysis of rolling element bearings with localized and distributed faults. Nonlinear Dyn. 2018, 93, 1765–1798. [Google Scholar] [CrossRef]
  75. Jang, J.Y.; Khonsari, M.M. On the Characteristics of Misaligned Journal Bearings. Lubricants 2015, 3, 27–53. [Google Scholar] [CrossRef]
  76. Singh, S.; Howard, C.Q.; Hansen, C.H. An extensive review of vibration modelling of rolling element bearings with localised and extended defects. J. Sound Vib. 2015, 357, 300–330. [Google Scholar] [CrossRef] [Green Version]
  77. Aboshosha, H.; Elawady, A.; El Ansary, A.; El Damatty, A. Review on dynamic and quasi-static buffeting response of transmission lines under synoptic and non-synoptic winds. Eng. Struct. 2016, 112, 23–46. [Google Scholar] [CrossRef]
  78. Ma, H.; Zeng, J.; Feng, R.; Pang, X.; Wang, Q.; Wen, B. Review on dynamics of cracked gear systems. Eng. Fail. Anal. 2015, 55, 224–245. [Google Scholar] [CrossRef]
  79. Ji, J.; Hansen, C.H.; Zander, A.C. Nonlinear Dynamics of Magnetic Bearing Systems. J. Intell. Mater. Syst. Struct. 2008, 19, 1471–1491. [Google Scholar] [CrossRef] [Green Version]
  80. Bovsunovsky, A.; Surace, C. Non-linearities in the vibrations of elastic structures with a closing crack: A state of the art review. Mech. Syst. Signal Process. 2015, 62-63, 129–148. [Google Scholar] [CrossRef]
  81. Cooley, C.G.; Parker, R. A Review of Planetary and Epicyclic Gear Dynamics and Vibrations Research. Appl. Mech. Rev. 2014, 66, 040804. [Google Scholar] [CrossRef]
  82. Wang, Q.; Zeng, J.; Wei, L.; Zhu, B. Carbody vibrations of high-speed train caused by dynamic unbalance of underframe suspended equipment. Adv. Mech. Eng. 2018, 10, 1–13. [Google Scholar] [CrossRef] [Green Version]
  83. del Campo, V.; Ragni, D.; Micallef, D.; Diez, F.J.; Ferreira, C.J.S. Estimation of loads on a horizontal axis wind turbine operating in yawed flow conditions. Wind. Energy 2015, 18, 1875–1891. [Google Scholar] [CrossRef]
  84. Sharma, A.; Upadhyay, N.; Kankar, P.K.; Amarnath, M. Nonlinear dynamic investigations on rolling element bearings: A review. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
  85. Papadopoulos, C.A. The strain energy release approach for modeling cracks in rotors: A state of the art review. Mech. Syst. Signal Process. 2008, 22, 763–789. [Google Scholar] [CrossRef]
  86. Barke, D.W.; Chiu, W.K. A Review of the Effects of Out-Of-Round Wheels on Track and Vehicle Components. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2005, 219, 151–175. [Google Scholar] [CrossRef]
  87. Hori, Y.; Kato, K. Studies on tribology. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2008, 84, 287–320. [Google Scholar] [CrossRef] [PubMed]
  88. Ibrahim, R. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
  89. Clouteau, D.; Cottereau, R.; Lombaert, G. Dynamics of structures coupled with elastic media—A review of numerical models and methods. J. Sound Vib. 2013, 332, 2415–2436. [Google Scholar] [CrossRef] [Green Version]
  90. Maheswari, R.U. Trends in non-stationary signal processing techniques applied to vibration analysis of wind turbine drive train—A contemporary survey. Mech. Syst. Signal Process. 2017, 85, 296–311. [Google Scholar] [CrossRef]
  91. Braun, S. The synchronous (time domain) average revisited. Mech. Syst. Signal Process. 2011, 25, 1087–1102. [Google Scholar] [CrossRef]
  92. Lei, Y.; Lin, J.; He, Z.; Zuo, M. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
  93. Ben-Brahim, L.; Gastli, A.; Yoshino, T.; Yokoyama, T.; Kawamura, A. Review of Medium Voltage High Power Electric Drives. IEEJ J. Ind. Appl. 2019, 8, 1–11. [Google Scholar] [CrossRef]
  94. Gardonio, P. Review of Active Techniques for Aerospace Vibro-Acoustic Control. J. Aircaft. 2002, 39, 206–214. [Google Scholar] [CrossRef]
  95. Hanselka, H. Adaptronics as a Key Technology for Intelligent Lightweight Structures. Adv. Eng. Mater. 2001, 3, 205–215. [Google Scholar] [CrossRef]
  96. Santos, I.F. Controllable Sliding Bearings and Controllable Lubrication Principles—An Overview. Lubricants 2018, 6, 16. [Google Scholar] [CrossRef] [Green Version]
  97. Aridogan, U.; Basdogan, I. A review of active vibration and noise suppression of plate-like structures with piezoelectric transducers. J. Intell. Mater. Syst. Struct. 2015, 26, 1455–1476. [Google Scholar] [CrossRef]
  98. Liu, W. A review on wind turbine noise mechanism and de-noising techniques. Renew. Energy 2017, 108, 311–320. [Google Scholar] [CrossRef]
  99. Abouel-seoud, S. Review Papers Tire and Engine Sources Contribution to Vehicle Interior Noise and Vibration Exposure Levels. Arch. Acoust. 2019, 44, 201–214. [Google Scholar] [CrossRef]
  100. Abuid, B.A.; Ameen, Y.M. Procedure for Optimum Design of a Two-Stage Spur Gear System. JSME Int. J. Ser. C 2003, 46, 1582–1590. [Google Scholar] [CrossRef] [Green Version]
  101. Fonseca, D.J.; Shishoo, S.; Lim, T.C.; Chen, D.S. A genetic algorithm approach to minimize transmission error of automotive spur gear sets. Appl. Artif. Intell. 2005, 19, 153–179. [Google Scholar] [CrossRef]
  102. Jiang, J.; Fang, Z. Design and analysis of modified cylindrical gears with a higher-order transmission error. Mech. Mach. Theory 2015, 88, 141–152. [Google Scholar] [CrossRef]
  103. Wang, Y. Optimized tooth profile based on identified gear dynamic model. Mech. Mach. Theory 2007, 42, 1058–1068. [Google Scholar] [CrossRef]
  104. Yildirim, N.; Gasparini, G.; Sartori, S. An improvement on helicopter transmission performance through use of high contact ratio spur gears with suitable profile modification design. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2008, 222, 1193–1210. [Google Scholar] [CrossRef]
  105. Karpat, F.; Ekwaro-Osire, S.; Cavdar, K.; Babalik, F.C. Dynamic analysis of involute spur gears with asymmetric teeth. Int. J. Mech. Sci. 2008, 50, 1598–1610. [Google Scholar] [CrossRef]
  106. Ouyang, T.; Huang, H.; Zhang, N.; Mo, C.; Chen, N. A model to predict tribo-dynamic performance of a spur gear pair. Tribol. Int. 2017, 116, 449–459. [Google Scholar] [CrossRef]
  107. Ouyang, T.; Huang, H.; Zhou, X.; Pan, M.; Chen, N.; Lv, D. A finite line contact tribo-dynamic model of a spur gear pair. Tribol. Int. 2018, 119, 753–765. [Google Scholar] [CrossRef]
  108. Ramadani, R.; Belsak, A.; Kegl, M.; Predan, J.; Pehan, S. Topology Optimization Based Design of Lightweight and Low Vibration Gear Bodies. Int. J. Simul. Model. 2018, 17, 92–104. [Google Scholar] [CrossRef]
  109. Xu, L.; Chen, N. Nonlinear dynamic study and vibration reduction of a power turret gear train with modified design parameters. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 229, 1745–1759. [Google Scholar] [CrossRef]
  110. Liou, C.-H.; Lin, H.H.; Oswald, F.B.; Townsend, D.P. Effect of Contact Ratio on Spur Gear Dynamic Load With No Tooth Profile Modifications. J. Mech. Des. 1996, 118, 439–443. [Google Scholar] [CrossRef]
  111. Theerarangsarit, K.; Ratanasumawong, C. Parallel-Axis Gear Design Methodology for Minimization of Power Loss and Its Effect on Vibration Characteristics. Eng. J. 2017, 21, 427–439. [Google Scholar] [CrossRef] [Green Version]
  112. Chong, T.H.; Bae, I.; Kubo, A. Multiobjective Optimal Design of Cylindrical Gear Pairs for the Reduction of Gear Size and Meshing Vibration. JSME Int. J. Ser. C 2001, 44, 291–298. [Google Scholar] [CrossRef] [Green Version]
  113. Komori, M.; Kubo, A.; Suzuki, Y. Simultaneous Optimization of Tooth Flank Form of Involute Helical Gears in Terms of Both Vibration and Load Carrying Capacity. JSME Int. J. Ser. C 2003, 46, 1572–1581. [Google Scholar] [CrossRef] [Green Version]
  114. Fuentes, A.; Nagamoto, H.; Litvin, F.L.; Gonzalez-Perez, I.; Hayasaka, K. Computerized design of modified helical gears finished by plunge shaving. Comput. Methods Appl. Mech. Eng. 2010, 199, 1677–1690. [Google Scholar] [CrossRef]
  115. Wang, C.; Cui, H.Y.; Zhang, Q.P.; Wang, W.M. Modified optimization and experimental investigation of transmission error, vibration and noise for double helical gears. J. Vib. Control. 2016, 22, 108–120. [Google Scholar] [CrossRef]
  116. Tanaka, E.; Houjoh, H.; Mutoh, D.; Motoshiromizu, H.; Ohno, K.; Tanaka, N. Vibration and Sound-Radiation Analysis for Designing a Low-Noise Gearbox with a Multi-Stage Helical Gear System. JSME Int. J. Ser. C 2003, 46, 1178–1185. [Google Scholar] [CrossRef] [Green Version]
  117. Wang, F.; Xu, X.; Fang, Z.; Chen, L. Design and analysis of herringbone gear with sixth-order transmission error based on meshing vibration optimization. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
  118. Litvin, F.L.; Fuentes, A.; Hayasaka, K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears. Mech. Mach. Theory 2006, 41, 83–118. [Google Scholar] [CrossRef]
  119. Su, J.; Fang, Z.; Cai, X. Design and analysis of spiral bevel gears with seventh-order function of transmission error. Chin. J. Aeronaut. 2013, 26, 1310–1316. [Google Scholar] [CrossRef] [Green Version]
  120. Astoul, J.; Mermoz, E.; Sartor, M.; Linares, J.; Bernard, A. New methodology to reduce the transmission error of the spiral bevel gears. CIRP Ann. 2014, 63, 165–168. [Google Scholar] [CrossRef]
  121. Mu, Y.; Fang, Z. Design and analysis of high contact ratio spiral bevel gears by modified curvature motion method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 3396–3409. [Google Scholar] [CrossRef]
  122. Mu, Y.; Li, W.; Fang, Z.; Zhang, X. A novel tooth surface modification method for spiral bevel gears with higher-order transmission error. Mech. Mach. Theory 2018, 126, 49–60. [Google Scholar] [CrossRef]
  123. Argyris, J.; Fuentes, A.; Litvin, F.L. Computerized integrated approach for design and stress analysis of spiral bevel gears. Comput. Methods Appl. Mech. Eng. 2002, 191, 1057–1095. [Google Scholar] [CrossRef]
  124. Fuentes-Aznar, A.; Orzáez, R.R.; Gonzalez-Perez, I. Computational approach to design face-milled spiral bevel gear drives with favorable conditions of meshing and contact. Meccanica 2018, 53, 2669–2686. [Google Scholar] [CrossRef]
  125. Yang, B.; Choi, S.; Kim, Y. Vibration reduction optimum design of a steam-turbine rotor-bearing system using a hybrid genetic algorithm. Struct. Multidiscip. Optim. 2005, 30, 43–53. [Google Scholar] [CrossRef]
  126. Ohta, H.; Kato, S.; Matsumoto, J.; Nakano, K. A Design of Crowning to Reduce Ball Passage Vibrations of a Linear Guideway Type Recirculating Linear Ball Bearing. J. Tribol. 2005, 127, 257–262. [Google Scholar] [CrossRef]
  127. Kirk, R.G.; Mondschein, B.; AlSaeed, A.A.; Gallimore, D.; Frank, A.; Crouch, J.; Tiller, M.; Vo, T.; Thrush, K.; Lloyd, R. Influence of Turbocharger Bearing Design on Observed Linear and Nonlinear Vibration. In Proceedings of the STLE/ASME 2010 International Joint Tribology Conference, San Francisco, CA, USA, 17–20 October 2010; pp. 175–177. [Google Scholar]
  128. Chasalevris, A.; Dohnal, F. A journal bearing with variable geometry for the suppression of vibrations in rotating shafts: Simulation, design, construction and experiment. Mech. Syst. Signal Process. 2015, 52–53, 506–528. [Google Scholar] [CrossRef]
  129. Cao, J.; Allaire, P.; Dimond, T. Reduction of vibration and power loss in industrial turbochargers with improved tilting pad bearing design. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; pp. 1–9. [Google Scholar]
Machines 09 00212 g001 550
Figure 1. Cumulative production of papers and citations per year.
Figure 1. Cumulative production of papers and citations per year.
Machines 09 00212 g001
Machines 09 00212 g002 550
Figure 2. Thematic map, according to the papers found.
Figure 2. Thematic map, according to the papers found.
Machines 09 00212 g002
Machines 09 00212 g003 550
Figure 3. Design processes of spur gears which consider the minimization of vibration as a design goal. (a) Design procedure of a two-stage spur gear system through a min–max method combined with a direct search technique [100]. (b) The design process of parallel-axis gear by changing gear parameters [111]; (c) the design of gear body based on topology optimization [108]; (d) the general design process of pair gears for minimum vibrations found in the literature.
Figure 3. Design processes of spur gears which consider the minimization of vibration as a design goal. (a) Design procedure of a two-stage spur gear system through a min–max method combined with a direct search technique [100]. (b) The design process of parallel-axis gear by changing gear parameters [111]; (c) the design of gear body based on topology optimization [108]; (d) the general design process of pair gears for minimum vibrations found in the literature.
Machines 09 00212 g003
Machines 09 00212 g005 550
Figure 5. Principal papers found grouped by the approach used to solve the problem of minimizing vibrations from the design stage in geared systems.
Figure 5. Principal papers found grouped by the approach used to solve the problem of minimizing vibrations from the design stage in geared systems.
Machines 09 00212 g005
Table
Table 2. Results of the design methods for reducing vibration in principal mechanical transmission elements.
Table 2. Results of the design methods for reducing vibration in principal mechanical transmission elements.
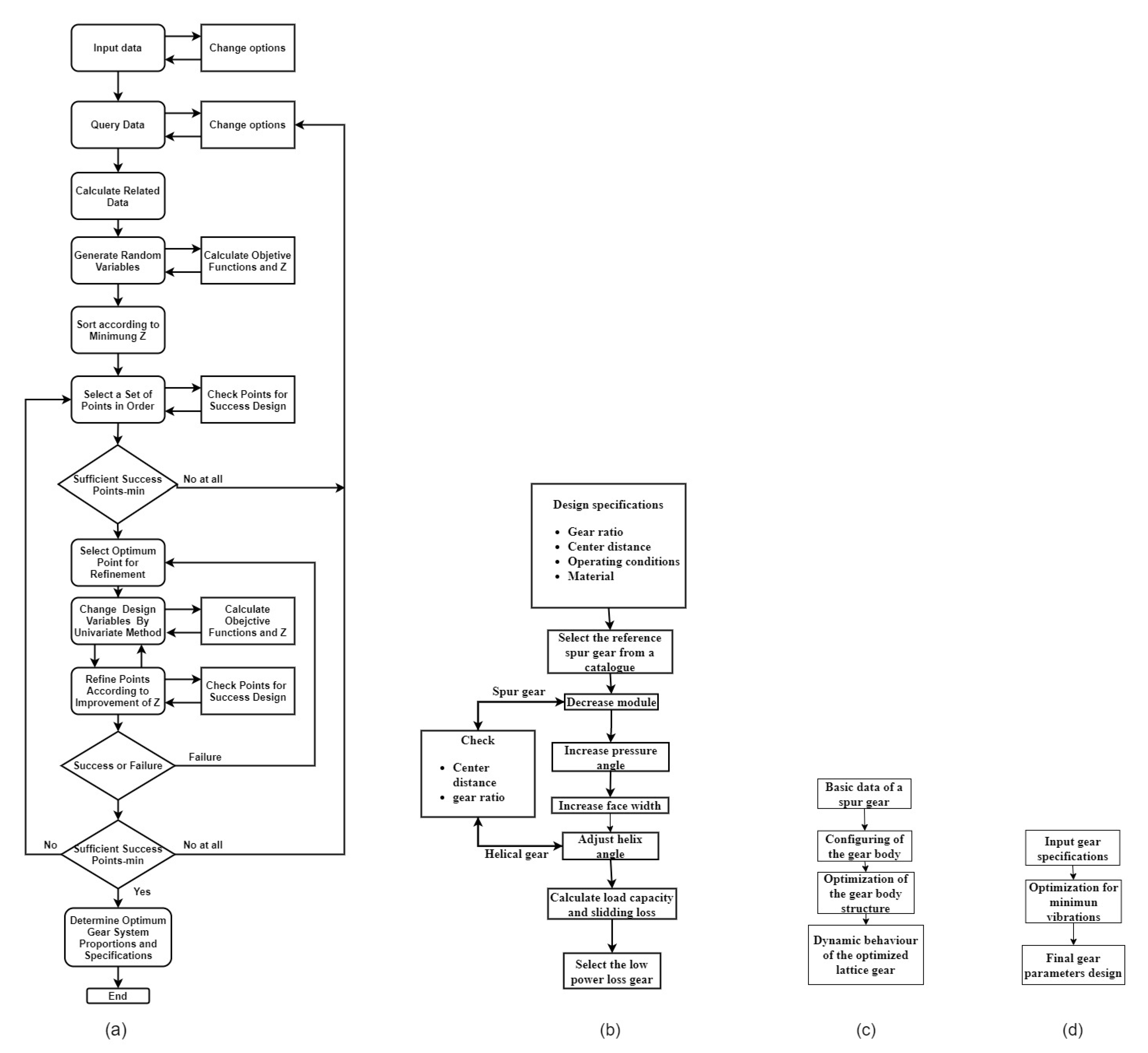
Transmission ElementMethodApplicationResults
Spur gearRefined min–max technique and direct min/max search method [100]Two-stage spur gear systemReduction of dynamic factor by 22% and 53% in the first and second teeth meshing zone, respectively
Genetic algorithm [101]Two mating gears22,1 microns of TE
H-TE [102]Gear pairHigh effective contact ratio with the higher-order TE
HCR and profile modification [104]Two-stage helicopter transmissionVibration decrease of three to four times compared with regular design
Dynamic behavior of spur gears with asymmetric teeth [105]Involute spur gear pairsDesign rules for spur gears with asymmetric teeth
Tribo-dynamic model [106]Spur gear pairConclusions about dynamic mesh force and load ratio
Unified tribo-dynamic model [107]Spur gear of ink vibratorOptimal range of the crown radius and round corner radius for reducing maximum pressure
Topology optimization [108]Titanium alloy’s gearLower frequency ranges in some dominating frequency components in the lattice structure proposed
Optimization of the dynamic response of the turret gear system by improving the modulus and the pressure angle [109]Three-stage gear trainReduction of vibration of 28–60%
Helical gearMulti-objective optimization technique through goal programming method [112]Gear pair used in an elevator reduction driveReduction of the vibrational excitation force (N/mm) by 60%
Optimization of tooth flank form [113]Gear pairReduction of the vibrational excitation force (N/mm) in the range of 16–50%
Model for excitation calculation [11]Gear pairMesh stiffness variation in the frequency domain and reasonable computational time
Computerized method for geometry modification [114]Gear pairReduction on the TE
Tooth profile modification [12]Gear pairVibration reduction for the studied load conditions
Modification of different gear parameters [111]Gear pairMaximum vibration reduction of 85% for the studied load condition
Constant mesh stiffness [13]Gear pairLowest RMS of the Dynamic TE for the evaluated gears
Analysis of dynamic behavior to add ribs in helical gearbox [116]Second-stage helical reduction gearsConcordance with experimental measurements and the proposed method
Optimization design method for six order TE [117]Herringbone gear couplingReduction of RMS acceleration of 40% in resonance velocity of sixth-order TE compared with second-order TE
Spiral bevel gearLocal synthesis algorithm for reducing TE [118]Gear pairReduced level of TE for prototypes of optimized gear drives studied
Seventh-order polynomial function of TE [119]Gear pairAdvantages in load sharing curves and tensile stress
Optimization process to reduce the TE [120]Gear pair30% reduction in the quasi-static TE
Seventh-order TE for HCR spiral bevel gears [121]Gear pairImprovements in the dynamics meshing quality of spiral bevel gears
H-TE for HCR spiral bevel gears [122]Gear pairReduction of TE for different load conditions
Synthesis, TCA, and stress analysis [123]Gear pairReduction of the shift of bearing contact caused by misalignment
Integrated computerized approach of design through a five-cut process [124]Gear pairUniform evolution of contact and bending stresses
BearingHybrid genetic algorithm [125]Two journal bearingsOptimum values of bearing length and bearing clearance
Design of crowning [126]Linear ball bearingReduction of 33% in the amplitude of displacement for the maximum linear velocity tested
Design of VGJB [128]Journal bearingsDecrease in the vibration amplitude at resonance by up to 70% compared to a conventional journal bearing
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Tuirán Villalba, R.; Maury Ramírez, H.; Águila Estrada, H. Classification of Design Methodologies to Minimize Vibrations in Gears and Bearings in the 21st Century: A Review. Machines 2021, 9, 212. https://doi.org/10.3390/machines9100212

AMA Style

Tuirán Villalba R, Maury Ramírez H, Águila Estrada H. Classification of Design Methodologies to Minimize Vibrations in Gears and Bearings in the 21st Century: A Review. Machines. 2021; 9(10):212. https://doi.org/10.3390/machines9100212

Chicago/Turabian Style

Tuirán Villalba, Rafael, Heriberto Maury Ramírez, and Héctor Águila Estrada. 2021. "Classification of Design Methodologies to Minimize Vibrations in Gears and Bearings in the 21st Century: A Review" Machines 9, no. 10: 212. https://doi.org/10.3390/machines9100212

APA Style

Tuirán Villalba, R., Maury Ramírez, H., & Águila Estrada, H. (2021). Classification of Design Methodologies to Minimize Vibrations in Gears and Bearings in the 21st Century: A Review. Machines, 9(10), 212. https://doi.org/10.3390/machines9100212

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop