Abstract
This research proposes a strategy for applying support objects—equipment, tools, and even furniture/environment from which humans can receive reaction force through their hands—for fall prevention in the elderly. This paper presents an assessment example of support objects based on balance recovery characteristics and a discussion regarding their application according to the assessment results. The balance recovery characteristics depend on the direction in which reaction force can be obtained based on the shape of the support object and direction in which the force is easily exerted on the hand. Evaluation indices for assessing the height and shape of nonportable support objects and determining a position of the tip on the ground of a cane, a typical portable support object, in the anterior direction are briefly introduced based on the authors’ previous works. The strategy for the application of support objects utilizing the evaluation indices is proposed; better use of support objects, their locations, new-shaped ones, and support devices with a new design concept are discussed and introduced based on the values of the calculated indices according to the type/usage of the support objects.
1. Introduction
In developed countries, the population is aging. In Japan, the proportion of population aged 65 and over reached 28.1% of the total population in 2018, and it is expected to increase to 38.4% by 2065 [1]. It has been reported that the fall of the elderly during walking can be fatal. Further, the population of caregivers that support the elderly during walking is insufficient for meeting the increasing demand. Thus, in the field of mechanical engineering, there have been some reports of research and the development of devices that support walking [2,3,4]. Many of these devices have been developed based on the concept of enabling the elderly who depend on support to walk (e.g., the elderly who suffer from general paralysis or paraplegia). However, these are functionally excessive and expensive for the elderly who are relatively healthy and can walk with some support. Furthermore, these elderly people account for the majority of the elderly population. Therefore, for support of this elderly, it is necessary to establish a walking support method that is simpler, cheaper, and independent of the support of caregivers.
The use of handrails or canes is a simple and cheap approach for supporting walking. The effects of using handrails or canes are classified into the following two categories [5].
- I.
- Partial weight bearing of legs
- II.
- Obtaining kinematic information of whole body
For I, the effect involves reducing the magnitude of force and joint torque that needs to be exerted on each leg by applying the force of several tens of Newton to the handrail/cane; i.e., the effect comprises decreasing the muscle activation of lower limbs. For II, the effect involves obtaining the somatosensory information of the whole body from various receptors of the arm by touching the handrail/cane with almost no force (several Newtons). The effect of II is called the “light touch effect”. This effect has been researched recently [5,6,7]. In an experiment where subjects who had suffered from a stroke walked while holding the cane with their nonparetic hand, it was found that they walked with a vertical downward force of 2.3 N acting on the cane, and the semitendinosus muscle, tensor fascia latae muscle, and vastus medialis muscle of the paretic leg were more active when compared to when they walked with a force of 49.3 N acting on the cane [5]. To maintain and improve walking ability, it is expected that the elderly walks with a certain amount of muscle activation on their legs, rather than with partial weight bearing of their legs. Therefore, the elderly who can walk with some support should actively walk with a handrail/cane in order to obtain the effect of II, as above.
However, in this use, in which the effect of II is obtained and has been clarified through previous research, such as [5,6,7], a quantitative evaluation index for determining the installation position or usage method of the handrail/cane has not been clarified; the installation position or usage method are examined and determined via sensory evaluation or the personal knowledge/experience of an informed person (doctors, caregivers, and others). Therefore, when considering the super-aged society and lack of caregivers, the authors have attempted to construct evaluation indices objectively for determining the height of a handrail and the position of a cane tip for the usage in which the effect of II is obtained. To this end, the mechanical effects that contribute to fall prevention using these objects were focused on. Furthermore, elderly people use not only handrails and canes, but also tables and walls to prevent falls. Consequently, the authors generalized equipment, tools, and even furniture/environment from which humans can receive reaction force through their hands and defined them as “support objects”. This research aims to establish not only a support method for fall prevention and a training method for walking ability improvement using support objects, but also a design methodology for the support objects, support devices, and living/facility environment that can considerably prevent falls. A concept of this research is the assessment and design of support objects for individuals with their height and weight (mass) as basic input information. Figure 1 shows these application examples.
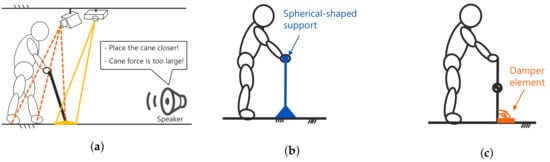
Figure 1.
Application examples of support objects. (a) walking instruction system; (b) new-shaped
support object; and, (c) cane with damper element.
As a first step toward achieving the abovementioned goals, we have already conducted research that is focused on the relationship between the position/shape of the support objects and fall prevention. The authors classified support objects by portability. For nonportable support objects, such as handrails, tables, and walls, we proposed an assessment method for environments that include them based on balance recovery characteristics [8]. These characteristics represent the ability to recover from a falling state depending on the direction in which the reaction force can be obtained based on the shape of the support objects and the direction in which the force is easily exerted on the hand. For portable support objects, it is necessary to determine the position of the contact point of the support objects with the ground in order to obtain reaction force, because they need to be carried by a walking user. Therefore, we considered the cane as a typical portable support object, and proposed an assessment method for determining the position of the cane tip that is effective for preventing falls according to the physical characteristics of the elderly [9]. In [9], by focusing on the decrease in grip strength and increase in reaction time of the elderly, the mechanical interface between the hand and the cane was modeled by a dynamic pair, which is represented by viscoelastic elements and movable elements. Using an analytical model with the dynamic pair, the assessment method was examined through numerical simulation and experiment. Based on the previous works, the authors considered support objects to be applied in order to achieve better balance recovery characteristics.
The related research has been conducted in various fields. IJmker et al., reported that each muscle activity in the lower extremity was reduced in walking with holding a handrail as compared to walking without touching the handrail, but not with light-touching the handrail in experiment [6]. Stramel et al., developed a light-touch cane robot that can follow a human and conducted experiments while using it to walk in a virtual environment with visual perturbations. The result suggested that the stride width was narrower and, thus, the stability of walking in a virtual environment was more improved when compared to walking in real-world walking [7]. However, these are only researches on the physical effect or on the light touch effect, not on the mechanical effects of handrails and canes that contribute to fall prevention, depending on the height of the handrails and the position of the cane tip. Further, Di et al., developed an intelligent cane robot that detects and passively prevents falls [10], but the conceptual approach is different from this research, which aims to achieve a simpler and cheaper approach with support objects for fall prevention. To our knowledge, this paper represents the first investigation of the application of support objects focusing on the mechanical effects of handrails and canes that contribute to fall prevention for individuals. This investigation will provide a simpler and cheaper approach for fall prevention to help assist walking by increasingly elderly people, as mentioned at the beginning.
This paper proposes a strategy for the application of support objects for fall prevention in the elderly based on our previous works [8,9]. An assessment example of the support objects is provided using the evaluation index that is based on the balance recovery characteristics with the height and weight of the user as basic input information. This index was proposed, and the calculation results of the index were obtained in our previous report [8]. In addition, some physical ability conditions of support object users and environmental conditions are set; under each condition, the application of support objects is discussed according to the assessment result. To help readers understand, our basic idea and results presented in our previous reports [8,9] are briefly introduced in Section 2 “Modeling Reaction Force Characteristics of Support Objects” to Section 4 “Assessment Method of Anterior Position of Cane Tip Based on Model with Dynamic Pair” in this paper: reaction force characteristics of the support objects considered in this paper; an assessment method for the height and shape of a nonportable support object based on the balance recovery characteristics; and, an assessment method for the anterior position of the cane tip based on the model with the dynamic pair. Following these contents, the application of support objects is discussed in Section 5 “Proposal of Strategy for Application of Support Objects” as the main and original part of this paper.
2. Modeling Reaction Force Characteristics of Support Objects
2.1. Support Objects in This Paper
The support objects considered in this research and the fixed coordinate system are shown in Figure 2 and Figure 3, and are listed in Table 1. In Figure 2 and Figure 3, the X-axis positive direction is the walking direction, the Z-axis positive direction is the vertically upward direction, and the Y-axis is the direction perpendicular to the -plane.
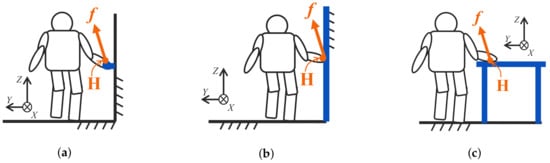
Figure 2.
Nonportable support objects. (a) support object #1: handrail (cylindrical shape); (b) support
object #2: wall (vertical-planar shape); and, (c) support object #3: table (horizontal-planar shape).
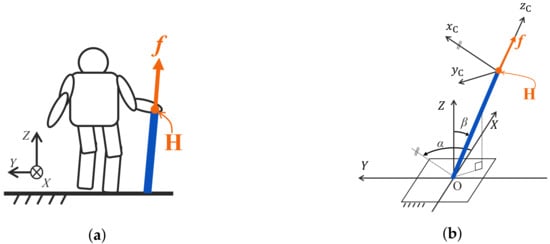
Figure 3.
Portable support object. (a) support object #4: cane (line-segment shape); and, (b) definition
of moving coordinate system O − xCyCzC and angles α and β.

Table 1.
Support objects considered in this research.
In Figure 2, Nos. 1–3 represent support objects that are installed in the environment or those corresponding with the environment itself. These objects were classified as nonportable support objects.
No. 1 is a circular handrail. The axis of the handrail is the X-axis direction in Figure 2a, and the normal force is obtained in the radial direction. Note that the radial size (thickness) of the handrail is ignored. In addition, when considering the state in which the hand is wrapped around the handrail, the static friction force is obtained in the X-axis direction. The support object with such reaction force characteristics was called a cylindrical-shaped support object.
Nos. 2 and 3 denote a wall and a table, respectively. The wall is a plane parallel to the -plane in Figure 2b, and the table is a plane that is parallel to the -plane in Figure 2c. The normal force is obtained in the direction perpendicular to these planes. It is assumed that the point corresponding to the hand and the plane corresponding to the support object are in point contact; thus, static friction force is obtained in the directions on the -plane and -plane, respectively. The support objects with such reaction force characteristics were called vertical-planar- and horizontal-planar-shaped support objects, respectively.
In the support objects Nos. 1–3, the effect of the pure reaction force moment originally obtained from them on the balance recovery should be considered. However, for the sake of simplicity, the effect is assumed to be sufficiently small and only the effect of the translational reaction force is considered.
In Figure 3, No. 4 represents a cane with a single leg that is carried around as walking support. This object was classified as a portable support object. It is assumed that the cane and ground (plane parallel to the -plane) can relatively rotate around the contact point at the tip of the cane. Further, although the effect of the slip between support objects and the ground should be considered essentially, because the inclination angles of the cane were within non-slip range in the experiment of walking with a cane by a middle-aged subject [9], it is assumed that the posture of the cane with respect to the ground is maintained at an angle that does not allow the cane tip to slip; thus, the posture is not specifically considered. Based on these assumptions, the reaction force received through the cane is obtained in the longitudinal direction of the cane. The support object with such reaction force characteristics was called a line-segment-shaped support object.
2.2. Modeling Reaction Force Characteristics
Let be the reaction force obtained from each support object to represent the difference in reaction force obtained from support objects according to the shape of them. Subsequently, acting on the point H corresponding to the position of the hand in Figure 2 and Figure 3 satisfies the following equations.
where in Equations (1)–(3) and in Equation (4) are the coefficients of static friction between the hand and the support object, and the support object and the ground, respectively. For the sake of simplicity, the coefficients are treated as constant values. and in Equation (4) are rotation matrices that represent the rotation of around the Z-axis and around the X-axis, respectively. and are the angles that are shown in Figure 3b, which are the angles formed by the X- and -axes and Z- and -axes, respectively. is a moving coordinate system fixed to the cane. The direction of the -axis coincides with the longitudinal direction of the cane from the ground to the hand.
Equations (1)–(4) are called friction cones [11]. These equations show the directional characteristics of the reaction force that is received from support objects. Note that, for nonportable support objects, the authors assumed that the support objects were fixed to the ground (actually they are fixed or almost fixed), and represented reaction force which can be obtained from support objects at the hand as a friction cone. Additionally, for portable support object, the authors assumed that a cane was connected to the hand rigidly compared to the ground when a human uses a cane and, thus, focused on reaction force acting on the cane from the ground and represented reaction force which can be obtained from the ground at the cane tip as a friction cone. Using these models, our ideas on the balance recovery characteristics that are based on the shape of the support objects are described in Section 3 and later.
3. Assessment Method of Support Object Based on Balance Recovery Characteristics
The evaluation index that assesses the effect of a single support object on fall prevention that is based on the balance recovery characteristics for nonportable support objects is described [8]. The reaction force characteristic solid (RFCS) is shown as a solid representing the balance recovery characteristics. This solid comprises the common part of the friction cone and the manipulating force ellipsoid [12] in the 7-DOF (degree of freedom) serial mechanism, which is the model of a human’s upper limb. Based on this RFCS and the reaction force obtained from the support objects required to recover balance, the evaluation index for the assessment of the support objects, S, was obtained in [8].
3.1. Reaction Force Characteristic Solid (RFCS)
3.1.1. Analysis Model
The upper limb on one side was modeled as a rigid 7-DOF serial link mechanism, as shown in Figure 4a. The other part of the whole body was modeled as an inverted pendulum with a revolute joint at a position corresponding to the foot; its axis is on the horizontal plane. In the coordinate system that is shown in Figure 4a–c, the direction of X-, Y-, and Z-axes have the same definition as provided in Section 2.1.
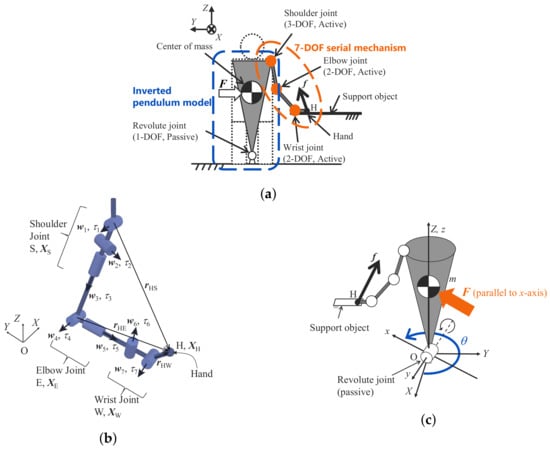
Figure 4.
Serial mechanism with 7-DOF and inverted pendulum as human model adapted from [8].
(a) overview; (b) serial mechanism with 7-DOF; and, (c) inverted pendulum.
For the rigid 7-DOF serial link mechanism, the shoulder joint was modeled as a 3-DOF ball joint, and the elbow and the wrist joints were modeled as 2-DOF universal joints, as shown in Figure 4a,b. Each joint of the mechanism is an active joint. In Figure 4b, S, E, and W represent the points corresponding to the centers of the shoulder, elbow, and wrist joint, respectively. H represents the point corresponding to the hand. , and are the three-dimensional vectors that represent the positions of S, E, W, and H, respectively. and are the torque generated by each revolute joint i and the three-dimensional unit vector representing the direction of the axis of each revolute joint i, respectively.
For the inverted pendulum, the revolute joint is a passive joint, and it is considered to have one degree of freedom in the direction in which the center of mass falls, as shown in Figure 4c. In the model, the coordinate system rotated by around the Z-axis with respect to the fixed coordinate system is set; the y-axis is defined as the axis of rotation of the revolute joint.
In Figure 4a,c, the fall in this model was defined as the state in which the center of mass of the inverted pendulum model is in contact with the ground. In addition, we considered the moment when the inverted pendulum model begins to collapse, and the fall occurs unless the reaction force from the support object is obtained. This moment was defined as “the moment when the balance is about to be lost”. At this moment, we assumed that the posture of the inverted pendulum, as shown in Figure 4a,c, was vertical to the ground. The state at this moment was represented as the state in which an external force acted on the center of mass of the inverted pendulum in the direction parallel to the x-axis shown in Figure 4c because its direction is the moveable (rotatable) direction of the inverted pendulum. Furthermore, “fall prevention”, which is, “balance recovery” implies that the static moments around the axis of the revolute joint with respect to the inverted pendulum are balanced when the balance is about to be lost. In Figure 4c, the balance recovery in any direction are represented by changing .
3.1.2. Manipulating Force Ellipsoid
Because each segment of the upper limb can perform a relative rotational motion at each joint, the direction in which the force is easily exerted on the hand changes, depending on the posture of each segment of the upper limb. Therefore, the manipulating force ellipsoid in the 7-DOF serial link mechanism was adopted in order to represent this direction.
The manipulating force ellipsoid is obtained from the condition that magnitude of torque vector is less than one. This condition means that the value of each torque can change within a certain limitation. Based on the model that is explained in Section 3.1.1, the manipulating force ellipsoid could be obtained as
where is a seven-dimensional vector that represents the torque that is generated by each revolute joint, is a three-dimensional vector that represents the reaction force acting on point H, and is the Jacobian matrix that satisfies the following equations
Equation (5) represents the interior and surface of the ellipsoid composed of . Figure 5 shows an overview of the manipulating force ellipsoid as an example.
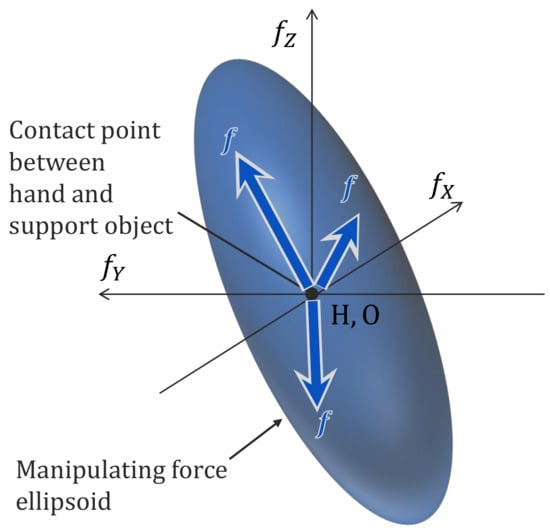
Figure 5.
Overview of manipulating force ellipsoid.
3.1.3. Reaction Force Characteristic Solid (RFCS)
By combining the manipulating force ellipsoid that is introduced in Section 3.1.2 and the friction cone explained in Section 2.2, the direction in which the reaction force from the support object at the hand is easily obtained when considering the shape characteristics of the object can be represented. We defined the solid consisting of the components of that satisfies Equations (5) and (1), (2), or (3), i.e., the common part of the manipulating force ellipsoid and the friction cone, as Reaction Force Characteristic Solid (RFCS). The direction in which the distance between the surface of the RFCS and center point of the manipulating force ellipsoid is large is the direction in which the reaction force considering the shape of support objects is obtained easily. In the next section, based on this RFCS, the evaluation index that is used for the assessment of the support objects considering the balance recovery characteristics is shown.
3.2. Evaluation Index Regarding Balance Recovery Characteristics Based on RFCS
Based on the RFCS, the margin of the magnitude of reaction force that is required for balance recovery, S, was formulated in [8] by the following process.
- Based on the RFCS, the reaction force effective for balance recovery is derived.
- The reaction force whose direction is the same as and whose magnitude is necessary for balance recovery is derived.
- The margin S, which is the ratio of the magnitude of to the magnitude of , is derived.
Figure 6a,b show the inverted pendulum model viewed from the and axes directions, respectively. In the figures, and are three-dimensional vectors that respresent the relative positions of the point H and the center of mass from the point O corresponding to the foot in the coordinate system , respectively. Additionally, is a projection vector of on the -plane, is a vector perpendicular to and the y-axis, and is an angle between and . When considering the moment balance around the rotation axis of the inverted pendulum model, the following equations were obtained in the process above

Figure 6.
Model of balance recovery adapted from [8]. (a) View from −y axis; and, (b) view from +z axis.
The larger the value of S, the better the balance can be recovered, even if the magnitude of the force exerted by the hand is small.
Assuming that the balance recovery characteristics largely depended on the magnitude of this scalar S, S was defined as an evaluation index for assessing support objects in terms of the balance recovery characteristics [8]. In our previous work [8], the relationship between the normalized height (the height of the support objects divided by the user’s height) and the index calculated while using experimental data was obtained. For example, the index value had a peak at approximately 0.5 of when experimental data in a subject touching the horizontal-planar-shaped support object were used for the calculation. The margin S will be used as an evaluation index of support objects in Section 5.1.
4. Assessment Method of Anterior Position of Cane Tip Based on Model with Dynamic Pair
In this section, as described in Section 1, the cane is considered to be a portable support object. By focusing on the distance between the toes and the cane tip, evaluation indices that represented the relationship between the distance and fall prevention effect were discussed in our previous report in order to assess the anterior position of the cane tip on the ground for anterior fall prevention [9]. In [9], first, forward dynamic analysis by numerical simulation using an analytical model was conducted to obtain evaluation indices to determine the distance between the toes and cane tip. In this simulation, a dynamic pair was applied to the analytical model. Next, the anterior position of the cane tip was determined as an illustrative example using these evaluation indices.
4.1. Dynamic Analysis Using Model with Dynamic Pair
4.1.1. Analysis Model Used in the Simulation
Figure 7 shows the analytical model used in the dynamics simulation. In this model, the human body and cane are represented by a planar four-link mechanism, including a dynamic pair. The directions of the X-, Y-, and Z-axes have the same definition as Section 2.1.
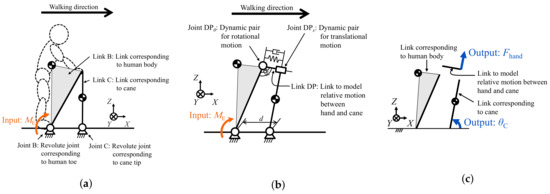
Figure 7.
Analytical model used in the simulation adapted from [9]. (a) Model without dynamic pair;
(b) model with dynamic pair (this model was used in the simulation); and, (c) the definition of outputs
i n the simulation.
In Figure 7a, the body and cane when the balance is about to be lost during walking are modeled as separate rigid bodies (Link B and C), respectively. In addition, passive revolute joints (Joint B and C) are installed at the position corresponding to the toes and the cane tip, respectively. The state in which the balance is about to be lost is represented by applying a clockwise external force moment, , in a certain amount of time around the axis of the Joint B. The magnitude of is , which corresponds to the inertia applied to human’s center of mass and generating 0.5 G. In addition, the duration of action of is 0.1 s to represent the moment when the balance is about to be lost, which is for a short time compared to the whole simulation time (1.0 s). Note that the slip at the contact point between the cane tip and the ground is not considered following the descriptions in Section 2.1.
When considering a decrease in grip strength and an increase in reaction time with aging, it was assumed that the mechanical interface between the hand and the cane was modeled as a dynamic pair that had the following two characteristics
- i.
- Movable direction: translational and rotational directions.
- ii.
- Viscoelastic characteristics: linear elastic and damping effects in each movable direction.
This is because the hand and the cane were connected more rigidly as compared to the foot and the ground, and the cane tip and the ground. Figure 7b shows the analytical model with the dynamic pair comprising Joints and , and the Link DP connecting them. The symbol DP means a part of the dynamic pair.
The input of this simulation is in Figure 7b, and the outputs are angular displacement, , and the magnitude of force acting on the hand from the cane in the longitudinal direction, , in Figure 7c. Here, is defined as the internal translational force that is applied to Link DP from Link C and obtained as an output of the numerical simulation. Because Link DP is perpendicular to Link C and they are connected by the prismatic joint, Joint , is applied to Link DP in the direction parallel to Link C, that is, in the longitudinal direction of the cane as a result. Under the kinematic constraint conditions represented in Figure 7b, the response of the link at each instant of time was obtained by solving the equation of motion of the entire system that comprises rigid links that correspond to the body, cane, and dynamic pair. Moreover, in order to examine the trend of the simulation results according to distance between the toes and the cane, some of the distances d shown in Figure 7b were given to the simulation.
4.1.2. Simulation Result
As the result of the numerical simulation, while is being applied, the smaller the value of the distance between the toes and the cane tip d in Figure 7b, the quicker the oscillation of converges. This result indicates that the energy that is given by to the entire model is dissipated by the damper element of the dynamic pair, and it is dissipated further as the value of d is smaller. This could be attributed to the fact that the smaller the value of d, the greater is the frequency of the cane, and the quicker the cane moves.
The smaller the value of d, the larger is the value of , because d is a moment arm for generating a moment balanced with .
4.2. Evaluation Indices for Anterior Position of Cane Tip
The evaluation indices for the anterior position of the cane tip presented in the previous report [9] based on the simulation results are briefly described in this section.
4.2.1. Amount of Energy Dissipation by Damper Element of Dynamic Pair
The simulation results suggested that the larger the value of energy dissipated by the damper element of the dynamic pair, which changes according to the distance between the toes and cane tip, the greater the fall prevention effect. Therefore, the amount of energy dissipation by the damper element of the dynamic pair was adopted as an evaluation index in order to represent the relationship between the distance from the toes to the cane tip and the fall preventing effect.
4.2.2. Magnitude of Force Acting on Hand from Cane
The smaller the magnitude of the force acting on the hand from the cane, the better is the ability to prevent a fall; this magnitude of the force was adopted as another index for representing the relationship above.
4.2.3. Ability to Perform Negative Work at Each Joint
It is possible that energy dissipation is effective in preventing falls, even if it is performed in not the damper element of the dynamic pair but the other elements. Although the relative motion of each segment of the body was ignored in Figure 7, each of them actually undergoes relative motion. Therefore, it is considered that energy could be dissipated by performing negative work in each joint of a human.
To perform negative work at each joint, it is necessary that there be a sufficient margin of the magnitude of torque at each joint for the maximum possible magnitude of the torque and sufficient margin of joint displacement for the range of motion of each joint. Consequently, by combining these margins, another evaluation index, which comprehensively represents the evaluation of the ability to perform negative work of each joint, was obtained. In our previous work [9], the relationship between the normalized distance (the distance from the toes to the cane tip divided by the user’s height) and the index calculated while using experimental data was obtained. For example, the index value had a peak at approximately 0.1 of when experimental data in a subject walking with the cane were used for the calculation.
4.3. Method for Determination of Cane Tip Position Useful for Preventing Anterior Fall
In [9], based on the evaluation indices that were introduced in Section 4.2, the cane tip position useful for preventing anterior fall was determined as an illustrative example. The optimization method was adopted for the example.
The numerical simulation that is presented in Section 4.1 was repeatedly conducted by changing d in the range of in Figure 7b. From the simulation results, regression equations (ED: energy dissipation by a dynamic pair) and (F: force acting on a hand from a cane) with respect to regarding the evaluation indices in Section 4.2.1 and Section 4.2.2 were obtained, respectively. In addition, according to the calculated values of the evaluation index in Section 4.2.3 using experimental data, a regression equation (NW: negative work at each joint of a human) with respect to was obtained.
Using the three objective functions, the optimization problem for finding a cane tip position useful for preventing anterior fall was formulated as
where E is the objective function of the optimization problem, consisting of the objective functions , , and , their weighting factors, and , , and , which are the maximum values of the objective functions , , and in the range of , respectively. Further, , and are the weighting factors for these objective functions, respectively. In this range of , the optimal solution that maximizes f was determined.
In our previous report [9], the anterior position of the cane tip was determined as an illustrative example by solving Equation (10). For example, the result was obtained as , assuming an elderly person whose grip strength had decreased and the reaction time had increased and setting appropriate values for , , and . This result indicates that, for a person with a height of 1.7 m, the optimum distance between the toes and the cane tip is approximately 0.15 m, which is within the range of the generally recommended distance (0.15–0.20 m) [13].
5. Proposal of Strategy for Application of Support Objects
Based on the results that are presented in Section 2 to Section 4 [8,9], the application of support objects under conditions close to those of practical scenarios is discussed in this section, which is the main and original part of this paper. To do this, first, an elderly person and a single support object were virtually set, and an assessment example of the support objects is shown based on the evaluation index S regarding the balance recovery characteristics that are introduced in Section 3. Next, the physical ability conditions of the user of the support object and the environmental conditions are set, and under the conditions the application of the support objects is investigated using their assessment results. Through this investigation, the authors propose a strategy for the application of support objects utilizing the evaluation indices [8,9].
5.1. Assessment Example for a Single Support Object
5.1.1. Prerequisites
To show an assessment example for individuals, as mentioned in the introduction section, assuming an elderly user of support objects, the physical parameters were set as an example, as shown in Table 2 with reference to research conducted by Okada et al. [14]. The values represent the mean of subjects in [14], and the standard deviations are 5.7 age, 0.067 m, and 10.6 kg, respectively. In addition, assuming that each segment length is proportional to height, each segment length of the user was determined based on each segment length of the subject in which the trend of the calculated index best corresponded with the trend of the sensory evaluation in the experiment of walking with the support objects. Moreover, the mass of the user was adopted as the value of mass m in the inverted pendulum model in Figure 4c.

Table 2.
Detail of a user of support objects.
In this assessment, the following walking cases were considered:
- Case 1.
- Walking with a handrail
- Case 2.
- Walking while touching the top of a table
- Case 3.
- Walking while pinching the edge of a table by his/her hand
- Case 4.
- Walking while touching a wall
- Case 5.
- Walking while touching a wall that has low friction
- Case 6.
- Walking with a cane
The models of the support objects in Case 1–Case 5, which are nonportable support objects, correspond with the following: 1. Cylindrical shape, 2. horizontal-planar shape, 3. horizontal-planar shape (reaction force can be obtained in the upper and lower direction), 4. vertical-planar shape, and 5. vertical-planar shape (low friction force can be obtained), respectively. Moreover, the model of the support object in Case 6, which is a portable support object, corresponds with the following: 6. line-segment shape. Each RFCS was derived based on the direction in which the reaction force is obtained according to the shape and use of each support object.
For the models of Case 1–Case 3, the heights are those of the heights of the general handrail and the dining table from the ground. The height of the cylindrical-shaped support object is 800 mm above the floor, which is the height of a typical handrail in Japan. The height of the horizontal-planar-shaped support object is 700 mm above the floor, which is the height of a typical dining table in Japan. The calculations of the evaluation index S in Section 3.2 were performed using the derived RFCS and data that were obtained in the experiment of walking with support objects. These experimental data were obtained by walking with the support objects whose heights were the closest to the heights above. In addition, these experimental data were also obtained from the subject in which the trend of the calculated index most closely matched the trend of the sensory evaluation that was related to safety.
For the model of Case 4, there is no height parameter similar to the models of Case 1–Case 3. The index S was calculated while using these the experimental data of walking while touching the vertical-planar-shaped support object by the same subject as the calculation in Case 1–Case 3 and the derived RFCS. In addition, in order to consider the meaning of the index value in comparison with the others, the calculation of the index S was conducted for the model of Case 5, which has a considerably lower friction coefficient assuming a wall where almost no friction force is obtained.
For the model of Case 6, the experimental data of the subject that walked with a cane by closest to (=0.0861) introduced in Section 4.3 as an example were adopted. Using these data and the derived RFCS, the evaluation index S was calculated.
5.1.2. Assessment Results and Discussion
As a result of calculating the evaluation index S, the values of the index were in the ascending order of Cases 1, 3, 4, 2, 5, and 6, as shown in Table 3. The following are the three points that were considered to be important from the calculation results.

Table 3.
Example of assessment of living space.
First, the index value in Case 2 is the lowest among the values in Case 1–Case 4. The evaluation index becomes a larger value because of its definition when the following A and/or B are
- A.
- There are many directions in which the reaction force can be obtained.
- B.
- There is a sufficient margin for the magnitude of force to recover balance.
Because the value in Case 2 is smaller than that in Case 4, it is considered that B contributes to the magnitude of the index more than A (Case 2 and Case 4 had no difference from the viewpoint of A). In addition, in Case 4, the user walked while touching a relatively high position (approximately the shoulder position) and, thus, it was considered that the moment necessary to recover balance could be obtained by a smaller-magnitude force when the balance was about to be lost on the wall side. This fact also suggests that B contributed to a larger value of the evaluation index.
Second, the index value in Case 2 is the lowest among those in Case 1–Case 4, while the value in Case 3 is higher than that in Case 4. Although the shapes of support objects are the same for the models in Case 2 and Case 3, it is shown that the balance recovery characteristics are improved by changing the usage of the support objects. Further consideration that is based on these results shows that, if the elderly who cannot pinch the table because of aging or illness are users of the support objects, only evaluation index values in Case 2 are obtained. Therefore, the environment where only a table is installed is more dangerous for the elderly with weakened grip strength than an environment where there is only a wall. In this case, it would be necessary to introduce another support object or device that increases the evaluation value.
Finally, although the index values in Case 2–Case 5 are smaller than that in Case 1, each of these has a certain evaluation value, which is larger than the value in Case 6. Among the support objects used in Case 1–Case 5, the tool that is generally used to assist walking is a handrail, which is used in Case 1. Nevertheless, if the support objects that were used in Case 2–Case 5 exist in the environment, these can be assessed as effective in preventing falls as compared with an environment without any support (). Moreover, the value in Case 6 is less than half that in Case 5. That is, the presence of not only a table or a wall, but also a wall that has low friction in the environment is assessed and found to be more effective in preventing falls than using a cane. This indicates that it is safer to walk while touching a table or a wall without using the cane when there is a table or a wall around. However, because the cane is portable, a certain fall prevention effect should be obtained while using the cane if there is nothing around.
Therefore, based on discussion, the recommended usage of support objects can be prioritized as Priority 1–Priority 3:
- Priority 1.
- Walk while touching the handrail.
- Priority 2.
- If there are no handrails around and there is a table or wall, walk while touching it.
- Priority 3.
- Carry a cane always, and if there is nothing around, use it to walk.
The discussion results of this section suggest that walking with the most fall prevention effect can be achieved using support objects that are based on the above priority.
In this research, the height of the support objects and physical parameters of the user were specifically set, and then the assessment for that user was performed. Therefore, the assessment method based on the balance recovery characteristics could be applied to the design of the height of a cylindrical-shaped and a horizontal-planar support object according to physical parameters (e.g., the optimum design of the height of support objects according to each individual’s height). As future work, the design methodology for support objects based on the balance recovery characteristics should be established.
5.2. Application of Support Objects According to Physical Characteristics and Environmental Conditions
5.2.1. Setting of Physical Characteristics and Environmental Conditions
Based on the calculation results and discussion in Section 5.1, the application of support objects is examined under specific physical characteristics and environmental conditions:
- Condition 1.
- Physical characteristics: both arms are healthy/One arm is healthy
- Condition 2.
- Physical characteristics: walking ability
- Condition 3.
- Environmental conditions: environment in which support objects are used
Although the evaluation index value presented in Section 5.1 was calculated under the condition that a single support object is used with only one arm, note that this section assumes that the support objects can be used with both arms if both arms are healthy. The discussion below assumes that the evaluation value can be represented as the sum of the evaluation index values of the support objects when the support objects are used with both arms.
5.2.2. Discussion under Each Condition
Condition 1. Physical Characteristics: Both Arms Are Healthy/One Arm Is Healthy
According to the above assumption, if both arms are healthy, it is clear that two support objects should be actively used to prevent falls. Further, under the same condition, it is desirable to install two parallel handrails in the living environment of the elderly; they should be even, uninterrupted, and reachable by both hands. In this case, the index value is . However, it is obvious that the installation of handrails above is difficult because of the environmental and financial restrictions. Therefore, to use the two support objects with both arms, the living environment needs to be designed when considering the location of the support objects. For example, in a space with a relatively narrow width, such as a hallway, an evaluation value of could be obtained by touching the walls on both sides. In addition, in an environment where the wall can be touched by only one arm in a wide space, installing the table in a place where the other arm can reach will yield the evaluation value of , as shown in Figure 8. These values are equivalent to the use of a handrail with one arm (evaluation value: ).
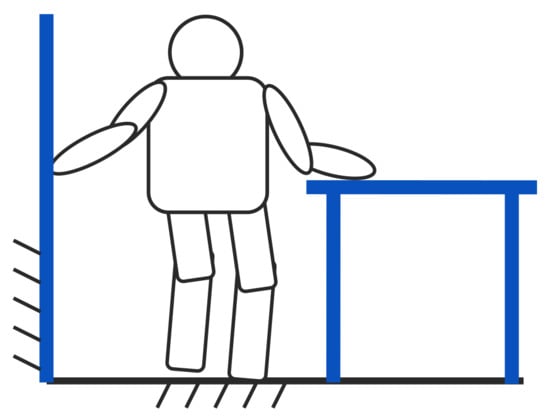
Figure 8.
Use of both arms: Touching a wall and a table by each hand.
Further, if the above discussion can be considered in the design phase of the living or facility environment, it will be possible to deal with the installation of support objects more flexibly and reduce cost as compared to after moving-in. Furthermore, even after moving in, it is possible to realize an environment that promotes fall prevention that is based on balance recovery characteristics by devising the arrangement of support objects. Therefore, design methodology for the environment based on the balance recovery characteristics is expected to be established as future work.
Consider an elderly person suffering from mild monoplegia that is caused by a cerebral hemorrhage or cerebral infarction, and consider the case where only one arm is healthy. Under this condition, it is necessary to install a handrail at least on the unaffected side when considering the flow line in the living environment of the elderly. Further, it is desirable to obtain support on the affected side. To promote fall prevention, it is necessary to develop tools/devices that can obtain the force equivalent to the reaction force obtained from a table/wall/handrail on the affected side. Figure 9 shows an example of a tool that supports the affected side. This figure shows a tool whose wall side is freely movable in the vertical plane and whose shoulder side is fixed to the body.
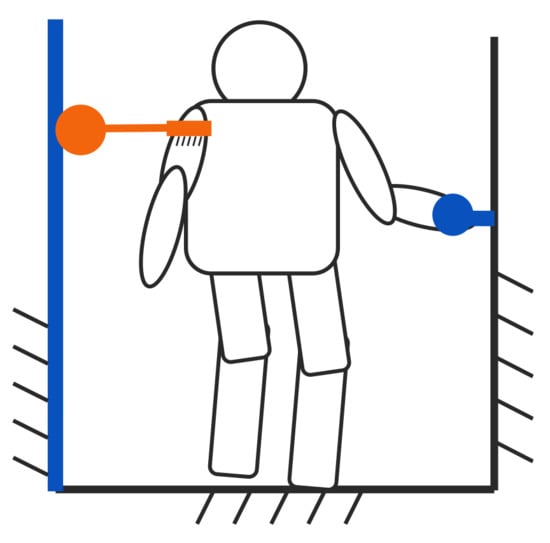
Figure 9.
Example of a support tool on affected-side.
Condition 2. Physical Characteristics: Walking Ability
An aid to encourage excessive weight bearing of their legs is not necessary, even for the elderly whose walking ability deteriorates due to the weakness of their legs, to maintain/improve walking ability, as mentioned in Section 1. Further, it would be better if muscle activation of their legs is performed to some extent. Therefore, it is desirable that elderly people who have sufficient walking ability using support objects should actively use them and perform walking in order to obtain the light touch effect. A cane is highly versatile, because it is portable although it has a low evaluation value in terms of balance recovery characteristics. Thus, it is preferable to carry a cane and walk with it in several places if the user has sufficient walking ability.
Furthremore, it is desirable for the elderly to be able to train themselves to walk using a cane because there is a shortage of caregivers. This will enable them to actively walk using a cane. As part of future work, a cane walking teaching system is expected to be developed (see Figure 1a, Section 1), which indicates the target position of the cane tip and the foot using the assessment method that was introduced in this paper according to physical parameters of cane users.
For the elderly who do not have sufficient walking ability, even if using support objects, it is recommended that a handrail be installed in their living environment first. In addition, if using the handrail is still not sufficient, then the use of support objects on both arms is desirable, as described in Condition 1. In such a case, support objects with new reaction force characteristics and/or new walking support devices should be introduced, which can help to achieve better balance recovery characteristics or the fall prevention effect.
One of the support objects with new reaction force characteristics is, for example, a spherical-shaped support object (see Figure 1b, Section 1). If the shape is spherical, then it is theoretically possible to obtain a normal force in all directions of the three-dimensional space from the support object and, thus, it is assumed that the balance recovery characteristic is high. A cylindrical-shaped support object whose longitudinal direction extends in the vertical direction, such as a vertical handrail, is assumed to have a high balance recovery characteristic, because a normal force in all directions of the horizontal plane can be obtained from this object. In order to actually use the spherical-shaped and the vertical cylindrical-shaped support object during walking, they must be installed throughout the environment. Therefore, although the design of the support objects that are based on the above concept and their introduction into the environment require further investigation, the establishment of the design methodology of the new-shaped support objects is desirable.
One of the new walking support devices is a cane with the function that dissipates energy or a cane that has the property of being less likely to vibrate, instead of dissipating the energy by the damper element of the dynamic pair presented in Section 4. In their design, the cane with the damper element (see Figure 1c, Section 1) or with a function similar to a dynamic vibration absorber can be considered. Thus, the development of walking assistance devices that are designed with new concepts is desirable.
Condition 3. Environmental Conditions: Environment in Which Support Objects Are Used
In the living space, especially in Japan, there are several relatively small spaces (Figure 10a). Therefore, it is possible to provide walking support using multiple support objects in a narrow space, such as in scenarios comprising walking with a handrail on one side, while touching a wall on the other side, as described in Condition 1. In contrast, medical facilities or nursing homes are wider than the living space (Figure 10b). In such environments, it is not possible to use support objects as in the living space. Therefore, to assist the walking of the elderly, a handrail should be installed on one side, while they use a cane on the other side, or a handrail should be installed in a position that can also be reached on the other side. Further, because it is necessary to walk in a wider space outdoors (Figure 10c) and the installation of handrails is limited, the balance recovery characteristics would be evaluated as low. In this case, using the cane in both hands, i.e., obtaining the evaluation value of can be suggested to improve the evaluation of the balance recovery characteristics. However, it is obvious that the evaluation value as compared to that indoors is smaller, which is more dangerous. Therefore, in an outdoor environment, it is necessary to introduce a walking support machine, as described in Condition 2, or provide support via a caregiver.
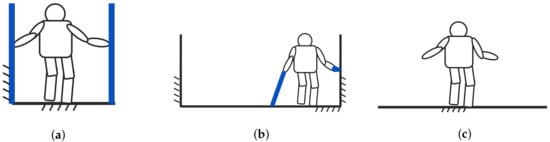
Figure 10.
Difference of width according to environments in which support object is used. (a) Living
space; (b) medical facility or nursing home; and, (c) outdoors.
6. Conclusions and Future Work
This paper presented an assessment example of support objects that are based on balance recovery characteristics and a discussion on the application of support objects according to the assessment in order to propose a strategy for the application of support objects for the fall prevention in the elderly during walking. The research was performed based on our previous works. In our previous works, balance recovery characteristics were defined as the ability to recover from a fallen state [8]. Based on these characteristics, the evaluation index for an assessment of the height and shape of a nonportable support object was introduced. For a portable support object, the evaluation indices for an assessment of the position of the cane tip in the anterior direction were introduced [9]. In this paper, by calculating these evaluation indices, an assessment example was provided and the application of support objects was discussed.
As the result of the discussion in this paper, (1) the strategy for the application of support objects utilizing the evaluation indices regarding the balance recovery characteristics introduced in the previous reports is proposed. (2) By calculating the values of the evaluation indices, an assessment example of not only a handrail and a cane (used to generally assist walking), but also a wall and a table are demonstrated. Furthermore, (3) according to the type/usage of the support objects, better use of them, their locations, new-shaped ones, and support devices with a new design concept are discussed and introduced.
As limitations of proposed approach, because some prerequisites and assumption were set in the assessment and the discussion in this paper, the effectiveness of the results needs to be validated (e.g., individual differences in the physical parameter of support object users, assessments in the case of using both arms). In addition, further applications of the strategy discussed in this paper would help to establish a design methodology for support objects or the environment. As future work, the authors will validate the effectiveness of this approach through experiment and simulation in order to realize the proposed strategy for the application of the support objects and the establishment of their design methodology.
Author Contributions
Conceptualization, S.M. and Y.T.; methodology, S.M.; software, S.M.; validation, S.M.; formal analysis, S.M.; investigation, S.M.; resources, S.M. and Y.T.; data curation, S.M.; writing—original draft preparation, S.M.; writing—review and editing, S.M. and Y.T.; visualization, S.M.; supervision, Y.T.; project administration, Y.T.; funding acquisition, Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI Grant Number 17H03162.
Acknowledgments
This research was in part supported by JSPS KAKENHI Grant Number 17H03162.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cabinet Office. Annual Report on the Ageing Society FY 2019; Cabinet Office: Tokyo, Japan, 2019. [Google Scholar]
- Raj, A.K.; Neuhaus, P.D.; Moucheboeuf, A.M.; Noorden, J.H.; Lecoutre, D.V. Mina: A sensorimotor robotic orthosis for mobility assistance. J. Rob. 2011, 2011. [Google Scholar] [CrossRef]
- Farris, R.J.; Quintero, H.A.; Goldfarb, M. Preliminary evaluation of a powered lower limb orthosis to aid walking in paraplegic individuals. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 652–659. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, T.; Kawamoto, H.; Sankai, Y. Control method of robot suit HAL working as operator’s muscle using biological and dynamical information. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3063–3068. [Google Scholar]
- Boonsinsukh, R.; Panichareon, L.; Phansuwan-Pujito, P. Light touch cue through a cane improves pelvic stability during walking in stroke. Arch. Phys. Med. Rehab. 2009, 90, 919–926. [Google Scholar] [CrossRef] [PubMed]
- IJmker, T.; Lamoth, C.; Houdijk, H.; Tolsma, M.; Van Der Woude, L.; Daffertshofer, A.; Beek, P. Effects of handrail hold and light touch on energetics, step parameters, and neuromuscular activity during walking after stroke. J. Neuroeng. Rehabil. 2015, 12, 70. [Google Scholar] [CrossRef] [PubMed]
- Stramel, D.M.; Carrera, R.M.; Rahok, S.A.; Stein, J.; Agrawal, S.K. Effects of a Person-Following Light-Touch Device During Overground Walking With Visual Perturbations in a Virtual Reality Environment. IEEE Robot. Autom. Let. 2019, 4, 4139–4146. [Google Scholar] [CrossRef]
- Matsuda, S.; Matsuura, D.; Sugahara, Y.; Takeda, Y. Assessment of living space for assisting stable walks by elderly people based on evaluation of balance recovery capability (Indices for evaluation for stable walk by a single support object). Trans. JSME 2017, 83, 17-00282. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Matsuda, S.; Takeda, Y. Proposal of method for assessment of anterior position of cane tip for fall prevention during walking by elderly people based on model with dynamic pair. Trans. JSME 2020, 86, 20-00063. (In Japanese) [Google Scholar] [CrossRef]
- Di, P.; Hasegawa, Y.; Nakagawa, S.; Sekiyama, K.; Fukuda, T.; Huang, J.; Huang, Q. Fall detection and prevention control using walking-aid cane robot. IEEE/ASME Trans. Mechatron. 2015, 21, 625–637. (In Japanese) [Google Scholar] [CrossRef]
- Nakamura, Y.; Nagai, K.; Yoshikawa, T. Mechanics of Coordinative Manipulation by Multiple Robotic Mechanisms. J. Rob. Soc. Jpn. 1986, 4, 489–498. (In Japanese) [Google Scholar] [CrossRef]
- Yoshikawa, T. Foundations of Robotics: Analysis and Control; The MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Consumer Product Safety Association. SG Standard for Walking Sticks. 2020. Available online: https://www.sg-mark.org/SG/0073 (accessed on 20 July 2020). (In Japanese).
- Okada, H.; Ae, M.; Fujii, N.; Morioka, Y. Body Segment Inertia Properties of Japanese Elderly. Biomechanisms 1996, 13, 125–139. (In Japanese) [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).