Unbalance Estimation for a Large Flexible Rotor Using Force and Displacement Minimization
Abstract
1. Introduction
2. Theoretical Background of Model-Based Unbalance Identification Methods
2.1. Modal Expansion and Equivalent Force Derivation-Based Method
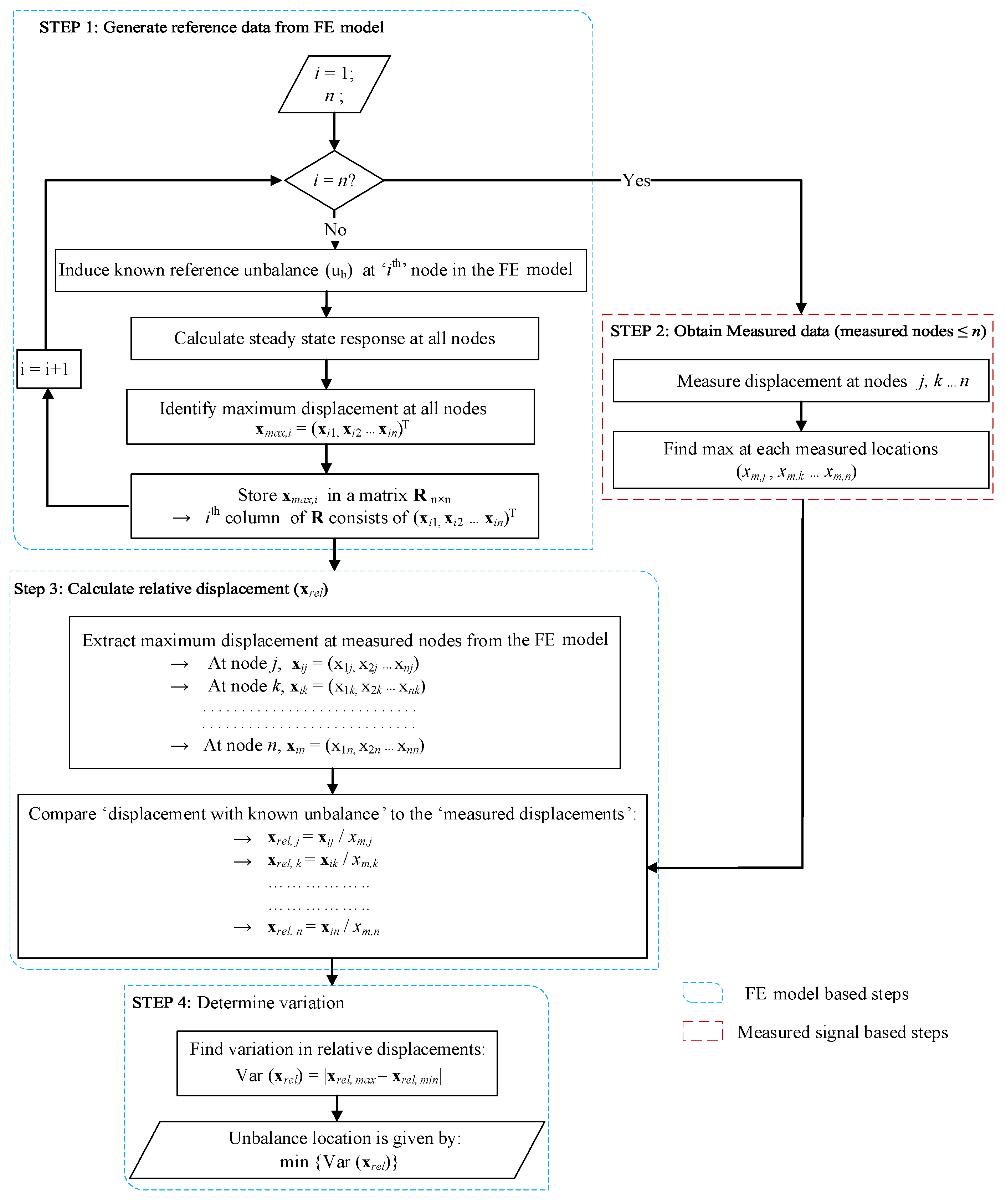
2.2. Displacement Comparison and Minimization Method
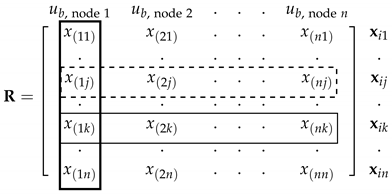
2.2.1. Identifying Unbalance Location
2.2.2. Estimating Unbalance Parameters
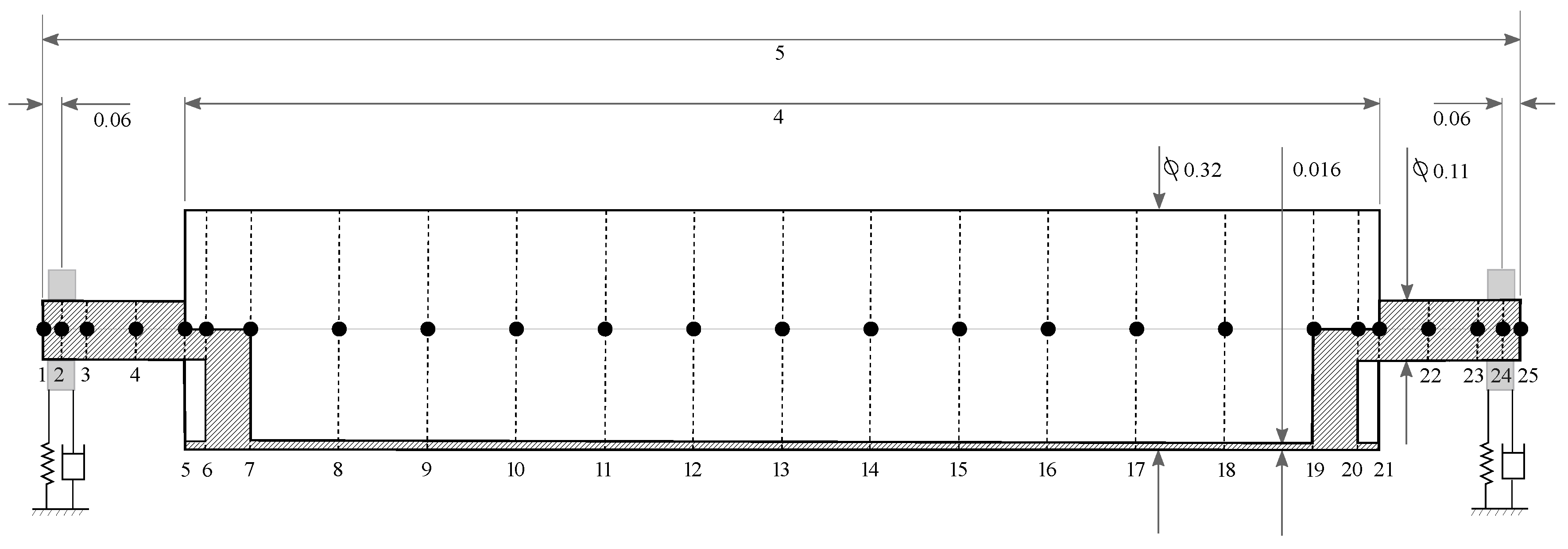
3. Test Rig Description and Modeling
3.1. Experimental Setup
3.2. Modeling Description
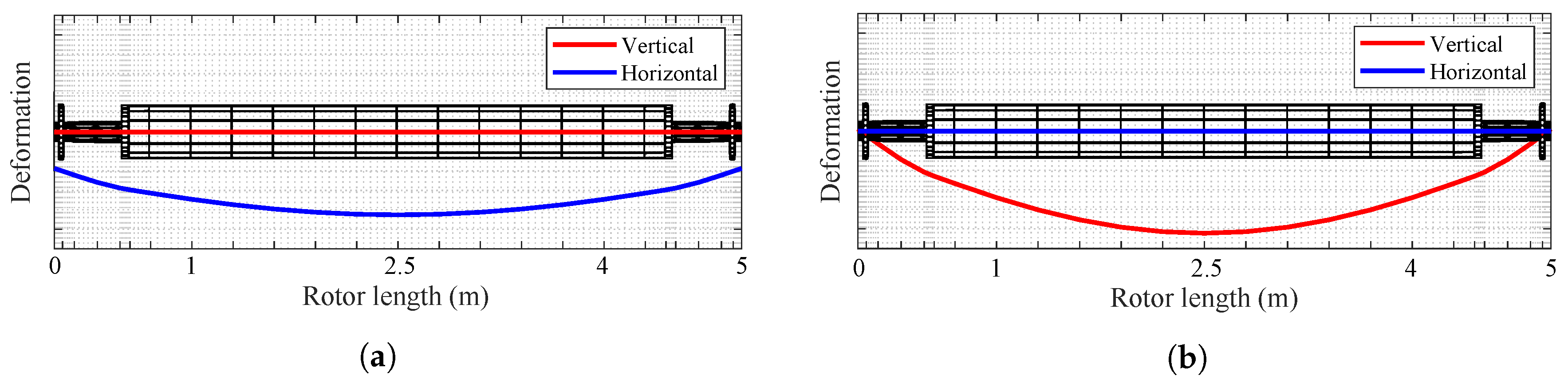
4. Numerical Simulation
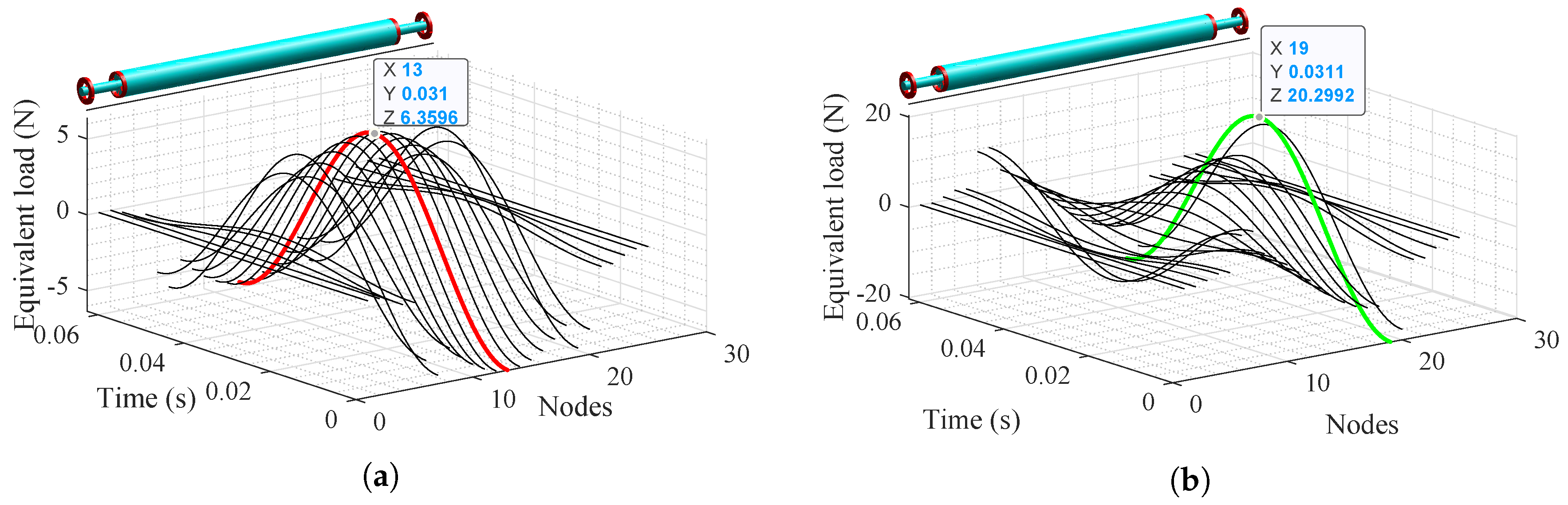
4.1. Unbalance Estimation Using Equivalent Load Minimization and Modal Expansion
4.1.1. Identifying Unbalance Location
4.1.2. Estimating Unbalance Parameters
4.2. Unbalance Estimation Using Displacement Comparison and Minimization
4.2.1. Identifying Unbalance Location
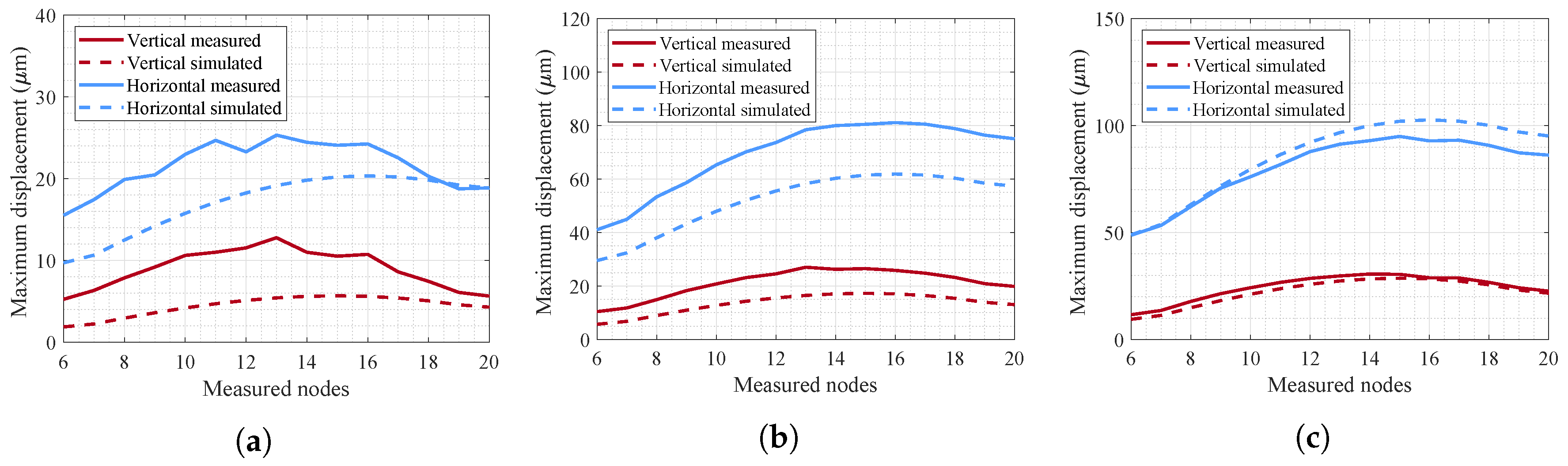
4.2.2. Identifying Unbalance Parameters and Sensitivity Analysis
5. Experimental Verification
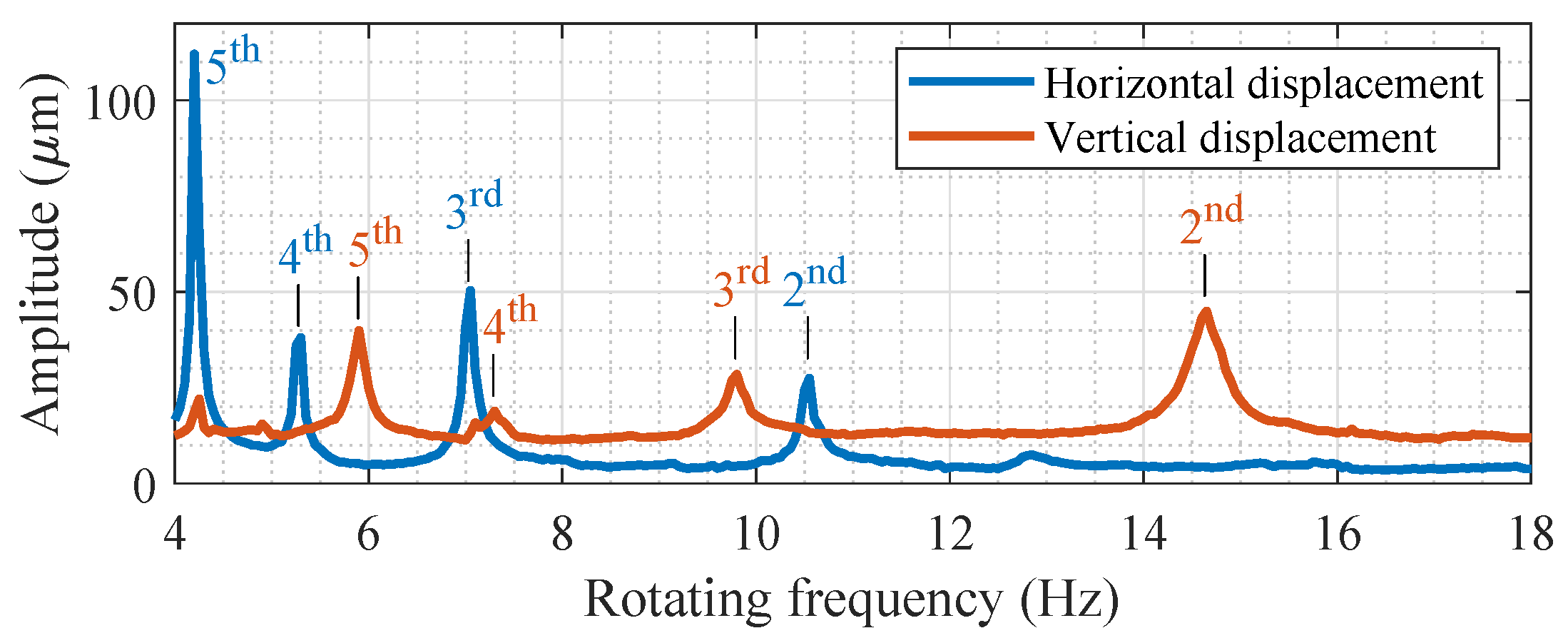
5.1. Obtaining Measured Signal and Pre-Processing
- The operation speed of the roll was set at 960 rpm (16 Hz). The acceptable speed range for this rotor is 4–18 Hz.
- Measuring probes were driven to the first measuring point.
- 100 revolutions of the rotor center point movement were measured from the first measuring point.
- Measuring probes were driven to the next measuring point.
- Steps 3 and 4 were repeated until the measurement is conducted also in the last measuring point.
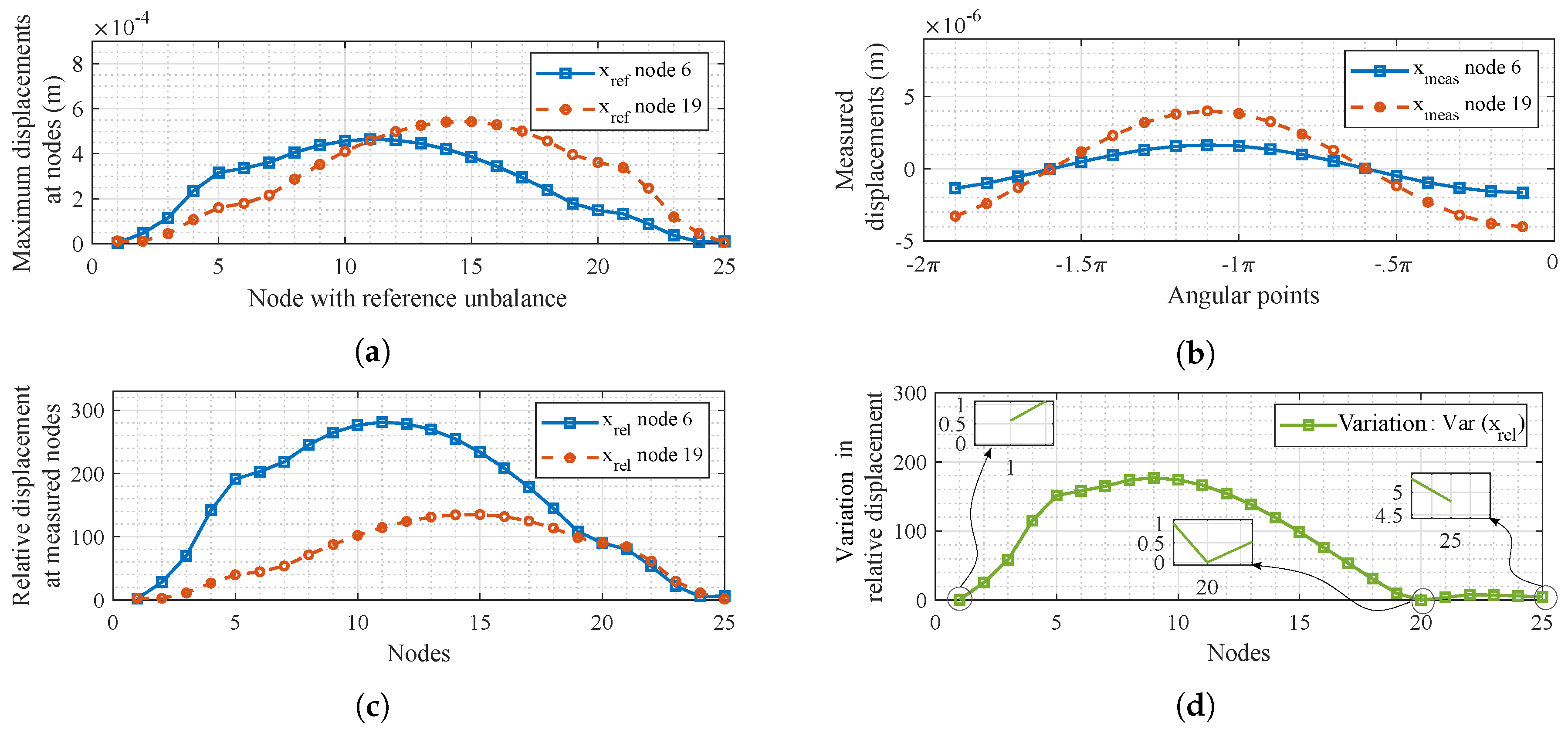
5.2. Identification and Estimation of Unbalance
5.2.1. Force Method
5.2.2. Displacement Method
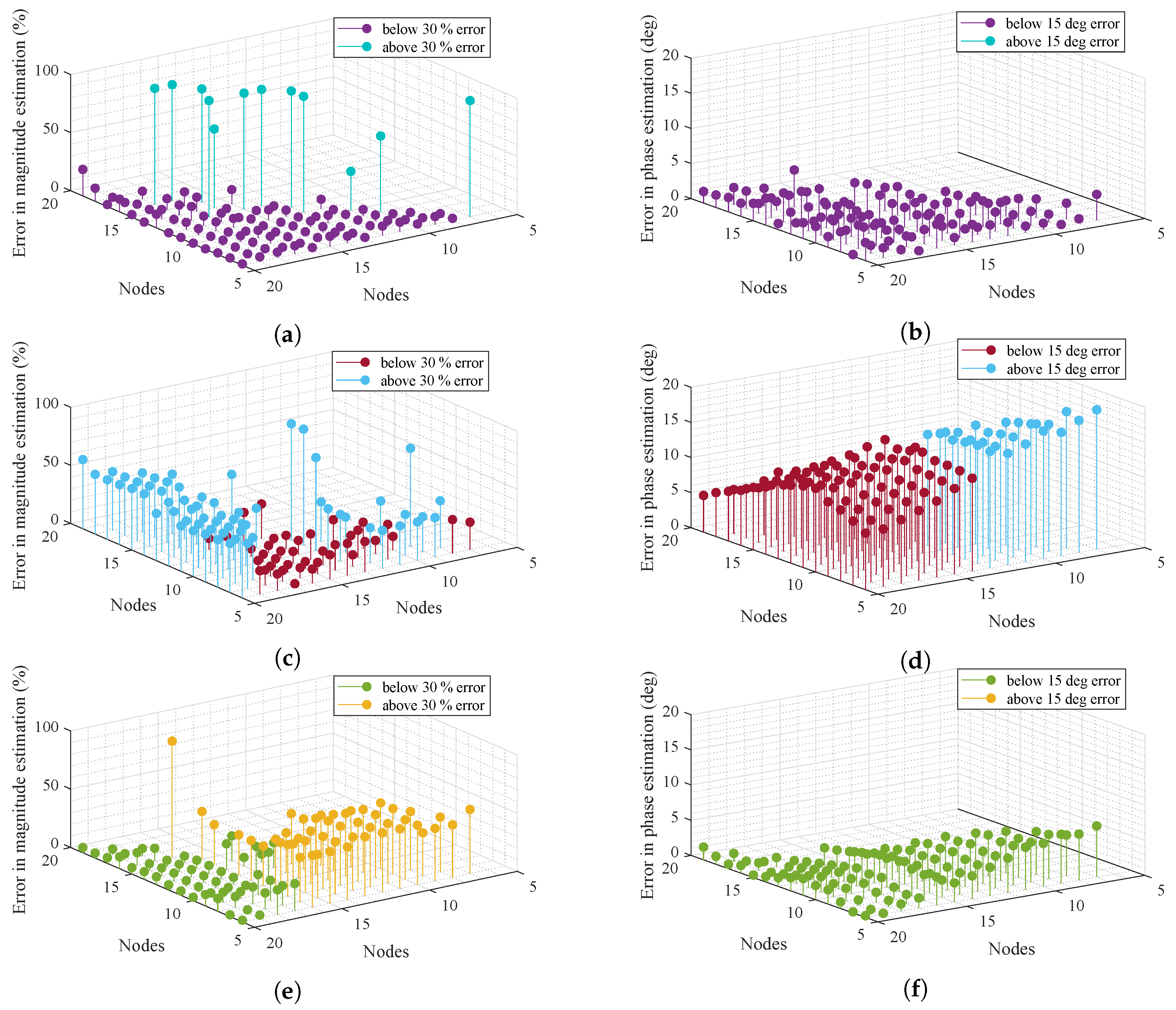
5.2.3. Estimation for Different Combinations of Two Measured Nodes Using Displacement Method
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

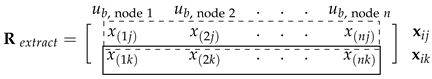
References
- Lees, A.W.; Sinha, J.K.; Friswell, M.I. Model-based identification of rotating machines. Mech. Syst. Signal Process. 2009, 23, 1884–1893. [Google Scholar] [CrossRef]
- Shrivastava, A.; Mohanty, A.R. Estimation of single plane unbalance parameters of a rotor-bearing system using Kalman filtering based force estimation technique. J. Sound Vib. 2018, 418, 184–199. [Google Scholar] [CrossRef]
- ISO. Mechanical Vibration—Balance Quality Requirements for Rotors in a Constant (Rigid) State—Part 1: Specification and Verification of Balance Tolerances; Standard ISO 1940–1:2003; International Organization for Standardization: Geneva, Switzerland, 2003. [Google Scholar]
- Pennacchi, P. Robust estimate of excitations in mechanical systems using M-estimators—Theoretical background and numerical applications. J. Sound Vib. 2008, 310, 923–946. [Google Scholar] [CrossRef]
- Vyas, N.S.; Satishkumar, D. Artificial neural network design for fault identification in a rotor-bearing system. Mech. Mach. Theory 2001, 36, 157–175. [Google Scholar] [CrossRef]
- Platz, R.; Markert, R. Fault Models for Online Identification of Malfunctions in Rotor Systems. In Proceedings of the Transactions of the 4th International Conference Acoustical and Vibratory Surveillance, Methods and Diagnostic Techniques, University of Compiegne, Compiegne, France, 16–18 October 2001; Volume 2, pp. 435–446. [Google Scholar]
- Markert, R.; Platz, R.; Seidler, M. Model based fault identification in rotor systems by least squares fitting. Int. J. Rotating Mach. 2001, 7, 311–321. [Google Scholar] [CrossRef]
- Sekhar, A.S. Crack identification in a rotor system: A model-based approach. J. Sound Vib. 2004, 270, 887–902. [Google Scholar] [CrossRef]
- Sekhar, A.S. Identification of unbalance and crack acting simultaneously in a rotor system: Modal expansion versus reduced basis dynamic expansion. Modal Anal. 2005, 11, 1125–1145. [Google Scholar] [CrossRef]
- Jain, J.R.; Kundra, T.K. Model based online diagnosis of unbalance and transverse fatigue crack in rotor systems. Mech. Res. Comm. 2004, 31, 557–568. [Google Scholar] [CrossRef]
- Jalan, A.K.; Mohanty, A.R. Model based fault diagnosis of a rotor–bearing system for misalignment and unbalance under steady-state condition. J. Sound Vib. 2009, 327, 604–622. [Google Scholar] [CrossRef]
- Sinha, J.K.; Lees, A.W.; Friswell, M.I. Estimating unbalance and misalignment of a flexible rotating machine from a single run-down. J. Sound Vib. 2004, 272, 967–989. [Google Scholar] [CrossRef]
- Bachschmid, N.; Pennacchi, P.; Vania, A. Identification of multiple faults in rotor systems. J. Sound Vib. 2002, 254, 327–366. [Google Scholar] [CrossRef]
- Pennacchi, P.; Bachschmid, N.; Vania, A. A model-based identification method of transverse cracks in rotating shafts suitable for industrial machines. Mech. Syst. Signal Process. 2006, 20, 2112–2147. [Google Scholar] [CrossRef][Green Version]
- Pennacchi, P.; Bachschmid, N.; Vania, A.; Zanetta, G.A.; Gregori, L. Use of modal representation for the supporting structure in model-based fault identification of large rotating machinery: Part 1—Theoretical remarks. Mech. Syst. Signal Process. 2006, 20, 662–681. [Google Scholar] [CrossRef]
- Pennacchi, P.; Bachschmid, N.; Vania, A.; Zanetta, G.A.; Gregori, L. Use of modal representation for the supporting structure in model-based fault identification of large rotating machinery: Part 2—Application to a real machine. Mech. Syst. Signal Process. 2006, 20, 682–701. [Google Scholar] [CrossRef]
- Pennacchi, P. Robust estimation of excitations in mechanical systems using M-estimators—Experimental applications. J. Sound Vib. 2009, 319, 140–162. [Google Scholar] [CrossRef]
- Cedillo, S.G.T.; Bonello, P. An equivalent unbalance identification method for the balancing of nonlinear squeeze-film damped rotordynamic systems. J. Sound Vib. 2016, 360, 53–73. [Google Scholar] [CrossRef]
- Ocampo, J.C.; Wing, E.S.G.; Moroyoqui, F.J.R.; Pliego, A.A.; Ortega, A.B.; Mayén, J. A novel methodology for the angular position identification of the unbalance force on asymmetric rotors by response polar plot analysis. Mech. Syst. Signal Process. 2017, 95, 172–186. [Google Scholar] [CrossRef]
- Sudhakar, G.N.D.S.; Sekhar, A.S. Identification of unbalance in a rotor bearing system. J. Sound Vib. 2011, 330, 2299–2313. [Google Scholar] [CrossRef]
- Yao, J.; Liu, L.; Yang, F.; Scarpa, F.; Gao, J. Identification and optimization of unbalance parameters in rotor-bearing systems. J. Sound Vib. 2018, 431, 54–69. [Google Scholar] [CrossRef]
- Nelson, H. A finite rotating shaft element using Timoshenko beam theory. J. Mech. Des. 1980, 102, 793–803. [Google Scholar] [CrossRef]
- Chen, W.J.; Gunter, E.J. Introduction to Dynamics of Rotor-Bearing Systems; Trafford: Victoria, BC, Canada, 2005. [Google Scholar]
- Feng, N.; Hahn, E. Including foundation effects on the vibration behaviour of rotating machinery. Mech. Syst. Signal Process. 1995, 9, 243–256. [Google Scholar] [CrossRef]
- Friswell, M.I.; Penny, J.E.; Lees, A.W.; Garvey, S.D. Dynamics of Rotating Machines; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Kuosmanen, P.; Väänänen, P. New highly advanced roll measurement technology. In Proceedings of the 5th International Conference on New Available Techniques, The World Pulp and Paper Week, Stockholm, Sweden, 4–7 June 1996; pp. 1056–1063. [Google Scholar]
- Heikkinen, J.E.; Ghalamchi, B.; Viitala, R.; Sopanen, J.; Juhanko, J.; Mikkola, A.; Kuosmanen, P. Vibration analysis of paper machine’s asymmetric tube roll supported by spherical roller bearings. Mech. Syst. Signal Process. 2018, 104, 688–704. [Google Scholar] [CrossRef]
- Choudhury, T.; Kurvinen, E.; Sopanen, J. Model Based Unbalance Identification for Paper Machine’s Tube Roll. In IFToMM World Congress on Mechanism and Machine Science; Springer: Krakow, Poland, 2019; pp. 3375–3384. [Google Scholar] [CrossRef]
- ISO. Mechanical Vibration—Rotor Balancing—Part 12: Procedures and Tolerances for Rotors with Flexible Behavior; Standard ISO 21940-12:2016; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- McFadden, P. A revised model for the extraction of periodic waveforms by time domain averaging. Mech. Syst. Signal Process. 1987, 1, 83–95. [Google Scholar] [CrossRef]
- Bishop, R.; Gladwell, G. The vibration and balancing of an unbalanced flexible rotor. J. Mech. Eng. Sci. 1959, 1, 66–77. [Google Scholar] [CrossRef]
- Kellenberger, W. Should a flexible rotor be balanced in N or (N + 2) planes? J. Eng. Ind. 1972, 94, 548–558. [Google Scholar] [CrossRef]



| Tending End of the Rotor | Driving End of the Rotor | |||||||
|---|---|---|---|---|---|---|---|---|
| Balancing masses (g) | 2883 | 1056 | 159 | 0 | 2592 | 499 | 0 | 292 |
| Phases (deg) | 0 | 90 | 180 | 270 | 0 | 90 | 180 | 270 |
| Test Case | Mass (g) | Eccentricity (mm) | Magnitude (kg·m) | Phase (degree) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 98.6 | 112.5 | 0.011 | 90 |
| 2 | 300.1 | 112.5 | 0.033 | 180 |
| 3 | 497.9 | 112.5 | 0.056 | 270 |
| Critical Speeds (Hz) | 2nd Comp. * (Hz) | 3rd Comp. (Hz) | 4th Comp. (Hz) | 5th Comp. (Hz) | |
|---|---|---|---|---|---|
| Horizontal | 21.10 | 10.55 | 7.05 | 5.3 | 4.2 |
| Vertical | 29.35 | 14.65 | 9.8 | 7.3 | 5.9 |
| Rotor properties | |
| Density | 7764 kg/m * |
| Poisson’s ratio | |
| Young’s modulus | Pa * |
| Rotor mass (measured) | 719.72 kg |
| Bearing properties | |
| Bearing stiffness coefficient | |
| Vertical | N/m |
| Horizontal | N/m |
| Bearing damping coefficient | |
| Vertical | Ns/m |
| Horizontal | Ns/m |
| Number of Measured DOFs | Measured Nodes (Transverse Vibrations at Each Node = 2 DOFs) |
|---|---|
| 6 | 6, 14, 19 |
| 4 | 6, 19 |
| Test No. | No. of Measured DOFs | Unbalance Location (Node) | Unbalance Magnitude (kg·m) | Unbalance Phase (Degree) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | Identified | Actual | Estimated | Error % | Actual | Estimated | Abs. Error | ||
| 1 | 6 | 20 | 19 | 0.011 | 0.006 | 41.34 | 90 | 90.5 | 0.5 |
| 2 | 6 | 20 | 19 | 0.033 | 0.020 | 41.37 | 180 | 178.6 | 1.4 |
| 3 | 6 | 20 | 19 | 0.056 | 0.032 | 41.36 | 270 | 270.5 | 0.5 |
| 1 | 4 | 20 | 13 | 0.011 | 0.005 | 58.88 | 90 | 90.5 | 0.5 |
| 2 | 4 | 20 | 13 | 0.033 | 0.014 | 58.91 | 180 | 178.6 | 1.4 |
| 3 | 4 | 20 | 13 | 0.056 | 0.023 | 58.89 | 270 | 270.5 | 0.5 |
| Test Cases | No. of Measured DOFs | Unbalance Location (Node) | Unbalance Magnitude (kg·m) | Unbalance Phase (Degree) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | Identified | Actual | Estimated | Error % | Actual | Estimated | Abs. Error | ||
| 1 | 2 | 20 | 20 | 0.011 | 0.011 | 0.00 | 90 | 90 | 0 |
| 2 | 2 | 20 | 20 | 0.033 | 0.033 | 0.00 | 180 | 180 | 0 |
| 3 | 2 | 20 | 20 | 0.056 | 0.056 | 0.00 | 270 | 270 | 0 |
| Speeds (rpm) | Test Cases | Unbalance Parameters | Actual Values | Measurement Noise | Modeling Error | ||||
|---|---|---|---|---|---|---|---|---|---|
| 5% | 15% | 25% | 1% | 2% | 5% | ||||
| 960 | 1 | magnitude | 0.011 | 0.011 | 0.012 | 0.013 | 0.011 | 0.011 | 0.012 |
| phase | 90 | 90.03 | 90.74 | 90.64 | 90 | 90.82 | 90.53 | ||
| 2 | magnitude | 0.033 | 0.035 | 0.038 | 0.042 | 0.033 | 0.033 | 0.034 | |
| phase | 180 | 179.99 | 179.35 | 179.64 | 97.8 | 98.4 | 101.6 | ||
| 3 | magnitude | 0.056 | 0.058 | 0.064 | 0.070 | 0.056 | 0.056 | 0.057 | |
| phase | 270 | 269.79 | 271.26 | 273.10 | 270 | 269.7 | 269.4 | ||
| 2200 | 1 | magnitude | 0.011 | 0.011 | 0.012 | 0.013 | 0.010 | 0.010 | 0.011 |
| phase | 90 | 90.07 | 90.38 | 90.54 | 90 | 90.21 | 90.64 | ||
| 2 | magnitude | 0.033 | 0.035 | 0.038 | 0.042 | 0.033 | 0.032 | 0.035 | |
| phase | 180 | 180 | 180.08 | 180.19 | 180 | 180.53 | 180.64 | ||
| 3 | magnitude | 0.056 | 0.058 | 0.064 | 0.070 | 0.055 | 0.054 | 0.058 | |
| phase | 270 | 270.04 | 269.82 | 269.47 | 270 | 270.07 | 270.14 | ||
| Test Cases | No. of Measured DOFs | Unbalance Location (Node) | Unbalance Magnitude (kg·m) | Unbalance Phase (Degree) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | Identified | Actual | Estimated | Error % | Actual | Estimated | Abs. Error | ||
| 1 | 6 | 20 | 19 | 0.011 | 0.012 | 7.44 | 90 | 95.1 | 5.1 |
| 2 | 6 | 20 | 19 | 0.033 | 0.029 | 12.71 | 180 | 167.4 | 12.6 |
| 3 | 6 | 20 | 19 | 0.056 | 0.034 | 38.61 | 270 | 274.9 | 4.9 |
| 1 | 4 | 20 | 13 | 0.011 | 0.007 | 34.52 | 90 | 89.1 | 0.9 |
| 2 | 4 | 20 | 13 | 0.033 | 0.021 | 36.08 | 180 | 171.3 | 8.7 |
| 3 | 4 | 20 | 13 | 0.056 | 0.024 | 55.81 | 270 | 271.2 | 1.2 |
| Test Cases | No. of Measured DOFs | Unbalance Location (Node) | Unbalance Magnitude (kg·m) | Unbalance Phase (Degree) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | Identified | Actual | Estimated | Error % | Actual | Estimated | Abs. Error | ||
| 1 | 2 | 20 | 14 | 0.011 | 0.010 | 3.95 | 90 | 91.3 | 1.3 |
| 2 | 2 | 20 | 19 | 0.033 | 0.040 | 20.21 | 180 | 171.8 | 8.1 |
| 3 | 2 | 20 | 19 | 0.056 | 0.054 | 2.66 | 270 | 269.8 | 0.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhury, T.; Viitala, R.; Kurvinen, E.; Viitala, R.; Sopanen, J. Unbalance Estimation for a Large Flexible Rotor Using Force and Displacement Minimization. Machines 2020, 8, 39. https://doi.org/10.3390/machines8030039
Choudhury T, Viitala R, Kurvinen E, Viitala R, Sopanen J. Unbalance Estimation for a Large Flexible Rotor Using Force and Displacement Minimization. Machines. 2020; 8(3):39. https://doi.org/10.3390/machines8030039
Chicago/Turabian StyleChoudhury, Tuhin, Risto Viitala, Emil Kurvinen, Raine Viitala, and Jussi Sopanen. 2020. "Unbalance Estimation for a Large Flexible Rotor Using Force and Displacement Minimization" Machines 8, no. 3: 39. https://doi.org/10.3390/machines8030039
APA StyleChoudhury, T., Viitala, R., Kurvinen, E., Viitala, R., & Sopanen, J. (2020). Unbalance Estimation for a Large Flexible Rotor Using Force and Displacement Minimization. Machines, 8(3), 39. https://doi.org/10.3390/machines8030039







